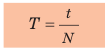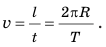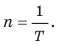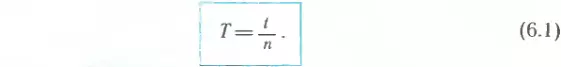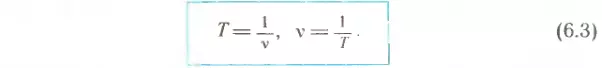
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Определение и формулы
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Определение и формулы
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Полезные факты
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Определение и формула
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с2). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙103 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙106. Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Задание EF18273
Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Центростремительное ускорение автомобиля равно…
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
Ответ: 4
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17763
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза
б) уменьшить в 2 раза
в) увеличить в 4 раза
г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
- Радиус окружности R1 = R.
- Радиус окружности R2 = 4R.
- Центростремительное ускорение: aц.с. = a1 = a2.
Найти нужно ν2.
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Или:
Отсюда:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 22k
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Движение по окружности с постоянной по модулю скоростью
теория по физике 🧲 кинематика
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Движение по окружности
Движение по окружности – простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
Если угол поворота мал, то ∆ l ≈ ∆ s .
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории – предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости – радиан в секунду ( р а д с ).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
Нормальное ускорение
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
a n = ∆ v → ∆ t , ∆ t → 0
Модуль центростремительного ускорения можно вычислить по формуле:
a n = v 2 R = ω 2 R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → – v A → .
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a → = ∆ v → ∆ t , ∆ t → 0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .
Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:
R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R
При ∆ φ → 0 , направление вектора ∆ v → = v B → – v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:
a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
Здесь R → – радиус вектор точки на окружности с началом в ее центре.
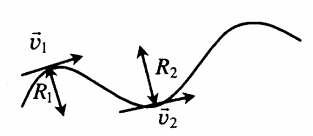
Тангенциальное ускорение
В общем случае ускорение при движении по окружности состоит из двух компонентов – нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
a τ = ∆ v τ ∆ t ; ∆ t → 0
Здесь ∆ v τ = v 2 – v 1 – изменение модуля скорости за промежуток ∆ t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/fizika/kinematika/dvizhenie-po-okruzhnosti/
[/spoiler]
Содержание:
Равномерное движение материальной точки по окружности:
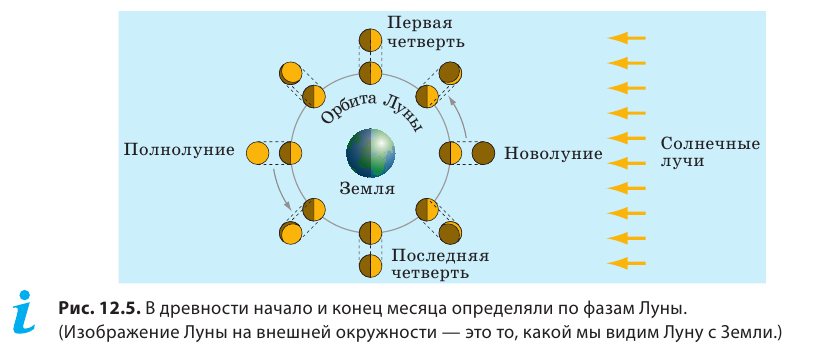
Более 5000 лет назад жрецы древнего Вавилона, наблюдая за Луной, определили такой хорошо известный нам интервал времени, как неделя. Как они это сделали? В чем особенность движения Луны? Встречается ли на Земле подобное движение?
Движение по окружности
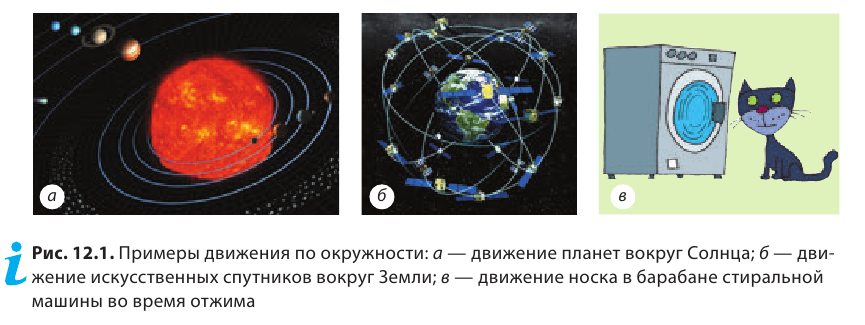
Попробуйте представить линию, вдоль которой движутся ребенок, кружащийся на карусели, носок в барабане стиральной машины во время отжима, кончик ножа блендера при изготовлении коктейля или смузи. Уверены, что вы легко определили: этой линией является окружность. Итак, в перечисленных случаях имеем дело с движением по окружности; простейшим является равномерное движение по окружности. Далее, говоря о равномерном движении по окружности любого физического тела, будем считать это тело материальной точкой. Равномерно по окружности движутся, например, кабинки колеса обозрения. Близким к равномерному движению по окружности является движение планет вокруг Солнца (рис. 12.1, а), естественного спутника (Луны) или искусственных спутников вокруг Земли* (рис. 12.1, б). Приведите примеры движения по окружности. В каких случаях это движение можно считать равномерным? Можно ли считать движение точек обода колеса велосипеда относительно его рамы равномерным движением по окружности? Обоснуйте свой ответ.
Равномерное движение материальной точки по окружности — это такое криволинейное движение, при котором точка, двигаясь по круговой траектории, за любые равные интервалы времени проходит одинаковый путь.
Определение периода вращения
Равномерное движение по окружности — это периодическое движение, то есть движение, повторяющееся через определенные равные интервалы времени. Например, кончик секундной стрелки часов, двигаясь равномерно вдоль циферблата, повторяет свое движение через каждые 60 с (рис. 12.2).
Любое периодическое движение характеризуется такими физическими величинами, как период и частота. При равномерном движении по окружности говорят о периоде вращения и частоте вращения.
Период вращения — это физическая величина, равная времени, за которое материальная точка, равномерно движущаяся по окружности, совершает один оборот. Период вращения обозначают символом T. Единица периода вращения в СИ — секунда: [T]=c. Период вращения равен одной секунде, если за одну секунду совершается один оборот. Кончик секундной стрелки часов совершает один оборот за 60 с, поэтому период его вращения, как и каждой точки секундной стрелки, равен 60 с T =(60c .) Подумайте, каковы периоды вращения точек минутной и часовой стрелок часов. Когда взбивают молочный коктейль блендером, каждая точка его ножа за 30 с делает 6000 оборотов (рис. 12.3). Чтобы определить время одного оборота, нужно время вращения (t = 30 с) разделить на количество оборотов за это время (N = 6000): 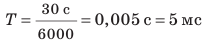
Определение частоты вращения
Указывая технические характеристики устройств, используют не период вращения, а частоту вращения (рис. 12.4). Частота вращения — это физическая величина, которая равна количеству оборотов за единицу времени. Частоту вращения обозначают символом n и определяют по формуле: 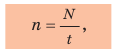
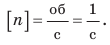
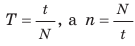
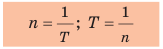
- Заказать решение задач по физике
Как возникли единицы времени: сутки и неделя
Как измерить время? Ответ на этот вопрос подсказала людям сама природа. Дело в том, что многие движения, происходящие в природе, являются периодическими, а период такого движения может служить единицей времени. Например, вращение Земли вокруг своей оси — периодическое движение. Ежедневный восход (закат) Солнца, обусловленный этим движением, подсказал нашим предкам единицу времени сутки, которые равны периоду вращения Земли вокруг своей оси. Несколько единиц времени были получены в древнем Вавилоне. Наблюдая за ночным небом, жрецы заметили, что «молодая» Луна появляется на небосклоне приблизительно каждые 28 суток. Периодическое рождение лунного диска служило своего рода вечными «часами». Так возникла единица времени месяц*. За это время Луна, вращаясь вокруг Земли, проходит полный цикл изменения фаз: новолуние, первая четверть, полнолуние, последняя четверть (рис. 12.5). Именно поэтому жрецы разделили лунный месяц на четыре части (поколичеству лунных фаз) и получили семь дней — единицу времени, которая называется неделя.
Определяем скорость равномерного движения по окружности
Кроме периода вращения и его частоты важной характеристикой движения по окружности является скорость движения. Если тело равномерно движется по окружности, то за время, равное периоду вращения t(=T, )тело совершает один оборот, то есть проходит путь, равный длине окружности. Длину окружности l можно вычислить по известной вам из математики формуле: 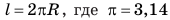
Сейчас, как правило, используют понятие календарного месяца, который не зависит от фаз Луны и длится от 28 до 31 суток.
Именно об этой скорости идет речь, когда, например, определяют скорость движения человека, кружащегося на карусели, говорят о скорости полета искусственных спутников Земли и т. д.
Итоги:
Равномерное движение материальной точки по окружности — это такое криволинейное движение, при котором точка, двигаясь по круговой траектории, за любые равные интервалы времени проходит одинаковый путь. Равномерное движение по окружности — это периодическое движение, то есть движение, повторяющееся через определенные одинаковые интервалы времени. Период вращения T — физическая величина, равная времени, в течение которого материальная точка, равномерно движущаяся по окружности, совершает один оборот. Единица периода вращения в СИ — секунда (с). Частота вращения n — это физическая величина, которая равна количеству оборотов за единицу времени. Единица частоты вращения в СИ — оборот в секунду (об/с, или 1/с). Период вращения T и частоту вращения n определяют по формулам: 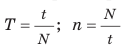
- Колебательное движение
- Физический и математический маятники
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними
- Равномерное и неравномерное движение
- Равномерное движение
- Неравномерное движение
- Вращательное движение тела
Равномерное движение по окружности характеризуют периодом и частотой обращения.
Период обращения — это время, за которое совершается один оборот.
Если, например, за время t=4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой T и определяется по формуле
Итак, чтобы найти период обращения, надо время, за которое совершено n оборотов, разделить на число оборотов.
Другой характеристикой равномерного движения по окружности является частота обращения.
Частота обращения — это число оборотов, совершаемых за 1 с. Если, например, за время t = 2 с тело совершило n = 10 оборотов, то легко сообразить, что за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой ν (читается: ню) и определяется по формуле
Итак, чтобы найти частоту обращения, надо число оборотов разделить на время, в течение которого они произошли.
За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с-1 (читается: секунда в минус первой степени). Раньше эту единицу называли «оборот в секунду», но теперь это название считается устаревшим.
Сравнивая формулы (6.1) и (6.2), можно заметить, что период и частота — величины взаимно обратные. Поэтому
Формулы (6.1) и (6.3) позволяют найти период обращения T, если известны число n и время оборотов t или частота обращения ν. Однако его можно найти и в том случае, когда ни одна из этих величин неизвестна. Вместо них достаточно знать скорость тела v и радиус окружности r, по которой оно движется. Для вывода новой формулы вспомним, что период обращения — это время, за которое тело совершает один оборот, т. е. проходит путь, равный длине окружности (lокр = 2πr, где π≈3,14— число «пи», известное из курса математики). Но мы знаем, что при равномерном движении время находится делением пройденного пути на скорость движения. Таким образом,
Итак, чтобы найти период обращения тела, надо длину окружности, по которой оно движется, разделить на скорость его движения.
Видео, не по теме но интересно
1. Что такое период обращения? 2. Как можно найти период обращения, зная время и число оборотов? 3. Что такое частота обращения? 4. Как обозначается единица частоты? 5. Как можно найти частоту обращения, зная время и число оборотов? 6. Как связаны между собой период и частота обращения? 7. Как можно найти период обращения, зная радиус окружности и скорость движения тела?
1.Равномерное
движение по окружности
2.Угловая скорость
вращательного движения.
3.Период вращения.
4.Частота вращения.
5.Связь линейной
скорости с угловой.
6.Центростремительное
ускорение.
7.Равнопеременное
движение по окружности.
8.Угловое ускорение
в равнопеременном движении по окружности.
9.Тангенциальное
ускорение.
10.Закон равноускоренного
движения по окружности.
11. Средняя угловая
скорость в равноускоренном движении
по окружности.
12.Формулы,
устанавливающие связь между угловой
скоростью, угловым ускорением и углом
поворота в равноускоренном движении
по окружности.
1
.Равномерное
движение по окружности
– движение, при котором материальная
точка за равные интервалы времени
проходит равные отрезки дуги окружности,
т.е. точка движется по окружности с
постоянной по модулю скоростью. В этом
случае скорость равна отношению дуги
окружности, пройденной точкой ко времени
движения, т.е.
и называется
линейной скоростью движения по окружности.
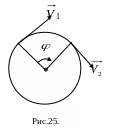
Как и в криволинейном
движении вектор скорости направлен по
касательной к окружности в направлении
движения (Рис.25).
2. Угловая
скорость в равномерном движении по
окружности
– отношение угла поворота радиуса ко
времени поворота:
В равномерном
движении по окружности угловая скорость
постоянна. В системе СИ угловая скорость
измеряется в(рад/c).
Один радиан – рад это центральный угол,
стягивающий дугу окружности длиной
равной радиусу. Полный угол содержит
радиан, т.е. за один оборот радиус
поворачивается на угол
радиан.
3. Период
вращения –
интервал времени Т, в течении которого
материальная точка совершает один
полный оборот. В системе СИ период
измеряется в секундах.
4. Частота
вращения –
число оборотов
,
совершаемых за одну секунду. В системе
СИ частота измеряется в герцах ( 1Гц =
1
)
. Один герц – частота, при которой за
одну секунду совершается один оборот.
Легко сообразить, что
Если за время t
точка совершает n
оборотов по окружности то
.
Зная период и
частоту вращения, угловую скорость
можно вычислять по формуле:
или
5 Связь
линейной скорости с угловой.
Длина дуги окружности равна
где
центральный
угол, выраженный в радианах, стягивающий
дугу
радиус
окружности. Теперь линейную скорость
запишем в виде
,
где
.
Ч
асто
бывает удобно использовать формулы:
или
Угловую скорость часто называют
циклической частотой, а частоту
линейной
частотой.
6. Центростремительное
ускорение.
В равномерном движении по окружности
модуль скорости остаётся неизменным
,
а направление её непрерывно меняется
(Рис.26). Это значит, что тело, движущееся
равномерно по окружности, испытывает
ускорение, которое направлено к центру
и называется центростремительным
ускорением.
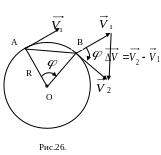
Пусть за промежуток
времени
прошло путь равный дуге окружности
.
Перенесём вектор
,
оставляя его параллельным самому себе,
так чтобы его начало совпало с началом
вектора
в точке В. Модуль изменения скорости
равен
,
а модуль центростремительного ускорения
равен
На Рис.26 треугольники
АОВ и ДВС равнобедренные и углы при
вершинах О и В равны, как углы с взаимно
перпендикулярными сторонами АО
и
ОВ
Это значит, что треугольники АОВ и ДВС
подобные. Следовательно
Если
то
есть интервал времени
принимает сколь угодно малые значения,
то дугу
можно
приближенно считать равной хорде АВ,
т.е.
.
Поэтому можем записать
Учитывая,
что ВД=
,
ОА=R
получим
Умножая обе части последнего равенства
на
,
получим
и далее выражение для модуля
центростремительного ускорения в
равномерном движении по окружности:
.
Учитывая,
что
получим две часто применяемые формулы:
,
.
Итак, в равномерном
движении по окружности центростремительное
ускорение постоянно по модулю.
Легко сообразить,
что в пределе при
,
угол
.
Это значит, что углы при основании ДС
треугольника ДВС стремятся значению
,
а вектор изменения скорости
становится
перпендикулярным к вектору скорости
,
т.е. направлен по радиусу к центру
окружности.
7. Равнопеременное
движение по окружности
– движение по окружности, при котором
за равные интервалы времени угловая
скорость изменяется на одну и ту же
величину.
8. Угловое
ускорение в равнопеременном движении
по окружности
– отношение изменения угловой скорости
к интервалу времени
,
в течении которого это изменение
произошло, т.е.
,
где
начальное
значение угловой скорости,
конечное
значение угловой скорости,
угловое ускорение, в системе СИ измеряется
в
.
Из последнего равенства получим формулы
для вычисления угловой скорости
и
,
если
.
Умножая обе части
этих равенств на
и учитывая, что
,
–
тангенциальное ускорение, т.е. ускорение,
направленное по касательной к окружности
, получим формулы для вычисления линейной
скорости:
и
,
если
.
9. Тангенциальное
ускорение
численно равно изменению скорости в
единицу времени и направлено вдоль
касательной к окружности. Если
>0,
>0,
то движение равноускоренное. Если
<0
и
<0
– движение.
10. Закон
равноускоренного движения по окружности.
Путь, пройденный по окружности за время
в равноускоренном движении, вычисляется
по формуле:
.
Подставляя сюда
,
,
сокращая на
,
получим закон равноускоренного движения
по окружности:
,
или
,
если
.
Если же движение равнозамедленное, т.е.
<0,
то
.
1
1.Полное
ускорение в равноускоренном движении
по окружности.
В равноускоренном движении по окружности
центростремительное ускорение с
течением времени возрастает, т.к.
благодаря тангенциальному ускорению
возрастает линейная скорость. Очень
часто центростремительное ускорение
называют нормальным и обозначают как
.
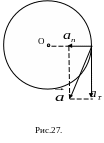
Так как
полное ускорение в данный момент
определяют по теореме Пифагора
(Рис.27).
12. Средняя
угловая скорость в равноускоренном
движении по окружности.
Средняя линейная скорость в равноускоренном
движении по окружности равна
.
Подставляя сюда
и
и сокращая на
получим
.
Если
,
то
.
12. Формулы,
устанавливающие связь между угловой
скоростью, угловым
ускорением
и углом поворота в равноускоренном
движении по окружности.
Подставляя в
формулу
величины
,
,
,
,
и сокращая на
,
получим
.
Если
,
то
и далее
,
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #