Sunshine
Высший разум
(836624)
3 года назад
Объёмный расход — в гидравлике объём жидкости или газа, протекающей через поперечное сечение потока в единицу времени.
Q = V/t, или V умноженное на S,
где:
Q — объёмный расход жидкости или газа, м³/с;
V — объём жидкости или газа, проходящий через поперечное сечение потока за время t, м³;
t — время, за которое жидкость или газ объёмом V проходит через поперечное сечение потока, с;
υ {displaystyle upsilon } {displaystyle upsilon } — скорость потока, м/с;
S — площадь поперечного сечения потока, м².
Алексей Коршунов
Мастер
(1723)
13 лет назад
Если что-то движется, то оно движется либо в том месте, которое оно занимает, либо в том месте, где его нет. Однако оно не может двигаться в том месте, которое оно занимает (так как в каждый момент времени оно занимает все это место) , но оно также не может двигаться и в том месте, где его нет. Следовательно, движение невозможно.
Древнегреческий герой Ахилл собирается состязаться в беге с черепахой. Если черепаха стартует немного раньше Ахилла, то ему, чтобы ее догнать, сначала нужно добежать до места ее старта. Но к тому моменту, как он туда доберется, черепаха проползет некоторое расстояние, которое нужно будет преодолеть Ахиллу, прежде чем догнать черепаху. Но за это время черепаха уползет вперед еще на некоторое расстояние. А поскольку число таких отрезков бесконечно, быстроногий Ахилл никогда не догонит черепаху.
Igor
Мастер
(1354)
13 лет назад
Изменением изменения объема воды от времени при разных условиях занимается гидродинамика – одна из наиболее хорошо развитых дисциплин механики сплошных сред. Там тебе и производные, и градиенты, и дивергенции с объемом и временем – пруд пруди. Ландавшица почитай, к примеру.
Решение.
[ begin{align}
& I=frac{Delta q}{Delta t}(1),Delta q=Ncdot e(2),N=frac{m}{M}cdot {{N}_{A}}(3),m=rho cdot V,(4),V=Scdot l(5), \
& I=frac{frac{rho cdot Scdot l}{M}{{N}_{A}}cdot e}{Delta t}=frac{rho cdot Scdot l}{Mcdot Delta t}{{N}_{A}}cdot e,upsilon =frac{l}{Delta t}(6),I=frac{rho cdot Scdot upsilon }{M}{{N}_{A}}cdot e. \
& upsilon =frac{Icdot M}{rho cdot Scdot {{N}_{A}}cdot e}(7).upsilon =frac{80cdot {{10}^{-3}}cdot 63,536cdot {{10}^{-3}}}{8,9cdot {{10}^{3}}cdot 0,8cdot {{10}^{-6}}cdot 6,02cdot {{10}^{23}}cdot 1,6cdot {{10}^{-19}}}=7,41cdot {{10}^{-6}}. \
end{align} ]
Где S — площадь поперечного сечения проводника; I — сила тока в проводнике; Δq – заряд, который проходит через поперечное сечение S проводника за время Δt; N — число электронов, определим, как количество атомов в определенной массе меди, так как на каждый атом меди приходится один свободный электрон, m – масса медного провода, V – объем провода, l – длина провода, NА – число Авогадро, NА = 6,02∙1023 кг/моль, ρ – плотность меди, e = 1,6∙10–19 Кл — модуль заряда электрона.
Ответ: 7,41 мкм/с.
V – объём
S – площадь поперечного сечения
v – скорость
t – время
Найти
- V
- S
- v
- t
Известно, что:
=
Вычислить ‘V‘
|
|
Макеты страниц
В этом параграфе мы применим закон сохранения энергии к движению жидкости или газа по трубам. Движение жидкости по трубам часто встречается в технике и быту. По трубам водопровода подается вода в городе в дома, к местам ее потребления. В машинах по трубам поступает масло для смазки, топливо в двигатели и т. д. Движение жидкости по трубам нередко встречается и в природе. Достаточно сказать, что кровообращение животных и человека — это течение крови по трубкам — кровеносным сосудам. В какой-то мере течение воды в реках тоже является разновидностью течения жидкости по трубам. Русло реки — это своеобразная труба для текущей воды.
Как известно, неподвижная жидкость в сосуде согласно закону Паскаля передает внешнее давление по всем направлениям и во все точки объема без изменения. Однако, когда жидкость течет без трения по трубе, площадь поперечного сечения которой на разных участках различна, давление оказывается неодинаковым вдоль трубы. Выясним, почему давление в движущейся жидкости зависит от площади поперечного сечения трубы. Но сначала ознакомимся с одной важной особенностью всякого потока жидкости.
Предположим, что жидкость течет по горизонтально расположенной трубе, сечение которой в разных местах различное, например по трубе, часть которой показана на рисунке 207.

Рис. 207
Если бы мы мысленно провели несколько сечений вдоль трубы, площади которых соответственно равны 





Как же может жидкость, протекшая через широкое сечение, успеть за такое же время «протиснуться» через узкое? Очевидно, что для этого при прохождении узких частей трубы скорость движения должна быть больше, и как раз во столько раз, во сколько раз площадь сечения меньше.
Действительно, рассмотрим некоторое сечение движущегося столба жидкости, совпадающее в начальный момент времени с одним из сечений трубы (рис. 208). За время 






В единицу же времени протекает объем жидкости — 

Объем жидкости, протекающей в единицу времени через сечение трубы, равен произведению площади поперечного сечения трубы на скорость течения.
Как мы только что видели, этот объем должен быть одним и тем же в разных сечениях трубы. Поэтому, чем меньше сечение трубы, тем больше скорость движения.
Сколько жидкости проходит через одно сечение трубы за некоторое время, столько же ее должно пройти за такое

Рис. 208
же время через любое другое сечение.
При этом мы считаем, что данная масса жидкости всегда имеет один и тот же объем, что она не может сжаться и уменьшить свой объем (о жидкости говорят, что она несжимаема). Хорошо известно, например, что в узких местах реки скорость течения воды больше, чем в широких. Если обозначить скорость течения жидкости в сечениях площадями 


Отсюда видно, что при переходе жидкости с участка трубы с большей площадью сечения на участок с меньшей площадью сечения скорость течения увеличивается, т. е. жидкость движется с ускорением. А это по второму закону Ньютона означает, что на жидкость действует сила. Что это за сила?
Этой силой может быть только разность между силами давления в широком и узком участках трубы. Таким образом, в широком участке давление жидкости должно быть больше, чем в узком участке трубы.
Это же следует из закона сохранения энергии. Действительно, если в узких местах трубы увеличивается скорость движения жидкости, то увеличивается и ее кинетическая энергия. А так как мы приняли, что жидкость течет без трения, то этот прирост кинетической энергии должен компенсироваться уменьшением потенциальной энергии, потому что полная энергия должна оставаться постоянной. О какой же потенциальной энергии здесь идет речь? Если труба горизонтальна, то потенциальная энергия взаимодействия с Землей во всех частях трубы одна и та же и не может измениться. Значит, остается только потенциальная энергия упругого взаимодействия. Сила давления, которая заставляет жидкость течь по трубе, — это и есть упругая сила сжатия жидкости. Когда мы говорим, что жидкость несжимаема, то имеем лишь в виду, что она не может быть сжата настолько, чтобы заметно изменился ее объем, но очень малое сжатие, вызывающее появление упругих сил, неизбежно происходит. Эти силы и создают давление жидкости. Вот это сжатие жидкости и уменьшается в узких частях трубы, компенсируя рост скорости. В узких местах труб давление жидкости должно быть поэтому меньше, чем в широких.
В этом состоит закон, открытый петербургским академиком Даниилом Бернулли:
Давление текущей жидкости больше в тех сечениях потока, в которых скорость ее движения меньше, и,

Рис. 209
наоборот, в тех сечениях, в которых скорость больше, давление меньше.
Как это ни покажется странным, но когда жидкость «протискивается» через узкие участки трубы, то ее сжатие не увеличивается, а уменьшается. И опыт хорошо это подтверждает.
Если трубу, по которой течет жидкость, снабдить впаянными в нее открытыми трубками — манометрами (рис. 209), то можно будет наблюдать распределение давления вдоль трубы. В узких местах трубы высота столба жидкости в манометрической трубке меньше, чем в широких. Это означает, что в этих местах давление меньше. Чем меньше сечение трубы, тем больше в ней скорость течения и меньше давление. Можно, очевидно, подобрать такое сечение, в котором давление равно внешнему атмосферному давлению (высота уровня жидкости в манометре будет тогда равна нулю). А если взять еще меньшее сечение, то давление жидкости в нем будет меньше атмосферного.
Такой поток жидкости можно использовать для откачки воздуха. На этом принципе действует так называемый водоструйный насос. На рисунке 210 изображена схема такого насоса. Струю воды пропускают через трубку А с узким отверстием на конце. Давление воды у отверстия трубы меньше атмосферного. Поэтому

Рис. 210

Рис. 211
газ из откачиваемого объема через трубку В втягивается к концу трубки А и удаляется вместе с водой.
Все сказанное о движении жидкости по трубам относится и к движению газа. Если скорость течения газа не слишком велика и газ не сжимается настолько, чтобы изменялся его объем, и если, кроме того, пренебречь трением, то закон Бернулли верен и для газовых потоков. В узких частях труб, где газ движется быстрее, давление его меньше, чем в широких частях, и может стать меньше атмосферного. В некоторых случаях для этого даже не требуется трубы.
Можно проделать простой опыт. Если дуть на лист бумаги вдоль его поверхности, как показано на рисунке 211, можно увидеть, что бумага станет подниматься вверх. Это происходит из-за понижения давления в струе воздуха над бумагой.
Такое же явление имеет место при полете самолета. Встречный поток воздуха набегает на выпуклую верхнюю поверхность крыла летящего самолета, и за счет этого происходит понижение давления. Давление над крылом оказывается меньше, чем давление под крылом. Именно поэтому возникает подъемная сила крыла.
Упражнение 62
1. Допустимая скорость течения нефти по трубам равна 2 м/сек. Какой объем нефти проходит через трубу диаметром 1 м в течение 1 ч?
2. Измерьте количество воды, вытекающей из водопроводного крана за определенное время 
3. Каким должен быть диаметр трубопровода, по которому должно протекать 
Оглавление
- Глава 1. Общие сведения о движении
- § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА
- § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ
- § 3. ПЕРЕМЕЩЕНИЕ
- § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА
- § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ
- § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ
- § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР
- § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ
- § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ
- § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ
- § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ)
- § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ
- Глава 2. Прямолинейное неравномерное движение
- § 13. СРЕДНЯЯ СКОРОСТЬ
- § 14. МГНОВЕННАЯ СКОРОСТЬ
- § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
- § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ
- § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ
- § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ
- § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ
- § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ
- § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ
- Глава 3. Криволинейное движение
- § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ
- § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ
- § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА
- Динамика
- Глава 4. Законы движения
- § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА
- § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ
- § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ
- § 31. ИНЕРТНОСТЬ ТЕЛ
- § 32. МАССА ТЕЛ
- § 33. МАССА ЛУНЫ
- § 34. СИЛА
- § 35. ВТОРОЙ ЗАКОН НЬЮТОНА
- § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение)
- § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР
- § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА
- § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА
- Глава 5. Силы природы
- § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ
- § 41. СИЛА УПРУГОСТИ
- § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ
- § 44. СИЛА ТЯЖЕСТИ
- § 45. ВЕС ТЕЛ
- § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ
- § 47. МАССА ЗЕМЛИ
- § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ
- § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ
- § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ
- Глава 6. Применение законов движения
- § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ
- § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ
- § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ
- § 54. НЕВЕСОМОСТЬ
- § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ
- § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО
- § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ
- § 58. ДВИЖЕНИЕ ПЛАНЕТ
- § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ
- § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ
- § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ
- § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ
- § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ
- § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА
- Равновесие тел
- Глава 7. Элементы статики
- § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ
- § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ
- § 67. ПРАВИЛО МОМЕНТОВ
- § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ
- Законы сохранения в механике
- Глава 8. Закон сохранения импульса
- § 70. СИЛА И ИМПУЛЬС
- § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
- § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ
- Глава 9. Механическая работа и мощность
- § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ
- § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ
- § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ
- § 77. РАБОТА СИЛЫ ТЯЖЕСТИ
- § 78. РАБОТА СИЛЫ УПРУГОСТИ
- § 79. РАБОТА СИЛЫ ТРЕНИЯ
- § 80. МОЩНОСТЬ
- Глава 10. Закон сохранения энергии
- § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА
- § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ
- § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН
- § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
- § 91. СТОЛКНОВЕНИЕ ТЕЛ
- § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ
- § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ
- Заключение
- Лабораторные работы
- 1. Определение ускорения тела при равноускоренном движении
- 2. Определение коэффициента трения скольжения
- 3. Изучение движения тела по параболе
- 4. Выяснение условия равновесия рычага
- 5. Определение центра тяжести плоской пластины
- Ответы к упражнениям
Сила тока с точки зрения гидравлики
Думаю, вы не раз слышали такое словосочетание, как «сила тока«. А для чего нужна сила? Ну как для чего? Чтобы совершать полезную или бесполезную работу. Главное, чтобы что-то делать. Каждый из нас обладает какой-либо силой. У кого-то сила такая, что он может одним ударом разбить кирпич в пух и в прах, а другой не сможет поднять даже соломинку. Так вот, дорогие мои читатели, электрический ток тоже обладает силой.
Представьте себе шланг, с помощью которого вы поливаете свой огород
Давайте теперь проведем аналогию. Пусть шланг — это провод, а вода в нем — электрический ток. Мы чуть-чуть приоткрыли краник и вода сразу же побежала по шлангу. Медленно, но все-таки побежала. Сила струи очень слабая.
А давайте теперь откроем краник на полную катушку. В результате струя хлынет с такой силой, что можно даже полить соседский огород.
В обоих случаях диаметр шланга одинаков.
А теперь представьте, что вы наполняете ведро. Напором воды из какого шланга вы его быстрее наполните? Разумеется из зеленого, где напор воды очень сильный. Но почему так происходит? Все дело в том, что объем воды за равный промежуток времени из желтого и зеленого шланга выйдет тоже разный. Или иными словами, из зеленого шланга количество молекул воды выбежит намного больше, чем из желтого за равный период времени.
Разберем еще один интересный пример. Давайте допустим, что у нас есть большая труба, и к ней заварены две другие, но одна в два раза меньше диаметром, чем другая.
Из какой трубы объем воды будет выходить больше за секунду времени? Разумеется с той, которая толще в диаметре, потому что площадь поперечного сечения S2 большой трубы больше, чем площадь поперечного сечения S1 малой трубы. Следовательно, сила потока через большую трубу будет больше, чем через малую, так как объем воды, который протекает через поперечное сечение трубы S2, будет в два раза больше, чем через тонкую трубу.
Что такое сила тока?
Итак, теперь давайте все что мы тут пописали про водичку применим к электронике. Провод — это шланг. Тонкий провод — это тонкий в диаметре шланг, толстый провод — это толстый в диаметре шланг, можно сказать — труба. Молекулы воды — это электроны. Следовательно, толстый провод при одинаковом напряжении можно протащить больше электронов, чем тонкий. И вот здесь мы подходим вплотную к самой терминологии силы тока.
Сила тока — это количество электронов, прошедших через площадь поперечного сечения проводника за какое-либо определенное время.
Все это выглядит примерно вот так. Здесь я нарисовал круглый проводок, «разрезал» его и получил ту самую площадь поперечного сечения. Именно через нее и бегут электроны.
За период времени берут 1 секунду.
Формула силы тока
Формула для чайников будет выглядеть вот так:
где
I — собственно сила тока, Амперы
N — количество электронов
t — период времени, за которое эти электроны пробегут через поперечное сечение проводника, секунды
Более правильная (официальная) формула выглядит вот так:
где
Δq — это заряд за какой-то определенный промежуток времени, Кулон
Δt — тот самый промежуток времени, секунды
I — сила тока, Амперы
В чем прикол этих двух формул? Дело все в том, что электрон обладает зарядом приблизительно 1,6 · 10-19 Кулон. Поэтому, чтобы сила тока была в проводе (проводнике) была 1 Ампер, нам надо, чтобы через поперечное сечение прошел заряд в 1 Кулон = 6,24151⋅1018 электронов. 1 Кулон = 1 Ампер · 1 секунду.
Итак, теперь можно официально сказать, что если через поперечное сечение проводника за 1 секунду пролетят 6,24151⋅1018 электронов, то сила тока в таком проводнике будет равна 1 Ампер! Все! Ничего не надо больше придумывать! Так и скажите своему преподавателю по физике).
Если преподу не понравится ваш ответ, то скажите типа что-то этого:
Сила тока — это физическая величина, равная отношению количества заряда прошедшего через поверхность (читаем как через площадь поперечного сечения) за какое-то время. Измеряется как Кулон/секунда. Чтобы сэкономить время и по другим морально-эстетическим нормам, Кулон/секунду договорились называть Ампером, в честь французского ученого-физика.
Сила тока и сопротивление
Давайте еще раз глянем на шланг с водой и зададим себе вопросы. От чего зависит поток воды? Первое, что приходит в голову — это давление. Почему молекулы воды движутся в рисунке ниже слева-направо? Потому, что давление слева, больше чем справа. Чем больше давление, тем быстрее побежит водичка по шлангу — это элементарно.
Теперь такой вопрос: как можно увеличить количество электронов через площадь поперечного сечения?
Первое, что приходит на ум — это увеличить давление. В этом случае скорость потока воды увеличится, но ее много не увеличишь, так как шланг порвется как грелка в пасти Тузика.
Второе — это поставить шланг бОльшим диаметром. В этом случае у нас количество молекул воды через поперечное сечение будет проходить больше, чем в тонком шланге:
Все те же самые умозаключения можно применить и к обыкновенному проводу. Чем он больше в диаметре, тем больше он сможет «протащить» через себя силу тока. Чем меньше в диаметре, то желательно меньше его нагружать, иначе его «порвет», то есть он тупо сгорит. Именно этот принцип заложен в плавких предохранителях. Внутри такого предохранителя тонкий проводок. Его толщина зависит от того, на какую силу тока он рассчитан.
Как только сила тока через тонкий проводок предохранителя превысит силу тока, на которую рассчитан предохранитель, то плавкий проводок перегорает и размыкает цепь. Через перегоревший предохранитель ток уже течь не может, так как проводок в предохранителе в обрыве.
Поэтому, силовые кабели, через которые «бегут» сотни и тысячи ампер, берут большого диаметра и стараются делать из меди, так как ее удельное сопротивление очень мало.
Сила тока в проводнике
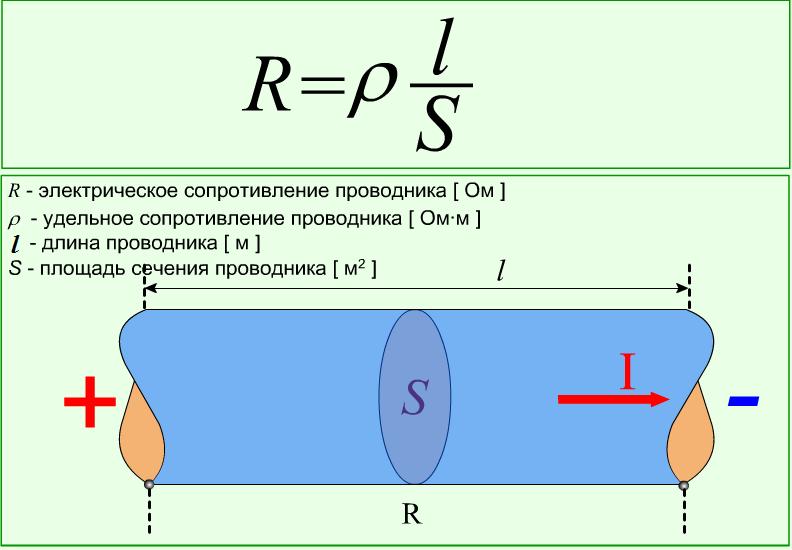
Очень часто можно увидеть задачки по физике с вопросом: какая сила тока в проводнике? Проводник, он же провод, может иметь различные параметры: диаметр, он же площадь поперечного сечения; материал, из которого сделан провод; длина, которая играет также важную роль.
Да и вообще, сопротивление проводника рассчитывается по формуле:
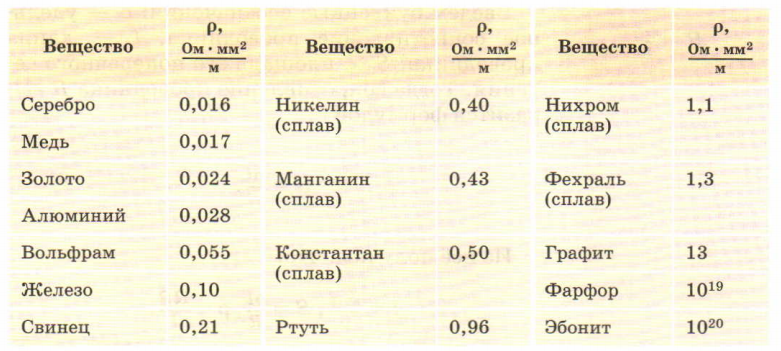
Таблица с удельным сопротивлением из разных материалов выглядит вот так.
Для того, чтобы найти силу тока в проводнике, мы должны воспользоваться законом Ома для участка цепи. Выглядит он вот так:
Задача
У нас есть медный провод длиной в 1 метр и его площадь поперечного сечения составляет 1 мм2 . Какая сила тока будет течь в этом проводнике (проводе), если на его концы подать напряжение в 1 Вольт?
Решение:
Как измерить силу тока?
Для того, чтобы измерить значение силы тока, мы должны использовать специальные приборы — амперметры. В настоящее время силу тока можно измерить с помощью цифрового мультиметра, который может измерять и силу тока, и напряжение и сопротивление и еще много чего. Для того, чтобы измерить силу тока, мы должны вставить наш прибор в разрыв цепи вот таким образом.
Более подробно как это сделать, можете прочитать в этой статье.
Также советую посмотреть обучающее видео, где очень умный преподаватель объясняет простым языком, что такое «сила тока».