Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:
Работа силы
В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.
Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).
Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:
Важно!
Механическая работа совершается, если:
- На тело действует сила.
- Под действием этой силы тело перемещается.
- Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).
Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.
Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.
Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:
Работа различных сил
Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.
| Работа силы тяжести |
Модуль силы тяжести: Fтяж = mg Работа силы тяжести: A = mgs cosα |
| Работа силы трения скольжения |
Модуль силы трения скольжения: Fтр = μN = μmg Работа силы трения скольжения: A = μmgs cosα |
| Работа силы упругости |
Модуль силы упругости: Fупр = kx Работа силы упругости: |
Работа силы упругости
Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):
Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:
s = x1 – x2
Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:
Работы силы трения покоя
Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.
Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.
A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)
Знак работы силы
Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:
- Если α = 0о, то cosα = 1.
- Если 0о < α < 90o, то cosα > 0.
- Если α = 90о, то cosα = 0.
- Если 90о < α < 180o, то cosα < 0.
- Если α = 180о, то cosα = –1.
Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180о). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0о). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.
Геометрический смысл работы
Графическое определение
Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.
A = Sфиг
Мощность
Определение
Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:
Рассмотрим частные случаи определения мощности в таблице.
Мощность при равномерном прямолинейном движении тела |
Работа при равномерном прямолинейном движении определяется формулой: A = Fтs Fт — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна: |
Мощность при равномерном подъеме груза |
Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому: |
Мгновенная мощность при неравномерном движении |
Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость: |
Мощность силы трения при равномерном движении по горизонтали |
Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения: |
Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?
Коэффициент полезного действия
Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.
Определения:
- Работа затраченная — полная работа силы, совершенной над телом (или телом).
- Работа полезная — часть полной работы силы, которая вызывает непосредственно перемещение тела.
- Коэффициент полезного действия (КПД) — процентное отношение полезной работы к работе затраченной. КПД обозначается буквой «эта» — η. Единицы измерения эта величина не имеет. Она показывает эффективность работы механизма или другой системы, совершающей работу, в процентах.
КПД определяется формулой:
Работа может определяться как произведение мощности на время, в течение которого совершалась работа:
A = Nt
Поэтому формулу для вычисления КПД можно записать в следующем виде:
Частые случаи определения КПД рассмотрим в таблице ниже:
Устройство |
Работа полезная и полная |
КПД |
| Неподвижный блок, рычаг |
Aполезн = mgh Асоверш. |
 |
| Наклонная плоскость |
Aполезн = mgh Асоверш. = Fl l — совершенный путь (длина наклонной плоскости). |
 |
Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.
В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:
Задание EF17557
Какую мощность развивает сила тяги трактора, перемещая прицеп со скоростью 18 км/ч, если она составляет 16,5 кН?
Ответ:
а) 916 Вт
б) 3300 Вт
в) 82500 Вт
г) 297000 Вт
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать формулу для расчета мощности.
3.Выполнить общее решение задачи.
4.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Сила тяги, перемещающая прицеп, равна: Fт = 16,5 кН.
• Скорость перемещения прицепа под действием силы тяги: v = 18 км/ч.
Переведем единицы измерения в СИ:
16,5 кН = 16,5∙103 Н
18 км/ч = 18000/3600 м/с = 5 м/с
Мощность равна отношению работы ко времени, в течение которого эта работа совершалась:
N=At
Но работа равна произведению силы, перемещения и косинуса угла между векторами силы и перемещения. В данном случае будем считать, что угол равен нулю, следовательно косинус — единице. Тогда работа равна:
A = Fs
Тогда мощность равна:
N=Fst=Fv=16,5·103·5=82500 (Вт)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17574
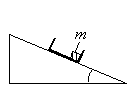
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Время движения |
Ускорение |
Модуль работы силы трения |
Алгоритм решения
1.Установить наличие и характер зависимости кинематических характеристик движения от массы тела.
2.Вывести формулу для модуля работы силы трения.
3.Установить, как изменится модуль работы силы трения при уменьшении массы тела вдвое.
Решение
При скольжении с наклонной плоскости происходит равноускоренное движение. Положение тела в любой момент времени при таком движении можно определить с помощью кинематических уравнений:
x=xo+v0xt+axt22
y=yo+v0yt+ayt22
Из этих уравнений видно, что ускорение и время никак не зависят от массы тела. Следовательно, при уменьшении массы тела в 2 раза его время движения и ускорение не изменятся.
Чтобы выразить модуль работы силы трения, выберем такую систему отсчета, чтобы вектор силы трения был расположен вдоль оси Ox.Тогда сила трения будет равна:
Fтр = μmg
Известно, что работа определяется формулой:
A = Fs cosα
Тогда работа силы трения равна:
A = μmgs cosα
Вектор силы трения всегда направлен противоположно вектору перемещения. Поэтому косинус угла между ними равен –1. Но нас интересует только модуль работы. Поэтому будем считать, что он равен:
A = μmgs
Модуль работы силы трения и масса тела зависят прямо пропорционально. Следовательно, если массу тела уменьшить вдвое, то и модуль работы силы трения уменьшится вдвое.
Поэтому правильная последовательность цифр в ответе: 332.
Ответ: 332
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18646
В первой серии опытов брусок перемещают при помощи нити равномерно и прямолинейно вверх по наклонной плоскости. Во второй серии опытов на бруске закрепили груз, не меняя прочих условий.
Как изменятся при переходе от первой серии опытов ко второй сила натяжения нити и коэффициент трения между бруском и плоскостью?
Для каждой величины определите соответствующий характер её изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
| Сила натяжения нити | Коэффициент трения |
Алгоритм решения
- Определить, какая величина изменилась во второй серии опытов.
- Определить, как зависит от этой величины сила натяжения нити.
- Определить, как зависит от этой величины коэффициент трения.
Решение
Когда к бруску подвесили груз, увеличилась масса. Когда тело на нити перемещается вверх прямолинейно и равномерно, сила натяжения нити определяется модулем силы тяжести:
T = mg
Эта формула показывает, что сила натяжения нити и масса тела зависят прямо пропорционально. Если, добавив к бруску груз, масса увеличится, то сила натяжения нити тоже увеличится.
Коэффициент трения — это величина, которая зависит только от материалов и типа поверхности. Поэтому увеличение массы тела на него никак не повлияют.
Верная последовательность цифр в ответе: 13.
Ответ: 13
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18271
Определите коэффициент полезного действия атомной электростанции, расходующей за неделю уран-235 23592U массой 1,4 кг, если её мощность равна 38 МВт. При делении одного ядра урана-235 выделяется энергия 200 МэВ.
Алгоритм решения
1.Записать исходные данные и перевести их в СИ.
2.Записать формулу для определения КПД атомной электростанции.
3.Решить задачу в общем виде.
4.Подставить известные данные и вычислить искомую величину.
5.Массовое число: A = 235.
6.Зарядовое число: Z = 92.
Решение
Запишем исходные данные:
• Энергия, выделяемая при делении одного ядра урана-235: Q0 = 200 МэВ.
• Масса урана-235: m = 1,4 кг.
• Время, в течение которого происходит деление: t = 1 неделя.
• Мощность атомной электростанции: N = 38 МВт.
Переведем все единицы измерения в СИ:
1 эВ = 1,6∙10–19 Дж
200 МэВ = 200∙106∙1,6∙10–19 Дж = 320∙10–13 Дж
1 неделя = 7∙24∙60∙60 с = 604,8∙103 с
38 МВт = 38∙106 Вт
КПД атомной электростанции есть отношение полезной работы к выделенной за это же время энергии:
η=AполезнQ100%
Полезную работу мы можем вычислить по формуле:
A=Nt
Выделенное количество теплоты мы можем рассчитать, вычислив количество атомов, содержащихся в 1,4 кг урана-235 и умножив их на энергию, выделяемую при делении одного такого атома.
Количество атомов равно произведению количество молей на постоянную Авогадро:
Nкол.атомов = νNA
Количество молей равно отношения массы вещества к его молярной массе, следовательно:
Молярная масса численно равна массовому числу в граммах на моль. Следовательно:
M = A (г/моль) = A∙10–3 (кг/моль)
Отсюда количество атомов равно:
Энергия, выделенная всеми атомами, равна:
Теперь можем вычислить КПД:
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 12k
§ 3. Сила, второй закон Ньютона
Сила является мерой взаимодействия (взаимного действия). Если действие велико (мало), то говорят о большой (малой) силе. Сила обозначается буквой `F` (первая буква слова force).
При взаимодействии чем больше сила, тем больше ускорение тела, на которое эта сила действует. Следовательно, ускорение прямо пропорционально действующей силе: `a~F`.
Но уже говорилось о том, что ускорение зависит от массы тела: `a~1/m`.
Обобщая эти зависимости получим:
Теперь рассмотрим свойства силы, устанавливаемые опытным путём:
1) Результат действия (проявления) силы зависит от направления действующей силы, следовательно, сила – величина векторная.
2) Результат действия (проявления) силы зависит от величины приложенной силы.
3) Результат действия (проявления) силы зависит от точки приложения силы.
4) За единицу силы принято значение такой силы, которая вызывает ускорение `1 “м”//”c”^2` у тела массой `1` кг. Единицу силы назвали в честь Исаака Ньютона `1` Ньютон. (Произносить фамилию считается правильным таким образом, как произносится фамилия в том государстве, где проживал или проживает учёный.)
`[vecF]=1″H”=1 “кг”*”м”/(“с”^2)` (Ньютон).
5) Если на тело одновременно действуют несколько сил, то каждая сила действуетнезависимо от других. (Принцип суперпозиции сил). Тогда все силы необходимо сложить векторно и получить результирующую силу (рис. 4).
Из приведённых свойств силы следует, как обобщение опытных фактов, второй закон Ньютона:
Сумма всех сил, действующих на тело, равна произведению массы тела на ускорение, сообщаемое этой суммой сил:
`sumvecF=mveca`.
Данное выражение можно представить и в другой форме: так как `veca=(vecv_”к”-vecv_0)/t`, то второй закон Ньютона примет вид: `sumvecF=m(vecv_”к”-vecv_0)/t`.
Произведение массы тела и его скорости называют импульсом тела: `vecp=mvecv`,
тогда получим новое выражение для второго закона Ньютона:
`sumvecF=(mvecv_”к”-mvecv_0)/t=(vecp_”к”-vecp_0)/t=(Deltavecp)/t`.
`sum vecF=(vecp_”к”-vecp_0)/t` – второй закон Ньютона в импульсной форме для среднего значения силы. Здесь `vecp_”к”-vecp_0=Deltavecp` – изменение импульса тела, `t` – время изменения импульса тела.
`sumvecF=(dvecp)/(dt)` – второй закон Ньютона в импульсной форме для мгновенного значения силы.
Из второго закона в частности следует, что ускорение тела, подвергающегося действию нескольких сил, равно сумме ускорений, сообщаемых каждой силой:
`veca=sumveca_i=veca_1+veca_2+…+veca_i=(sumvecF)/m=`
`=(vecF_1+vecF_2+…+vecF_i)/m=(vecF_1)/m+(vecF_2)/m+…+(vecF_i)/m`.
Первая форма записи второго закона `(sumvecF=mveca)` справедлива только при малых скоростях по сравнению со скоростью света. И, разумеется, выполняется второй закон Ньютона только в инерциальных системах отсчёта. Также следует отметить, что второй закон Ньютона справедлив для тел неизменной массы, конечных размеров и движущихся поступательно.
Второе (импульсное) выражение имеет более общий характер и справедливо при любых скоростях.
Как правило, в школьном курсе физики сила со временем не меняется. Однако последняя импульсная форма записи позволяет учесть зависимость силы от времени, и тогда изменение импульса тела будет найдено с помощью определённого интеграла на исследуемом интервале времени. В более простых случаях (сила изменяется со временем по линейному закону) можно брать среднее значение силы.
Иногда очень полезно знать, что произведение `vecF*t` называют импульсом силы, и его значение `vecF*t=Deltavecp` равно изменению импульса тела.
Для постоянной силы на графике зависимости силы от времени можем получить, что площадь фигуры под графиком равна изменению импульса (рис. 5).
Но даже если сила будет изменяться со временем, то и в этом случае, разбивая время на малые интервалы `Deltat` такие, что величина силы на этом интервале остаётся неизменной (рис. 6), а потом, суммируя полученные «столбики», получим:
Площадь фигуры под графиком `F(t)` численно равна изменению импульса.
В наблюдаемых природных явлениях сила, как правило, меняется со временем. Мы же часто, применяя простые модели процессов, считаем силы постоянными. Сама же возможность использования простых моделей появляется из возможности подсчёта средней силы, т. е. такой постоянной силы, у которой площадь под графиком от времени будет равна площади под графиком реальной силы.
Следует добавить ещё одно очень важное следствие второго закона Ньютона, связанное с равенством инертной и гравитационной масс.
Неразличимость гравитационной и инертной масс означает, что и ускорения, вызванные гравитационным взаимодействием (законом всемирного тяготения) и любым другим тоже неразличимы.
Мяч массой `0,5` кг после удара, длящегося `0,02` с, приобретает скорость `10` м/с. Найти среднюю силу удара.
В данном случае рациональнее выбрать второй закон Ньютона в импульсной форме, т. к. известны начальная и конечная скорости, а не ускорение, и известно время действия силы. Также следует отметить, что сила, действующая на мяч, не остаётся постоянной. По какому закону меняется сила со временем, не известно. Для простоты мы будем пользоваться предположением, что сила постоянная, и её мы будем называть средней.
Тогда `sumvecF=(Deltavecp)/t`, т. е. `vecF_(“ср”)*t=Deltavecp`. В проекции на ось, направленной вдоль линии действия силы, получим: `F_”ср”*t=p_”к”-p_0=mv_”к”`. Окончательно для искомой силы получим:
`F_”ср”=(mv_”к”)/t`.
Количественно ответ будет таким:
`F_”ср”=(0,5″кг”*10″м”/”с”)/(0,02″с”)=250″H”`.
|
1 / 1 / 2 Регистрация: 27.10.2012 Сообщений: 209 |
|
|
1 |
|
Найти время действия силы26.03.2013, 18:21. Показов 3846. Ответов 9
Здравствуйте, дорогие форумчане. Миниатюры
0 |
|
Я не экстрасенс 382 / 339 / 34 Регистрация: 22.01.2013 Сообщений: 1,126 |
|
|
26.03.2013, 18:38 |
2 |
|
Модуль импульса удара судя по рис. равен 5 кг*м/с
1 |
|
1 / 1 / 2 Регистрация: 27.10.2012 Сообщений: 209 |
|
|
26.03.2013, 18:46 [ТС] |
3 |
|
Ответ будет 0.5 ?
0 |
|
4179 / 2822 / 709 Регистрация: 16.09.2012 Сообщений: 11,484 |
|
|
26.03.2013, 18:47 |
4 |
|
Визуально №1.
0 |
|
1 / 1 / 2 Регистрация: 27.10.2012 Сообщений: 209 |
|
|
26.03.2013, 18:50 [ТС] |
5 |
|
Визуально №1. Почему?
0 |
|
Я не экстрасенс 382 / 339 / 34 Регистрация: 22.01.2013 Сообщений: 1,126 |
|
|
26.03.2013, 18:54 |
6 |
|
5=25*0.2
2 |
|
4179 / 2822 / 709 Регистрация: 16.09.2012 Сообщений: 11,484 |
|
|
26.03.2013, 19:06 |
7 |
|
P2=P+P1
1 |
|
Я не экстрасенс 382 / 339 / 34 Регистрация: 22.01.2013 Сообщений: 1,126 |
|
|
26.03.2013, 23:34 |
8 |
|
приблизительно … =5,5 ну, это будет… А если серьезно, качество рисунка позволяет разглядеть лишь треугольник 3х4.
0 |
|
Комп_Оратор) 8849 / 4591 / 619 Регистрация: 04.12.2011 Сообщений: 13,700 Записей в блоге: 16 |
|
|
27.03.2013, 00:56 |
9 |
|
А если серьезно, качество рисунка позволяет разглядеть лишь треугольник 3х4. Ну так, треугольник Пифагора и получается :
1 |
|
1 / 1 / 2 Регистрация: 27.10.2012 Сообщений: 209 |
|
|
27.03.2013, 06:42 [ТС] |
10 |
|
Спасибо всем за помощь)
0 |
Мы уже говорили об основах классической механики. Настала пора поговорить о них подробнее и затронуть в обсуждении чуть больше, чем просто основу. В этой статье мы подробно разберем основные законы классической механики. Как вы уже догадались, речь пойдет о законах Ньютона.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Основные законы классической механики Исаак Ньютон (1642-1727) собрал и опубликовал в 1687 году. Три знаменитых закона были включены в труд, который назывался «Математические начала натуральной философии».
Был долго этот мир глубокой тьмой окутан
Да будет свет, и тут явился Ньютон.
(Эпиграмма 18-го века)
Но сатана недолго ждал реванша –
Пришел Эйнштейн, и стало все как раньше.
(Эпиграмма 20-го века)
Что стало, когда пришел Эйнштейн, читайте в отдельном материале про релятивистскую динамику. А мы пока приведем формулировки и примеры решения задач на каждый закон Ньютона.
Первый закон Ньютона
Первый закон Ньютона гласит:
Существуют такие системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно, если на них не действуют никакие силы или действие других сил скомпенсировано.
Проще говоря, суть первого закона Ньютона можно сформулировать так: если мы на абсолютно ровной дороге толкнем тележку и представим, что можно пренебречь силами трения колес и сопротивления воздуха, то она будет катиться с одинаковой скоростью бесконечно долго.
Инерция – это способность тела сохранять скорость как по направлению, так и по величине, при отсутствии воздействий на тело. Первый закон Ньютона еще называют законом инерции.
До Ньютона закон инерции был сформулирован в менее четкой форме Галилео Галилеем. Инерцию ученый называл «неистребимо запечатленным движением». Закон инерции Галилея гласит: при отсутствии внешних сил тело либо покоится, либо движется равномерно. Огромная заслуга Ньютона в том, что он сумел объединить принцип относительности Галилея, собственные труды и работы других ученых в своих “Математических началах натуральной философии”.
Понятно, что таких систем, где тележку толкнули, а она покатилась без действия внешних сил, на самом деле не бывает. На тела всегда действуют силы, причем скомпенсировать действие этих сил полностью практически невозможно.
Например, все на Земле находится в постоянном поле силы тяжести. Когда мы передвигаемся (не важно, ходим пешком, ездим на машине или велосипеде), нам нужно преодолевать множество сил: силу трения качения и силу трения скольжения, силу тяжести, силу Кориолиса.
Второй закон Ньютона
Помните пример про тележку? В этот момент мы приложили к ней силу! Интуитивно понятно, что тележка покатится и вскоре остановится. Это значит, ее скорость изменится.
В реальном мире скорость тела чаще всего изменяется, а не остается постоянной. Другими словами, тело движется с ускорением. Если скорость нарастает или убывает равномерно, то говорят, что движение равноускоренное.
Если рояль падает с крыши дома вниз, то он движется равноускоренно под действием постоянного ускорения свободного падения g. Причем любой дугой предмет, выброшенный из окна на нашей планете, будет двигаться с тем же ускорением свободного падения.
Второй закон Ньютона устанавливает связь между массой, ускорением и силой, действующей на тело. Приведем формулировку второго закона Ньютона:
Ускорение тела (материальной точки) в инерциальной системе отсчета прямо пропорционально приложенной к нему силе и обратно пропорционально массе.
Если на тело действует сразу несколько сил, то в данную формулу подставляется равнодействующая всех сил, то есть их векторная сумма.
В такой формулировке второй закон Ньютона применим только для движения со скоростью, много меньшей, чем скорость света.
Существует более универсальная формулировка данного закона, так называемый дифференциальный вид.
В любой бесконечно малый промежуток времени dt сила, действующая на тело, равна производной импульса тела по времени.
Третий закон Ньютона
В чем состоит третий закон Ньютона? Этот закон описывает взаимодействие тел.
3 закон Ньютона говорит нам о том, что на любое действие найдется противодействие. Причем, в прямом смысле:
Два тела воздействуют друг на друга с силами, противоположными по направлению, но равными по модулю.
Формула, выражающая третий закон Ньютона:
Другими словами, третий закон Ньютона – это закон действия и противодействия.
Пример задачи на законы Ньютона
Вот типичная задачка на применение законов Ньютона. В ее решении используются первый и второй законы Ньютона.
Десантник раскрыл парашют и опускается вниз с постоянной скоростью. Какова сила сопротивления воздуха? Масса десантника – 100 килограмм.
Решение:
Движение парашютиста – равномерное и прямолинейное, поэтому, по первому закону Ньютона, действие сил на него скомпенсировано.
На десантника действуют сила тяжести и сила сопротивления воздуха. Силы направлены в противоположные стороны.
По второму закону Ньютона, сила тяжести равна ускорению свободного падения, умноженному на массу десантника.
Ответ: Сила сопротивления воздуха равна силе тяжести по модулю и противоположна направлена.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
А вот еще одна физическая задачка на понимание действия третьего закона Ньютона.
Комар ударяется о лобовое стекло автомобиля. Сравните силы, действующие на автомобиль и комара.
Решение:
По третьему закону Ньютона, силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению. Сила, с которой комар действует на автомобиль, равна силе, с которой автомобиль действует на комара.
Другое дело, что действие этих сил на тела сильно отличаются вследствие различия масс и ускорений.
Исаак Ньютон: мифы и факты из жизни
На момент публикации своего основного труда Ньютону было 45 лет. За свою долгую жизнь ученый внес огромный вклад в науку, заложив фундамент современной физики и определив ее развитие на годы вперед.
Он занимался не только механикой, но и оптикой, химией и другими науками, неплохо рисовал и писал стихи. Неудивительно, что личность Ньютона окружена множеством легенд.
Ниже приведены некоторые факты и мифы из жизни И. Ньютона. Сразу уточним, что миф – это не достоверная информация. Однако мы допускаем, что мифы и легенды не появляются сами по себе и что-то из перечисленного вполне может оказаться правдой.
- Факт. Исаак Ньютон был очень скромным и застенчивым человеком. Он увековечил себя благодаря своим открытиям, однако сам никогда не стремился к славе и даже пытался ее избежать.
- Миф. Существует легенда, согласно которой Ньютона осенило, когда на наго в саду упало яблоко. Это было время чумной эпидемии (1665-1667), и ученый был вынужден покинуть Кембридж, где постоянно трудился. Точно неизвестно, действительно ли падение яблока было таким роковым для науки событием, так как первые упоминания об этом появляются только в биографиях ученого уже после его смерти, а данные разных биографов расходятся.
- Факт. Ньютон учился, а потом много работал в Кембридже. По долгу службы ему нужно было несколько часов в неделю вести занятия у студентов. Несмотря на признанные заслуги ученого, занятия Ньютона посещались плохо. Бывало, что на его лекции вообще никто не приходил. Скорее всего, это связано с тем, что ученый был полностью поглощен своими собственными исследованиями.
- Миф. В 1689 году Ньютон был избран членом Кембриджского парламента. Согласно легенде, более чем за год заседания в парламенте вечно поглощенный своими мыслями ученый взял слово для выступления всего один раз. Он попросил закрыть окно, так как был сквозняк.
- Факт. Неизвестно, как бы сложилась судьба ученого и всей современной науки, если бы он послушался матери и начал заниматься хозяйством на семейной ферме. Только благодаря уговорам учителей и своего дяди юный Исаак отправился учиться дальше вместо того, чтобы сажать свеклу, разбрасывать по полям навоз и по вечерам выпивать в местных пабах.
Дорогие друзья, помните – любую задачу можно решить! Если у вас возникли проблемы с решением задачи по физике, посмотрите на основные физические формулы. Возможно, ответ перед глазами, и его нужно просто рассмотреть. Ну а если времени на самостоятельные занятия совершенно нет, специализированный студенческий сервис всегда к вашим услугам!
В самом конце предлагаем посмотреть видеоурок на тему “Законы Ньютона”.
Дано определение силы в механике. Описаны факторы, определяющие действие на тело силы: направление, точка приложения и численное значение. Сформулированы второй и третий Законы Ньютона. Дано понятие равнодействующей силы.
 Сила в механике
Сила в механике
Определение силы
Твердые тела могут вступать во взаимодействие, в результате которого изменяется характер их движения. Мерой этого взаимодействия является физическая величина, которую называют силой.
Сила – векторная величина, количественная мера механического взаимодействия физических тел, приводящего к изменению их скорости или к их деформациям.
Действие силы на тело определяется тремя факторами:
- направлением;
- точкой приложения;
- численным значением.
Это означает, что сила является векторной величиной (вектором).
Обозначение силы
На схемах вектор силы обозначается отрезком, на конце которого ставится стрелка. Начало отрезка указывает точку приложения силы, а стрелка указывает направление действия силы. Длина отрезка в выбранном масштабе соответствует численному значению силы (рис.1).
В тексте чаще всего сила обозначается латинской буквой F со стрелкой или чертой над ней. Чтобы различать силы, их обозначают посредством нижнего индекса, который ставится после буквы F. Например: Fтяж — сила тяжести; Fупр — сила упругости; Fтр — сила трения; Fм — сила тяги мышц. Иногда за конкретным видом силы стандартно закрепляется определенная буква латинского алфавита, например буква Р (со стрелкой сверху) обозначает вес тела.
Точка приложения силы
При расчетах очень важно знать точку приложения силы. В прикладной механике такие силы называют сосредоточенными. Например, точкой приложения силы тяжести является центр масс (центр тяжести) тела. Также, зная направление и точку приложения силы, можно определить линию действия силы.
Прямая, вдоль которой направлена сила, проходящая через точку ее приложения называется линией действия силы.
Численное значение силы
Численное значение силы (модуль) измеряется в Ньютонах (Н).
С точки зрения механики, все силы возникают при взаимодействии двух или более тел, и у каждой силы есть противодействующая ей сила. Об этом говорит третий закон Ньютона.
Третий закон Ньютона
«Силы, с которыми действуют два тела друг на друга, равны по численному значению и противоположны по направлению. При этом одна сила приложена к одному телу, другая – к другому».
Третий закон Ньютона записывается в следующем виде: F1= — F2.
Второй закон Ньютона (основной закон динамики)
«Ускорения, которые силы сообщают телам, прямо пропорциональны величинам этих сил и обратно пропорциональны массам тел и направлены в сторону действия сил».
Это позволяет определить численное значение силы, если известна масса тела и его ускорение по формуле: F=m*a.
Равнодействующая сила
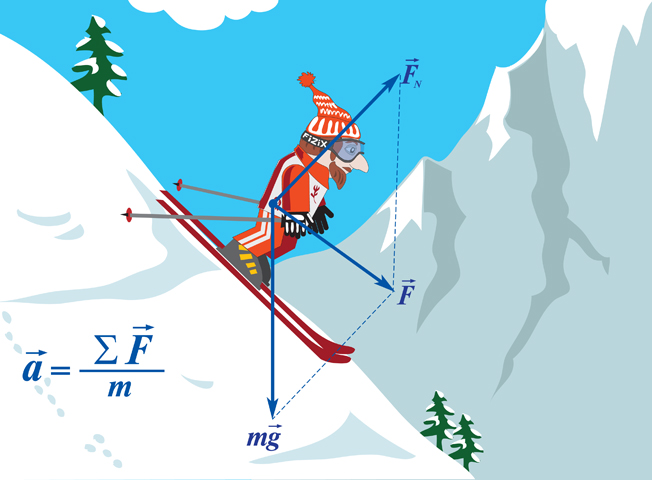
Если на тело действует несколько сил, приложенных к одной точке, можно найти равнодействующую (результирующую) силу, действие которой на тело эквивалентно воздействию на тела нескольких сил.
Равнодействующая сила – это сила, которая производит на тело такое же действие, как несколько одновременно действующих сил.
Так как сила – это векторная величина, к ней можно применять правила операции над векторами, например, сложение. Чтобы найти равнодействующую силу, необходимо сложить два или несколько векторов (рис.2).
Для анализа силовых упражнений, необходимо познакомится с некоторыми видами сил:
- силой тяжести,
- весом тела,
- силой реакции опоры,
- силой упругости,
- силой тяги мышц.
С уважением, А.В. Самсонова
Похожие записи:
Биомеханика рывка и толчка в тяжелой атлетике
Приведена рецензия на книгу докт. пед. наук, профессора А.А. Шалманова «Биомеханика движения штанги в рывке и толчке у…
Мышечно-сухожильный комплекс
Приведена рецензия на книгу В.Т.Тураева и В.В. Тюпа «Мышечно-сухожильный комплекс: анатомия, биомеханика, спортивная практика» зав. кафедрой биомеханики НГУ…
Сила тяжести
Дано определение силы тяжести. Показано, что сила тяжести является частным случаем силы гравитации. Описаны факторы, определяющие силу тяжести:…
Типы телосложения (соматотип) по Башкирову
Описана краткая биография П.Н. Башкирова и его научные труды. Дается классификация типов телосложения человека: долихоморфного (астенического), мезоморфного…
Типы телосложения (конституции) по Э. Кречмеру
Описана биография Эрнста Кречмера – немецкого психиатра и психолога, разработавшего типологию тела человека. Дано описание типов телосложения…
Типы конституции женщин по И.Б. Галанту
Описана биография известного советского психиатра И.Б.Галанта, предложившего естественную систему конституциональных типов женщин. Дана характеристика предложенных И.Б.Галантом конституциональных…









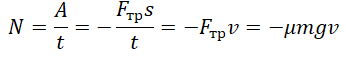
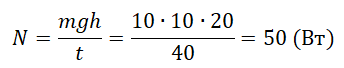


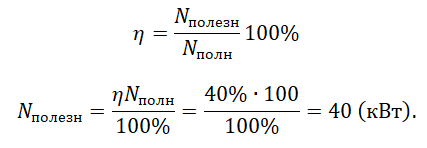
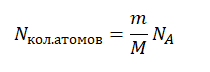
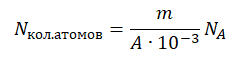
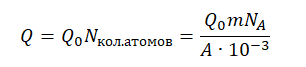
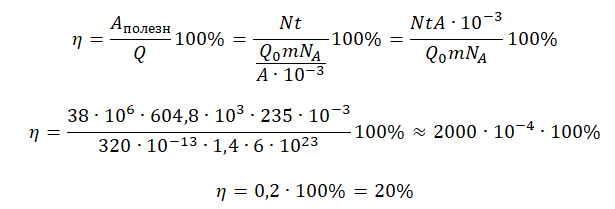


 ладно, возьмем 5
ладно, возьмем 5 


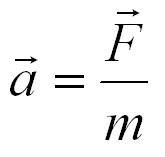
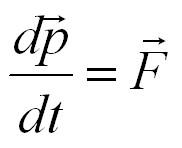
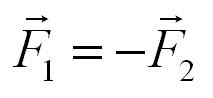

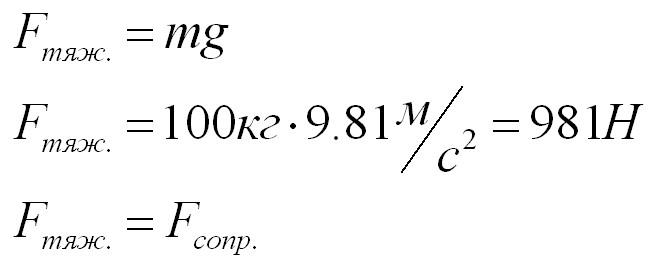
 Сила в механике
Сила в механике

