На прошлых уроках мы познакомились с определением механического движения, узнали, каким бывает движение, изучили его свойства и характеристики. Теперь нам известны формулы для расчета скорости при равномерном движении ($upsilon = frac{S}{t}$) и средней скорости при неравномерном ($upsilon_{ср} = frac{S}{t}$).
На данном уроке мы посмотрим на эти формулы с другой стороны — научимся использовать их для расчета пути и времени движения, а также рассмотрим графики скорости и пути для равномерного движения.
Формулы для расчета пути и времени движения при равномерном движении тела
Скорость тела при равномерном движении вычисляется по формуле $upsilon = frac{S}{t}$. Отсюда, если мы знаем скорость и время, то можем найти пройденный путь:
$S = upsilon t$.
Чтобы определить путь, пройденный телом при равномерном движении, нужно скорость тела умножить на время его движения.
Выразим время:
$t = frac{S}{upsilon}$.
Чтобы рассчитать время при равномерном движении, нужно путь, пройденный телом, разделить на скорость его движения.
Формулы для расчета пути и времени движения при неравномерном движении тела
При неравномерном движении мы используем определение средней скорости, которую можем найти по формуле:
$upsilon_{ср} = frac{S}{t}$.
Чтобы определить путь при неравномерном движении, нужно среднюю скорость движения умножить на время:
$large S = upsilon_{ср} t$.
Также мы можем рассчитать время, разделив путь, пройденный телом, на среднюю скорость его движения:
$t = frac{s}{upsilon_{ср}}$.
График скорости равномерного движения
Так как скорость – это векторная величина, она характеризуется и модулем, и направлением. В зависимости от выбранного направления скорость по знаку может быть как положительной, так и отрицательной.
На рисунке 1 изображен динозавр, автомобиль и дом. Зададим ось координат $x$.
Если динозавр начнет двигаться к дому, то его скорость будет положительной, так как направление движения совпадает с направлением оси $x$. Если же динозавр направится к автомобилю, то его скорость будет отрицательной, так как направление движения противоположно направлению оси $x$.
Итак, график скорости равномерного движения имеет вид, представленный на рисунке 2.
Из графика видно, что скорости с течением времени не изменяется – они постоянны в любой выбранный момент времени. Если мы посмотрим на график положительной скорости, то увидим, что $upsilon = 6 frac{м}{с}$, на график отрицательной — $upsilon = -4 frac{м}{с}$.
Зная скорость и время, мы можем рассчитать пройденный путь за определенный промежуток времени. Рассчитаем какой путь пройдет тело с положительной скоростью за $4 space с$.
$S = upsilon t = 6 frac{м}{с} cdot space 4 c = 24 space м$.
График пути равномерного движения
Пример графика зависимости пути равномерного движения представлен на рисунке 3.
Здесь $S$ — ось пройденных путей, $t$ — ось времени. По этому графику мы можем найти путь, пройденный телом за определенный промежуток времени. Например, за 1 с тело проходит путь длиной 2 м, за 2 с – 4 м, за 3 с – 6 м.
Зная путь и время, мы можем рассчитать скорость. Для удобства расчета возьмем самый первый отрезок пути: $t = 1 space с$, $S = 2 space м$. Тогда,
$upsilon = frac{S}{t} = frac{2 space м}{1 space с} = 2 frac{м}{с}$.
Задачи
Задача №1
Самым быстрым животным на Земле считается гепард. Он способен развивать скорость до $120 frac{км}{ч}$, но сохранять ее способен в течение короткого промежутка времени. Если за несколько секунд он не настигнет добычу, то, вероятнее всего, уже не сможет ее догнать. Найдите путь, который пробежит гепард на максимальной скорости за $3$ секунды.
Переведем единицы измерения скорость в СИ и решим задачу.
$120 frac{км}{ч} = 120 cdot frac{1000 space м}{3600 space с} approx 33 frac{м}{с}$.
Дано:
$upsilon = 120 frac{км}{ч}$
$t = 3 space c$
СИ:
$upsilon = 33 frac{м}{с}$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Гепард двигается равномерно в течение 3 с.
Путь, который он проходит за это время:
$S = upsilon t$,
$S = 33 frac{м}{с} cdot 3 с approx 100 space м$
Ответ: $S = 100 space м$.
Задача №2
Колибри – самые маленькие птицы на нашей планете. При полете они совершают около 4000 взмахов в минуту. Тем не менее, они способны пролетать очень большие расстояния. Например, некоторые виды данной птицы перелетают Мексиканский залив длиной $900 км$ со средней скоростью $40 frac{км}{ч}$. Сколько времени у них занимает такой полет?
Переведем единицы измерения скорость в СИ и решим задачу.
$40 frac{км}{ч} = 40 cdot frac{1000 м}{3600 с} approx 11 frac{м}{с}$,
$900 space км = 900 space 000 м$.
Дано:
$upsilon_{ср} = 40 frac{км}{ч}$
$S = 900 space км$
CИ:
$upsilon_{ср} = 11 frac{м}{с}$
$S = 900 space 000 space м$
$t-?$
Показать решение и ответ
Скрыть
Решение:
Полет колибри будет примером неравномерного движения. Зная среднюю скорость и путь, рассчитаем время перелета:
$t = frac{s}{upsilon_{ср}}$,
$t = frac{900 space 000 space м}{11 frac{м}{с}} approx 82 space 000 space с$.
Переведем время в часы:
$1 space ч = 60 space мин = 60 cdot 60 space c = 3600 space c$.
Тогда:
$t = frac{82 space 000 space c}{3600 space c} approx 23 space ч$.
Ответ: $t = 23 space ч$.
Больше задач на расчет пути и времени движения с подробными решениями смотрите в отдельном уроке.
Упражнения
Упражнение №1
Пользуясь таблицей 1 из прошлого урока, найдите скорости страуса, автомобиля, искусственного спутника Земли. Определите пути, пройденные ими за $5 space с$.
Дано:
$upsilon_1 = 22 frac{м}{с}$
$upsilon_2 = 20 frac{м}{с}$
$upsilon_3 = 8000 frac{м}{с}$
$t = 5 space с$
$S_1 — ?$
$S_2 — ?$
$S_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Путь, пройденный страусом:
$S_1 = upsilon_1 t$,
$S_1 = 22 frac{м}{с} cdot 5 space с = 110 space м$.
Путь, пройденный автомобилем:
$S_2 = upsilon_2 t$,
$S_2 = 20 frac{м}{с} cdot 5 space с = 100 space м$.
Путь, пройденный искусственным спутником Земли:
$S_3 = upsilon_3 t$,
$S_3 = 8000 frac{м}{с} cdot 5 space с = 40 space 000 space м = 40 space км$.
Ответ: $S_1 = 110 space м$, $S_2 = 100 space м$, $S_3 = 40 space км$.
Упражнение №2
На велосипеде можно без особого напряжения ехать со скоростью $3 frac{м}{с}$. На какое расстояние можно уехать за $1.5 space ч$?
Дано:
$t = 1.5 space ч$
$upsilon = 3 frac{м}{с}$
СИ:
$t = 5400 space с$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем путь, который можно проехать на велосипеде с указанной скоростью:
$S = upsilon t$,
$S = 3 frac{м}{с} cdot 5400 space с = 16 space 200 space м = 16.2 space км$.
Ответ: $S = 16.2 space км$.
Упражнение №3
На рисунке 4 показан график зависимости пути равномерного движения тела от времени ($S$ — ось пройденного пути, $t$ — ось времени). По этому графику найдите, чему равен путь, пройденный телом за $2 space ч$. Затем рассчитайте скорость тела.
Определим из графика путь, пройденный телом за $2 space ч$. Этому времени на графике соответствует значение пути, равное $200 space км$. Запишем условие задачи и решим ее.
Дано:
$S = 200 space км$
$t = 2 space ч$
$upsilon — ?$
Показать решение и ответ
Скрыть
Решение:
Скорость равномерного движения рассчитываем по формуле:
$upsilon = frac{S}{t}$.
$upsilon = frac{200 space км}{2 space ч} = 100 frac{км}{ч}$.
Ответ: $upsilon = 100 frac{км}{ч}$.
Упражнение №4
График зависимости скорости равномерного движения тела от времени представлен на рисунке 5. По этому графику определите скорость движения тела. Рассчитайте путь, который пройдет тело за $2 space ч$, $4 space ч$.
Из графика видно, что скорость тела равна $8 frac{м}{с}$. Этот график представляет собой прямую, параллельную оси времени, потому что движение равномерное, и скорость тела не изменяется с течением времени. Запишем условие задачи и решим ее.
Дано:
$t_1 = 2 space ч$
$t_2 = 4 space ч$
$upsilon = 8 frac{м}{с}$
СИ:
$t_1 = 7200 space с$
$t_2 = 14 space 400 space с$
$S_1 — ?$
$S_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Путь рассчитаем по формуле: $S = upsilon t$.
За $2 space ч$ тело пройдет путь:
$S_1 = upsilon t_1$,
$S_1 = 8 frac{м}{с} cdot 7200 space с = 57 space 600 space м = 57.6 space км$.
За $4 space ч$ тело пройдет путь:
$S_2 = upsilon t_2$,
$S_2 = 8 frac{м}{с} cdot 14 space 400 space с = 115 space 200 space м = 115.2 space км$.
Ответ: $S_1 = 57.6 space км$, $S_2 = 115.2 space км$.
Упражнения №5
По графикам зависимости путей от времени (рисунок 6) двух тел, движущихся равномерно, определите скорости этих тел. Скорость какого тела больше?
Для того, чтобы рассчитать скорость тела, нам нужно знать путь и время, за которое этот путь был пройден. Возьмем эти значения для двух тел из их графиков. Первое тело (I) проходит путь, равный $4 space м$, за $2 space с$. Второе тело (II) проходит путь, равный $4 space м$, за $4 space с$. Запишем условие задачи и решим ее.
Дано:
$S = 4 space м$
$t_1 = 2 space с$
$t_2 = 4 space с$
$upsilon_1 — ?$
$upsilon_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем скорость первого тела:
$upsilon_1 = frac{S}{t_1}$,
$upsilon_1 = frac{4 space м}{2 space с} = 2 frac{м}{с}$.
Рассчитаем скорость второго тела:
$upsilon_2 = frac{S}{t_2}$,
$upsilon_2 = frac{4 space м}{4 space с} = 1 frac{м}{с}$.
Получается, что скорость первого тела больше скорости второго.
Ответ: $upsilon_1 = 2 frac{м}{с}$, $upsilon_2 = 1 frac{м}{с}$, $upsilon_1 > upsilon_2$.
«Формула времени. Решение задач»
Скорость, время и расстояние — физические величины, взаимосвязаны процессом движения. Виды движений: 1) равномерное (прямолинейное, криволинейное и по окружности), 2) равноускоренное (с постоянным ускорением), 3) гармоническое. Для каждого вида движения своя формула времени.
Время обозначается как t. Единица измерения времени – с (секунды).
Самая простая формула при равномерном прямолинейном движении. Время, необходимое для прохождения пути равняется частному от деления пути на скорость равномерного прямолинейного движения: t = S / v.
При равноускоренном движении время равняется частному от деления разницы конечной и начальной скорости на ускорение: t = (v — v0) / a или частному от деления пути на разность конечной и начальной скорости: t = S / (v — v0).
Решение задач через формулу времени
Задача № 1.
Конькобежец может развивать скорость до 13 м/с. За какое время он пробежит дистанцию длиной 2,6 км?
Ответ: 200 с.
Задача № 2.
Двигаясь с ускорением 5 м/с2 скорость космической ракеты увеличилась на 100 м/с. За какое время произошло такое изменение скорости?
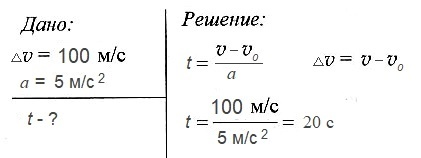Ответ: 20 с.
Задача № 3.
Пункты А и В находятся на берегу реки на некотором расстоянии друг от друга. Моторная лодка проходит расстояние АВ вниз по течению реки за время t1 = 3 ч, а плот то же расстояние – за время t0 =12 ч. Какое время t2 затратит моторная лодка на обратный путь?
Решение. Обозначим расстояние между пунктами А и В через L, скорость моторной лодки относительно воды через vл , а скорость течения через vт. Тогда t0 = L / vт , t1 = L / (vл + vт) , t2 = L / (vл — vт) . Исключая из записанной системы уравнений L, vл и vт
находим 
Ответ: 6 ч.
Конспект урока «Формула времени. Решение задач».
Следующая тема: «».
Содержание материала
- Формула времени. Решение задач
- Видео
- Формулы для расчета пути и времени движения при неравномерном движении тела
- Скорость
- График пути равномерного движения
- Единицы измерения времени
- Первые часы
- Как люди измеряли время?
- Способы вычисления расстояния и времени
Формула времени. Решение задач
Скорость, время и расстояние — физические величины, взаимосвязаны процессом движения. Виды движений: 1) равномерное (прямолинейное, криволинейное и по окружности), 2) равноускоренное (с постоянным ускорением), 3) гармоническое. Для каждого вида движения своя формула времени.
Время обозначается как t. Единица измерения времени – с (секунды).
Самая простая формула при равномерном прямолинейном движении. Время, необходимое для прохождения пути равняется частному от деления пути на скорость равномерного прямолинейного движения: t = S / v.
При равноускоренном движении время равняется частному от деления разницы конечной и начальной скорости на ускорение: t = (v — v) / a или частному от деления пути на разность конечной и начальной скорости: t = S / (v — v).
Видео
Формулы для расчета пути и времени движения при неравномерном движении тела
При неравномерном движении мы используем определение средней скорости, которую можем найти по формуле
$$upsilon_{ср} = frac{S}{t}$$
Чтобы определить путь при неравномерном движении, нужно среднюю скорость движения умножить на время:
$$large S = upsilon_{ср} t$$
Также мы можем рассчитать время, разделив путь, пройденный телом, на среднюю скорость его движения:
$$t = frac{s}{upsilon_{ср}}$$
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.
Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.
Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.
Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
График пути равномерного движения
Пример графика зависимости пути равномерного движения представлен на рисунке 3.
Здесь $S$ — ось пройденных путей, $t$ — ось времени. По этому графику мы можем найти путь, пройденный телом за определенный промежуток времени. Например, за 1 с тело проходит путь длиной 2 м, за 2 с – 4 м, за 3 с – 6 м.
Зная путь и время, мы можем рассчитать скорость. Для удобства расчета возьмем самый первый отрезок пути: $t = 1 с, s = 2 м$. Тогда,
$upsilon = frac{s}{t} = frac{2 м}{1 с} = 2 frac{м}{с}$.
Единицы измерения времени
Основной единицей измерения момента силы в системах СИ и СГС является: [t]=c
Единицы измерения времени основываются на периоде вращения Земли около своей оси и вокруг Солнца, Луни вокруг Земли. Внесистемные единицы измерения времени: час, минута, сутки и т.д.
Первые часы
Сначала было достаточно палочки, на которой каменным топором можно делать зарубки и тем самым отсчитывать прошедшие дни. Но это скорее был календарь, а не часы.
Первые и самые древние часы – солнечные. Их действие основано на изменении длины тени предметов по мере того, как солнце движется по небосводу. Такие часы представляли собой гномон – длинный шест, воткнутый в землю. Солнечные часы применялись в Древнем Египте и Китае. О них было доподлинно известно уже в 1200 году до нашей эры.
Затем появились водяные, песочные и огненные часы. Работа этих механизмов не была привязана к движению небесных светил. Долгое время водяные часы были главным инструментом для измерения времени.
Первые механические часы были изготовлены китайскими мастерами в 725 году нашей эры. Однако широкое распространение они получили относительно недавно.
В средневековой Европе механические часы устанавливались в башнях соборов и имели только одну стрелку – часовую. Карманные часы появились только в 1675 году (изобретение запатентовал Гюйгенс), а наручные – намного позже.
Как люди измеряли время?
Для измерения времени нужны какие-либо повторяющиеся с одинаковым периодом события. Например, смена дня и ночи. Солнце каждый день встает на востоке и садится на западе, а Луна каждый синодический месяц проходит весь цикл фаз освещенности солнцем — от тоненького серпа полумесяца до полнолуния.
Древним людям ничего не оставалось, как привязать отсчет времени к движению небесных тел и событиям, связанным с ним. А именно – к смене дней, ночей и сезонов года.
В году 4 сезона и 12 месяцев. Именно столько раз за весну, лето, осень и зиму Луна меняет свои фазы.
По мере развития прогресса методы измерения времени совершенствовались, появились солнечные, водяные, песочные, огненные, механические, электронные и, наконец, молекулярные часы.
Способы вычисления расстояния и времени
Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:
S=v*t, где v — понятно что такое,
S — расстояние, которое требуется найти,
t — время, за которое объект прошел это расстояние.
Таким образом вычисляется значение расстояния.
Или вычисляем значение времени, за которое пройдено расстояние:
t=S/v, где v — все та же скорость,
S — расстояние, пройденный путь,
t — время, значение которого в данном случае нужно найти.
Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.
Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.
И это еще не предел!
Теги
Формулы скорости, времени, расстояния?
Как выразить эти понятия друг одно через другие?
Анонимный вопрос
2 ноября 2018 · 236,8 K
Если вам известна скорость v и время t, то вы сможете найти расстояние S по формуле S=vt.
Обратите внимание на единицы измерения! Если вам дана скорость в километрах в час, то и время должно быть выражено в часах (или в метрах в секунду и секундах соответственно).
Выразить скорость из этой формулы можно следующим образом: v=S/t
А если вы хотите посчитать время, то воспользуйтесь формулой t=S/v
204,0 K
Комментировать ответ…Комментировать…
V = S : t
t = S : V
S = V * t
S = расстояние
V = скорость
t = время
: = деление
* = умножение
Пример :
Решил найти расстояние ( S)
Для этого скорость ( V) которая равна 4км/ч *время ( t) 4 часа
Ответ : 16 км Читать далее
21,2 K
Подскажите а как посчитать, за если я прохожу допустим растояние 9 метров за 7 минут, то за сколько я пройду 300 метров?
Комментировать ответ…Комментировать…
Учусь в гимназии №17. Увлекаюсь математикой, русским языком, родным языком, литературой и… · 20 мая 2021
(Обратите внимание, что для записи формулы пути используются строчные буквы s, v и t. Это сделано, чтобы не путать их с обозначением площади — S и объёма — V.) Читать далее
20,0 K
Комментировать ответ…Комментировать…
Чтобы найти скорость, нужно расстояние разделить на время движения: v = S: t. Время – это продолжительность каких-то действий, событий. Время движения обозначается маленькой латинской буквой t. Чтобы найти время, нужно расстояние разделить на скорость движения: t = S: v. Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
5,7 K
Комментировать ответ…Комментировать…
Короче!
Если у вас расстояние нужно найти то:
S=t*v, S=50*20(пример)
Если нужно найти время то:
t=S:V
Если нужно найти скорость то :
V=S:T.
Это все формулы. Читать далее
59,9 K
спасибо, Warrior! Было не понятно, но
ты помог мне выровнять математику!
Комментировать ответ…Комментировать…
Расчёт
пути и времени движения
«Движение
– это жизнь»
Аристотель
В
данной теме будем применять приобретённые знания о механическом движении на
практике. Прежде чем начать решать задачи, вспомним, необходимые определения. Путь
– это физическая величина, равная длине траектории, по которой двигалось тело,
в течение данного промежутка времени. Путь является скалярной величиной,
то есть, не имеет направления. Скорость при равномерном движении – это
величина, равная отношению пройденного пути к промежутку времени, за который
этот путь пройден.
Скорость
является векторной величиной, то есть, характеризуется как числовым значением,
так и направлением.
Средняя
скорость при неравномерном движении – это величина, равная отношению всего
пройденного пути к общему времени в пути.
Задача
1.
Какой путь пройдет автомобиль, двигаясь равномерно со скоростью 75 км/ч за 20 минут?
В
первую очередь, необходимо научиться правильно оформлять задачи по физике.
При решении любой задачи нужно писать «дано». То есть, в левой части
листа необходимо записать слово «дано», после которого ставится двоеточие, а
дальше в столбик перечисляете все исходные данные, которые указаны в условии
задачи. В нашем случае – это скорость и время в пути. После этого, нужно
очеркнуть данные и ниже (уже под линией) записать, что необходимо найти.
В задаче спрашивается, какой путь пройдет автомобиль. Дальше приступаем
непосредственно к решению задачи.
А
теперь обратите внимание вот на что: скорость в условии задачи дана в км/ч, то есть,
сколько километров автомобиль проходит за час. А время в условии дано в
минутах. Поэтому, прежде чем делать вычисления, необходимо перевести минут в
часы.
В
общем и целом, этот способ правильный. Но, чтобы не запутаться с единицами
измерения, можно (и даже нужно) переводить данные в систему СИ сразу после
того, как записано «дано». Напомним, что для перевода км/ч в м/с или м/с в
км/ч необходимо
1 м/с = 3,6 км/ч
1 км/ч = 1/3,6 м/с
Время
в системе СИ измеряется в секундах. В одной минуте шестьдесят секунд, поэтому,
чтобы перевести минуты в секунды, нужно минуты умножить на 60. После того, как
перевели все данные в систему СИ, необходимо очеркнуть и эту колонку, а правее
пишитсяе само решение. Решение и ответ будут одинаковыми. Однако рекомендуется
переводить данные в систему СИ.
Задача
2.
Мотоциклист проехал 5 км вдвое быстрее, чем следующие 7 км. Найдите его среднюю скорость, если общее время в пути составило 10 минут.
Получившееся
выражение, в котором остались, только те величины, которые были даны
изначально, называется расчетной формулой. Только в расчетную формулу необходимо
подставлять числовые значения, а до этого, все делается в буквенном виде.
Задача
3.
Самолет взлетел, после чего пролетел 120 км на определенной высоте, а потом приземлился. Известно, что пути, пройденные в процессе взлета и посадки равны 120 км каждый. Во время взлета и посадки, скорость самолета была равна 200 м/с, а во время остального
пути – 250 м/с. Какое время самолет затратил на весь путь? Какова средняя
скорость?
Сразу
хочется обратить ваше внимание на распространенную ошибку. Среднюю
скорость нельзя находить как среднее арифметическое разных скоростей на разных
участках движения. В этом можно убедиться с помощью простых расчетов:
если подсчитать среднюю скорость, как среднее арифметическое скоростей, то
получим 216,7 м/с. Этот результат неправильный. Теперь подсчитаем среднюю
скорость как отношение всего пройденного пути к общему времени в пути. В
результате получим 214,3 м/с. Получается вроде небольшая разница. В
результате неверных расчётов за каждую секунду, пройденное расстояние
увеличивается на 2,4 м/с. Поэтому, при неверном расчете за час пройденное
расстоянии будет больше на 8,6 км, а это существенно.
Задача
4.
Средняя скорость движения велосипедиста равна 8 м/с. Известно, что первую часть
своего пути велосипедист проехал за 3 минуты. За какое время велосипедист
проехал вторую часть, если общий путь составил 2 км?
Задача
5.
Определите по графику скорость равномерного движения тела.
Здесь,
конечно, никаких данных, кроме самого графика нет, поэтому, «дано» писать не
нужно. В таких заданиях, в первую очередь нужно посмотреть на оси графика:
какие величины они обозначают и в каких единицах измеряются. Вертикальная ось –
обозначает пройденный путь в метрах, а горизонтальная ось – время в минутах.
Значит, это график зависимости пройденного пути от времени. При равномерном
движении скорость постоянна, значит, можно путь, пройденный за определенный
промежуток времени, разделить на это время и, таким образом, найти скорость.
Для наибольшей точности желательно найти точку, на графике, наиболее близкую к
пересечению клеточек. Когда нашли такую точку, смотрим на соответствующие
координаты, то есть, на значения пути и времени. Для этого из точки опускаем
перпендикуляры на обе оси. Теперь, когда получили значение координат, можно определить скорость.
Основные
выводы:
В
качестве итогов урока, рассмотрим общий алгоритм решения задач на движение.
