Как найти время если задача вдогонку

Задача № 1.

Расстояние между домами Оли и Вали 160 м. Они вышли в школу одновременно. Валя шла со скоростью 100 м/мин, а Оля шла вдогонку Вале со скоростью 120 м/мин. Через сколько минут Оля догонит Валю?

Решение:

1) 120- 100 = 20 (м/мин)- скорость сближения девочек

160 : 20 = 8 (мин)- нужно Оле, чтобы догнать Валю.

Ответ: 8 минут.

Задача № 2.

За какое время мотоцикл догонит грузовой автомобиль, если расстояние между ними 45 км, а скорость мотоцикла больше скорости грузовика на 15 км/ч?

Решение: 

45 : 15 = 3 (ч)

Ответ: через 3 часа.

Задача № 3.

Из лагеря геологоразведчиков выехал вездеход со скоростью 30 км/ч. Через 2 ч вслед за ним был послан другой вездеход. С какой скоростью он должен ехать, чтобы догнать первый через 4 ч после своего выхода?

Решение:

1) 2 + 4 = 6 (ч) – был в пути 1 вездеход

2) 6 * 30 = 180 (км) – проехал 1 вездеход

3) 180 : 4=45 (км/ч) – скорость I I вездехода

Ответ: 45 км/ч.

Задача № 4.

1) 170 – 20 = 150 (км) –  на столько увеличилось расстояние между автомобилем и мотоциклом за 5 часов.

2) 150:5 = 30 (км/ч) – скорость удаления автомобиля от мотоцикла.

3) 70 – 30 = 40 (км/ч) – скорость мотоцикла.

Ответ: 40 км/ч.

Задача № 5.

Расстояние между двумя станциями 40 км. Из этих станций одновременно в одном направлении вышли скорый и товарный поезд, причем товарный поезд шел впереди. Через сколько часов скорый поезд догонит товарный, если его скорость равна 80 км/ч, а скорость товарного поезда 60 км/ч?

Решение:

1) 80 – 60 = 20 (км/ч) – скорость сближения поездов.

2) 40:20 = 2 (ч) – через такое время скорый поезд догонит товарный.

Ответ: через 2 часа.

Здесь можно пройти Тест по этой теме.

Задачи в которых двигаются вдогонку из разных пунктов решаются по определенному правилу. Два объекта могут сближаться или удаляться в зависимости от их скоростей.

• Если скорость объекта, который впереди больше, то они удаляются. 

• Если скорость объекта, который впереди меньше, то они сближаются

Движение является способом существования всего, что человек видит вокруг себя. Поэтому задачи на перемещение разных объектов в пространстве являются типичными проблемами, которые предлагается разрешить школьникам. В данной статье подробно рассмотрим движение вдогонку и формулы, которые необходимо знать, чтобы уметь решать задачи такого типа.

Что такое движение?

Перед тем, как переходить к рассмотрению формул движения вдогонку, необходимо разобраться с этим понятием подробнее.

Под движением подразумевают изменение пространственных координат объекта за определенный промежуток времени. Например, автомобиль, который движется по дороге, самолет, который летит в небесах, или кошка, бегущая по траве, – все это примеры движения.

Важно отметить, что рассматриваемый движущийся объект (автомобиль, самолет, кошка) считают безмерным, то есть его размеры не имеют совершенно никакого значения для решения проблемы, поэтому ими пренебрегают. Это своего рода математическая идеализация, или модель. Для подобного объекта существует название: материальная точка.

Движение вдогонку и его особенности

Теперь перейдем к рассмотрению популярных школьных задач на движение вдогонку и формул для него. Под этим видом движения понимают перемещение двух или более объектов в одном направлении, которые отправляются в свой путь из разных пунктов (материальные точки имеют разные начальные координаты) или/и в разное время, но из одного и того же пункта. То есть создается ситуация, при которой одна материальная точка пытается догнать другую (другие), поэтому эти задачи получили такое название.

Согласно определению, особенностями движения вдогонку являются следующие:

• Наличие двух и более движущихся объектов. Если двигаться будет только одна материальная точка, то ей “некого” будет догонять.
• Прямолинейное перемещение в одном направлении. То есть объекты осуществляют движение вдоль одной и той же траектории и в одном направлении. Движение навстречу друг другу не входит в число рассматриваемых задач.
• Пункт отправления играет важную роль. Идея заключается в том, чтобы в момент начала движения объекты были разделены в пространстве. Такое разделение будет иметь место, если они стартуют в одинаковое время, но из разных пунктов или же из одного пункта, но в разное время. Старт двух материальных точек из одного пункта и в одинаковое время к задачам вдогонку не относится, поскольку в этом случае один объект будет постоянно удаляться от другого.

Формулы движения вдогонку

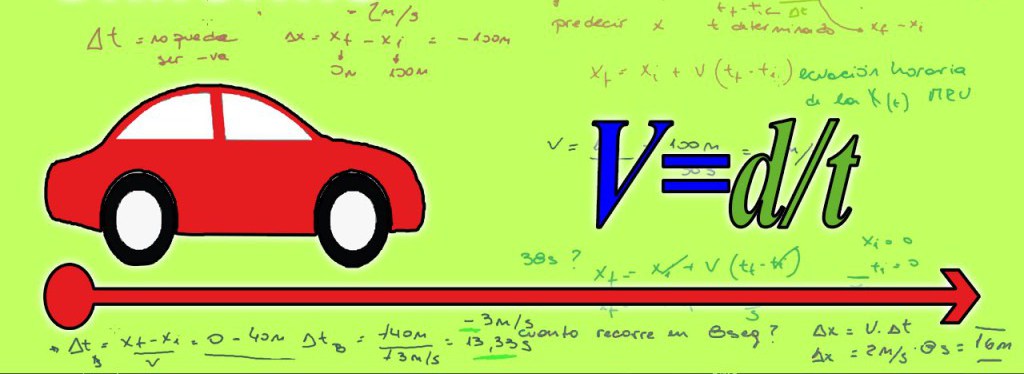
В 4 классе общеобразовательной школы обычно рассматриваются подобные задачи. Это означает, что формулы, которые необходимы для решения, должны быть максимально простыми. Такому случаю удовлетворяет равномерное прямолинейное движение, в котором фигурируют три физических величины: скорость, пройденный путь и время движения:

• Скорость – величина, показывающая расстояние, которое проходит тело за единицу времени, то есть она характеризует быстроту изменения координат материальной точки. Обозначается скорость латинской буквой V и измеряется, как правило, в метрах в секунду (м/с) или в километрах в час (км/ч).
• Путь – это расстояние, которое проходит тело за время своего движения. Он обозначается буквой S (D) и выражается обычно в метрах или километрах.
• Время – период движения материальной точки, который обозначается буквой T и приводится в секундах, минутах или часах.

Описав основные величины, приведем формулы движения вдогонку:

• s = v*t;
• v = s/t;
• t = s/v.

Решение любой задачи рассматриваемого типа базируется на применении этих трех выражений, которые необходимо запомнить каждому школьнику.

Пример решения задачи №1

Приведем пример задачи движения вдогонку и решения (формулы, необходимые для него, приведены выше). Проблема формулируется следующим образом: “Грузовик и легковой автомобиль одновременно выезжают из пунктов A и B со скоростями 60 км/ч и 80 км/ч соответственно. Оба транспортных средства движутся в одном направлении так, что автомобиль приближается к пункту A, а грузовик удаляется от обоих пунктов. Через какое время автомобиль догонит грузовик, если расстояние между A и B составляет 40 км?”.

Перед тем как решать задачу, необходимо научить ребят определять суть проблемы. В данном случае она заключается в неизвестном времени, которое проведут оба транспортных средства в пути. Предположим, что это время равно t часам. То есть через время t автомобиль догонит грузовик. Найдем это время.

Рассчитаем расстояние, которое пройдет каждый из движущихся объектов за время t, имеем: s₁ = v₁*t и s₂ = v₂*t, здесь s₁, v₁ = 60 км/ч и s₂, v₂ = 80 км/ч – пройденные пути и скорости движения грузовика и автомобиля до того момента, когда второй догонит первого. Поскольку расстояние между пунктами A и B равно 40 км, то автомобиль, догнав грузовик, пройдет путь на 40 км больше, то есть s₂ – s₁ = 40. Подставляя в последнее выражение формулы для путей s₁ и s₂, получим: v₂*t – v₁*t = 40 или 80*t – 60*t = 40, откуда t = 40/20 = 2 ч.

Отметим, что данный ответ можно получить, если использовать понятие скорости сближения между движущимися объектами. В задаче она равна 20 км/ч (80-60). То есть при этом подходе возникает ситуация, когда один объект движется (автомобиль), а второй относительно него стоит на месте (грузовик). Поэтому достаточно поделить расстояние между пунктами A и B на скорость сближения, чтобы решить задачу.

Пример решения задачи №2

Приведем еще один пример задач на движение вдогонку (формулы для решения используются те же): “Из одного пункта выезжает велосипедист, а через 3 часа в ту же сторону выезжает автомобиль. Через какое время после начала своего движения автомобиль догонит велосипедиста, если известно, что он движется в 4 раза быстрее?”.

Решать эту задачу следует так же, как и предыдущую, то есть необходимо определить, какой путь пройдет каждый участник движения до момента, когда один догонит другого. Предположим, что автомобиль догнал велосипедиста через время t, тогда получаем следующие пройденные пути: s₁ = v₁*(t+3) и s₂ = v₂*t, здесь s₁, v₁ и s₂, v₂ – пути и скорости велосипедиста и автомобиля соответственно. Заметим, что до того, как автомобиль догнал велосипедиста, последний находился в пути t + 3 часа, так как он выехал на 3 часа раньше.

Зная, что оба участника отправились из одного пункта, и пройденные ими пути будут равны, получаем: s₂ = s₁ или v₁*(t+3) = v₂*t. Скорости v₁ и v₂ нам не известны, однако в условии задачи сказано, что v₂ = 4*v₁. Подставляя это выражение в формулу для равенства путей, получим: v₁*(t+3) = 4*v₁*t или t+3 = 4*t. Решая последнее, приходим к ответу: t = 3/3 = 1 ч.

Некоторые советы

Формулы движения вдогонку являются простыми, тем не менее школьников в 4 классе важно научить мыслить логически, понимать значение величин, с которыми они имеют дело, и осознавать проблему, которая перед ними стоит. Ребят рекомендуется призывать к рассуждениям вслух, а также к командной работе. Кроме того, для наглядности задач можно использовать компьютер и проектор. Все это способствует развитию у них абстрактного мышления, коммуникативных навыков, а также математических способностей.

Рассмотрим задачи на движение вдогонку, в которых объекты движутся в одном направлении, но выезжают из разных пунктов, находящихся на некотором расстоянии друг от друга.

При движении вдогонку объекты могут как сближаться, так и удаляться.

Если скорость объекта, который идет впереди, меньше скорости идущего вслед за ним объекта, то второй догоняет первого и они сближаются.

Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:

   

   

Если скорость идущего впереди объекта больше скорости объекта, который движется следом, то второй не сможет  догнать первого и они удаляются друг от друга.

Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:

   

   

Скорость, время и расстояние связаны между собой формулой пути:

   

Задача 1.

Расстояние между двумя пунктами 20 км. Из этих пунктов в одном направлении одновременно выехали автомобиль и мотоциклист, причем автомобиль двигался впереди. Через 5 часов расстояние между ними стало 170 км. Найти скорость мотоциклиста, если скорость автомобиля 70 км/ч.

Решение:

	v, км/ч	t, ч	s, км
Автомобиль	70	5	?
Мотоциклист	?	5	?

1) 170-20=150 (км) на столько увеличилось расстояние между автомобилем и мотоциклистом за 5 часов

2) 150:5=30 (км/ч) скорость удаления автомобиля от мотоциклиста

3) 70-30=40 (км/ч) скорость мотоциклиста.

Ответ: 40 км/ч.

Задача 2.

Расстояние между двумя станциями 40 км. Из этих станций одновременно в одном направлении вышли скорый и товарный поезда, причем товарный поезд едет впереди. Через сколько часов скорый поезд догонит товарный, если его скорость равна 80 км/ч, а скорость товарного поезда — 60 км/ч?

Решение:

	v, км/ч	t, ч	s, км
Пассажирский	80	?	? на 40 км больше
Товарный	60	?	?

1) 80-60=20 (км/ч) скорость сближения поездов

2) 40:20=2 (ч) через такое время скорый поезд догонит товарный.

Ответ: через 2 ч.

Задача 3.

Расстояние между пунктами равно 50 км. Из этих пунктов одновременно в одном направлении выезжают велосипедист и мотоциклист, причем велосипедист едет впереди. Скорость велосипедиста равна 13 км/ч, скорость мотоциклиста — 38 км/ч. На каком расстоянии от пункта своего выезда мотоциклист догонит велосипедиста?

Решение:

	v, км/ч	t, ч	s, км
Мотоциклист	38	?	? на 50 км больше
Велосипедист	13	?	?

1) 38-13=25 (км/ч) скорость сближения мотоциклиста и велосипедиста

2) 50:25=2 (ч) через столько часов после своего выезда мотоциклист догонит велосипедиста

3) 38∙2=76 (км) на таком расстоянии от пункта своего выезда мотоциклист догонит велосипедиста.

Ответ: 76 км.

Тема
нашего урока задачи на движение в одном направлении «вдогонку»

Эту
тему подсказал мой знакомый, с которым недавно произошла вот такая история,
когда он собирался в путешествие.

–
Господин шкипер, здравствуйте!

Не
поможете ли Вы мне? Дело в том, что я хотел отправиться в путешествие. Первую
часть пути мы должны проплыть на паруснике, а потом пересесть на поезд и уехать
в город Владивосток. Но я опоздал, и парусник отплыл без меня. Я созвонился с
капитаном парусника. Он сказал, что ждать меня они уже не могли, и отплыли без
меня. Сейчас они остановились в небольшом посёлке в 48 км отсюда. Но
скоро отправляются дальше. Помогите, пожалуйста, догнать парусник как можно
скорее. Ведь если я через 5 часов не догоню их, то опоздаю и на поезд. И
тогда – конец моему путешествию.

–
Ну что же, мы постараюсь Вам помочь, но для этого необходимо уточнить некоторые
детали.

Вы
сказали, что парусник находится в 48 км отсюда? А теперь узнайте у капитана
парусника, с какой скоростью он движется?

–
Да, я узнал – его скорость равна 6 км/ч.

–
Так, хорошо. Скорость моего катера – 18 км/ч. Надо узнать,
сколько времени понадобится катеру, чтобы догнать парусник. Для того, чтобы
разобраться в ситуации, надо просто подумать… Давайте выполним рисунок.

Итак,
вот река. Вот здесь находимся мы, а вот, на расстоянии 48 км
отсюда находится парусник. Скорость парусника 6 км/ч, скорость
моего катера – 18 км/ч. Надо узнать, через сколько часов мы сможем
догнать катер.

–
Пожалуйста, давайте скорее поплывём, ведь парусник уже отплывает. А по пути и
решим эту задачу.

–
Ну что же, в путь.

–
Итак, мы отплыли одновременно с парусником. Мы сейчас посчитаем, сколько
времени нам понадобиться, чтобы доплыть до посёлка. Расстояние
до посёлка 48 км разделим на скорость нашего катера – 18 км/ч.

48 : 18 =

–
Да, но ведь парусник за это время далеко отплывёт от посёлка. Такой способ
решения нам не подходит. Попробую нарисовать рисунок.

Так,
вот река, вот место, откуда мы отплыли, а вот посёлок, откуда уже одновременно
с нами отплыл парусник. Вот направление и скорость парусника и
нашего катера.

Через
час
парусник проплывёт ещё 6 км, ведь его скорость 6 км/ч, а мы – 18 км (наша
скорость 18 км/ч). Замечательно, расстояние между нами сократится. Пройдёт
ещё час. Парусник отдаляется ещё на 6 км, но мы все равно становимся к нему
ещё ближе. Я понял!!! За каждый час мы будем приближаться к паруснику на
одинаковое количество километров. Ага, это наша скорость сближения.
Сейчас я её узнаю. Мы догоняем парусник со скоростью18 км/ч, но за это время он
уплывает на 6 км/ч.

Значит,
скорость сближения меньше нашей скорости на 6 км/ч. Мы от 18 – 6, получается 12
км/ч.

1)
18 – 6 = 12 (км/ч)

Это
наша скорость сближения при движении вдогонку. Именно на столько
за каждый час будет сокращаться расстояние между катером и парусником.
Та-а-а-к. Я знаю, что расстояние между катером и парусником было 48 км,
и теперь узнал, что скорость нашего сближения – 12 км/ч. Сейчас я
найду время, за которое катер догонит парусник. Чтобы найти время, надо
расстояние разделить на скорость.

2)
48 : 12 = 4 (ч).

Ура!
Я успею на поезд!

А
вы знаете, мне так понравилось решать задачи на движение вдогонку. И теперь я
не буду так переживать – ведь я знаю, что вовремя доплыву до пункта отправления
поезда. Вы знаете, мне захотелось ещё решать такие задачи. Сейчас со своего
телефона я зайду в интернет и попытаюсь найти ещё одну. Ага, вот и нашёл. Вот
моя задача.

Пассажирский поезд отправился
во Владивосток. Когда от станции отправления он отошёл на расстояние 342 км, от
того же вокзала в том же направлении вышел скорый поезд. С какой скоростью шёл
скорый поезд, если скорость пассажирского 50 км/ч, и скорый догнал его через 9
часов?

Да, нелёгкая задача.
Но, как говорится, «просто надо подумать». И, конечно, изобразить всё на
рисунке.

В задаче известно, что первоначально
расстояние между поездами было 342 км, и скорый поезд догнал
пассажирский за 9 ч, т. е. через 9 ч оно стало равно 0. У нас есть расстояние,
и время, за которое это расстояние было сокращено до 0, т.е.
поезда сблизились. Значит, мы можем найти скорость сближения
поездов по формуле.

1) 342 : 9 = 38 (км/ч).

Это – скорость
сближения поездов. А что такое «скорость сближения» при движении в
одном направлении? Это разница между скоростями движущихся объектов.
А, проще говоря, на сколько одна скорость больше другой. Скорый поезд,
конечно, двигался быстрее пассажирского. И теперь мы знаем, на сколько быстрее
– на 38 км/ч. Значит, мы можем узнать скорость скорого поезда. Мы
к скорости пассажирского поезда прибавляем скорость сближения поездов.

2) 50 + 38 = 88 (км/ч).

Да неплохая скорость
для поезда! Скоро я тоже поеду на таком. А пока могу решить ещё одну задачу.
Вот, например, такую.

Из города А выехал
мотоциклист, а из города Б одновременно с ним выехал велосипедист. Скорость
мотоциклиста 80 км/ч, а скорость велосипедиста – 12 км/ч. Через 3 ч мотоциклист
догнал велосипедиста. На каком расстоянии друг от друга находятся города А и Б?

Конечно, делаю рисунок.

Дорога, города А и Б, направление
движения и скорость.

За один час мотоциклист
проедет 80 км, а велосипедист – 12 км. При этом они сближаются. Вспомним, что при
движении в одном направлении вдогонку скорость сближения равна разности
скоростей.

Находим её.

1) 80 – 12 = 68 (км/ч)
– скорость сближения.

Нам известна скорость
сближения и время, за которое мотоциклист догнал велосипедиста, т.е.
преодолел то расстояние, которое было между ними первоначально. Вспоминаем формулу
решения задач на движение.

Чтобы найти расстояние,
мы скорость умножаем на время. Выполняем действие:

2) 68 · 3 = 204(км).
Вот мы и узнали расстояние между городами. Ответ. Расстояние между городами 204
км.

Вот как здорово! Пока я
решал задачи, мы догнали парусник и теперь я вместе со всеми отправлюсь в город
Владивосток. Спасибо шкиперу за то, что он помог мне догнать моих друзей. А ещё
я сегодня понял, что если два объекта движутся из разных точек в одном
направлении вдогонку, то скорость сближения – это разность двух скоростей.