В море часто требуется получить время какого-либо астрономического явления, главным образом захода и восхода Солнца и кульминации Солнца и Луны. В общем случае для любого светила эта задача решается путем определения из параллактического треугольника часового угла этого светила в заданном его положении. Для кульминаций эта общая задача упрощается, так как для верхней кульминации tM=0°, а для нижней tм=180°, откуда время кульминации любого светила можно рассчитать с любой точностью (например, до 1c). Практически высокой точности не требуется, достаточно 1м, поэтому в МАЕ для Солнца, планет и Луны приводится предвычисленное местное среднее время кульминации их на меридиане Гринвича.
Определение времени кульминации Луны, Солнца и планет (до 1м). Для Солнца и Луны предвычисленное Тм на Гринвиче, обозначенное Тк, приводится на правой странице внизу для верхней (в) и нижней (н) кульминаций. Для планет приводится только время верхней кульминации на среднюю дату листа
— внизу левой страницы (см. рис. 53).
Это местное время на меридиане Гринвича (Тк) относится только к меридиану с долготой λ=0°. Для наблюдателя с долготой λм следует получить свое Tм, которое отличается от Тк, так как за время поворота Земли (сферы) на величину λм светило, имеющее собственное движение, переместится в другую точку сферы. На рис.54 в положении 1 Луна кульминирует на меридиане Гринвича (Тк), собственное движение Луны (прямое) показано стрелкой. Если наблюдатель М расположен в западной долготе λW, то за время поворота сферы на угол Е0Е, Луна переместится из 1′ в положение 2 и кульминация ее наступит позже на угол ∆Tλ, на который должна дополнительно повернуться сфера, поэтому
Для наблюдателя в восточной долготе кульминация, наоборот, наступит раньше (по местному времени), чем на Гринвиче, т.е.
145

|
TM=TK–∆Tλ |
(112) |
|||
|
В МАЕ величина и знак поправки ∆Tλ определяются по формуле |
||||
|
∆Тλ = |
m∆ |
λ |
(113) |
|
|
360о |
||||
где ∆ — разность Тк с предыдущими сутками, если долгота восточная, и с последующими сутками, если долгота западная. Обычно при восточной долготе знак « — », при западной «+».
Примечание. У планет собственное движение бывает обратным, тогда знаки — противоположные.
По формуле (ИЗ) в МАЕ составлена таблица (приложение 1,Б), в которую входят с разностью ∆, вычисленной по ежедневным таблицам — от данных суток к предыдущим при λOst и наоборот при λw (для планет разности получаются трехсуточные и их надо делить на 3), и долготой места. Для Солнца разности ∆ не превышают 1м, поэтому поправкой ∆Tλ обычно пренебрегают и принимают Тк=Тк,
Пример 29. 5 мая 1977 г. в λс=141°27’Ost (№=—10) определить Тс верхней кульминации Луны и Солнца.
Решение. Из МАЕ на стр. 109 внизу выбираем (см. рис. 53):
146

Для Луны разность ∆ образована от 1Ч28М на 5/V к 0Ч26М на 4/V, а так как время уменьшилось, то знак «—».
Лунные сутки, т.е. промежуток между двумя кульминациями, продолжительнее средних приблизительно на 50м, поэтому в некоторые дни кульминации Луны на Гринвиче не происходит (в МАЕ эти случаи отмечены прочерком). Например, если 2/V 1977 г. Тк=23Ч27С, то, прибавив «лунные тки» 24Ч50М, получим следующую кульминацию Луны 0417M4/V (точнее, 0Ч26М), а 3/V кульминации не будет. В подобных случаях следует брать последующую кульминацию (при восточной долготе) и интерполировать «через дату» с предыдущей кульминацией (при λw — наоборот).
Пример 30. 3 мая 1977 г. в λс=157°20’W (№=10W). Определить Т0
верхней кульминации Луны. Решение.
147

Может оказаться, что и по судовому времени на эту дату кульминации нет, тогда берется ближайшая кульминация.
Определение времени кульминации звезд, планет, Луны и Солнца «через часовой угол» (до 1с). Эта задача — частный случай общей задачи определения времени по часовому углу. При верхней кульминации tМ=0о(360о), а при нижней
– 180о, переводя его в и входя в МАЕ обратным входом, получаем Тгр и затем Тс (см. пример 31).
Пример 31. 6 мая 1977 г. в λ=102о30’Ost (№=8 Ost) определить Тс верхней кульминации звезды α Гидры.
Решение.
§34. ОБОСНОВАНИЕ РАСЧЕТА ВРЕМЕНИ ВИДИМОГО ВОСХОДА (ЗАХОДА) СОЛНЦА И ЛУНЫ И ВРЕМЕНИ СУМЕРЕК
При движении Солнца по суточной параллели аа1 (рис. 55) утром его центр сначала приходит на h=—12° — этот момент называется началом навигационных сумерек (СО, затем на h=—6° — начало гражданских сумерек (С’1), затем его край появляется на видимом горизонте (положение С2) — это видимый восход Солнца. При h=0 (положение С3) имеем истинный восход Солнца.
Сумерками называется явление постепенного убывания освещенности
148
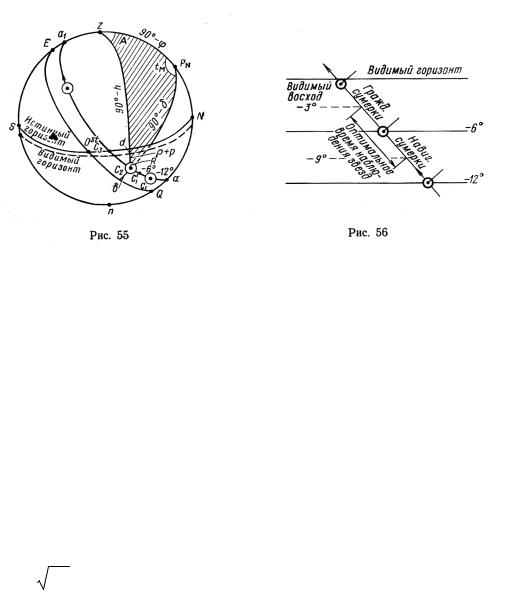
при заходе Солнца или возрастания ее при восходе. В мореходной астрономии сумерки условно разделены на гражданские и навигационные.
Гражданскими сумерками называется промежуток времени от захода Солнца до снижения его центра на —6° (утром — наоборот), освещенность при этом падает от 700 до 1 лк; видны предметы в море и горизонт, можно читать, появляются яркие звезды (рис. 56).
Навигационными сумерками называется промежуток времени от h =–6° до h =–12°. В это время предметы уже не видны, но горизонт еще виден, видны все навигационные звезды. Полная темнота наступает после конца астрономических сумерек (h=—18°), но в навигации они значения не имеют.
Примечание. Наилучшее время для наблюдений звезд, как экспериментов, не навигационные сумерки, а промежуток h =–9°, т.е. между средними моментами этих сумерек. Однако в МАЕ никак не отражен и его приходится рассчитывать.
выяснилось из от h =–3° до этот промежуток
Основания расчета tм и Тс восхода (захода) Солнца и сумерек. В
момент видимого восхода центр Солнца находится ниже истинного горизонта
|
(С2 на рис.55) , и его высота может быть подсчитана по формуле |
|
|
h=–d–р+р–R |
(114) |
где d — наклонение видимого горизонта, зависящее от возвышения еМ
глаза (d=l,76 еМ );
р — астрономическая рефракция, приподнимающая изображение Солнца;
149
р — параллакс Солнца;
R — видимый угловой радиус Солнца.
Эти величины можно выбрать в табл. 11-а и 8 МТ—75. Принимая е=0, т.е. с уровня моря, р=—34,3′; R =–16,0′ из указанных таблиц, получим h =–50,3′.
Из параллактического треугольника zРNС2 (см. рис. 55) по данным φ, δ, и полученной h имеем:
sin h=sinφ sinδ+cosφ cos δ cos tM,
|
откуда |
|||||||||
|
costM |
= sinh−sinϕsinδ |
||||||||
|
cosϕcosδ |
|||||||||
|
или, заменяя cos t на |
более выгодную функцию |
sin2 |
t |
, т.е. |
|||||
|
2 |
|||||||||
|
cost =1 − 2sin |
2 t |
после преобразования получим |
|||||||
|
2 |
|||||||||
|
sin2 |
tM |
= 0,5secϕsecδ[cos(ϕ −δ) −sinh] |
(115) |
||||||
|
2 |
По формуле (115) последовательно, принимая h=—50,3′; h=—6° и h=— 12°, получаем часовые углы и затем время захода, конца гражданских и навигационных сумерек и аналогично для восхода.
Расчет tM и времени восхода, захода Луны. При подсчете высоты Луны в момент видимого восхода ее края применяется та же формула (114), но при значениях величин рe=+57′ и Re=—15,5′;
рe=—34,3′ — 15,5’+57’=7,2′.
С этим значением высоты по формуле (115) рассчитаны tM, а затем и время восхода (захода) Луны, помещенное в МАЕ.
150
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Что такое кульминация звёзд
Как оказалось, не все знают, что такое кульминация звёзд. По определению, кульминация означает наиболее высокий момент чего-либо. Собственно говоря, в астрономии под этим подразумевают наивысший момент движения космического объекта.
Итак, кульминация звезды — это момент её прохождения сквозь небесный меридиан во время суточного движения светила.
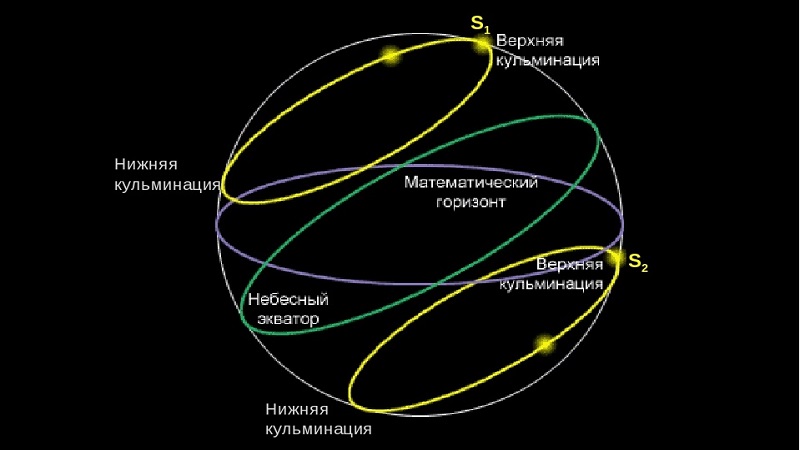
Стоит напомнить, что небесный меридиан является кругом сферы неба, который проходить сквозь зенит, полюс мира, а также южный полюс мира и надир.
Полюс мира представляет собой, можно сказать, отправную точку. Она лежит на небесной сфере, и как раз вокруг неё происходит видимое суточное движение звёзд. Причем перемещаются они по кругу параллельно экватору.
На Земле, как и в космосе — всегда есть на что посмотреть. Например сериалы Нетфликс, которые не оставят вас равнодушными.
Какая бывает кульминация звезд
Любое светило в течение суток пересекает меридиан неба в двух точках. Другими словами, вот этот момент и называется кульминацией.
Период между описываемым пересечением звёздных тел составляет половину суток, то есть 12 часов.
Так как кульминация звёзд происходит два раза за сутки, то она бывает двух видов:
- верхняя, когда высота светила достигает максимального значения;
- нижняя, наоборот, наступает в то время, когда высота звезды минимальна.
Как рассчитывается кульминация звёзд
Поскольку высота полюса мира над горизонтом равна географической широте местности, то определить значения момента пересечений звёздного тела и небесного меридиана не так уж сложно.
В действительности, верхняя и нижняя кульминация звезды рассчитывается по формуле:

где h — высота, ф — географическая широта и δ — склонение.
Получается, что если известно склонение и высота звезды в момент кульминации, то можно рассчитать географическую широту местности, откуда проводятся наблюдения.
Что интересно, незаходящая звезда для определённой географической широты наблюдается и в верхней, и в нижней кульминации. А вот если светило находится далеко от небесного экватора в сторону юга, то его пересечение с меридианом может быть незаметно.

Для понимания, как и когда происходит кульминация звёзд можно обратиться к нашему главному светилу. Правда, самый простой пример, это Солнце. Оно, как и другие звёзды, два раза в сутки пересекает небесный меридиан. И все мы хорошо знаем это время. Во-первых, верхняя солнечная кульминация-это полдень. Во-вторых, спустя половину суток (12 часов), наступает полночь или нижняя кульминация.
Как видно, люди долгое время наблюдали за движением небесных тел. Они выделили определённые особенности и научились применять их в своей жизни. В целом, само наблюдение за загадочными и светящимися звёздными точками, небесной сферой и космосом безумно увлекательное и красивое зрелище.
Оценка статьи:
![]() Загрузка…
Загрузка…
Кульминация (астрономия) – момент прохождения светила через небесный меридиан в процессе его суточного движения. Иначе: моменты прохождения светилом точек пересечения суточной параллели светила и небесного меридиана.
Различают верхнюю и нижнюю кульминации. В момент верхней кульминации светило поднимается на максимальную высоту над горизонтом. В момент нижней кульминации светило опускается на минимальную высоту, в некоторых случаях может оказаться под горизонтом.
Также различают верхнюю кульминацию к северу и к югу от зенита. Если светило кульминирует к югу от зенита, то, в момент кульминации, его астрономический азимут равен 0°, а если светило кульминирует к северу от зенита, то его азимут в момент кульминации равен 180°.
Зная склонение светила δ и широту места наблюдения φ можно вычислить зенитные расстояния этого светила в моменты кульминаций:
zн = 180º – (φ + δ);
zв; ю. з = φ – δ;
zв; c.з = δ – φ.
Наборот, наблюдая какую-либо звезду в верхней и нижней кульминации можно определить её склонение и широту места наблюдения. Если верхняя кульминация звезды происходит к югу от зенита, то
δ = 90° – (zн+zв; ю. з) /2;
φ = 90° – (zн-zв; ю. з) /2;
а если к северу от зенита, то
δ = 90° – (zн-zв; ю. з) /2;
φ = 90° – (zн+zв; ю. з) /2.
В этой статье мы будем решать задачи, связанные со временем в астрономии. Научимся определять звездное время, часовые углы. Увидим, что в разных местах одновременно время – разное.
Напомню основные положения прошлой статьи:
Звездное время измеряется часовым углом
точки весеннего равноденствия и поэтому всегда
. У небесного светила с прямым восхождением
часовой угол
Звездное время в пункте с географической долготой
связано со звездным гринвичским временем
равенством
причем отсчитывается к востоку от Гринвича и выражается в часах, минутах и секундах времени. Для перевода градусных единиц в единицы времени существуют таблицы, можно воспользоваться примером расчета выше.
В один и тот же физический момент звездное время и
в двух пунктах различается на разность географической долготы
и
этих пунктов, т. е.
Используемые в практической жизни средние солнечные сутки продолжительнее звездных суток приблизительно на Зм56с.
Местное среднее время
где — уравнение времени, a
—истинное солнечное время, измеряемое часовым углом Солнца, увеличенным на 12ч, т. е.
Местное среднее время и
двух пунктов связано между собой равенством:
а со средним гринвичским временем (называемым всемирным временем) – равенством
В практической жизни используется либо поясное время
либо декретное время
где — номер часового пояса, равный целому числу часов.
Для двух пунктов, расположенных в разных часовых поясах n1 и n2,
Если система счета времени не указана, то всегда подразумевается время, действующее на данной территории.
Задача 1.
Определить звездное время в моменты верхней и нижней кульминации звезды Фомальгаута ( Южной Рыбы), прямое восхождение которой 22 ч 54 м 53 с.
В момент верхней кульминации всегда , поэтому
22 ч 54 м 53 с.
В нижней кульминации всегда 12 ч, поэтому
22 ч 54 м 53 c +12 ч=34 ч 54 м 53 с- 24 ч=10 ч 54 м 53 с.
Ответ: в верхней кульминации 22 ч 54 м 53 с, в нижней
10 ч 54 м 53 с.
Задача 2.
Найти звездное время в моменты, в которые часовой угол звезды Ригеля ( Ориона) соответственно равен (-3 ч 17 м 43 с) и 1 ч 42 м 29 с. Прямое восхождение этой звезды 5 ч 12 м 08 с.
-3 ч 17 м 43 с+ 5 ч 12 м 08 с=1 ч 54 м 25 с
1 ч 42 м 29 с+ 5 ч 12 м 08 с=6 ч 54 м 37 с
Ответ: 1 ч 54 м 25 с,
6 ч 54 м 37 с
Задача 3.
Определить звездное время в пунктах с географической долготой 2 ч 13 м 23 с и в момент, когда в пункте с долготой 4 ч 37 м 11 с звезда Кастор (
Близнецов) находится в верхней кульминации. Прямое восхождение Кастора 7 ч 31 м 25 с.
Когда звезда в верхней кульминации, ее часовой угол равен 0. Поэтому звездное время
7 ч 31 м 25 с.
Время в пункте с нулевой долготой может быть найдено так:
7 ч 31 м 25 с-4 ч 37 м 11 с =2 ч 54 м 14 с.
Теперь добавим к этому звездному времени долготы тех мест, которые нас интересуют:
2 ч 54 м 14 с+2 ч 13 м 23 с=5 ч 07 м 37 с
Переведем во время долготу второго места:
5ч 39 м 52 с, я для этого пользовалась таблицей.
Вычисляем звездное время в этом пункте:
2 ч 54 м 14 с+5ч 39 м 52 с =8ч 34 м 06 с.
Ответ: 5 ч 07 м 37 с,
8 ч 34 м 06 с.
Задача 4.
Решить предыдущую задачу для тех же пунктов, но для момента времени, в который звезда Капелла ( Возничего) находится в нижней кульминации в Иркутске (
6 ч 57 м 05 с). Прямое восхождение Капеллы 5 ч 13 м 00 с.
В нижней кульминации часовой угол звезды 12 ч. Поэтому
12+5ч 13 м 00с=17 ч 13 м 00 с.
Так как Иркутск восточнее Гринвича, то
17 ч 13 м 00 с -6 ч 57 м 05 с =10 ч 15 м 55 с.
Теперь добавим к этому звездному времени долготы тех мест, которые нас интересуют:
10 ч 15 м 55 с +2 ч 13 м 23 с=12 ч 29 м 18 с
Переведем во время долготу второго места:
5ч 39 м 52 с, я для этого пользовалась таблицей.
Вычисляем звездное время в этом пункте:
10 ч 15 м 55 с +5ч 39 м 52 с =15ч 55 м 47 с.
Ответ: 12ч 29 м 18 с,
15 ч 55 м 47 с.
Задача 5.
Вычислить часовые углы звезд Алголя ( Персея) и Альтаира (
Орла) в 8 ч 20 м 30 с по звездному времени. Прямое восхождение этих звезд соответственно равно 3 ч 04 м 54 с и 19 ч 48 м 21 с. Часовые углы выразить в градусных единицах.
8 ч 20 м 30 с-3 ч 04 м 54 с=5 ч 15 м 36 с
8 ч 20 м 30 с-19 ч 48 м 21 с =-11 ч 27 м 51 с
Добавим 24 часа, чтобы часовой угол был положительным:
-11 ч 27 м 51 с +24 ч 00 м 00 с=12 ч 32 м 09 с.
Осталось перевести результаты в единицы времени:
5 ч 15 м 36 с=
12 ч 32 м 09 с=
Ответ: 5 ч 15 м 36 с,
,
12 ч 32 м 09 с,
.
Задача 6.
Прямое восхождение звезды Миры ( Кита) 2 ч 16 м 49 с, Сириуса (
Большого Пса) 6 ч 42 м 57 с и Проциона (
Малого Пса) 7 ч 36 м 41 с. Чему равны часовые углы этих звезд в моменты верхней и нижней кульминации Сириуса?
Для верхней кульминации Сириуса , для нижней –
12 ч. Звездное время для верхней кульминации
6 ч 42 м 57 с
Для нижней
18 ч 42 м 57 с
Определяем часовые углы звезд Миры
6 ч 42 м 57 с-2 ч 16 м 49 с=4 ч 26 м 08 с
18 ч 42 м 57 с -2 ч 16 м 49 с=16 ч 26 м 08 с
И Проциона:
6 ч 42 м 57 с-7 ч 36 м 41 с=-0 ч 53 м 44 с
18 ч 42 м 57 с -7 ч 36 м 41 с=11 ч 06 м 16 с
Ответ: в верхней кульминации Сириуса его часовой угол ч, у Миры
4ч 26 м 08 с, у Проциона
-0 ч 53 м 44 с, в нижней кульминации Сириуса его часовой угол 12 ч, у Миры
16 ч 26 м 08 с, у Проциона
11 ч 06 м 16 с.
Задача 7.
Найти часовые углы звезд Кастора ( Близнецов) и Шеата (
Пегаса) в момент, когда часовой угол звезды Беги (
Лиры) равен 4ч15м10с. Прямое восхождение Кастора 7 ч 31 м 25 с, Беги 18 ч 35 м 15 с и Шеата 23 ч 01 м 21 с.
Найдем звездное время по данным для Беги:
4 ч 15 м 10 с+18 ч 35 м 15 с=22 ч 50 м 25 с.
Теперь с легкостью рассчитываем часовые углы Кастора:
22 ч 50 м 25 с-7 ч 31 м 25 с=15ч 19 м 0 с
И Шеата:
22ч 50м 25 с-23 ч 01 м 21 с =-0ч 10 м 56 с
Или 23 ч 49 м 04 с.
Ответ: часовой угол Кастора 15ч 19 м 0 с, Шеата 23 ч 49 м 04 с.
Задача 8.
Часовой угол звезды Миры ( Кита) в Гринвиче равен 2ч16м47с. Определить в этот момент звездное время в пунктах с географической долготой 2ч 03 м 02 с и
. Прямое восхождение Миры 2 ч 16 м 49 с.
Переведем долготу второго места во временные единицы:
=3ч 20 м 00 с+16м+ 2 м 56 с+ 2 с=3 ч 38 м 58 с.
Звездное время в Гринвиче равно
2 ч 16 м 47 с+2 ч 16 м 49 с=4ч 33 м 36 с
Оба места расположены восточнее Гринвича, поэтому
4ч 33 м 36 с+2ч03м02с=6ч 36 м 38 с
4ч 33 м 36 с+3 ч 38 м 58 с =8ч 12 м 34 с
Ответ: 6ч 36 м 38 с,
8ч 12 м 34 с.
Задача 9.
Найти звездное время и часовой угол звезды Мицара ( Большой Медведицы) в Гринвиче и в пункте с географической долготой 6 ч 34 м 09 с в тот момент, когда в Якутске (
8 ч 38 м 58 с) часовой угол звезды Альдебарана (
Тельца)
. Прямое восхождение Мицара 13 ч 21 м 55 с, а Альдебарана 4 ч 33 м 03 с.
Переводим для начала часовой угол Альдебарана во временные единицы:
=20ч+1 ч 20 м+36 м+2м 56с =21ч 58м 56 с.
Звездное время в Якутске:
21 ч 58 м 56 с+4 ч 33 м 03 с=26 ч 31 м 59 с=2 ч 31 м 59 с.
Теперь, зная долготу Якутска, определяем звездное время в Гринвиче. Якутск восточнее Гринвича, поэтому
2 ч 31 м 59 с-8 ч 38 м 58 с=26 ч 31 м 59 с-8 ч 38 м 58 с=17 ч 53 м 01 с
Часовой угол Мицара в Гринвиче равен
17 ч 53 м 01 с-13 ч 21 м 55 с=4 ч 31 м 06 с
Теперь из Гринвича смещаемся в пункт с долготой 6ч34м09с:
17 ч 53 м 01 с+6 ч 34 м 09 с=24 ч 27 м 10 с=0 ч 27 м 10 с.
Часовой угол Мицара здесь равен
0 ч 27 м 10 с -13 ч 21 м 55 с=24 ч 27 м 10 с-13 ч 21 м 55 с=11 ч 05 м 15 с.
Ответ: звездное время в Гринвиче 17 ч 53 м 01 с, часовой угол Мицара
4 ч 31 м 06 с, звездное время в месте с долготой 6 ч 34 м 09 с:
0 ч 27 м 10 с, часовой угол Мицара здесь равен
11 ч 05 м 15 с.
Задача 10.
Какое прямое восхождение у звезд, находящихся в верхней и нижней кульминации в двух различных пунктах наблюдения, если в одном из них, расположенном восточнее другого на , часовой угол звезды Проциона (
Малого Пса) равен (-2 ч 16 м 41 с)? Прямое восхождение Проциона 7 ч 36 м 41 с.
Звездное время в первом пункте:
-2 ч 16 м 41 с+7 ч 36 м 41 с=5 ч 20 м 00 с
Если звезды в верхней кульминации, их часовые углы равны 0:
5ч 20м 00 с
А если в нижней, то 12 ч, тогда
5ч 20м 00 с-12ч=-6 ч 40 м 00с=17 ч 20 м 00 с
Теперь перебираемся во второй пункт, который по условию задачи западнее. Давайте установим, насколько: = 2 ч+24 м+2 м 48 с=2ч 26 м 48 с.
Звездное время в более западном пункте меньше на его долготу:
5 ч 20 м 00 с-2 ч 26 м 48 с=2 ч 53 м 12 с
Теперь вычислим прямое восхождение звезд в верхней кульминации:
2 ч 53 м 12 с
2 ч 53 м 12 с -12ч=-9 ч 06 м 48 с=14 ч 53 м 12 с
Ответ: в верхней кульминации в первом пункте 5 ч 20 м 00 с, в нижней –
17 ч 20 м 00 с, в верхней кульминации во втором пункте
2 ч 53 м 12 с , в нижней
14 ч 53 м 12 с.
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Для понимания звездного времени рассмотрим небесную сферу. На модели небесной сферы можно показать связь звездного времени с прямым восхождением (α) и часовым углом (t). Звездное время – это промежуток времени, между двумя последовательными одноименными кульминациями, точки весеннего равноденствия на одном и том же меридиане.S = α + t или S = tγ. . Часовой угол t – это дуга небесного экватора от ее верхней точки Q’ до круга склонения светила m по ходу часовой стрелки. Часовой угол изменяется от 0- 24 h(0 – 360 ͦ ). Прямое восхождение α – дуга небесного экватора от точки γ до круга склонения светила против хода часовой стрелки и изменяется от 0 до 24h(0 – 360 ͦ.). Другими словами, звездное время это и есть часовой угол точки весеннего равноденствия, то есть дуга небесного экватора от ее верхней точки Q’ до точки весеннего равноденствия по ходу часовой стрелки [1] ,[3],[4].
На небесной сфере, показано связь звездного времени с прямым восхождением (α) и часовым углом (t).
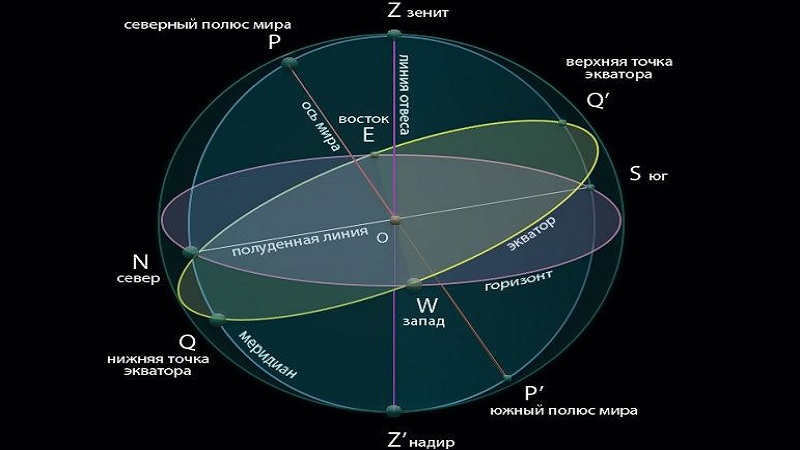
Рис. 1 – Небесная сфера
На небесной сфере отмечены следующие точки: Z –зенит, Z’ – надир, Z Z’ – отвесная линия, *M – небесный объект, NS – истинный горизонт, γ – точка весеннего равноденствия, t – часовой угол, α – прямое восхождение, S – звездное время.
Рассмотрим некоторые примеры решения задач с использованием звездного времени.
Задача 1.
Условие: Определить звездное время в городе Белгороде в момент известного звездного времени в городе Уфе Sу = 0h59m.
Дано: Sу = 0h59m, λу = 3h 43,8 m , λБ = 2 h 1,4 m
Решение
S1 – S2 = λ1 – λ2
SБ = Sу – λу + λБ
SБ = 0h 59 m
SБ= 0h 59 m – (3h 43,8 m – 2 h 1,4 m ) = 0h 59 m – 1h 42,4 m = 23 h 16,6 m
Таблица 1
|
Город |
λ |
|
|
Уфа |
3h 43,8 m |
0h 59 m |
|
Белгород |
2 h 1,4 m |
23 h 16,6 m |
Ответ: SБ = 23 h 16,6 m
Задача 2.
Условие: :Найти звездное время в моменты восхода и захода точек равноденствий, в моменты обеих кульминаций (4 основных точек эклиптики) и указать моменты принимаемой за начало звездных суток.
Решение:
В основе звездного времени лежат звездные сутки – промежуток времени между двумя последовательными верхними кульминациями точки весеннего равноденствия на одном и том же меридиане.
За начало звездных суток принят момент верхней кульминации точки весеннего равноденствия (S = 0h).
Точка верхней кульминации и точка нижней кульминации должны быть диаметрально противоположены, следовательно, если мы принимаем точки весеннего равноденствия верхней кульминации за 0h, то нижняя кульминация наступит через 12h.
Точки восхода и захода также диаметрально противоположны. За верхней кульминацией идет заход, то есть через 6h, а заход и восход также диаметрально противоположны, то есть наступит через 12h, 6h+ 12h= 18h.
Точка весеннего равноденствия и точка осеннего равноденствия на небесной сфере взаимно диаметрально противоположны. Это означает, что у них разница в верхней кульминации 12h, то есть, если в точке весеннего равноденствия в верхней кульминации 0h, то в точке осеннего равноденствия верхняя кульминация будет равна 0h+ 12h=12h . Нижняя кульминация равна 0h (из-за разницы в 12h). Затем по аналогии заполняем остальные колонки таблицы.
Точка летнего солнцестояния и точка зимнего солнцестояния, как и точки весеннего, осеннего равноденствия – взаимно диаметрально противоположны.
Поэтому, раз мы изначально за начало звездных суток приняли момент верхней кульминации точка весеннего равноденствия 0h, то по вертикали данного столбца разница должна быть в 6 h(0h , 6 h, 12h,18h). И по аналогии заполняем оставшиеся колонки таблицы соблюдая разницу во времени (6 h). Результат выполнения задания представлен в таблице.
Таблица 2
|
Точка |
Звездное время S в момент |
|||
|
восхода |
верхней кульминации |
захода |
нижней кульминации |
|
|
22.03 точка весеннего равноденствия |
18h |
0h |
6h |
12h |
|
22.06. точка летнего солнцестояния |
0h |
6h |
12h |
18h |
|
22.09. точка осеннего равноденствия |
6h |
12h |
18h |
0h |
|
22.12. точка зимнего солнцестояния |
12h |
18h |
0h |
6h |
Физический смысл звездного времени:
1. Для одного и того же физического момента уравнение времени на всех земных меридианах одинаково.
2. Звездное время в двух пунктах земной поверхности в один и тот же физический момент не совпадает, так как у городов различная долгота λ, а звездное время и долгота связаны соотношением: S1 – S2 = λ1 – λ2.
3. Часовые углы различных небесных светил в один и тот же момент времени в одном и том же пункте наблюдения будут различаться, так как светила имеют разное прямое восхождение α , а t и α связаны соотношением t = S – α.
Литература:
-
Кононович Э.В., Мороз В.И. Общий курс астрономии: Учебное пособие / под ред. В.В. Иванова. – М.: Едиториал УРСС, 2001;
-
Астрономический ежегодник на 2014 год. – СПб.: Наука, 2013;
-
Геодезическая астрономия применительно к решению инженерно-геодезических задач / И.С. Пандул. – СПб.: Политехника, 2010;
-
Труды ИПА РАН. Вып. 10. В.А. Брумберг, Н.И. Глебова, М.В. Лукашева, А.А. Малков, Е.В. Питьева, Л.И. Румянцева, М.Л. Свешников, М.А. Фурсенко. Расширенное объяснение к «Астрономическому ежегоднику». – СПб.: ИПА РАН, 2004.
