Как найти время нахождения в пути

А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

vср=(v1+v2+v3+…+vn)/n

где v1, v2, v3, vn – значения скоростей объекта на отдельных участках пути S,

n – количество этих участков,

vср – средняя скорость объекта на всем протяжении всего пути.

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

vср=(S1+S2+…+Sn)/t,

где vср – средняя скорость объекта на всем протяжении пути,

S1, S2, Sn – отдельные неравномерные участки всего пути,

t – общее время, за которое объект прошел все участки.

Можно записать использовать и такой вид вычислений:

vср=S/(t1+t2+…+tn),

где S – общее пройденное расстояние,

t1, t2, tn – время прохождения отдельных участков расстояния S.

Но можно записать эту же формулу и в более точном варианте:

vср=S1/t1+S2/t2+…+Sn/tn,

где S1/t1, S2/t2, Sn/tn – формулы вычисления скорости на каждом отдельном участке всего пути S.

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.

Математика

5 класс

Урок № 35

Задачи на движение

Перечень вопросов, рассматриваемых в теме:

1. Понятия скорости, времени, расстояния.
2. Формулы нахождения скорости, времени, расстояния.
3. Понятия скорости сближения, скорости удаления.

Глоссарий по теме

Расстояние – это длина от одного пункта до другого.

Большие расстояния, в основном, измеряются в метрах и километрах.

Расстояние обозначается латинской буквой S.

Чтобы найти расстояние, надо скорость умножить на время движения:

S = v ∙ t

Скорость – это расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.

Скорость обозначается латинской буквой v.

Чтобы найти скорость, нужно расстояние разделить на время движения:

v = S : t

Время – это продолжительность каких-то действий, событий.

Время движения обозначается маленькой латинской буквой t.

Чтобы найти время, нужно расстояние разделить на скорость движения:

t = S : v

Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.

Чтобы найти скорость сближения, нужно сложить скорости объектов.

Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.

Чтобы найти скорость удаления, нужно сложить скорости объектов.

Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.

Основная литература

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К., Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.

2. Потапов М. К., Шевкин А. В. Математика. Книга для учителя. 5 – 6 классы — М.: Просвещение, 2010

Дополнительная литература

1. Чесноков А. С., Нешков К. И. Дидактические материалы по математике 5 кл. – М.: Академика учебник, 2014

2. Бурмистрова Т. А. Математика. Сборник рабочих программ. 5–6 классы // Составитель Бурмистрова Т. А.

3. Потапов М. К. Математика: дидактические материалы. 6 кл. // Потапов М. К., Шевкин А. В. — М.: Просвещение, 2010

Теоретический материал для самостоятельного изучения

Очень часто нам встречаются задачи на нахождение скорости, времени и расстояния. Что же всё это такое? Сейчас нам предстоит в этом разобраться.

Расстояние – это длина от одного пункта до другого. (Например, расстояние от дома до школы 2 километра). В основном большие расстояния измеряются в метрах и километрах. Общепринятое обозначение расстояния – заглавная латинская буква S.

Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. Скорость обозначается маленькой латинской буквой v.

Рассмотрим задачу:

Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 200 метров. Первый школьник добежал за 50 секунд. Второй за 100 секунд. Кто из ребят бежал быстрее?

Решение:

Быстрее бежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. Чтобы найти скорость, нужно расстояние разделить на время движения.

Давайте найдём скорость первого школьника. Для этого разделим 200 метров на время движения первого школьника, то есть на 50 секунд:

200 м : 50 с = 4

Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч). 

У нас расстояние дано в метрах, а время в секундах. Значит, скорость измеряется в метрах в секунду:

200 м : 50 с = 4 (м/с)

Скорость движения первого школьника составляет 4 метра в секунду.

Теперь найдём скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника:

200 м : 100 c = 2 (м/с)

Скорость движения первого школьника – 4 (м/с).

Скорость движения второго школьника – 2 (м/с).

4 (м/с) > 2 (м/с)

Скорость первого школьника больше. Значит, он бежал до спортплощадки быстрее.

Иногда возникает ситуация, когда требуется узнать, за какое время тело преодолеет то или иное расстояние. Время движения обозначается маленькой латинской буквой t.

Рассмотрим задачу:

От дома до спортивной секции 1200 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 600 метров в минуту. За какое время мы доедем до спортивной секции?

Решение:

Если за одну минуту мы будем проезжать 600 метров, то сколько таких минут нам понадобится для преодоления тысячи двухсот метров? Очевидно, что надо разделить 1200 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 600 метров. Тогда мы получим время, за которое мы доедем до спортивной секции:

1200 : 600 = 2 (мин)

Ответ: мы доедем до спортивной секции за 2 минуты.

Скорость, время и расстояние связаны между собой.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:

S = v ∙ t

Рассмотрим задачу:

Мы вышли из дома и направились в магазин. Мы дошли до магазина за 15 минут. Наша скорость была 60 метров в минуту. Какое расстояние мы прошли?

Решение:

Если за одну минуту мы прошли 60 метров, то сколько таких отрезков по шестьдесят метров мы пройдём за 15 минут? Очевидно, что умножив 60 метров на 15 минут, мы определим расстояние от дома до магазина:

v = 60 (м/мин)

t = 15 (минут)

S = v ∙ t = 60 ∙ 15 = 900 (метров)

Ответ: мы прошли 900 метров.

Если известно время и расстояние, то можно найти скорость:

v = S : t

Рассмотрим задачу:

Расстояние от дома до школы 800 метров. Школьник дошёл до этой школы за 8 минут. Какова была его скорость?

Скорость движения школьника – это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 800 метров, то какое расстояние он преодолевал за одну минуту?

Чтобы ответить на этот вопрос, нужно разделить расстояние на время движения школьника:

S = 800 метров

t = 8 минут

v = S : t = 800 : 8 = 100 (м/мин)

Ответ: скорость школьника была 100 м/мин.

Если известна скорость и расстояние, то можно найти время:

t = S : v

Рассмотрим задачу:

От дома до спортивной секции 600 метров. Мы должны дойти до неё пешком. Наша скорость будет 120 метров в минуту (120 м/мин). За какое время мы дойдём до спортивной секции?

Если за одну минуту мы будем проходить 120 метров, то сколько таких минут со ста двадцатью метрами будет в шестистах метрах?

Чтобы ответить на этот вопрос, нужно 600 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 120. Тогда мы получим время, за которое мы дойдём до спортивной секции:

S = 600 метров

v = 120 (м/мин)

t = S : v = 600 : 120 = 5 (минут).

Ответ: мы дойдём до спортивной секции за 5 минут.

Итак, все рассмотренные нами формулы мы можем представить в виде треугольника для лучшего запоминания:

Теперь рассмотрим типы задач на движение.

Задачи на сближение.

Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.

Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причём скорость первого будет 100 метров в минуту, а второго – 105 метров в минуту, то скорость сближения будет составлять 100 плюс 105, то есть 205 метров в минуту. Значит, каждую минуту расстояние между пешеходами будет уменьшаться на 205 метров.

Чтобы найти скорость сближения, нужно сложить скорости объектов.

Задача.

Из двух пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.

Решение:

1. Найдём скорость сближения велосипедистов:

13 км/ч + 15 км/ч = 28 км/ч

1. Определим расстояние между населёнными пунктами. Для этого скорость сближения умножим на время движения:

28 ∙ 3 = 84 км

Ответ: расстояние между населёнными пунктами 84 км.

Задачи на скорость удаления.

Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.

Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причём скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4 плюс 6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиваться на 10 километров.

Чтобы найти скорость удаления, нужно сложить скорости объектов.

Рассмотрим задачу:

С причала одновременно в противоположных направлениях отправились теплоход и катер. Скорость теплохода составляла 60 км/ч, скорость катера 130 км/ч. Какое расстояние будет между ними через 2 часа?

Решение:

1. Определим скорость удаления. Для этого сложим их скорости:

60 + 130 = 190 км/ч.

Получили скорость удаления равную 190 км/ч. Данная скорость показывает, что за час расстояние между теплоходом и катером будет увеличиваться на 190 километров.

1. Чтобы узнать какое расстояние будет между ними через два часа, нужно 190 умножить на 2:

190 ∙ 2 = 380 км.

Ответ: через 2 часа расстояние между теплоходом и катером будет составлять 380 километров.

Задачи на движение объектов в одном направлении.

В предыдущих пунктах мы рассматривали задачи, в которых объекты (люди, машины, лодки) двигались либо навстречу друг другу, либо в противоположных направлениях. В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.

Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.

Рассмотрим задачу:

Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 130 км/ч, а скорость автобуса 90 км/ч. Какое расстояние будет между ними через 1 час? Через 3 часа?

Решение:

1. Найдём скорость удаления. Для этого из большей скорости вычтем меньшую:

130 км/ч − 90 км/ч = 40 км/ч

1. Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 3 часа в три раза больше:

40 ∙ 3 = 120 км

Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через три часа – 120 км.

Рассмотрим ситуацию, в которой объекты начали своё движение из разных пунктов, но в одном направлении.

Задача.

Пусть на одной улице имеется дом, школа и аттракцион. Дом находится на одном конце улицы, аттракцион на другом, школа между ними. От дома до школы 900 метров. Два пешехода отправились в аттракцион в одно и то же время. Причём первый пешеход отправился в аттракцион от дома со скоростью 90 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 85 метров в минуту. Какое расстояние будет между пешеходами через 3 минуты? Через сколько минут после начала движения первый пешеход догонит второго?

Решение:

1. Определим расстояние, пройденное первым пешеходом за 3 минуты. Он двигался со скоростью 90 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 270 метров:

90 ∙ 3 = 270 метров

1. Определим расстояние, пройденное вторым пешеходом за 3 минуты. Он двигался со скоростью 85 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 255 метров:

85 ∙ 3 = 255 метров

1. Теперь найдём расстояние между пешеходами. Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (900м) прибавить расстояние, пройденное вторым пешеходом (255м), и из полученного результата вычесть расстояние, пройденное первым пешеходом (270м):

900 + 255 = 1155 м

1155 – 270 = 885 м

Либо из расстояния от дома до школы (900 м) вычесть расстояние, пройденное первым пешеходом (270 м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (255 м):

900 – 270 = 630 м

630 + 255 = 885 м

Таким образом, через три минуты расстояние между пешеходами будет составлять 885 метров.

1. Теперь давайте ответим на вопрос: через сколько минут после начала движения первый пешеход догонит второго?

В самом начале пути между пешеходами было расстояние 900 м. Через минуту после начала движения расстояние между ними будет составлять 895 метров, поскольку первый пешеход двигается на 5 метров в минуту быстрее второго:

90 ∙ 1 = 90 м

85 ∙ 1 = 85 м

900 + 85 – 90 = 985 – 90 = 895 м

Через три минуты после начала движения расстояние уменьшится на 15 метров и будет составлять 885 метров. Это был наш ответ на первый вопрос задачи:

90 ∙ 3 = 270 м

85 ∙ 3 = 255 м

900 + 255 – 270 = 1155 – 270 = 885 м

Можно сделать вывод, что каждую минуту расстояние между пешеходами будет уменьшаться на 5 метров.

А раз изначальные 900 метров с каждой минутой уменьшаются на одинаковые 5 метров, то мы можем узнать сколько раз 900 метров содержат по 5 метров, тем самым определяя через сколько минут первый пешеход догонит второго:

900 : 5 = 180 минут.

Ответ: через три минуты расстояние между пешеходами будет составлять 885 метров, первый пешеход догонит второго через 180 минут = 3 часа.

Разбор решения заданий тренировочного модуля

№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте

Заполните таблицу:

	S	v	t
1.	135 км	9 км/ч	____ ч
2.	____ м	12 м/с	4 с
3.	132 м	____ м/мин	11 мин

Для заполнения пропусков воспользуемся формулами нахождения скорости, времени, расстояния:

1. Надо найти время: t = S : v

135 : 9 = 15 часов.

1. Надо найти расстояние: S = v ∙ t

12 ∙ 4 = 48 м.

1. Надо найти скорость: v = S : t

132 : 11 = 12 м/мин.

Верный ответ:

	S	v	t
1.	135 км	9 км/ч	15 часов
2.	48 м	12 м/с	4 с
3.	132 м	12 м/мин	11 мин

№2. Тип задания: единичный / множественный выбор

Выберите верный ответ к задаче:

Из пунктов А и В, расстояние между которыми 300 км, отправились одновременно навстречу друг другу мотоциклист и автомобилист. Скорость автомобиля 60 км/ч, а мотоцикла 30 км/ч. Какое расстояние будет между ними через 3 часа?

Варианты ответов:

1. 70
2. 30
3. 270
4. 240

Эта задача относится к типу задач на сближение, т.е. нам надо:

1. сложить скорости мотоциклиста и автомобилиста:

60 + 30 = 90 км/ч – скорость сближения;

1. узнать, сколько километров они пройдут за 3 часа вместе. Для этого:

90 ∙ 3 = 270 км;

1. из общего расстояния нам осталось вычесть пройденное:

300 – 270 = 30 км

Верный ответ: 2. 30 км.

«Скоро приедем?»: как оценить время в пути

За прошедший год мы много работали над качеством предсказания времени в пути (ETA) в навигаторе 2ГИС и на 30% увеличили количество маршрутов, у которых прогнозное время совпадает с реальным с точностью до минуты. Меня зовут Кирилл, я Data Scientist в 2ГИС, и я расскажу, как максимально точно рассчитывать время прибытия из точки А в точку Б в условиях постоянного изменения дорожной ситуации.

Поговорим про то, как мы постепенно меняли подходы к оценке времени в пути: от простой аддитивной модели до использования ML-моделей прогноза пробок и корректировки ETA. Ввели Traversal Time на смену GPS скоростей, а ещё проводили эксперименты и оценивали качество изменений алгоритма, чистили мусор из данных и закатывали модели в продакшн. Обо всём по порядку.

Почему нам важно правильно оценивать время в пути

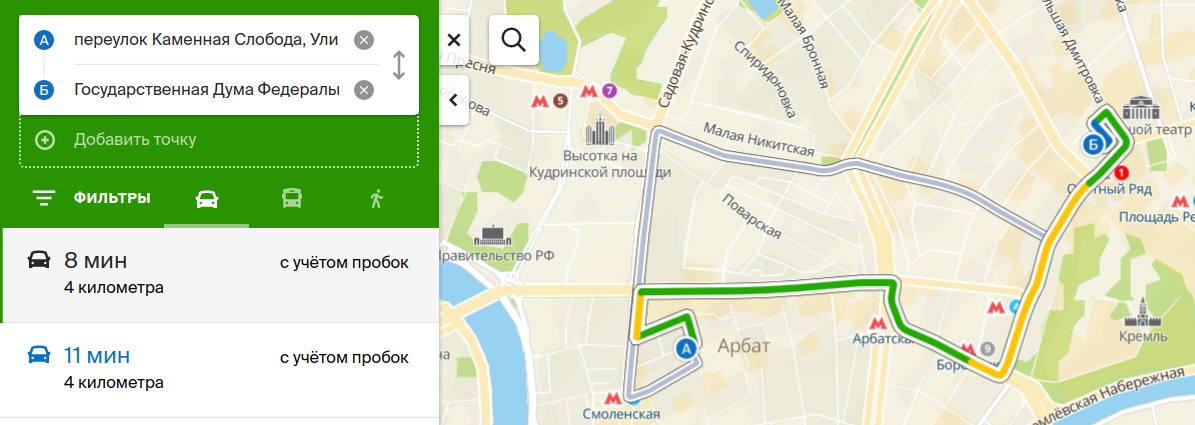
Во-первых, оценка времени пути помогает выбрать подходящий маршрут из точки А в точку Б (сравнить время и решить, что подходит лучше).

Во-вторых, от времени в пути зависит стоимость поездки в такси или доставки товара, поэтому правильная оценка времени напрямую влияет на ценообразование для наших партнеров.

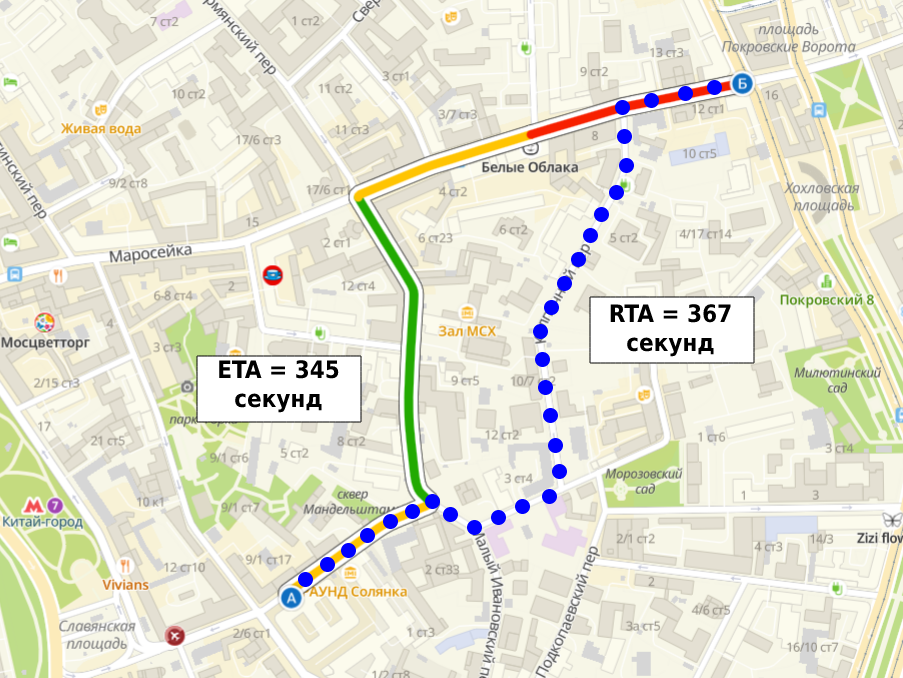
Важно определить, что мы понимаем под оценкой времени. Для этого используем два типа времени в пути (Time of Arrival):

• ETA (Estimated Time of Arrival) — это ожидаемое время в пути (наша оценка времени);

• RTA (Real Time of Arrival) — это реальное время в пути (время, которое прошло от начала и до завершения поездки пользователем).

Мы должны сделать так, чтобы наше ETA было как можно ближе к RTA.

Какие метрики оцениваем

Оценка ETA — задача регрессионного анализа. Его классические метрики MAE (Mean Absolute Error) и RMSE (Root Mean Squared Error) отражают, на сколько минут в среднем отличается прогнозное время от реального (для некоторой случайной поездки):

Однако у такого подхода есть несколько проблем:

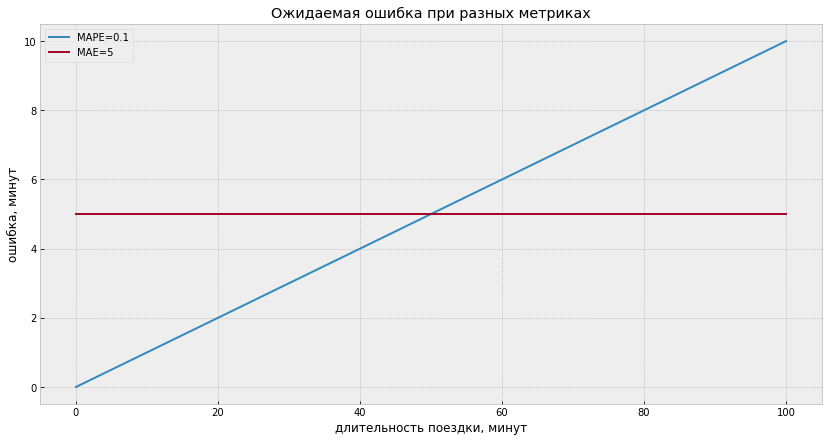
• Длительность поездок может быть разной: 5 минут, 60 минут или даже несколько часов. Одна и та же ошибка прогноза — например, в 5 минут — будет восприниматься во всех трех случаях по-разному. Чем длиннее поездка, тем менее критичной будет казаться ошибка. Вспоминая, что ETA влияет на ценообразование, этот пример становится еще более актуальным.

• Есть проблемы с интерпретацией результатов: если алгоритм в среднем ошибается на 10 минут — это хорошо или плохо? Ответить на этот вопрос невозможно, если мы не знаем среднюю длительность поездки. То есть в каждом новом эксперименте должна быть такая же средняя длительность поездки, как и в предыдущих. Если это требование нарушено, метрики экспериментов некорректно сравнивать между собой.

• Нет сведений о том, в какую сторону алгоритм ошибается чаще. Постоянное занижение или завышение ETA — это очень плохо, даже если средняя ошибка низкая. Пользователи это заметят и попытаются скорректировать время в пути самостоятельно: например, прибавить 5 минут к прогнозному времени. Нашей оценке будут доверять меньше.

Поэтому для оценки качества ETA мы используем две другие метрики одновременно:

1. MAPE (Mean Absolute Percentage Error) показывает, на сколько процентов в среднем прогнозное время отличается от реального. Чем меньше ошибка, тем лучше.

Эта метрика решает трудности, связанные с интерпретацией результатов: теперь не нужно ничего знать о длительности поездки, чтобы понять, хорошо ли работает алгоритм и насколько большой будет ошибка для различных поездок. 

1. ETA/RTA (Estimated Time of Arrival / Real Time of Arrival) показывает среднее значение отношения прогнозного времени к реальному. В идеале оно должно быть около единицы, то есть в среднем алгоритм не должен стабильно завышать или занижать прогнозное время в пути.

ETA/RTA — вспомогательная метрика для проверки того, насколько (и в какую сторону) в среднем сдвинуто предсказанное время относительно реального. Для оценки качества предсказаний алгоритма в первую очередь нужно смотреть на MAPE. 

Для анализа мы также используем и множество других метрик, однако эти две — наиболее значимые.

Вычисляем базовый алгоритм расчёта ETA

С метриками определились, а что дальше? 

В нашем распоряжении есть дорожный граф, в котором ребра — это маленькие кусочки дорог, соединённые между собой. Каждое ребро такого графа может включать в себя несколько дорожных полос, но обязательно является однонаправленным. Помимо этого, есть также множество других постоянных характеристик ребра, например:

• геометрия (длина и ширина);

• ограничение на максимальную скорость;

• тип покрытия;

• наличие на ребре светофора.

Таким образом, считаем, что маршрут из А в Б — это путь в дорожном графе, начинающийся в вершине А и заканчивающийся в вершине Б.

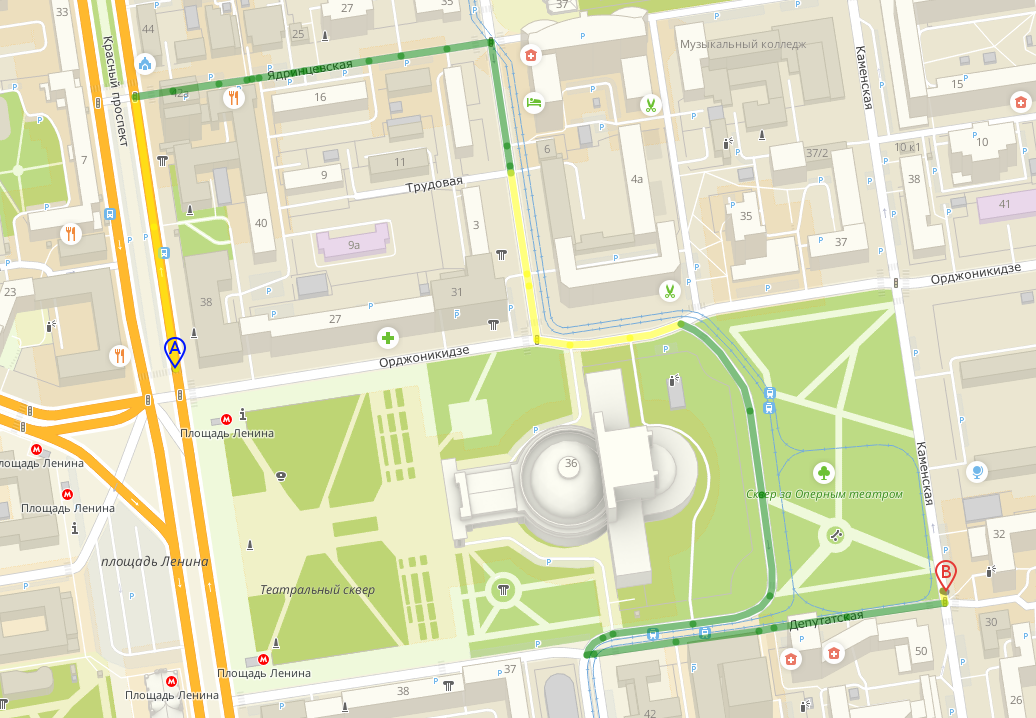
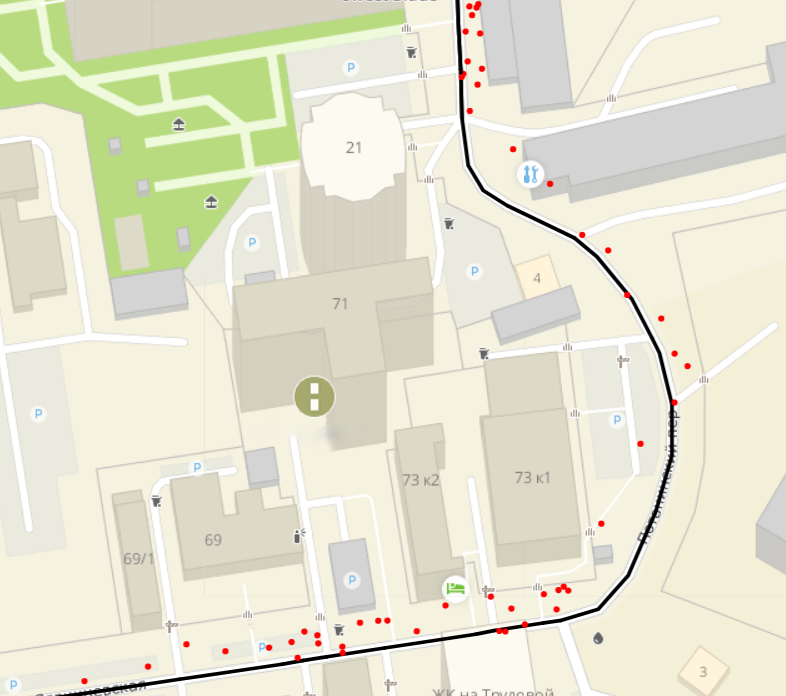
Также мы получаем GPS-данные с устройств пользователей-автомобилистов. Это текущее местоположение (широта и долгота) устройства, скорость, с которой устройство движется, азимут и прочее. Эти GPS-точки с каждого устройства приходят с интервалом в несколько секунд, что позволяет не просто собирать данные, но и анализировать целые траектории движения.

Более того, есть также алгоритм, который умеет притягивать GPS-точки к соответствующему ребру дорожного графа с довольно хорошей точностью. Поэтому для каждого ребра можно насчитать различные статистики:

• текущая скорость;

• текущая загруженность (например, число GPS-точек в единицу времени);

• «обычная» скорость в это время (например, средняя за всю предыдущую неделю).

Есть несколько вариантов расчёта статистик. Первый: пересчитывать их постоянно, с приходом новых точек — например, считать скорость на основе последних 100 точек. Второй: пересчитывать статистики каждые N минут на основе всех точек, полученных за это время.

Мы остановились на втором варианте и пересчитываем текущие статистики раз в пять минут, а «обычные» статистики — раз в неделю. Эти значения оказались оптимальными: если пересчитывать чаще, то данные не успевают накопиться (из-за чего статистики сильно «скачут»), а если реже, то не успеваем быстро адаптироваться к новой дорожной ситуации.

Всё готово к тому, чтобы рассказать про базовый алгоритм расчёта ETA: 

1. Считаем время проезда по каждому ребру в маршруте на основе текущей скорости на ребре.

2. Добавляем к полученному времени «штрафы» — дополнительное время за совершение сложных манёвров, таких как повороты и развороты.

Алгоритм можно выразить простой формулой:

С преимуществами алгоритма всё понятно: он простой, быстрый и даже работает, предсказывая что-то близкое к правде! Но в таком виде у него есть существенные недостатки. Посмотрим на них.

Какие недостатки алгоритма нужно исправить

1. Алгоритм сильно зависит от текущих скоростей на ребрах

Эта скорость должна быть не какой-то абстрактной величиной, а точной оценкой средней скорости водителя на этом ребре. Поэтому нужно очень тщательно настроить алгоритм расчёта скоростей на ребрах, иначе предсказания будут далеки от истинных значений.

2. Не учитывается изменение скоростей по рёбрам во время движения

Некорректно брать текущую скорость на ребре, если мы приедем к нему, например, только через 40 минут. За это время на ребре может, например, начаться пробка, и скорость упадет в несколько раз, что повлияет на итоговое время в пути.

3. Нет персонализации предсказаний

Для любого пользователя на одном и том же маршруте будет предсказано одно и то же ETA, без учёта его манеры вождения.

4. Не учитывается общая дорожная ситуация и особенности построенного маршрута

Игнорируется много информации о состоянии дорог в маршруте, о текущих пробках в городе и конкретном районе, по которому предстоит ехать, количество участков с затрудненным движением и так далее.

5. Проблема с подбором корректных «штрафов»

В разных городах время на маневры может значительно отличаться. Более того, оно может быть уникальным для каждого перекрестка: нужно учитывать наличие светофоров, количество полос, качество и геометрию дороги и так далее. Эта задача ещё сложнее, чем расчет текущей скорости на ребре графа, поэтому в первых версиях алгоритма мы использовали постоянные штрафы на каждый вид манёвров.

Дальше расскажу про то, как мы поэтапно исправляли описанные недостатки.

Настраиваем схему экспериментов

Прежде чем модифицировать существующий алгоритм, нужно научиться оценивать эффект от изменений. Первая сложность — как оптимизировать две метрики? Что делать в ситуациях, когда одна метрика стала лучше, а другая — хуже? 

Мало того, что две метрики в целом неудобно оптимизировать, так у них ещё есть особенности, которые мешают интерпретировать результат: 

• Во-первых, может быть ситуация, когда обе метрики стали лучше, а алгоритм — хуже. 

• Во-вторых, эти метрики взаимосвязаны: оптимальное значение MAPE достигается при ETA/RTA чуть меньшем, чем 1 (например, при ETA/RTA = 0.95). Из-за этого изменения (которые не делают ничего, кроме как немного двигают ETA всех маршрутов) могут влиять в том числе на MAPE.

Предположим, что мы как-то меняем существующий алгоритм и сравниваем его со старым по метрикам ETA/RTA и MAPE. По ним очевидный вывод: алгоритм стал лучше.

Теперь посмотрим на значения ETA/RTA поездок, полученные старым алгоритмом:

Видно, что в течение дня ETA/RTA смещён в среднем на 20% в сторону недопредсказания, но дисперсия значений очень низкая, что хорошо. Однако MAPE — это среднее отклонение относительно зелёной линии (то есть значения ETA/RTA=1), а не относительно среднего значения синих точек. Поэтому в данном случае MAPE высокий.

Если компенсировать этот сдвиг путем умножения ETA на 1.25, то получаем практически идеальный алгоритм с оптимальным ETA/RTA и низким MAPE:

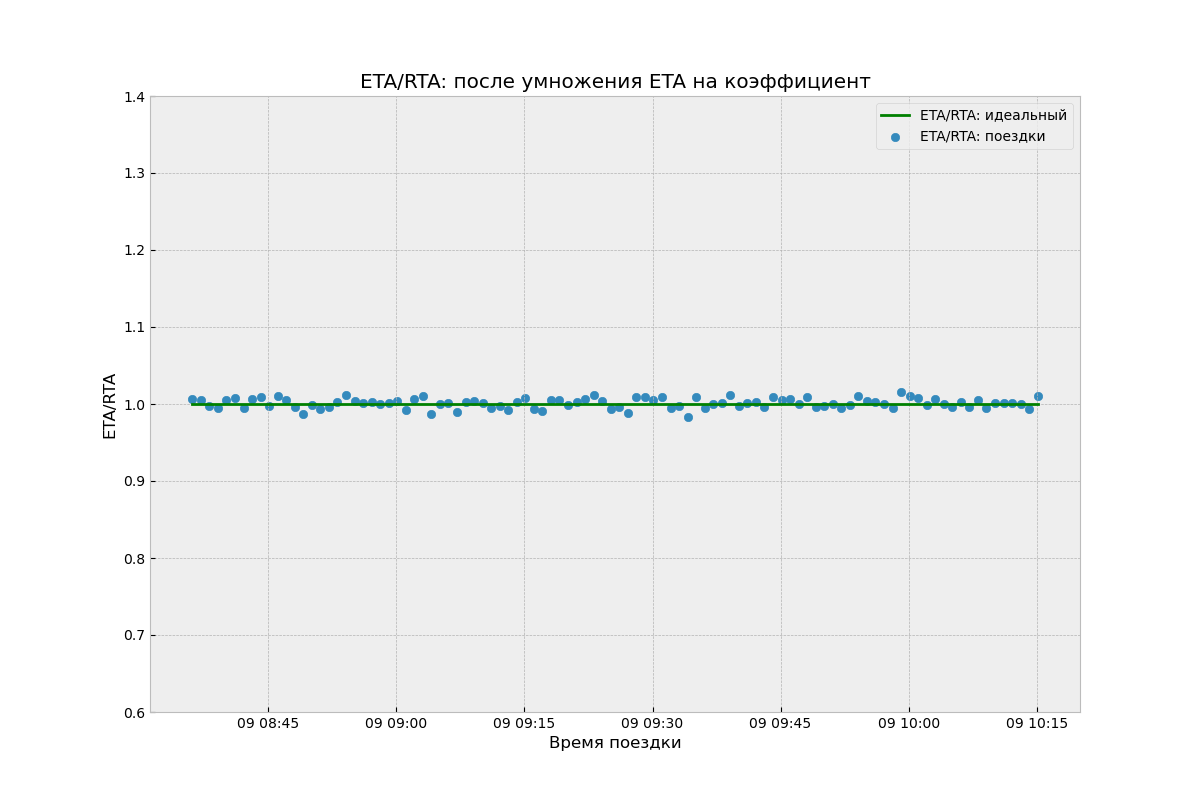
А теперь посмотрим на график ETA/RTA поездок, полученных новым алгоритмом:

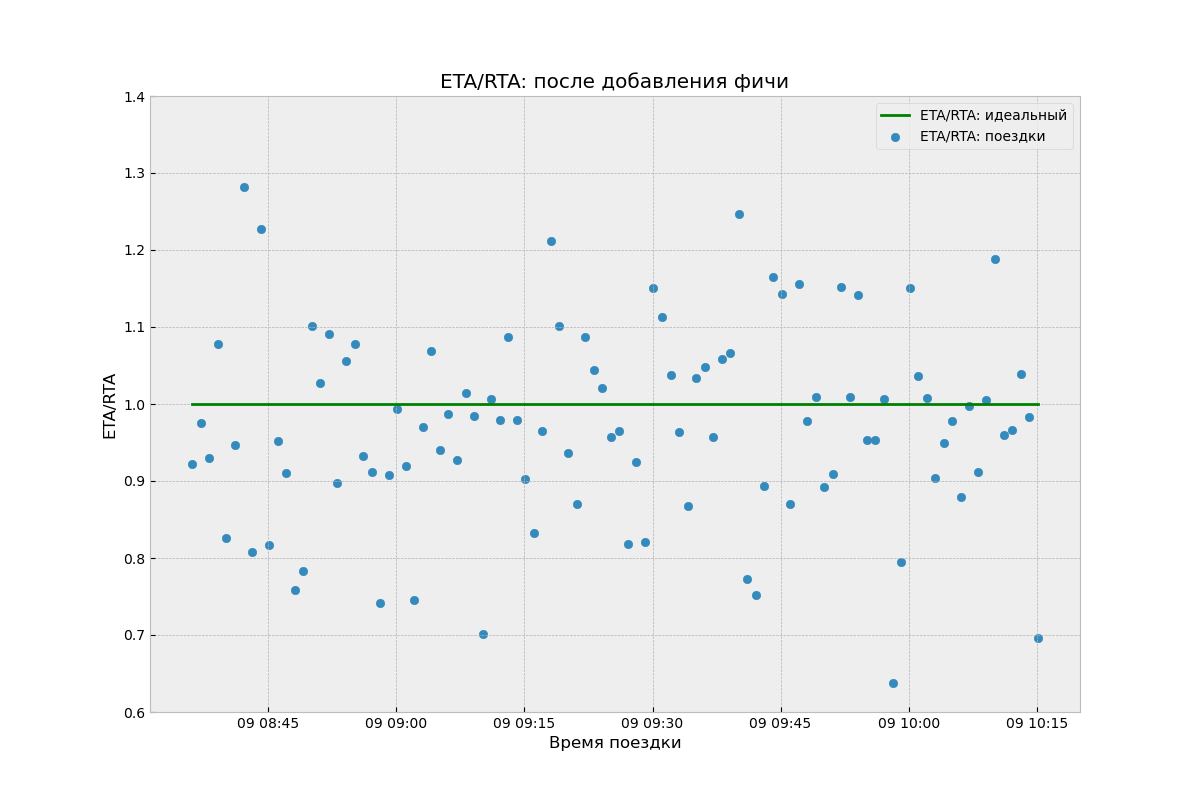
Он несмещённый, но имеет огромную дисперсию! Алгоритм однозначно стал хуже, но по метрикам этого не было видно. По графикам получаем один вывод, по метрикам — другой. Нужно что-то с этим сделать.

Чтобы выйти из этой ситуации, мы придумали свою метрику и назвали её NFCAM — Normalized First Central Absolute Momentum.

Фактически она показывает MAPE алгоритма при «идеальном» ETA/RTA, равном единице, и лишена двух вышеописанных недостатков. Заметим также, что любой смещённый алгоритм можно подвинуть к «идеальному» ETA/RTA путём умножения на величину, обратную ETA/RTA (которую можно насчитать из статистики). 

По NFCAM видно, что алгоритм до добавления фичи был лучше, чем после, а простой сдвиг умножением не влияет на значение метрики. FCAM отличается от NFCAM отсутствием нормирующего члена в знаменателе, поэтому неустойчив к умножению.

После того, как определились с метрикой, появился следующий вопрос: а как проводить эксперименты? 

Все эксперименты мы проводим в два этапа:

1. Офлайн-тестирование: делаем датасет из поездок, для которых известна построенная геометрия маршрута и RTA. Заменяем скорости на ребрах/штрафы за манёвры на вычисленные новым алгоритмом и замеряем метрики.

2. Онлайн-тестирование: А/Б тестирование на реальных маршрутах.

Онлайн-тестирование нужно, чтобы проверить, не испортилось ли качество построения маршрутов (для этого у нас тоже есть специальная метрика). В офлайн-тестировании мы этого проверить не можем, так как RTA есть только для построенного маршрута, а значит, мы не можем перестраивать его в соответствии с новым алгоритмом — ведь тогда пользователь поехал бы иначе, а значит, RTA был бы другим.

Если обновленный алгоритм успешно проходит оба этапа, то есть для контрольной группы NFCAM становится лучше, то изменение выкатывается в продакшн.

Важно также отметить, что датасет мы формируем не из всех доступных поездок: среди поездок встречается очень много «мусора», который нужно отфильтровать. Чтобы попасть в датасет, «хорошая» поездка должна удовлетворять нескольким критериям:

• Начинается и заканчивается недалеко от точек А и Б.

• Реальная траектория движения не слишком отличается от предложенной (например, если предложенный маршрут был длиной 1 км, а пользователь проехал 8 км, такой маршрут отбросится).

• Средняя скорость пользователя не аномальная (исключаем «телепортации» из-за некачественного GPS-устройства).

При этом мы не требуем, чтобы траектория движения полностью совпадала с предложенным маршрутом.

Улучшаем шаг за шагом

Traversal time

Решаем проблему 1. Улучшаем расчет текущих скоростей.

Мы уже упомянули о том, что сейчас алгоритм вычисления ETA по большей части зависит от текущих скоростей на рёбрах. Как правильно вычислять эти скорости? 

Вспоминаем, что у нас есть GPS-точки, которые притягиваются к рёбрам. Первый и самый простой способ — усреднить все скорости GPS-точек на ребре и полученное число считать текущей скоростью. У такого подхода есть серьезные недостатки:

• GPS-скорости очень ненадежны и часто значительно отличаются от настоящих.

• Поскольку точки идут с интервалом в несколько секунд, неизвестно, какая скорость была между ними (фактически — игнорируем ускорение при расчетах).

• Большое влияние на среднюю скорость оказывают выбросы: например, при каждой остановке будет присылаться нулевые скорости, которые нужно как-то фильтровать.

Более удачным способом вычислить текущую скорость оказался подход, использующий не GPS-скорости, а GPS-координаты. В нём мы пытаемся найти среднее время прохождения ребра пользователем (от начала и до конца ребра): 

(суммирование происходит по всем пользователям, которые проезжали по ребру в выбранный период)

А уже на основе полученного времени — traversal time — мы считаем текущую скорость. Traversal time позволил значительно улучшить качество предсказания ETA по сравнению с подходом, в котором считали скорость только на основе GPS-скоростей.

Скорости из статистики

К сожалению, на ребре может быть недостаточно данных для расчёта скорости, которую можно было бы использовать для расчёта времени в пути по этому ребру. Но чтобы построить маршрут через это ребро, какая-то скорость всё же нужна. Для этого мы используем скорости из статистики следующим образом:

• если недавно для этого ребра была рассчитана текущая скорость, берём её;

• определяем «класс» ребра и берём скорость, типичную для этого класса;

• если «класс» ребра не получается определить, берём ограничение скорости по знаку.

Раньше мы использовали скорости, которые «обычно» бывают в это время, но без них метрики оказались лучше.

Модель прогноза скоростей

Решаем проблему 2. Прогнозируем изменение скоростей по мере движения пользователя по маршруту.

Дальше нужно было научиться предсказывать изменение скоростей (дорожной ситуации) по мере того, как пользователь двигается по маршруту. Для этого нужно заменить константные скорости на рёбрах на скорости, которые зависят от ETA кусочка маршрута, построенного из точки старта до выбранного ребра.

Для этого создали новую характеристику ребра — прогнозные скорости. Это скорости на час вперед от текущего момента с пятиминутным шагом, то есть 12 чисел для каждого ребра, которые, как и текущие скорости, пересчитываются раз в пять минут. Шаг в пять минут выбрали по аналогии с интервалом обновления текущих скоростей. Больший период прогноза, чем час, не оказывает никакого влияния на метрики ETA/RTA и MAPE.

Для формирования прогнозных скоростей сделали отдельный сервис с ML-моделями прогноза:

• для каждого города свой набор моделей;

• для каждого пятиминутного шага используется отдельная модель.

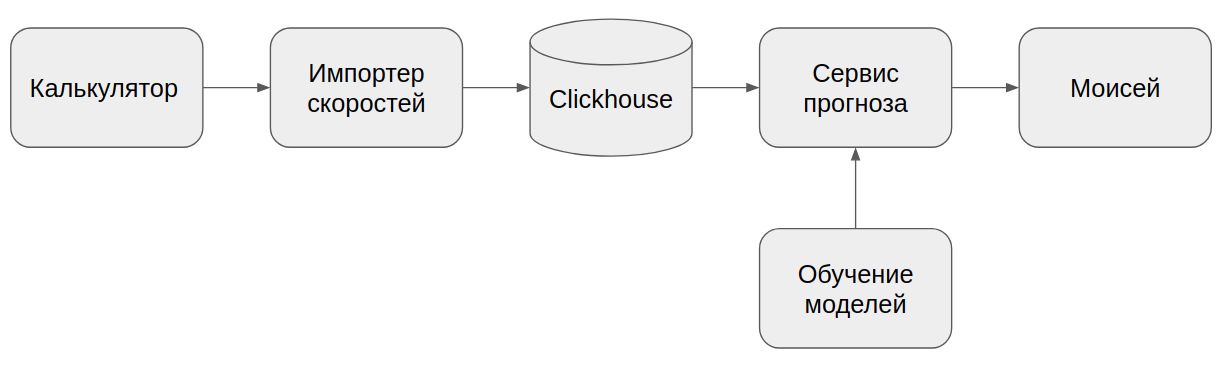
На вход сервис ждёт текущие скорости рёбер в дорожном графе. Затем они добавляются в БД Clickhouse, которая быстро считает признаки для нашего огромного объёма данных: среднюю и медианную скорости за последний час, неделю; количество полос на ребре; текущее время и прочее. Для тех рёбер, по которым недостаточно актуальной статистики, прогнозные скорости не вычисляются. 

Сформированные признаки подаются на вход моделям, которые возвращают прогнозные скорости. Всё это упаковывается в файл и возвращается в сервис расчёта ETA.

Модели периодически автоматически переобучаются, чтобы учитывать изменение сезона и общей дорожной ситуации в городах. Качество каждой модели вычисляется так: 

• Выбираем некоторый момент в прошлом, предсказываем для него скорости через N минут (зависит от модели).

• Считаем уже знакомую метрику RMSE между полученными скоростями и скоростями, которые будут текущими через N минут (то есть с «реальными» скоростями из будущего относительно момента предсказания).

Новые модели сравниваем со старыми на одинаковом наборе данных: если RMSE стал лучше, то модель меняется на новую. Также на стейджинге у нас развёрнут отдельный сервис прогноза для экспериментов. 

Для ускорения работы сервиса мы убрали самые вычислительно тяжёлые признаки и конвертируем обученные модели в onnx-формат.

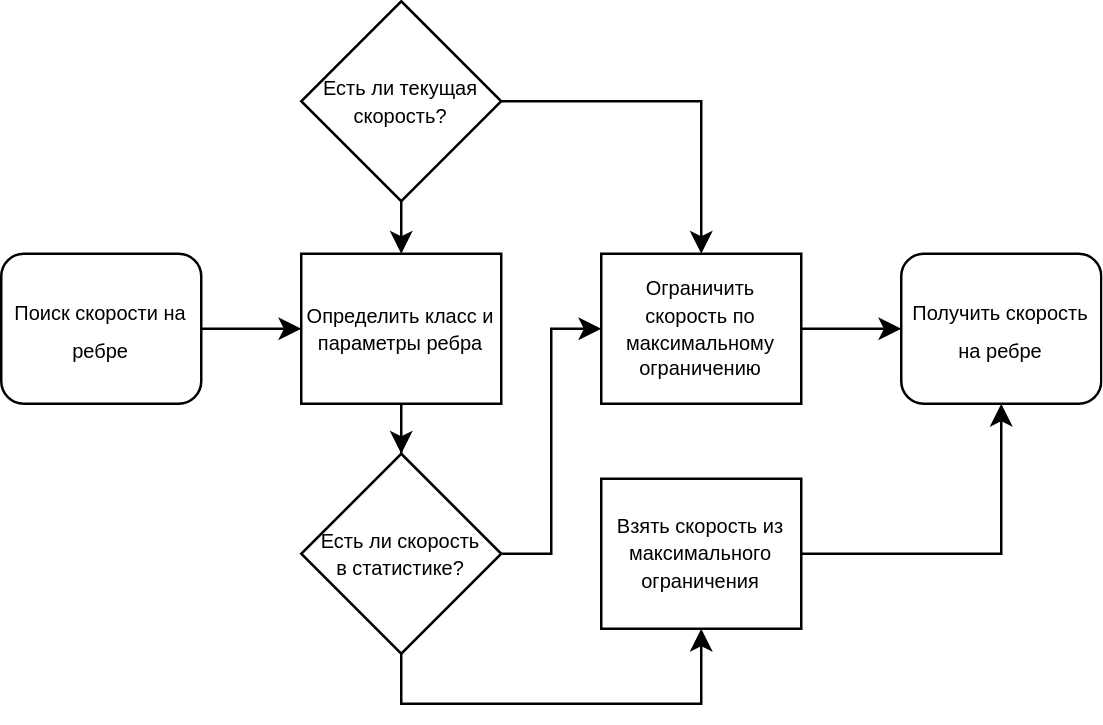
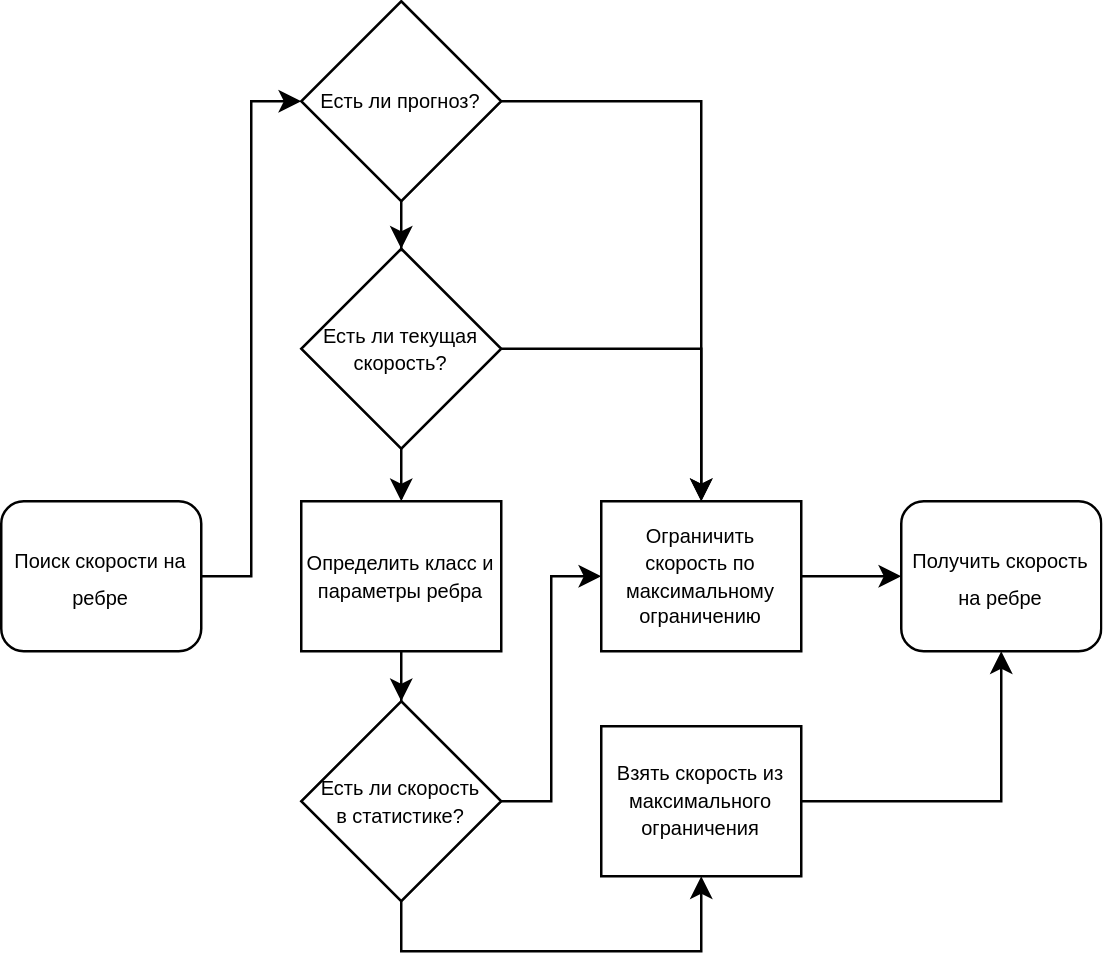
С добавлением прогнозных скоростей общая схема получения скорости на ребре выглядит так:

Модель корректировки ETA

Решаем проблемы 3 и 4. Добавляем персонализацию и учитываем дополнительные данные при предсказании ETA.

Затем нужно было как-то разобраться со сдвигом ETA/RTA: из-за того, что во всех городах используется один и тот же алгоритм, трудно отрегулировать все параметры так, чтобы ETA/RTA везде был около 1. В некоторых городах он был сильно занижен, а в других — завышен. 

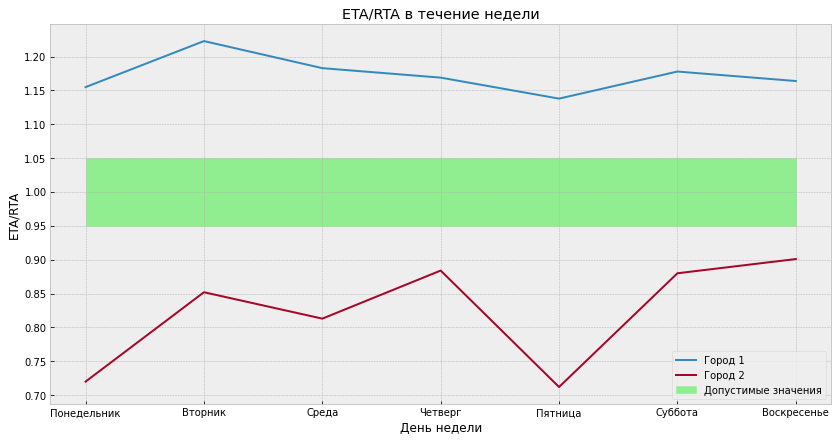
К тому же мы столкнулись с тем, что все пользователи навигатора делятся на две совершенно разные по стилю вождения группы: обычные пользователи и… таксисты 🙂

Последние ездят значительно быстрее, и для них ETA/RTA получается выше, чем для обычных пользователей. В итоге трудно сделать так, чтобы у обеих групп ETA/RTA не был сдвинут.

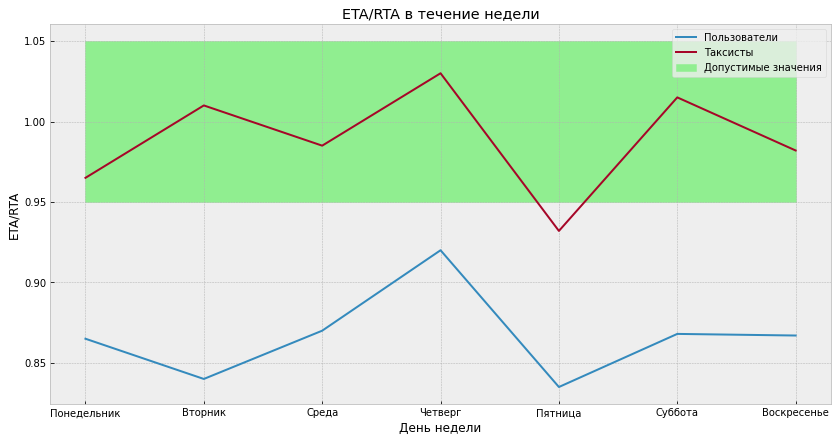
Первоначально мы с этим боролись так, как было описано выше: на основе статистических данных рассчитывали коэффициент коррекции…

… по каждому городу для обеих групп пользователей, а затем ETA поездок умножали на этот коэффициент. Таким образом решили проблему сдвига ETA/RTA и добавили персонализацию — для обычных пользователей и таксистов время в пути отличается.

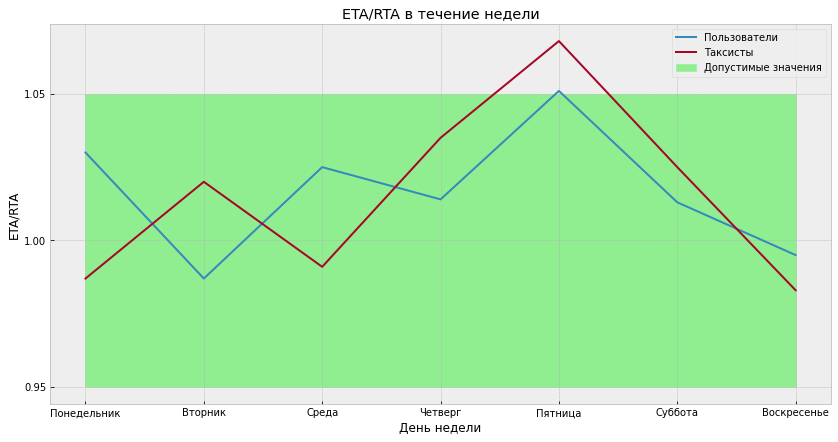
Затем мы улучшили этот механизм, и на смену константной корректировке пришла модельная корректировка, которая учитывает особенности каждого построенного маршрута.

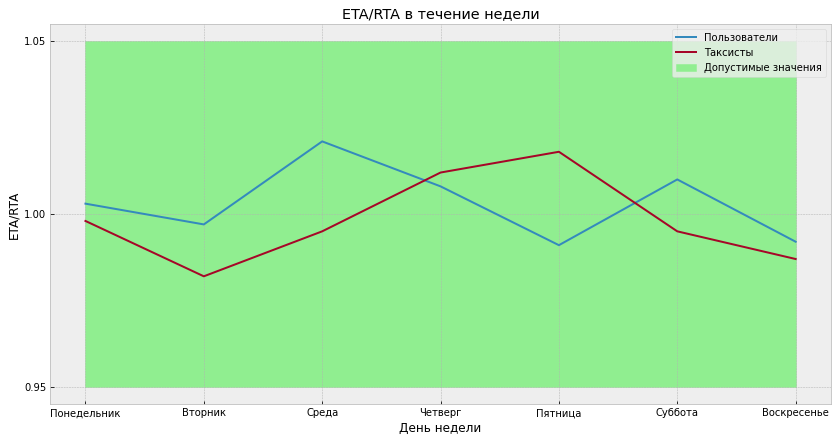
После построении маршрута и вычисления ETA считаются также его различные признаки, связанные со скоростями, геометрией, местоположением промежуточных точек и текущим временем. Затем эти признаки подаются на вход ML-модели, которая пытается скорректировать прежде посчитанный ETA. То есть модель не полностью заменяет базовый алгоритм, а только улучшает его результаты, используя дополнительную информацию.

В итоге вычисление ETA можно представить так: 

Модели обучаются каждый день, потому что, во-первых, они получаются гораздо «легче» моделей прогноза, а во-вторых, они сильнее зависят от изменений дорожной ситуации. 

Немного про штрафы

Решаем проблему 5. Уменьшаем влияние штрафов на итоговый результат.

В модели корректировки уже используется полная информация о манёврах в маршруте, поэтому определение штрафов за них мы переложили на модель. Формула расчета ETA немного упростилась, а качество — улучшилось:

Однако полностью от штрафов мы не отказались: они до сих пор используются при поиске оптимального маршрута (оптимальным мы считаем тот, у которого наилучший ETA), чтобы не строить геометрически слишком сложные маршруты. Поэтому в итоге у нас есть три разных времени в пути, каждое из которых очень важно:

• ETA со штрафами: используется при построении маршрута.

• ETA без штрафов: используется как признак в модели корректировки.

• ETA скорректированный: используется как финальная оценка времени в пути по маршруту.

Результаты

Теперь, наконец, посмотрим, как повлияли все эти улучшения на метрики.

ETA/RTA

В результате ETA/RTA во всех городах теперь находится в пределах от 0.95 до 1.05, а в большинстве из них практически равен единице. Проблему сдвига ETA/RTA получилось полностью решить при помощи модели коррекции.

MAPE

MAPE улучшился в среднем на 0.08, а в отдельных городах улучшение достигло 0.13. Теперь в среднем мы ошибаемся менее чем на 20% при прогнозировании времени в пути.

Процент плохих маршрутов

Плохим маршрутом мы считаем тот, в котором ошибка прогнозирования оказалось больше 50%. Их количество удалось снизить на 4.5% от общего количества маршрутов, и теперь вероятность подобной ошибки — менее 10%.

Можно с уверенностью сказать, что время в пути теперь определяется намного точнее, чем это было раньше, а значительных ошибок прогнозирования стало существенно меньше. Последнее особенно радует, потому что пользователи воспринимают эти ошибки крайне негативно.

Мы не останавливаемся на достигнутом и продолжаем улучшать алгоритмы вычисления времени в пути, в особенности, хотим учитывать личные предпочтения при построении геометрии маршрута.