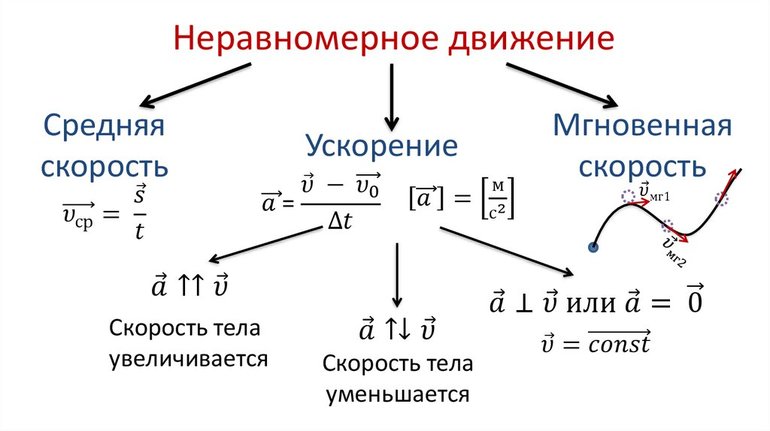
Основные понятия
Наука, изучающая механическое движение без учёта причин, его вызвавших, называется кинематикой. При перемещении в физике принимается, что любой объект состоит из множества одинаково движущихся материальных точек. Поэтому вместо того, чтобы рассматривать тело в целом, изучается только поведение одной точки.
Любое движение описывается рядом параметров. К основным из них относят:

- Траекторию — линию, по которой происходит перемещение в пространстве.
- Пройденное расстояние — путь, ограниченный начальными и конечными координатами.
- Координаты — изменение положения точки в пространстве относительно принятого начала.
- Скорость — быстрота изменения положения.
- Ускорение — нарастание скорости во времени.
Под перемещением понимают движение за некий промежуток времени, описываемый вектором: ∆r = r — r0. Направление вектора принимается от положения материальной точки в начальный момент, к изменению её расположения в установленный. Скорость же представляет вектор, определяющий направление перемещения и быстроту изменения движения относительно начальных координат, то есть какого-либо тела отсчёта.
Движение принято разделять на два вида: прямолинейное и криволинейное. В качестве примера для первого вида можно привести езду поезда на ровном участке железной дороги, бег спринтера на короткие дистанции, перемещение воды в прямой трубе. В реальности же чаще приходится сталкиваться с криволинейным перемещением, таким как падение тела, полёт футбольного мяча после удара.
Какой бы ни была траектория движения, под перемещением понимают минимальное расстояние, которое находится между отправной и конечной координатой. Фактически это — отрезок, соединяющий две точки. Но движение кроме траектории описывается и скоростью, то есть быстротой прохождения заданных участков.
Неравномерность перемещения обозначает изменение быстроты движения. Физическая величина, определяемая как отношение пройденного пути ко времени, затраченному на движение, называется средней скоростью. Этот параметр специально ввели для описания неравномерного движения в физике.
Суть и определение
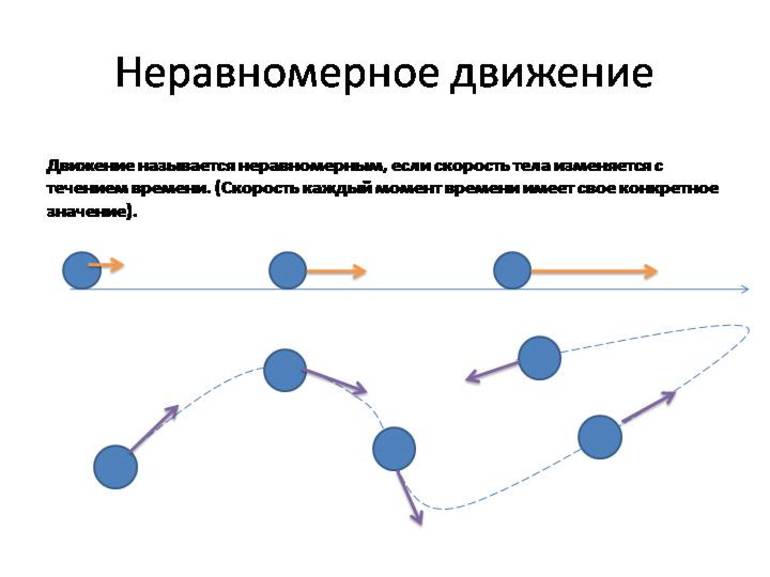
Суть неравномерного движения изучают в седьмом классе средней школы на уроках физики. В школьном учебнике приводится определение, что неравномерным считается такое изменение материальной точки в пространстве, при котором меняется скорость. При этом отмечается, что она может изменяться и по направлению.
Исходя из этого, можно сделать заключение, что движение, сопровождающее изменением скорости или траектории, является неравномерным. Например, вращение шара по окружности, выстрел из лука. При этом перемещение может быть равноускоренным, то есть состоять из чередования различных неравномерных движений. Как пример можно привести переключение скоростей в передвигающемся автомобиле.
Средняя скорость — это относительный параметр. Определяется он отношением пройденного пути к затраченному для этого времени. Предполагать, что для его нахождения можно просто сложить известные мгновенные скорости и разделить результат на их количество, в корне неверно. Под мгновенной характеристикой понимается скорость, существующая в определённой точке на данный момент.
Например, спидометр, установленный в машине, регистрирует ежесекундно именно мгновенную скорость. Поэтому для нахождения среднего показателя используется следующая формула: V = s / t, где:
- V — искомая средняя скорость;
- s — пройденный путь;
- t — затраченное на прохождение время.
В качестве единицы измерения используется отношение метров на секунды в соответствии с Международной системой измерений (СИ). Следует отметить, что когда траектория пути не является прямолинейной, то пройденное материальной точкой расстояние будет больше, чем её перемещение. Для описания такого случая вводится понятие средней путевой скорости, являющейся скалярной величиной. При этом её значение будет отличаться от средней скорости перемещения.

Случается так, что движение точки через один и тот же промежуток времени изменяется на одинаковую величину. В этом случае движение называют равнопеременным. Оно может быть как равнозамедленным, так и равноускоренным. Ускорение или замедление не зависит от изменения скорости за единицу времени. Но, зная поведение тела и его начальную скорость, можно вычислить, с какой скоростью оно будет двигаться в любой промежуток времени. Для этого используют выражение: v = v0 + a * Δt.
График движения
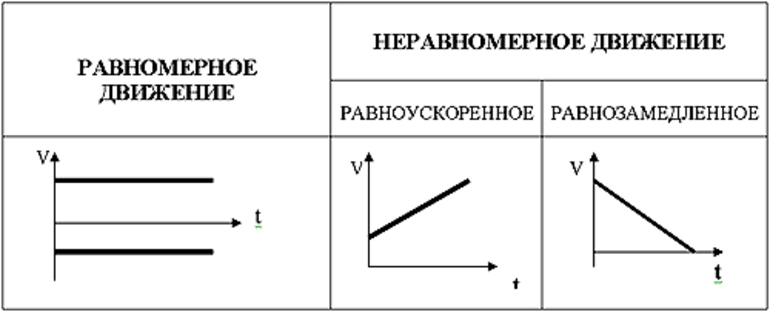
Существует простая геометрическая интерпретация траектории движения, по которой двигалась материальная точка. Когда тело перемещается с одной и той же скоростью, равняющейся v, то длительность пройденного отрезка будет определяться выражением: ∆t = t2 − t1, где t1 и t2 — начальный и конечный момент времени. Вполне логично предположить, что за указанный промежуток времени тело переместится на расстояние, равное: s = v * (t 2 — t 1) = v * ∆t.
В этом случае график пути в декартовой системе координат будет выглядеть как прямая. При этом пройденное расстояние, по сути, будет определяться площадью прямоугольника, построенного вниз от линии пути до оси времени. Скорость будет соответствовать вертикальной стороне фигуры, а изменение времени — горизонтальной.
Теперь можно рассмотреть, как будет выглядеть график неравномерного движения. Средняя скорость тела зависит от времени на конкретно взятом промежутке, ограниченном моментами t1 и t2. Пусть рассматриваемый отрезок будет разбит на промежутки, равные ∆t. Можно предположить, что в каждом таком отрезке скорость движения остаётся неизменной. Плавное её изменение можно заменить аппроксимацией ступенчатого вида. Иными словами, в каждом таком промежутке увеличение v (t) будет определяться выражением: v (t) ] = [ti, ti + ∆t].
Тогда ∆t будет совпадать с площадью прямоугольника, находящегося под ступенькой. Таким образом, путь будет определяться суммой всех площадей на графике. Когда ∆t направлена в сторону нуля, то сумма площадей этих прямоугольников будет располагаться под скоростью. То есть фактически — обозначать путь, пройденный телом с начальной точки до конечной.
Исходя из сказанного, можно утверждать, что расстояние, которая проходит точка при неравномерном движении, определяется площадью, находящейся под графиком скорости на установленном промежутке времени. Это определение является общим для любого типа перемещений.
Математическое описание
Движение характеризуется различными параметрами, которые можно описать формулами и уравнениями. С точки зрения математики под термином понимается изометрия пространства в себя. При решении задач, связанных с неравномерным движением, используются следующие формулы:
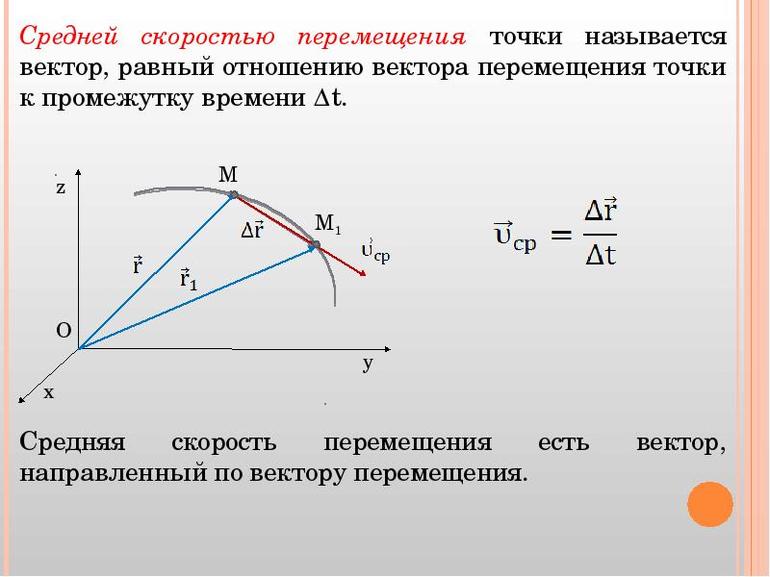
- Вектор средней скорости. Определяется как отношение вектора изменения ко времени, за которое произошло перемещение: vср = Δs / Δt.
- Средняя путевая скорость. Для её вычисления используется отношение пройденного пути к отрезку времени, за которое преодолено это расстояние: v ¯ = l / Δt. Более общим выражением, описывающим этот параметр, будет отношение изменения координаты объекта к промежутку времени: v = Δx / Δt.
- Мгновенная скорость. Определяется формулой: v = lim Δs / Δt = lim Δr / Δt. При этом предел времени стремится к нулю. То есть характеристика численно равняется отношению изменения координаты ко времени, за которое оно произошло. Направление вектора параметра совпадает с траекторией движения. Следует отметить, что для прямолинейного движения скорость изменяется только по значению, а направление остаётся неизменным.
- Равнопеременное движение. Если вектор обозначить как Δv, то изменение скорости можно обозначить как Δv = v — v0. В случае когда Δt 1 = Δt 2 = … = Δtn, тогда Δv1 = Δv2 = … = Δvn. Отсюда Δv1 / Δt1 = Δv2 / Δt2 = … = Δv3 / Δt3 = cost. Другими словами, это характеристика движения, при которой a = (v — v 0) / t.
- Ускорение. Показывает зависимость изменения скорости от вектора к промежутку времени. Для неравномерного перемещения используется формула: a ср = Δv / Δt. Из неё следует, что мгновенное ускорение будет равняться: a = lim Δv / Δt = v’. Ускорение — это параметр, который определяется не только изменением модуля, но и вектором. Смысл заключается в том, что любое движение по окружности будет являться ускоренным из-за изменения направления в течение времени.
- Равнопеременное перемещение. График движения описывается уравнением: v = v0 + a * t.
Нужно отметить, что при равноускоренном движении расстояние изменяется в соответствии с квадратной зависимостью: s = v0 * t + at2 / 2. В координатных прямых зависимость будет иметь вид: x = x0 + vo * t + a * t / 2. При этом график будет иметь вид параболы.
При расчётах довольно часто применяется закон сложения скоростей. Он позволяет определить параметр относительно зафиксированной системы отсчёта. Согласно этому способу: v2 = v1 + v. Понять справедливость утверждения можно, представив муху, ползущую по поверхности пластинки. Её скорость будет определяться относительно проигрывателя суммой движения и тем параметром, который имеет точка пластинки по отношению к площади, на которой находится в рассматриваемый момент тело.
Примеры решения задач

С помощью формулы неравномерного движения в физике решаются различные задания на расчёт ускорения и вычисление параметров перемещения в реальных условиях. Одной из типовых задач, предлагающихся для самостоятельного решения ученикам в школе, является следующая.
Пусть имеется автомобиль, который ехал по прямому шоссе со скоростью 90 км/час одну минуту. Затем он заехал на подъём, который преодолевал две минуты. Его движение замедлилось до 60 км/ч. Для съезда с него машина затратила 0,5 минут, спидометр при этом показывал 120 км/ч. Нужно вычислить среднюю скорость.
При использовании теоретических знаний и закона сложения формула, позволяющая найти ответ, будет выглядеть следующим образом: V = s / t = (s1 + s2 + s3) / (t1 + t2 + t3). По условию задачи, движение можно разделить на три части: прямое (шоссе), замедленное (подъём), ускоренное (спуск). Для каждого из участков нужно определить пройденное автомобилем расстояние. Так, s1 = v1 * t1 = 90 * 1/60 = 1,5 км; s2 = v2 * t2 = 60 * 2/60 = 2 км; s3 = v3 * t3 = 120 * 0,5/60 = 1 км. Подставив полученные значения, можно вычислить ответ: v = (1,5 + 2 + 1) / (3,5 / 60) = 77 км /ч. Число шестьдесят используется в формуле для перевода времени в систему СИ.

Вот ещё одна из типичных задач. Пусть велосипедист проехал за первый час десять километров. За последующие три часа он преодолел тридцать километров. Нужно найти среднюю скорость. Для решения задачи нужно обозначить всё расстояние, что проехал велосипедист, буквой r, а время, которое он затратил для его преодоления — t. Тогда V = r /t = (r1 + r2) / (t1 + t2) = (10 +30) / (1+3) = 40 / 4 = 10 км/ч.
Приведённые задачи относятся к заданиям среднего уровня. Из примеров более сложного типа можно привести следующий. Имеется шарик. Нужно так его направить на желобе, чтобы он скатывался с ускорением за три-четыре секунды. Замерить затраченное время секундомером.
Вначале следует определить длину жёлоба: l = v * t. Скорость будет определяться как (Vнач + Vкон) / 2, так как Vкон = Vнач + a * t. Учитывая, что Vнач = 0, то Vкон = 2 + Vср, а Vкон = a * t. Следовательно: a = (2 * Vср) / t. Из опыта было установлено — время равняется четырём секундам, а необходимое расстояние жёлоба — 120 см. Отсюда v = 120 / 4 = 30 см/с. Исходя из этого, Vк = 60 см/с, а ускорение будет: a = 2V /t = 60 /4 = 15 см/с2. Задача решена.
Содержание:
Неравномерное движение:
Наверняка вам случалось ехать на автобусе или автомобиле из одного города в другой. Вспомните: транспортное средство время от времени тормозит, останавливается, потом снова набирает скорость… Стрелка спидометра все время колеблется и только иногда замирает на месте. Можно ли назвать такое движение равномерным? Конечно, нет. А как называют такое движение? Как его описывают?
В повседневной жизни мы обычно имеем дело с неравномерным движением. Так, неравномерным является движение автобуса (рис. 11.1) и других транспортных средств, движение падающих тел, движение спортсменов на беговой дорожке. А еще вспомните, например, как катится мяч, как вы движетесь во время прогулки, на уроках физкультуры и т. д.

Неравномерное движение — это движение, при котором тело за равные интервалы времени проходит разный путь. Обратите внимание! При неравномерном движении значение скорости движения тела со временем изменяется. Попробуйте привести примеры неравномерного движения. Теперь мы можем классифицировать виды механического движения (см. таблицу): по форме траектории — прямолинейное, криволинейное; по характеру движения тела – равномерное, неравномерное

Вычисляем среднюю скорость движения тела
Предположим, что поезд прошел 150 км (расстояние между двумя станциями) за 2,5 ч. Если разделить 150 км на 2,5 ч, получим скорость движения поезда — 60 км/ч. Но ведь поезд двигался неравномерно! В таком случае говорят, что получена средняя скорость движения поезда (рис. 11.2).

Средняя скорость движения тела 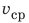 — это физическая величина, равная отношению всего пути l, который прошло тело, к интервалу времени t, за который этот путь пройден:
— это физическая величина, равная отношению всего пути l, который прошло тело, к интервалу времени t, за который этот путь пройден: 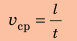 Обратите внимание! В данном случае t — это сумма времени движения тела и времени, потраченного на возможные остановки.
Обратите внимание! В данном случае t — это сумма времени движения тела и времени, потраченного на возможные остановки.
График скорости неравномерного движения тела
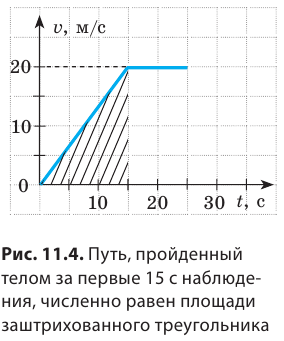
Рассмотрим график скорости неравномерного движения некоторого тела (рис. 11.3) и определим: как двигалось тело; какой путь прошло тело за 25 с наблюдения; какой была средняя скорость движения тела на данном пути. По графику видим, что скорость движения тела в течение первых 15 с равномерно увеличивалась от 0 до 20 м/с. Чтобы вычислить путь, пройденный телом за это время, вспомним: числовое значение пути, который прошло тело, равно числовому значению площади фигуры под графиком скорости движения этого тела. Итак, определим площадь заштрихованного треугольника (рис. 11.4). Из рисунка видим, что площадь заштрихованного треугольника равна половине площади прямоугольника с «длиной» 20 м/с и «шириной» 15 с. Площадь прямоугольника, в свою очередь, равна произведению его длины и ширины. Таким образом, путь 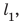 пройденный телом за 15 с, равен:
пройденный телом за 15 с, равен:
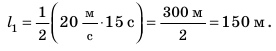
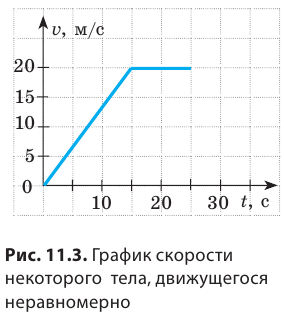
Следующий интервал времени 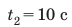 с тело двигалось равномерно со скоростью
с тело двигалось равномерно со скоростью 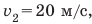 поэтому путь
поэтому путь 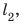 пройденный телом за это время, равен:
пройденный телом за это время, равен: 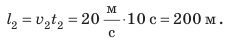 Весь путь l, пройденный телом за 25 с наблюдения, составил 350 м:
Весь путь l, пройденный телом за 25 с наблюдения, составил 350 м:
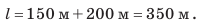 Зная весь путь l и все время t движения тела, найдем среднюю скорость его движения:
Зная весь путь l и все время t движения тела, найдем среднюю скорость его движения: 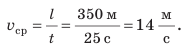 График пути для данного движения приведен на рис. 11.5.
График пути для данного движения приведен на рис. 11.5.
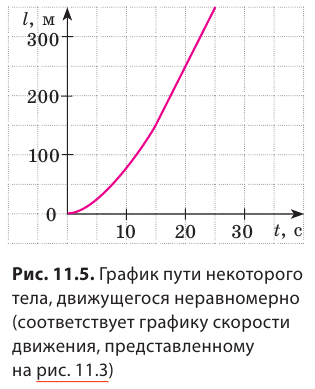
Обратите внимание! Путь не может уменьшаться, поэтому график пути либо поднимается, либо остается горизонтальным, но никогда не опускается.
- Заказать решение задач по физике
Пример
Полтора часа мальчик ехал на велосипеде со скоростью 20 км/ч. Потом велосипед сломался, и последний километр пути мальчик шел пешком. Какой была средняя скорость движения мальчика на всем пути, если пешком он шел полчаса? Анализ физической проблемы. Выполним пояснительный рисунок. Для определения средней скорости движения нужно найти путь, который преодолел мальчик, и время его движения. Время движения выражено в часах, путь — в километрах, поэтому среднюю скорость движения найдем в километрах в час.
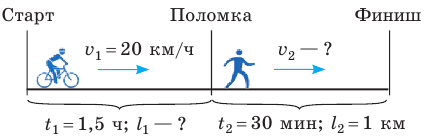
Дано:
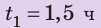 ,
,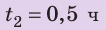 ,
,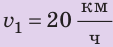 ,
,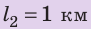
Найти:
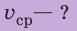
Решение:
По определению: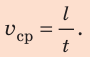
Путь l, который преодолел мальчик, равен: 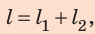 где
где 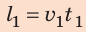 — путь, который он проехал на велосипеде;
— путь, который он проехал на велосипеде; 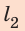 — путь, пройденный пешком. Все время, затраченное на путешествие:
— путь, пройденный пешком. Все время, затраченное на путешествие: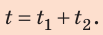
Подставив выражения для l и t в формулу средней скорости движения, получим:
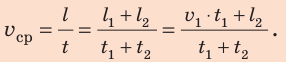
Проверим единицу, найдем значение искомой величины:
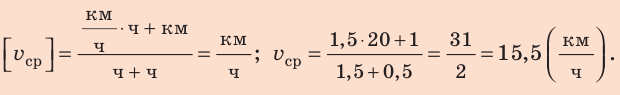
Анализ результатов. Мальчик ехал на велосипеде со скоростью 20 км/ч, шел пешком со скоростью 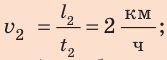 найденная средняя скорость его движения меньше 20 км/ч и больше 2 км/ч. Результат правдоподобен.
найденная средняя скорость его движения меньше 20 км/ч и больше 2 км/ч. Результат правдоподобен.
Ответ: 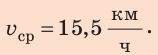
Итоги:
Неравномерное движение — это движение, при котором тело за равные интервалы времени проходит разный путь. Виды механического движения: по форме траектории — прямолинейное и криволинейное; по зависимости скорости движения от времени — равномерное и неравномерное. Средняя скорость движения тела равна отношению всего пути, пройденного телом, к интервалу времени, за который этот путь пройден: 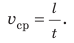
- Вращательное движение тела
- Равномерное движение материальной точки по окружности
- Колебательное движение
- Физический и математический маятники
- Относительность движения
- Поступательное движение
- Равномерное и неравномерное движение
- Равномерное движение
Как определить время:
а) при равномерном движении тела;
б) при неравномерном движении тела?

reshalka.com
ГДЗ учебник по физике 7 класс Перышкин. §17. Вопросы. Номер №2
Решение
а) Чтобы определить время при равномерном движении, надо путь, пройденным телом, разделить на скорость его движения:
t
=
S
v
, где t − время, S − путь, v − скорость.
б) Чтобы определить время при неравномерном движении, надо путь, пройденным телом, разделить на среднюю скорость его движения:
t
=
S
v
с
р
, где t − время, S − путь,
v
с
р
− средняя скорость.
Путь при неравномерном движении.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Сейчас мы будем рассматривать неравномерное движение – то есть движение, при котором абсолютная величина скорости меняется со временем. Оказывается, существует простая геометрическая интерпретация пути, пройденного телом при произвольном движении.
Начнём с равномерного движения. Пусть скорость тела постоянна и равна . Возьмём два момента времени: начальный момент
и конечный момент
. Длительность рассматриваемого промежутка времени равна
.
Очевидно, что за промежуток времени тело проходит путь:
(1)
Давайте построим график зависимости скорости от времени. В данном случае это будет прямая, параллельная оси абсцисс (рис. 1).
 |
| Рис. 1. Путь при равномерном движении |
Нетрудно видеть, что пройденный путь равен площади прямоугольника, расположенного под графиком скорости. В самом деле, первый множитель в формуле (1) есть вертикальная сторона этого прямоугольника, а второй множитель
– его горизонтальная сторона.
Теперь нам предстоит обобщить эту геометрическую интерпретацию на случай неравномерного движения.
Пусть скорость тела зависит от времени, и на рассматриваемом промежутке
график скорости выглядит, например, так (рис. 2):
 |
| Рис. 2. Неравномерное движение |
Дальше мы рассуждаем следующим образом.
1. Разобьём наш промежуток времени на небольшие отрезки величиной
.
2. Предположим, что на каждом таком отрезке тело движется с постоянной скоростью
. То есть, плавное изменение скорости заменим ступенчатой аппроксимацией*: в течение каждого небольшого отрезка времени тело движется равномерно, а затем скорость тела мгновенно и cкачком меняется.
На рис. 3 показаны две ступенчатые аппроксимации. Ширина ступенек на правом рисунке вдвое меньше, чем на левом.
 |
| Рис. 3. Ступенчатая аппроксимация |
Путь, пройденный за время равномерного движения – это площадь прямоугольника, расположенного под ступенькой. Поэтому путь, пройденный за всё время такого “ступенчатого” движения – это сумма площадей всех прямоугольников на графике.
3. Теперь устремляем к нулю. Ясно, что в пределе наша ступенчатая аппроксимация перейдёт в исходный график скорости на рис. 2. Сумма площадей прямоугольников перейдёт в площадь под графиком скорости; следовательно, эта площадь и есть путь, пройденный телом за время от
до
. (рис. 4
 |
| Рис. 4. Путь при неравномерном движении |
В итоге мы приходим к нужному нам обобщению геометрической интерпретации пути, полученной выше для случая равномерного движения.
| Аппроксимация – это приближённая замена достаточно сложного объекта более простой моделью, которую удобнее изучать. |
Геометрическая интерпретация пути.Путь, пройденный телом при любом движении, равен площади под графиком скорости на заданном промежутке времени.
Посмотрим, как работает эта геометрическая интерпретация в важном частном случае равноускоренного движения.
Задача. Тело, имеющее скорость в начальный момент
, разгоняется с постоянным ускорением
. Найти путь, пройденный телом к моменту времени
.
Решение. Зависимость скорости от времени в данном случае имеет вид:
(2)
График скорости – прямая, изображённая на рис. 5. Искомый путь есть площадь трапеции, расположенной под графиком скорости.
 |
| Рис. 5. Путь при равноускоренном движении |
Меньшее основание трапеции равно . Большее основание равно
. Высота трапеции равна
. Поскольку площадь трапеции есть произведение полусуммы оснований на высоту, имеем:
Эту формулу можно переписать в более привычном виде:
Она, разумеется, вам хорошо известна из темы “Равноускоренное движение”.
Задача. График скорости тела является полуокружностью диаметра (рис. 6). Максимальная скорость тела равна
. Найти путь, пройденный телом за время
.
Решение. Как вы знаете, площадь круга радиуса равна
. Но в данной задаче необходимо учесть, что радиусы полуокружности имеют разные размерности: горизонтальный радиус есть время
, а вертикальный радиус есть скорость
.
Поэтому пройденный путь, вычисляемый как площадь полукруга, равен половине произведения на горизонтальный радиус и на вертикальный радиус:
 |
| Рис. 6. К задаче |
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Путь при неравномерном движении.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Содержание материала
- Формула времени. Решение задач
- Видео
- Формулы для расчета пути и времени движения при неравномерном движении тела
- Скорость
- График пути равномерного движения
- Единицы измерения времени
- Первые часы
- Как люди измеряли время?
- Способы вычисления расстояния и времени
Формула времени. Решение задач
Скорость, время и расстояние — физические величины, взаимосвязаны процессом движения. Виды движений: 1) равномерное (прямолинейное, криволинейное и по окружности), 2) равноускоренное (с постоянным ускорением), 3) гармоническое. Для каждого вида движения своя формула времени.
Время обозначается как t. Единица измерения времени – с (секунды).
Самая простая формула при равномерном прямолинейном движении. Время, необходимое для прохождения пути равняется частному от деления пути на скорость равномерного прямолинейного движения: t = S / v.
При равноускоренном движении время равняется частному от деления разницы конечной и начальной скорости на ускорение: t = (v — v) / a или частному от деления пути на разность конечной и начальной скорости: t = S / (v — v).

Видео
Формулы для расчета пути и времени движения при неравномерном движении тела
При неравномерном движении мы используем определение средней скорости, которую можем найти по формуле
$$upsilon_{ср} = frac{S}{t}$$
Чтобы определить путь при неравномерном движении, нужно среднюю скорость движения умножить на время:
$$large S = upsilon_{ср} t$$
Также мы можем рассчитать время, разделив путь, пройденный телом, на среднюю скорость его движения:
$$t = frac{s}{upsilon_{ср}}$$
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.
Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.
Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.
Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
График пути равномерного движения
Пример графика зависимости пути равномерного движения представлен на рисунке 3.

Здесь $S$ — ось пройденных путей, $t$ — ось времени. По этому графику мы можем найти путь, пройденный телом за определенный промежуток времени. Например, за 1 с тело проходит путь длиной 2 м, за 2 с – 4 м, за 3 с – 6 м.
Зная путь и время, мы можем рассчитать скорость. Для удобства расчета возьмем самый первый отрезок пути: $t = 1 с, s = 2 м$. Тогда,
$upsilon = frac{s}{t} = frac{2 м}{1 с} = 2 frac{м}{с}$.
Единицы измерения времени
Основной единицей измерения момента силы в системах СИ и СГС является: [t]=c
Единицы измерения времени основываются на периоде вращения Земли около своей оси и вокруг Солнца, Луни вокруг Земли. Внесистемные единицы измерения времени: час, минута, сутки и т.д.
Первые часы
Сначала было достаточно палочки, на которой каменным топором можно делать зарубки и тем самым отсчитывать прошедшие дни. Но это скорее был календарь, а не часы.
Первые и самые древние часы – солнечные. Их действие основано на изменении длины тени предметов по мере того, как солнце движется по небосводу. Такие часы представляли собой гномон – длинный шест, воткнутый в землю. Солнечные часы применялись в Древнем Египте и Китае. О них было доподлинно известно уже в 1200 году до нашей эры.

Затем появились водяные, песочные и огненные часы. Работа этих механизмов не была привязана к движению небесных светил. Долгое время водяные часы были главным инструментом для измерения времени.
Первые механические часы были изготовлены китайскими мастерами в 725 году нашей эры. Однако широкое распространение они получили относительно недавно.
В средневековой Европе механические часы устанавливались в башнях соборов и имели только одну стрелку – часовую. Карманные часы появились только в 1675 году (изобретение запатентовал Гюйгенс), а наручные – намного позже.
Как люди измеряли время?
Для измерения времени нужны какие-либо повторяющиеся с одинаковым периодом события. Например, смена дня и ночи. Солнце каждый день встает на востоке и садится на западе, а Луна каждый синодический месяц проходит весь цикл фаз освещенности солнцем — от тоненького серпа полумесяца до полнолуния.
Древним людям ничего не оставалось, как привязать отсчет времени к движению небесных тел и событиям, связанным с ним. А именно – к смене дней, ночей и сезонов года.
В году 4 сезона и 12 месяцев. Именно столько раз за весну, лето, осень и зиму Луна меняет свои фазы.
По мере развития прогресса методы измерения времени совершенствовались, появились солнечные, водяные, песочные, огненные, механические, электронные и, наконец, молекулярные часы.

Способы вычисления расстояния и времени
Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:
S=v*t, где v — понятно что такое,
S — расстояние, которое требуется найти,
t — время, за которое объект прошел это расстояние.
Таким образом вычисляется значение расстояния.
Или вычисляем значение времени, за которое пройдено расстояние:
t=S/v, где v — все та же скорость,
S — расстояние, пройденный путь,
t — время, значение которого в данном случае нужно найти.

Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.
Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.
И это еще не предел!
