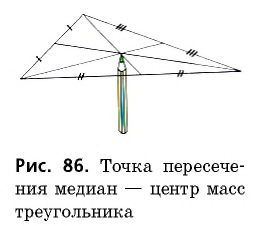
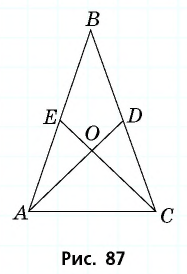
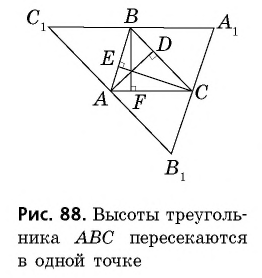
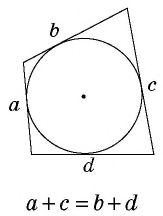
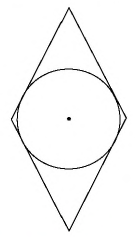
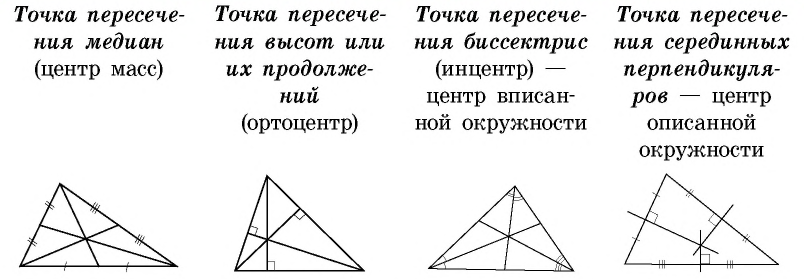
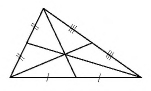
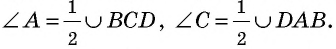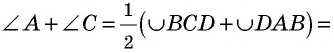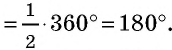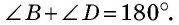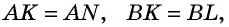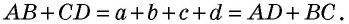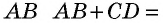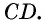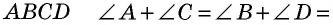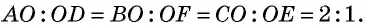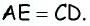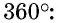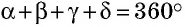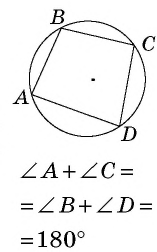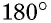Общие сведения о фигуре
Параллелограмм — это четырехугольник на плоскости, у которого присутствует равенство противоположных сторон, причем они лежат на параллельных прямых.
Ромб, прямоугольник и квадрат — его частные случаи. Из него состоят более сложные объемные фигуры. Например, параллелепипед и куб.
Высота параллелограмма — отрезок, который является перпендикуляром, проведенным к нижней стороне геометрической фигуры.

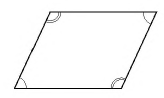
Всего можно провести четыре высоты. Две из них можно провести из вершин углов, которые лежат в параллелограмме и являются тупыми. Другие две высоты проводятся из острых углов (находятся вне фигуры). Углы делятся на шесть типов: острые, прямые, тупые, развернутые, выпуклые и полные.
Первый тип, градусная размерность которого меньше 90, является острым. Если значение равно 90, то он является прямым, и соответствует второму типу.
В случае, когда выполняется условие 90 < a < 180, то угол считается тупым. При равенстве a = 180 — развернутый. При неравенстве 180 < a < 360 — выпуклый (смежный с ним угол является острым).
Полным называется угол, градусная мера которого соответствует 360.
Для решения задач и выполнения расчетов необходимо знать следующие аспекты: свойства и признаки параллелограмма, а также уметь находить его углы, стороны, диагонали, периметр и площадь. Кроме того, следует знать не только основные соотношения фигуры, которая вписана в окружность, но и в случае, когда окружность находится внутри нее.
Информация о признаках
Признаки позволяют выяснить принадлежность фигуры к параллелограмму. Например, существует произвольный четырехугольник, и нужно выяснить, является ли он параллелограммом. Необходимо отметить, что при условии совпадения хотя бы одного из признаков, этот четырехугольник является им. Проверку следует производить, руководствуясь следующими утверждениями:
- Параллельность и равенство двух любых сторон.
- Равенство противолежащих сторон.
- Углы, которые являются противолежащими, равны.
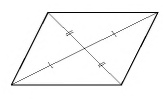
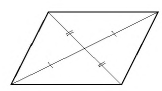
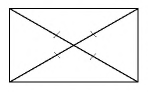
- Точка пересечения диагоналей (центр симметрии) делит их на два равных отрезка.
- При выполнении равенства (d — диагонали): (d1)^2 + (d2)^2 = a 2 + b 2 + c 2 + d 2 .
Последний признак можно записать для упрощения расчетов следующим образом: sqr (d1) + sqr (d2) = 2 * (a 2 + b 2 ). Равенство можно упростить, поскольку противоположные стороны равны.
Основные свойства
Для решения задач и проектирования деталей необходимо знать основные свойства параллелограмма. Некоторые из них были получены при доказательстве и следствиях из теорем. К ним относятся следующие:

- Ромб, квадрат и прямоугольник — параллелограммы.
- Противоположные стороны одинаково равны и параллельны.
- Противолежащие углы равны.
- Суммарное значение градусной меры всех внутренних углов параллелограмма составляет 360.
- Сумма углов, прилегающих к одной из вершин, составляет 180 градусов.
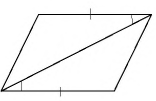
- Диагональ делит фигуру на два треугольника, которые равны между собой по всем признакам.
- Две диагонали (одна — большая, а другая — меньшая) делят параллелограмм на две пары треугольников, которые равны между собой.
- Диагонали фигуры пересекаются, а точка пересечения делит их пополам (через нее можно провести среднюю линию, которая параллельна сторонам).
- Точка пересечения двух диагоналей является симметрией фигуры.
- Биссектрисы соседних углов пересекаются под углом в 90 градусов, а противоположных являются параллельными.
- sqr (d1) + sqr (d2) = 2 * ((a)^2 + (b)^2).
Однако для выполнения расчетов признаков и свойств параллелограмма недостаточно. В некоторых случаях требуется вычислить периметр и площадь фигуры. Соотношения используются не только в учебных заведениях, но и в научных исследованиях. Простым примером является нахождение площади поперечного сечения проводника. Это может понадобиться для дальнейшего вычисления электрического сопротивления.
Определение периметра
Периметром (P) любой фигуры является сумма длин всех ее сторон. Следовательно, для параллелограмма найти это значение является несложным. Базовая формула периметра параллелограмма имеет следующий вид: P = a + b + c + d = 2 * (a + b). Кроме того, существуют и другие соотношения для нахождения этой величины:

- Если известны одна из сторон и две диагонали.
- Нахождение периметра через сторону, высоту и синус угла.
В первом случае соотношение для стороны «a» записывается следующим образом: P = 2 * a + sqrt [2 * (d1 * d1 + d2 * d2 — 2 * a^(2))]. Для «b» запись изменяется таким образом: P = 2*b + sqrt [2 * (d1^(2) + d2^(2) — 2 * b^(2))].
Во втором случае, когда известна сторона «а», угол BAD и высота Ha, периметр записывается формулой вида: P = 2 * [a + Ha / sin (BAD)]. Для стороны «b», угла BAD и высоты Hb равенство принимает следующий вид: P = 2 * [b + Hb / sin (BAD)]. Если проанализировать последние два соотношения, то величины «Hb / sin (BAD)» и «Hа / sin (BAD)» являются стороной «b» и «a» соответственно.
Вычисление площади
Площадь параллелограмма (S) — это пространство, которое ограничено его сторонами, и равно произведению одной из сторон на высоту, проведенную к одноименному основанию. Базовая формула нахождения значения S является следующей: S = a * Ha = b * Hb. Кроме того, существует два способа нахождения ее значения, когда известны следующие величины:

- По сторонам и углу.
- Две диагонали и синус углов f или g между ними.
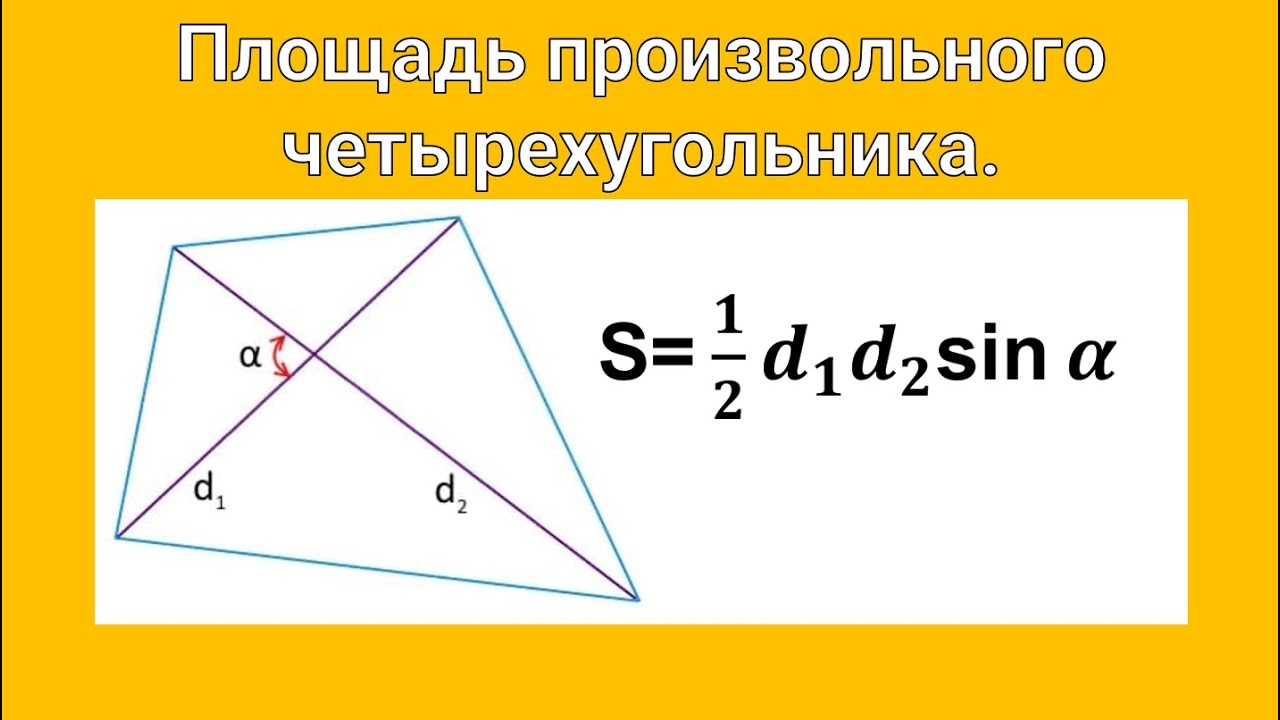
Можно записать соотношение следующим образом: S = a * b * sin (BAD) = a * b * sin (ABC). В последнем случае математическая запись площади имеет следующий вид: S = 0,5 * d1 * d2 * sin (f) = 0,5 * d1 * d2 * sin (g).
Кроме того, существует формула Герона, которая позволяет вычислить площадь параллелограмма. Для этого необходимо вычислить полупериметр (p) треугольника со сторонами a, b и d: p = P / 2 = (a + b + d).
Формула имеет вид: S = sqrt[p * (p — a) * (p — b) * (p — d)].
Соотношения сторон и диагоналей
В некоторых задачах необходимо определить неизвестные длины сторон или диагонали. Можно попытаться вывести соотношения, однако эта процедура занимает некоторое время. Следовательно, проще воспользоваться уже готовыми формулами. Стороны параллелограмма можно определить четырьмя основными выражениями. При этом следует знать следующие величины:
- Диагонали и угол.
- Другую сторону и диагонали.
- Высоту и значение синуса угла в градусах.
- Площадь и высоту.
В первом случае для вычисления длины стороны «а», следует воспользоваться следующей формулой: a = [sqrt (d1 *d1 + d2 * d2 — 2 * d1 * d2 * cos (f))] / 2 = [sqrt (d1 * d1 + d2 * d2 + 2 * d1 * d2 * cos (g))] / 2. Значение стороны «b» вычисляется немного иначе: b = [sqrt (d1 * d1 + d2 * d2 + 2 * d1 * d2 * cos (f))] / 2 = [sqrt (sqr (d1) + sqr (d2) — 2 * d1 * d2 * cos (g))] / 2.
При известных значениях диагоналей и одной из сторон, соотношение имеет более простой вид, чем в первом случае: a = [sqrt (2 * (sqr (d1) + sqr (d2) — 2 * b 2 ))] / 2 и b = [sqrt (2 * (sqr (d1) + sqr (d2) — 2 * a 2 ))] / 2.
Когда известны высоты и угол BAD, можно найти стороны a и b: a = Hb / sin (BAD) и b = Ha / sin (BAD). Если известны площадь и высота, то соотношение принимает следующий вид: a = S / Ha и b = S / Hb.
Диагональ параллелограмма — отрезок, который соединяет его противоположные внутренние углы. Фигура имеет две диагонали, одна из которых длинная (d1), а другая является короткой (d2). Их можно найти, используя 4 соотношения. Это возможно в том случае, когда известны следующие данные:
- Стороны и косинус угла ABC.
- Cos (BAD) и стороны.
- Одну известную диагональ и стороны.
- Площадь, диагональ и угол между d1 и d2.
В первом случае можно воспользоваться следующими формулами (теорема косинусов): d1 = sqrt[a 2 + b 2 — 2 * a * b * cos (ABC)] и d2 = sqrt[a 2 + b 2 + 2 * a * b * cos (ABC)]. Во втором: d1 = sqrt[a 2 + b 2 + 2 * a * b * cos (BAD)] и d2 = sqrt[a 2 + b 2 — 2 * a * b * cos (BAD)].
Когда известны две стороны и одна из диагоналей, то можно воспользоваться третьим случаем: d1 = sqrt[2 * a 2 + 2 * b 2 — (d2)^2] и d2 = sqrt[2 * a 2 + 2 * b 2 — (d1)^2]. В последнем случае равенства для нахождения диагоналей имеют такой вид: d1 = 2 * S / [(d2) * sin (f)] = 2 * S / [(d2) * sin (g)] и d2 = 2 * S / [(d1) * sin (f)] = 2 * S / [(d1) * sin (g)].
Параллелограмм и окружность
Существуют определенный тип задач, в которых речь идет о параллелограмме и окружности. Всего бывает два варианта: вписанная и описанная окружности. Следует отметить, что не всегда это возможно. Существуют определенные условия, при которых возможны такие операции. Кроме того, следует обратить особое внимание на дополнительные свойства, которые появляются при комбинации данных фигур. Можно не только чередовать комбинации, но и использовать одновременно.
Для решения сложного типа задач и выполнения расчетов, в некоторых случаях рекомендуется применять вписанные и описанные окружности. Например, при проектировании деталей, необходимо полностью подогнать ее размеры, поскольку они должны быть правильной формы. При помощи окружности (вписанной или описанной) можно выявить ряд дефектов, которые могут привести к некорректной работе механизма.
Круг и прямоугольник
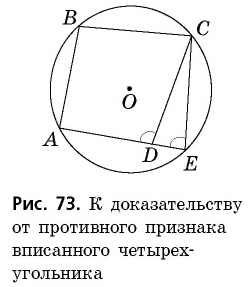
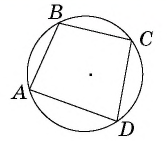
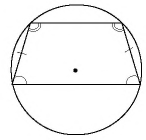
Главное условие: любой четырехугольник можно вписать в окружность, когда сумма его двух противоположных углов составляет 180 градусов. У параллелограмма есть одно свойство: сумма углов, которые прилегают к любой из вершин, составляет 180 градусов. Кроме того, сумма всех его углов составляет 360, а, следовательно, сумму противоположных углов составляет 360 — 180 = 180 (градусов).
Однако при попытке описать около него окружность ничего не выйдет, поскольку есть одно свойство: противоположные углы у него равны. Ими могут быть тупые и острые. Сумма градусной меры тупых углов будет больше 180, а острых — меньше.
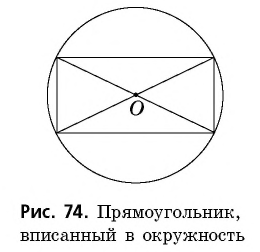
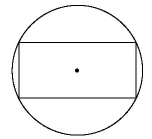
Когда противоположные углы будут равны 90, то значит их сумма составит 180. В этом случае нужно рассматривать частный случай — прямоугольник.
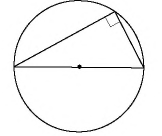
Появляется очень важное свойство: диагонали прямоугольника пересекаются и точкой пересечения (центром окружности) делятся пополам, а также являются диаметрами окружности.
Для нахождения радиуса окружности, следует воспользоваться следующим соотношением (при условии, что известны стороны прямоугольника): R = [sqrt (a 2 + b 2 )] / 2 = d / 2. Величина «d» является диаметром.
Ромб и квадрат
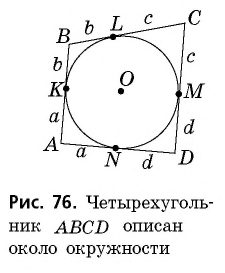
В параллелограмм также можно вписать окружность. Однако для этого необходимо выполнение определенного условия. Оно заключается в следующем: суммы противолежащих сторон параллелограмма должны быть равны. Нужно отметить, что это выполняется только для ромба и квадрата.

Ромбом называется параллелограмм, стороны которого равны, а углы не равны 90 градусов. Квадрат — геометрическая фигура, у которой все стороны и углы равны. Из последнего определения можно найти значение градусной меры одного угла: 360 / 4 = 90.
Последняя фигура является частным случаем ромба. Радиус окружности находится с помощью формулы: r = S / p = 0,5 * H. В этом соотношении переменные S, p и H — площадь, полупериметр и высота соответственно.
Для нахождения S можно воспользоваться такими соотношениями:
- Известны длина стороны (а) и высота (H): S = a * H.
- Через диагонали d1 и d2: S = d1 * d2 / 2.
Полупериметром фигуры называется половина от значения ее периметра. Соотношение записывается таким образом: p = P / 2 = 4 * a.
Таким образом, знать основные свойства и признаки параллелограмма необходимо, поскольку от этого может зависеть не только качество сдачи экзаменов, решения задач, но и проектирование различных деталей.
Источник: https://nauka.club/matematika/parallelogramm-ego-svoystva.html
площа па
Параллелограммом называют четырехугольник у которого противоположные стороны параллельны между собой. Основные задачи в школе по данной теме заключаются в вычислении площади параллелограмма, его периметра, высоты, диагоналей. Указанные величины и формулы для их вычисления будут приведены ниже.
Свойства параллелограмма
Противоположные стороны параллелограмма как и противоположные углы равны между собой: AB=CD, BC=AD,
Еще одно замечательное свойство которое часто применяют при решении задач состоит в том, что сумма квадратов диагоналей в параллелограмме равна сумме квадратов всех сторон:
AC^2+BD^2=2*(AB^2+BC^2).
Основные признаки параллелограммов:
1. Четырехугольник у которого противоположные стороны попарно параллельны является параллелограммом. 2. Четырехугольник с равными противоположными сторонами является параллелограммом. 3. Четырехугольник с равными и параллельными противоположными сторонами является параллелограммом. 4. Если диагонали четырехугольника в точке пересечения делятся пополам то это параллелограмм.
5. Четырехугольник у которого противоположные углы попарно равны является параллелограммом
Биссектрисы параллелограмма
Биссектрисы противоположных углов в параллелограмме могут быть параллельными или совпадать.
Биссектрисы соседних углов ( прилегающие к одной стороне ) пересекаются под прямым углом (перпендикулярные).
Высота параллелограмма
Высота параллелограмма — это отрезок который проведен с угла перпендикулярно к основанию. Из этого следует что из каждого угла можно провести две высоты.
Формула площади параллелограмма
- Площадь параллелограмма равна произведению стороны на высоту проведенную к ней. Формула площади следующая
- Вторая формула не менее популярная при вычислениях и определяется так: площадь параллелограмма равна произведению соседних сторон на синус угла между ними
- На основе приведенных формул Вы будете знать как вычислить площадь параллелограмма.
Периметр параллелограмма
Формула для вычисления периметру параллелограмма имеет вид то есть периметр равен удвоенному значению суммы сторон. Задачи на параллелограмм будут рассмотрены в соседних материалах, а пока изучайте формулы. Большинство задач по вычислению сторон, диагоналей параллелограмма достаточно просты и сводятся к знанию теоремы синусов и теоремы Пифагора.
Посмотреть материалы:
Источник: https://yukhym.com/ru/geometriya/perimetr-ploshchad-parallelogramma.html
Формулы параллелограмма
Для расчёта всех основных параметров параллелограмма воспользуйтесь калькулятором.
- Противоположные стороны параллельны и равны.
- Противоположные углы равны
- Точка пересечения диагоналей делит их пополам.
- Сумма углов четырехугольника прилегающих к любой стороне равна 180°
- В четырехугольнике сумма квадратов диагоналей равна сумме квадратов его сторон
- Сумма углов параллелограмма равна 360°
- Каждая диагональ делит параллелограмма на два равных треугольника
- Биссектрисы противоположных углов параллелограмма всегда параллельны
- Биссектрисы соседних углов параллелограмма всегда пересекаются под прямым углом (90°)
Длины сторон через диагонали и угол между ними

Длина стороны через диагонали и известную сторону
$$ AB = sqrt{AC^2 + BD^2 — 2 * BC^2 over 2} $$ $$ BC = sqrt{AC^2 + BD^2 — 2 * AB^2 over 2} $$
Длины сторон через высоты и угол между сторонами

Длина диагонали через стороны и углы между ними

Длина диагонали через стороны и известную диагональ
$$ AC = sqrt{2 * AB^2 + 2 * BC^2 — BD^2} $$ $$ BD = sqrt{2 * AB^2 + 2 * BC^2 — AC^2} $$
Длина диагонали через площадь параллелограмма, известную диагональ и угол между диагоналями


- Косинус острого угла
- Косинус тупого угла
- Синус острого и тупого угла через площадь и стороны параллелограмма
$$ cos(α) = {AB^2 + BC^2 — BD^2 over 2 * AB * BC} $$ $$ cos(β) = {AB^2 + BC^2 — AC^2 over 2 * AB * BC} $$ $$ sin(α) = sin(β) = {S over AB * BC} $$ 
- Косинус острого угла через стороны и диагонали
- Косинус тупого угла через стороны и диагонали
- Синус острого и тупого угла через площадь и диагонали
$$ cos(α) = {AC^2 + BD^2 — 4 * AB^2 over 2 * AC * BD} $$ $$ cos(α) = {BC^2 — AB^2 over AC * BD} $$ $$ cos(β) = {AC^2 + BD^2 — 4 * BC^2 over 2 * AC * BD} $$ $$ cos(β) = {AB^2 — BC^2 over AC * BD} $$ $$ sin(α) = sin(β) = {2 * S over AC * BD} $$


Источник: http://calc-online24.ru/formula/parallelogram
Периметр параллелограмма
Параллелограмм это геометрическая фигура имеющая четыре параллельные стороны, противоположных друг другу. В школьной программе все задания по решению параллелограмма, направлены на нахождение высоты, площади, диагонали и периметра. О них и пойдет речь.
Параллелограмм обладает свойствами, такими как:
В параллелограмме и углы и стороны, которые противоположны между собой одинаковы: АВ = CD, BC =AD. Так же как углы АВС = ADC и ВАD = BCD.
Диагонали проведенные из углов параллелограмма в месте пересечения разделятся на две одинаковые части. АО = ОС, ОВ = OD.
Сумма двух углов, одной стороны всегда 180 градусов.
углы: А + В = 1800, В + С = 1800, С + D =1800, A + D = 1800 .
Любая диагональ разделяет параллелограмм на две одинаковые фигуры (треугольник) как по площади так и по размеру.
-
У параллелограмма есть несколько основных признаков.
Зачастую встречается такое интересное свойство как, сума диагоналей в квадрате одинакова с суммой сторон в квадрате.
АС2 + BD2 = (AB2 + BC2). AC2 + BD2 = 2 * (AB2 + BC2)
— Четырехугольная фигура с противоположными сторонами параллельными друг другу и есть параллелограмм. — Четырехугольная фигура имеющая одинаковые противоположные стороны, есть параллелограмм.
— Четырехугольная фигура имеющая одинаковые параллельные и противоположные стороны, есть параллелограмм.
— Когда встречающиеся диагонали четырехугольной фигуры в месте пересечения разделяются на равные части. Данная фигура является параллелограммом.
— Четырехугольная фигура в которой противоположные углы одинаковы называется параллелограммом.
- Периметр параллелограмма находится по формуле
Р = 2 (а+b)
- что означает что периметр равняется двойной сумме сторон.
- Биссектриса параллелограмма
Из школьной программы помню определение которое засело в памяти на всю жизнь — Биссектриса это крыса, что ходит по углам и делит угол пополам. Если же говорить научным языком, то: Биссектрисы углов находящихся на одной стороне встречаются в точке пересечения под углом в 90 градусов.
Так же они могут совпадать и быть параллельны друг другу.
Так же в параллелограмме можно найти высоту, она обозначается в виде отрезка исходящего из угла к основанию, следовательно, от каждого угла их можно провести две.
Площадь параллелограмма это произведение стороны и высоты приведенную к ней. Находится по формуле.
S = a * ha = b * hb
Есть еще один способ вычисления, но им не так часто пользуются в расчетах. Она звучит как площадь параллелограмма это произведение рядом лежащих сторон умноженный на синус угла находящегося между ними.
S = a * b * sin(?) = a * b * sin(?)
Все приведенные в данной статье формулы помогут Вам в решении различных задач по нахождению величин параллелограмма, это не сложно но очень интересно.
Заметка: если Вы находитесь в поиске персонала. Империя кадров поможет вам в этом вопросе. Просто перейдите по ссылке персонал временный (http://www.imperia.ru/client/temp_staff/) и узнайте подробнее.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Источник: https://reshit.ru/perimetr-parallelogramma
Формула площади и периметра параллелограмма

Параллелограмм – это четырехугольник, у которого стороны попарно параллельны. Частными вариантами параллелограмма являются ромб, прямоугольник и квадрат.
Любой параллелограмм характеризуется сторонами a и b и высотой h (см. рисунок). Также при решении задач может понадобиться угол α между сторонами параллелограмма. Именно эти характеристики используются в формулах параллелограмма при вычислении площади и периметра.
Формула периметра параллелограмма
Периметр P параллелограмма можно получить, зная его стороны:
Формулы площади параллелограмма
- Площадь параллелограмма S можно вычислить, зная его сторону и высоту h, проведенную к этой стороне:
- Также площадь параллелограмма S можно вычислить, зная его стороны и угол α между ними:
- Поделитесь статьей с одноклассниками «ПАРАЛЛЕЛОГРАММ формулы площади и периметра».

Параллелограмм – это четырёхугольник, у которого противолежащие стороны попарно параллельны, т.е. лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Формула площади параллелограмма:
Площадь геометрической фигуры – часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади параллелограмма выражается числом заключающихся в него квадратных единиц.
1) Площадь параллелограмма равна произведению длины его основания на длину высоты (a, h).
- S – площадь параллелограмма
- a – длина основания
- h – длина высоты
Формула периметра параллелограмма:
Периметр геометрической фигуры – суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.
1) Периметр параллелограмма равен удвоенной сумме 2-х его смежных сторон (a, b).
- P – периметр параллелограмма
- a – длина 1-ой стороны параллелограмма
- b – длина 2-ой стороны параллелограмма
Параллелограмм – это четырехугольник, противоположные стороны которого параллельны и не образуют прямой угол. Диагонали в точке пересечения делятся пополам, но они не равны и не перпендикулярны.
Высоты – это перпендикулярные расстояния между двумя противоположными сторонами, их длина определяется с помощью функции синуса прямоугольных треугольников, которые они совместно со сторонами параллелограмма образуют.
Функция кнопки insert 7 букв сканворд
Формулы
- P – периметр
- S – площадь
- a,b – стороны
- d1,2 – диагонали
- h a – высота на сторону a
- h b – высота на сторону b
При предоставлении услуг веб-сайт «Calculat.org» использует файлы куки.
Вы не любите рекламу? Мы ее тоже не любим, тем не менее доходы от рекламы предоставляют возможность функционирования нашего веб-сайта и бесплатного обслуживания наших посетителей. Пожалуйста, подумайте, не стоит ли отменить блокировку рекламы на этом веб-сайте. Спасибо.
- Мария Сухоруких
- Распечатать
Источник: https://4apple.org/formula-ploshhadi-i-perimetra-parallelogramma/
Формула периметра параллелограмма
Параллелограмм это четырехугольник, у которого противоположные стороны попарно параллельны.
По свойству параллелограмма его противоположные стороны равны. Поэтому для нахождения периметра параллелограмма ABCD со сторонами AB = CD = a и AC = BD = b будет справедлива формула:
- Чтобы найти периметр параллелограмма, нужно сумму двух непараллельных сторон умножить на два.
- [ P_{ riangle ABCD} = a+b+a+b = 2cdot a+2cdot b=2cdot left (a+b
ight) ] - [ LARGE P_{ riangle ABCD} = 2cdot left (a+b
ight) ] - где: P — периметр параллелограмма a — длина малой стороны параллелограмма b — длина большой стороны параллелограмма
Формулы периметраРасчёт Площадь Математика Тригонометрия Формулы Теория
Найти периметр параллелограмма ABCD со сторонами a = 7.62 см и b = 9.33 см.
Для нахождения периметра параллелограмма воспользуемся формулой ( P_{ riangle ABCD} = 2cdot left (a+b
ight) )
Подставляя данные задачи в эту формулу, получим:
( P_{ riangle ABCD} = 2cdot left (7.62 + 9.33
ight) = 2 cdot 16.95 = 33.9 ) см
( P_{ riangle ABCD} = 33.9 ) см
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
- Формула периметра треугольникаПериметр треугольника равен сумме длин его сторон
- Формула периметра равнобедренного треугольникаПериметр равнобедренного треугольника равен сумме длин его сторон
- Формула периметра равностороннего треугольникаПериметр равностороннего треугольника равен тройной сумме длины его стороны
- Периметр круга радиуса r равен удвоенному произведению радиуса r на число пи (~3.1415)
- Формула периметра трапецииПериметр трапеции равен сумме длин всех четырех сторон
- Формула периметра прямоугольникаПериметр прямоугольника — это сумма длины и ширины, умноженная на «2».
- Формула периметра квадратаПериметр квадрата равен сумме 4-х длин его сторон или произведению длины любой его стороны на четыре (так как у квадрат длины всех сторон равны)
- Периметр ромба равен сумме длин всех его сторон, или длинна стороны умноженная на 4
- Сила взаимодействия двух неподвижных точечных электрических зарядов в вакууме прямо пропорциональна произведению их модулей и обратно пропорциональна квадрату расстояния между ними.
- Согласно нормам Всемирной Организацией Здравоохранения (ВОЗ)
- 1 Ампер это сила тока, при которой через проводник проходит заряд 1 Кл за 1 сек.
- 1 ом представляет собой электрическое сопротивление между двумя точками проводника, когда постоянная разность потенциалов 1 вольт, приложенная к этим точкам, создаёт в проводнике ток 1 ампер, а в проводнике не действует какая-либо электродвижущая сила.
- Сколько в ампере ватт, как перевести амперы в ватты и киловаттыМощность – это скорость расходования энергии, выраженная в отношении энергии ко времени: 1 Вт = 1 Дж/1 с. Один ватт равен отношению одного джоуля (единице измерения работы) к одной секунде.
Источник: https://calcsbox.com/post/formula-perimetra-parallelogramma.html
Калькулятор периметра параллелограмма через диагонали
Параллелограмм — четырехугольник, стороны которого являются попарно параллельными отрезками. Параллелограмм представляет собой фигуру, частными случаями которой являются ромб, прямоугольник и квадрат — четырехугольники, знакомые нам с самого детства.
Геометрия параллелограмма
Четырехугольник считается параллелограммом, если соблюдается хотя бы одно из нижеперечисленных условий:
- противоположные стороны параллельны друг другу;
- противоположные стороны равны друг другу;
- пересекающиеся диагонали в точке пересечения делятся пополам.
Параллелограмм и его частные случаи — наиболее встречающаяся в реальной жизни фигура.
В трехмерном пространстве параллелограмм превращается в четырехугольную призму, форму которой имеет большинство рукотворных объектов: кирпичи, системные блоки компьютеров, стены, книги или коробки.
Косоугольные фигуры встречаются реже, однако форму таких параллелограммов имеют грани резцов металлообрабатывающих станков или элементы дизайна и декора, такие как ковры или геометрические узоры на стенных покрытиях.
Параллелограмм также можно увидеть прямо на улице. Прямоугольные или косоугольные окна — это параллелограммы. Кроме того, прямо под ногами вы можете увидеть один из наиболее банальных воплощений ромба в реальности — тротуарную плитку. Столь широкое распространение данной фигуры в повседневной жизни делает вопрос определения площади и периметра параллелограмма актуальной задачей.
Периметр параллелограмма
Периметр представляет собой количественную оценку общей длины сторон любой фигуры. Параллелограмм имеет четыре стороны, которые попарно равны и параллельны друг другу. Исходя из этого, периметр геометрической фигуры выражается простой формулой:
P = 2 (a + b)
Путем подстановок мы можем найти стороны геометрической фигуры при помощи диагоналей и одной из ее высот. Наш онлайн-калькулятор позволяет определить периметр параллелограмма, зная три переменных: две диагонали и высоту четырехугольника.
Естественно, что вы можете воспользоваться и самой простой формулой для подсчета периметра, однако программный код калькулятора требует введения 3 переменных, поэтому для его корректной работы помимо длин сторон введите значение высоты, равное ha = b или hb = a.
К примеру, если a = 3, b = 4, то укажите, что hb = 3 или ha = 4. Такая подстановка превратит параллелограмм в квадрат, однако при известных сторонах периметр не зависит от величины углов геометрической фигуры, что позволит нам корректно рассчитать требуемый параметр.
Рассмотрим пару примеров.
Примеры из жизни
Пример №1
Давайте определим периметр четырехугольника, зная, что его диагонали равны 3 и 5 см, а высота фигуры составляет 2 см. Свойства четырехугольника подсказывают нам, что высота численно не может быть больше длин диагоналей, поэтому параметр h всегда меньше и d1, и d2. Введем эти данные в форму калькулятора и получим мгновенный ответ:
P = 11,45 см
Зная эти переменные, мы можем определить периметр любого параллелограмма.
Пример №2
Определить периметр абстрактного параллелограмма можно и по стандартной, самой простой формуле. Если стороны четырехугольника равны a = 3 и b = 4, то нам понадобится ввести эти данные в калькулятор, а также указать, что ha = 4. Мы получим ответ в виде:
P = 14,
что полностью соответствует расчетам по классической формуле P = 2 (a + b).
Заключение
Параллелограмм и его частные случаи занимают в деятельности человека важное место.
В реальной жизни вам понадобится определять периметры и площади прямоугольников, квадратов, ромбов или параллелограммов, которые являются гранями соответствующих призм или полноценными фигурами на плоскости.
Используйте наши калькуляторы для выполнения расчетов при решении повседневных, школьных или профессиональных задач.
Источник: https://BBF.ru/calculators/131/
Как найти периметр параллелограмма
В школьной программе, по геометрии, можно часто встретить задания, в которых необходимо найти периметр параллелограмма. Для его нахождения нужно использовать всего лишь одну простую формулу.
1
Что такое параллелограмм?
- Параллелограмм – в переводе с греческого означает параллельный.
- По своей структуре параллелограмм – это четырехугольник, стороны которого параллельны друг другу. Две его боковые стороны ложатся наискось. Каждая из сторон равна друг другу, т. е, равны противоположные углы. Но каждая из прилегающих сторон может отличаться размером.
- В основном четырехугольник обозначается большими заглавными буквами ABCD.
- Еще одной особенностью параллелограмма, является тот факт, что он может являться квадратом, прямоугольником или ромбом.
- Чтобы вычислить является ли четырехугольник параллелограммом, необходимо использовать правила нахождения параллелограмма. Одним из таких правил является тот факт, когда его диагонали пересекаются и точкой пересечения делятся пополам.
- Считается, что общая сумма углов, которые лежат параллельно, должна равняться 180 °С, т.е. A + B + C + D = 180 °С. Чтобы вычислить, нужно использовать правило параллельных прямых.
2
Что такое площадь параллелограмма?
- Площадью параллелограмма называется геометрическая фигура, у которой есть основание, высота, а также боковые стороны равны между собой.
- Для того, чтобы приступить к вычислению площади параллелограмма необходимо знать его высоту, а также измерить боковые стороны.
- Существуют специальные теоремы и доказательства, при помощи которых легко вычислить площадь параллелограмма.
3
Как найти периметр параллелограмма?
- Чтобы найти общую численную характеристику параллелограмма необходимо использовать формулу. Такая формула может изменяться, зависимости от заданных значений.
- Чтобы найти периметр необходимо воспользоваться основной формулой: P = 2 * (a + b), где а – верхняя сторона, b – боковая сторона.
- Например, одна из боковых сторон параллелограмма – а равна 4 см, а сторона b, которая перпендикулярно ей – 6 см. Вычисли периметр, используя формулу: a = 6 см, b = 4 см. P = 2 * (6+4) = 10 * 2 = 20 см.
- Значит, периметр данного параллелограмма будет равен 20 см.
- Значение периметра может измеряться при помощи единицы измерения длины.
- Периметр параллелограмма всегда равен удвоенной сумме двух его сторон.
Кроме периметра, также при помощи формул можно найти любое значение данной геометрической фигуры: высоту, площадь, площадь по вписанной окружности и другие необходимые параметры.
Источник: https://sovetclub.ru/kak-najti-perimetr-parallelogramma
Параллелограмм и его виды
50. Построим две пары параллельных прямых: AB ∥ CD и AD ∥ BC (чер. 57). Совокупность этих четырех прямых с их четырьмя точками пересечения составляют фигуру, называемую параллелограммом. На чер. 57 имеем параллелограмм ABCD. Прямые, его составляющие, называются сторонами параллелограмма; иногда под этим названием понимают не всю бесконечную прямую AB, а только ее отрезок между точками A и B. Точки пересечения сторон называются вершинами параллелограмма. Параллелограмм выделяет из плоскости определенную ее часть, называемую его площадью. Параллелограмм имеет 4 внутренних угла; поэтому иногда дают определение параллелограмма в следующей форме:
Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны.
Параллелограмм является, следовательно, частным видом общего понятия «четырехугольник»; мы легко можем построить вообще какой-нибудь четырехугольник, выделяющий из плоскости определенную ее часть: для этого надо построить какой-нибудь отрезок AB (чер. 58), из точки A построить какой-либо новый отрезок AC, составляющий с AB угол, отличный от выпрямленного, из точки C также построить новый отрезок CD, чтобы точка D лежала по ту же сторону прямой AC (бесконечной), как и точка B, и, наконец, построить отрезок BD, концами которого служат уже построенные точки B и D. То же можно выполнить иначе: взять 4 произвольных точки A, B, D и C и соединить их попарно прямыми, каждую с двумя соседними, наблюдая лишь, чтобы эти прямые выделяли из плоскости определенную часть.
О четырехугольниках и вообще о многоугольниках смотри гл. VII.
51. Изучение углов параллелограмма. Пронумеруем внутренние углы цифрами 1, 2, 3 и 4 и возьмем еще два из внешних углов: ∠5 и ∠6 (чер. 57). Тогда:
1) ∠1 + ∠4 = выпрямл. углу; 2) ∠1 и ∠2 = выпрямленному углу и т. д.
В самом деле, углы 1 и 4 суть внутренние односторонние при параллельных AB и DC и секущей AD, а мы знаем (п. 33), что сумма таких углов равна выпрямленному; то же применимо и к углам 1 и 2, которые являются внутренними односторонними при параллельных AD и BC и секущей AB. Можно то же применить и к парам углов 2 и 3 или к 3 и 4.
2) ∠1 = ∠3 и ∠2 = ∠4.
Так как ∠1 = ∠5, как соответственные при параллельных AB и DC и секущей AD, но ∠5 = ∠3, как внутренние накрест-лежащие углы при параллельных AD и BC и секущей CD, то ∠1 = ∠3; также найдем: ∠4 = ∠6 и ∠6 = ∠2, следов., ∠4 = ∠2.
Эти результаты можно выразить словами:
В параллелограмме: 1) два соседних угла в сумме составляют выпрямленный угол и 2) два противоположных угла равны между собою.
52. Изучение сторон параллелограмма. Здесь мы будем рассматривать стороны, как отрезки, а потому изобразим параллелограмм так, как на чер. 59.
Точки A, B, C и D (чер. 57), кроме сторон, определяют еще прямые AC и BD (на чер. 57 они не начерчены), называемые диагоналями параллелограмма. Построив только одну из них BD (чер. 59), получим два треугольника: ∆ABD и ∆DBC, у которых одна сторона BD общая. Кроме того, пронумеровав углы, составляемые диагональю BD со сторонами параллелограмма, как на чертеже, найдем ∠1 = ∠2, как внутренние накрест-лежащие при параллельных AB и DC и секущей BD, затем ∠3 = ∠4, как внутренние накрест-лежащие при параллельных AD и BC и секущей BD. Следовательно два угла (∠1 и ∠3) и сторона между ними BD одного треугольника (∆ABD) соответственно равны двум углам (∠2 и ∠4) и стороне между ними (DB) другого треугольника (∆CDB), поэтому (п. 47) и ∆ABD = ∆CDB. Отсюда заключаем, что и их остальные части равны, причем равные стороны должны лежать против равных углов: AD (против ∠1 в ∆ABD) должна, следовательно, равняться BC (против ∠2 в ∆CDB) и также AB (против ∠3) равняется DC (против ∠4). Этот результат можно выразить словами:
Параллельные стороны параллелограмма равны между собою.
53. В упражнениях 3 и 4 п. 34 мы уже строили параллелограмм. Но построение параллельных прямых несколько длинно. Теперь является возможным ускорить построение параллелограмма. Возьмем произвольный угол A (чер. 60) и на сторонах его отложим два произвольных отрезка AB и AC; затем, принимая B за центр, построим окружность радиусом, равным отрезку AC, и, принимая C за центр, построим другую окружность, радиусом, равным отрезку AB. Наконец, одну из точек пересечения этих окружностей, ту именно, которая лежит внутри взятого угла A, соединим прямыми DC и DB с точками C и B. На нашем чертеже даны только дуги этих кругов, которых достаточно для определения положения точки D; на практике так всегда и поступают. Тогда получим четырехугольник DBAC, выделяющий из плоскости ее определенную часть; согласно построению, 1) BD = AC и 2) AB = CD. Возникает вопрос: построен ли у нас параллелограмм, или нет?
Для решения этого вопроса построим диагональ CB; тогда получим 2 треугольника: ACB и DBC, у которых сторона CB общая и, согласно построению, AC = BD и AB = CD, т. е. 3 стороны одного треугольника равны соответственно трем сторонам другого, а такие треугольники, мы знаем (п. 46), равны, т. е. ∆ACB = ∆CBD. Отсюда заключаем о равенстве углов 1 и 2 (против равных сторон); следов., AC ∥ BD, так как ∠3 = ∠4, и, следов., AB ∥ CD, так как ∠3 и ∠4 суть внутренние накрест-лежащие углы при прямых AB и CD и секущей CB. Отсюда следует, что ACDB есть параллелограмм, т. е.:
Если построен 4-угольник, выделяющий из плоскости определенную часть, у которого противоположные стороны равны, то этот 4-угольник есть параллелограмм.
54. Упражнения. Надо освоиться с выше данным построением параллелограмма и выполнять это построение быстро и свободно.
- На данном угле построить параллелограмм. Много ли таких параллелограммов возможно построить?
- Построить параллелограмм на данной стороне. Много ли возможно построить таких параллелограммов?
- Построить параллелограмм по данной стороне и по углу. Много ли таких параллелограммов можно построить?
- Построить параллелограмм по двум сторонам. Много ли таких параллелограммов можно построить?
- Построить параллелограмм по двум сторонам и углу между ними.
- Построить параллелограмм на данной диагонали. Много ли возможно построить таких параллелограммов?
- Построить параллелограмм, если даны три его вершины. Сколько можно построить таких параллелограммов?
После решения этой задачи получим фигуру, изучение которой позволит установить некоторые свойства треугольника:
а) прямая, соединяющая середины двух сторон треугольника, параллельна третьей его стороне и равна ее половине;
б) если дан какой-либо треугольник, то можно построить другой треугольник, чтобы каждая сторона нового была в 2 раза больше (или, наоборот, в 2 раза меньше) соответствующей стороны старого треугольника, причем площадь нового треугольника окажется в 4 раза больше (или, наоборот, – меньше) площади старого.
(На стран. 99 дана фигура, которую можно получить здесь, решая предложенную задачу; в п. 107, на той же странице, дано изучение этой фигуры, однако, с несколько иной точки зрения). - 8. Построить параллелограмм по двум сторонам и диагонали.
Полезно, прежде чем приступить к построениям, требуемым в вышеизложенных задачах, дать себе отчет, какие из 4 вершин параллелограмма даны, и наметить мысленно заранее приблизительное положение остальных вершин.
55. Можно еще построить параллелограмм следующим образом: построим две параллельных прямых AB ∥ DC (чер. 61) и на каждой из них отложим по равному отрезку AB = DC. Затем соединим точки A и D и точки B и С (но нельзя соединять A с C и B с D, – тогда получится 4-угольник, не выделяющий из плоскости определенную ее часть); тогда получим 4-угольник ABCD, у которого AB ⊫ DC (равна и параллельна), выделяющий из плоскости определенную ее часть.
Не трудно выяснить, что построенный 4-угольник есть параллелограмм. Для этого построим диагональ AC и пронумеруем полученные при концах диагонали углы. Легко видеть, что ∆ABC = ∆CDA; в самом деле, у них сторона AC общая, затем по построению AB = CD и, кроме того, ∠1 = ∠2, так как AB ∥ CD, т. е. 2 стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого, а мы знаем (п. 47), что в этом случае треугольники равны. Отсюда заключаем, что ∠3 = ∠4, а так как эти углы суть внутренние накрест-лежащие при прямых CB и AD и секущей CA, то CB ∥ AD; кроме того, из равенства же треугольников имеем CB = AD. Теперь выяснено, что ABCD есть параллелограмм. Этот результат можно выразить словами:
Если в четырехугольнике, выделяющем из плоскости определенную ее часть, две стороны равны и параллельны, то и другие две равны и параллельны, и этот четырехугольник есть параллелограмм.
56. Изучение диагоналей параллелограмма. Уже было замечено, что в параллелограмме возможно построить две диагонали. Пусть построен параллелограмм ABCD (чер. 62) и его диагонали AC и BD. Мы уже знаем, что противоположные стороны параллелограмма равны, т. е. AB = CD и AD = BC. Воспользуемся этим и найдем равные треугольники.
Нетрудно увидать, что ∆AOB = ∆COD. В самом деле, мы знаем, что AB = CD; затем, пронумеровав углы, найдем, что ∠1 = ∠3, как внутренние накрест-лежащие при параллельных AB и CD и секущей AC, а также ∠2 = ∠4, как внутренние накрест-лежащие при параллельных AB и CD и секущей BD, т. е. два угла и сторона между ними одного треугольника равны соответственно двум углам и стороне между ними другого, а такие треугольники, как знаем (п. 47), равны. Также можно найти равенство ∆OBC = ∆ODA. Из равенства треугольников OAB и OCD следует, что OA = OC (против равных углов 2 и 4) и BO = OD (против равных углов 1 и 3), т. е. диагонали в точке O разделили друг друга на 2 равных отрезка или пополам. Этот результат можно выразить словами:
Диагонали параллелограмма делят друг друга пополам.
Точка O, в которой AC и BD делятся пополам, называется серединою отрезка AC и серединою отрезка BD.
57. При помощи построения параллелограмма мы можем теперь каждый данный отрезок разделить пополам, или, другими словами, найти середину этого отрезка.
Пусть дан отрезок AB (чер. 63); требуется найти его середину. Примем AB за одну из диагоналей параллелограмма, который и надо построить для решения задачи. Такая задача была уже предложена (зад. 6 п. 54); дадим здесь ее решение. Прежде всего мы замечаем, что у нас уже имеются две противоположных вершины искомого параллелограмма A и B, – другие две вершины должны лежать где-либо по разные стороны прямой AB. Так как стороны параллелограмма нам не даны, то мы можем взять произвольный отрезок, которому должна равняться каждая из одной пары параллельных сторон параллелограмма, и радиусом, равным этому отрезку, опишем дугу I, принимая за центр точку A, и дугу II, принимая за центр точку B. Также, выбрав произвольный отрезок для другой пары сторон параллелограмма (впрочем, он должен быть больше разности между первым отрезком и диагональю AB и меньше их суммы, – иначе окружности не пересекутся, см. п. 25), мы радиусами, разными этому отрезку, опишем дугу III, принимая B за центр, и дугу IV, принимая A за центр, – точка C, где пересекаются дуги I и III, и точка D, где пересекаются дуги II и IV, должны служить другими двумя вершинами параллелограмма. Соединив их прямыми с точками A и B, получим искомый параллелограмм, диагональю которого служит данный отрезок AB. Ясно, что таких параллелограммов можно построить бесчисленное множество, так как выбор сторон AC и BC зависит от нас.
Нам важна вторая диагональ этого построенного параллелограмма, диагональ CD; построив ее, мы, на основании предыдущего п., можем утверждать, что задача решена, что точка O, где CD пересекается с AB, есть середина AB.
Заметим, что нет надобности строить стороны параллелограмма AC, CB, BD и DA, – нужно лишь построить его вторую диагональ CD.
58. Задача. Построить параллелограмм по его диагоналям и одной стороне.
Пусть даны отрезки a, b и c (чер. 64); требуется построить такой параллелограмм, чтобы отрезки a и b служили его диагоналями и отрезок c одною из его сторон.
Чтобы разобраться в этой задаче, начертим (хотя бы от руки) параллелограмм и будем считать, что его диагонали и одна из сторон (напр., отмеченная на чертеже черточкою) нам известны. Зная свойство диагоналей (п. 56), мы придем к заключению, что мы можем построить ∆AOB, в котором нам все три стороны известны: AB данная, AO и OB суть половины данных диагоналей. Поэтому построение должно быть выполнено в таком порядке: 1) надо, согласно п. 57, разделить пополам каждую из данных диагоналей a и b, 2) построить ∆, у которого сторонами служат найденные половины диагоналей и данная сторона параллелограмма c (п. 38) и 3) дополнить построенный треугольник до параллелограмма, для чего надо продолжить его 2 стороны, которые являются половинами данных диагоналей, отложить на продолжениях опять половины диагоналей и концы этих отрезков соединить с концами стороны c.
Иногда данные могут быть таковы, что задача невозможна, – это можно узнать при выполнении 2-го построения.
59. Можно ускорить решение задачи деления данного отрезка пополам, для чего следует описывать дуги из концов данного отрезка не различными, а одинаковыми радиусами.
Пусть требуется отрезок AB (чер. 65) разделить пополам; для этого, принимая последовательно точки A и B за центры, построим две окружности I и II одинаковыми радиусами и их точки пересечения C и D соединим прямою, – точка O, где CD пересекает AB, и является серединою отрезка AB. Можно, конечно, строить не полные окружности, а лишь их дуги, достаточные для определения положения точек C и D. Для того, чтобы эти окружности пересеклись, необходимо, чтобы их общий радиус был больше половины отрезка AB.
Если построить самый параллелограмм, то увидим, что все его стороны равны между собою: AC = CB = BD = DA, так как окружности описывались одинаковыми радиусами. Следовательно, здесь мы построили особый параллелограмм, все стороны которого равны между собою, – такой параллелограмм называется ромбом.
Упражнение. Разделить данный отрезок на 4, на 8 и т. д. равных частей.
60. Изучение ромба. Для того, чтобы параллелограмм обратился в ромб, достаточно, чтобы две его соседние стороны были равны. Если, напр., построен параллелограмм ABCD (чер. 66) так, что AB = BC, то, на основании свойств сторон параллелограмма, имеем CD = AB и AD = BC, откуда следует, что AB = BC = CD = DA, т. е., что этот параллелограмм есть ромб.
Упражнения.
- Строить различные ромбы на данной стороне.
- Строить различные ромбы на данном угле.
- Построить ромб по данной его стороне и углу.
- Строить различные ромбы на данной диагонали.
- Построить ромб по его стороне и диагонали.
То обстоятельство, что ромб есть особенный параллелограмм (параллелограмм с равными сторонами), дает основание думать, что эта особенность должна отразиться и на других частях ромба. Оказывается, что она отражается на его диагоналях.
Пусть построен ромб ABCD (чер. 66) и его диагонали AC и BD. Тогда прежде всего мы уже знаем, что каждая диагональ делится в точке O пополам, так как ромб есть тоже параллелограмм (п. 56). Теперь надо воспользоваться особенностью ромба: в ромбе все стороны равны, но мы уже знаем, что в параллелограмме противоположные стороны равны, и мы этим воспользовались в п. 56, где нашли, что, благодаря этому, точка O есть середина каждой диагонали; теперь, следовательно, надо обратить внимание на равенство двух соседних сторон, т. е., напр., на равенство AB = BC; возникает мысль: не повлечет ли это равенство за собою следствием равенство двух треугольников, сторонами которых служат AB и BC, т. е. ∆AOB и ∆BOC? Рассмотрим эти треугольники: у них 1) сторона BO общая, 2) AB = BC, как стороны ромба, и 3) AO = OC, так как точка O есть середина диагонали AC. Мы знаем, что если три стороны одного треугольника равны соответственно трем сторонам другого, то такие треугольники равны; следовательно, ∆AOB = ∆OBC. Отсюда следует: 1) ∠ABO = ∠OBC (эти углы расположены против равных сторон AO и OC) и 2) ∠AOB = ∠BOC (против равных сторон AB и BC). Первое равенство углов указывает, что ∠ABC ромба разделен диагональю BD на два равных угла. Если бы мы рассмотрели треугольники OBC и OCD, то также нашли бы, что ∠BCD ромба делится диагональю CA на два равных угла; то же можно получить и про остальные два угла. Поэтому имеем первое свойство диагоналей ромба:
1) Диагонали ромба делят его углы пополам.
Рассматривая 2-е из найденных равенств, т. е. равенство ∠AOB = ∠BOC, видим, что здесь выпрямленный угол AOC делится также диагональю BD пополам; не трудно также увидать, что все 4 угла при точке O равны между собою, т. е. ∠AOB = ∠BOC = ∠COD = ∠DOA (это можно увидать, напр., из того, что ∠AOD = ∠BOC, как вертикальные, и по той же причине ∠COD = ∠BOA, – следовательно, все 4 угла равны между собою), причем каждый из них получился от разделения на две равных части выпрямленного угла (напр., ∠COD получился от разделения на 2 равных части выпрямленного угла BOD и т. д.). Принято называть углы, получающиеся от разделения выпрямленного угла на две равных части, прямыми углами; следовательно, у нас получились прямые углы: ∠AOB, ∠BOC, ∠COD, ∠DOA. Коротко выражают ту же мысль словами: прямым углом называется половина выпрямленного угла.
Вот необходимые нам свойства прямых углов:
a) Все прямые углы равны между собою.
Это следует из того, что все выпрямленные углы равны между собою, а, следовательно, и их половины (прямые углы) тоже равны.
b) Если один из четырех углов, образуемых двумя пересекающимися прямыми, прямой, то и остальные три угла прямые.
В самом деле, если при точке пересечения прямых a и b (чер. 67) получились углы 1, 2, 3 и 4, из которых, напр., ∠1 прямой, то и ∠2 прямой, так как ∠1 и ∠2 вместе составляют выпрямленный угол, но ∠3 = ∠1, как вертикальные, следовательно, и ∠3 прямой, так же и ∠4 прямой, потому что он равен ∠2.
Две прямые линии, которые, пересекаясь, образуют прямые углы, называются перпендикулярными прямыми (иногда взаимно-перпендикулярными).
Поэтому второе свойство диагоналей ромба можно выразить в такой форме:
2) Диагонали ромба взаимно перпендикулярны.
61. Пользуясь первым свойством диагоналей ромба, мы можем всякий данный угол разделить пополам:
Пусть дан ∠A (чер. 68); требуется разделить его пополам. Для этого придется построить такой ромб, чтобы ∠A был его углом и построить диагональ этого ромба чрез точку A.
Отложим на сторонах угла A два равных (но произвольных) отрезка AB = AC; тогда у нас будут построены 3 вершины ромба A, B и C, четвертая же вершина должна лежать где-то внутри угла A. Затем, принимая последовательно точки B и C за центры, построим круги (или только их дуги, достаточные для определения четвертой вершины ромба) радиусами, равными отрезкам AB и AC; точка пересечения этих кругов, точка D, расположенная внутри угла A, и дает нам четвертую вершину ромба. Соединив ее с B и C прямыми (впрочем, для деления угла пополам это лишнее, и на первый раз нужно лишь для того, чтобы увидать, что получился ромб), получим ромб ABDC; построив его диагональ AD, разделим угол A на два равных угла на ∠BAD и ∠DAC.
Луч, делящий угол пополам, называется биссектором этого угла; AD есть биссектор угла BAC (чер. 68).
Ясно, что всякий угол может быть вышеописанным способом разделен пополам, или у всякого угла есть биссектор.
Если вообразить, что построенный биссектор AD угла BAC вращается около вершины угла A в ту или иную сторону, то равенство углов BAD и DAC нарушается: один угол увеличивается, а другой уменьшается. Поэтому:
Всякий угол может быть разделен пополам лишь одним способом.
Или:
У всякого угла имеется лишь один биссектор.
62. Упражнения.
- Построить ромб по его углу и диагонали, проходящей через вершину этого угла.
Надо построить данный угол, его биссектор, на нем отложить данную диагональ и чрез конец ее построить прямые, параллельные сторонам угла. - Построить четырехугольник по его двум противоположным углам и по диагонали, соединяющей вершины этих углов, причем четырехугольник должен быть симметричным относительно данной диагонали.
Как располагается другая диагональ этого четырехугольника относительно данной? - Разделить данный угол на 4, на 8 и т. д. равных частей.
- Построить биссекторы двух смежных углов. Показать, что они перпендикуляры между собою.
63. Задача. Построить на данной прямой при данной ее точке прямой угол.
Раз мы умеем строить ромб, то мы умеем, вообще говоря, строить прямые углы. Для решения задачи этого п. Надо расположить ромб так, чтобы точка пересечения его диагоналей совпала с данною точкою A (чер. 69) и одна диагональ шла по данной прямой AB. Для этого от точки A в обе стороны отложим на данной прямой равные (но произвольные) отрезки AC = AD; тогда точки C и D можно принять за две вершины ромба. Для построения двух других вершин надо, принимая последовательно точки C и D за центры, построить две окружности (или их дуги, достаточные для получения точек пересечения) одним и тем же радиусом, большим, чем отрезок AC (иначе окружности не пересекутся). Соединив прямыми точки пересечения наших окружностей K и L с точками C и D, получим ромб CKDL; его диагональ KL должна пройти чрез середину диагонали CD, т. е. чрез точку A; построив эту диагональ KL, получим 4 прямых угла (п. 60).
Важно ускорить и упростить это построение:
1) Нет надобности строить стороны ромба, 2) можно построить лишь одну точку пересечения окружностей, напр., точку K, и тогда , построив отрезок KA, получим два прямых угла; если его продолжить, то получим еще два прямых угла. На чертеже изображены пунктиром те линии, построение которых излишне.
64. Задача. Построить параллелограмм с прямым углом.
Строим произвольную прямую AB и выбираем на ней произвольную точку A (чер. 70), при которой строим (п. 63) прямой угол; на стороне AC этого прямого угла выбираем произвольную точку C и на прямой AB точку E. Затем, принимая последовательно точки C и E за центры, строим две окружности (или дуги): первую (центр C) радиусом, равным отрезку AE, и второю (центр E) радиусом, равным отрезку AC; точка пересечения этих окружностей точка D, лежащая по ту же сторону прямой AB, как и точка C и должна служить четвертою вершиною этого параллелограмма. Построив, наконец, прямые CD и DE, получим искомый параллелограмм ACDE, у которого ∠A прямой (сравнить это построение с п. 53).
Рассмотрим остальные углы этого параллелограмма: 1) мы знаем, что ∠D = ∠A, как противоположные углы параллелограмма (п. 51), следовательно, угол D тоже прямой; 2) затем знаем, что ∠C + ∠A = выпрямленному углу, как соседние углы параллелограмма (п. 51, 1), но ∠A прямой, т. е. равен половине выпрямленного угла, следовательно, и ∠C равен половине выпрямленного, т.е. тоже есть прямой угол, затем ∠E = ∠C и, следовательно, ∠E тоже прямой. Итак, оказалось:
Если в параллелограмме один угол прямой, то и остальные углы прямые.
Такой параллелограмм с прямыми углами называется прямоугольником.
65. Так как прямоугольник есть особенный параллелограмм, то эта особенность должна отразиться, как и в ромбе, на его диагоналях.
Пусть построен прямоугольник ABCD (чер. 71) и построены его диагонали AC и BD. Конечно, основное свойство диагоналей параллелограмма остаётся и здесь: диагонали делят друг друга пополам. Но нам надо открыть какую-либо особенность диагоналей, зависящую от того, что теперь у нашего параллелограмма все углы прямые. Рассмотрим пару треугольников, в каждый из которых входил бы один из прямых углов, и важно, чтобы входили два соседних прямых угла, напр., ∠A и ∠D (соседние углы ведь вообще в параллелограмме не равны, а противоположные всегда равны). Такими треугольниками являются ∆ABD (∠A прямой) и ∆ACD (∠D прямой). У этих треугольников сторона AD общая, затем сторона AB первого равна стороне CD второго и между ними равные углы, так как мы знаем, что прямые углы равны между собою (п. 60, а). Следовательно, две стороны (AD и AB) и угол между ними (прямой ∠A) одного треугольника равны соответственно двум сторонам (AD и CD) и углу между ними (прямой ∠D) другого треугольника, а мы знаем, что такие треугольники равны. Отсюда выводим, что AC = BD, т. е. оказывается, что диагонали равны между собою.
Итак:
Диагонали прямоугольников равны между между собою.
66. Наконец, можно построить такой прямоугольник, чтобы у него все стороны были равны (построение ясно: строим прямой угол A (чер. 72) и на его сторонах откладываем равные отрезки AB = AD, затем обычным приёмом находим четвертую вершину C). Такой параллелограмм является в одно и то же время и прямоугольником (у него все углы прямые, так как один угол прямой) и ромбом (у него все стороны равны, так как две соседних равны), – она называется квадратом. Его диагонали должны обладать свойствами диагоналей и параллелограмма, и ромба, и прямоугольника, т. е.:
Диагонали квадрата взаимно делятся пополам, делят углы квадрата пополам и взаимно перпендикулярны и, наконец, равны между собою.
67. Упражнения.
- Построить прямоугольник по его сторонам.
- Построить прямоугольник по диагонали и одной из его сторон.
- Построить квадрат по его стороне.
- Построить квадрат по его диагонали.
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Параллелограмм и его свойства
Сумма внутренних углов любого четырехугольника равна (360^circ).
Свойства параллелограмма:
(blacktriangleright) Противоположные стороны попарно равны;
(blacktriangleright) Диагонали точкой пересечения делятся пополам;
(blacktriangleright) Противоположные углы попарно равны, а сумма соседних равна (180^circ).
Признаки параллелограмма.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – параллелограмм:
(blacktriangleright) если противоположные стороны попарно равны;
(blacktriangleright) если две стороны равны и параллельны;
(blacktriangleright) если диагонали точкой пересечения делятся пополам;
(blacktriangleright) если противоположные углы попарно равны.
Площадь параллелограмма
Площадь параллелограмма равна произведению высоты на основание, к которому проведена эта высота.
Задание
1
#1783
Уровень задания: Легче ЕГЭ
Периметр параллелограмма равен (100), его большая сторона равна (32). Найдите меньшую сторону параллелограмма.
Так как у параллелограмма противоположные стороны равны, то его периметр равен удвоенной сумме его непараллельных сторон, тогда сумма большей и меньшей сторон равна (100 : 2 = 50), значит, меньшая сторона параллелограмма равна (50 – 32 = 18).
Ответ: 18
Задание
2
#1784
Уровень задания: Равен ЕГЭ
Периметр параллелограмма равен (15). При этом одна сторона этого параллелограмма на (5) больше другой. Найдите меньшую сторону параллелограмма.
У параллелограмма противоположные стороны равны. Пусть (BC = AB +
5), тогда периметр параллелограмма (ABCD) равен (AB + BC + CD + AD =
AB + AB + 5 + AB + AB + 5 = 4cdot AB + 10 = 15), откуда находим (AB
= 1,25). Тогда меньшая сторона параллелограмма равна (1,25).
Ответ: 1,25
Задание
3
#273
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (BE) – высота, (BE = ED = 5). Площадь параллелограмма (ABCD) равна 35. Найдите длину (AE).
Площадь параллелограмма равна произведению основания на высоту, проведённую к этому основанию, тогда (35 = BE cdot AD = 5cdot(5 + AE)), откуда находим (AE = 2).
Ответ: 2
Задание
4
#1785
Уровень задания: Равен ЕГЭ
Из точки (C) параллелограмма (ABCD) опустили перпендикуляр на продолжение стороны (AD) за точку (D). Этот перпендикуляр пересёк прямую (AD) в точке (E), причём (CE = DE). Найдите (angle B) параллелограмма (ABCD). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle EDC = angle DCE). Так как (angle DEC = 90^{circ}), а сумма углов треугольника равна (180^{circ}), то (angle EDC =
45^{circ}), тогда (angle ADC = 180^{circ} – 45^{circ} =
135^{circ}). Так как в параллелограмме противоположные углы равны, то (angle B = angle ADC = 135^{circ}).
Ответ: 135
Задание
5
#1686
Уровень задания: Равен ЕГЭ
Диагональ (BD) параллелограмма (ABCD) перпендикулярна стороне (DC) и равна (4). Найдите площадь параллелограмма (ABCD), если (AD=5).
По теореме Пифагора находим: (AB^2=AD^2 – BD^2 = 25 – 16 = 9) (Rightarrow) (AB = 3). (S_{ABCD} = 4cdot3 = 12).
Ответ: 12
Задание
6
#1685
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (P_{triangle AOB} = 8), (P_{triangle AOD} = 9), а сумма смежных сторон равна (7). Найдите произведение этих сторон параллелограмма (ABCD).
(P_{triangle AOB} = AO + OB + AB), (P_{triangle AOD} = AO + OD + AD), (BO = OD) (Rightarrow) (P_{triangle AOD} – P_{triangle AOB} = AD – AB = 1), но (AD + AB = 7) (Rightarrow) (AD = 4), (AB = 3) (Rightarrow) (ADcdot AB = 12).
Ответ: 12
Задание
7
#3617
Уровень задания: Равен ЕГЭ
Стороны параллелограмма равны (9) и (15). Высота, опущенная на первую сторону, равна (10). Найдите высоту, опущенную на вторую сторону параллелограмма.
Площадь параллелограмма равна произведению высоты на сторону, к которой высота проведена. Следовательно, с одной стороны, площадь (S=9cdot 10), с другой стороны, (S=15cdot h), где (h) – высота, которую нужно найти.
Следовательно, [9cdot 10=15cdot hquadLeftrightarrowquad h=6]
Ответ: 6
Задачи из раздела «Геометрия на плоскости» являются обязательной частью аттестационного экзамена у выпускников средней школы. Теме «Параллелограмм и его свойства» в ЕГЭ традиционно отводится сразу несколько заданий. Они могут требовать от школьника как краткого, так и развернутого ответа с построением чертежа. Поэтому если одним из ваших слабых мест являются именно задачи на вычисление площадей параллелограмма или его сторон и углов, то вам непременно стоит повторить или вновь разобраться в материале.
Сделать это легко и эффективно вам поможет образовательный портал «Школково». Наши опытные специалисты подготовили необходимый теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко решить задачи ЕГЭ на вычисление площадей, сторон, углов или свойства биссектрисы параллелограмма. Найти базовую информацию вы можете в разделе «Теоретическая справка».
Чтобы успешно решить задачи ЕГЭ по теме «Параллелограмм и его свойства», предлагаем попрактиковаться в выполнении соответствующих упражнений. Большая подборка заданий представлена в блоке «Каталог». Специалисты портала «Школково» регулярно дополняют и обновляют данный раздел.
Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

УСТАЛ? Просто отдохни
На этой странице вы узнаете
- Чем отличаются признаки от свойств?
- Сколько крыс у биссектрисы?
- Гибридом чего будет квадрат?
Когда мы видим изображение с множеством деталей, наш мозг автоматически раскладывает их на простые фигуры. Этот процесс занимает доли секунды. Разные геометрические фигуры вызывают у нас разные ощущения, эмоции и ассоциации.А что будет, если мы задержим взгляд на одной из них и разберем подробнее? Давайте сделаем так с параллелограммом.
Параллелограмм
Параллелограмм – это четырёхугольник, чьи стороны попарно параллельны и равны.

Параллелограмм мы видим достаточно часто.


Признаки параллелограмма
У параллелограмма есть три основных признака. Если для четырехугольника выполняется хотя бы один из признаков, такой четырехугольник можно называть параллелограммом.
Признаки параллелограмма:
- Две противоположные стороны четырехугольника параллельны и равны.
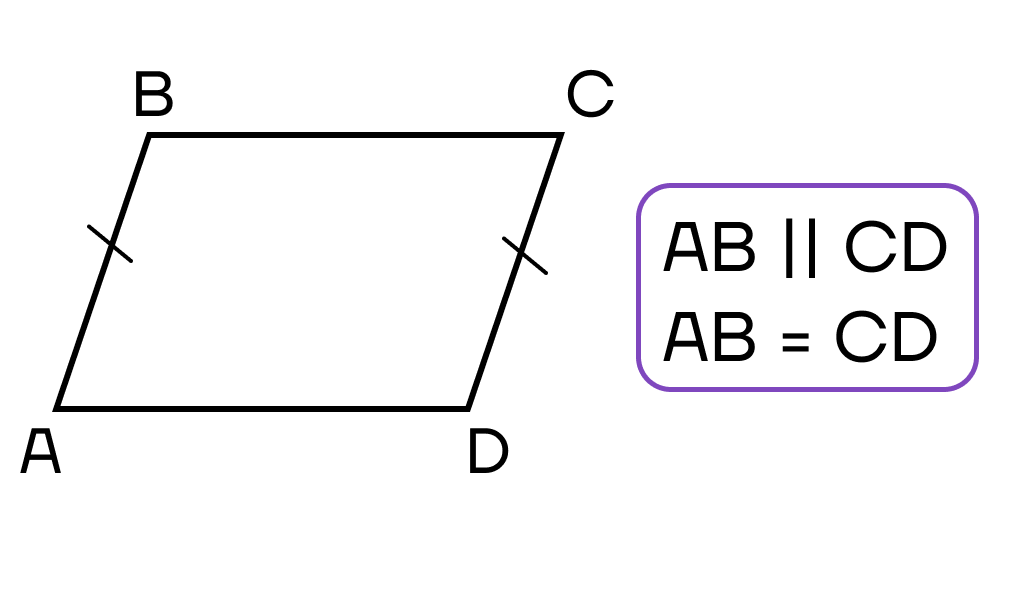
- Противоположные стороны четырехугольника попарно равны.
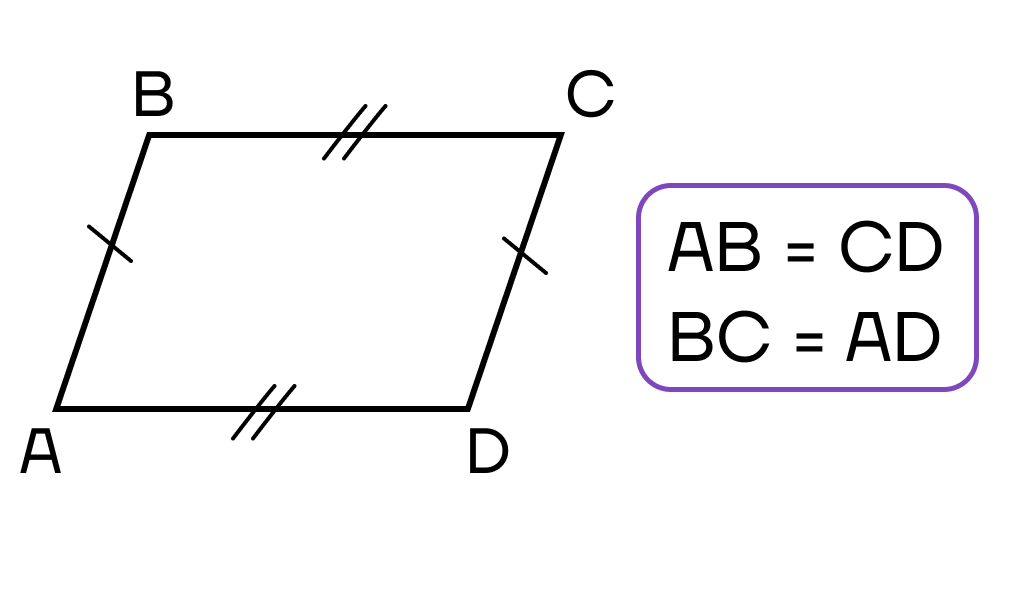
- Диагонали четырехугольника пересекаются и в точке пересечения делятся пополам.

Свойства параллелограмма
Свойства нельзя путать с признаками, хоть они и очень похожи. Свойствами параллелограмма обладает фигура, уже являющаяся параллелограммом, тогда как признаки предназначены для выявления параллелограммов среди четырехугольников.
Свойства параллелограмма:
- Противолежащие стороны равны.

- Противолежащие стороны параллельны.
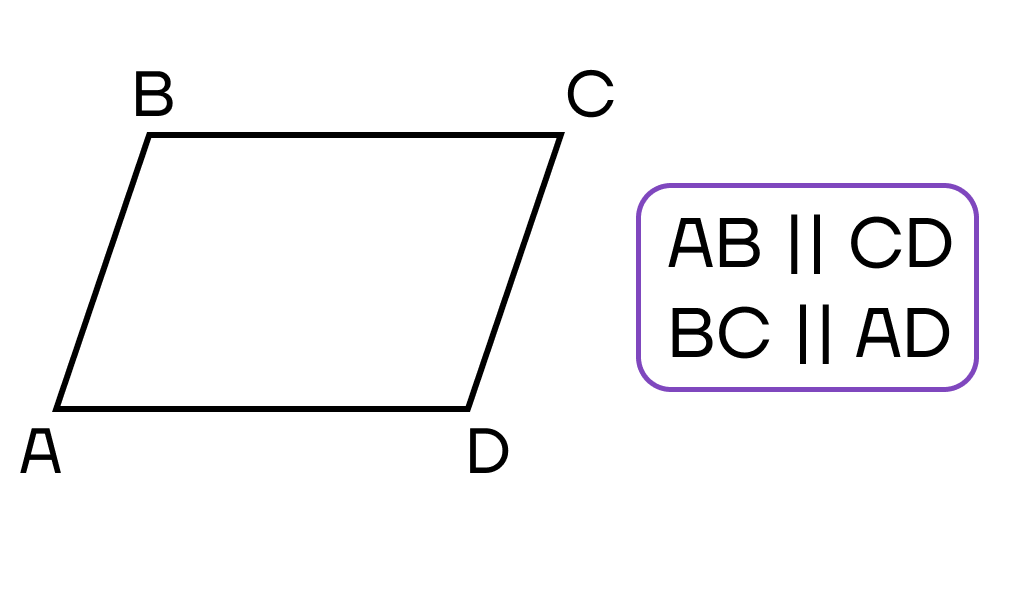
- Противолежащие углы равны.
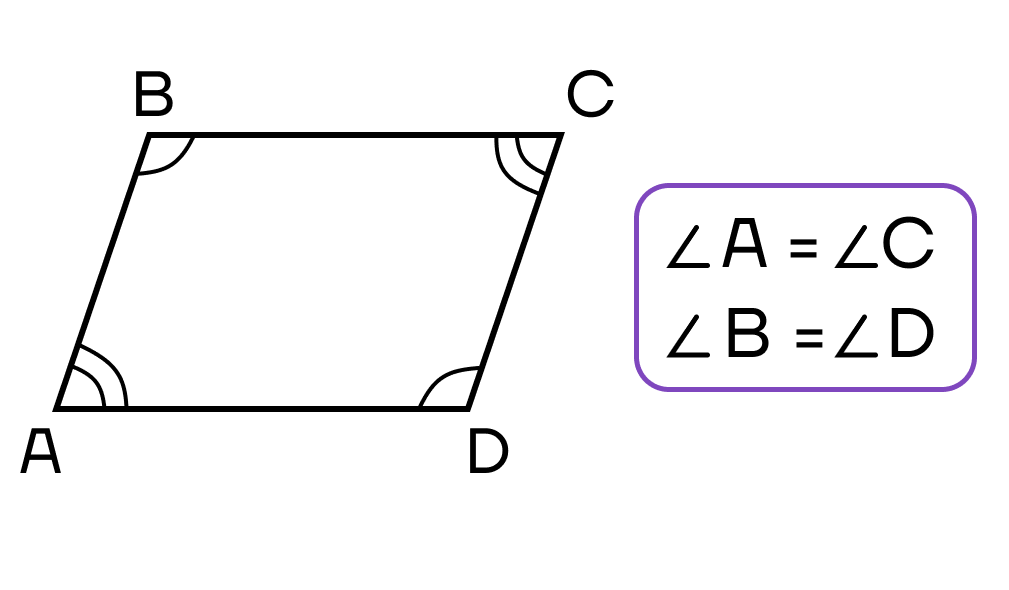
- Сумма всех углов 3600.
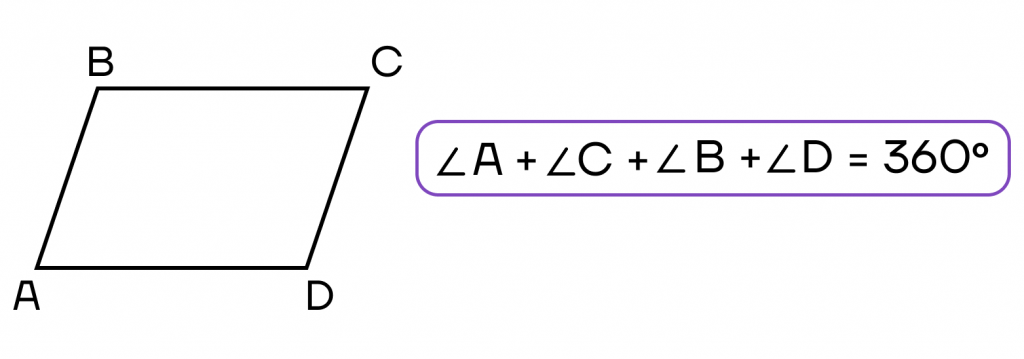
- Диагонали пересекаются и точкой пересечения делятся пополам.
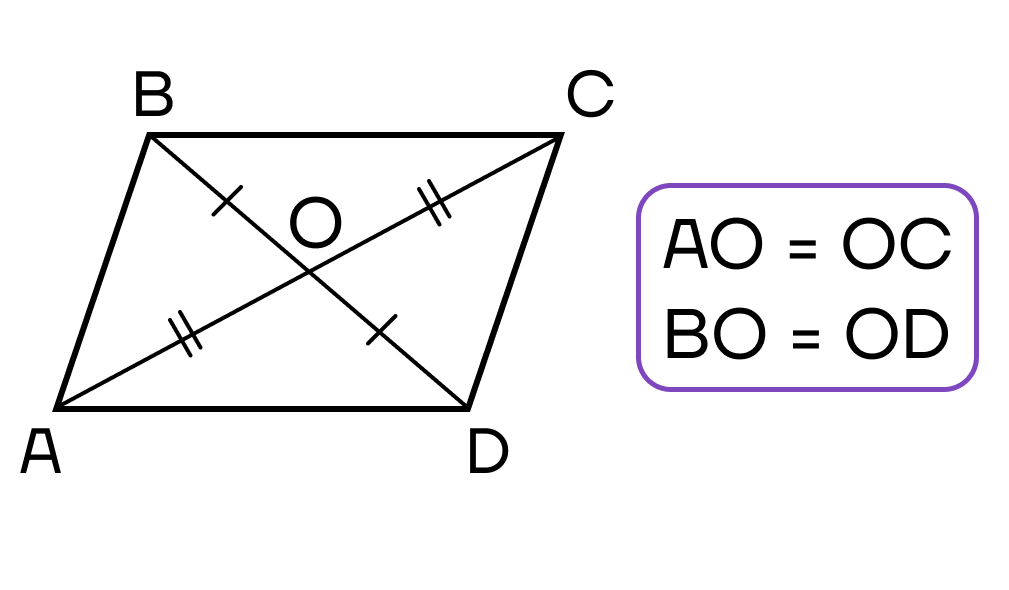
- Сумма углов, прилежащих к любой стороне, равна 1800.
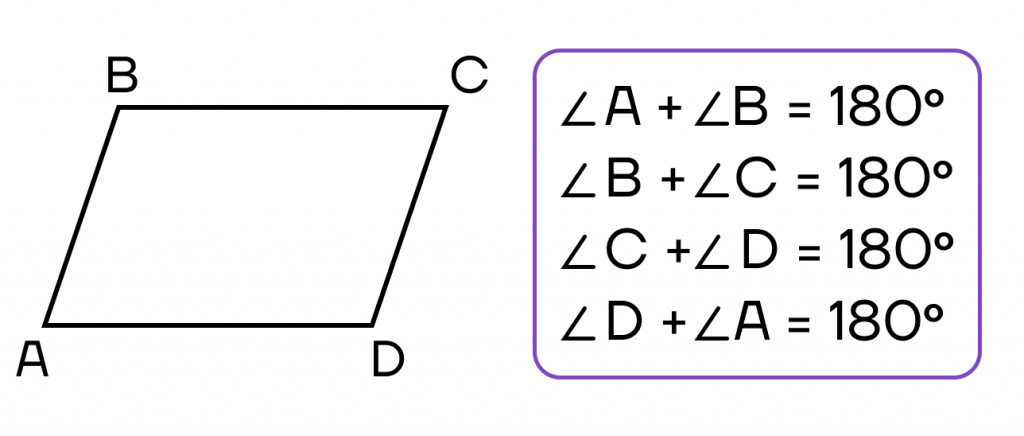
- Сумма квадратов диагоналей равна сумме квадратов всех сторон.
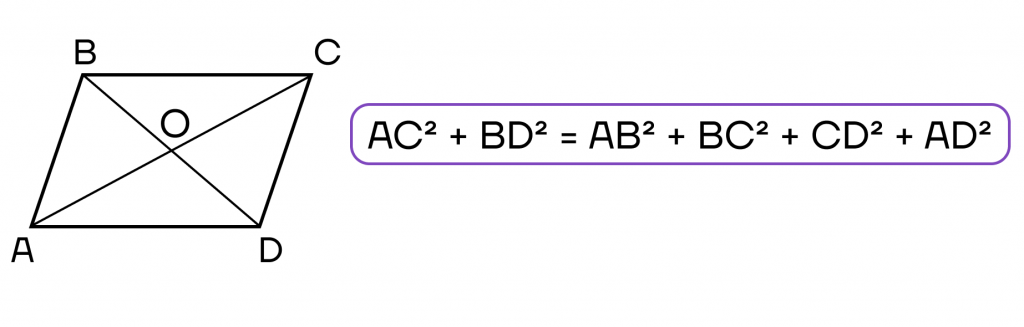
- Диагонали делят параллелограмм на четыре треугольника с одинаковой площадью.

- Каждая диагональ делит параллелограмм на два равных треугольника

Биссектриса в параллелограмме
Можно ли провести биссектрису в параллелограмме? Да. Биссектриса параллелограмма – это луч, исходящий из вершины угла параллелограмма, делящий этот угол на два равных угла и пересекающий одну из сторон параллелограмма.

Значение биссектрисы легко запомнить, используя фразу “Биссектриса – это крыса, она бегает по углам и делит угол пополам”.
Так как у треугольника три угла – соответственно, и крыс-биссектрис тоже три.
Два факта связанные с биссектрисой в параллелограмме:
- Биссектриса, проведенная из угла параллелограмма, отсекает от него равнобедренный треугольник.

- Биссектрисы углов, принадлежащих одной стороне параллелограмма, пересекаются под прямым углом.
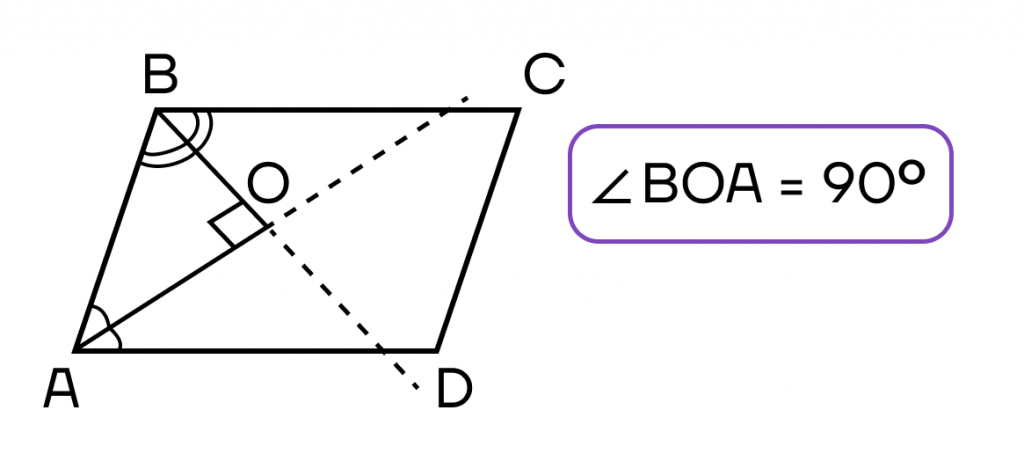
Площадь параллелограмма
Есть три формулы площади параллелограмма, которые применяются в зависимости от известных величин
- Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
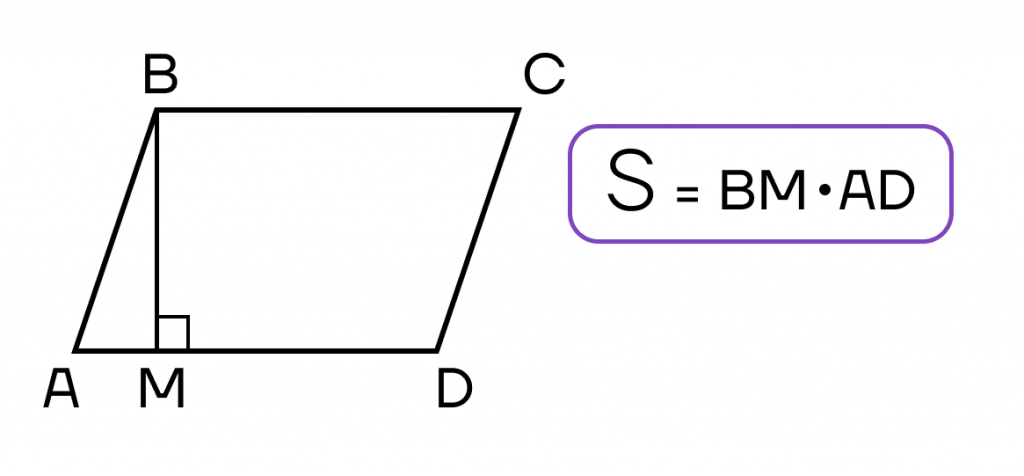
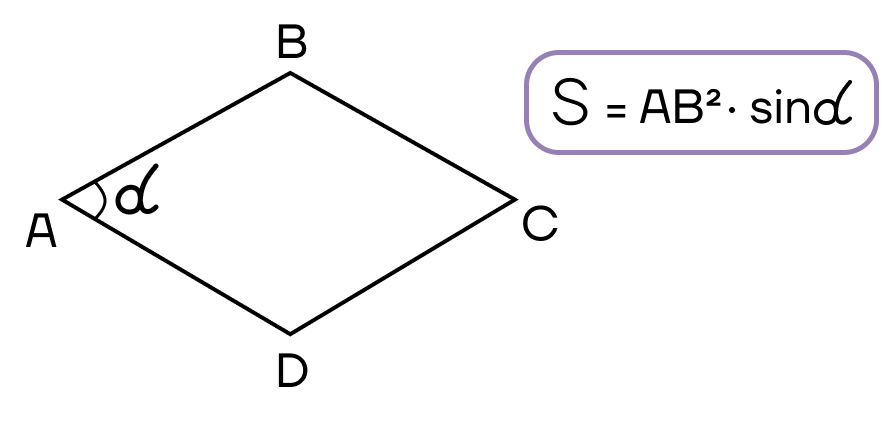
- Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними.

- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними.

Прямоугольник
Как параллелограмм связан с прямоугольником?
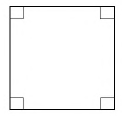
Прямоугольник – это параллелограмм, углы которого по 900.
Данную фигуру часто называют частным случаем параллелограмма. Из этого следует, что для прямоугольника применимы те же признаки и свойства, что для параллелограмма, но и имеется ряд собственных.
В жизни прямоугольником можно назвать дверь, картину или фотографию:
Признаки прямоугольника
- Параллелограмм, имеющий хотя бы один прямой угол.
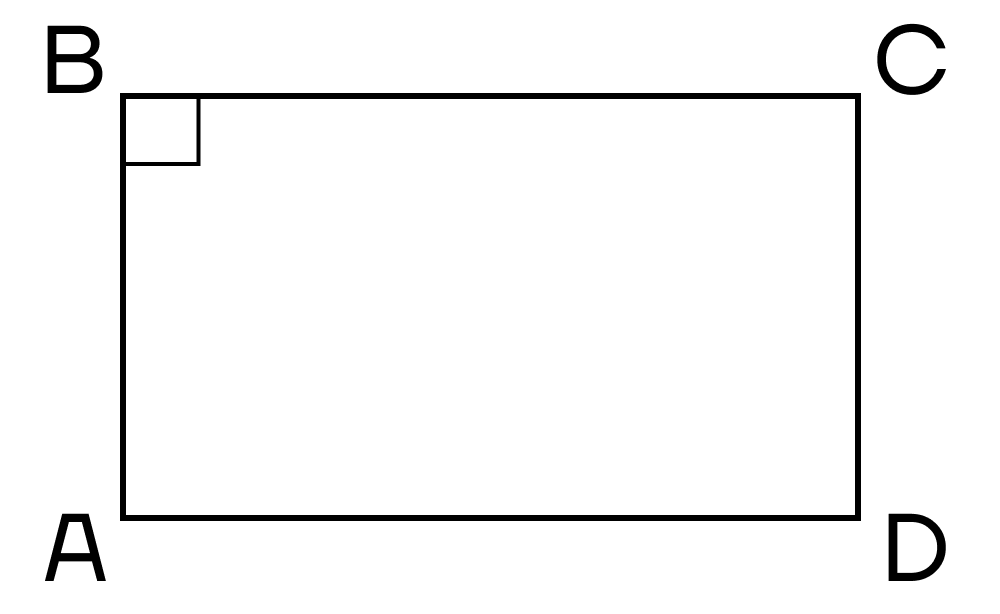
- Параллелограмм, все углы которого равны.
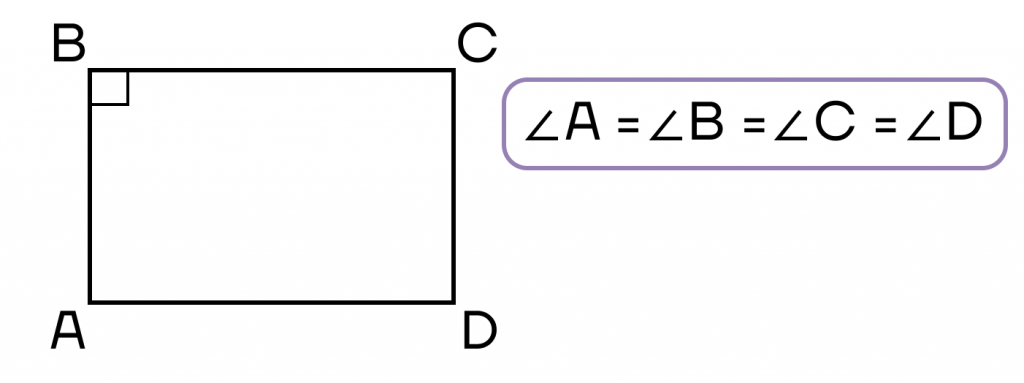
- Параллелограмм, диагонали которого равны.
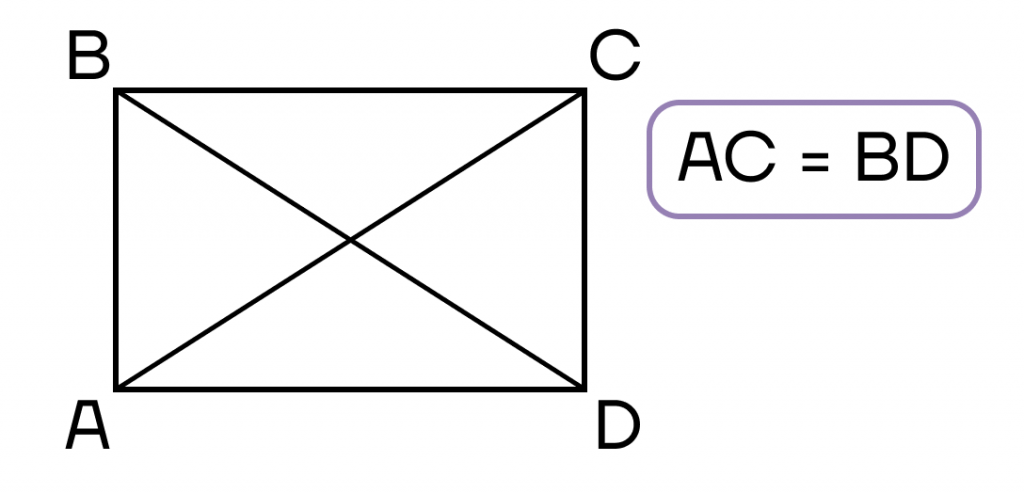
- Четырехугольник, у которого три прямых угла.

Свойства прямоугольника
- Все углы прямые.

- Диагонали равны.

- Стороны прямоугольника одновременно являются и его высотами.
- Сумма квадратов двух прилежащих сторон равна квадрату диагонали.
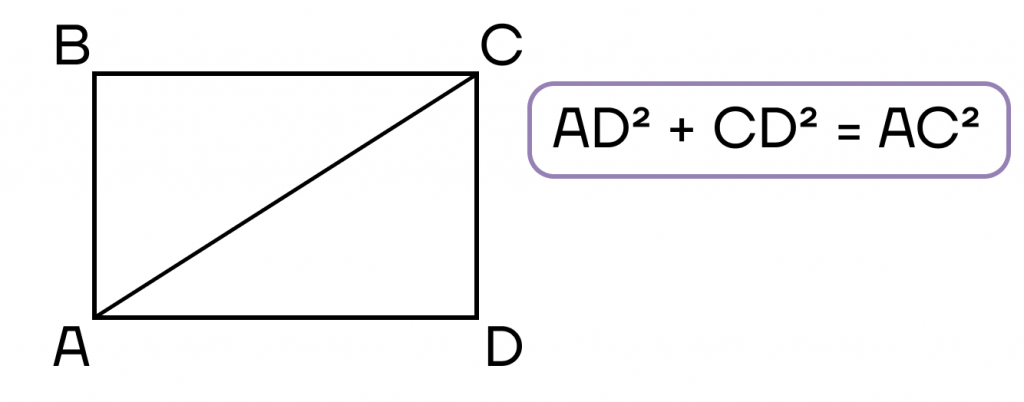
Биссектриса и площадь прямоугольника
Биссектриса делит угол прямоугольника на два угла по 450 и пересекает одну из сторон прямоугольника.
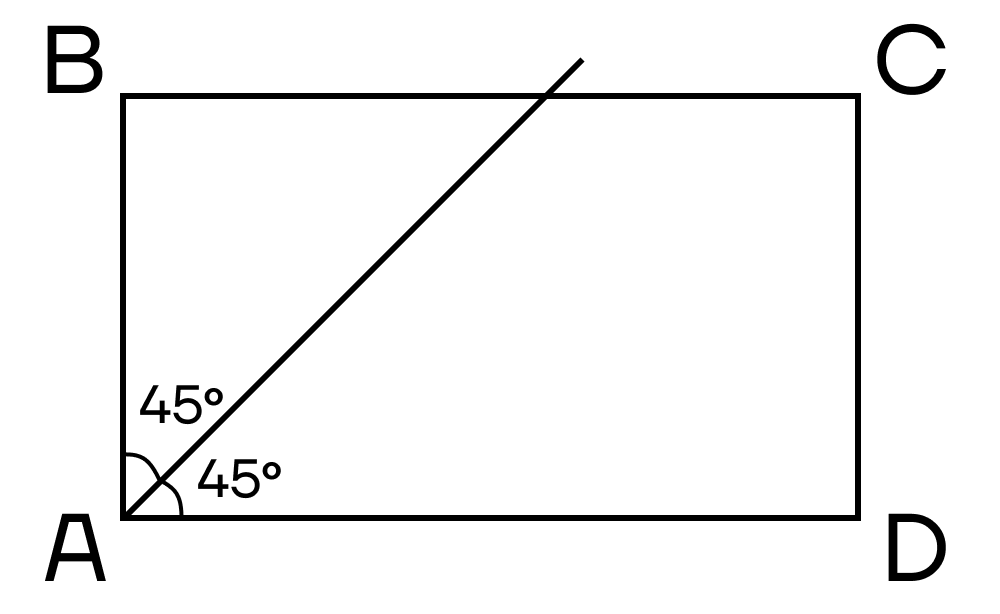
Теперь рассмотрим два способа нахождения площади прямоугольника:
- Площадь прямоугольника равна произведению двух соседних сторон.
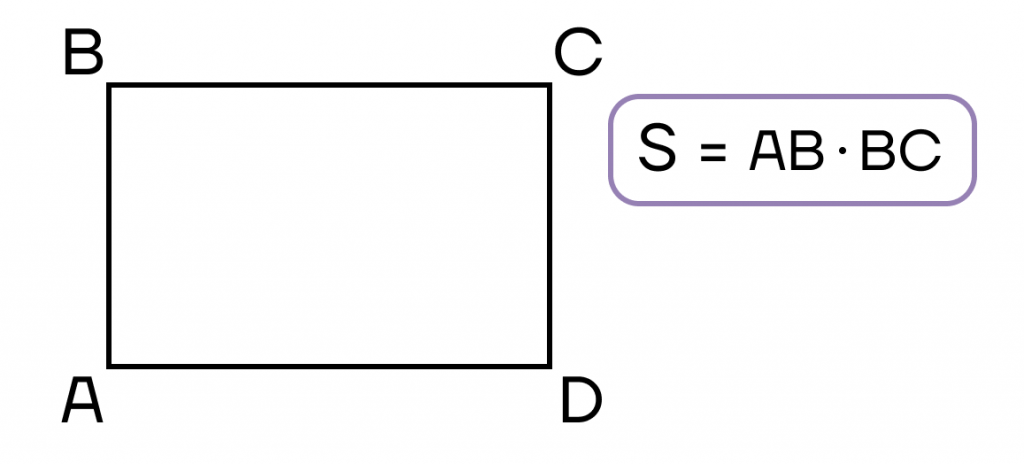
- Площадь прямоугольника равна половине произведения квадрата диагонали на синус угла между диагоналями.
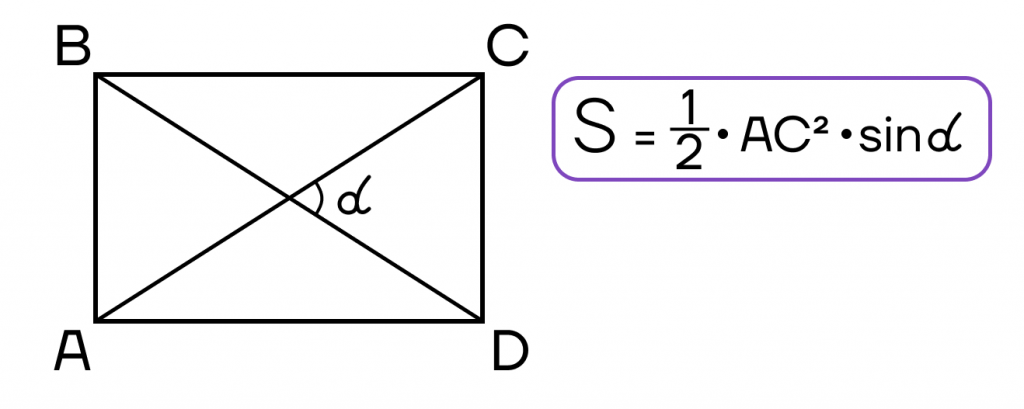
Ромб
Пожалуй, это самая неустойчивая фигура.

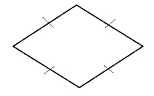
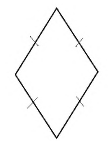
Ромб – это параллелограмм, у которого все стороны равны.

Ромб можно увидеть на знаке машины “Митсубиси”, их там целых три.
А также в игровых наградах:

Также является частным случаем параллелограмма и обладает его признаками и свойствами, но имеет и собственные.
Всё о ромбе
Признаки ромба:
- Две смежные стороны параллелограмма равны.
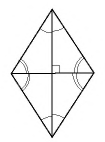
- Диагонали параллелограмма пересекаются под прямым углом.
- Диагональ параллелограмма делит каждый угол пополам.
- Четырехугольник, у которого все стороны равны.
Свойства ромба:
- Все стороны равны.

- Диагонали пересекаются под прямым углом и точкой пересечения делятся пополам.

- Диагонали являются биссектрисами.

- Высоты в ромбе равны.
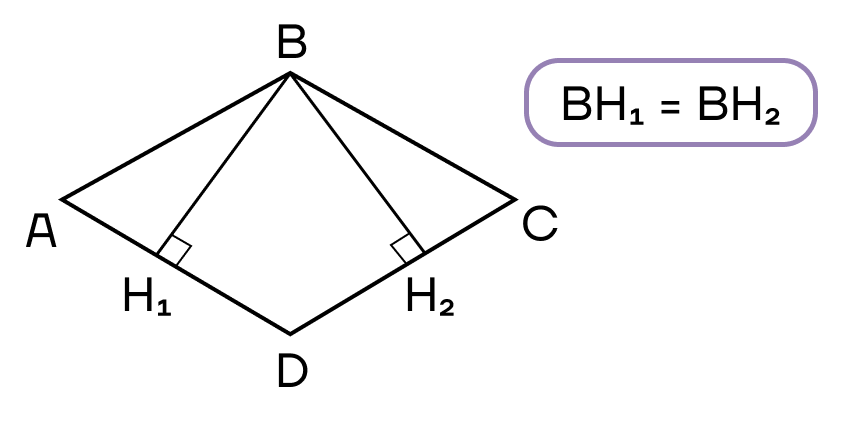
Как уже отмечено в свойствах ромба, биссектрисой ромба является диагональ.
Как найти площадь ромба?
Для нахождения площади ромба есть три разные формулы:
- Площадь ромба равна произведению стороны и высоты ромба.
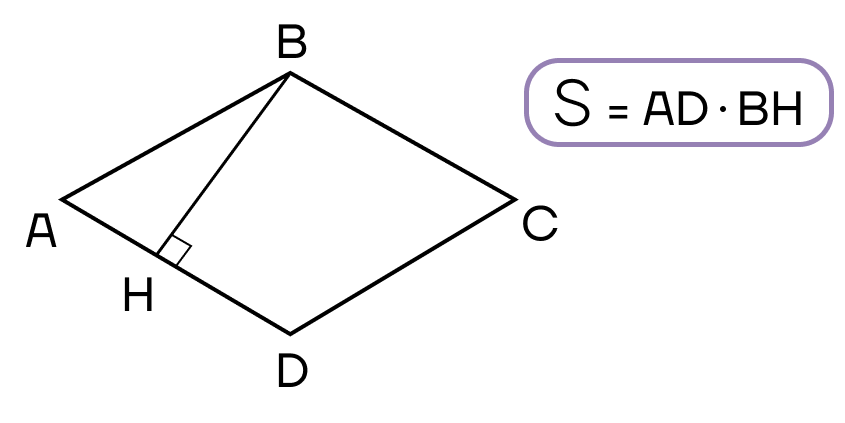
- Площадь ромба равна половине произведения его диагоналей.
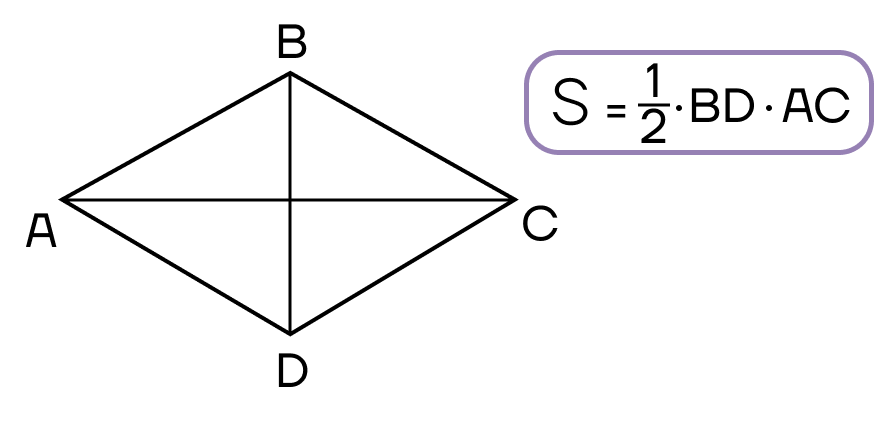
- Площадь ромба равна произведению квадрата стороны на синус угла ромба.
Квадрат
А вот квадрат, наоборот, достаточно устойчив.

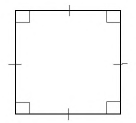
Квадрат – это четырехугольник, у которого все углы и стороны равны.
Если внимательно посмотреть на определение, то можно заметить, что квадрат объединяет в себе и параллелограмм, и прямоугольник, и ромб.
Нечто, сочетающее в себе разнородные элементы, называют гибридом. Квадрат будет иметь все признаки и свойства родительских фигур:параллелограмма, прямоугольника и ромба.

Квадратом может быть крышка подарочной коробки или окно.


Рассмотрим признаки и свойства данной фигуры.
Всё о квадрате
Признаки квадрата:
- Ромб, у которого хотя бы один угол прямой.
- Ромб, у которого все углы равны.
- Ромб, у которого диагонали равны.
- Четырехугольник, диагонали которого равны и перпендикулярны.
Свойства квадрата:
- Диагональ квадрата равна 2 стороны квадрата.
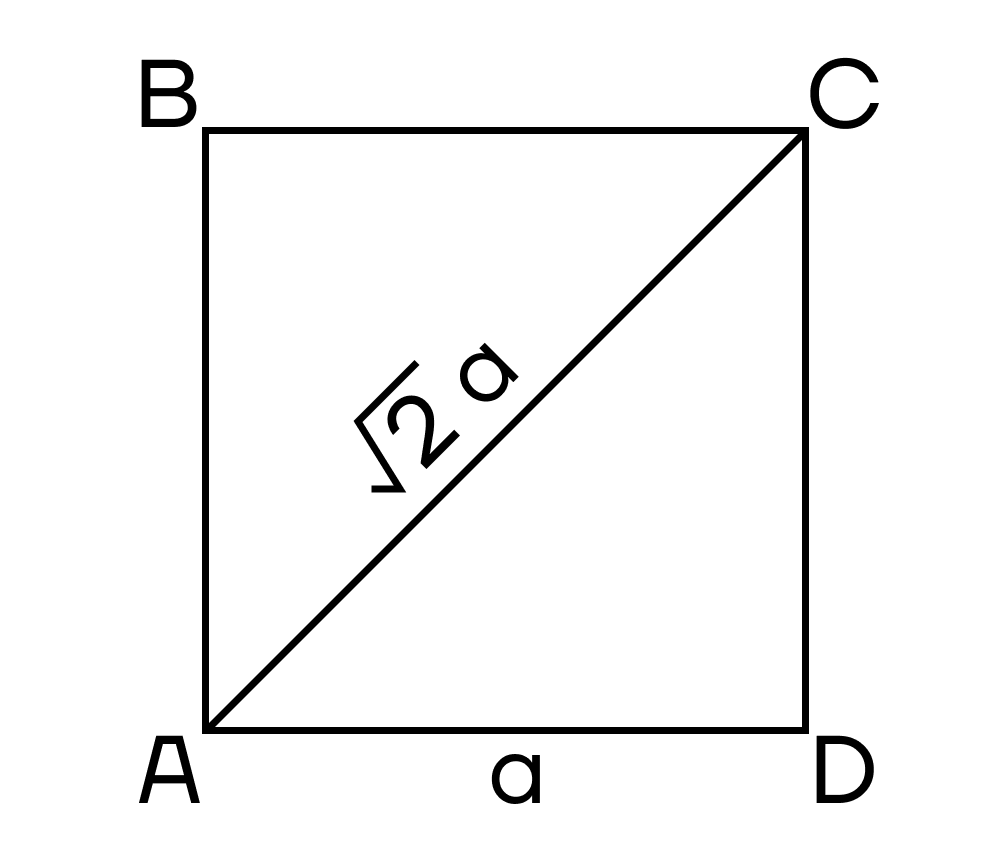
- Диагонали делят квадрат на четыре равных треугольника.

Биссектрисой квадрата, как и у ромба, является диагональ.
Рассмотрим формулы для нахождения площади квадрата:
- Площадь квадрата равна квадрату его стороны.
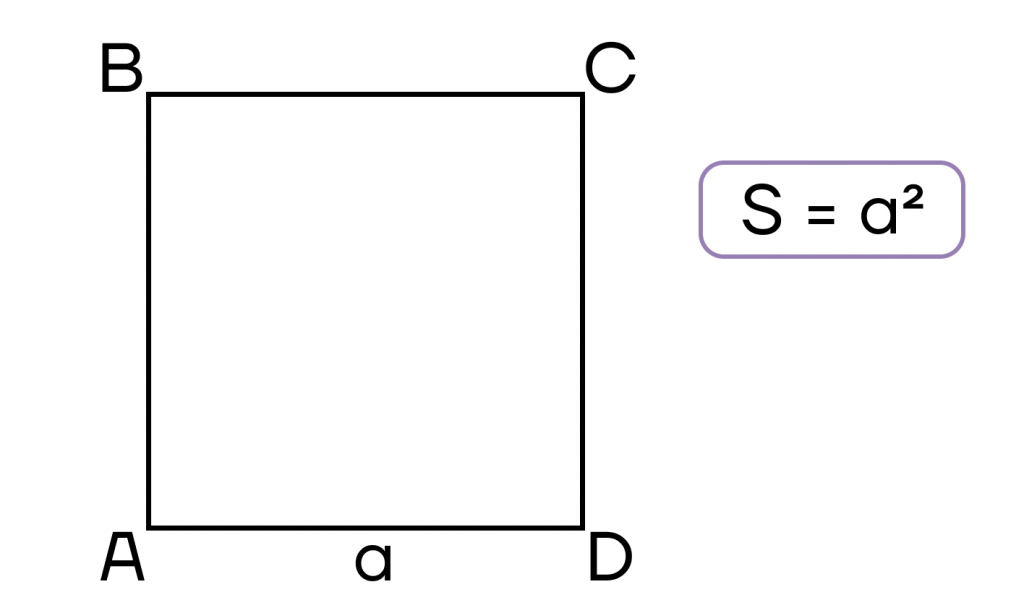
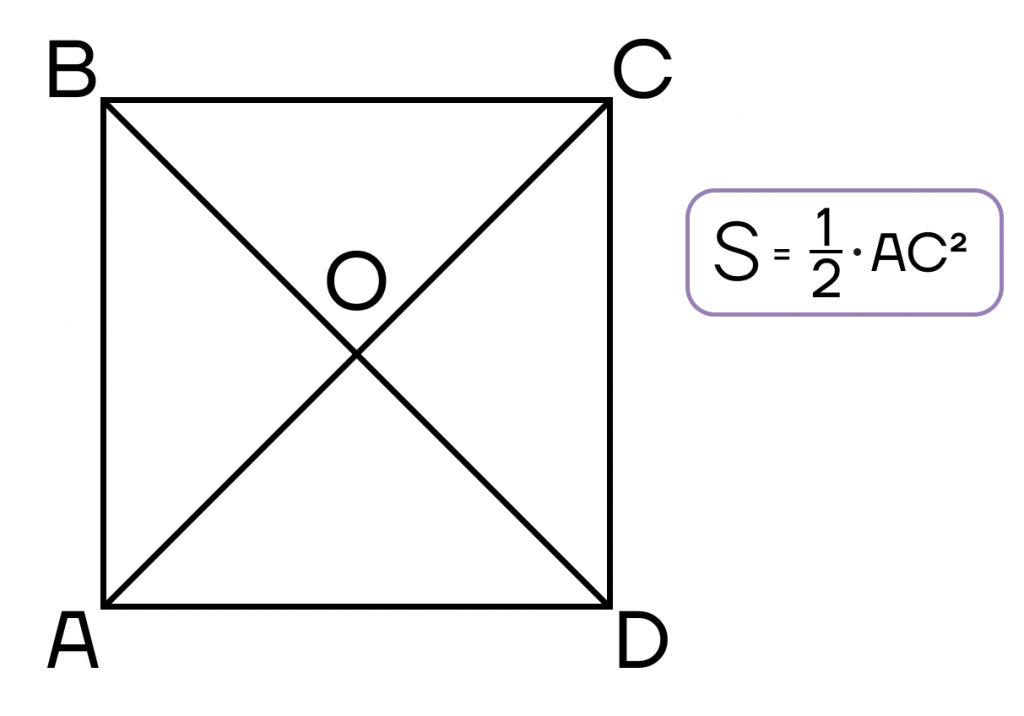
- Площадь квадрата равна половине квадрата диагонали.
Фактчек
- Параллелограмм – это четырёхугольник, чьи стороны попарно параллельны и равны.
- Прямоугольник – это параллелограмм, углы которого по 900 и диагонали которого равны.
- Ромб – это параллелограмм, у которого все стороны равны, а также диагонали перпендикулярны друг другу
- Квадрат – это четырехугольник, у которого все углы и стороны равны. Квадрат является гибридом параллелограмма, прямоугольника и ромба.
Проверь себя
Задание 1.
Найдите площадь параллелограмма, если его стороны 5 и 8, а угол между ними 300
- 40
- 20
- 10
- 25
Задание 2.
Найдите площадь прямоугольника, если его диагональ 12, а угол между диагоналями 600
- 83
- 6
- 63
- 4
Задание 3.
Найдите площадь ромба, если его диагонали 6 и 10
- 30
- 60
- 15
- 25
Задание 4.
У четырехугольника диагонали пересекаются под углом 300, а его стороны попарно параллельны и равны. Что это за фигура?
- Квадрат
- Ромб
- Прямоугольник
- Параллелограмм
Задание 5.
У четырехугольника две противоположные стороны параллельны и равны и есть один прямой угол. Что это за фигура?
- Квадрат
- Ромб
- Прямоугольник
- Параллелограмм
Ответы: 1. – 2; 2. – 3; 3. – 1; 4. – 4; 5. – 3
Содержание:
С четырехугольником вы уже знакомились на уроках математики. Дадим строгое определение этой фигуры.
Определение четырехугольника:
Четырехугольником называется фигура, состоящая из четырех точек (вершин четырехугольника) и четырех отрезков, которые их последовательно соединяют (сторон четырехугольника). При этом никакие три его вершины не лежат на одной прямой и никакие две стороны не пересекаются.
На рисунке 1 изображен четырехугольник с вершинами
Говорят, что две вершины четырехугольника являются соседними вершинами, если они соединены одной стороной; вершины, которые не являются соседними, называют противолежащими вершинами. Аналогично стороны четырехугольника, имеющие общую вершину, являются соседними сторонами, а стороны, не имеющие общих точек,— противолежащими сторонами. На рисунке 1 стороны 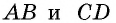
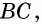
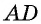
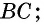
Четырехугольник обозначают, последовательно указывая все его вершины, причем буквы, которые стоят рядом, должны обозначать соседние вершины. Например, четырехугольник на рисунке 1 можно обозначить 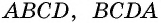
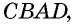
Определение
Диагональю четырехугольника называется отрезок, соединяющий две противолежащие вершины.
В четырехугольнике 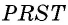
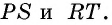
Определение
Периметром четырехугольника называется сумма длин всех его сторон. Периметр четырехугольника (как и треугольника) обозначают буквой
Любой четырехугольник ограничивает конечную часть плоскости, которую называют внутренней областью этого четырехугольника (на рис. 3, а, б она закрашена).
На рисунке 3 изображены два четырехугольника и проведены прямые, на которых лежат стороны этих четырехугольников. В четырехугольнике 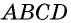
Определение
Четырехугольник называется выпуклым, если он лежит по одну сторону от любой прямой, содержащей его сторону.
Действительно, четырехугольник 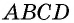
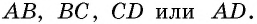
выпуклые четырехугольники (другие случаи будут оговорены отдельно).
Определение
Углом (внутренним углом) выпуклого четырехугольника 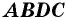
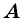
Угол, смежный с внутренним углом четырехугольника при данной вершине, называют внешним углом четырехугольника при данной вершине.
Углы, вершины которых являются соседними, называют соседними углами, а углы, вершины которых являются противолежащими,— противолежащими углами четырехугольника.
Теорема (о сумме углов четырехугольника)
Сумма углов четырехугольника равна
Доказательство:
В данном четырехугольнике 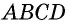
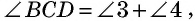
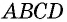
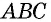
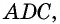
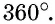
Пример:
Углы четырехугольника 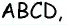
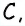
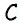
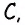
Решение:
Углами, соседними с углом 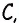
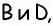
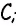
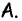
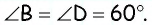
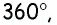
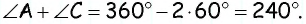
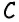
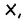
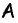
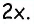
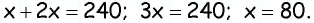
Ответ:
Определение параллелограмма
Определение параллелограмма
Рассмотрим на плоскости две параллельные прямые, пересеченные двумя другими параллельными прямыми (рис. 7).
В результате такого пересечения образуется четырехугольник, который имеет специальное название — параллелограмм.
Определение
Параллелограммом называется четырехугольник, противолежащие стороны которого попарно параллельны.
На рисунке 7 изображен параллелограмм 
Пример:
На рисунке 8 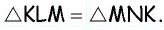
Решение:
Из равенства треугольников 
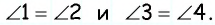
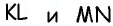
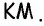
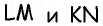
Как и в треугольнике, в параллелограмме можно провести высоты (рис. 9).
Определение
Высотой параллелограмма называется перпендикуляр, проведенный из точки одной стороны к прямой, которая содержит противолежащую сторону.
Очевидно, что к одной стороне параллелограмма можно провести бесконечно много высот (рис. 9, а),— все они будут равны как расстояния между параллельными прямыми, а из одной вершины параллелограмма можно провести две высоты к разным сторонам (рис. 9, б). Часто, говоря «высота параллелограмма», имеют в виду ее длину.
Свойства параллелограмма
Непосредственно из определения параллелограмма следует, что любые два его соседних угла являются внутренними односторонними при параллельных прямых, которые содержат противолежащие стороны. Это означает, что сумма двух соседних углов параллелограмма равна
Докажем еще несколько важных свойств сторон, углов и диагоналей параллелограмма.
Теорема (свойства параллелограмма)
В параллелограмме:
- противолежащие стороны равны;
- противолежащие углы равны;
- диагонали точкой пересечения делятся пополам.
Свойства 1 и 2 иллюстрирует рисунок 10, а, а свойство 3 — рисунок 10, б.
Доказательство:
Проведем в параллелограмме 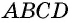
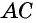
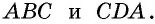
У них сторона 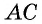
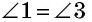
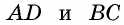
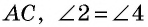
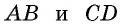
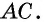
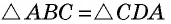
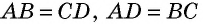
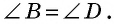
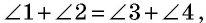
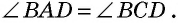
Для доказательства свойства 3 проведем в параллелограмме 
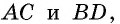
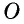
Рассмотрим треугольники 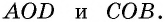
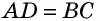
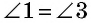
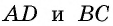
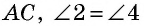
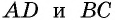
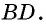
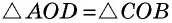
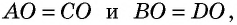
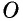
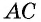
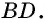
Пример №1
Сумма двух углов параллелограмма равна 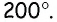
Решение:
Пусть дан параллелограмм 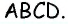

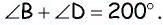
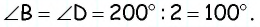
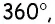
Ответ:
Пример №2
В параллелограмме 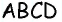
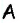
Решение:
Пусть в параллелограмме 
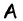
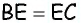
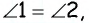

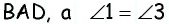
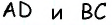
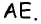
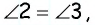
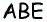
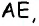
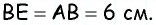
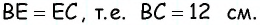
Ответ: 36 см.
Признаки параллелограмма
Теоремы о признаках параллелограмма
Для того чтобы использовать свойства параллелограмма, во многих случаях необходимо сначала убедиться, что данный четырехугольник действительно является параллелограммом. Это можно доказать либо по определению (см. задачу в п. 2.1), либо по признакам — условиям, гарантирующим, что данный четырехугольник — параллелограмм. Докажем признаки параллелограмма, которые чаще всего применяются на практике.
Теорема (признаки параллелограмма)
- Если две противолежащие стороны четырехугольника параллельны и равны, то этот четырехугольник — параллелограмм.
- Если противолежащие стороны четырехугольника попарно равны, то этот четырехугольник — параллелограмм.
- Если диагонали четырехугольника точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Доказательство:
1) Пусть в четырехугольнике 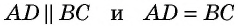
Проведем диагональ 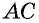
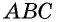
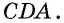
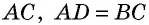
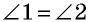
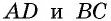
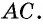
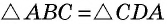
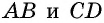
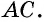
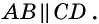
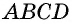
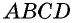
2) Пусть в четырехугольнике 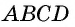
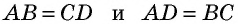
Снова проведем диагональ 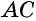
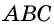
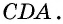
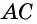
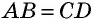
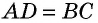
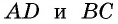
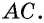
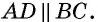
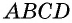
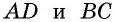
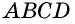
3) Пусть в четырехугольнике 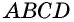
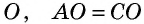
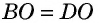
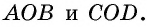
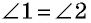
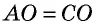
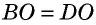
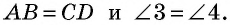
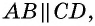
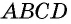
Теорема доказана полностью.
Пример №3
В параллелограмме 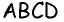

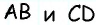
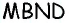
Решение:
Рассмотрим четырехугольник 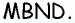
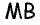
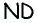
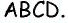
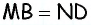
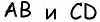
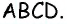
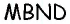
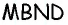
Попробуйте самостоятельно найти другие способы решения этой задачи, основанные на применении других признаков и определения параллелограмма.
Необходимые и достаточные условия
Каждый из признаков параллелограмма указывает на определенную особенность, наличия которой в четырехугольнике достаточно для того, чтобы утверждать, что он является параллелограммом. Вообще в математике признаки иначе называют достаточными условиями. Например, перпендикулярность двух прямых третьей — достаточное условие параллельности данных двух прямых.
В отличие от признаков, свойства параллелограмма указывают на ту особенность, которую обязательно имеет любой параллелограмм. Свойства иначе называют необходимыми условиями. Поясним такое название примером: равенство двух углов необходимо для того, чтобы углы были вертикальными, ведь если этого равенства нет, вертикальными такие углы быть не могут.
В случае верности теоремы «Если 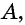
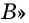
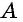
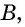
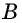
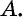
Таким образом, необходимые условия (свойства) параллелограмма следуют из того, что данный четырехугольник — параллелограмм; из достаточных условий (признаков) следует то, что данный четырехугольник — параллелограмм.
Сравнивая свойства и признаки параллелограмма, нетрудно заметить, что одно и то же условие (например, попарное равенство противолежащих сторон) является и свойством, и признаком параллелограмма. В таком случае говорят, что условие является необходимым и достаточным. Необходимое и достаточное условие иначе называют критерием. Например, равенство двух углов треугольника — критерий равнобедренного треугольника.
Немало примеров необходимых и достаточных условий можно найти в других науках и в повседневной жизни. Все мы знаем, что воздух — необходимое условие для жизни человека, но не достаточное (человеку для жизни нужно еще много чего, среди прочего — пища). Выигрыш в лотерею — достаточное условие для материального обогащения человека, но оно не является необходимым — ведь улучшить свое финансовое положение можно и другим способом. Попробуйте самостоятельно найти несколько примеров необходимых и достаточных условий.
Виды параллелограммов
Прямоугольник
Определение
Прямоугольником называется параллелограмм, у которого все углы прямые.
На рисунке 28 изображен прямоугольник
Поскольку прямоугольник является частным случаем параллелограмма, он имеет все свойства параллелограмма: противолежащие стороны прямоугольника параллельны и равны, противолежащие углы равны, диагонали точкой пересечения делятся пополам и т.д. Однако прямоугольник имеет некоторые особые свойства. Докажем одно из них.
Теорема (свойство прямоугольника)
Диагонали прямоугольника равны.
Доказательство:
Пусть дан прямоугольник 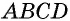
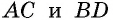
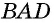
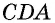
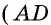
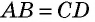
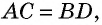
Имеет место и обратное утверждение (признак прямоугольника): если диагонали параллелограмма равны, то этот параллелограмм является прямоугольником. Докажите это утверждение самостоятельно. Таким образом, можно утверждать, что равенство диагоналей параллелограмма — необходимое и достаточное условие (критерий) прямоугольника.
Опорная задача
Если все углы четырехугольника прямые, то этот четырехугольник — прямоугольник. Докажите.
Решение:
Пусть в четырехугольнике 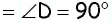
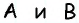
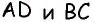
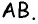

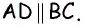
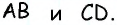
Ромб
Определение
Ромбом называется параллелограмм, у которого все стороны равны.
На рисунке 30 изображен ромб
Он обладает всеми свойствами параллелограмма, а также некоторыми дополнительными свойствами, которые мы сейчас докажем.
Теорема (свойства ромба)
Диагонали ромба перпендикулярны и делят его углы пополам.
Эти свойства ромба иллюстрируются рисунком 31.
Доказательство:
Пусть диагонали ромба 
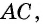
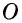
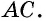
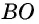
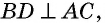
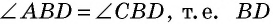
Аналогично доказываем, что диагонали ромба являются биссектрисами и других его углов. Теорема доказана.
Опорная задача
Если все стороны четырехугольника равны, то этот четырехугольник — ромб. Докажите.
Решение:
Очевидно, что в четырехугольнике, все стороны которого равны, попарно равными являются и противолежащие стороны. Следовательно, по признаку параллелограмма такой четырехугольник — параллелограмм, а по определению ромба параллелограмм, у которого все стороны равны, является ромбом.
Решая задачи, помещенные в конце этого параграфа, вы докажете другие признаки прямоугольника и ромба.
Квадрат
На рисунке 33 изображен еще один вид параллелограмма — квадрат.
Определение
Квадратом называется прямоугольник, у которого все стороны равны.
Иначе можно сказать, что квадрат — это прямоугольник, который является ромбом. Действительно, поскольку квадрат является прямоугольником и ромбом и, конечно же, произвольным параллелограммом, то:
- все стороны квадрата равны, а противолежащие стороны параллельны;
- все углы квадрата прямые;
- диагонали квадрата равны, перпендикулярны, делят углы квадрата пополам и делятся точкой пересечения пополам.
Связь между отдельными видами параллелограммов. Равносильные утверждения
Исходя из определений произвольного параллелограмма и его отдельных видов, мы можем схематически отобразить связь между ними (рис. 34).
На схеме представлены множества параллелограммов, прямоугольников и ромбов. Такой способ наглядного представления множеств называют диаграммами Эйлера — Венна. Диаграмма Эйлера — Венна для параллелограммов демонстрирует, что множества прямоугольников и ромбов являются частями (подмножествами) множества параллелограммов, а множество квадратов — общей частью (пересечением) множеств прямоугольников и ромбов. Диаграммы Эйлера — Венна часто используют для подтверждения или проверки правильности логических рассуждений.
Подытоживая материал этого параграфа, обратим также внимание на то, что возможно и другое определение квадрата: квадратом называется ромб с прямыми углами. В самом деле, оба приведенных определения описывают одну и ту же фигуру. Такие определения называют равносильными. Вообще два утверждения называются равносильными, если они или оба выполняются, или оба не выполняются. Например, равносильными являются утверждения «В треугольнике две стороны равны» и «В треугольнике два угла равны», ведь оба они верны, если рассматривается равнобедренный треугольник, и оба ложны, если речь идет о разностороннем треугольнике.
Равносильность двух утверждений также означает, что любое из них является необходимым и достаточным условием для другого. В самом деле, рассмотрим равносильные утверждения «Диагонали параллелограмма равны» и «Параллелограмм имеет прямые углы». Из того, что диагонали параллелограмма равны, следует, что он является прямоугольником, т.е. имеет прямые углы, и наоборот: параллелограмм с прямыми углами является прямоугольником, т.е. имеет равные диагонали. На этом примере легко проследить логические шаги перехода от признаков фигуры к ее определению и далее — к свойствам. Такой переход довольно часто приходится выполнять в процессе решения задач.
Трапеция
Как известно, любой параллелограмм имеет две пары параллельных сторон. Рассмотрим теперь четырехугольник, который имеет только одну пару параллельных сторон.
Определение
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Параллельные стороны трапеции называют ее основаниями, а непараллельные стороны — боковыми сторонами. На рисунке 37 в трапеции 
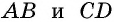
Углы, прилежащие к одной боковой стороне, являются внутренними односторонними при параллельных прямых, на которых лежат основания трапеции. По теореме о свойстве параллельных прямых из этого следует, что сумма углов трапеции, прилежащих к боковой стороне, равна 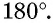
Определение
Высотой трапеции называется перпендикуляр, проведенный из точки одного основания к прямой, содержащей другое основание.
Очевидно, что в трапеции можно провести бесконечно много высот (рис. 38),— все они равны как расстояния между параллельными прямыми.
Чаще всего в процессе решения задач высоты проводят из вершин углов при меньшем основании трапеции.
Частные случаи трапеций
Как среди треугольников и параллелограммов, так и среди трапеций выделяются отдельные виды, обладающие дополнительными свойствами.
Определение
Прямоугольной трапецией называется трапеция, в которой одна из боковых сторон перпендикулярна основаниям.
На рисунке 39 изображена прямоугольная трапеция. У нее два прямых угла при меньшей боковой стороне. Эта сторона одновременно является и высотой трапеции.
Определение
Равнобедренной трапецией называется трапеция, в которой боковые стороны равны.
На рисунке 40 изображена равнобедренная трапеция 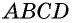
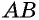
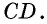
У равнобедренной трапеции так же, как и у равнобедренного треугольника, углы при основании равны. Докажем это в следующей теореме.
Теорема (свойство равнобедренной трапеции)
В равнобедренной трапеции углы при основании равны.
Доказательство:
Пусть 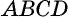
Перед началом доказательства заметим, что этой теоремой утверждается равенство углов при каждом из двух оснований трапеции, т. е. необходимо доказать, что
Проведем высоты 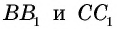
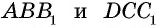
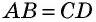
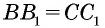
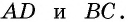
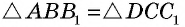
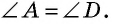
Теорема доказана.
Имеет место также обратное утверждение (признак равнобедренной трапеции):
- если в трапеции углы при основании равны, то такая трапеция является равнобедренной.
Докажите этот факт самостоятельно.
Пример №4
Меньшее основание равнобедренной трапеции равно боковой стороне, а диагональ перпендикулярна боковой стороне. Найдите углы трапеции.
Решение:
Пусть дана равнобедренная трапеция 
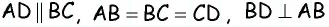
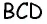
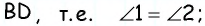
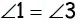

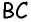
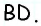
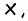
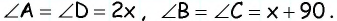

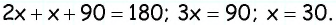
Ответ:
Построение параллелограммов и трапеций
Задачи на построение параллелограммов и трапеций часто решают методом вспомогательного треугольника. Напомним, что для этого необходимо выделить в искомой фигуре треугольник, который можно построить по имеющимся данным. Построив его, получаем две или три вершины искомого четырехугольника, а остальные вершины находим по данным задачи.
Пример №5
Постройте параллелограмм по двум диагоналям и углу между ними.
Решение:
Пусть 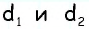
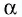
Пусть параллелограмм 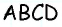
Треугольник 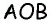
Таким образом, мы получим вершины 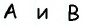
Вершины 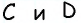
Построение
1. Разделим отрезки 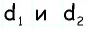
2. Построим треугольник 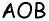
3. На лучах 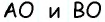
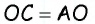
4. Последовательно соединим точки
Доказательство:
Четырехугольник 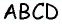
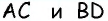
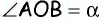
Исследование
Задача имеет единственное решение при любых значениях
В некоторых случаях для построения вспомогательного треугольника на рисунке-эскизе необходимо провести дополнительные линии.
Пример №6
Постройте трапецию по четырем сторонам.
Решение:
Пусть 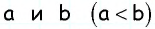
Анализ
Пусть искомая трапеция 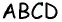
Проведем через вершину 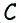
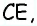
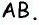
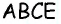

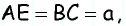
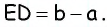


Построение
1. Построим отрезок
2. Построим треугольник 
3. Построим луч, проходящий через точку 


4. На луче 
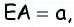
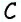
5. Соединим точки
Доказательство:
По построению 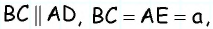

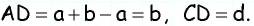
Исследование
Задача имеет единственное решение, если числа 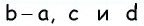
Теорема Фалеса
Для дальнейшего изучения свойств трапеции докажем важную теорему.
Теорема (Фалеса)
Параллельные прямые, которые пересекают стороны угла и отсекают на одной из них равные отрезки, отсекают равные отрезки и на другой стороне.
Доказательство:
Пусть 
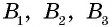
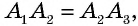
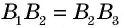
Проведем через точку 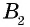
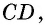
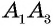
Четырехугольники 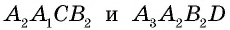
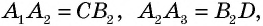
Рассмотрим треугольники 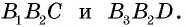
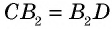
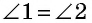
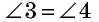
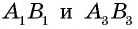
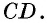
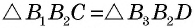
Теорема доказана.
Заметим, что в условии данной теоремы вместо сторон угла можно рассматривать две произвольные прямые, поэтому теорема Фалеса может формулироваться и следующим образом: параллельные прямые, которые пересекают две данные прямые и отсекают на одной из них равные отрезки, отсекают равные отрезки и на другой прямой.
Пример №7
Разделите данный отрезок на 
Решение:
Решим задачу для 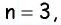

Для этого проведем из точки 
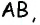
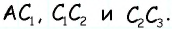
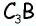
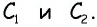

Средняя линия треугольника
Теорема Фалеса помогает исследовать еще одну важную линию в треугольнике.
Определение
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
На рисунке 49, а отрезок 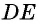
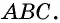
Теорема (свойство средней линии треугольника)
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Доказательство:
Пусть 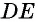
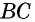
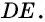
Проведем теперь среднюю линию 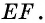
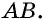
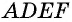
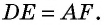
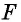
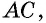
Теорема доказана.
Опорная задача (теорема Вариньона) Середины сторон четырехугольника являются вершинами параллелограмма. Докажите.
Решение:
Пусть точки 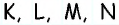
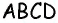
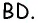
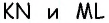
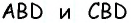
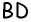
Средняя линия трапеции
Определение
Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции.
На рисунке 52 отрезок 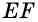
Теорема (свойство средней линии трапеции) Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство:
Пусть 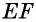
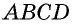
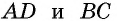
Проведем прямую 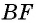
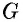
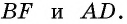
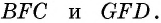
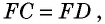
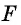
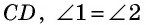
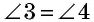
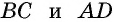
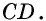
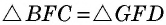
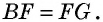
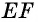
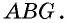
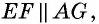
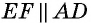
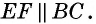
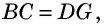
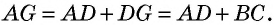
Теорема доказана.
Пример №8
Через точки, делящие боковую сторону трапеции на три равные части, проведены прямые, параллельные основаниям трапеции. Найдите длины отрезков этих прямых, заключенных внутри трапеции, если ее основания равны 2 м и 5 м.
Решение:
Пусть в трапеции 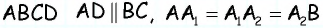
По теореме Фалеса параллельные прямые, которые проходят через точки 
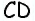
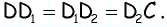
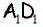
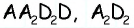
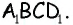
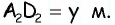
Ответ: 3 м и 4 м.
Вписанные углы
Градусная мера дуги
В седьмом классе изучение свойств треугольников завершалось рассмотрением описанной и вписанной окружностей. Но перед тем как рассмотреть описанную и вписанную окружности для четырехугольника, нам необходимо остановиться на дополнительных свойствах углов.
До сих пор мы изучали только те углы, градусная мера которых не превышала 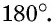
На рисунке 58 угол 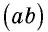
Используем понятие плоского угла для определения центрального угла в окружности.
Определение
Центральным углом в окружности называется плоский угол с вершиной в центре окружности.
На рисунке 59, а, б стороны угла с вершиной в центре окружности 
Для того чтобы уточнить, какой из двух плоских углов со сторонами 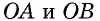
На рисунке 59, а центральному углу 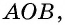
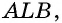
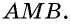
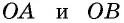
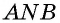
Определение
Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.
Градусную меру дуги, как и саму дугу, обозначают так: 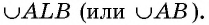
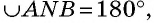
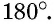
Концы хорды 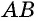
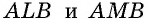
Вписанный угол
Определение
Вписанным углом называется угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.
На рисунке 60 изображен вписанный угол 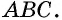
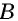
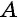
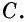
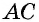
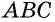
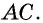
Теорема (о вписанном угле)
Вписанный угол измеряется половиной дуги, на которую он опирается.
Доказательство:
Пусть в окружности с центром 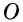
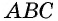
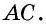
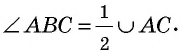
1) Пусть центр окружности лежит на одной из сторон данного угла (рис. 61, а). В этом случае центральный угол 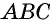
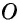
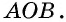
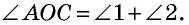
т.е.
2) Пусть центр окружности лежит внутри угла 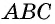
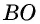
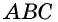
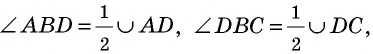
3) Аналогично в случае, когда центр окружности лежит вне вписанного угла (рис. 60, б),
Теорема доказана.
Только что доказанную теорему можно сформулировать иначе.
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.
Пример №9
Найдите угол 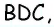
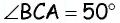
Решение:
Для того чтобы найти угол 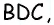
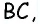
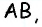

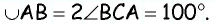
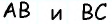
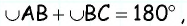
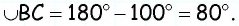
Ответ:
Следствия теоремы о вписанном угле
По количеству и значимости следствий теорема о вписанном угле является одной из «богатейших» геометрических теорем. Сформулируем наиболее важные из этих следствий.
Следствие 1
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Действительно, по теореме о вписанном угле градусная мера каждого из вписанных углов на рисунке 63 равна половине дуги
Следствие 2
Вписанный угол, опирающийся на полуокружность,— прямой, и наоборот: любой прямой вписанный угол опирается на полуокружность.
Действительно, поскольку градусная мера полуокружности равна 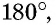
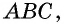
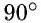
Следствие 3
Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы. Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.
Первое из приведенных утверждений вытекает из следствия 2. Если в треугольнике 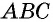
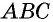
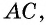
Тогда гипотенуза 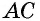
Отметим еще один интересный факт: медиана прямоугольного треугольника, проведенная к гипотенузе, делит данный треугольник на два равнобедренных треугольника с общей боковой стороной. Из этого, в частности, следует, что углы, на которые медиана делит прямой угол, равны острым углам треугольника (рис. 65, б).
В качестве примера применения следствий теоремы о вписанном угле приведем другое решение задачи, которую мы рассмотрели в п. 7.2.
Пример №10
Найдите угол 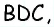
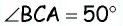
Решение:
Проведем хорду 
Поскольку вписанный угол 
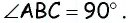
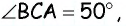
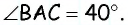
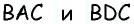
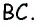
Ответ:
Вписанные четырехугольники
Определение
Четырехугольник называется вписанным в окружность, если все его вершины лежат на этой окружности.
Четырехугольник 
Как известно, около любого треугольника можно описать окружность. Для четырехугольника это можно сделать не всегда. Докажем свойство и признак вписанного четырехугольника.
Теорема (овписанном четырехугольнике)
- Сумма противолежащих углов вписанного четырехугольника равна
(свойство вписанного четырехугольника).
- Если сумма противолежащих углов четырехугольника равна
то около него можно описать окружность (признак вписанного четырехугольника).
Доказательство:
1) Свойство. Пусть четырехугольник 
Следовательно,
Аналогично доказываем, что
2) Признак. Пусть в четырехугольнике 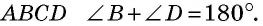
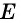
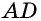
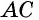
Тогда четырехугольник 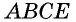
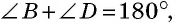
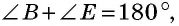
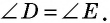
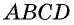
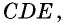
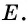
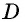
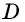
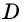
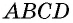
Теорема доказана.
Следствие 1
Около любого прямоугольника можно описать окружность.
Если параллелограмм вписан в окружность, то он является прямоугольником
Прямоугольник, вписанный в окружность, изображен на рисунке 74.
Центр описанной окружности является точкой пересечения диагоналей прямоугольника (см. задачу 255).
Следствие 2
Около равнобедренной трапеции можно описать окружность.
Если трапеция вписана в окружность, то она равнобедренная.
Равнобедренная трапеция, вписанная в окружность, изображена на рисунке 75.
Описанные четырехугольники
Определение
Четырехугольник называется описанным около окружности, если все его стороны касаются этой окружности.
Четырехугольник 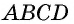
Оказывается, что не в любой четырехугольник можно вписать окружность. Докажем соответствующие свойство и признак.
Теорема (об описанном четырехугольнике)
- В описанном четырехугольнике суммы противолежащих сторон равны (свойство описанного четырехугольника).
- Если в четырехугольнике суммы противолежащих сторон равны, то в него можно вписать окружность (признак описанного четырехугольника).
Доказательство:
1) Свойство. Пусть стороны четырехугольника 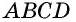
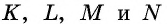
По свойству отрезков касательных 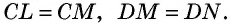
2) Признак. Пусть в четырехугольнике 
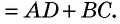
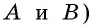
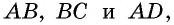
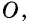
Предположим, что это не так. Тогда прямая 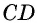
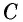
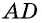
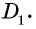
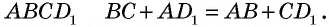
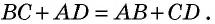
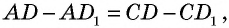
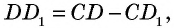
Таким образом, наше предположение неверно. Аналогично можно доказать, что прямая 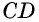
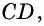
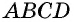
Замечание. Напомним, что в данной теореме рассматриваются только выпуклые четырехугольники.
Следствие
В любой ромб можно вписать окружность. Если в параллелограмм вписана окружность, то он является ромбом
Ромб, описанный около окружности, изображен на рисунке 78. Центр вписанной окружности является точкой пересечения диагоналей ромба (см. задачу 265, а).
Пример №11
В равнобедренную трапецию с боковой стороной 6 см вписана окружность. Найдите среднюю линию трапеции.
Решение:
Пусть 
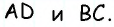
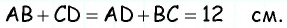
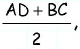
Ответ: 6 см
Геометрические софизмы
Многим из вас, наверное, известна древнегреческая история об Ахиллесе, который никак не может догнать черепаху. История математики знает немало примеров того, как ложные утверждения и ошибочные результаты выдавались за истинные, а их опровержение давало толчок настоящим математическим открытиям. Но даже ошибки и неудачи могут принести пользу математикам. Эти ошибки остались в учебниках и пособиях в виде софизмов — заведомо ложных утверждений, доказательства которых на первый взгляд кажутся правильными, но на самом деле таковыми не являются. Поиск и анализ ошибок, содержащихся в этих доказательствах, часто позволяют определить причины ошибок в решении других задач. Поэтому в процессе изучения геометрии софизмы иногда даже более поучительны и полезны, чем «безошибочные» задачи и доказательства.
Рассмотрим пример геометрического софизма, связанного с четырехугольниками, вписанными в окружность.
Окружность имеет два центра.
Доказательство:
Обозначим на сторонах произвольного угла 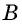
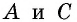
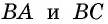
Эти перпендикуляры должны пересекаться (ведь если бы они были параллельны, то параллельными были бы и стороны данного угла — обоснуйте это самостоятельно). Обозначим точку 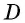
Через точки 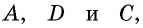
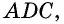
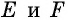
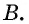
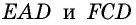
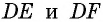
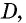
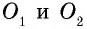
Ошибка этого «доказательства» заключается в неправильности построений на рисунке 79. В четырехугольнике 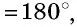
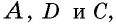
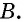
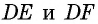
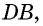
Среди задач к этому и следующим параграфам вы найдете и другие примеры геометрических софизмов и сможете самостоятельно потренироваться в их опровержении. Надеемся, что опыт, который вы при этом приобретете, поможет в дальнейшем избежать подобных ошибок при решении задач.
Четырехугольник и окружность в задачах. Метод вспомогательной окружности
При решении задач об окружностях и четырехугольниках иногда следует использовать специальные подходы. Один из них заключается в рассмотрении вписанного треугольника, вершины которого являются вершинами данного вписанного четырехугольника.
Пример №12
Найдите периметр равнобедренной трапеции, диагональ которой перпендикулярна боковой стороне и образует с основанием угол 
Решение:
Пусть дана вписанная трапеция 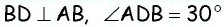
Заметим, что окружность, описанная около трапеции, описана также и около прямоугольного треугольника 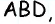

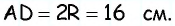
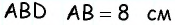
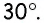
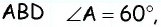

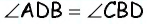
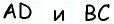
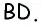
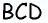
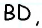

Ответ: 40 см.
Особенно интересным и нестандартным является применение окружности (как описанной, так и вписанной) при решении задач, в условиях которых окружность вообще не упоминается.
Пример №13
Из точки 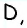
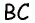
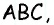


Решение:
В четырехугольнике 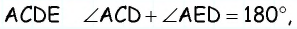
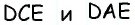
Метод решения задач с помощью дополнительного построения описанной или вписанной окружности называют методом вспомогательной окружности.
Замечательные точки треугольника
Точка пересечения медиан
В седьмом классе в ходе изучения вписанной и описанной окружностей треугольника рассматривались две его замечательные точки — точка пересечения биссектрис (иначе ее называют инцентром треугольника) и точка пересечения серединных перпендикуляров к сторонам.
Рассмотрим еще две замечательные точки треугольника.
Теорема (о точке пересечения медиан треугольника)
Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, начиная от вершины треугольника.
Доказательство:
Пусть в треугольнике 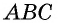
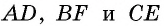
Докажем, что они пересекаются в некоторой точке 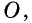
Пусть 
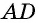
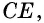
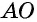
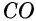
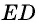
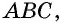
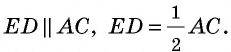
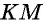
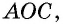
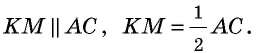
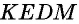

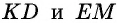
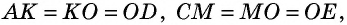
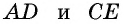
Аналогично доказываем, что и третья медиана 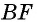
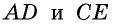
Точку пересечения медиан треугольника иначе называют центроидом или центром масс треугольника. В уместности такого названия вы можете убедиться, проведя эксперимент: вырежьте из картона треугольник произвольной формы, проведите в нем медианы и попробуйте удержать его в равновесии, положив на иглу или острый карандаш в точке пересечения медиан (рис. 86).
Пример №14
Если в треугольнике две медианы равны, то он равнобедренный. Докажите.
Решение:
Пусть в треугольнике 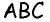
Рассмотрим треугольники 


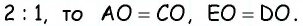
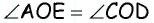
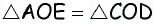
Но по определению медианы эти отрезки — половины сторон 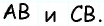
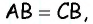
Точка пересечения высот
Теорема (о точке пересечения высот треугольника)
Высоты треугольника (или их продолжения) пересекаются в одной точке.
Доказательство:
Пусть 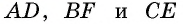
Проведя через вершины треугольника прямые, параллельные противолежащим сторонам, получим треугольник 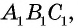
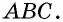
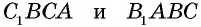
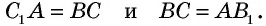
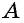
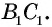
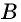
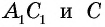
Таким образом, высоты 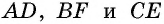
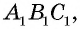
Точку пересечения высот (или их продолжений) иначе называют ортоцентром треугольника.
Таким образом, замечательными точками треугольника являются:
- точка пересечения биссектрис — центр окружности, вписанной в треугольник;
- точка пересечения серединных перпендикуляров к сторонам — центр окружности, описанной около треугольника;
- точка пересечения медиан — делит каждую из медиан в отношении 2:1, начиная от вершины треугольника;
- точка пересечения высот (или их продолжений).
ИТОГОВЫЙ ОБЗОР ГЛАВЫ I
ЧЕТЫРЕХУГОЛЬНИК
Теорема о сумме углов четырехугольника.
Сумма углов четырехугольника равна
Справочный материал по параллелограмму
Параллелограммом называется четырехугольник, противолежащие стороны которого попарно параллельны
Признаки параллелограмма
Если две противолежащие стороны четырехугольника параллельны и равны, то этот четырехугольник — параллелограмм
Если противолежащие стороны четырехугольника попарно равны, то этот четырехугольник- параллелограм.
Противолежащие углы параллелограмма равны.
Диагонали параллелограмма точкой пересечения делятся пополам
Если противолежащие углы четырехугольника попарно равны, то этот четырехугольник — параллелограмм
Если диагонали четырехугольника точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм
Виды параллелограммов
Прямоугольником называется параллелограм у которого все углы прямые
Ромбом называется параллелограмм, у которого все стороны равны
Квадратом называется прямоугольник, у которого все стороны равны
Свойство прямоугольника
Диагонали прямоугольника равны
Признак прямоугольника
Если все углы четырехугольника равны, то этот четырехугольник является прямоугольником
Свойства ромба
Диагонали ромба перпендикулярны и делят его углы пополам
Признак ромба
Если все стороны четырехугольника равны, то этот четырехугольник является ромбом
Свойства квадрата
Все стороны квадрата равны, а противолежащие стороны параллельны
Все углы квадрата прямые
Диагонали квадрата равны, перпендикулярны, делят углы квадрата пополам и точкой пересечения делятся пополам
Трапеция
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие непараллельны
Прямоугольной трапецией называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям
Равнобедренной трапецией называется трапеция, у которой боковые стороны равны.
Свойство равнобедренной
В равнобедренной трапеции углы при основании равны.
Признак равнобедренной
Если в трапеции углы при основании равны, то такая трапеция равнобедренная
Теорема Фалеса
Параллельные прямые, которые пересекают стороны угла и отсекают на одной из них равные отрезки, отсекают равные отрезки и на другой стороне
Средние линии треугольника и трапеции
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции
Свойство средней линии треугольника
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны
Свойство средней линии трапеции
Средняя линия трапеции параллельна основаниям и равна их полусумме
Углы в окружности
Центральным углом в окружности называется плоский угол с вершиной в центре окружности
Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла
Вписанным углом называется угол, вершина которого лежит на окружности, а стороны пересекают эту окружность
Теорема о вписанном угле Вписанный угол измеряется половиной дуги, на которую он опирается
Следствия теоремы о вписанном угле
Вписанные углы, опирающиеся на одну и ту же дугу, равны
Вписанный угол, опирающийся на полуокружность, прямой, и наоборот: любой прямой вписанный угол опирается на полуокружность
Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы. Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы
Вписанные четырехугольники
Четырехугольник называется вписанным в окружность, если все его вершины лежат на этой окружности
Признак вписанного четырехугольника
Если сумма противолежащих углов четырехугольника равна 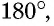
Около любого прямоугольника можно описать окружность
Около равнобедренной трапеции можно описать окружность
Свойство вписанного четырехугольника
- Сумма противолежащих углов вписанного четырехугольника равна
- Если параллелограмм вписан в окружность, то он является прямоугольником
- Если трапеция вписана в окружность, то она равнобедренная
Описанные четырехугольники
Четырехугольник называется описанным около окружности, если все его стороны касаются этой окружности
Признак описанного четырехугольника
Если в выпуклом четырехугольнике суммы противолежащих сторон равны, то в него можно вписать окружность
В любой ромб можно вписать окружность
Свойство описанного четырехугольника
- В описанном четырехугольнике суммы противолежащих сторон равны
- Если в параллелограмм вписана окружность, то он является ромбом
Замечательные точки треугольника
Теорема о точке пересечения медиан треугольника Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, начиная от вершины треугольника
Теорема о точке пересечения высот треугольника Высоты треугольника (или их продолжения) пересекаются в одной точке
Историческая справка
Большая часть теоретических положений, связанных с четырехугольником, была известна еще в Древней Греции. Например, параллелограмм упоминается в работах Евклида под названием «параллельно-линейная площадь». Основные свойства четырехугольников были установлены на практике и только со временем доказаны теоретически.
Одним из творцов идеи геометрического доказательства по праву признан древнегреческий ученый Фалес Милетский (ок. 625-547 гг. до н. э.). Его считали первым среди прославленных «семи мудрецов» Эллады. Механик и астроном, философ и общественный деятель, Фалес значительно обогатил науку своего времени. Именно он познакомил греков с достижениями египтян в геометрии и астрономии. По свидетельству историка Геродота, Фалес предсказал затмение Солнца, которое произошло 28 мая 585 г. до н. э. Он дал первые представления об электричестве и магнетизме. Достижения Фалеса в геометрии не ограничиваются теоремой, названной его именем. Считается, что Фалес открыл теорему о вертикальных углах, доказал равенство углов при основании равнобедренного треугольника, первым описал окружность около прямоугольного треугольника и обосновал, что угол, который опирается на полуокружность, прямой. Фалесу приписывают и доказательство второго признака равенства треугольников, на основании которого он создал дальномер для определения расстояния до кораблей на море.
В молодые годы Фалес побывал в Египте. Согласно легенде, он удивил египетских жрецов, измерив высоту пирамиды Хеопса с помощью подобия треугольников (о подобии треугольников – в следующей главе).
Изучая замечательные точки треугольника, нельзя не вспомнить имена еще нескольких ученых.
Теорему о пересечении высот треугольника доказал в XV в. немецкий математик Региомонтан (1436-1476) – в его честь эту теорему иногда называют задачей Региомонтана.
Выдающийся немецкий ученый Леонард Эйлер (1707-1783), который установил связь между замечательными точками треугольника, является уникальной исторической фигурой. Геометрия и механика, оптика и баллистика, астрономия и теория музыки, математическая физика и судостроение – вот далеко не полный перечень тех областей науки, которые он обогатил своими открытиями. Перу Эйлера принадлежит более 800 научных работ, причем, по статистическим подсчетам, он делал в среднем одно изобретение в неделю! Человек чрезвычайной широты интересов, Эйлер был академиком Берлинской, Петербургской и многих других академий наук, он существенным образом повлиял на развитие мировой науки. Недаром французский математик Пьер Лаплас, рассуждая об ученых своего поколения, утверждал, что Эйлер – «учитель всех нас».
Среди украинских математиков весомый вклад в исследование свойств четырехугольников внес Михаил Васильевич Остроградский (1801-1862). Этот выдающийся ученый, профессор Харьковского университета, получил мировое признание благодаря работам по математической физике, математическому анализу, аналитической механике. Талантливый педагог и методист, Остроградский создал «Учебник по элементарной геометрии», который, в частности, содержал ряд интересных и сложных задач на построение вписанных и описанных четырех. М. В. Остроградский угольников и вычисление их площадей.
- Теорема синусов и теорема косинусов
- Параллельность прямых и плоскостей
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Центральные и вписанные углы
- Углы и расстояния в пространстве
- Подобие треугольников
- Решение прямоугольных треугольников








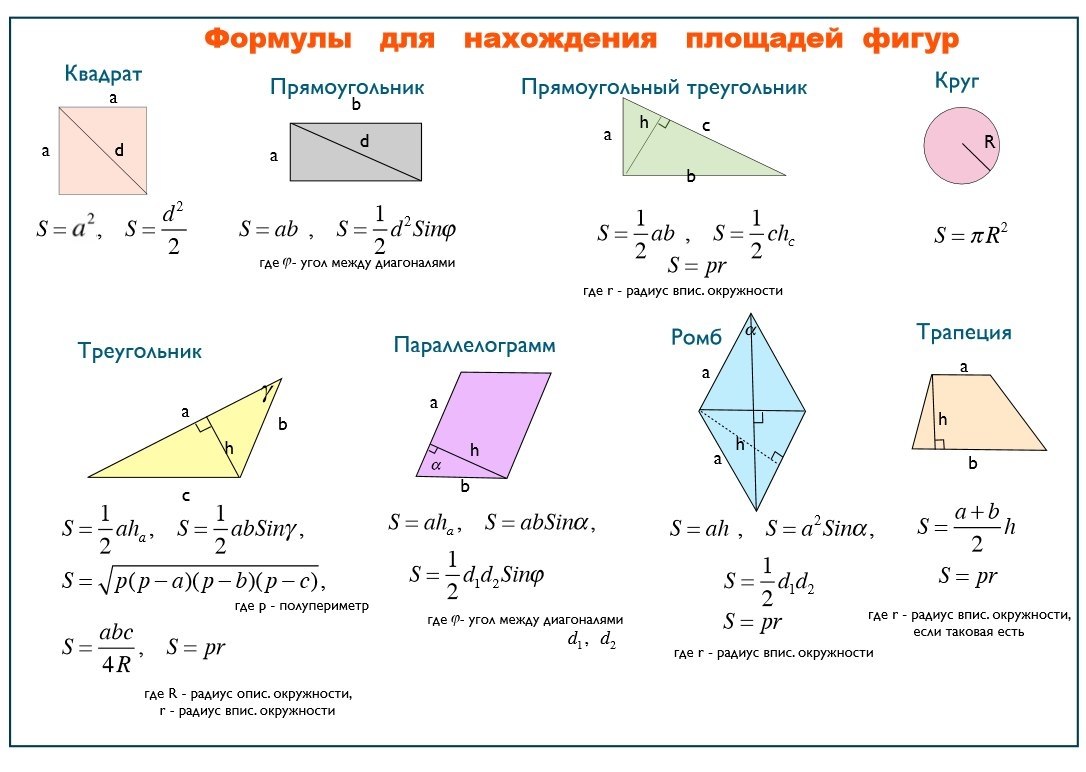




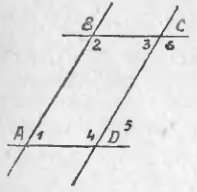
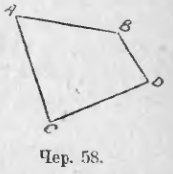
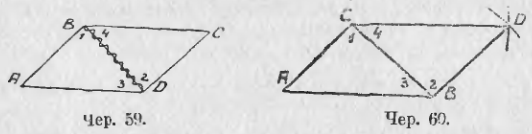
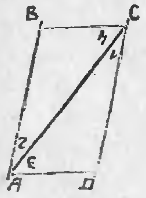
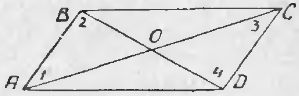
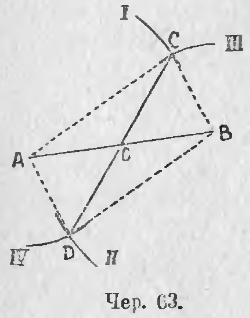
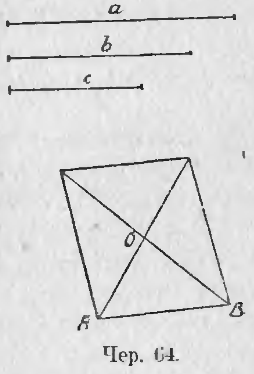
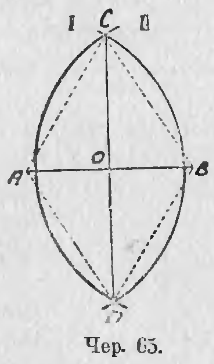
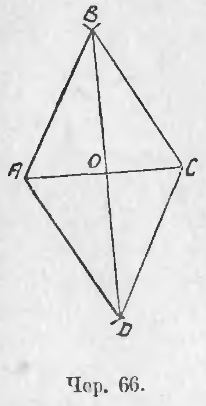
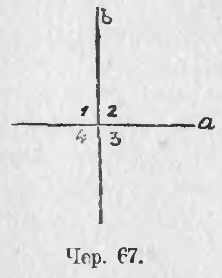
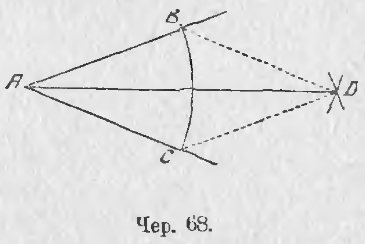
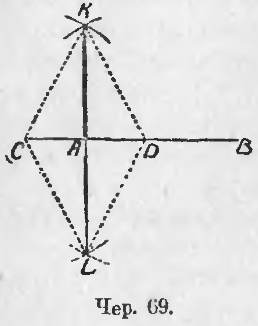
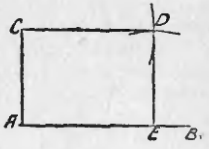
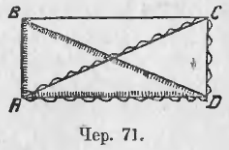
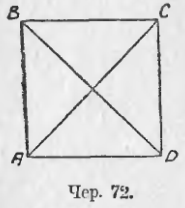



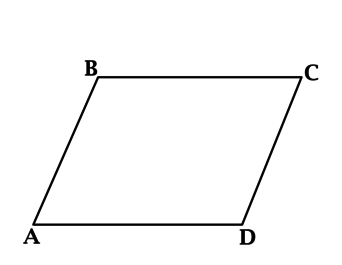
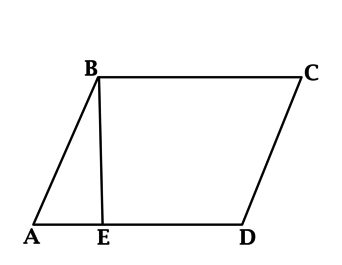
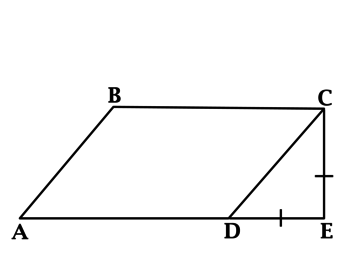







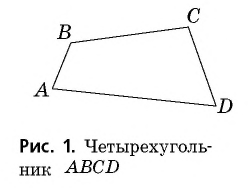
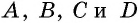
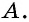
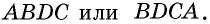
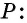
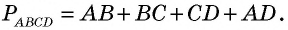
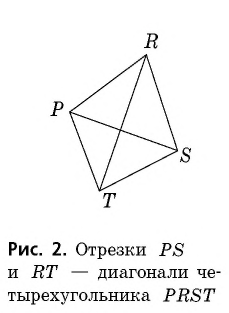
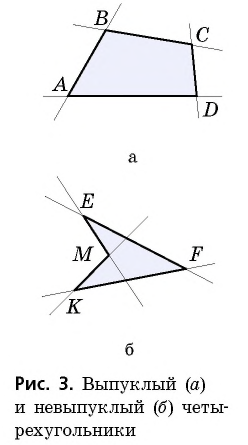
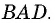
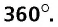
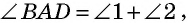
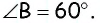
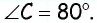
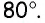
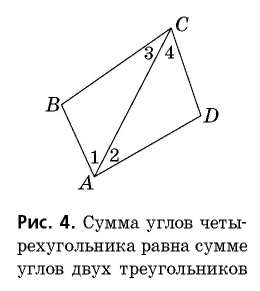
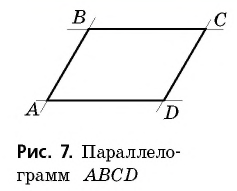
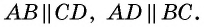
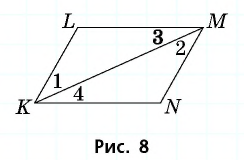
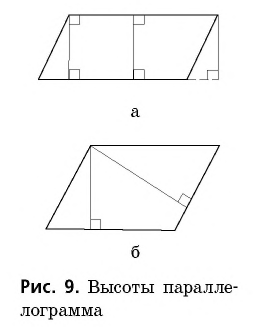
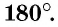
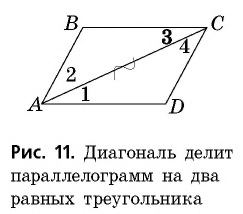
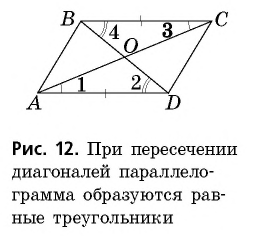
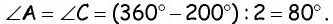

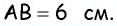
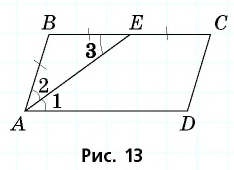
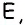
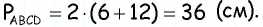
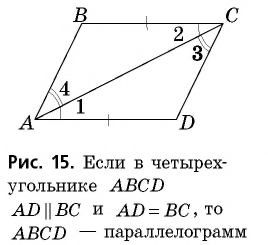
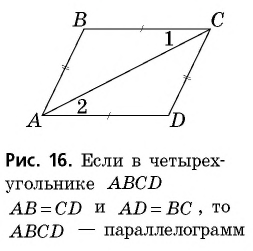
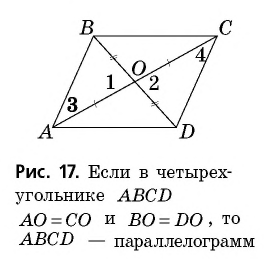
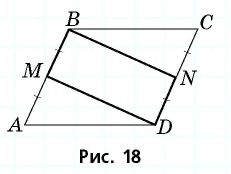

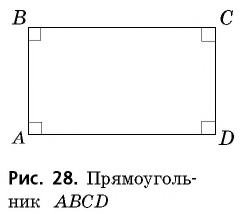
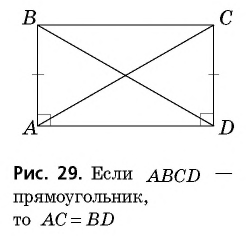
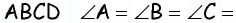
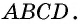
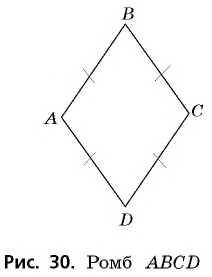
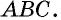
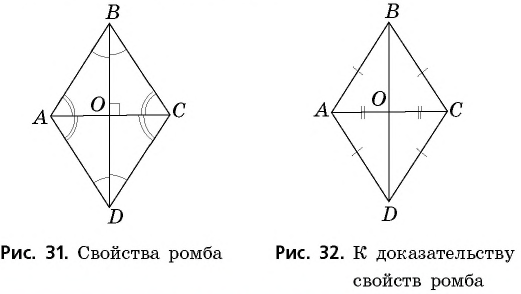
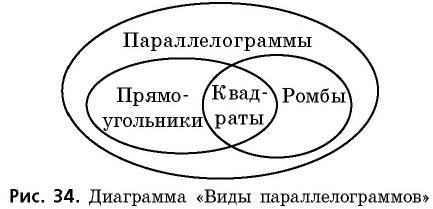
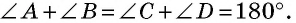
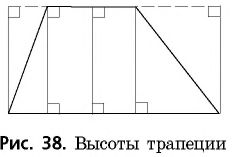
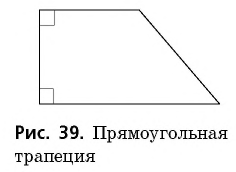
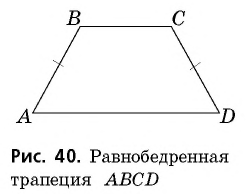
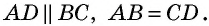
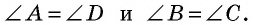
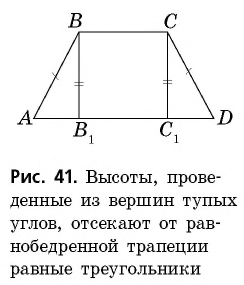
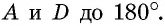
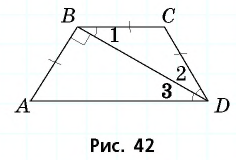
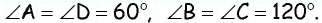
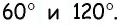
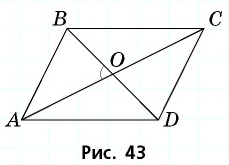
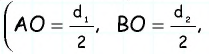
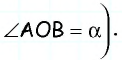
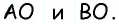
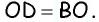
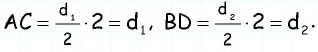
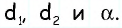
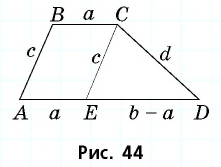
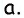
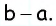
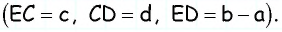
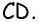
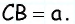
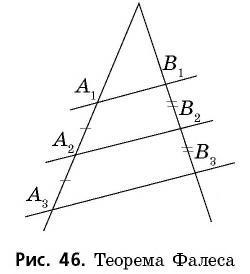
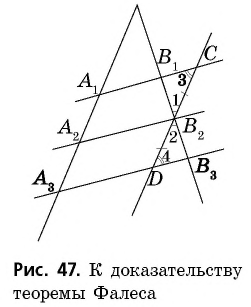
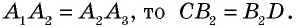
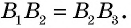
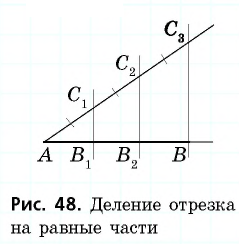
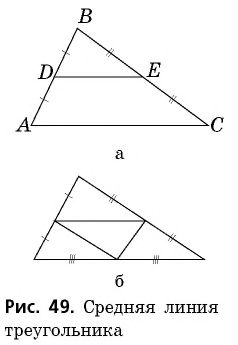
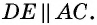
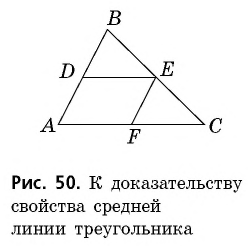
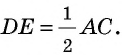
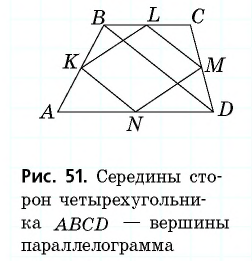
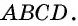
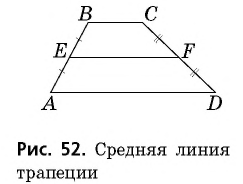
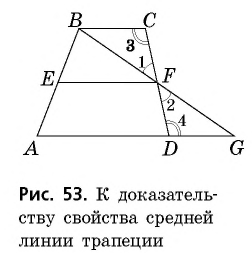
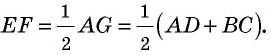
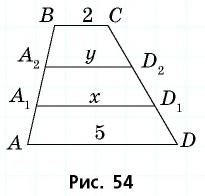
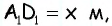
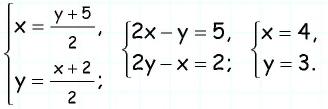
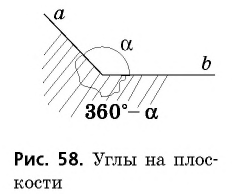
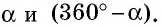
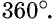
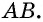
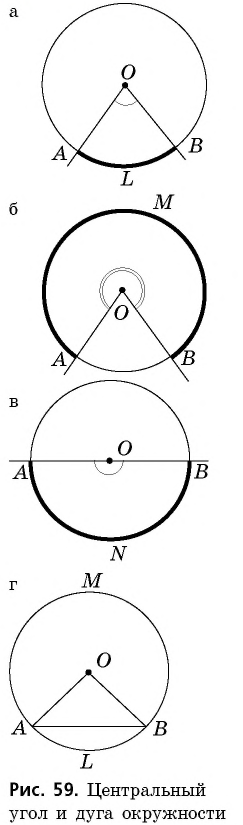
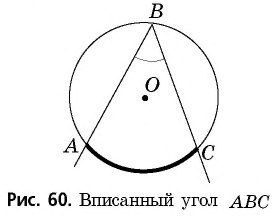
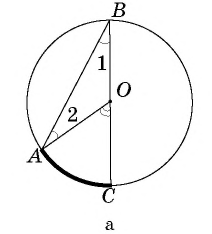
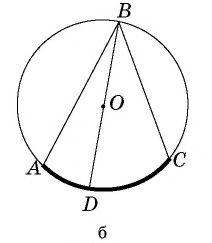
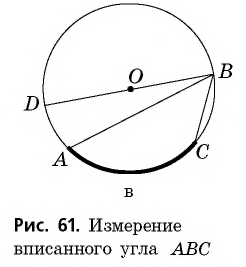
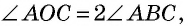
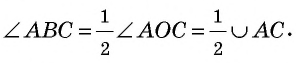
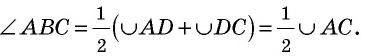
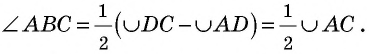
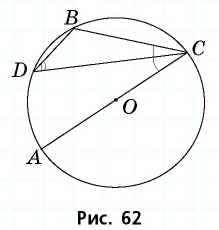
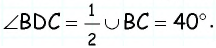
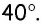
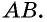
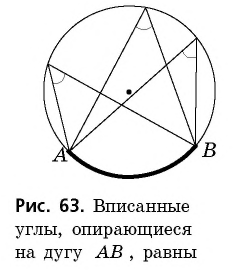
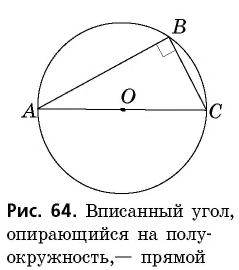
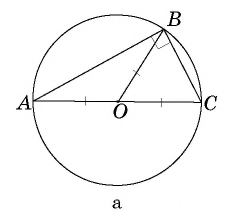
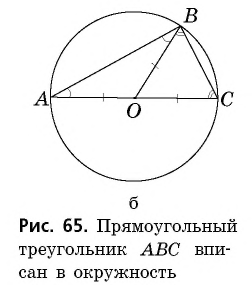
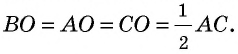
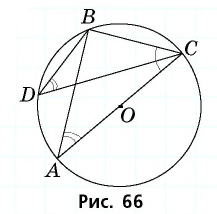
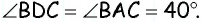

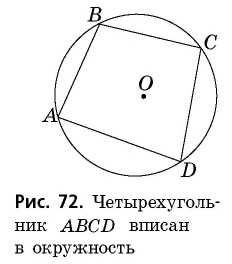
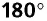 (свойство вписанного четырехугольника).
(свойство вписанного четырехугольника).