Наш калькулятор движения тела — это инструмент, который поможет вам проанализировать параболическое движение тела. Он может определить время полета, а также компоненты скорости, дальность полета и максимальную высоту полета. Продолжайте читать, если вы хотите понять, что такое движение тела, познакомьтесь с определением движения и определите вышеупомянутые значения с помощью уравнений движения тела.
Что такое движение тела (снаряда)? Определение движения снаряда
Представьте себе лучника, посылающего в воздух стрелу. Она начинает двигаться вверх и вперед при некотором наклоне к земле. Чем дальше она летит, тем медленнее она поднимается — и, наконец, она начинает снижаться, двигаясь теперь вниз и вперед и, наконец, снова ударяясь о землю. Если бы вы могли проследить ее путь, это была бы кривая, называемая траекторией в форме параболы. Любой объект, движущийся таким образом, движется как снаряд.
На снаряд действует только одна сила — сила тяжести. Сопротивление воздуха всегда не учитывается. Если вы начертите диаграмму свободного тела такого объекта, вам нужно будет нарисовать только один направленный вниз вектор и обозначить его «гравитация». Если бы на тело действовали какие-либо другие силы, то — по определению движения снаряда — это не был бы снаряд.
Калькулятор движения снаряда
Анализ движения снаряда
Движение снаряда довольно логично. Предположим, вы знаете начальную скорость объекта V, угол запуска α и начальную высоту h. Наш калькулятор движения снаряда выполняет следующие действия, чтобы найти все оставшиеся параметры:
1. Вычислите составляющие скорости.
- Скорость и ее горизонтальная и вертикальная составляющие
Горизонтальная составляющая скорости Vx равна V * cos (α).
Вертикальная составляющая скорости Vy равна V * sin (α).
Три вектора — V, Vx и Vy — образуют прямоугольный треугольник.
Если вертикальная составляющая скорости равна 0, то это случай горизонтального движения снаряда. Если дополнительно α = 90 °, то это случай свободного падения.
2. Запишите уравнения движения.
Расстояние
- Пройденное расстояние по горизонтали можно выразить как x = Vx * t, где t — время.
Вертикальное расстояние от земли описывается формулой y = h + Vy * t — g * t² / 2, где g — ускорение свободного падения.
Скорость
- Горизонтальная скорость равна Vx.
Вертикальную скорость можно выразить как Vy — g * t.
Ускорение
- Горизонтальное ускорение равно 0.
Вертикальное ускорение равно -g (потому что на снаряд действует только сила тяжести).
3.Рассчитайте время полета.
График движения снаряда: время полета
Полет заканчивается, когда снаряд попадает в землю. Можно сказать, что это происходит, когда вертикальное расстояние от земли равно 0. В случае, когда начальная высота равна 0, формулу можно записать как: Vy * t — g * t² / 2 = 0. Тогда из это уравнение, мы находим, что время полета
t = 2 * Vy / g = 2 * V * sin (α) / g.
Однако, если мы бросаем объект с некоторой возвышенности, тогда формула не так хорошо сокращается, как раньше, и мы получаем квадратное уравнение для решения: h + Vy * t — g * t² / 2 = 0. После решения этой задачи уравнение, получаем:
t = [V * sin (α) + √ ((V * sin (α)) ² + 2 * g * h)] / g
4. Рассчитайте дальность полета снаряда.
График движения снаряда: дальность
Дальность полета снаряда — это общее горизонтальное расстояние, пройденное за время полета. Опять же, если мы запускаем объект с земли (начальная высота = 0), то мы можем записать формулу как R = Vx * t = Vx * 2 * Vy / g. Его также можно преобразовать в форму: R = V² * sin (2α) / g
Ситуация усложняется для начального значения высоты, отличного от 0. Затем нам нужно заменить длинную формулу из предыдущего шага на t:
R = Vx * t = V * cos (α) * [V * sin (α) + √ (V * sin (α)) ² + 2 * g * h)] / g
5. Рассчитайте максимальную высоту.
График движения снаряда: максимальная высота
Когда снаряд достигает максимальной высоты, он перестает двигаться вверх и начинает падать. Это означает, что его вертикальная составляющая скорости изменяется с положительной на отрицательную, другими словами, она равна 0 на короткий момент времени t (Vy = 0).
Если Vy — g * t (Vy = 0) = 0, то мы можем переформулировать это уравнение к t (Vy = 0) = Vy / g.
Теперь мы просто находим расстояние по вертикали от земли в это время: hmax = Vy * t (vy = 0) — g * (t (Vy = 0)) ² / 2 = Vy² / (2 * g) = V² * sin (α) ² / (2 * г)
К счастью, в случае запуска снаряда с некоторой начальной высоты h нам нужно просто добавить это значение в окончательную формулу: hmax = h + V² * sin (α) ² / (2 * g)
Уравнения движения снаряда
Уфф, это было много вычислений! Подведем итог, чтобы сформировать наиболее важные уравнения движения снаряда:
Запуск объекта с земли (начальная высота h = 0)
- Составляющая горизонтальной скорости: Vx = V * cos (α)
Вертикальная составляющая скорости: Vy = V * sin (α)
Время полета: t = 2 * Vy / г
Дальность полета снаряда: R = 2 * Vx * Vy / g
Максимальная высота: hmax = Vy² / (2 * g)
Запуск объекта с некоторой высоты (начальная высота h> 0)
- Составляющая горизонтальной скорости: Vx = V * cos (α)
Вертикальная составляющая скорости: Vy = V * sin (α)
Время полета: t = [Vy + √ (Vy² + 2 * g * h)] / g
Дальность полета снаряда: R = Vx * [Vy + √ (Vy² + 2 * g * h)] / g
Максимальная высота: hmax = h + Vy² / (2 * g)
Использование нашего калькулятора движения снаряда наверняка сэкономит вам много времени. Он также может работать «наоборот». Например, введите время полета, расстояние и начальную высоту и смотрите, как он выполняет все вычисления за вас!
Часто задаваемые вопросы
Должен ли снаряд перемещаться горизонтально?
Нет, движение снаряда и его уравнения охватывают все движущиеся объекты, где единственной силой, действующей на них, является гравитация. Сюда входят объекты, которые подбрасываются прямо вверх, те, которые выбрасываются горизонтально, те, которые имеют горизонтальный и вертикальный компонент, и те, которые просто отбрасываются.
Как может снаряд упасть вокруг Земли?
На снаряд действует только одна сила — сила тяжести. Это означает, что объект в конечном итоге упадет на Землю. Но что делать, если объект движется по горизонтали так быстро, что к тому времени, как он достигает земли, земли уже нет? Это принцип, по которому работают спутники.
Как найти ускорение при движении снаряда?
На объект в метательном движении действует только одна сила — гравитация. Это означает, что любое изменение вертикальной скорости происходит из-за ускорения свободного падения, которое на Земле составляет 9,81 м / с2. В горизонтальном направлении скорость не изменяется, так как сопротивление воздуха считается незначительным, поэтому ускорение равно 0.
Какие факторы влияют на движение снаряда, выпущенного горизонтально?
Начальная скорость, начальная высота, с которой запускается снаряд, и сила тяжести будут влиять на снаряд, запущенный горизонтально. Сопротивление воздуха также будет иметь влияние в реальной жизни, но для большинства теоретических расчетов оно незначительно и поэтому игнорируется. Если у снаряда есть крылья, это также повлияет на его движение, так как он будет скользить.
Что такое снаряд?
Снаряд — это объект, который движется в воздухе и не имеет силы, действующей на него, кроме ускорения свободного падения (это означает, что он не может быть самоходным). Вы, наверное, можете вспомнить множество примеров: брошенный мяч или камень, стрела из лука. Даже Луна — это снаряд по отношению к Земле!
Каковы характеристики движения снаряда?
Свойства движения снаряда заключаются в том, что горизонтальная скорость объекта не изменяется, что его вертикальная скорость постоянно изменяется из-за силы тяжести, что форма его траектории будет параболой и что на объект не влияет сопротивление воздуха.
Кто первым и когда точно описал движение снаряда?
Галилей был первым человеком, который точно описал движение снаряда, разбив движение на горизонтальную и вертикальную составляющие и осознав, что график движения любого объекта всегда будет параболой. Он описал это в своей книге «О движении», опубликованной примерно в 1590-х годах.
Почему снаряд летит по кривой?
Объект следует параболе из-за того, что гравитация влияет на две его составляющие движения — горизонтальную и вертикальную. Горизонтальная составляющая вообще не подвержена влиянию силы тяжести, поэтому изменяется линейно. Однако вертикальная часть постоянно находится под действием силы тяжести, поэтому она будет увеличиваться в высоте, а затем уменьшаться, ускоряясь под действием силы тяжести.
Почему 45 градусов — оптимальный угол для снарядов?
Уравнение для расстояния, пройденного снарядом под действием силы тяжести, имеет вид sin (2θ) v2 / g, где θ — угол, v — начальная скорость, а g — ускорение свободного падения. Предполагая, что v2 / g постоянна, наибольшее расстояние будет, когда sin (2θ) будет максимальным, то есть когда 2θ = 90 градусов. Это означает θ = 45 градусов.
В статье подробно, начиная с основ и базовых определений, рассказано о движении тела брошенного под углом к горизонту. Здесь вы найдете формулы параметров движения: общее время, дальность полета, максимальная высота. Также в конце приложены примеры задач с решениями.
Определение. Баллистическое движение — это движение некоторого тела в поле тяжести Земли при условии, что тело имеет вертикальную и горизонтальную проекции скорости.
Вначале вспомним основные формулы для равноускоренного движения.
Изменение скорости с течением времени задаётся соотношением
vₓ = v₀ₓ + aₓt,
где vₓ — конечная проекция скорости, v₀ₓ — начальная проекция скорости, aₓ — проекция ускорения тела.
Изменение координаты x во времени можно найти, используя следующее соотношение:
x = x₀ + v₀ₓt + aₓt² / 2,
где x — конечная координата тела, x₀ — начальная координата, v₀ₓ — начальная проекция скорости тела вдоль оси OX, aₓ — проекция ускорения тела.

Замечание 1. Перемещением тела за время t называется величина Sₓ = x – x₀.
Замечание 2. Так как эти выражения справедливы для проекций, то их можно записать и в векторном виде.
Баллистическое движение — это случай равноускоренного движения (с постоянным ускорением свободного падения g). Любое тело, брошенное под углом α к горизонту, имеет некоторую вертикальную и горизонтальную проекции скорости (рис. 1).
Далее движение необходимо разбить на два участка:
- Горизонтальное
- Вертикальное
По горизонтали тело движется с одинаковой скоростью (обычно пренебрегаем силами различного трения):
v₁ = v₀cos(α)
А по вертикали это обычное движение тела, брошенного вертикально вверх с начальной скоростью:
v₂ = v₀sin(α)
Общее время движения
Разобьём траекторию на два участка. Первый — участок, на котором тело продолжает подниматься, а второй — участок, где тело спускается. Обозначим t₁ время подъёма тела (от нуля до максимальной высоты подъема), t₂ — время спуска тела.
Из уравнения движения:
v₀sin(α) – gt₁ = 0
(так как конечная проекция скорости в верхней точке траектории равна нулю),
t₁ = v₀sin(α) / g.
Найдём время спуска:
–gt₂ = –v₀sin(α),
(т. к. конечная скорость тела будет такая же, как и начальная),
t₂ = v₀sin(α) / g.
Общее время движения:
t = t₁ + t₂ = 2v₀sin(α) / g.
Замечание.Время спуска и время подъёма тела одинаковые. Это связано с тем, что движение симметрично.
Дальность полета
Так как по горизонтали (вдоль оси ОХ) движение тела равномерное, то, зная общее время движения, найдём дальность полета L:
L = tv₁ = (2v₀sin(α) / g) · v₀cos(α) = 2v₀²sin(α)cos(α) / g.
Замечание. Используя формулу из тригонометрии
2sin(α)cos(α) = sin(2α),
получим:
L = 2v₀²sin(2α) / g.
Следовательно, максимальная дальность полета тела будет при броске под углом 45° к горизонту (так как sin(90°) = 1).
Максимальная высота подъёма тела
Рассмотрим движение тела в проекции на ось OY:
H = v₀sin(α)t₁ – gt₁² / 2.
После подставления времени подъёма получим
H = v₀²sin²(α) / (2g).
Давайте теперь решим некоторые задачи.
Задачи
Задача 1. Пуля, летящая горизонтально со скоростью v = 500 м/с, пробивает первый листок бумаги. Найти, на каком расстоянии S находится второй листок бумаги, если известно, что его пуля пробила на h = 20 см ниже, чем первый.
Решение. Найдём, за какое время пуля прошла расстояние между листами. Нам известно, что за это же время она опустилась на высоту h = 20 см. Тогда:
h = gt² / 2,
t = √(2h/g).
Теперь, зная время движения пули между листами, найдём расстояние, которое прошла пуля за это время:
S = tv = v · √(2h/g) = 100 м.
Ответ: S = 100 м.
Задача 2. Школьник может бросить мяч в спортивном зале с максимальной скоростью v = 25 м/с. Пренебрегая силами сопротивления воздуха, найти максимальную дальность полета мяча в спортивном зале, если высота зала равна h = 4 м. Считать, что мяч не ударяется о потолок.
Решение. Пусть мальчик бросил мяч под некоторым углом α к горизонту. Тогда дальность полета мяча равна:
L = 2v₀²sin(α)cos(α) / g.
Как обсуждалось выше, тело имеет максимальную дальность полета, если его бросить под углом α = 45° к горизонту. Но в данной задаче возможно, что при таком угле мяч ударится о потолок. Проверим, какова максимальная высота подъёма мяча при условии, что угол равен α = 45°.
H = v₀²sin²(α) / (2g) = 16 м.
Следовательно, угол, под которым мальчик бросит мяч, будет значительно меньше. Найдём максимальный угол, при котором мяч не столкнется с потолком. Этот угол будет соответствовать предельному случаю, когда мяч побывает на высоте h = 4 м.
h = v₀²sin²(α) / (2g) => sin²(α) = 2gh / v₀².
Из основного тригонометрического тождества
sin²(α) + cos²(α) = 1
найдём cos²(α):
cos²(α) = 1 – 2gh / v₀².
Подставив все выражения в дальность полета L, получим:
L = 2√(2gh(v₀² – 2gh)) / g = 42 м.
Ответ: L = 42 м.
Замечание. Если в задаче не приведены числовые значения (задача в общем виде), то необходимо записать 2 ответа. Первый ответ при условии высокого потолка, при h > H —
L = 2v₀²sin(α)cos(α) / g, α = 45°.
И при h < H получаем ответ
L = 2√(2gh(v₀² – 2gh)) / g.
Список литературы
- Черноуцан А. Учебно-справочное пособие для старшеклассников и абитуриентов. М., 2000.
- Белолипецкий С. Н., Еркович О. С., Казаковцева В. А., Цвецинская Т. С. Задачник по физике. М., 2005.
Автор: Роман Федоренко
|
Это можно узнать только экспериментально, на стрельбах, или рассчетно эмпирически, с учетом многих факторов. Погодные условия, давление воздуха, высота над уровнем моря и так далее – параметров куча. Есть специальные баллистические калькуляторы, но они позволяют только рассчитать только поправки на стрельбу. Основная зависимость – от калибра и вида патрона. Если от времени, когда вы услышали звук от выстрела, сможете мысленно сказать “Двадцать Два”, то к вашему счастью, стреляли явно не по вас…. автор вопроса выбрал этот ответ лучшим ДРЕССИРОВЩИК 8 лет назад Если разговор о расстоянии в 0.5 км, 1 км и 2 км, то разговор соответственно не о пистолетной пуле и не об охотничьих жеканах (они столько не пролетят!), тогда логически предположим что среднестатистическая стрелковая (армейская) пуля имеет скорость полёта 700 – 1000 м/с, а есть и быстрее, делаем расчёт надеюсь считать не разучились пол километра – пол секунды и так дальше, очень важно если вы услышали выстрел, то падать на землю поздно, так как звук зачастую прилетает медленней самой пули. Знаете ответ? |
Внешняя
баллистика – это наука, изучающая
движение пули в воздухе (т.е. после
прекращения действия на нее пороховых
газов).
Вылетев из канала
ствола под действием пороховых газов,
пуля движется по инерции. Для того чтобы
определить, как же движется пуля
необходимо рассматривать траекторию
ее движения. Траекторией
называется кривая линия, описываемая
центром тяжести пули во время полета.
Пуля при полете в
воздухе подвергается действиям двух
сил: силы тяжести и силы сопротивления
воздуха. Сила тяжести заставляет
постепенно понижаться, а сила сопротивления
воздуха непрерывно замедляет движение
пули и стремится опрокинуть ее. В
результате действия этих сил скорость
полета пули постепенно уменьшается,
а ее траектория представляет собой по
форме неравномерно изогнутую кривую.
Сопротивление
воздуха полету пули вызывается тем, что
воздух представляет собой упругую
среду, поэтому в этой среде затрачивается
часть энергии пули,
что вызывается тремя основными причинами:
-
трением воздуха;
-
образованием
завихрений; -
образованием
баллистической волны.
Равнодействующая
этих сил составляет силу сопротивления
воздуха.
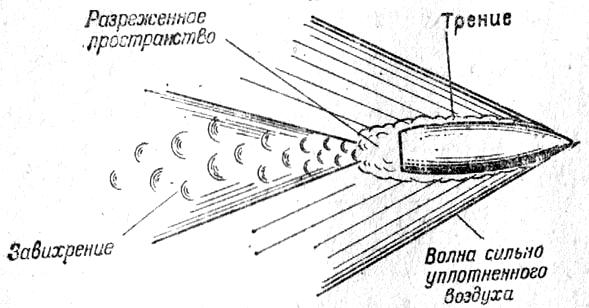
Рис. 2.
Образование
силы сопротивления воздуха.
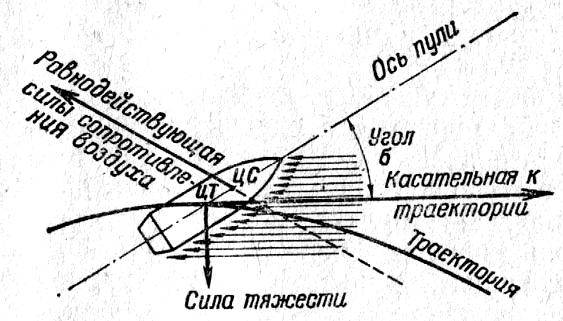
Рис. 3.
Действие
силы сопротивления воздуха на полет
пули:
ЦТ – центр тяжести;
ЦС – центр сопротивления воздуха.
Частицы воздуха,
соприкасающиеся с движущейся пулей
создают трение и уменьшают скорость
полета пули. Примыкающий к поверхности
пули слой воздуха, в котором движение
частиц изменяется в зависимости от
скорости называется пограничным слоем.
Этот слой воздуха, обтекая пулю, отрывается
от ее поверхности и не успевает сразу
же сомкнуться за донной частью.
За донной частью
пули образуется разряженное пространство,
вследствие чего появляется разность
давления на головную и донную части.
Эта разность создает силу, направленную
в сторону обратную движению пули, и
уменьшающую скорость ее полета. Частицы
воздуха, стремясь заполнить разрежение,
образовавшееся за пулей, создают
завихрение.
Пуля при полете
сталкивается с частицами воздуха и
заставляет их колебаться. Вследствие
этого перед пулей повышается плотность
воздуха и образуется звуковая волна.
Поэтому полет пули сопровождается
характерным звуком. При скорости полета
пули, меньшей скорости звука, образование
этих волн оказывает незначительное
влияние на ее полет, т.к. волны
распространяются быстрее скорости
полета пули. При скорости полета пули,
большей скорости звука, от набегания
звуковых волн друг на друга создается
волна сильно уплотненного воздуха
–
баллистическая волна, замедляющая
скорость полета пули, т.к. пуля тратит
часть своей энергии на создание этой
волны.
Действие силы
сопротивления воздуха на полет пули
очень велико: оно вызывает уменьшение
скорости и дальности полета. Например,
пуля при начальной скорости
800 м/с в
безвоздушном пространстве полетела бы
на дальность
32620 м;
дальность же полета этой пули при наличии
сопротивления воздуха равна лишь
3900 м.
Величина силы
сопротивления воздуха в основном зависит
от:
-
скорости полета
пули; -
формы и калибра
пули; -
от поверхности
пули; -
плотности воздуха
и возрастает с
увеличением скорости полета пули, ее
калибра и плотности воздуха.
При сверхзвуковых
скоростях полета пули, когда основной
причиной сопротивления воздуха является
образование уплотнения воздуха перед
головной частью (баллистической волны)
выгодны пули с удлиненной остроконечной
головной частью.
Таким образом,
сила сопротивления воздуха уменьшает
скорость движения пули и опрокидывает
её. В результате этого пуля начинает
«кувыркаться», возрастает сила
сопротивления воздуха, уменьшается
дальность полета и понижается её действие
по цели.
Стабилизация пули
в полете обеспечивается приданием пуле
быстрого вращательного движения вокруг
своей оси, а также – хвостовым оперением
гранаты. Скорость вращения при вылете
из нарезного оружия составляет: пуль
3000-3500 об/с, проворачивание оперенных
гранат 10-15 об/с. Вследствие вращательного
движения пули, воздействия силы
сопротивления воздуха и силы тяжести
происходит отклонение пули в правую
сторону от вертикальной плоскости,
проведенной через ось канала ствола, –
плоскости
стрельбы.
Отклонение пули от нее при полете в
сторону вращения называется деривацией.
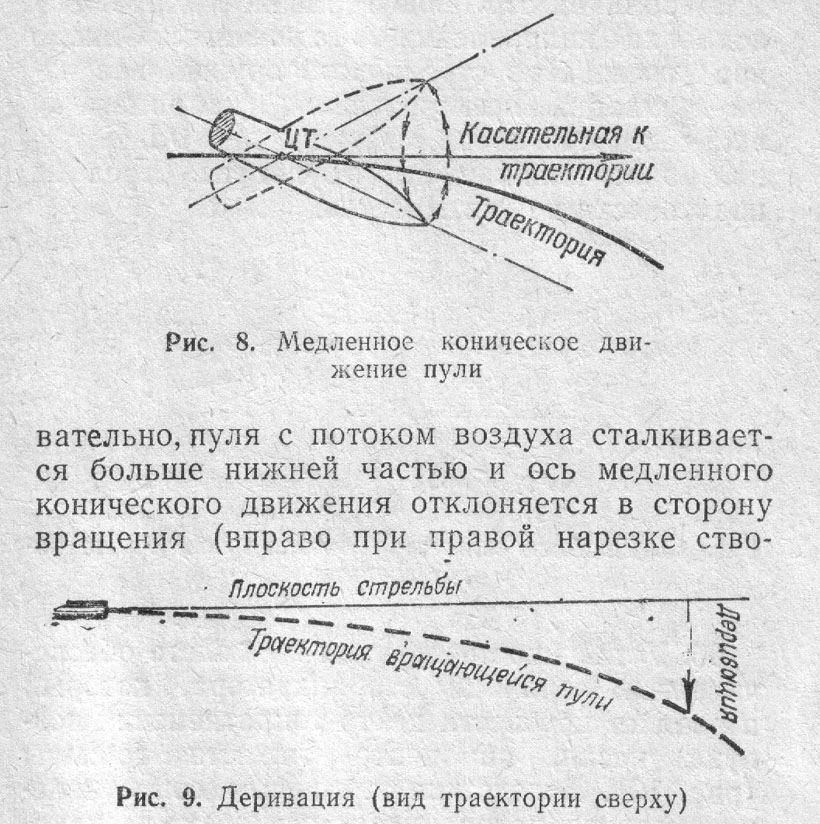
Рис. 4. Деривация
(вид траектории сверху).
В результате
действия этих сил пуля совершает полет
в пространстве по неравномерно изогнутой
кривой линии, называемой траекторией.
Продолжим
рассмотрение элементов и определений
траектории пули.
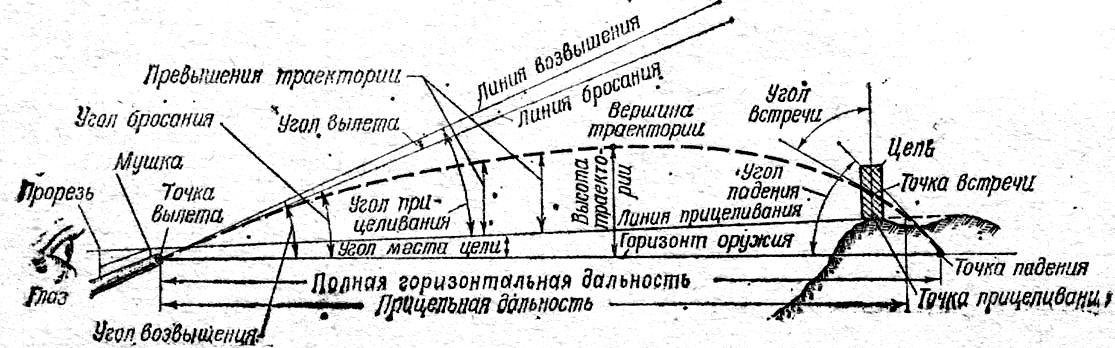
Рис. 5. Элементы
траектории.
Центр дульного
среза ствола называется точкой
вылета. Точка
вылета является началом траектории.
Горизонтальная
плоскость проходящая через точку вылета
называется горизонтом
оружия. На
чертежах, изображающих оружие и траекторию
сбоку, горизонт оружия имеет вид
горизонтальной линии. Траектория дважды
пересекает горизонт оружия: в точке
вылета и в точке падения.
Прямая линия,
являющаяся продолжением оси канала
ствола наведенного
оружия,
называется
линией возвышения.
Вертикальная
плоскость, проходящая через линию
возвышения называется
плоскостью стрельбы.
Угол, заключенный
между линией возвышения и горизонтом
оружия называется
углом возвышения.
Если этот угол отрицательный, то он
называется
углом склонения (снижения).
Прямая линия,
являющаяся продолжением оси канала
ствола в
момент вылета пули,
называется линией
бросания.
Угол, заключенный
между линией бросания и горизонтом
оружия, называется углом
бросания.
Угол, заключенный
между линией возвышения и линией
бросания, называется углом
вылета.
Точка пересечения
траектории с горизонтом оружия называется
точкой падения.
Угол, заключенный
между касательной к траектории в точке
падения и горизонтом оружия называется
углом падения.
Расстояние от
точки вылета до точки падения называется
полной
горизонтальной дальностью.
Скорость пули в
точке падения называется
окончательной скоростью.
Время движения
пули от точки вылета до точки падения
называется полным
временем полета.
Наивысшая точка
траектории называется
вершиной траектории.
Кратчайшее
расстояние от вершины траектории до
горизонта оружия называется
высотой траектории.
Часть траектории
от точки вылета до вершины называется
восходящей ветвью,
часть траектории от вершины до точки
падения называется нисходящей
ветвью траектории.
Точка на цели (или
вне её),
в которую наводится оружие, называется
точкой
прицеливания (ТП).
Прямая линия от
глаза стрелка до точки прицеливания
называется линией
прицеливания.
Расстояние от
точки вылета до пересечения траектории
с линией прицеливания, называется
прицельной дальностью.
Угол, заключенный
между линией возвышения и линией
прицеливания, называется
углом прицеливания.
Угол, заключенный
между линией прицеливания и горизонтом
оружия называется
углом места цели.
Прямая, соединяющая
точку вылета с целью, называется линией
цели.
Расстояние от
точки вылета до цели по линии цели
называется наклонной
дальностью.
При стрельбе
прямой наводкой линия цели практически
совпадает с линией прицеливания, а
наклонная дальность – с прицельной
дальностью.
Точка пересечения
траектории с поверхностью цели (земли,
преграды) называется точкой
встречи.
Угол, заключенный
между касательной к траектории и
касательной к поверхности цели (земли,
преграды) в точке встречи, называется
углом встречи.
Форма траектории
зависит от величины угла возвышения.
С увеличением угла возвышения высота
траектории и полная горизонтальная
дальность полета пули увеличивается.
Но это происходит до известного предела.
За этим пределом высота траектории
продолжает увеличиваться,
а полная горизонтальная дальность
начинает уменьшаться.
Угол возвышения,
при котором полная горизонтальная
дальность полета пули становится
наибольшей, называется углом
наибольшей дальности
(величина этого угла составляет около
35°).
Различают настильные
и навесные траектории:
-
Настильной
– называется траектория, получаемая
при углах возвышения меньших угла
наибольшей дальности. -
Навесной
–
называется траектория, получаемая при
углах возвышения больших угла наибольшей
дальности.
Настильная и
навесная траектории, получаемые при
стрельбе из одного и того же оружия при
одной и той же начальной скорости и
имеющие одинаковую полную горизонтальную
дальность, называются – сопряжёнными.
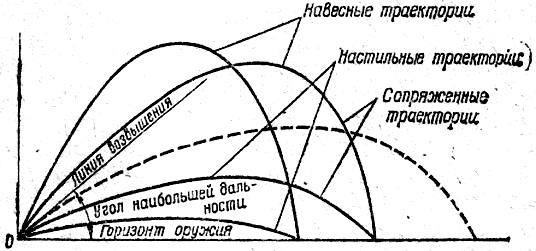
Рис. 6. Угол наибольшей
дальности,
настильные, навесные
и сопряжённые траектории.
Траектория более
настильна, если она меньше поднимается
над линией цели, и чем меньше угол
падения. Настильность траектории влияет
на величину дальности прямого выстрела,
а также на величину поражаемого и
мертвого пространства.
При стрельбе из
стрелкового оружия и гранатометов
используются только настильные
траектории. Чем настильнее траектория,
тем на большем протяжении местности
цель может быть поражена с одной
установкой прицела (тем меньшее влияние
на результаты стрельбы оказывает ошибка
в определении установки прицела): в этом
заключается практическое значение
траектории.
Прямой выстрел.
Поражаемое, прикрытое и мертвое
пространства
Прямой выстрел,
поражаемое, прикрытое и мертвое
пространства наиболее близко соприкасаются
с вопросами стрелковой практики.
Большинство целей
для танков, БМП, стрелкового оружия
имеют значительные размеры по высоте
и требуют для их поражения прямого
попадания. Получить прямое попадание
можно при прямом выстреле и в случае,
если траектория проходит через поражаемое
пространство цели. Настильность
траектории влияет на величину дальности
прямого выстрела.
При прямом
выстреле
траектория пули на всем своем протяжении
до цели не поднимается выше цели и не
опускается ниже ее основания. Он может
быть получен при различных установках
прицела, положениях цели (относительно
горизонта оружия) и точки прицеливания.
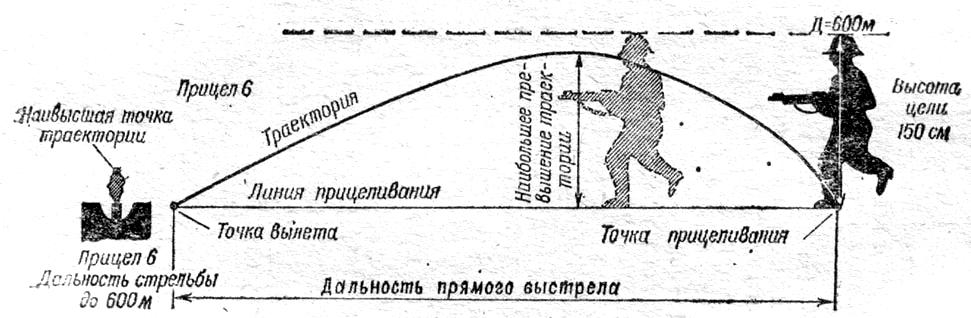
Рис. 7. Прямой
выстрел.
Если имеет место
прямой выстрел, то при правильном
направлении стрельбы пуля (траектория)
обязательно пройдет через цель и будет
получено прямое попадание.
Дальность прямого
выстрела – это такая дальность стрельбы,
при которой высота траектории равна
высоте цели.
Значение дальности
прямого выстрела состоит в том, что в
пределах этой дальности обеспечивается
высокая вероятность попадания в цель
с первого выстрела, а в случае промаха
при первом выстреле – возможность
попадания в нее при последующих выстрелах
с одной исходной установкой прицела.
В пределах дальности
прямого выстрела в напряженные моменты
боя стрельба может вестись без перестановки
прицела, при этом точка прицеливания
по высоте, как правило, выбирается на
нижнем краю цели.
Поражаемым
пространством
(глубиной
поражаемого пространства)
называется расстояние на местности, на
протяжении которого нисходящая ветвь
траектории не превышает высоты цели.
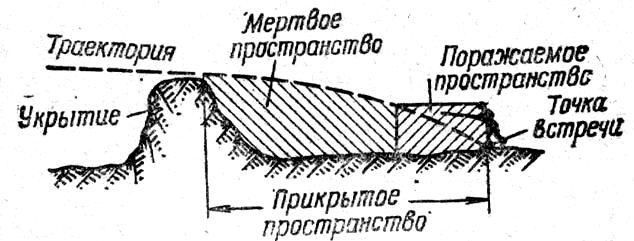
Рис. 8. Поражаемое,
прикрытое и мертвое пространства.
Глубина поражаемого
пространства зависит от:
-
высоты
цели (глубина будет тем больше, чем выше
цель); -
настильности
траектории (глубина будет тем больше,
чем настильнее траектория); -
угла
наклона местности (на переднем скате
она уменьшается, на обратном скате
увеличивается).
Пространство за
укрытием, не пробиваемым пулями, от его
гребня до точки встречи называется
прикрытым
пространством.
Часть прикрытого
пространства, на котором цель не может
быть поражена при данной траектории,
называется мертвым
пространством. Глубина
мертвого пространства равна разности
прикрытого и поражаемого пространства.
Таким образом,
необходимо отметить,
что движение пули представляет собой
сложный и динамичный процесс, требующий
тщательного изучения.
Формула расчета времени за которое пройдет пуля
Пользователь удален
Профи
(892),
закрыт
2 года назад
3eta dæity
Оракул
(85402)
2 года назад
x = v*cos(a)*t
y = h + v*sin(a)*t – g*t^2/2
Если стреляют горизонтально, то а=0, рассмотрим этот случай. v – начальная скорость. h – это начальная высота пули над уровнем ровной поверхности.
Пуля упадёт на землю, если не встретит никакого препятствия, через t = sqrt(2h/g).
Пройденная пулей дистанция до падения (дальность): L = v*sqrt(2h/g).

