Как найти время протекания тока через проводник

Закон Джоуля-Ленца

Электричество – неотъемлемый признак нашей эпохи. Абсолютно всё вокруг завязано на нём. Любой современный человек, даже без технического образования, знает, что электрический ток, текущий по проводам, способен в некоторых случаях нагревать их, зачастую до очень высоких температур. Казалось бы, это заведомо всем известно и не стоит упоминания. Однако, как объяснить это явление? Почему и как происходит нагрев проводника?

Опыты Ленца

Перенесемся в 19 век-эпоху накопления знаний и подготовки к технологическому прыжку 20 века. Эпоха, когда по всему миру различные учёные и просто изобретатели-самоучки чуть ли не ежедневно открывают что-то новое, зачастую тратя огромное количество времени на исследования и, при этом, не представляя конечный результат.

Один из таких людей, русский учёный Эмилий Христианович Ленц, увлекался электричеством, на тогдашнем примитивном уровне, пытаясь рассчитывать электрические цепи. В 1832 году Эмилий Ленц “застрял” с расчётами, так как параметры его смоделированной цепи “источник энергии – проводник – потребитель энергии” сильно разнились от опыта к опыту. Зимой 1832-1833 года учёный обнаружил, что причиной нестабильности является кусочек платиновой проволоки, принесённый им с холода. Отогревая или охлаждая проводник, Ленц также заметил что существует некая зависимость между силой тока, электрическим сопротивлением и температурой проводника.

При определённых параметрах электрической цепи проводник быстро оттаивал и даже слегка нагревался. Измерительных приборов в те времена практически никаких не существовало – невозможно было точно измерить ни силу тока, ни сопротивление. Но это был русский физик, и он проявил смекалку. Если это зависимость, то почему бы ей не быть обратимой?

Для того чтобы измерить количество тепла, выделяемого проводником, учёный сконструировал простейший “нагреватель” – стеклянная ёмкость, в которой находился спиртосодержащий раствор и погружённый в него платиновый проводник-спираль. Подавая различные величины электрического тока на проволоку, Ленц замерял время, за которое раствор нагревался до определённой температуры. Источники электрического тока в те времена были слишком слабы, чтобы разогреть раствор до серьёзной температуры, потому визуально определить количество испарившегося раствора не представлялось возможным. Из-за этого процесс исследования очень затянулся – тысячи вариантов подбора параметров источника питания, проводника, долгие замеры и последующий анализ.

Закон Джоуля-Ленца

В итоге, спустя десятилетие, в 1843 году Эмилий Ленц выставил на всеобщее обозрение научного сообщества результат своих опытов в виде закона. Однако, оказалось, что его опередили! Пару лет назад английский физик Джеймс Прескотт Джоуль уже проводил аналогичные опыты и также представил общественности свои результаты. Но, тщательно проверив все работы Джеймса Джоуля, русский учёный выяснил что собственные опыты гораздо точнее, наработан больший объём исследований, потому, русской науке есть чем дополнить английское открытие.

Научное сообщество рассмотрело оба результата исследований и объединила их в одно, тем самым закон Джоуля переименовали в закон Джоуля-Ленца. Закон утверждает, что количество теплоты, выделяемое проводником при протекании по нему электрического тока , равно произведению силы этого тока в квадрате, сопротивлению проводника и времени, за которое по проводнику течёт ток. Или формулой:

Q — количество выделяемого тепла (Джоули)

I — сила тока, протекающего через проводник (Амперы)

R — сопротивление проводника (Омы)

t — время прохождения тока через проводник (Секунды)

Почему греется проводник

Как же объясняется нагрев проводника? Почему он именно греется, а не остаётся нейтральным или охлаждается? Нагрев происходит из-за того, что свободные электроны, перемещающиеся в проводнике под действием электрического поля, бомбардируют атомы молекул металла, тем самым передавая им собственную энергию, которая переходит в тепловую. Если изъясняться совсем просто: преодолевая материал проводника, электрический ток как бы “трётся”, соударяется электронами о молекулы проводника. Ну а , как известно, любое трение сопровождается нагревом. Следовательно, проводник будет нагреваться пока по нему бежит электрический ток.

Из формулы также следует – чем выше удельное сопротивление проводника и чем выше сила тока протекающего по нему, тем выше будет нагрев . Например, если последовательно соединить проводник-медь (удельное сопротивление 0,018 Ом·мм²/м) и проводник-алюминий (0,027 Ом·мм²/м), то при протекании через цепь электрического тока алюминий будет нагреваться сильнее чем медь из-за более высокого сопротивления. Поэтому, кстати, не рекомендуется в быту делать скрутки медных и алюминиевых проводов друг с другом – будет неравномерный нагрев в месте скрутки. В итоге – подгорание с последующим пропаданием контакта.

Применение закона Джоуля-Ленца в жизни

Открытие закона Джоуля-Ленца имело огромные последствия для практического применения электрического тока. Уже в 19 веке стало возможным создать более точные измерительные приборы, основанные на сокращении проволочной спирали при её нагреве протекающим током определённой величины – первые стрелочные вольтметры и амперметры. Появились первые прототипы электрических обогревателей, тостеров, плавильных печей – использовался проводник с высоким удельным сопротивлением, что позволяло получить довольно высокую температуру.

Были изобретены плавкие предохранители, биметаллические прерыватели цепи (аналоги современных тепловых реле защиты), основанные на разнице нагрева проводников с разным удельным сопротивлением. Ну и, конечно же, обнаружив что при определённой силе тока проводник с высоким удельным сопротивлением способен нагреться докрасна , данный эффект использовали в качестве источника света. Появились первые лампочки.

Проводник (угольная палочка, бамбуковая нить, платиновая проволока и т.д.) помещали в стеклянную колбу, откачивали воздух для замедления процесса окисления и получали незатухаемый, чистый и стабильный источник света – электрическую лампочку

Заключение

Таки образом, можно сказать что на законе Джоуля-Ленца держится чуть ли не вся электрика и электротехника. Открыв этот закон, появилась возможность уже заранее предсказать некоторые будущие проблемы в освоении электричества. Например, из-за нагрева проводника передача электрического тока на большое расстояние сопровождается потерями этого тока на тепло. Соответственно, чтобы компенсировать эти потери нужно занизить передаваемый ток, компенсируя это высоким напряжением. А уже на оконечном потребителе, понижать напряжение и получать более высокий ток.

Закон Джоуля-Ленца неотступно следует из одной эпохи технологического развития в другую. Даже сегодня мы постоянно наблюдаем его в быту – закон проявляется всюду, и не всегда люди ему рады. Сильно греющийся процессор персонального компьютера, пропадание света из-за обгоревшей скрутки «медь-алюминий»,выбитая вставка-предохранитель, выгоревшая из-за высокой нагрузки электропроводка – всё это тот самый закон Джоуля-Ленца.

Источник

Работа электрического тока. Закон Джоуля-Ленца.

Для определения работы, которая совершается током, проходящим по некоторому участку цепи, нужно воспользоваться определением напряжения: . Значит,

где А — работа тока; q — электрический заряд, который прошел за определенное время через исследуемый участок цепи. Подставив в последнее равенство формулу q = It, имеем:

Работа электрического тока на участке цепи является произведением напряжения на концах это­го участка на силу тока и на время, на протяжении которого совершалась работа.

Закон Джоуля-Ленца .

Закон Джоуля — Ленца гласит: количество теплоты, которое выделяется в проводнике на участке электрической цепи с сопротивлением R при протекании по нему постоянного тока I в течение времени t равно произведению квадрата тока на сопротивление и время:

Закон был установлен в 1841 г. английским физиком Дж. П. Джоулем, а в 1842 г. подтверж­ден точными опытами русского ученого Э. X. Ленца. Само же явление нагрева проводника при прохождении по нему тока было открыто еще в 1800 г. французским ученым А. Фуркруа, которо­му удалось раскалить железную спираль, пропустив через нее электрический ток.

Из закона Джоуля — Ленца видно, что при последовательном соединении проводников, поскольку ток в цепи всюду одинаков, максимальное количество тепла будет выделяться на про­воднике с наибольшим сопротивлением. Это применяется в технике, например, для распыления металлов.

При параллельном соединении каждый проводник находятся под одинаковым напряжением, но токи в них разные. Из формулы (Q = I 2 Rt) видно, что, так как, согласно закону Ома , то

Следовательно, на проводнике с меньшим сопротивлением будет выделяться больше тепла.

Если в формуле (А = IUt) выразить U через IR, воспользовавшись законом Ома, получим Закон Джоуля — Ленца. Это лишний раз подтверждает тот факт, что работа тока расходуется на выделение тепла на активном сопротивлении в цепи.

Источник

Электрический ток и закон Ома

теория по физике 🧲 постоянный ток

Электрический ток — направленное движение заряженных частиц под действием внешнего электрического поля.

Условия существования электрического тока:

• наличие заряженных частиц;
• наличие электрического поля, которое создается источниками тока.

Носители электрического тока в различных средах

Среда	Носители электрического тока
Металлы	Свободные электроны
Электролиты (вещества, проводящие ток вследствие диссоциации на ионы)	Положительные и отрицательные ионы
Газы	Ионы и электроны
Полупроводники	Электроны и дырки (атом, лишенный одного электрона)
Вакуум	Электроны

Электрическая цепь и ее схематическое изображение

Электрическая цепь — это совокупность устройств, соединенных определенным образом, которые обеспечивают путь для протекания электрического тока.

Основные элементы электрической цепи:

• Источник тока (генератор, гальванический элемент, батарея, аккумулятор).
• Потребители тока (лампы, нагревательные элементы и прочие электроприборы).
• Проводники — части цепи, обладающие достаточным запасом свободных электронов, способных перемещаться под действием внешнего электрического поля. Проводники соединяют источники и потребители тока в единую цепь.
• Ключ (переключатель, выключатель) для замыкания и размыкания цепи.

Электрическая цепь также может содержать:

• резистор — элемент электрической цепи, обладающий некоторым сопротивлением;
• реостат — устройство для регулировки силы тока и напряжения в электрической цепи путём получения требуемой величины сопротивления;
• конденсатор — устройство, способное накапливать электрический заряд и передавать его другим элементам цепи;
• измерительные приборы — устройства, предназначенные для измерения параметров электрической цепи.

Определение

Электрическая схема — графическое изображение электрической цепи, в котором реальные элементы представлены в виде условных обозначений.

Условные обозначения некоторых элементов электрической цепи

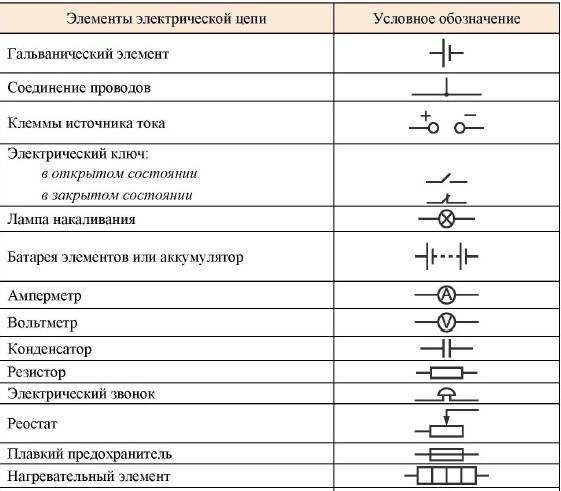
Простейшая электрическая цепь содержит в себе источник и потребитель тока, проводники, ключ. Схематически ее можно отобразить так:

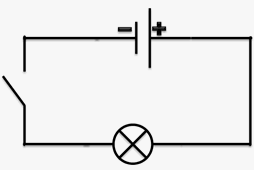
По металлическим проводам перемещаются отрицательно заряженные электроны, т.е. ток идет от «–» к «+» источника. Направление движения электронов называют действительным. Но исторически в науке принято условное направление тока от «+» источника к «–».

Действия электрического тока (преобразования энергии)

Электрический ток способен вызывать различные действия:

• Тепловое — электрическая энергия преобразуется в тепло. Такое преобразование обеспечивает электроплита, электрический камин, утюг.
• Химическое — электролиты под действием постоянного электрического тока подвергаются электролизу. К положительному электроду (аноду) в процессе электролиза притягиваются отрицательные ионы (анионы), а к отрицательному электроду (катоду) — положительные ионы (катионы).
• Магнитное (электромагнитное) — при наличии электрического тока в любом проводнике вокруг него наблюдается магнитное поле, т.е. проводник с током приобретает магнитные свойства.
• Световое — электрический ток разогревает металлы до белого каления, и они начинают светиться подобно вольфрамовой спирали внутри лампы накаливания. Другой пример — светодиоды, в которых свет обусловлен излучением фотонов при переходе электрона с одного энергетического уровня на другой.
• Механическое — параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются.

Основные параметры постоянного тока

Постоянный ток — электрический ток, который с течением времени не изменяется по величине и направлению.

Основными параметрами электрического тока являются:

• Сила тока. Обозначается как I. Единица измерения — А (Ампер).
• Напряжение. Обозначается как U. Единица измерения — В (Вольт).
• Сопротивление. Обозначается как R. Единица измерения — Ом.

Сила тока

Сила тока показывает, какой заряд q проходит через поперечное сечение проводника за 1 секунду:

I = q t . . = Δ q Δ t . . = N q e t .

N — количество электронов, q e = 1 , 6 · 10 − 19 Кл — заряд электрона, t — время (с).

Заряд, проходящий по проводнику за время t при силе тока, равной I:

Пример №1. Источник тока присоединили к двум пластинам, опущенным в раствор поваренной соли. Сила тока в цепи 0,2 А. Какой заряд проходит между пластинами в ванне за 2 минуты?

2 минуты = 120 секунд

q = I t = 0 , 2 · 120 = 24 ( К л )

Заряд, проходящий за время ∆t при равномерном изменении силы тока от I₁ до I₂:

Δ q = I 1 + I 2 2 . . Δ t

Сила тока и скорость движения электронов:

n — (м –3 ) — концентрация, S (м 2 ) — площадь сечения проводника, v — скорость электронов.

Внимание!

Электроны движутся по проводам со скоростью, равной долям мм/с. Но электрическое поле распространяется со скоростью света: c = 3∙10 8 м/с.

Сопротивление

Сопротивление металлов характеризует тормозящее действие положительных ионов кристаллической решетки на движение свободных электронов:

ρ — удельное сопротивление, показывающее, какое сопротивление имеет проводник длиной 1 м и площадью поперечного сечения 1 м 2 , изготовленный из определенного материала. l — длина проводника (м), S — площадь его поперечного сечения.

Пример №2. Медная проволока имеет электрическое сопротивление 6 Ом. Какое электрическое сопротивление имеет медная проволока, у которой в 2 раза больше длина и в 3 раза больше площадь поперечного сечения?

Сопротивление первого и второго проводника соответственно:

Поделим электрическое сопротивление второго проводника на сопротивление первого:

R 2 R 1 . . = ρ 2 l 3 S . . ÷ ρ l S . . = ρ 2 l 3 S . . · S ρ l . . = 2 3 . .

Отсюда сопротивление второго проводника равно:

Напряжение

Напряжение характеризует работу электрического поля по перемещению положительного заряда:

Пример №3. Перемещая заряд в первом проводнике, электрическое поле совершает работу 20 Дж. Во втором проводнике при перемещении такого же заряда электрическое поле совершает работу 40 Дж. Определить отношение U₁/U₂ напряжений на концах первого и второго проводников.

U 1 U 2 . . = A 1 q . . ÷ A 2 q . . = A 1 q . . · q A 2 . . = A 1 A 2 . . = 20 40 . . = 1 2 . .

Закон Ома для участка цепи

Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению:

Иллюстрация закона Ома.

Сила тока направлена в сторону движения заряженных частиц (электронов). Силе тока противостоит сопротивление: чем оно больше, тем меньше сила тока (тем меньше проходит электронов через проводник в единицу времени). Но росту силы тока способствует напряжение, которое словно толкает заряженные частицы, заставляя их упорядоченно перемещаться.

Закон Ома для участка цепи с учетом формулы для расчета сопротивления:

Для сравнения и расчета сопротивления часто используют вольтамперную характеристику. Так называют графическое представление зависимости силы тока от напряжения. Пример вольтамперной характеристики:

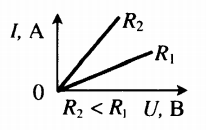
Чем круче график, тем меньше сопротивление проводника. При расчете сопротивления важно учитывать единицы измерения величин, указанных на осях.

Пример №4. На рисунке изображен график зависимости силы тока от напряжения на одной секции телевизора. Каково сопротивление этой секции:

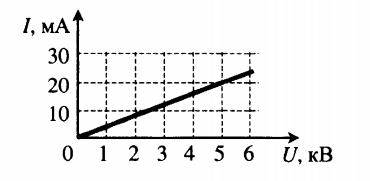
Точке графика, соответствующей 5 кВ, соответствует сила тока, равна 20 мА.

Сначала переведем единицы измерения величин в СИ:

R = U I . . = 5000 0 , 02 . . = 250000 ( О м ) = 250 ( к О м )

При определении сопротивления резистора ученик измерил напряжение на нём: U = (4,6 ± 0,2) В. Сила тока через резистор измерялась настолько точно, что погрешностью можно пренебречь: I = 0,500 А. По результатам этих измерений можно сделать вывод, что сопротивление резистора, скорее всего,

Источник

Как найти силу тока?

Расчет электрических параметров необходим для правильных построений цепей. Поскольку целью использования электричества в электротехнике является задача по выполнению током работы, то встает вопрос о том, как найти силу тока. Данный параметр используют при вычислениях мощности и в расчетах потребления электрической энергии.

Существуют разные способы определения этого важного параметра, которые мы рассмотрим в данной статье.

Формулами

Параметры электрического тока всегда взаимосвязаны. Например, изменение величины нагрузки отображается на показателях других величин. Причем эти изменения подчиняются соответствующим законам, которые выражаются через формулы. Поэтому на практике для нахождения силы тока часто используют соответствующие формулы.

Через заряд и время

Вспомним определение (рис.1): электричество – это величина заряда, движимого силами электрического поля, преодолевающего за единицу времени условную плоскость проводника, называемую поперечным сечением проводника.

Рис. 1. Определение понятия сила тока

Таким образом, если известен электрический заряд, прошедший через проводник за определенное время, то не трудно найти величину этого заряда прошедшего за единицу времени, то есть: I = q/t

Через мощность и напряжение

В паспорте электроприбора обычно указывается его номинальная мощность и параметры электрической сети, для работы с которой он предназначен. Имея в распоряжении эти данные, можно вычислить силу тока по формуле: I = P/U.

Данное выражение вытекает из формулы для расчета мощности: P = IU.

Через напряжение или мощность и сопротивление

Силу электричества на участке цепи определяют по закону Ома. Для этого необходимо знать следующие параметры: сопротивление и напряжение на этом участке. Тогда I = U/R. Если известна мощность нагрузки, то ее можно выразить через квадрат силы тока умноженной на сопротивление участка: P = I 2 R, откуда

Для полной цепи эту величину вычисляют по закону Ома, но с учетом параметров источника питания.

Через ЭДС, внутреннее сопротивление и нагрузку R

Применяя закон Ома, адаптированный для полной цепи, вы можете вычислить максимальный ток по формуле I = ε / (R+r′), если известны параметры:

• внешнее сопротивление проводников (R);
• ЭДС источника питания (ε);
• внутреннее сопротивление источника, обладающего ЭДС (r′).

Закон Джоуля-Ленца

Казалось бы, что расчет силы тока по количеству тепла, выделяющегося в результате нагревания проводника, не имеет практического применения. Однако это не так. Рассмотрим это на примере.

Пусть требуется найти силу тока во время работы электрочайника. Для этого доведите до кипения 1 кг воды и засеките время в секундах. Предположим, начальная температура составляла 10 ºС. Тогда Q = Cm(τ – τ) = 4200 Дж/кг× 1 кг (100 – 10) = 378 000 Дж.

Рис. 2. Закон Джоуля-Ленца

Из закона Джоуля-Ленца (изображение на рис. 2) вытекает формула:

Измерив сопротивление электроприбора и подставив значения в формулу, получим величину потребляемого тока.

Измерительными приборами

Если под руками имеются измерительные приборы, то с их помощью довольно просто найти силу тока. Необходимо лишь соблюдать правила измерений и не забывать о правилах безопасности.

Амперметром

Пользуясь приборами для измерения ампеража, следует помнить, что они подключаются в цепи последовательно. Внутреннее сопротивление амперметра очень маленькое, поэтому прибор легко выводится из строя, если проводить измерения пределами значений, для которых он рассчитан.

Схема подключения амперметра показана на рисунке 3. Обратите внимание на то, что на участке измеряемой электрической цепи обязательно должна быть нагрузка.

Рис. 3. Схема подключения амперметра

Большинство аналоговых амперметров, например, таких, как на рисунке 4, предназначены для измерений параметров в цепях с постоянными токами.

Рис. 4. Аналоговый амперметр

Обратите внимание распределение шкалы амперметра. Цена первого деления 50 А, а всех последующих – 10 А. Максимальная величина, которую можно измерить данным амперметром не должна превышать 300 А. Для измерений электрической величины в меньших либо в больших пределах следует применять соответствующие приборы, предназначенные для таких диапазонов. В этом смысле универсальность амперметра ограничена.

При измерениях постоянных токов необходимо соблюдать полярность щупов при подключении амперметра. Для подключения прибора требуется разрывать цепь. Это не всегда удобно. Иногда вычисление силы тока по формуле является предпочтительней, особенно если приходится проводить измерения в сложных электротехнических схемах.

Мультиметром

Преимущество мультиметра в том, что этот прибор многофункциональный. Современные мультиметры цифровые. У них есть режимы для измерений в цепях постоянных и переменных токов. В режиме измерения силы тока этот измерительный прибор подключается в цепь аналогично амперметру.

Перед включением мультиметра в цепь, всегда проверяйте режим измерений, а пределы измерения выбирайте заведомо большие предполагаемой силы тока. После первого измерения можно перейти в режим с меньшим диапазоном.

Для работы с переменным напряжением переводите прибор в соответствующий режим. Считывайте значения с дисплея после того, как цифры перестанут мелькать.

Примеры

Покажем на простых примерах, как решать задачи на вычисление силы тока по формуле.

Задача 1.

Рис. 5. Пример 1

Решение: При параллельном соединении нагрузочных элементов U = const, то есть, напряжение одинаково на всех резисторах и составляет 100 В. Тогда, по закону Ома I = U/R

Для вычисления искомого параметра на всем участке цепи, нам необходимо знать общее сопротивление этого участка. Учитывая тот факт, что при параллельном соединении нагрузочных элементов в цепи их общее сопротивление равно:

Имеем: 1/R= 1/5 + 1/25 + 1/50 = 13/50; R = 50/13 ≈ 3.85 (Ом)

Тогда: I = U/R = 100 В/3,85 Ом ≈26 А.

Ответ:

• Сила тока на сопротивлениях: I₁ =20 А; I₂ = 4А; I₃ = 2 А.
• Сила тока, поступающего на рассматриваемый участок цепи равна 26 А.

Задача 2.

Решение:

Воспользуемся формулой для нахождения силы тока, включающей напряжение и мощность: I = P/U.

• 2 кВт преобразим в ватты: 2 кВт = 2000 Вт.
• Подставляем данные: I = 2 000 Вт/ 220 В ≈ 9 А
• Ответ: Нагревательный элемент электрочайника рассчитан на 9 А.

Задача 3.

Решение.

Применяя закон Ома для полной цепи, запишем: I = ε / (R+r′)

I = 6 В / (5 Ом + 1 Ом) = 1 А.

Ответ: сила тока 1 А.

Задача 4.

Решение:

За время t электричество выполнит работу A = U*I*t.

Напряжение сети известно – оно составляет 220 В.Силу тока находим по формуле: I = U/R, тогда A = (U 2 /R)*t или

A = ((220 В) 2 / 40 Ом) * 2 ч = 2420 Втч = 2,42 кВтч

Ответ: За 2 часа работы электроплита потребляет 2,42 кВт часов электроэнергии.

Применяя формулы для вычисления параметров электричества, пользуясь фундаментальными законами физики можно находить неизвестные данные для составных элементов цепей и электроприборов с целью оценки их состояния. В каждом отдельном случае необходимо определить известные параметры тока, которые можно использовать в дальнейших вычислениях. Обычно, это напряжение, мощность или сопротивление нагрузки.

Если можно обойтись без измерений амперметром – лучше прибегнуть к вычислениям, даже если при этом потребуется измерить напряжение. Такое измерение можно проводить без разрыва электрической цепи, чего нельзя сделать при помощи амперметра.

Источник

Электричество — неотъемлемый признак нашей эпохи. Абсолютно всё вокруг завязано на нём. Любой современный человек, даже без технического образования, знает, что электрический ток, текущий по проводам, способен в некоторых случаях нагревать их, зачастую до очень высоких температур. Казалось бы, это заведомо всем известно и не стоит упоминания. Однако, как объяснить это явление? Почему и как происходит нагрев проводника?

Опыты Ленца

Перенесемся в 19 век-эпоху накопления знаний и подготовки к технологическому прыжку 20 века. Эпоха, когда по всему миру различные учёные и просто изобретатели-самоучки чуть ли не ежедневно открывают что-то новое, зачастую тратя огромное количество времени на исследования и, при этом, не представляя конечный результат.

Один из таких людей, русский учёный Эмилий Христианович Ленц, увлекался электричеством, на тогдашнем примитивном уровне, пытаясь рассчитывать  электрические цепи. В 1832 году  Эмилий Ленц «застрял» с расчётами, так как параметры его смоделированной цепи «источник энергии — проводник — потребитель энергии» сильно разнились от опыта к опыту. Зимой 1832-1833 года учёный обнаружил, что причиной нестабильности является кусочек платиновой проволоки, принесённый им с холода. Отогревая или охлаждая проводник, Ленц также заметил что  существует некая  зависимость между силой тока, электрическим сопротивлением  и температурой проводника.

При определённых параметрах электрической цепи проводник быстро оттаивал и даже слегка нагревался. Измерительных приборов в те времена практически никаких не существовало — невозможно было точно измерить ни силу тока, ни сопротивление. Но это был русский физик, и он проявил смекалку. Если это зависимость, то почему бы ей не быть обратимой?

Для того чтобы измерить количество тепла, выделяемого проводником, учёный сконструировал простейший «нагреватель» — стеклянная ёмкость, в которой находился  спиртосодержащий раствор и погружённый в него платиновый проводник-спираль. Подавая различные величины электрического тока на проволоку, Ленц замерял время, за которое раствор нагревался до определённой температуры. Источники электрического тока в те времена  были слишком слабы, чтобы разогреть раствор до серьёзной температуры, потому визуально определить количество испарившегося  раствора не представлялось возможным. Из-за этого процесс исследования очень затянулся — тысячи вариантов подбора параметров источника питания, проводника, долгие замеры и последующий анализ.

Закон Джоуля-Ленца

В итоге, спустя десятилетие, в 1843 году Эмилий Ленц выставил на  всеобщее обозрение научного сообщества результат своих опытов в виде закона. Однако, оказалось, что его опередили! Пару лет назад английский физик Джеймс Прескотт Джоуль уже проводил аналогичные опыты и также представил общественности свои результаты. Но, тщательно проверив все работы Джеймса Джоуля, русский учёный выяснил что собственные опыты гораздо точнее, наработан больший объём исследований, потому, русской науке есть чем дополнить английское открытие.

Научное сообщество рассмотрело оба результата исследований и объединила их в одно, тем самым закон Джоуля переименовали в закон Джоуля-Ленца. Закон утверждает, что количество теплоты, выделяемое проводником при протекании по нему электрического тока , равно произведению силы этого тока в квадрате, сопротивлению проводника и времени, за которое по проводнику течёт ток. Или формулой:

Q=I²Rt

где

Q — количество выделяемого тепла (Джоули)

I — сила тока, протекающего через проводник (Амперы)

R — сопротивление проводника (Омы)

t — время прохождения тока через проводник (Секунды)

Почему греется проводник

Как же объясняется нагрев проводника? Почему он именно греется, а не остаётся нейтральным или охлаждается? Нагрев происходит из-за того, что свободные электроны, перемещающиеся в проводнике под действием электрического поля, бомбардируют атомы молекул металла, тем самым передавая им собственную энергию, которая переходит в тепловую. Если изъясняться совсем просто: преодолевая материал проводника, электрический ток как бы «трётся», соударяется электронами о молекулы проводника. Ну а , как известно, любое трение сопровождается нагревом. Следовательно, проводник будет нагреваться пока по нему бежит электрический ток.

Из формулы также следует —  чем выше удельное сопротивление проводника и чем выше сила тока протекающего по нему, тем выше будет нагрев . Например, если последовательно соединить проводник-медь (удельное сопротивление  0,018 Ом·мм²/м) и проводник-алюминий (0,027 Ом·мм²/м), то при протекании через цепь электрического тока алюминий будет нагреваться сильнее чем медь из-за более высокого сопротивления. Поэтому, кстати, не рекомендуется в быту делать скрутки медных и алюминиевых проводов друг с другом — будет неравномерный нагрев в месте скрутки. В итоге —  подгорание с последующим пропаданием контакта.

Применение закона Джоуля-Ленца в жизни

Открытие закона Джоуля-Ленца имело огромные последствия для практического применения электрического тока. Уже в 19 веке стало возможным создать более точные измерительные приборы, основанные на сокращении проволочной спирали при её нагреве протекающим током определённой величины — первые стрелочные вольтметры и амперметры. Появились первые прототипы электрических обогревателей, тостеров, плавильных печей – использовался проводник с высоким удельным сопротивлением, что позволяло получить довольно высокую температуру.

Были изобретены плавкие предохранители, биметаллические прерыватели цепи (аналоги современных тепловых реле защиты), основанные на разнице нагрева проводников с разным удельным сопротивлением. Ну и, конечно же, обнаружив что при определённой силе тока проводник с высоким удельным сопротивлением способен нагреться докрасна , данный эффект использовали в качестве источника света. Появились первые лампочки.

Проводник (угольная палочка, бамбуковая нить, платиновая проволока и т.д.) помещали в стеклянную  колбу, откачивали воздух для замедления процесса окисления и получали  незатухаемый, чистый и стабильный источник света – электрическую лампочку

Заключение

Таки образом, можно сказать что на законе Джоуля-Ленца держится чуть ли не вся электрика и электротехника. Открыв этот закон, появилась возможность уже заранее предсказать  некоторые будущие проблемы в освоении электричества. Например, из-за нагрева проводника передача электрического тока на большое расстояние сопровождается потерями этого тока на тепло. Соответственно, чтобы компенсировать эти потери  нужно занизить передаваемый ток, компенсируя это высоким напряжением. А уже на оконечном потребителе, понижать напряжение и получать более высокий ток.

Закон Джоуля-Ленца неотступно следует из одной эпохи технологического развития  в другую. Даже сегодня мы постоянно наблюдаем его в быту – закон проявляется всюду, и не всегда люди ему рады. Сильно греющийся процессор персонального компьютера, пропадание света из-за обгоревшей скрутки  «медь-алюминий»,выбитая вставка-предохранитель, выгоревшая из-за высокой нагрузки электропроводка – всё это тот самый закон Джоуля-Ленца.

Раз уж заговорили про ДжОУля )) Читайте статья про ОУ — Операционный усилитель.

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

На
прошлом уроке мы с вами говорили о действиях, которые способен оказывать
электрический ток, протекая в различных средах. Познакомившись с тремя
действиями тока, уместно задать себе вопрос: от чего зависит эффективность каждого
из действий, то есть от чего зависит количество теплоты, выделяемой в нити
накала электролампы, масса выделенной в опыте меди, подъёмная сила
изготовленного электромагнита?

Эффективность этих
действий будет зависеть от нескольких причин. Электрический ток, как вы знаете,
— это направленное
движение заряженных частиц. Поэтому чем больше электрический заряд,
перенесённый частицами через поперечное сечение проводника за какое-то
определённое время, тем интенсивнее будет действие тока.

Здесь можно провести
аналогию: эффективность действия воды на водяной мельнице или
гидроэлектростанции, конечно же, определяется массой ежесекундно протекающей в
таком устройстве воды. Поэтому важнейшей характеристикой электрического тока
является величина, называемая силой тока.

Сила
тока — это физическая величина, численно равная электрическому заряду,
протекающему через поперечное сечение проводника за единицу времени. Обозначают силу тока буквой I.

Пусть q — заряд, протекающий через сечение
проводника за некоторый отрезок времени t. Тогда очевидно, что для нахождения ежесекундно
протекающего заряда мы должны разделить весь заряд на значение промежутка
времени, что и приводит нас к формуле силы тока:

Единицу силы тока не
вводят через какие-либо формулы, а просто выбирают по договорённости, как это
было уже сделано с единицами массы, времени и длины.

Здесь вы можете сказать,
что подобная договорённость лишена логики: брать в качестве основной величины
не единицу заряда, которая рассматривается значительно раньше, а единицу силы
тока, то есть величину, которая получается путём логической операции с
электрическим зарядом.

Вы абсолютно правы! Но
все дело в том, что для всех основных единиц нужно создать эталоны, то есть
устройства, позволяющие собрать и сохранить без потерь сведения о выбранной
единице. Так вот, для единицы силы тока можно с гораздо большей точностью
выбрать и сохранить эталон, чем для единицы электрического заряда, чем и объясняется
такая «нелогичность» в выборе основной единицы.

В
1948 г. на Генеральной конференции по мерам и весам решили, что в основе
определения единицы силы тока должно лежать явление взаимодействия двух
проводников с током. Это явление можно пронаблюдать на опыте. Если по двум
параллельным проводникам пропустить ток, то, в зависимости от направления тока,
проводники либо притянутся, либо оттолкнутся.

При
этом сила притяжения или отталкивания между проводниками прямо пропорциональна
силе тока в них, то есть чем больше сила тока, тем сильнее взаимодействуют
проводники.

Но
чтобы ввести точный эталон, необходимо соблюдать очень жёсткие условия опыта. Проводники
должны быть тонкими и бесконечно длинными, при этом они должны находиться в
вакууме на расстоянии 1 м друг от друга.

Поэтому, за единицу силы тока принимают такую силу тока, при которой бесконечно
длинные параллельные проводники, находящиеся
на расстоянии одного метра друг
от друга в вакууме, на
каждом метре своей длины взаимодействуют с силой 2 ∙ 10⁻⁷
Н.

Эту
единицу силы тока называют ампером. Названа
она так в честь французского физика А. Ампера,
и является основной единицей силы тока в СИ.

1
А — это очень большое значение силы тока. Поэтому в науке, технике и на
практике часто используют кратные и дольные единицы силы тока:

Познакомившись с единицей
силы тока, мы можем дать и строгое определение единицы электрического заряда
(количества электричества). Зная формулу для расчёта силы тока, можно записать:
q = It. Учитывая, что единицей силы тока является ампер, а
единицей времени — секунда, получим, что 1 Кл — это заряд, протекающий за 1 с
через поперечное сечение проводника с током силой 1 А.

Ещё
одна очень важная особенность силы тока заключается в следующем: сила тока
во всех участках проводника, по которому протекает электрический ток, одинакова.
Всё дело в том, что, когда в проводнике протекает ток, заряд нигде ни в какой его
части не скапливается. Так, если в начале проводника, например, металлической
проволочки, сила тока равна 1 А, то и в любом поперечном сечении проводника, и
в конце его она тоже обязательно 1 А.

 Прибор,
с помощью которого измеряют силу тока в цепи, называют амперметром.

Амперметр
и по своему принципу действия, и по устройству похож на гальванометр. Его
работа основана на магнитном действии тока.

Чем
больше сила тока, проходящего по катушке, тем сильнее она взаимодействует с
магнитом, тем больше угол поворота стрелки прибора. Поскольку с помощью
амперметра измеряют силу тока, то он устроен так, чтобы включение его в цепь практически не влияло на силу
тока в цепи.

Чтобы
отличить амперметр от гальванометра, на его шкале ставят букву «А». На схемах
амперметр изображают кружком с буквой «А» в центре:

Будьте
внимательны при работе с амперметрами, так как каждый из них рассчитан на некоторую
максимальную силу тока. Иначе прибор может попросту сгореть.

Амперметр включается в
цепь последовательно с тем прибором, силу тока в котором нужно измерить.
Иными словами, чтобы контролировать значение силы тока, протекающего в
интересующей нас части цепи, мы должны обязательно сделать разрыв цепи и
включить в разрыв амперметр, чтобы весь заряд, протекающий в этой части цепи,
проходил через прибор.

Обратите
внимание и на то, что у каждой клеммы прибора стоит свой знак: или «плюс», или
«минус». Это значит, что клемму со знаком «плюс» надо обязательно соединить с
проводом, идущим от положительного полюса источника тока, а клемму со знаком «минус»
— с отрицательным.

Если
цепь состоит из нескольких последовательно соединённых проводников или приборов
(это такое соединение, при котором начало одного проводника соединяется с
концом другого), то амперметр будет показывать во всех точках цепи одно и
то же значение силы тока.

Пример решения задачи.

Задача. По графику зависимости перенесённого
заряда от времени найдите силу тока в проводнике. Какое количество электронов
проходит через сечение проводника за 5 с?