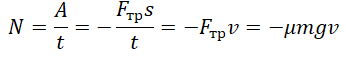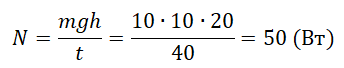Как найти время зная мощность и работу?
яфі аіві
Ученик
(98),
закрыт
7 лет назад
Виталий Данилович
Мудрец
(12520)
7 лет назад
Мощность – это работа в единицу времени. Мол, Ватт – это Джоуль за секунду. А киловаттчас – это киловатт, умноженный на час. Как найти, за какой время нажжётся два киловаттчаса, если мощность – полкиловатта? Правильный ответ: разделить работу на мощность.
Сила, перемещающая тело, совершает работу. Работа – это разность энергии тела в начале процесса и в его конце. А мощность – это работа за одну секунду. Коэффициент полезного действия (КПД) – это дробное число. Максимальный КПД равен единице, однако, часто, КПД меньше единицы.
Работы силы, формула
Сила, приложенная к телу и перемещающая его, совершает работу (рис. 1).

Рис. 1. Сила перемещает тело и совершает работу
Работа силы — это скалярное произведение вектора силы на вектор перемещения.
Работу, совершаемую силой, можно посчитать, используя векторный или скалярный вид записи такой формулы:
Векторный вид записи
[ large boxed{ A = left( vec{F} , vec{S} right) }]
Для решения задач правую часть этой формулы удобно записывать в скалярном виде:
[ large boxed{ A = left| vec{F} right| cdot left| vec{S} right| cdot cos(alpha) }]
( F left( H right) ) – сила, перемещающая тело;
( S left( text{м} right) ) – перемещение тела под действием силы;
( alpha ) – угол между вектором силы и вектором перемещения тела;
Работу обозначают символом (A) и измеряют в Джоулях. Работа – это скалярная величина.
В случае, когда сила постоянная, формула позволяет рассчитать работу, совершенную силой за полное время ее действия.
Если сила изменяется со временем, то в каждый конкретный момент времени будем получать мгновенную работу. Эти, мгновенные значения для разных моментов времени будут различаться.
Рассмотрим несколько случаев, следующих из формулы:
- Когда угол между силой и перемещением острый, работа силы положительная;
- А если угол тупой — работа отрицательная, так как косинус тупого угла отрицательный;
- Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
Работа — разность кинетической энергии
Работу можно рассчитать еще одним способом — измеряя кинетическую энергию тела в начале и в конце процесса движения. Рассмотрим такой пример. Пусть автомобиль, движется по горизонтальной прямой и, при этом увеличивает свою скорость (рис. 2). Масса автомобиля 1000 кг. В начале его скорость равнялась 1 м/с. После разгона скорость автомобиля равна 10 метрам в секунду. Найдем работу, которую пришлось проделать, чтобы ускорить этот автомобиль.

Рис. 2. Автомобиль движется прямолинейно и увеличивает свою скорость
Для этого посчитаем энергию движения автомобиля в начале и в конце разгона.
( E_{k1} left(text{Дж} right) ) – начальная кинетическая энергия машины;
( E_{k2} left(text{Дж} right) ) – конечная кинетическая энергия машины;
( m left( text{кг}right) ) – масса автомобиля;
( displaystyle v left( frac{text{м}}{c}right) ) – скорость, с которой машина движется.
Кинетическую энергию будем вычислять, используя формулу:
[ large E_{k} = m cdot frac{v^{2}}{2} ]
[ large E_{k1} = 1000 cdot frac{1^{2}}{2} = 500 left(text{Дж} right) ]
[ large E_{k2} = 1000 cdot frac{10^{2}}{2} = 50000 left(text{Дж} right) ]
Теперь найдем разницу кинетической энергии в конце и вначале разгона.
[ large boxed{ A = Delta E_{k} }]
[ large Delta E_{k} = E_{k2} — E_{k1} ]
[ large Delta E_{k} = 50000 – 500 = 49500 left(text{Дж} right) ]
Значит, работа, которую потребовалось совершить, чтобы разогнать машину массой 1000 кг от скорости 1 м/с до скорости 10 м/с, равняется 49500 Джоулям.
Примечание: Работа – это разность энергии в конце процесса и в его начале. Можно находить разность кинетической энергии, а можно — разность энергии потенциальной.
[ large boxed{ A = Delta E }]
Работа силы тяжести — разность потенциальной энергии
Рассмотрим теперь следующий пример. Яблоко массой 0,2 кг упало на садовый стол с ветки, находящейся на высоте 3 метра от поверхности земли. Столешница располагается на высоте 1 метр от поверхности (рис. 3). Найдем работу силы тяжести в этом процессе.

Рис. 3. На рисунке указано начальное 1 положение тела (яблока) и его конечное 2 положение, отмечены высоты для подсчета работы по вертикальному перемещению тела
Посчитаем потенциальную энергию яблока до его падения и энергию яблока на столешнице.
( E_{p1} left(text{Дж} right) ) – начальная потенциальная энергия яблока;
( E_{p2} left(text{Дж} right) ) – конечная потенциальная энергия яблока;
Примечание: Работу можно рассчитать через разность потенциальной энергии тела.
Потенциальную энергию будем вычислять, используя формулу:
[ large E_{p} = m cdot g cdot h]
( m left( text{кг}right) ) – масса яблока;
Величина ( displaystyle g approx 10 left(frac{text{м}}{c^{2}} right) ) – ускорение свободного падения.
( h left( text{м}right) ) – высота, на которой находится яблоко относительно поверхности земли.
Начальная высота яблока над поверхностью земли равна 3 метрам
[ large E_{p2} = 0,2 cdot 10 cdot 3 = 6 left(text{Дж} right) ]
Потенциальная энергия яблока на столе
[ large E_{p1} = 0,2 cdot 10 cdot 1 = 2 left(text{Дж} right) ]
Теперь найдем разницу потенциальной энергии яблока в конце падения и перед его началом.
[ large Delta E_{p} = E_{p2} — E_{p1} ]
[ large Delta E_{p} = 2 – 6 = — 4 left(text{Дж} right) ]
Важно помнить: Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
Чтобы работа получилась положительной, в правой части формулы перед ( Delta E_{p}) дополнительно допишем знак «минус».
[ large boxed{ A = — Delta E_{p} }]
Значит, работа, которую потребовалось совершить силе тяжести, чтобы яблоко массой 0,2 кг упало с высоты 3 м на высоту 1 метр, равняется 4 Джоулям.
Примечания:
- Если тело падает на землю, работа силы тяжести положительна;
- Когда мы поднимаем тело над землей, мы совершаем работу против силы тяжести. Наша работа при этом положительна, а работа силы тяжести будет отрицательной;
- Сила тяжести относится к консервативным силам. Для консервативных сил перед разностью потенциальной энергии мы дописываем знак «минус»;
- Работа силы тяжести не зависит от траектории, по которой двигалось тело;
- Работа для силы (displaystyle F_{text{тяж}}) зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени.
Рисунок 4 иллюстрирует факт, что для силы (displaystyle F_{text{тяж}}) работа зависит только от разности высот и не зависит от траектории, по которой тело двигалось.

Рис. 4. Разность высот между начальным и конечным положением тела во всех случаях на рисунке одинакова, поэтому, работа силы тяжести для представленных случаев будет одинаковой
Мощность
В механике мощность часто обозначают символами N или P и измеряют в Ваттах в честь шотландского изобретателя Джеймса Уатта.
Примечание: Символ (vec{N}) используется для обозначения силы реакции опоры — она измеряется в Ньютонах и является векторной величиной. Чтобы не возникло путаницы, мощность вместо N будем обозначать символом P. Символ P – первая буква в английском слове power – мощность.
Мощность – это работа, совершенная за одну секунду (энергия, затраченная за 1 сек).
Расчет работы осуществляем, используя любую из формул:
[ large A = Delta E_{k} ]
[ large A = Delta E_{p} ]
[ large A = F cdot S cdot cos(alpha) ]
Разделив эту работу на время, в течение которого она совершалась, получим мощность.
[ large boxed{ P = frac{A}{Delta t} }]
Если работа совершалась равными частями за одинаковые интервалы времени – мощность будет постоянной величиной.
Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.
Еще одна формула для расчета мощности
Есть еще один способ расчета мощности, когда сила перемещает тело и при этом скорость тела не меняется:
[ large P = left( vec{F} , vec{v} right) ]
Формулу можно записать в скалярном виде:
[ large P = left| vec{F} right| cdot left| vec{v} right| cdot cos(alpha) ]
( F left( H right) ) – сила, перемещающая тело;
( displaystyle v left( frac{text{м}}{c} right) ) – скорость тела;
( alpha ) – угол между вектором силы и вектором скорости тела;
Когда векторы (vec{F}) и (vec{v}) параллельны, запись формулы упрощается:
[ large boxed{ P = F cdot v }]
Примечание: Такую формулу для расчета мощности можно получить из выражения для работы силы, разделив обе части этого выражения на время, в течение которого работа совершалась (а если точнее, найдя производную обеих частей уравнения).
КПД
КПД – коэффициент полезного действия. Обычно обозначают греческим символом (eta) «эта». Единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах.
Примечания:
- Процент – это дробь, у которой в знаменателе число 100.
- КПД — это либо правильная дробь, или дробь, равная единице.
Вычисляют коэффициент (eta) для какого-либо устройства, механизма или процесса.
[ large boxed{ eta = frac{ A_{text{полезная}}}{ A_{text{вся}}} }]
(eta) – КПД;
( large A_{text{полезная}} left(text{Дж} right)) – полезная работа;
(large A_{text{вся}} left(text{Дж} right)) – вся затраченная для выполнения работы энергия;
Примечание: КПД часто меньше единицы, так как всегда есть потери энергии. Коэффициент полезного действия не может быть больше единицы, так как это противоречит закону сохранения энергии.
[ large boxed{ eta leq 1 }]
Величина (eta) является дробной величиной. Если числитель и знаменатель дроби разделить на одно и то же число, полученная дробь будет равна исходной. Используя этот факт, можно вычислять КПД, используя мощности:
[ large boxed{ eta = frac{ P_{text{полезная}}}{ P_{text{вся затраченная}}} }]
Выводы
- Сила, приложенная к телу и перемещающая его, совершает работу;
- Когда угол между силой и перемещением острый, работа силы положительная, а если угол тупой — работа отрицательная; Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
- Работу можно вычислить, измеряя кинетическую энергию тела в начале и в конце его движения;
- Вычислить работу можно через разность потенциальной энергии тела в начальной и в конечной высотах над землей;
- Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
- Мы совершаем работу против силы тяжести, когда поднимаем тело над землей. При этом наша работа положительная, а работа силы тяжести — отрицательная;
- Сила тяжести — это консервативная сила. Поэтому, работа силы (displaystyle F_{text{тяж}}) не зависит от траектории, по которой двигалось тело, а зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени;
- Мощность – это работа, совершенная за одну секунду, или затраченная за 1 сек. энергия;
- Коэффициент полезного действия обозначают греческим символом (eta) «эта», единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах;
- КПД — это либо правильная дробь, или дробь, равная единице.
- Можно вычислять КПД, подставляя в формулу работу, или мощности
Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:
![]()
Работа силы
В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.
Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).
Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:
![]()

Важно!
Механическая работа совершается, если:
- На тело действует сила.
- Под действием этой силы тело перемещается.
- Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).
Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.
Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.
Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:
![]()
Работа различных сил
Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.
| Работа силы тяжести |
Модуль силы тяжести: Fтяж = mg Работа силы тяжести: A = mgs cosα |
| Работа силы трения скольжения |
Модуль силы трения скольжения: Fтр = μN = μmg Работа силы трения скольжения: A = μmgs cosα |
| Работа силы упругости |
Модуль силы упругости: Fупр = kx Работа силы упругости:
|
Работа силы упругости
Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):

Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:
s = x1 – x2
Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:

Работы силы трения покоя
Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.

Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.
A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)
Знак работы силы
Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:
- Если α = 0о, то cosα = 1.
- Если 0о < α < 90o, то cosα > 0.
- Если α = 90о, то cosα = 0.
- Если 90о < α < 180o, то cosα < 0.
- Если α = 180о, то cosα = –1.
Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180о). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0о). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.
Геометрический смысл работы
Графическое определение
Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.

A = Sфиг
Мощность
Определение
Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:

Рассмотрим частные случаи определения мощности в таблице.
Мощность при равномерном прямолинейном движении тела |
Работа при равномерном прямолинейном движении определяется формулой: A = Fтs Fт — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна:
|
Мощность при равномерном подъеме груза |
Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому:
|
Мгновенная мощность при неравномерном движении |
Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость:
|
Мощность силы трения при равномерном движении по горизонтали |
Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения:
|
Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?
Коэффициент полезного действия
Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.
Определения:
- Работа затраченная — полная работа силы, совершенной над телом (или телом).
- Работа полезная — часть полной работы силы, которая вызывает непосредственно перемещение тела.
- Коэффициент полезного действия (КПД) — процентное отношение полезной работы к работе затраченной. КПД обозначается буквой «эта» — η. Единицы измерения эта величина не имеет. Она показывает эффективность работы механизма или другой системы, совершающей работу, в процентах.
КПД определяется формулой:

Работа может определяться как произведение мощности на время, в течение которого совершалась работа:
A = Nt
Поэтому формулу для вычисления КПД можно записать в следующем виде:

Частые случаи определения КПД рассмотрим в таблице ниже:
Устройство |
Работа полезная и полная |
КПД |
| Неподвижный блок, рычаг |
Aполезн = mgh Асоверш. |
 |
| Наклонная плоскость |
Aполезн = mgh Асоверш. = Fl l — совершенный путь (длина наклонной плоскости). |
 |
Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.
В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:
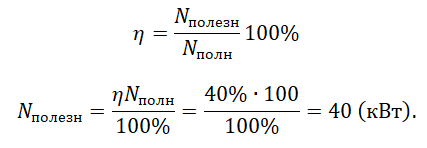
Задание EF17557
Какую мощность развивает сила тяги трактора, перемещая прицеп со скоростью 18 км/ч, если она составляет 16,5 кН?
Ответ:
а) 916 Вт
б) 3300 Вт
в) 82500 Вт
г) 297000 Вт
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать формулу для расчета мощности.
3.Выполнить общее решение задачи.
4.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Сила тяги, перемещающая прицеп, равна: Fт = 16,5 кН.
• Скорость перемещения прицепа под действием силы тяги: v = 18 км/ч.
Переведем единицы измерения в СИ:
16,5 кН = 16,5∙103 Н
18 км/ч = 18000/3600 м/с = 5 м/с
Мощность равна отношению работы ко времени, в течение которого эта работа совершалась:
N=At
Но работа равна произведению силы, перемещения и косинуса угла между векторами силы и перемещения. В данном случае будем считать, что угол равен нулю, следовательно косинус — единице. Тогда работа равна:
A = Fs
Тогда мощность равна:
N=Fst=Fv=16,5·103·5=82500 (Вт)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17574
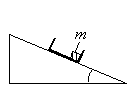 С вершины наклонной плоскости из состояния покоя скользит с ускорением лёгкая коробочка, в которой находится груз массой m (см. рисунок). Как изменятся время движения, ускорение и модуль работы силы трения, если с той же наклонной плоскости будет скользить та же коробочка с грузом массой m/2? Для каждой величины определите соответствующий характер изменения:
С вершины наклонной плоскости из состояния покоя скользит с ускорением лёгкая коробочка, в которой находится груз массой m (см. рисунок). Как изменятся время движения, ускорение и модуль работы силы трения, если с той же наклонной плоскости будет скользить та же коробочка с грузом массой m/2? Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Время движения |
Ускорение |
Модуль работы силы трения |
Алгоритм решения
1.Установить наличие и характер зависимости кинематических характеристик движения от массы тела.
2.Вывести формулу для модуля работы силы трения.
3.Установить, как изменится модуль работы силы трения при уменьшении массы тела вдвое.
Решение
При скольжении с наклонной плоскости происходит равноускоренное движение. Положение тела в любой момент времени при таком движении можно определить с помощью кинематических уравнений:
x=xo+v0xt+axt22
y=yo+v0yt+ayt22
Из этих уравнений видно, что ускорение и время никак не зависят от массы тела. Следовательно, при уменьшении массы тела в 2 раза его время движения и ускорение не изменятся.
Чтобы выразить модуль работы силы трения, выберем такую систему отсчета, чтобы вектор силы трения был расположен вдоль оси Ox.Тогда сила трения будет равна:
Fтр = μmg
Известно, что работа определяется формулой:
A = Fs cosα
Тогда работа силы трения равна:
A = μmgs cosα
Вектор силы трения всегда направлен противоположно вектору перемещения. Поэтому косинус угла между ними равен –1. Но нас интересует только модуль работы. Поэтому будем считать, что он равен:
A = μmgs
Модуль работы силы трения и масса тела зависят прямо пропорционально. Следовательно, если массу тела уменьшить вдвое, то и модуль работы силы трения уменьшится вдвое.
Поэтому правильная последовательность цифр в ответе: 332.
Ответ: 332
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18646
В первой серии опытов брусок перемещают при помощи нити равномерно и прямолинейно вверх по наклонной плоскости. Во второй серии опытов на бруске закрепили груз, не меняя прочих условий.
Как изменятся при переходе от первой серии опытов ко второй сила натяжения нити и коэффициент трения между бруском и плоскостью?
Для каждой величины определите соответствующий характер её изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
| Сила натяжения нити | Коэффициент трения |
Алгоритм решения
- Определить, какая величина изменилась во второй серии опытов.
- Определить, как зависит от этой величины сила натяжения нити.
- Определить, как зависит от этой величины коэффициент трения.
Решение
Когда к бруску подвесили груз, увеличилась масса. Когда тело на нити перемещается вверх прямолинейно и равномерно, сила натяжения нити определяется модулем силы тяжести:
T = mg
Эта формула показывает, что сила натяжения нити и масса тела зависят прямо пропорционально. Если, добавив к бруску груз, масса увеличится, то сила натяжения нити тоже увеличится.
Коэффициент трения — это величина, которая зависит только от материалов и типа поверхности. Поэтому увеличение массы тела на него никак не повлияют.
Верная последовательность цифр в ответе: 13.
Ответ: 13
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18271
Определите коэффициент полезного действия атомной электростанции, расходующей за неделю уран-235 23592U массой 1,4 кг, если её мощность равна 38 МВт. При делении одного ядра урана-235 выделяется энергия 200 МэВ.
Алгоритм решения
1.Записать исходные данные и перевести их в СИ.
2.Записать формулу для определения КПД атомной электростанции.
3.Решить задачу в общем виде.
4.Подставить известные данные и вычислить искомую величину.
5.Массовое число: A = 235.
6.Зарядовое число: Z = 92.
Решение
Запишем исходные данные:
• Энергия, выделяемая при делении одного ядра урана-235: Q0 = 200 МэВ.
• Масса урана-235: m = 1,4 кг.
• Время, в течение которого происходит деление: t = 1 неделя.
• Мощность атомной электростанции: N = 38 МВт.
Переведем все единицы измерения в СИ:
1 эВ = 1,6∙10–19 Дж
200 МэВ = 200∙106∙1,6∙10–19 Дж = 320∙10–13 Дж
1 неделя = 7∙24∙60∙60 с = 604,8∙103 с
38 МВт = 38∙106 Вт
КПД атомной электростанции есть отношение полезной работы к выделенной за это же время энергии:
η=AполезнQ100%
Полезную работу мы можем вычислить по формуле:
A=Nt
Выделенное количество теплоты мы можем рассчитать, вычислив количество атомов, содержащихся в 1,4 кг урана-235 и умножив их на энергию, выделяемую при делении одного такого атома.
Количество атомов равно произведению количество молей на постоянную Авогадро:
Nкол.атомов = νNA
Количество молей равно отношения массы вещества к его молярной массе, следовательно:
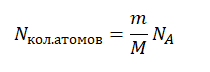
Молярная масса численно равна массовому числу в граммах на моль. Следовательно:
M = A (г/моль) = A∙10–3 (кг/моль)
Отсюда количество атомов равно:
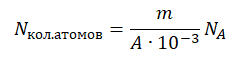
Энергия, выделенная всеми атомами, равна:
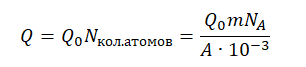
Теперь можем вычислить КПД:
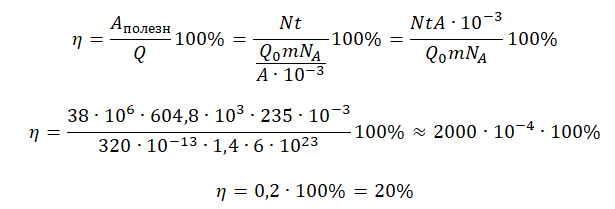
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 11.9k

4545456
+35
Решено
9 лет назад
Физика
5 – 9 классы
как найти время зная работу,силу тока,напряжение?
Смотреть ответ
2
Комментарии

danafizik
А=UIt отсюда t=A/UI

Ответ
4
(5 оценок)
8

Очаровашка99
9 лет назад
Светило науки – 136 ответов – 0 раз оказано помощи
I=A/Ut
t=A/IU
))))))))))))))))))))))))
(5 оценок)
Ответ проверен экспертом
3
(7 оценок)
6

MashaPutnaj
9 лет назад
Светило науки – 15179 ответов – 183972 помощи
ак найти время зная работу,силу тока,напряжение?
А= U*I*t t=A/U*I
А= U^2*t/R t= A*R/U^2
A=I^2*R*t t= A/I^2*R
(7 оценок)
https://vashotvet.com/task/8578837
Содержание:
Мощность:
Одинаковую работу можно совершить за разные промежутки времени. Например, можно поднять груз за минуту, а можно поднимать этот же груз в течение часа.
Физическую величину, равную отношению совершенной работы 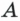
Единицей мощности в SI является джоуль в секунду (Дж/с), или ватт (Вт), названный так в честь английского изобретателя Дж. Уатта. Один ватт — это такая мощность, при которой работу в 1 Дж совершают за 1 с. Итак, 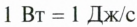
Человек может развивать мощность в сотни ватт. Чтобы оценить, насколько могущество человеческого разума, создавшего двигатели, больше «могущества» человеческих мускулов, приведем такие сравнения:
- мощность легкового автомобиля примерно в тысячу раз больше средней мощности человека;
- мощность авиалайнера примерно в тысячу раз больше мощности автомобиля;
- мощность космического корабля примерно в тысячу раз больше мощности самолета.
Мощность
Механическая работа всегда связана с движением тел. А движение происходит во времени. Поэтому и выполнение работы, как и превращение механической энергии, всегда происходит на протяжении определенного времени.
Работа выполняемая на протяжении определенного времени:
Простейшие наблюдения показывают, что время выполнения работы может быть разным. Так, школьник может подняться по лестнице на пятый этаж за 1-2 мин, а пожилой человек — не меньше чем за 5 мин. Грузовой автомобиль КрАЗ может перевезти определенный груз на расстояние 50 км за 1 ч. Но если этот груз частями начнет перевозить легковой автомобиль с прицепом, то потратит на это не меньше 12 ч.
Для описания процесса выполнения работы, учитывая его скорость, используют физическую величину, которая называется мощностью.
Что такое мощность
Мощность – это физическая величина, которая показывает скорость выполнения работы и равна отношению работы ко времени, за которое эта работа выполняется.
Так как при выполнении работы происходит превращение энергии, то можно считать, что мощность характеризует скорость превращения энергии.
Как рассчитать мощность
Для расчета мощности нужно значение работы разделить на время, за которое эта работа была выполнена:

Если мощность обозначить латинской буквой 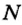 , то формула для расчета мощности будет такой
, то формула для расчета мощности будет такой

Единицы мощности
Для измерения мощности используется единица ватт (Вт). При мощности 1 Вт работа 1 Дж выполняется за 1 с:

Единица мощности названа в честь английского механика Джеймса Уатта, который внес значительный вклад в теорию и практику построения тепловых двигателей.
 Джеймс Уатт (1736-1819) – английский физик и изобретатель.
Джеймс Уатт (1736-1819) – английский физик и изобретатель.
Главная заслуга Уатта в том, что он отделил водяной конденсатор от нагревателя и сконструировал насос для охлаждения конденсатора. Фактически он увеличил разность температур между нагревателем и конденсатором (холодильником), благодаря чему увеличил экономичность паровой машины. Позже теоретически это обоснует Сади Карно.
Он один из первых высказал предположение, что вода – это сложное вещество, состоящее из водорода и кислорода.
Как и для других физических величин, для единицы мощности существуют производные единицы:
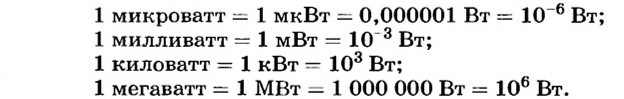
Пример №1
Определить мощность подъемного крана, если работу 9 МДж он выполняет за 5 мин.
Дано:
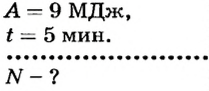
Решение
По определению 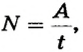 поэтому
поэтому
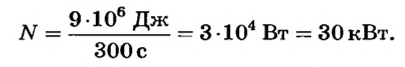
Ответ. Мощность крана 30 кВт.
Пример №2
Человек массой 60 кг поднимается на пятый этаж дома за 1 мин. Высота пяти этажей дома равна 16 м. Какую мощность развивает человек?
Дано:
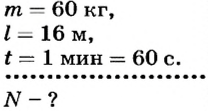
Решение
По определению 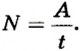
Работа определяется 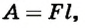
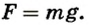
Тогда 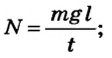
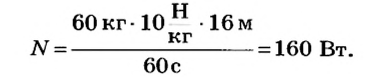
Ответ. Человек развивает мощность 160 Вт.
Зная мощность и время, можно рассчитать работу:

Скорость движения зависит от мощности
Мощность связана со скоростью соотношением:
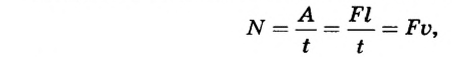
где 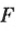 — сила, которая выполняет работу;
— сила, которая выполняет работу; 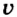 — скорость движения.
— скорость движения.
Если известны мощность двигателя и значения сил сопротивления, то можно рассчитать возможную скорость автомобиля или другой машины, которая выполняет работу:

Таким образом, из двух автомобилей при равных силах сопротивления большую скорость будет иметь тот, у которого мощность двигателя больше.
Каждый конструктор знает, что для увеличения скорости движения автомобиля, самолета или морского корабля нужно или увеличивать мощность двигателя, или уменьшать силы сопротивления. Поскольку увеличение мощности связано с увеличением потребления топлива, то средствам современного транспорта, как правило, придают специфическую обтекаемую форму, при которой сопротивление воздуха будет наименьшим, а все подвижные части изготавливают так, чтобы сила трения была минимальной.
Итоги:
- Существуют два вида механической энергии: кинетическая и потенциальная.
- Если тело перемещается или деформируется под действием силы, то выполняется механическая работа.
- Простыми механизмами являются рычаги и блоки.
- Ни один простой механизм не дает выигрыша в работе.
- Качество механизма определяется коэффициентом полезного действия, который определяет часть полезной работы в общей выполненной работе.
- Тело, при перемещении которого может быть выполнена работа, обладает энергией.
- Взаимодействующие тела обладают потенциальной энергией.
- Движущееся тело обладает кинетической энергией, которая зависит от скорости и массы тела.
- Потенциальная и кинетическая энергии могут превращаться друг в друга. Такие превращения происходят в равной мере, если отсутствуют силы трения.
- Сумму кинетической и потенциальной энергий называют полной механической энергией системы.
- В замкнутой системе при отсутствии сил трения сумма кинетической и потенциальной энергий остается постоянной.
- Закон сохранения и превращения энергии подтверждает невозможность существования вечного двигателя (perpetuum mobile).
- Мощность характеризует скорость превращения одного вида энергии в другой.
Механическая работа и мощность
С помощью импульса невозможно описать все случаи взаимодействия. Поэтому в физике применяют еще и понятие механической работы.
В механике работа зависит от значения и направления силы, а также перемещения точки ее приложения. Из курса физики 8 класса вам известно, что
A = Fs,
где F – значение силы, действующей на тело; s – модуль перемещения тела.
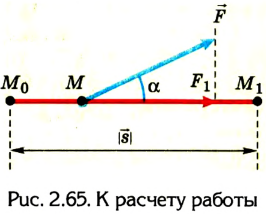
Если сила F постоянна, а перемещение 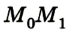 прямолинейное (рис. 2.65), то работа
прямолинейное (рис. 2.65), то работа 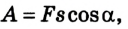
где s = 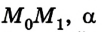 – угол между направлением действия силы и перемещения.
– угол между направлением действия силы и перемещения.
Робота является величиной скалярной. Произведение 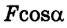 – проекция действующей силы на направление перемещения.
– проекция действующей силы на направление перемещения.
Легко заметить, что если 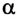 < 90°, то работа силы положительная, при
< 90°, то работа силы положительная, при 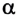 = 90° (сила перпендикулярна к перемещению) работа равна нулю, а при
= 90° (сила перпендикулярна к перемещению) работа равна нулю, а при 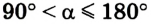 – отрицательная.
– отрицательная.
Пример №3
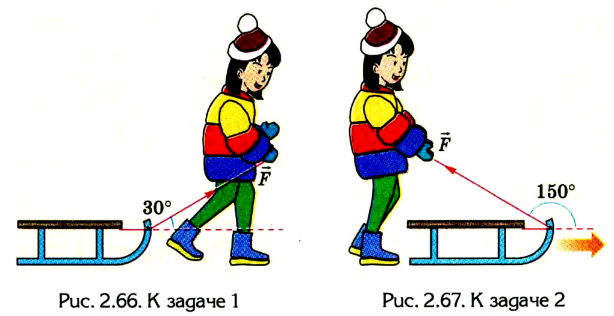
Девочка тянет санки равномерно, прикладывая к веревке силу 50 Н. Веревка натягивается под углом 30° к горизонту (рис. 2.66). Какую работу выполнит девочка, переместив санки на 20 м?
Дано:
F = 50 Н,
s = 20 м, 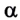 = 30°.
= 30°.
А-?
Решение
По определению 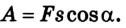
Соответственно 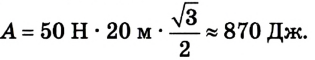
Ответ: А = 870 Дж (работа силы положительная, поскольку cos 30° > 0).
- Заказать решение задач по физике
Пример №4
Решим предыдущую задачу для случая, когда девочка удерживает санки, съехавшие с горки (рис. 2.67). В данном случае 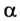 = 150°.
= 150°.
Дано:
F = 50 Н, s = 20 м,
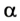 = 150°.
= 150°.
А – ?
Решение
А = Fscosa;
А = 50 Н • 20 м • (-0,87) 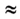 -870 Дж.
-870 Дж.
Ответ: А = -870 Дж (работа силы отрицательная, поскольку cos 150° < 0).
Таким образом, в зависимости от направления действия силы по отношению к перемещению работа может иметь положительные и отрицательные значения.
Например, работа, которую выполняет двигатель автомобиля, будет положительной, поскольку направление силы тяги автомобиля совпадает с направлением его движения. Положительной будет и работа человека, поднимающего какой-либо груз с земли на определенную высоту. Силы трения, действующие на автомобиль, выполняют отрицательную работу, поскольку направлены в противоположном направлении к перемещению.
Возможны случаи, когда работа равна нулю, хотя перемещение тела происходит. Например, если 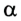 = 90°, то работа силы равна нулю, поскольку cos90° = 0. Сила тяжести, действующая на спутник Земли, который движется по круговой орбите, работы не выполняет.
= 90°, то работа силы равна нулю, поскольку cos90° = 0. Сила тяжести, действующая на спутник Земли, который движется по круговой орбите, работы не выполняет.
Мощность — это физическая величина, характеризующая скорость совершения работы. Поскольку во время выполнения работы происходит превращение энергии, можно сделать вывод, что мощность показывает скорость превращения одного вида энергии в другой.
В механике мощность обозначают буквой N и рассчитывают по формуле
N= — =—,
t t
где 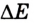 – изменение энергии; А – работа; t – время.
– изменение энергии; А – работа; t – время.
Если известны мощность и время, за которое совершена работа, то можно рассчитать и саму работу:
A = Nt.
Основная единица измерения мощности – ватт (Вт):
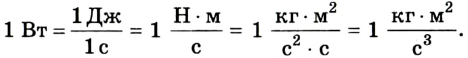
Всё о мощности
Одна и та же работа в разных случаях может быть выполнена за различные промежутки времени, т. е. она может совершаться неодинаково быстро. Например, при подъеме груза на определенную высоту подъемным краном (рис. 148) будет затрачено гораздо меньше времени, чем при использовании лебедки.
Для характеристики процесса выполнения работы важно знать не только ее численное значение, но и время, за которое она выполняется. Очевидно, что чем меньшее время требуется для выполнения данной работы, тем эффективнее работает машина, механизм и др.
Величина, характеризующая быстроту совершения работы, называется мощностью. Ее обычно обозначают буквой Р.
Если в течение промежутка времени Δt была совершена работа А, то средняя мощность равна отношению работы к этому промежутку времени:
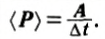
Из определения видно, что мощность численно равна работе, совершаемой в единицу времени. Таким образом, единицей мощности является джоуль в секунду 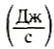 . Эта единица получила название ватт (Вт): 1 Вт = 1
. Эта единица получила название ватт (Вт): 1 Вт = 1 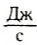 . Это название дано в честь английского ученого Джеймса Уатта — изобретателя универсального парового двигателя. Уаттом была впервые введена единица мощности, которая и до сих пор используется для характеристики мощности различных двигателей — 1 лошадиная сила (1 л. с. = 736 Вт).
. Это название дано в честь английского ученого Джеймса Уатта — изобретателя универсального парового двигателя. Уаттом была впервые введена единица мощности, которая и до сих пор используется для характеристики мощности различных двигателей — 1 лошадиная сила (1 л. с. = 736 Вт).
Понятно, что во времена Уатта на заре технической революции мощность построенной паровой машины было естественно сравнить с мощностью лошади — единственным в то время «двигателем».
Может ли человек развивать мощность, равную 1 л. с.? Ответ на этот вопрос положительный. Рассмотрим разбег спортсмена на короткие дистанции. Хорошие спортсмены дистанцию в 100 м пробегают за 10 с, т. е. их средняя скорость 10 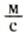 . Разбег длится 3 с, а работа A, которую совершают мышцы спортсмена, не может быть меньше, чем кинетическая энергия
. Разбег длится 3 с, а работа A, которую совершают мышцы спортсмена, не может быть меньше, чем кинетическая энергия 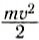 , приобретенная им за время разбега. Следовательно, средняя мощность не меньше, чем
, приобретенная им за время разбега. Следовательно, средняя мощность не меньше, чем
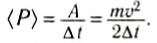
Если предположить, что масса спортсмена т = 80 кг, то
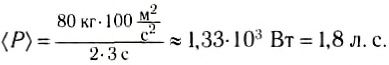
Разумеется, развивать такую мощность длительное время не сможет даже очень тренированный человек.Если известна мощность, то работа выражается равенством:
A = P∆t. (2)
Это позволяет ввести еще одну единицу работы (а значит, и энергии) следующим путем. За единицу работы можно принять работу, которая совершается некоторой силой в течение 1 с при мощности в 1 Вт. Она называется ватт-секундой. Понятно, что 1 Вт.c = 1 Дж. Часто используются более крупные внесистемные единицы работы и энергии: киловатт-час (кВт.ч) и мегаватт-час (МВт . ч):
1 кВт .ч= 1000кВт.3600 с = 3,6∙ 106 Дж;
1 МВт.ч= 1000кВт.3600 с = 3,6∙ 109 Дж.
При движении любого тела на него в общем случае действует несколько сил. Каждая сила совершает работу, и, следовательно, для каждой силы мы можем вычислить мощность.
Наиболее общее выражение для работы постоянной силы, направленной под углом 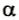 к направлению движения. А = F∆rcos
к направлению движения. А = F∆rcos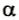 . Поэтому средняя мощность этой силы:
. Поэтому средняя мощность этой силы:
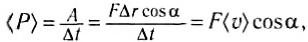 (3)
(3)
так как 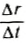 — модуль средней скорости тела.
— модуль средней скорости тела.
Ясно, что если модуль силы в некоторой момент времени равен F и модуль мгновенной скорости υ, а угол между ними 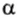 , то мгновенное значение мощности этой силы:
, то мгновенное значение мощности этой силы:
P = Fυcos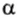 . (4)
. (4)
Как следует из формулы (4), при заданной мощности мотора сила тяги тем меньше, чем больше скорость движения автомобиля. Вот почему водители при подъеме в гору, когда нужна наибольшая сила тяги, переключают двигатель на пониженную передачу. Для движения по горизонтальному участку с постоянной скоростью достаточно, чтобы сила тяги преодолевала силу сопротивления движению. Формула (4) позволяет объяснить, что быстроходные поезда, автомобили, корабли, самолеты нуждаются в двигателях большой мощности и конструкции, обеспечивающей как можно меньшую силу сопротивления.
Любой двигатель или механическое устройство предназначены для выполнения определенной механической работы. Эта работа называется полезной работой. Для двигателя автомобиля — это работа по его перемещению, для токарного станка — работа по вытачиванию детали и т. п.
В любой машине, в любом двигателе полезная работа всегда меньше той энергии, которая затрачивается для приведения их в действие, потому что всегда существуют силы трения, работа которых приводит к нагреванию каких-либо частей устройства. А нагревание нельзя считать полезным результатом действия машины.
Поэтому каждое устройство характеризуется особой величиной, которая показывает, насколько эффективно используется подводимая к нему энергия. Эта величина называется коэффициентом полезного действия (КПД) и обычно обозначается греческой буквой η (эта).
Коэффициентом полезного действия называется отношение полезной )аботы, совершенной машиной за некоторый промежуток времени, ко всей утраченной работе (подведенной энергии) за тот же промежуток времени:
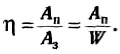 (5)
(5)
Коэффициент полезного действия обычно выражается в процентах, поскольку и полезную, и затраченную работы можно представить как произведение мощности на промежуток времени, в течение которого работала машина, то коэффициент полезного действия можно определить следующим образом:
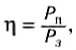
где Pn и Р3 — полезная мощность и затраченная мощность соответственно.
Главные выводы:
- Мощность численно равна работе, которую совершает сила в единицу времени.
- Мощность силы равна произведению силы на скорость тела и косинус угла между направлением силы и скорости в данный момент времени.
- Коэффициентом полезного действия называется отношение полезной работы, совершенной машиной за некоторый промежуток времени, ко всей затраченной работе (подведенной энергии) за тот же промежуток времени.
- Взаимодействие тел
- Механическая энергия и работа
- Золотое правило механики
- Потенциальная энергия
- Криволинейное движение
- Ускорение точки при ее движении по окружности
- Инерциальные системы отсчета
- Энергия в физике