Время и путь разгона автомобиля до
максимальной скорости являются самыми
распространенными и наглядными
характеристиками динамичности автомобиля.
Их определение производят графоаналитическим
способом с использованием графика
ускорений автомобиля. При проведении
расчетов полагаем, что разгон автомобиля
на каждой передаче производится до
достижения двигателем максимальных
оборотов.
Кривые ускорений автомобиля, начиная
с первой передачи, разбиваем на 3…4
интервала скоростей. Для каждого
интервала скоростей определяем среднее
ускорение и изменение скорости в пределах
интервала. Время разгона автомобиля в
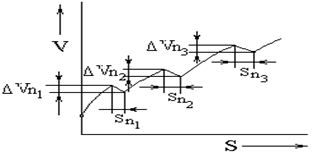
данном интервале скоростей определяется
по формуле-24
 ,
,
[с] (24)
где
![]()
– изменение скорости автомобиля в
интервале скоростей для которого
определяется время разгона, км/ч;
![]() =
=
![]()
![]()
– среднее ускорение в данном интервале
скоростей, м/с2;

При определении времени разгона
автомобиля учитывается и время на
переключение передач, которое определяется
по рекомендациям таблицы-10.
Таблица 10 – Время переключения передач
|
Тип |
Время |
|
|
Карбюраторные |
Дизельные |
|
|
Без |
1,3 |
1 |
|
С |
0,3 |
1 |
Выбираю время переключения передачи –
0,5 с.
Падение скорости автомобиля за время
переключения передач определяется по
формуле-25
 ,
,
км/ч (25)
где
![]()
– коэффициент учета вращающихся масс
при движении автомобиля накатом;
принимается![]() =1,05
=1,05
так как при накате
![]() =0
=0
(см. п.5.2.7);
![]()
– время переключения передачи, с; см.
табл.10;
Ψ – коэффициент сопротивления дороги,
соответствующий скорости движения
автомобиля при которой происходит
переключение передачи;

(cм. п.2.5 4)
Путь разгона автомобиля определяется
для тех же интервалов изменения скорости
автомобиля по формуле 26
 ,
,
м (26)
где
![]()
– средняя скорость движения в каждом
интервале скоростей, км/ч;
![]() =
=

Путь, проходимый автомобилем за время
переключения передач (движение накатом),
определяется по формуле-27
 ,
,
м (27)
Используя всю вышеприведенную информацию,
определяем время и путь разгона автомобиля
на горизонтальной дороге с асфальтобетонным
покрытием до максимальной скорости
![]() .
.
Все расчеты по данному подразделу сводим
в таблицу-11.
Таблица 10 – Расчет времени и пути разгона
проектируемого автомобиля до максимальной
скорости.
|
Номер |
Интервал |
Интервал |
ΔVi, |
jср |
Δt |
∑Δt |
Vср |
ΔS |
∑ΔSi, |
|
I |
2,6-5,2 |
1,17-1,26 |
2,6 |
1,22 |
0,592 |
0,592 |
3,9 |
0,641 |
0,641 |
|
5,2-7,8 |
1,26-1,29 |
2,6 |
1,28 |
0,564 |
1,156 |
6,5 |
1,018 |
1,659 |
|
|
7,8-10,3 |
1,29-1,26 |
2,5 |
1,28 |
0,543 |
1,699 |
9,05 |
1,365 |
3,024 |
|
|
10,3-13 |
1,26-1,17 |
2,7 |
1,22 |
0,615 |
2,314 |
11,65 |
1,990 |
5,014 |
|
|
13-15,5 |
1,17-1,02 |
2,5 |
1,10 |
0,631 |
2,945 |
14,25 |
2,498 |
7,512 |
|
|
Накат |
– |
– |
0,255 |
– |
0,5 |
3,445 |
– |
2,135 |
9,647 |
|
II |
15,2-19,5 |
1,02-1,22 |
4,3 |
1,12 |
1,066 |
4,511 |
17,35 |
5,138 |
14,785 |
|
19,5-24,3 |
1,22-1,13 |
4,8 |
1,18 |
1,130 |
5,641 |
21,9 |
6,874 |
21,659 |
|
|
24,3-29,2 |
1,13-0,98 |
4,9 |
1,06 |
1,284 |
6,925 |
26,75 |
9,541 |
31,2 |
|
|
Накат |
– |
– |
0,262 |
– |
0,5 |
7,425 |
– |
4,037 |
35,237 |
|
III |
28,9-34,8 |
0,98-0,83 |
5,9 |
0,91 |
1,801 |
9,226 |
31,85 |
15,934 |
51,171 |
|
34,8-43,5 |
0,83-0,75 |
8,7 |
0,79 |
3,059 |
12,285 |
39,15 |
33,267 |
84,438 |
|
|
43,5-52,2 |
0,75-0,66 |
8,7 |
0,71 |
3,404 |
15,689 |
47,85 |
45,245 |
129,683 |
|
|
Накат |
– |
– |
0,286 |
– |
0,5 |
16,189 |
– |
7,230 |
136,913 |
|
IV |
51,91-66 |
0,52-0,32 |
14,09 |
0,42 |
9,32 |
25,51 |
59 |
152,74 |
289,65 |
|
66-85 |
0,32-0, |
19 |
0,26 |
20,30 |
45,81 |
75,5 |
425,74 |
715,39 |
|
|
85-99 |
0, |
14 |
0,135 |
28,81 |
74,62 |
92 |
736,3 |
1451,69 |
По результатам расчетов строим графики
изменения времени и пути разгона
автомобиля до максимальной скорости.
Эти графики допускается строить в одних
координатных осях в соответствующих
масштабах. Переломы графиков в точках,
соответствующих моментам переключения
передач следует показывать условно,
так как в масштабах построения графиков,
эти падения скорости движения автомобиля
практически неуловимы.
Пример графиков времени и пути разгона
автомобиля до максимальной скорости
построенный в одних координатных осях
приведен на рисунке-7.

Рисунок 7 – График времени и пути разгона
проектируемого автомобиля до максимальной
скорости.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Расчет времени и пути разгона автомобиля



Время и путь разгона автомобиля до максимальной скорости являются самыми распространенными и наглядными характеристиками динамичности автомобиля. Их определение производят графоаналитическим способом с использованием графика ускорений автомобиля. При проведении расчетов полагаем, что разгон автомобиля на каждой передаче производится до достижения двигателем максимальных оборотов.
Кривые ускорений автомобиля, начиная с первой передачи, разбиваем на 3…4 интервала скоростей. Для каждого интервала скоростей определяем среднее ускорение и изменение скорости в пределах интервала. Время разгона автомобиля в данном интервале скоростей определяется по формуле 24
 ,[с] (24)
,[с] (24)
где  — изменение скорости автомобиля в интервале скоростей для которого определяется время разгона, км/ч;
— изменение скорости автомобиля в интервале скоростей для которого определяется время разгона, км/ч;
 =
= 
 — среднее ускорение в данном интервале скоростей, м/с 2 ;
— среднее ускорение в данном интервале скоростей, м/с 2 ;
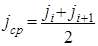
При определении времени разгона автомобиля учитывается и время на переключение передач, которое определяется по рекомендациям таблицы-10.
Таблица 10- Время переключения передач
Тип коробки передач
Время переключения передач, с
Выбираю время переключения передачи – 0,5 с.
Падение скорости автомобиля за время переключения передач определяется по формуле-25
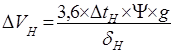 , км/ч (25)
, км/ч (25)
где  — коэффициент учета вращающихся масс при движении автомобиля накатом; принимается
— коэффициент учета вращающихся масс при движении автомобиля накатом; принимается  =1,05 так как при накате
=1,05 так как при накате  =0 (см. п. 5.2.7);
=0 (см. п. 5.2.7);
 — время переключения передачи, с; см. табл. 10;
— время переключения передачи, с; см. табл. 10;
Ψ – коэффициент сопротивления дороги, соответствующий скорости движения автомобиля при которой происходит переключение передачи;
 (cм. п. 2.5.4)
(cм. п. 2.5.4)
Путь разгона автомобиля определяется для тех же интервалов изменения скорости автомобиля по формуле 26
 , м (26)
, м (26)
где  — средняя скорость движения в каждом интервале скоростей, км/ч;
— средняя скорость движения в каждом интервале скоростей, км/ч;
 =
= 
Путь, проходимый автомобилем за время переключения передач (движение накатом), определяется по формуле-27
 , м (27)
, м (27)
Используя всю вышеприведенную информацию, определяем время и путь разгона автомобиля на горизонтальной дороге с асфальтобетонным покрытием до максимальной скорости  . Все расчеты по данному подразделу сводим в таблицу-10.
. Все расчеты по данному подразделу сводим в таблицу-10.
Таблица 10 – Расчет времени и пути разгона проектируемого автомобиля до максимальной скорости
| Номер передачи КПП | Интервал Vi, км/ч | Интервал j i, м/с 2 | ΔVi,км/ч | jср i, м/с 2 | Δt i, с | ∑Δt i, c | Vср i, км/ч | ΔS i, м | ∑ΔSi, м |
| 2,6-5,2 | 1,17-1,26 | 2,6 | 1,22 | 0,592 | 0,592 | 3,9 | 0,641 | 0,641 | |
| 5,2-7,8 | 1,26-1,29 | 2,6 | 1,28 | 0,564 | 1,156 | 6,5 | 1,018 | 1,659 | |
| 7,8-10,3 | 1,29-1,26 | 2,5 | 1,28 | 0,543 | 1,699 | 9,05 | 1,365 | 3,024 | |
| 10,3-13 | 1,26-1,17 | 2,7 | 1,22 | 0,615 | 2,314 | 11,65 | 1,990 | 5,014 | |
| 13-15,5 | 1,17-1,02 | 2,5 | 1,10 | 0,631 | 2,945 | 14,25 | 2,498 | 7,512 | |
| Накат | — | — | 0,255 | — | 0,5 | 3,445 | — | 2,135 | 9,647 |
| 15,2-19,5 | 1,02-1,22 | 4,3 | 1,12 | 1,066 | 4,511 | 17,35 | 5,138 | 14,785 | |
| 19,5-24,3 | 1,22-1,13 | 4,8 | 1,18 | 1,130 | 5,641 | 21,9 | 6,874 | 21,659 | |
| 24,3-29,2 | 1,13-0,98 | 4,9 | 1,06 | 1,284 | 6,925 | 26,75 | 9,541 | 31,2 | |
| Накат | — | — | 0,262 | — | 0,5 | 7,425 | — | 4,037 | 35,237 |
| 28,9-34,8 | 0,98-0,83 | 5,9 | 0,91 | 1,801 | 9,226 | 31,85 | 15,934 | 51,171 | |
| 34,8-43,5 | 0,83-0,75 | 8,7 | 0,79 | 3,059 | 12,285 | 39,15 | 33,267 | 84,438 | |
| 43,5-52,2 | 0,75-0,66 | 8,7 | 0,71 | 3,404 | 15,689 | 47,85 | 45,245 | 129,683 | |
| Накат | — | — | 0,286 | — | 0,5 | 16,189 | — | 7,230 | 136,913 |
| 51,91-66 | 0,52-0,32 | 14,09 | 0,42 | 9,32 | 25,51 | 59 | 152,74 | 289,65 | |
| 66-85 | 0,32-0,20 | 19 | 0,26 | 20,30 | 45,81 | 75,5 | 425,74 | 715,39 | |
| 85-99 | 0,20-0,07 | 14 | 0,135 | 28,81 | 74,62 | 92 | 736,3 | 1451,69 |
По результатам расчетов строим графики изменения времени и пути разгона автомобиля до максимальной скорости. Эти графики допускается строить в одних координатных осях в соответствующих масштабах. Переломы графиков в точках, соответствующих моментам переключения передач следует показывать условно, так как в масштабах построения графиков, эти падения скорости движения автомобиля практически неуловимы.
Пример графиков времени и пути разгона автомобиля до максимальной скорости построенный в одних координатных осях приведен на рисунке-7.
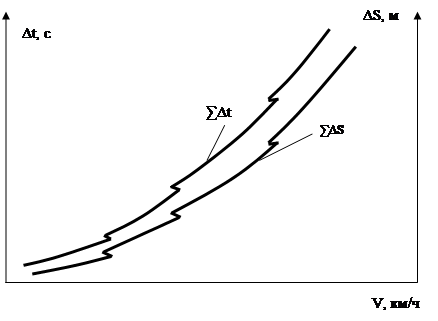
Рисунок 7 – График времени и пути разгона проектируемого автомобиля до максимальной скорости
Источник
Время разгона.
Основным фактором, который влияет на время разгона автомобиля, является мощность двигателя. Кроме этого, на разгон авто влияет огромное количество других факторов. Все зависит от уровня аэродинамики автомобиля, его веса, шин, подвески, установленной на авто типа коробки передач и прочего. Далее в деталях опишем каждый из факторов.
Силы, действующие на автомобиль при движении.

От чего зависит время разгона автомобиля.
1) Вес автомобиля. И так, чем автомобиль легче, тем легче ему разгонятся и проходить повороты. Производители спорткаров, которые предназначены для гонок по трекам, абсолютно всеми способами стараются уменьшить вес, при этом сохранив ему мощность.
3) На разгон автотранспорта влияют колёса. Производители устанавливают диски, изготовленные из легких сплавов. На колеса устанавливают низкопрофильные покрышки. Такие колеса весят немного. Больше информации о колесах можно узнать в интернете поэтому, останавливаться на их разновидностях не будем.
4) Аэродинамика автомобиля – один из наиболее актуальных вопросов в гонках. Существенное сопротивление воздуха на автомобиль оказывается при разгоне свыше 80 км/ч. Ненастроенная аэродинамика существенно увеличивает время разгона автомобиля.
7) Подвеска авто. Для быстрого старта и идеального прохождения поворотов, на спорткары устанавливают специальную спортивную жесткую подвеску.
8) Тип привода автомобиля. Именно от этого зависит разгон с места. При одинаковых мощностях двух автомобилей с задним и передним приводом, всегда выиграет первый.
Источник
Время и путь разгона автомобиля
При определении времени и пути разгона принимаются следующие допущения:
-разгон начинается с минимальной устойчивой скорости вращения коленчатого вала, а процесс трогания с места и разгон автомобиля до скорости, соответствующей низшей передаче коробки передач и минимальным оборотам коленчатого вала, ввиду сложности и малоизученности процессов, не рассматриваются;
-двигатель работает в режиме внешней скоростной характеристики.
Известно, что ускорение равно 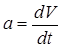 или
или 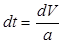 .
.
Используя численный метод, вправе записать
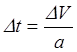 . (5.23)
. (5.23)
Если 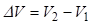 , что соответствует приращению скорости
, что соответствует приращению скорости 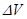 при разгоне от скорости V1 до V2, тогда
при разгоне от скорости V1 до V2, тогда 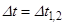 соответствует времени разгона от скорости V1 до V2.
соответствует времени разгона от скорости V1 до V2.
а – среднее ускорение в интервале скоростей V1 и V2.
а = 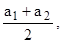
где а1, а2 – ускорение разгона при скоростях движения соответственно V1 и V2.
Из предыдущего следует, что Д = 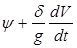 .
.
Отсюда 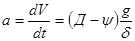 .
.
При скорости V1 имеем а1 = 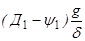 ,
,
при скорости V2 имеем а2 = 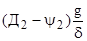 ,
,
где Д1, Д2 – динамические факторы автомобиля при скоростях соответственно V1 и V2;
y1, y2 – коэффициенты дорожного сопротивления при скоростях соответственно V1 и V2.
При движении на горизонтальной дороге имеем
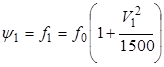 ,
, 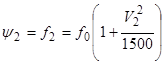 ..
..
После подстановки в уравнение (5.23) вышеприведенных зависимостей, время разгона от скорости V1 до V2 запишется
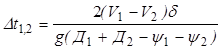 . (5.24)
. (5.24)
Суммарное время разгона на передаче находится суммированием времени в интервалах скоростей на этой передаче.
Чтобы время разгона было минимальным, переключение должно осуществляться при максимальном ускорении.
Потерю скорости при переключении передач находим, приняв, что при переключении передач двигатель отсоединен от трансмиссии. Если влиянием воздуха принебречь, тогда Д1= Д2=0. С достаточной для практических расчетов точностью можно принять, что y1=y2.
Что же касается времени переключения передач, то оно зависит от типа и конструкции привода переключения передач, субьективных особенностей водителя и находится в пределах (0,3…1,5)с. При расчетах принимается среднее значение времени переключения tn =0,8…1c.
После подстановки значений Д1= Д2=0; t1,2 = tn в формулу (5.24) определим падение скорости 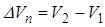 при переключении передачи
при переключении передачи
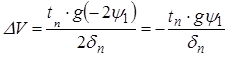 . (5.25)
. (5.25)
Знак «минус» указывает, что при переключении передач скорость уменьшается.
Заметим, что формула (5.25) получена с допущением, что влиянием соп-ротивления воздуха при переключении передач пренебрегаем, принимая Рв= 0.
Коэффициент дорожного сопротивления y1 соответствует скорости движения автомобиля начальный момент переключения.
Суммарное время разгона автомобиля равно
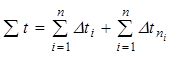 ,
,
где 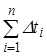 — суммарное время разгона на всех передачах;
— суммарное время разгона на всех передачах; 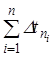 — суммарное время при переключении передач.
— суммарное время при переключении передач.
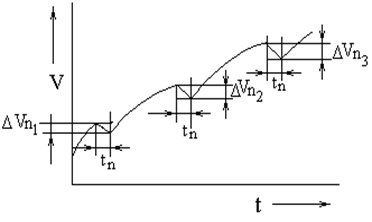 По результатам расчетов строится график времени разгона.
По результатам расчетов строится график времени разгона.
Заметим, что график времени разгона не начинается с нулевой скорости, поскольку нами принято допущение, что движение автомобиля начинается со скорости, соответствующей минимальным оборотам двигателя.
Рис.5.7 График времени разгона
Определение пути разгона производим после определения времени разгона.
Если учесть, что 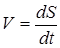 или dS = Vdt,
или dS = Vdt,
где DS – путь, проходимый автомобилем при разгоне от скорости V1 до V2;
Dt = Dt1,2 – время разгона от скорости V1 до V2, которое определяется по формуле (5.24);
За время переключения передачи, которое принимают одинаковым при каждом переключении tn =0,8…1c, автомобиль пройдет путь
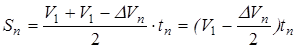 , (5.26)
, (5.26)
где V1— cкорость в начале переключения;
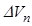 — падение скорости за время переключения передачи, которое
— падение скорости за время переключения передачи, которое
определяется по формуле (5.25) и берется по абсолютной величине.
Суммарный путь разгона автомобиля определяется так
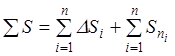 ,
,
где 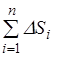 — суммарный путь разгона на всех передачах;
— суммарный путь разгона на всех передачах; 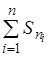 — суммарный путь, проходимый автомобилем, при переключении передач.
— суммарный путь, проходимый автомобилем, при переключении передач.
 По результатам расчетов строится график пути разгона.
По результатам расчетов строится график пути разгона.
Следует отметить, что график пути разгона аналогично графику времени разгона начинается со скорости, соответствующей минимальным оборотам двигателя, поскольку процесс трогания с места и разгон до скорости, соответствующей минимальным оборотам двигателя нами, согласно принятых допущений, не учитываются.
Рис.5.8 График пути разгона
1. Гришкевич А.И. Автомобили: Теория.- Минск : Вышэйш шк.,1986.-240 с., с.-27…54.
2. Литвинов А.С., Фаробин Я.Е. Автомобиль:Теория эксплуатационных свойств.-М.: Машиностроение, 1984.-272 с., с.-12-55.
3. Кошарний М.Ф. Основи механіки та енергетики автомобіля.-К.: Вища шк., 1992.-200 с., с. –92-112.
1. Перечислите силы сопротивления движению автомобиля.
2. Как влияет тип шины, опорная поверхность и скорость движения на величину силы сопротивления качению?
3. Из каких составляющих состоит аэтодинамическое сопротивление автомобиля?
4. Какие составляющие сопротивления воздуха учитывает коэффициент сопротивления воздуха?
5. Напишите уравнение тягового баланса автомобиля и объясните его составляющие.
6.Напишите уравнения мощностного баланса автомобиля и объясните его составляющие.
7.Что такое динамический фактор автомобиля и какой его физический смысл?
8.В чем отличие динамической характеристики автомобиля от динамического паспорта?
Источник
Определение ускорений, времени и пути разгона автомобиля
1.6.1 Определение ускорений
Для определения ускорения автомобиля используются расчетные данные динамической характеристики D и V.
Ускорение определяется из выражения:
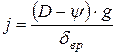 , м/с² (1.26)
, м/с² (1.26)
где ψ – коэффициент суммарного дорожного сопротивления, при
i =0,  ; (1.27)
; (1.27)
δ в p – коэффициент учета вращающихся масс:
 (1.28)
(1.28)
g – ускорение свободного падения;
ik – передаточное число КП на данной передаче.
На I передаче:  ;
;
На II передаче:  ;
;
На III передаче:  ;
;
На IV передаче:  ;
;
Для первой передачи:
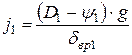 , м/с² (1.29)
, м/с² (1.29)
Для m – ной передачи:
 , м/с²
, м/с²
Определяем ускорение на первой передаче:
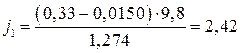

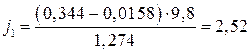
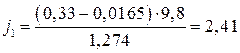
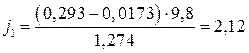
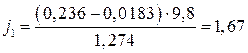
и т.д. для каждой передачи.
Ψ1 0,015 0,0153 0,0158 0,0165 0,0173 0,0183 V1,км/ч 9,6 21,3 32,9 44,7 56,4 67 j1,м/с 2 2,42 2,49 2,52 2,41 2,12 1,67
Продолжение таблицы 7
D2 0,256 0,262 0,264 0,251 0,217 0,168 Ψ2 0,0151 0,0156 0,0163 0,0174 0,0189 0,0206 V2,км/ч 12,3 27,3 42,4 57,4 72,4 86,1 J2 м/с 2 1,99 2,04 2,05 1,93 1,64 1,22 D3 0,237 0,242 0,244 0,229 0,196 0,149 Ψ3 0,0151 0,0157 0,0167 0,0178 0,0196 0,0214 V3,км/ч 13,2 29,5 45,7 61,9 78,1 92,8 J3 м/с 2 1,86 1,9 1,91 1,77 1,48 1,07
D4 0,154 0,152 0,145 0,124 0,087 0,038 Ψ4 0,0153 0,0165 0,0187 0,0217 0,0257 0,03 V4,км/ч 20,3 45,1 69,9 94,7 119,5 142,1 J4, м/с 2 1,24 1,21 1,13 0,91 0,55 0,07
1.6.2 Определение времени разгона автомобиля.
При проведении расчетов полагают, что разгон автомобиля на каждой передаче производится до достижения максимальных оборотов двигателя.
Для определения времени разгона кривые ускорения разбиваются на 3 интервала. В каждом интервале определяют:
 , м/с² (1.30)
, м/с² (1.30)
 , км/ч; (1.31)
, км/ч; (1.31)
время разгона автомобиля:
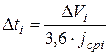 , с (1.32)
, с (1.32)
Время переключения передачи принимается Δtп = 0,3.
Падение скорости за время переключения передачи определяют по зависимости:
 , м/с (1.33)
, м/с (1.33)
 м/с
м/с
 м/с
м/с
 м/с
м/с
Расчет времени разгона на 1 и т.д. передачах производится с учетом уменьшения скорости за время переключения передач.
Для первой передачи:
 м/с 2
м/с 2
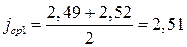 м/с 2
м/с 2
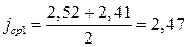 м/с 2
м/с 2
и т.д. для каждой передачи.
Для первой передачи:
 км/ч
км/ч
 км/ч
км/ч
 км/ч
км/ч
и т.д. для каждой передачи.
Для первой передачи:
 с
с
 с
с
 с
с
и т.д. для каждой передачи.
Результаты расчетов сводят в таблицу 8, и строят график разгона автомобиля. Время разгона при этом откладывается нарастающем итогом.
jсрi, м/с 2 2,46 2,51 2,47 2,02 2,05 1,99 1,95 1,97 7,84 1,23 1,17 1,02 Δti, с 1,32 1,28 1,33 2,06 2,05 2,09 2,32 2,28 2,45 5,6 5,9 6,75 ΔSi, м 7,5 9,64 14,3 11,3 19,8 28,9 13,7 23,8 36,6 50,8 94,2 154,3 Vсрi, км/ч 15,4 27,1 38,8 19,8 34,8 49,9 21,3 37.6 53,8 32,7 57,5 82,3
1.6.3 Определение пути разгона автомобиля.
Путь разгона определение в тех же интервалах изменения скорости:

 , м (1.34)
, м (1.34)
где V ср i – средняя скорость движения в каждом интервале:
 , км/ч (1.35)
, км/ч (1.35)
Определяем Δ S 1 для первой передачи:
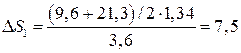 м
м
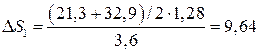 м
м
 м
м
и т.д. для каждой передачи.
Путь проходимый автомобилем за время переключения передач
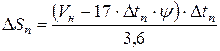 , м (1.36)
, м (1.36)
где V н – скорость в момент начала переключения передачи.
 м
м
 м
м
 м
м
Источник
Время на прочтение
3 мин
Количество просмотров 9.5K
Немного теории.
Для начала разберемся с тем, что такое лошадиные силы и устроим небольшой экскурс в школьную физику.
1 л.с. – это мощность, затрачиваемая при вертикальном подъёме груза массой 75 кг со скоростью 1 м/с.
Как известно, мощность показывает, какую работу совершает тело в единицу времени:
Работа равна произведению силы на перемещение: A = F*S. Учитывая, что скорость V=S/t, получим:
Получаем формулу для перевода лошадиных сил в принятую в международной системе СИ единицу измерения мощности – Ватт:
Перейдем к основной части, а именно – к техническим характеристикам автомобиля.
Некоторые характеристики и расчёты будут приводиться приближенно, поскольку мы не претендуем на умопомрачительную точность расчетов, важнее понять физику и математику процесса.
m = 2 тонны = 2000 кг – масса автомобиля (масса авто 1940 кг, считаем что в ней водитель массой 60 кг и больше ничего/никого).
P = 670 л.с. (по паспорту 625 л.с., но реально мощность выше – измерено на динамометрическом стенде в ролике DSC OFF https://www.youtube.com/watch?v=ysg0Depmyjc. В этой статье мы ещё обратимся к замерам отсюда.)
Разгон 0-100 км/ч: 3.2-3.3 с (по паспорту, замерам)
Разгон 100-200 км/ч: 7.5-7.6 с (по паспорту, замерам)
Мощность двигателя генерируется на маховике, потом через сцепление передается в КПП, далее через дифференциалы, привода, карданный вал передается на колёса. В результате эти механизмы поглощают часть мощности и итоговая мощность, поставляемая к колесам, оказывается меньше на 18-28%. Именно мощность на колесах определяет динамические характеристики автомобиля.
У меня нет сомнений в гениальности инженеров БМВ, но, для начала, возьмем для удобства потери мощности 20%.
Вернемся к нашим физическим баранам. Для вычисления разгона нам нужно связать мощность со скоростью и временем разгона. Для этого воспользуемся вторым законом Ньютона:
Вооружившись этими знаниями, получим конечную формулу:
Выражая отсюда t, получим итоговую формулу для вычисления разгона:
На самом деле в паспорте автомобиля указывается максимальная мощность, достигаемая двигателем при определенном числе оборотов. Ниже приведена зависимость мощности двигателя от числа оборотов (синяя линия). Строго говоря, параметры этой кривой зависят от номера передачи, так что для определенности скажем, что график для 5й передачи.

Главное, что мы должны усвоить из этого графика – мощность автомобиля не постоянна во время движения, а увеличивается по мере роста оборотов двигателя.
Перейдем к расчету разгона от 0 до 100 км/ч. Переведем скорость в м/с:
При разгоне от 0 до 100 км/ч автомобиль практически сразу переключается с первой передачи на вторую, и при достижении около 90 км/ч переключается на третью. Будем считать, что на всём протяжении разгона автомобиль разгоняется на второй передаче, причем максимальная мощность будет меньше 670 л.с., поскольку передача ниже пятой. Возьмём в качестве начальной мощности при 0 км/ч мощность 150 л.с. (при 2000 об/мин), конечную – 600 л.с. (7000 об/мин):

Чтобы не считать сложные интегралы для вычисления средней мощности, скажем следующие слова: учитывая приближенный характер наших расчетов, проскальзывание авто при ускорении, а также сопротивление воздуха (хотя при разгоне от 0 до 100 оно играет не такую большую роль, как при разгоне до 200 км/ч), будем считать, что мощность зависит от скорости линейно, тогда средняя мощность при разгоне от 0 до 100 км/ч составляет:
Пришло время учесть потери мощности, о которых было сказано ранее, а заодно перевести мощность в кВт (1 кВт = 1000 Вт) для удобства. Потери мощности 20%, значит эффективность 80%=0.8:
Теперь подставляем всё в конечную формулу:
Получили довольно близкий к “паспортным” 3.3 с результат, ура! Специально не стал ничего дополнительно подгонять, дабы подчеркнуть приближенный характер расчёта, хотя это было довольно просто сделать, взяв, например, чуть больше мощность.
Теперь, ради интереса и проверки самих себя, вычислим разгон 100-200 км/ч.
С ростом скорости растёт трение воздуха, для движения используются более высокие передачи КПП (3-я, 4-я, 5-я), но при этом уменьшается проскальзывание колес. Так что оставим среднюю мощность 375 л.с.
Так делать конечно же нельзя! После 2-й передачи двигатель работает на “комфортных” для себя оборотах 4000-7000 об/мин, поэтому средняя мощность будет гораздо выше, поскольку выше будет начальная мощность для каждой передачи. Здесь уже не получится считать, что автомобиль едет только на 4-й передаче на всем протяжении разгона, но можно считать, что он проехал одинаковые промежутки времени на 3-й, 4-й и 5-й передаче, и пусть график зависимости мощности от числа оборотов для них одинаков, поэтому построим общую условную кривую зависимости мощности от скорости:

Опять же, считаем для простоты зависимость мощности от скорости линейной, тогда получаем среднюю и реальную мощность:
Тогда итоговое время разгона 100-200 км/ч:
Время разгона “по паспорту” 7.6 с. И снова мы оказались близко к истине!
P.S. не хочу объяснять, откуда взялось (V^2 – V_0^2), можете повыводить на досуге 🙂
Ну и в общем-то всё. Приведенные рассуждения и вычисления не претендуют на истину в последней инстанции и большую точность, но показывают, что зная “школьные” формулы по физике, можно решать такие интересные задачки, связанные с жизнью.
На написание данной статьи меня подтолкнуло следующее видео:
Используемые в нём расчёты основаны на школьном курсе физики.
Начнём с того, что время t разгона до заданной скорости v (например, до 100 км/ч) определяется по формуле
t = v/a, (1)
где
a — ускорение.
Вообще говоря, в силу разных причин ускорение меняется по мере разгона, но мы можем оценить его максимальную величину a_max, тем самым найдя минимально возможное время разгона t_min.
Согласно второму закону Ньютона ускорение a любого тела прямо пропорционально приложенной к телу силе F и обратно пропорционально его массе m:
a = F/m. (2)
Как известно, на ровной дороге автомобиль ускоряется за счёт силы трения между шинами и поверхностью дороги. Максимальная величина силы трения F_max определяется по формуле
F_max = μ∙N, (3)
где
μ — коэффициент трения покоя (для большинства летних гражданских шин μ ≈ 1);
N — нормальная сила давления.
Заметим, что при пробуксовке ведущих колёс коэффициент трения покоя меняется на коэффициент трения скольжения, который приблизительно вдвое меньше. Поэтому при пробуксовке тяга, а в след за ней и ускорение, падают не менее чем вдвое.
Таким образом, зная силу N, приходящуюся на ведущие колёса автомобиля, можно определить максимальную тягу, создаваемую шинами, а уже по ней найти ускорение и время разгона.
1 ПОЛНОПРИВОДНЫЕ АВТОМОБИЛИ
Для полноприводных автомобилей эта сила N равна весу P автомобиля:
N = P = m∙g, (4)
где
m — масса автомобиля, кг;
g — ускорение свободного падения (9.81 м/с²).
Если подставить (2), (3) и (4) в (1), то получится
t_min = v/(μ∙g), (5)
что для v = 100 км/ч = 27.78 м/c даёт
t_min ≈ 27.78/9.81 = 2.83 с
2 МОНОПРИВОДНЫЕ АВТОМОБИЛИ
С моноприводными автомобилями ситуация иная. У них за счёт продольного переноса веса во время разгона сила N будет определяться по формуле
N = δ∙P ± m∙a∙H/B = m∙(δ∙g ± a∙H/B), (6)
где
δ — статическая доля веса автомобиля, приходящаяся на ведущую ось;
a — ускорение (2), с которым разгоняется автомобиль, м/с²;
H — высота центра тяжести автомобиля, мм;
B — колёсная база, мм.
При этом в случае заднеприводных автомобилей в формуле (6) используется знак “+”, а в случае переднеприводных — знак “−”.
Если подставить (3) и (6) в (2), то получится
a_max = μ∙(δ∙g ± a_max∙H/B),
откуда находим максимально возможное ускорение автомобиля:
a_max = δ∙μ∙g/(1 −+ μ∙H/B). (7)
Осталось подставить (7) в (1):
t_min = (1 −+ μ∙H/B)∙v/(δ∙μ∙g). (8)
В формулах (7) и (8) знак “−” уже используется для заднеприводных автомобилей, а знак “+” — для переднеприводных.
Из выражения (8) видно, что при равномерной загрузке осей заднеприводный автомобиль потенциально будет разгоняться быстрее переднеприводного.
Пример
Оценим минимально возможное время разгона а/м Lada Granta. Для этого автомобиля известно, что статическая развесовка составляет 60/40, а база равна 2476 мм. В качестве высоты центра тяжести примем ⅓ от полной высоты автомобиля, т.е. 500 мм. Тогда по формуле (8) получаем
t_min ≈ (1 + 500/2476)∙27.78/(0.6∙9.81) = 5.67 с
Видно, что по сравнению с полноприводным автомобилем это время оказалось вдвое дольше.
Теперь занизим центр тяжести нашей Гранты на 100 мм:
t_min ≈ (1 + 400/2476)∙27.78/(0.6∙9.81) = 5.48 с
С помощью такого занижения время разгона удалось сократить всего на 0.2 с
Посмотрим, что будет, если мы поставим гоночные шины с коэффициентом трения μ = 1.2:
t_min = (1 + 1.2∙400/2476)∙27.78/(0.6∙1.2∙9.81) = 4.70 с
Разница с исходным вариантом составляет уже почти 1 с, т.е. такая модификация сильнее влияет на сокращение времени разгона.
P.S. Дополнение по просьбе RomanSmirnov
Найдём оценку минимальной мощности, выдаваемой двигателем, при которой рассчитанное время разгона становится достижимым.
Кинетическая энергия T автомобиля (как и любого другого тела) определяется по формуле
T = m∙v²/2. (9)
Тогда мощность с колёс во время разгона не должна быть меньше:
W_min ≥ T/t_min. (10)
Здесь мы пренебрегли силами сопротивления качения и сопротивления воздуха.
Для рассмотренной выше Гранты со снаряженной массой 1160 кг на штатных шинах получается
W_min ≥ 1160∙27.78²/(2∙5.48) = 81.7 кВт = 110 л.с.
Обычно потери в трансмиссии составляют около 25%, что даёт оценку на минимальную мощность двигателя почти 140 л.с. К этому надо добавить мощность сил сопротивления, которые можно оценить в 10% от рассчитанной минимальной мощности с колёс.
Таким образом, если во время разгона мощность с колёс не будет падать ниже 120 л.с. (а мощность двигателя не будет падать ниже 150 л.с.), то минимально возможное время разгона становится достижимым.
Обычно во время разгона обороты двигателя не опускаются ниже 3000 об/мин. При таких оборотах мощность мотора составляет приблизительно половину от максимальной. Следовательно, минимально возможное время разгона можно ожидать на Гранте с двигателем не менее 300 л.с.
P.P.S. Дополнение, касающееся минимально возможного времени заезда на четверть мили
При равноускоренном движении пройденный путь S вычисляется по формуле
S = a∙t²/2,
откуда легко выражается время
t = √[2S/a]. (11)
По этой формуле для полноприводного автомобиля получается
t ≈ √[2∙402/9.81] = 9.05 c,
а для Гранты на штатных шинах —
t ≈ √[2∙402∙(1 + 500/2476)/(0.6∙9.81)] = 12.81 c.
____________________________________________________
Радиус качения шины, скорость и КПП
Степень сжатия, бензин и избыточное давление
Оценка влияния R/S на работу мотора
Турбулизаторы или вихревые генераторы
Расчёт минимально возможного времени разгона
Фаза впрыска
Почему нельзя крутить мотор на заводских прошивках?
Оптимальные формы каналов ГБЦ. Часть 1
Оптимальные формы каналов ГБЦ. Часть 2
Влияние перекрытия распредвалов на ВСХ мотора
Влияние состава смеси на мощность мотора
Влияние угла опережения зажигания на мощность мотора
Расчёт ряда КПП

reshalka.com
ГДЗ Физика 7-9 классы сборник вопросов и задач к учебнику Перышкина автор Марон. Прямолинейное равноускоренное движение. Ускорение. Перемещение при прямолинейном равноускоренном движении. Номер №1460
Решение 1
С каким ускорением движется Автомобиль “Ока”, если его скорость увеличивается от 0 до 100 км/ч за 30 с ? Какой путь пройдет автомобиль за время разгона?
Дано:
t = 30 c;
v
0
=
0
м/с;
v = 100 км/ч.
Найти:
a − ?
S − ?
СИ:
v = 27,8 м/с.
Решение:
Уравнение скорости:
v
=
v
0
+
a
t
;
a
=
v
–
v
0
t
;
a
=
27
,
8
−
0
30
=
0
,
93
м
/
с
2
;
S
=
a
t
2
2
;
S
=
0
,
93
∗
30
2
2
=
418
,
5
м.
Ответ: 0,93
м
/
с
2
; 418,5 м.
Решение 2
Гоночный автомобиль движется 3,4 с равноускоренно из состояния покоя. Скорость после разгона составила 100 км/ч. Найдите ускорение и пройденный путь.
Дано:
t = 3,4 c;
v
0
=
0
м/с;
v = 100 км/ч.
Найти:
a − ?
S − ?
СИ:
v = 27,8 м/с.
Решение:
Уравнение скорости:
v
=
v
0
+
a
t
;
a
=
v
–
v
0
t
;
a
=
27
,
8
−
0
3
,
4
=
8
,
2
м
/
с
2
;
S
=
a
t
2
2
;
S
=
8
,
2
∗
3
,
4
2
2
=
47
,
4
м.
Ответ: 8,2
м
/
с
2
; 47,4 м.
Решение 3
С каким ускорением движется Автомобиль ВАЗ, если его скорость увеличивается от 0 до 100 км/ч за 19 с ? Какой путь пройдет автомобиль за время разгона?
Дано:
t = 19 c;
v
0
=
0
м/с;
v = 100 км/ч.
Найти:
a − ?
S − ?
СИ:
v = 27,8 м/с.
Решение:
Уравнение скорости:
v
=
v
0
+
a
t
;
a
=
v
–
v
0
t
;
a
=
27
,
8
−
0
19
=
1
,
46
м
/
с
2
;
S
=
a
t
2
2
;
S
=
1
,
46
∗
19
2
2
=
269
м.
Ответ: 1,46
м
/
с
2
; 269 м.
Решение 4
Гепард за 2 с развивает скорость до 72 км/ч. Найдите ускорение и пройденный за это время путь.
Дано:
t = 2 c;
v
0
=
0
м/с;
v = 72 км/ч.
Найти:
a − ?
S − ?
СИ:
v = 20 м/с.
Решение:
Уравнение скорости:
v
=
v
0
+
a
t
;
a
=
v
–
v
0
t
;
a
=
20
−
0
2
=
10
м
/
с
2
;
S
=
a
t
2
2
;
S
=
10
∗
2
2
2
=
20
м.
Ответ: 10
м
/
с
2
; 20 м.
Решение 5
Конькобежец − спринтер дистанцию 50 м пробегает за 8,5 с. С каким ускорением двигался спортсмен? Какая установилась скорость после разгона?
Дано:
t = 8,5 c;
S = 50 м;
v
0
=
0
м/с.
Найти:
a − ?
v − ?
Решение:
Уравнение движения:
S
=
v
0
t
+
a
t
2
2
;
Так как спорстмен начинает движение, то
v
0
=
0
м/с.
S
=
a
t
2
2
;
2
S
=
a
t
2
;
a
=
2
S
t
2
;
a
=
2
∗
50
8
,
5
2
=
1
,
38
м
/
с
2
;
v = at;
v = 1,38 * 8,5 = 11,73 м/с.
Ответ: 1,38
м
/
с
2
; 11,73 м/с.
Решение 6
Легкоатлет− спринтер на дистанции 40 м разогнался до 39,6 км/ч. Найдите время его разгона и ускорение.
Дано:
S = 40 м.
v = 39,6 км/ч;
v
0
=
0
м/с.
Найти:
a − ?
t − ?
СИ:
v = 11 м/с.
Решение:
S
=
v
0
+
v
2
∗
t
;
2
S
=
(
v
0
+
v
)
∗
t
;
t
=
2
S
v
0
+
v
;
t
=
2
∗
40
0
+
11
=
7
,
3
с;
v
=
v
0
+
a
t
;
Так как
v
0
=
0
м/с, то v = at;
a
=
v
t
;
a
=
11
7
,
3
=
1
,
5
м
/
с
2
.
Ответ: 1,5
м
/
с
2
; 7,3 с.
Решение 7
Велосипедист за 15 с проехал путь 200 м. Найдите ускорение и скорость после разгона.
Дано:
t = 15 c;
S = 200 м;
v
0
=
0
м/с.
Найти:
a − ?
v − ?
Решение:
Уравнение движения:
S
=
v
0
t
+
a
t
2
2
;
Так как велосипедист начинает движение, то
v
0
=
0
м/с.
S
=
a
t
2
2
;
2
S
=
a
t
2
;
a
=
2
S
t
2
;
a
=
2
∗
200
15
2
=
1
,
78
м
/
с
2
;
v = at;
v = 1,78 * 15 = 26,7 м/с.
Ответ: 1,78
м
/
с
2
; 26,7 м/с.
Решение анализ
Среди 3−х автомобилей с наибольшим ускорением двигался гоночный автомобиль, затем автомобиль Ваз. Наименьшее ускорение имеет автомобиль “Ока”, т.к. ему нужно больше времени для разгона до 100 км/ч.
Среди 3−х спортсменом с наибольшим ускорением двигался велосипедист, затем легкоатлет−спринтер. Наименьшее ускорение имеет конькобежец − спринтер.
Ускорение гепарда выше ускорения автомобилей и спортсменов.



