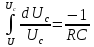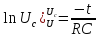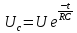Как найти время разряда конденсатора

Конденсаторы часто применяются в электрических схемах, помогая трансформировать электросигнал под определенные характеристики. Используя их основное свойство — накапливать электрический заряд, можно регулировать прохождение тока по цепи, убирать нежелательные пульсации напряжения или повысить энергоэффективность сети. При решении подобных задач в расчет берутся конкретные параметры того или иного электронакопителя, а также общие процессы, связанные с зарядом и разрядом конденсаторов.

• Заряд конденсатора
• Процессы зарядки и разрядки конденсаторов
• Емкость и энергия конденсатора
• Как зарядить конденсатор
• Время, необходимое для зарядки конденсатора
• Заряд конденсатора: формула
• Время разряда конденсатора

Заряд конденсатора

Устройство обычного конденсатора состоит из двух пластин (обкладок), подключаемых к выходам цепи, и диэлектрика между ними. При этом величина заряда, накаливаемого конденсатором, зависит от его емкостной характеристики основных параметров: площади обкладок, толщины и диэлектрических свойств прокладочного материала.

Емкость конденсатора определяется по формуле:

C = S • ε • ε0 / d,

где S – площадь обкладок, ε — диэлектрическая проницаемость прокладки, ε0 — диэлектрическая постоянная (8,85•10-12 Ф/м), d – расстояние между пластинами.

Конденсируемый же заряд равняется произведению емкости конденсатора на напряжение в цепи: q = С × U.

Процессы зарядки и разрядки конденсаторов

При включении конденсатора в цепь через него начинает проходить ток. С движением электронов по проводнику на одной обкладке устройства скапливается отрицательный заряд, а на другой (при недостатке электронов) — положительный. Между пластинами образуется индуктивное поле, создающее разность потенциалов определенного значения. В проводниках постоянного тока накопление заряда идет до тех пор, пока уровень напряжения на обкладках не сравняется с номинальным напряжением элемента питания, после чего течение электротока останавливается.

Когда цепь размыкается и на конденсатор не подается напряжение, он может сохранять заряд на протяжение определенного времени, а затем с исчезновением электрического поля между пластинами заряд начнет перетекать в проводник. Процесс разряда конденсатора характеризуется переходом электронов с одной обкладки на другую. Конденсатор разряжается полностью, когда количество свободных электронов на обеих пластинах сравнивается. При этом все электродинамические процессы в цепи прекращаются.

Емкость и энергия конденсатора

Конденсатор, как и всякий объект, получающий электрический заряд, обладает энергией. Для его зарядки требуется определенная работа, которая идет на разделение заряженных частиц — именно она считается энергией конденсаторного устройства. Ее можно увидеть, если заряженный конденсатор присоединить, например, к светодиоду. Накопитель отдаст заряд лампочке, и она на некоторое время загорится, тем самым энергия перейдет в свет и тепло.

Для определения энергии конденсатора в расчет берут количество заряда, толщину диэлектрика и напряженность электрического поля. Последняя является векторной величиной и представляет собой силу, действующую на точечный заряд.

Поскольку заряды на обкладках равны между собой по модулю, во внимание принимается только значение напряженности одной из них, а значит, эта величина делится пополам — Е/2. Общая же энергия определяется по формуле:

Wp = qEd/2.

Произведение напряженности на расстояние между пластинами само себе представляет разность потенциалов или напряжение — U = E × d. Таким образом, энергию можно выразить через заряд и напряжение на конденсаторе. Формула будет иметь следующий вид:

Wp = qU/2.

Учитывая, что заряд и напряжение находятся в зависимости от емкости конденсатора, можно вывести еще пару формул энергии:

 Wp = q2/2C

 Wp = CU2/2

Как зарядить конденсатор

Для зарядки конденсатора требуется генератор электротока. Возникающие при этом процессы удобнее разобрать на примере простой цепи, включающей в себя конденсатор (С) и резистор (R).

Зарядка конденсатора от источника постоянной ЭДС

В соответствии с законом Ома разность потенциалов, возникающая на резисторе и конденсаторе, суммарно равна электродвижущей силе генератора тока. Математически это можно представить следующими формулами:

UC = q/C – напряжение конденсатора;

UR = IR – напряжение резистора;

ε = UC + UR – ЭДС источника.

Для пояснения зарядного процесса определим равенство

IR = ε – q / C.

Эта формула представляет динамические изменения заряда силы тока. Более конкретно это может быть выражено уравнением:

I = dq / dt.

Изменение заряда во времени можно подставить к сопротивлению. Соответственно, получаем

R • dq / dt = ε – q / C.

В строгом смысле это уравнение предписывает бесконечное время зарядки конденсаторного устройства. Однако этим можно пренебречь, если учесть, что заряд фактически дискретен и может быть подвержен случайным изменением и флуктуациям. Таким образом, в данном выражении имеются в виду усредненная динамика зарядного процесса. На его основании можно записать изменение ЭДС и составляющих напряжений обоих элементов цепи:

dε = d(IR) + d(q/C).

Фактически ЭДС генератора не меняется во времени, а значит, dε = 0, а емкость конденсатора и сопротивление обладают постоянными значениями, поэтому их можно обозначить без d:

R • dI = — 1/C • dq.

Поделив данное уравнение на временной период, за который заряжается конденсатор, можно вывести выражение, учитывающее корреляцию между динамикой заряда и силой тока:

dI / dt = –I/RC.

Это уравнение означает отношение скорости, с которой уменьшается сила тока к ее фактическому значению.

В начале процесса заряда конденсатора значение q равняется нулю. В этот момент при наибольшей разнице напряжений источника питания и электронакопителя сила тока имеет максимальное значение. По мере увеличения заряда значение I постепенно падает. Когда конденсатор заряжается полностью, его напряжение сравнивается с ЭДС генератора, а сила тока принимает значение 0. Соответственно, электродинамический процесс прекращается.

Дополнительно можно рассмотреть, как в процессе зарядки трансформируется энергия. Вполне очевидно, что генератор тока является причиной возникновения электротока в цепи и, следовательно, заряда электронакопителя.

В этом усматривается некое противоречие: когда конденсатор получает от генератора тока заряд q, это значит, что ЭДС выполнила работу равную заряду (А = qe), однако энергия самого накопителя определяется по формуле W = q2 / 2C = qε / 2, что составляет только половину от работы, произведенной источником питания. Этот парадокс объясняется самим фактом прохождения тока по электроцепи, которое сопровождается выделением тепловой энергии на резисторе, то есть определенное количество энергопотери приходится на тепло.

Дифференциальные расчеты для малых отрезков времени процесса зарядки показывают, что энергия от генератора, действительно, разделяется на электрическую, идущую на заряд конденсаторного устройства, и тепловую. При этом сопротивление цепи само по себе никак не влияет на количество выделяемой теплоты, которое равняется энергии конденсатора.

Заряд конденсатора, ток

При подключении конденсатора к источнику тока в начале зарядки заряд на пластинах практически отсутствует. Максимальное значение I в этой ситуации объясняется минимальным сопротивлением. С увеличением заряженных частиц, возрастает сопротивление индуктивного поля, которое препятствует прохождению тока по проводнику.

Период времени, за начальную точку которого берут момент наибольшей силы тока, а за конечную полное прекращение движения заряженных частиц, носит название переходного периода зарядки конденсатора.

Начальный момент зарядки конденсатора характеризуется нулевым напряжением между его пластинами. Показатель U начинает возрастать с появлением на обкладках разноименно заряженных частиц. Большая сила тока в начале процесса обусловливает большую скорость увеличения напряжения. По мере ее падения рост напряжения замедляется, достигнув максимального значения при полной зарядке электронакопителя.

График увеличения напряжения имеет вид параболы, будучи противоположным графику снижения силы тока.

Математически динамическую взаимозависимость тока, напряжения и емкости конденсатора можно выразить следующим образом:

I = С • dV / dt.

Время, необходимое для зарядки конденсатора

Время зарядки конденсатора определяется его емкостью, электродвижущей силой генератора тока, напряжением и сопротивлением в цепи.

Заряд конденсатора описывается как экспоненциальный процесс. Чтобы оценить его время, принимается, что значение заряда увеличивается равномерно, при этом скорость заряда приравнивается к силе тока в начале процесса. Отсюда следует уравнение постоянной времени:

τ = q / I0 = RC.

Зависимость динамики напряжения от длительности зарядки определяется по следующей формуле:

U(t) = UC • (1 – e-t/τ).

Значение высчитывается с привлечением основания натурального логарифма (е), которое относится к функции экспоненты и равняется приблизительно 2,718. При этом UC обозначает напряжение ЭДС источника.

Процент заряда по постоянной времени τ определяется в соответствии с формулой:

(1 — 1/еτ) • 100%.

Таким образом, конденсатор достигает почти полной зарядки за 5 τ.

• 1 τ — 63,2%;

• 2 τ — 86,5%

• 3 τ — 95,1%

• 4 τ — 98,2%

• 5 τ — 99,3%

Учитывая экспоненциальный характер увеличения напряжения конденсатора, можно сказать, что время его зарядки до уровня ЭДС генератора длится бесконечно долго.

Заряд конденсатора: формула

Конденсатор заряжается довольно быстро. Обычно для этого достаточно нескольких миллисекунд. Равенство напряжения электродвижущей силы источника питания и электронакопителя определяет максимальный заряд конденсатора. Формула заряда может быть определена с учетом общих параметров конденсатора:

q = Uεε0S/d.

Также можно принять во внимание конструкционные особенности конденсатора. Так, для цилиндрического накопителя заряд равняется:

q = U2πεε0l/ln(r2/r1),

где l – высота цилиндров, r2 – радиус наружной пластины, r1 — радиус внутренней пластины.

Время разряда конденсатора

Если конденсатор переключить на нагрузку резистора, он сам станет источником питания и будет отдавать заряд в цепь. Движение тока при этом начинается от пластины с отрицательным зарядом на положительно заряженную пластину и далее по контуру. Напряжение в начальный момент будет такое же как и после полной зарядки накопителя. В соответствии с законом Ома можно определить и первоначальную силу тока:

IC = UC / R.

Отдавая заряд, конденсатор будет терять напряжение. Соответственно будет уменьшаться и сила тока. Снижение обоих показателей идет по экспоненциальной кривой с замедлением скорости падения. Это значит, что динамику разрядки конденсатора можно описать, как и в случае зарядки, при помощи постоянной времени τ.

Изменение основных электрических показателей при заряде и разряде конденсатора играют ключевую роль в электротехнике и радиоэлектронике. Эта функциональность в полной мере проявляется в цепях переменного тока, где оба процесса сменяют друг друга с определенной периодичностью. На частотно-зависимых качествах электронакопителей основан принцип действия таких электроустановок, как колебательные контуры, реле времени, цепи обратной связи, частотные фильтры и другие.

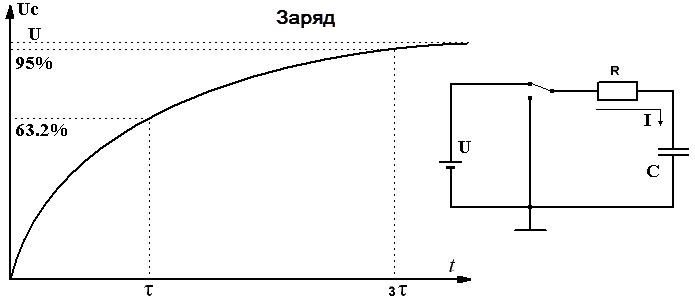
Электрическая цепь RC

Рассмотрим ток в электрической цепи, состоящей из конденсатора ёмкостью C и резистора сопротивлением R, соединённых параллельно.
Значение тока заряда или разряда конденсатора определится выражением I = C(dU/dt), а значение тока в резисторе,
согласно закону Ома, составит U/R, где U – напряжение заряда конденсатора.

Из рисунка видно, что электрический ток I в элементах C и R цепи будет иметь одинаковое значение и
противоположное направление, согласно закону Кирхгофа. Следовательно, его можно выразить следующим образом:

Решаем дифференциальное уравнение C(dU/dt)= -U/R

Интегрируем:

Из таблицы интегралов здесь используем преобразование

Получаем общий интеграл уравнения: ln|U| = – t/RC + Const.
Выразим из него напряжение U потенцированием: U = e^-t/RC * e^Const.
Решение примет вид:

U = e^-t/RC * Const.

Здесь Const – константа, величина, определяемая начальными условиями.

Следовательно, напряжение U заряда или разряда конденсатора будет меняться во времени по экспоненциальному закону
e^-t/RC.

Экспонента – функция exp(x) = e^x
e – Математическая константа, приблизительно равная 2.718281828…

---

Постоянная времени τ

Если конденсатор емкостью C последовательно с резистором сопротивлением R подключить к источнику постоянного напряжения U,
в цепи пойдёт ток, который за любое время t зарядит конденсатор до значения U_C и определится выражением:

Тогда напряжение U_C на выводах конденсатора будет увеличиваться от нуля до значения U по экспоненте:

U_C = U(1 – e^-t/RC)

При t = RC, напряжение на конденсаторе составит U_C = U(1 – e^-1) = U(1 – 1/e) .
Время, численно равное произведению RC, называется постоянной времени цепи RC и обозначается греческой буквой τ.

Постоянная времени τ = RC

За время τ конденсатор зарядится до (1 – 1/e)*100% ≈ 63,2% значения U.
За время 3τ напряжение составит (1 – 1/e³)*100% ≈ 95% значения U.
За время 5τ напряжение возрастёт до (1 – 1/e⁵)*100% ≈ 99% значения U.

---

Если к конденсатору емкостью C, заряженному до напряжения U, параллельно подключить резистор сопротивлением R,
тогда в цепи пойдёт ток разряда конденсатора.

Напряжение на конденсаторе при разряде будет составлять U_C = Ue^-t/τ = U/e^t/τ.

За время τ напряжение на конденсаторе уменьшится до значения U/e, что составит 1/e*100% ≈ 36.8% значения U.

За время 3τ конденсатор разрядится до (1/e³)*100% ≈ 5% от значения U.
За время 5τ до (1/e⁵)*100% ≈ 1% значения U.

Параметр τ широко применяется при расчётах RC-фильтров различных электронных цепей и узлов.

---

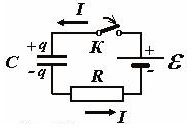
При
замыкании выключателя К в положение 2,
заряженный конденсатор С, обладающий
энергией W
= CU²/2,
начинает разряжаться, т.е. в цепи
появляется разрядный ток.

Согласно
закону Ома мгновенное значение силы
тока через сопротивление при разрядке
конденсатора равно i=U_c/R.

Поскольку
заряд конденсатора при разрядке
уменьшается с течением времени, то i
= –dq/dt.

Так
как dq
= CdU_c,
то получим i
= –CdU_c/dt.
Отсюда dU_c/U_c
= –dt/RC.

Интегрируя
полученное выражение с учетом того, что
при t=0,
U_c
= U,
имеем:

Следовательно,
напряжение на конденсаторе при его
разрядке уменьшается по экспоненциальному
закону, а разрядный ток определяется
по закону

(4)

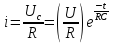
На
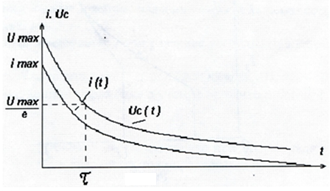
рис. 3 представлены графики зависимости
U_c(t)
и i(t)
при разрядке конденсатора.

Рис.
3

В
начальный момент времени разрядный ток
имеет максимальное значение i_max=U/R.
За время τ=RC
разрядный ток уменьшается в e
раз. Энергия, сосредоточенная в
электрическом поле заряженного
конденсатора, выделяется в виде тепла
на сопротивлении R.
Рассмотренные переходные процессы
используются в радиотехнике, для
измерения малых промежутков времени,
для получения мощных электрических
разрядов, в релаксационных генераторах
(генераторах пилообразного напряжения).

Итак,
в переходных процессах, происходящих
при заряде и разряде конденсатора, ток
и напряжение на конденсаторе с течением
времени изменяется по экспоненциальному
закону ().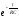

Произведение
RС
имеет
размерность времени
и
называется постоянной времени или
временем релаксации τ =RC.
За
время τ заряд конденсатора уменьшается
в e
раз.

Для
определения RС
часто
удобно измерять время, за которое
величина заряда или напряжения падает
до половины первоначального значения,
так называемое “половинное время”
t_1/2.
“Половинное
время” определяется из выражения

,

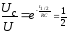
Взяв
натуральный логарифм от обеих частей
уравнения, получаем
,
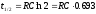
или

₍₅₎

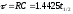
Способ
измерения постоянной времени состоит
в определении t_1/2
и
умножении полученной величины на 1,44.
Так как экспонента асимптотически
приближается к оси абсцисс, то точно
установить окончание процесса разряда
конденсатора (так же как и процесса
заряда) не представляется возможным.
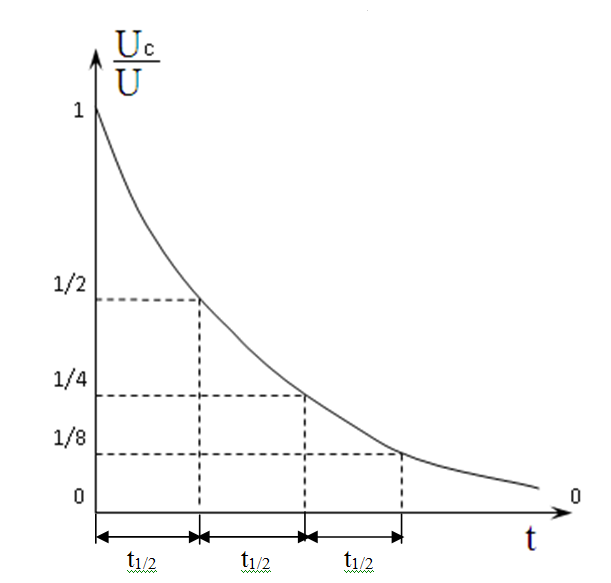
Поэтому целесообразно изме­рять время
уменьшения величины напряжения в 2 раза,
т.е. “половинное время”. За каждый
интервал времени
t_1/2=0,693ּRC
заряд на емкости уменьшается в два раза
(рис. 4).

Рис. 4

Кроме того,
постоянную времени можно найти графическим
способом. Из формулы (4) находим:

,
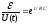
(6)

Логарифмируя левую
и правую части формулы (11), получаем

.
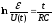
(7)

Построив
логарифмическую зависимость, y=f(x),
где
,
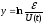
а,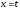
получим прямую, котангенс угла наклона
которой к оси Х есть время релаксации
, или постоянная времениRC:

.
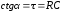
(8)

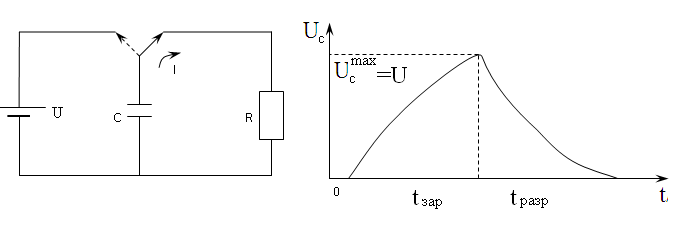
Если обкладки
конденсатора попеременно подключать
к источнику тока и к сопротивлению R
(рис. 5), то график процесса заряд-разряд
конденсатора будет иметь вид, показанный
на рис. 6. Процесс заряда-разряда можно
наблюдать с помощью осциллографа,
подавая на вход Y
напряжение с конденсатора C.

Рис. 5 Рис. 6

Соседние файлы в папке Лабы Физика 2 семестр

• #
• #
• #
• #
• #
• #
• #
• #

Калькуляторы рассчитывают параметры разрядки и зарядки конденсатора от источника постоянной ЭДС через сопротивление. Формулы, по которым идет расчет, приведены под калькуляторами.

Понять приводимые ниже формулы поможет картинка, изображающая электрическую схему заряда конденсатора от источника постоянной ЭДС (батареи):

Итак, при замыкании ключа К в цепи пойдет электрический ток, который будет приводить к заряду конденсатора.
По закону Ома сумма напряжений на конденсаторе и резисторе равна ЭДС источника, таким образом:

При этом заряд и сила тока зависят от времени. В начальный момент времени на конденсаторе нет заряда, сила тока максимальна, также как и максимальна мощность, рассеиваемая на резисторе.

Во время зарядки конденсатора, напряжение на нем изменяется по закону

где величину

называют постоянной времени RC-цепи или временем зарядки конденсатора.
Вообще говоря, согласно уравнению выше, заряд конденсатора бесконечно долго стремится к величине ЭДС, поэтому для оценки времени заряда конденсатора используют величину
— это время, за которое напряжение на конденсаторе достигнет значения 99,2% ЭДС.
Заряд на конденсаторе:

Энергия, запасенная в конденсаторе:

Работа, выполненная источником ЭДС: