Как найти время регулирования в матлабе - Сайт, где вы сможете решить свои вопросы

Перерегулирование и время переходного процесса являются показателями качества системы, процессы которой устойчивы и имеют конечную длительность.

Определение перерегулирования и времени переходного процесса в продукте Acsocad

В режиме просмотра графика необходимо щелкнуть на режим “=” для показа на графике перерегулирования и времени переходного процесса. При подведении к линии графика дополнительно выводится в числовом виде значение перерегулирования (O, %) и времени переходного процесса (Tp, с).

Определение перерегулирования и времени переходного процесса в продукте MATLAB Simulink

В MATLAB Simulink необходимо задать вход и выход исследуемой системы и запустить инструмент линейного анализа. Эта процедура подробно рассмотрена на странице “Анализ: годограф Найквиста и Михайлова, ЛАЧХ и ЛФЧХ”.
После запуска линеаризации выбирается режим графика “Step” и далее на рисунке вызывается меню путем нажатия правой кнопки мыши. В меню “Characteristics” выбираются подпункты меню “Peak Response” и “Setting Time”.

Для вывода текстовой информации о значениях показателей необходимо щелкнуть левой кнопкой мыши по отмеченным на графике точкам.

Источник

clc;
clear all;
%Задание передаточных функций элементов
%Объект
k1=0.3;T1=0.3; 
num1=[k1];den1=[T1 1];
k2=0.3;T2=0.3;
num2=[k2];den2=[T2 1];
k3=0.3;T3=0.3;
num3=[k3];den3=[1];
k4=0.3;T4=0.3;
num4=[k4];den4=[1];
k5=0.3;
num5=[k5];den5=[1];
k6=0.3;
num6=[k6];den6=[1];
%Контроллер
 
kcpr = (1/T1+1/T2)/(k1*k2*k3*k4*k5*k6);
num7=[kcpr];den7=[1 0];
%Здесь в качестве коэффициента регулятора взят предельный
%коэффициент, расчитанный из условия устойчивости
 
%Последовательное соединение блоков W1 и W2.
[num12,den12]=series(num1,den1,num2,den2);
 
%Последовательное соединение блоков W1W2W3W4 и W5W6.
[num23,den23]=series(num2,den2,num3,den3);
 
%Последовательное соединение блоков W3 и W4.
[num34,den34]=series(num3,den3,num4,den4);
 
%Последовательное соединение блоков W4 и W5.
[num45,den45]=series(num4,den4,num5,den5);
 
%Последовательное соединение блоков W6 и W7.
[num67,den67]=series(num6,den6,num7,den7);
 
%Последовательное соединение блоков W1W2W3W4 и W5W6.
[num4_7,den4_7]=series(num45,den45,num67,den67);
 
%Последовательное соединение блоков W1W2W3W4 и W5W6.
[num2_7,den2_7]=series(num23,den23,num4_7,den4_7);
 
%Последовательное соединение блоков W5 и W6.
[num56,den56]=series(num5,den5,num6,den6);
 
%Последовательное соединение блоков W1W2 и W3.
[num1_3,den1_3]=series(num12,den12,num3,den3);
 
%Последовательное соединение блоков W1W2 и W3W4.
[num1_4,den1_4]=series(num1_3,den1_3,num4,den4);
 
%Последовательное соединение блоков W1W2W3W4 и W5W6.
[num1_6,den1_6]=series(num1_4,den1_4,num56,den56);
 
%Последовательное соединение блоков W1W2W3W4W5W6 и W7.(Передаточная
%функция разомкнутой системы)
[num1_7,den1_7]=series(num1_6,den1_6,num7,den7);
 
%Передаточная функция ошибки замкнутой системы 
%относительно задающего входа yo.
num=[1];den=[1];%единичная передаточная функция
sign=-1;
[nume_yo,dene_yo]=feedback(num,den,num1_7,den1_7,sign);
[nume_f1,dene_f1]=feedback(num1,den1,num2_7,den2_7,sign);
[nume_f4,dene_f4]=feedback(num1_3,den1_3,num4_7,den4_7,sign);
 
%Вывод на экран найденых передаточных функций 
disp('Transfer function from command y* to error e; We_y*');
printsys(nume_yo,dene_yo,'p');
disp(' ')
disp('Transfer function from command f1 to error e; We_f1');
printsys(nume_f1,dene_f1,'p');
disp(' ')
disp('Transfer function from command f4 to error e; We_f4');
printsys(nume_f4,dene_f4,'p');
%Для определения статической ошибки можно воспользоваться оператором МАТЛАБа DCGAIN и, следовательно, добавить в скрипт файл следующие строки. 
%Определение статической ошибки
disp(' ')
disp('Coefficient of static error of y*')
Co=dcgain(nume_yo,dene_yo)
%Коэффициент скоростной ошибки по y*
disp('Coefficient of speed error from y*')
C1 = 1/(k1*k2*k3*k4*k5*k6*kcpr)
%Реакция системы на единичный скачок, когда в регуляторе
%установлен предельный коэффициетн усиления
t=0:.2:20;
%step(nume_yo,dene_yo,t)
lsim(nume_y1,dene_y1,2*t,t);

Источник

Переходная функцияh(t)
звена – это реакция звена на единичное
воз – действие1(t)
при условии, что до момента приложения
воздействия звено находилось в состоянии
покоя, т.е. начальные условия были
нулевыми.

Построим график переходной функции
h(t)
заданной нескорректированной системы
в приложенииSimulinkпакетаMatlab.

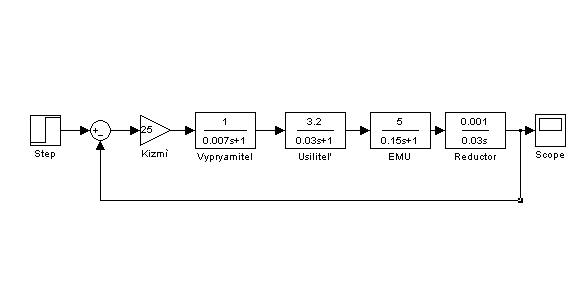
Рис. 7. Структурная схема замкнутой
системы

Рис. 8. Переходный процесс нескорректированной
системы (сходящийся)

Показатели качества нескорректированной
системы:

Полученные значения показателей качества
нескорректированной системы не
удовлетворяют требуемым (t_рег<=1.5;<=0%).

Оценка показателей качества нескорректированной системы

Перерегулирование нескорректированной
системы не удовлетворяет требуемому
(<=5%), а время
регулирования лежит в пределах требуемых
значений (t_рег<=2.5).

8. Проведение синтеза последовательного корректирующего устройства методом Соколова

Передаточная функция замкнутой
нескорректированной системы: Фн/ск=

Исходя из технических
требований к системе, известно, что
перерегулирование системы должно быть
%,
а время регулирования

tр=
1.5 с, значит данная система в скорректированном
состоянии должна удовлетворять второму
условию закона распределения нолей и
полюсов, когда достаточно медленное
время регулирования, но перерегулирование
системы мало. Для второго случая
передаточная нормированная функция
выглядит следующим образом:

Фн=,
гдеn=np-mp+зад-1=4-0+1-1=4

n=4, значит
передаточная нормированная функция
для данной системы будет иметь следующий
вид:

Фн=.

Зная нормированную передаточную
функцию Фн,
сформируем желаемую передаточную
функцию Фж(s)=Фн().Желаемая
передаточная функция выбирается с
использованием теоремы масштабов
преобразования Лапласа:

Тогда желаемая передаточная
функция для данной системы будет иметь
следующий вид:

Фж(s)=
Фн()==

p– аргумент нормированной
передаточной функции,

s– комплексный аргумент
Лапласа,

z– коэффициент масштаба
времени,

t_рег– заданное
время регулирования,

–
время регулирования нормированной
передаточной функции.

Тогда передаточная функция
корректирующего устройства имеет
следующий вид:

Wку==

Найдем передаточную функцию
скорректированной разомкнутой системы:

Wск==

9. Построение лах и лфх скорректированной разомкнутой системы в Matlab

Листинг программы:

w=tf([1],[ 0.007 0.076 0.367 0.882 0]);

margin(w);

Рис.9 Графики ЛАХ и ЛФХ
скорректированной разомкнутой систем

Оценка запасов устойчивости
скорректированной системы по модулю
(амплитуде) и по фазе

Запас устойчивости по амплитуде
=10,4
дБ,m=1-L=0.7

Запас устойчивости по фазе
.
Значит, система обладает достаточными
запасами устойчивости, как по амплитуде,
так и по фазе.

Сравнение с запасами устойчивости
нескорректированной системы

После введения корректирующего устройства
система стала более устойчивей, что
наглядно видно из ЛАХ и ЛФХ скорректированной
разомкнутой системы по увеличению
запасов устойчивости по модулю (m=0.7)
и по фазе (=62,7).

Построение графика переходной функции
h(t)
скорректированной системы в приложении
Octave

Передаточная
функция скорректированной замкнутой
системы имеет следующий вид:

Фск=

Листинг
программы:

w=tf([1],[0.007
0.076 0.367 0.882 1])

step(w)

Рис.10 График переходной
функции скорректированной систем

Оценка показателей качества
скорректированной системы

Время регулирования по графику
примерно равно tp=1,5c.

Перерегулирование системы:

Таким образом, с помощью метода Соколова
Н.И. было синтезировано последовательное
корректирующее устройство, которое
было введено в систему для достижения
требуемых показателей качества. В
результате была получена скорректированная
система, удовлетворяющая требуемым
показателям качества, но с незначительным
отклонением величины перерегулирования:
время регулирования равно 1.5 секунды и
величина перерегулирования равна 3%.

Источник

Лабораторная работа предназначена для закрепления навыков работы в MATLAB для построения и исследования динамических свойств линейных систем управления. Рассматривается процесс моделирования линейной системы в программе MATLAB Simulink методами передаточной функции и прямого аналогового моделирования.

Цель работы: освоить методику моделирования линейной системы в программе MATLAB Simulink методами передаточной функции и прямого аналогового моделирования.

Задание:

1. По исходным данным составить структурную схему системы автоматического управления в MATLAB Simulink с использованием блоков TransferFcn и др. Для моделирования передаточных функций:

выбрать закон регулирования, обеспечивающий астатизм в системе и наилучшее качество регулирования. Регулятор смоделировать с помощью блока PID, включив необходимые составляющие. Выбрать оптимальные настройки регулятора, обеспечивающие минимальное время регулирования при соблюдении ограничения на перерегулирования 20%;
вывести логарифмические частотные характеристики системы, определить запасы устойчивости;
провести оценку устойчивости системы по методу Гурвица и Найквиста;
вывести переходной процесс. Оценить качество регулирования по прямым показателям.

2. Собрать схему рассматриваемой системы в MATLAB Simulink по методу аналогового моделирования. Настроить начальные значения. Вывести график переходного процесса в блоке Scope.

3. Вывести на один осциллограф выходы схем, построенных в пункте 1 и 2. Получить кривые переходных процессов. Сделать сравнительный вывод о методах моделирования.

Пример.

Пусть система описывается следующими уравнениями:

где T1 = 1.5, T2 = 11, T3 = 34, k1 = 1.5, k2 = 2.

1. Исследование системы в MATLAB Simulink с помощью блоков передаточной функции

Схема в MATLAB Simulink, собранная с помощью блока TransferFcn имеет вид (рис.1):

Так как в системе присутствует интегрирующее звено, целесообразно для регулирования выбрать ПД закон регулирования. Параметры подобраны в блоке PID с помощью функции Tune (рис.2). В случае необходимости для достижения требуемых показателей качества переходного процесса в систему можно добавить еще одну пропорциональную составляющую регулятора – блок Gain после блока PID. С помощью коэффициента в блоке Gain подбирается необходимое перерегулирование.

На рисунке 3 приведены логарифмические частотные характеристики системы, пересечение амплитудной характеристикой разомкнутой системы оси 0 дБ происходит при фазе больше -180°, поэтому замкнутая система устойчива, запасы устойчивости по фазе составляют 60°, по модулю – 40.3 дБ.

Для построения годографа Найквиста можно использовать функцию nyquist(sys) в командной строке или использовать процедуру линейного анализа в Simulink.

Для этого необходимо настроить вход и выход системы для линейного анализа с помощью команд контекстного меню (рис.4). Либо вместо блока Constant поставить блок In, вместо Scope – блок Out. Далее выбираем команду меню Analysis – Control Design – Linear Analysis. В окне линейного анализа выбираем тип графика New Nyquist.

По виду годографа Найквиста (рис.5) делаем вывод, что так как годограф разомкнутой системы не охватывает точку (-1;j0), то замкнутая система устойчива.

Для определения устойчивости по прямому критерию и критерию Гурвица используем командную строку:

>> w1=tf(1,[1.5 0]);

>> w2=tf(1.5,[11 1]);

>> w3=tf(2,[34 1]);

>> wp=tf([0.8 0.02],1);

>> wraz=w1*w2*w3*wp

wraz =

         2.4 s + 0.06

  --------------------------

  561 s^3 + 67.5 s^2 + 1.5 s



>> wzam=feedback(wraz,1)

wzam =

            2.4 s + 0.06

  ---------------------------------

  561 s^3 + 67.5 s^2 + 3.9 s + 0.06

Прямой критерий устойчивости:

>> pole(wzam)           %определим корни знаменателя замкнутой системы

ans =

  -0.0489 + 0.0486i

  -0.0489 - 0.0486i

  -0.0225 + 0.0000i

Все корни отрицательные, следовательно система устойчива.

Определим устойчивость по критерию Гурвица:

>> [num,den]=tfdata(wzam,'v');

>> den

den =

  561.0000   67.5000    3.9000    0.0600

% Ввод определителя Гурвица

>> A=[67.5 0.06;561 3.9];

>> if det(A)>0

disp('система устойчива')

else

disp('система неустойчива'),end

система устойчива

По графику переходной функции на рис.2 можно оценить качество регулирования: время регулирования составило 98.8 с, перерегулирования 9.11%.

2. Исследование системы в MATLAB Simulink с помощью метода прямого аналогового моделирования.

Метод заключается в выделении старшей производной выходной величины в дифференциальном уравнении и дальнейшем интегрировании ее требуемое количество раз в зависимости от порядка производной.

Например, для апериодического звена первого порядка:

дифференциальное уравнение имеет вид:

Выделим старшую производную:

Для решения уравнения – получения сигнала y на выходе – его необходимо проинтегрировать. Тогда на структурной схеме апериодическое звено (рис.6а) можно заменить следующей схемой, собранной из пропорциональных и интегрирующих звеньев (рис.6б).

Для нашего примера, если использовать метод прямого аналогового моделирования с выделением старшей производной и последовательным интегрированием, получим следующую схему (рис.7):

Для сравнения результатов выведем схемы на один осциллограф (рис.8). Графики переходных процессов – кривые разгона приведены на рисунке 9.

Как видно на рис.9, графики кривых разгона близки, следовательно, методы моделирования дают сходные результаты. Однако метод прямого моделирования позволяет учесть начальные значения, которые устанавливаются в последнем блоке Integrator (на рис.6 обозначен y*(t)). Для схем на рисунке 8 установлено заданное значение y_з = 100, начальное значение y_н = 20.

Источник

Discrete-time or continuous-time PID controller

Description

The Discrete PID Controller block implements a PID controller (PID, PI,
PD, P only, or I only). The block is identical to the PID
Controller block with the Time domain parameter set to
Discrete-time.

The block output is a weighted sum of the input signal, the integral of the input
signal, and the derivative of the input signal. The weights are the proportional,
integral, and derivative gain parameters. A first-order pole filters the derivative
action.

The block supports several controller types and structures. Configurable options in
the block include:

Controller type (PID, PI, PD, P only, or I only) — See the
Controller parameter.
Controller form (Parallel or Ideal) — See the Form
parameter.
Time domain (continuous or discrete) — See the Time
domain parameter.
Initial conditions and reset trigger — See the Source and
External reset parameters.
Output saturation limits and built-in anti-windup mechanism — See the
Limit output parameter.
Signal tracking for bumpless control transfer and multiloop control — See the
Enable tracking mode parameter.

As you change these options, the internal structure of the block changes by activating
different variant subsystems. (For more information, see Implement Variations in Separate Hierarchy Using Variant Subsystems). To examine the internal structure of the block and its variant subsystems,
right-click the block and select > .

Control Configuration

In one common implementation, the PID Controller block operates in
the feedforward path of a feedback loop.

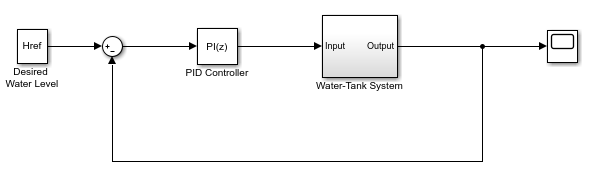
The input of the block is typically an error signal, which is the difference
between a reference signal and the system output. For a two-input block that permits
setpoint weighting, see Discrete PID
Controller (2DOF).

PID Gain Tuning

The PID controller gains are tunable either manually or automatically. Automatic
tuning requires Simulink^®
Control Design™ software. For more information about automatic tuning, see the
Select tuning method parameter.

Examples

Ports

Input

expand all

Port_1( u ) — Error signal input
scalar | vector

Difference between a reference signal and the output of the system
under control, as shown.

P — Proportional gain
scalar | vector

Proportional gain, provided from a source external to the block. External gain input is
useful, for example, when you want to map a different PID
parameterization to the PID gains of the block. You can also use
external gain input to implement gain-scheduled PID control. In
gain-scheduled control, you determine the PID coefficients by
logic or other calculation in your model and feed them to the
block.

Dependencies

To enable this port, set Controller parameters Source to external.

I — Integral gain
scalar | vector

Integral gain, provided from a source external to the block. External gain input is useful,
for example, when you want to map a different PID
parameterization to the PID gains of the block. You can also use
external gain input to implement gain-scheduled PID control. In
gain-scheduled control, you determine the PID coefficients by
logic or other calculation in your model and feed them to the
block.

When you supply gains externally, time variations in the integral gain are also integrated. This result occurs because of the way the PID gains are implemented within the block. For details, see the Controller parameters Source parameter.

Dependencies

To enable this port, set Controller parameters Source to
external, and set Controller to
a controller type that has integral action.

**I*T_s** — Integral gain multiplied by sample time
scalar | vector

Integral gain multiplied by the controller sample time, provided from a source external to the block. External gain input is useful, for example, when you want to map a different PID parameterization to the PID gains of the block. You can also use external gain input to implement gain-scheduled PID control. In gain-scheduled control, you determine the PID coefficients by logic or other calculations in your model and feed them to the block.

Note

PID tuning tools, such as the PID Tuner app and Closed-Loop PID Autotuner block, tune the gain I but not I*T_s. Therefore, multiply the integral gain value you obtain from a tuning tool by the sample time before you supply it to this port.

When you use I*T_s instead of I, the block requires fewer calculations to perform integration. This improves the execution time of the generated code.

Dependencies

To enable this port, set Controller parameters Source to external, set Controller to a controller type that has integral action, and enable the Use I*Ts parameter.

D — Derivative gain
scalar | vector

Derivative gain, provided from a source external to the block. External gain input is useful,
for example, when you want to map a different PID
parameterization to the PID gains of the block. You can also use
external gain input to implement gain-scheduled PID control. In
gain-scheduled control, you determine the PID coefficients by
logic or other calculation in your model and feed them to the
block.

When you supply gains externally, time variations in the derivative gain are also differentiated. This result occurs because of the way the PID gains are implemented within the block. For details, see the Controller parameters Source parameter.

Dependencies

To enable this port, set Controller parameters Source to
external, and set Controller to
a controller type that has derivative action.

N — Filter coefficient
scalar | vector

Derivative filter coefficient, provided from a source external to the block. External
coefficient input is useful, for example, when you want to map a different PID
parameterization to the PID gains of the block. You can also use the external input to
implement gain-scheduled PID control. In gain-scheduled control, you determine the PID
coefficients by logic or other calculation in your model and feed them to the
block.

Dependencies

To enable this port, set Controller parameters Source to
external, and set Controller to a
controller type that has a filtered derivative.

Reset — External reset trigger
scalar

Trigger to reset the integrator and filter to their initial conditions. The value of the
External reset parameter determines whether reset occurs on a
rising signal, a falling signal, or a level signal. The port icon indicates the selected
trigger type. For example, the following illustration shows a continuous-time PID block
with External reset set to
rising.

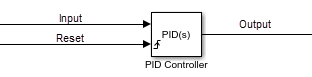
When the trigger occurs, the block resets the integrator and filter to the initial conditions specified by the Integrator Initial condition and Filter Initial condition parameters or the I₀ and D₀ ports.

Note

To be compliant with the Motor Industry Software Reliability Association (MISRA™) software standard, your model must use Boolean signals to drive the external reset ports of the PID controller block.

Dependencies

To enable this port, set External reset to any value other than none.

I₀ — Integrator initial condition
scalar | vector

Integrator initial condition, provided from a source external to the block.

Dependencies

To enable this port, set Initial conditions Source to
external, and set Controller to
a controller type that has integral action.

D₀ — Filter initial condition
scalar | vector

Initial condition of the derivative filter, provided from a source external to the
block.

Dependencies

To enable this port, set Initial conditions Source to
external, and set Controller to a
controller type that has derivative action.

up — Output saturation upper limit
scalar | vector

Upper limit of the block output, provided from a source external to the block. If the weighted
sum of the proportional, integral, and derivative actions exceeds the value provided at
this port, the block output is held at that value.

Dependencies

To enable this port, select Limit output and set the output
saturation Source to
external.

lo — Output saturation lower limit
scalar | vector

Lower limit of the block output, provided from a source external to the block. If the weighted
sum of the proportional, integral, and derivative
actions goes below the value provided at this
port, the block output is held at that
value.

Dependencies

To enable this port, select Limit output and set the output saturation
Source to external.

TR — Tracking signal
scalar | vector

Signal for controller output to track. When signal tracking is active, the difference between
the tracking signal and the block output is fed back to the integrator input. Signal
tracking is useful for implementing bumpless control transfer in systems that switch
between two controllers. It can also be useful to prevent block windup in multiloop
control systems. For more information, see the Enable tracking mode
parameter.

Dependencies

To enable this port, select the Enable tracking mode parameter.

T_DTI — Discrete-integrator time
scalar

Discrete-integrator time, provided as a
scalar to the block. You can use your own value of
discrete-time integrator sample time that defines
the rate at which the block is going to be run
either in Simulink or on external hardware. The value
of the discrete-time integrator time should match
the average sampling rate of the external
interrupts, when the block is used inside a
conditionally-executed subsystem.

In other words, you can specify
Ts for any of the integrator
methods below such that the value matches the
average sampling rate of the external interrupts.
In discrete time, the derivative term of the
controller transfer function is:

where α(z)
depends on the integrator method you specify with
this parameter.

Forward Euler
Backward Euler
Trapezoidal

For more information about discrete-time
integration, see the Discrete-Time
Integrator block reference page. For more
information on conditionally executed subsystems,
see Conditionally Executed Subsystems Overview.

Dependencies

To enable this port, set Time
Domain to
Discrete-time and
select the PID Controller is inside a
conditionally executed subsystem
option.

Output

expand all

Port_1( y ) — Controller output
scalar | vector

Controller output, generally based on a sum of the input signal, the integral of the input
signal, and the derivative of the input signal, weighted by the proportional, integral,
and derivative gain parameters. A first-order pole filters the derivative action. Which
terms are present in the controller signal depends on what you select for the
Controller parameter. The base controller transfer function for
the current settings is displayed in the Compensator formula
section of the block parameters and under the mask. Other parameters modify the block
output, such as saturation limits specified by the Upper Limit and
Lower Limit saturation parameters.

The controller output is a vector signal when any of the inputs is a vector signal. In that
case, the block acts as N independent PID controllers, where
N is the number of signals in the input vector.

Parameters

expand all

Controller — Controller type
`PID` (default) | `PI` | `PD` | `P` | `I`

Specify which of the proportional, integral, and derivative terms are in the controller.

PID: Proportional, integral, and derivative action.
PI: Proportional and integral action only.
PD: Proportional and derivative action only.
P: Proportional action only.
I: Integral action only.

Tip

The controller transfer function for the current setting is displayed in the Compensator formula section of the block parameters and under the mask.

Programmatic Use

Block Parameter: Controller

Type: string, character vector

Values: "PID", "PI", "PD", "P", "I"

Default: "PID"

Form — Controller structure
`Parallel` (default) | `Ideal`

Specify whether the controller structure is parallel or ideal.

Parallel

The controller output is the sum of the proportional, integral, and derivative actions, weighted independently by P, I, and D, respectively. For example, for a continuous-time parallel-form PID controller, the transfer function is:

For a discrete-time parallel-form controller, the transfer function is:

where the Integrator method and Filter method
parameters determine α(z) and
β(z), respectively.

Ideal

The proportional gain P acts on the sum of all actions. For example, for a continuous-time ideal-form PID controller, the transfer function is:

For a discrete-time ideal-form controller, the transfer function is:

where the Integrator method and Filter method parameters determine a(z) and b(z), respectively.

Tip

The controller transfer function for the current settings is displayed in the Compensator formula section of the block parameters and under the mask.

Programmatic Use

Block Parameter: Controller

Type: string, character vector

Values: "Parallel", "Ideal"

Default: "Parallel"

Time domain — Specify discrete-time or continuous-time controller
`Discrete-time` (default) | `Continuous-time`

When you select Discrete-time, it is
recommended that you specify an explicit sample time for the block. See the
Sample time (-1 for inherited) parameter. Selecting
Discrete-time also enables the
Integrator method, and Filter
method parameters.

When the PID Controller block is in a model with
synchronous state control (see the State Control (HDL Coder) block), you
cannot select Continuous-time.

Note

The PID Controller and Discrete PID
Controller blocks are identical except for the default value
of this parameter.

Programmatic Use

Block Parameter:
TimeDomain

Type: string, character
vector

Values:
"Continuous-time",
"Discrete-time"

Default:
"Discrete-time"

PID Controller is inside a conditionally executed subsystem — Enable the discrete-integrator time port
`off` (default) | `on`

For discrete-time PID controllers, enable the discrete-time integrator port to use
your own value of discrete-time integrator sample time. To ensure proper integration,
use the T_DTI port to provide a scalar value
of Δt for accurate discrete-time integration.

Dependencies

To enable this parameter, set Time Domain to
Discrete-time.

Programmatic Use

Block Parameter:
UseExternalTs

Type: string, character vector

Values:
"on", "off"

Default:
"off"

Sample time (-1 for inherited) — Discrete interval between samples
–1 (default) | positive scalar

Specify a sample time by entering a positive scalar value, such as 0.1. The default discrete
sample time of –1 means that the block inherits its sample time from upstream blocks.
However, it is recommended that you set the controller sample time explicitly,
especially if you expect the sample time of upstream blocks to change. The effect of the
controller coefficients P, I, D, and N depend on the sample time. Thus, for a given set
of coefficient values, changing the sample time changes the performance of the
controller.

See
Specify Sample Time for more information.

To implement a continuous-time controller, set Time domain to Continuous-time.

Tip

If you want to run the block with an externally specified or variable sample time, set this parameter to –1 and put the block in a Triggered Subsystem. Then, trigger the subsystem at the desired sample time.

Dependencies

To enable this parameter, set Time domain to Discrete-time.

Programmatic Use

Block Parameter: SampleTime

Type: scalar

Values: -1, positive scalar

Default: -1

Integrator method — Method for computing integral in discrete-time controller
`Forward Euler` (default) | `Backward Euler` | `Trapezoidal`

In discrete time, the integral term of the controller transfer function is
Iα(z), where
α(z) depends on the integrator method you
specify with this parameter.

Forward Euler

Forward rectangular (left-hand) approximation,

This method is best for small sampling times, where the Nyquist limit is large compared to the bandwidth of the controller. For larger sampling times, the Forward Euler method can result in instability, even when discretizing a system that is stable in continuous time.

Backward Euler

Backward rectangular (right-hand) approximation,

An advantage of the Backward Euler method is that discretizing a stable continuous-time system using this method always yields a stable discrete-time result.

Trapezoidal

Bilinear approximation,

An advantage of the Trapezoidal method is that discretizing a stable continuous-time system using this method always yields a stable discrete-time result. Of all available integration methods, the Trapezoidal method yields the closest match between frequency-domain properties of the discretized system and the corresponding continuous-time system.

Tip

The controller formula for the current setting is displayed in the
Compensator formula section of the block parameters and
under the mask.

Note

For the BackwardEuler or Trapezoidal methods, you cannot generate HDL code for the block if either:

Limit output is selected and Anti-Windup
Method is anything other than
none.
Enable tracking mode is selected.

For more information about discrete-time integration, see the Discrete-Time Integrator block reference page.

Dependencies

To enable this parameter, set Time Domain to Discrete-time and set Controller to a controller type with integral action.

Programmatic Use

Block Parameter: IntegratorMethod

Type: string, character vector

Values: "Forward Euler", "Backward Euler", "Trapezoidal"

Default: "Forward Euler"

Filter method — Method for computing derivative in discrete-time controller
`Forward Euler` (default) | `Backward Euler` | `Trapezoidal`

In discrete time, the derivative term of the controller transfer function is:

where α(z) depends on the filter method you specify
with this parameter.

Forward Euler

Forward rectangular (left-hand) approximation,

Backward Euler

Backward rectangular (right-hand) approximation,

An advantage of the Backward Euler method is that discretizing a stable continuous-time system using this method always yields a stable discrete-time result.

Trapezoidal

Bilinear approximation,

Tip

The controller formula for the current setting is displayed in the
Compensator formula section of the block parameters and
under the mask.

For more information about discrete-time integration, see the Discrete-Time Integrator block reference page.

Dependencies

To enable this parameter, set Time Domain to
Discrete-time and
enable Use filtered
derivative.

Programmatic Use

Block Parameter: FilterMethod

Type: string, character vector

Values: "Forward Euler", "Backward Euler", "Trapezoidal"

Default: "Forward Euler"

Main

Source — Source for controller gains and filter coefficient
internal (default) | external

Enabling external inputs for the parameters allows you to compute PID gains and filter
coefficients externally to the block and provide them to the block as signal
inputs.

internal

Specify the controller gains and filter coefficient using the block parameters P, I, D, and N.

external

Specify the PID gains and filter coefficient externally using block inputs. An additional input port appears on the block for each parameter that is required for the current controller type.

External gain input is useful, for example, when you want to map a
different PID parameterization to the PID gains of the block. You can also
use external gain input to implement gain-scheduled PID control. In
gain-scheduled control, you determine the PID gains by logic or other
calculation in your model and feed them to the block.

When you supply gains externally, time variations in the integral and
derivative gain values are integrated and differentiated, respectively. This
result occurs because in both continuous time and discrete time, the gains
are applied to the signal before integration or differentiation. For
example, for a continuous-time PID controller with external inputs, the
integrator term is implemented as shown in the following
illustration.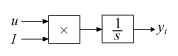

Within the block, the input signal u is multiplied by
the externally supplied integrator gain, I, before
integration. This implementation yields:

Thus, the integrator gain is included in the integral. Similarly, in the
derivative term of the block, multiplication by the derivative gain precedes
the differentiation, which causes the derivative gain D
to be differentiated.

Programmatic Use

Block Parameter: ControllerParametersSource

Type: string, character vector

Values: "internal", "external"

Default: "internal"

Proportional (P) — Proportional gain
1 (default) | scalar | vector

Specify a finite, real gain value for the proportional gain. When Controller form is:

Parallel — Proportional action is independent of the integral and derivative actions. For instance, for a continuous-time parallel PID controller, the transfer function is:

For a discrete-time parallel-form controller, the transfer function is:

where the Integrator method and Filter method
parameters determine α(z) and
β(z), respectively.
Ideal — The proportional gain multiples the integral and derivative terms. For instance, for a continuous-time ideal PID controller, the transfer function is:

For a discrete-time ideal-form controller, the transfer function is:

where the Integrator method and Filter method
parameters determine α(z) and
β(z), respectively.

Tunable: Yes

Dependencies

To enable this parameter, in the Main tab, set the controller-parameters
Source to internal and set
Controller to PID,
PD, PI, or
P.

Programmatic Use

Block Parameter: P

Type: scalar, vector

Default: 1

Integral (I) — Integral gain
1 (default) | scalar | vector

Specify a finite, real gain value for the integral gain.

Tunable: Yes

Dependencies

To enable this parameter, in the Main tab, set the controller-parameters
Source to internal, and set
Controller to a type that has integral action.

Programmatic Use

Block Parameter: I

Type: scalar, vector

Default: 1

**Integral (I*Ts)** — Integral gain multiplied by sample time
1 (default) | scalar | vector

Specify a finite, real gain value for the integral gain multiplied by the sample time.

Note

When you use I*Ts instead of I, the block requires fewer calculations to perform integration. This improves the execution time of the generated code.

Tunable: No

Dependencies

To enable this parameter, in the Main tab, set the controller-parameters Source to internal, set Controller to a type that has integral action, and enable the Use I*Ts parameter.

Programmatic Use

Block Parameter: I

Type: scalar, vector

Default: 1

**Use I*Ts** — Use integral gain multiplied by sample time
`off` (default) | `on`

For discrete-time controllers with integral action, the block takes the integral gain as an input and multiplies it by the sample time internally as a part of performing the integration. You can enable this parameter to specify integral gain multiplied by sample time as input (I*Ts) in place of the integral gain (I). Doing so reduces the number of internal calculations and is useful when you want to improve the execution time of your generated code.

Dependencies

To enable this parameter, set Controller to a controller type that has integral action.

Programmatic Use

Block Parameter: UseKiTs

Type: string, character vector

Values: "on", "off"

Default: "on"

Derivative (D) — Derivative gain
0 (default) | scalar | vector

Specify a finite, real gain value for the derivative gain.

Tunable: Yes

Dependencies

To enable this parameter, in the Main tab, set the controller-parameters
Source to internal, and set
Controller to PID or
PD.

Programmatic Use

Block Parameter: D

Type: scalar, vector

Default: 0

Use filtered derivative — Apply filter to derivative term
`on` (default) | `off`

For discrete-time PID controllers only, clear this option to replace the filtered derivative
with an unfiltered discrete-time differentiator. When you do so, the derivative term of
the controller transfer function becomes:

For continuous-time PID controllers, the derivative term is always filtered.

Dependencies

To enable this parameter, set Time domain to
Discrete-time, and set Controller to a
type that has derivative action.

Programmatic Use

Block Parameter: UseFilter

Type: string, character vector

Values: "on", "off"

Default: "on"

Filter coefficient (N) — Derivative filter coefficient
100 (default) | scalar | vector

Specify a finite, real gain value for the filter coefficient. The filter coefficient
determines the pole location of the filter in the derivative action of the
block. The location of the filter pole depends on the Time
domain parameter.

When Time domain is
Continuous-time, the pole
location is s = -N.

When Time domain is
Discrete-time, the pole
location depends on the Filter method
parameter.

Filter Method	Location of Filter Pole
`Forward Euler`	zpole=1−NTs
`Backward Euler`	zpole=11+NTs
`Trapezoidal`	zpole=1−NTs/21+NTs/2

The block does not support N = Inf (ideal unfiltered derivative). When the Time domain is Discrete-time, you can clear Use filtered derivative to remove the derivative filter.

Tunable: Yes

Dependencies

To enable this parameter, in the Main tab, set the controller-parameters
Source to
internal and set
Controller to
PID or
PD.

Programmatic Use

Block Parameter: N

Type: scalar, vector

Default: 100

Select tuning method — Tool for automatic tuning of controller coefficients
`Transfer Function Based (PID Tuner App)` (default) | `Frequency Response Based`

If you have Simulink
Control Design software, you can automatically tune the PID coefficients. To do so, use
this parameter to select a tuning tool, and click Tune.

Transfer Function Based (PID Tuner App): Use PID Tuner, which lets you interactively tune PID
coefficients while examining relevant system responses to validate
performance. By default, PID Tuner works with a linearization of
your plant model. For models that cannot be linearized, you can tune PID
coefficients against a plant model estimated from simulated or measured
response data. For more information, see
Introduction to Model-Based PID Tuning in Simulink (Simulink Control Design).
Frequency Response Based: Use Frequency Response Based PID Tuner, which tunes PID
controller coefficients based on frequency-response estimation data obtained
by simulation. This tuning approach is especially useful for plants that are
not linearizable or that linearize to zero. For more information, see
Design PID Controller from Plant Frequency-Response Data (Simulink Control Design).

Both of these tuning methods assume a single-loop control configuration. Simulink
Control Design software includes other tuning approaches that suit more complex
configurations. For information about other ways to tune a PID Controller
block, see Choose a Control Design Approach (Simulink Control Design).

Enable zero-crossing detection — Detect zero crossings on reset and on entering or leaving a saturation state
`on` (default) | `off`

Zero-crossing detection can accurately locate signal discontinuities without resorting to excessively small time steps that can lead to lengthy simulation times. If you select Limit output or activate External reset in your PID Controller block, activating zero-crossing detection can reduce computation time in your simulation. Selecting this parameter activates zero-crossing detection:

At initial-state reset
When entering an upper or lower saturation state
When leaving an upper or lower saturation state

For more information about zero-crossing detection, see Zero-Crossing Detection.

Programmatic Use

Block Parameter: ZeroCross

Type: string, character vector

Values: "on", "off"

Default: "on"

Initialization

Source — Source for integrator and derivative initial conditions
`internal` (default) | `external`

Simulink uses initial conditions to initialize the integrator and derivative-filter
(or the unfiltered derivative) output at the start of a simulation or at a specified
trigger event. (See the External reset parameter.) These initial
conditions determine the initial block output. Use this parameter to select how to
supply the initial condition values to the block.

internal: Specify the initial conditions using the Integrator Initial
condition and Filter Initial condition
parameters. If Use filtered derivative is not selected,
use the Differentiator parameter to specify the initial
condition for the unfiltered differentiator instead of a filter initial
condition.
external: Specify the initial conditions externally using block inputs. Additional
input ports I_o and
D_o appear on the block.
If Use filtered derivative is not selected, supply the
initial condition for the unfiltered differentiator at
D_o instead of a filter
initial condition.

Programmatic Use

Block Parameter:
InitialConditionSource

Type: string, character vector

Values:
"internal", "external"

Default:
"internal"

Integrator — Integrator initial condition
0 (default) | scalar | vector

Simulink uses the integrator initial condition to initialize the integrator at the start of a simulation or at a specified trigger event (see External reset). The integrator initial condition and the filter initial condition determine the initial output of the PID controller block.

The integrator initial condition cannot be NaN or Inf.

Dependencies

To use this parameter, in the Initialization tab, set
Source to internal, and set
Controller to a type that has integral action.

Programmatic Use

Block Parameter: InitialConditionForIntegrator

Type: scalar, vector

Default: 0

Filter — Filter initial condition
0 (default) | scalar | vector

Simulink uses the filter initial condition to initialize the derivative filter at the start of a simulation or at a specified trigger event (see External reset). The integrator initial condition and the filter initial condition determine the initial output of the PID controller block.

The filter initial condition cannot be NaN or Inf.

Dependencies

To use this parameter, in the Initialization tab, set
Source to internal, and use a
controller that has a derivative filter.

Programmatic Use

Block Parameter: InitialConditionForFilter

Type: scalar, vector

Default: 0

Differentiator — Initial condition for unfiltered derivative
0 (default) | scalar | vector

When you use an unfiltered derivative, Simulink uses this parameter to initialize the differentiator at the start of a simulation or at a specified trigger event (see External reset). The integrator initial condition and the derivative initial condition determine the initial output of the PID controller block.

The derivative initial condition cannot be NaN or Inf.

Dependencies

To use this parameter, set Time domain to Discrete-time, clear the Use filtered derivative check box, and in the Initialization tab, set Source to internal.

Programmatic Use

Block Parameter: DifferentiatorICPrevScaledInput

Type: scalar, vector

Default: 0

Initial condition setting — Location at which initial condition is applied
`Auto` (default) | `Output`

Use this parameter to specify whether to apply the Integrator Initial condition and Filter Initial condition parameter to the corresponding block state or output. You can change this parameter at the command line only, using set_param to set the InitialConditionSetting parameter of the block.

Auto: Use this option in all situations except when the block is in a triggered subsystem or a function-call subsystem and simplified initialization mode is enabled.
Output: Use this option when the block is in a triggered subsystem or a function-call subsystem and simplified initialization mode is enabled.

For more information about the Initial condition setting parameter, see the Discrete-Time Integrator block.

This parameter is only accessible through programmatic use.

Programmatic Use

Block Parameter: InitialConditionSetting

Type: string, character vector

Values:
"Auto", "Output"

Default:
"Auto"

External reset — Trigger for resetting integrator and filter values
`none` (default) | `rising` | `falling` | `either` | `level`

Specify the trigger condition that causes the block to reset the integrator and filter to initial conditions. (If Use filtered derivative is not selected, the trigger resets the integrator and differentiator to initial conditions.) Selecting any option other than none enables the Reset port on the block for the external reset signal.

none

The integrator and filter (or differentiator) outputs are set to initial conditions at the beginning of simulation, and are not reset during simulation.

rising

Reset the outputs when the reset signal has a rising edge.

falling

Reset the outputs when the reset signal has a falling edge.

either

Reset the outputs when the reset signal either rises or falls.

level

Reset the outputs when the reset signal either:

Is nonzero at the current time step
Changes from nonzero at the previous time step to zero at the current time step

This option holds the outputs to the initial conditions while the reset signal is nonzero.

Dependencies

To enable this parameter, set Controller to a type that has derivative or
integral action.

Programmatic Use

Block Parameter: ExternalReset

Type: string, character vector

Values:
"none",
"rising",
"falling",
"either","level"

Default: "none"

Ignore reset when linearizing — Force linearization to ignore reset
`off` (default) | `on`

Select to force Simulink and Simulink
Control Design linearization commands to ignore any reset mechanism specified in the External reset parameter. Ignoring reset states allows you to linearize a model around an operating point even if that operating point causes the block to reset.

Programmatic Use

Block Parameter: IgnoreLimit

Type: string, character vector

Values: "off", "on"

Default: "off"

Enable tracking mode — Activate signal tracking
`off` (default) | `on`

Signal tracking lets the block output follow a tracking signal that you provide at the TR port. When signal tracking is active, the difference between the tracking signal and the block output is fed back to the integrator input with a gain Kt, specified by the Tracking gain (Kt) parameter. Signal tracking has several applications, including bumpless control transfer and avoiding windup in multiloop control structures.

Bumpless control transfer

Use signal tracking to achieve bumpless control transfer in systems that switch between two
controllers. Suppose you want to transfer control between a PID controller and
another controller. To do so, connecting the controller output to the
TR input as shown in the following illustration.

For more information, see Bumpless Control Transfer.

Multiloop control

Use signal tracking to prevent block windup in multiloop control approaches, as in the following model.

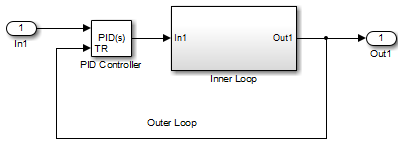
The Inner Loop subsystem contains the blocks shown in the following diagram.

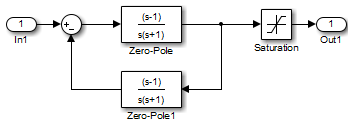
Because the PID controller tracks the output of the inner loop, its output never exceeds the saturated inner-loop output. For more details, see Prevent Block Windup in Multiloop Control.

Dependencies

To enable this parameter, set Controller to a type that has
integral action.

Programmatic Use

Block Parameter:
TrackingMode

Type: string, character vector

Values: "off", "on"

Default: "off"

Tracking coefficient (Kt) — Gain of signal-tracking feedback loop
1 (default) | scalar

When you select Enable tracking mode, the difference between the signal TR and the block output is fed back to the integrator input with a gain Kt. Use this parameter to specify the gain in that feedback loop.

Dependencies

To enable this parameter, select Enable tracking mode.

Programmatic Use

Block Parameter: Kt

Type: scalar

Default: 1

Saturation

Output saturation

Limit Output — Limit block output to specified saturation values
`off` (default) | `on`

Activating this option limits the block output, so that you do not need a separate Saturation block after the controller. It also allows you
to activate the anti-windup mechanism built into the block (see the
Anti-windup method parameter). Specify the output saturation
limits using the Lower limit and Upper limit
parameters. You can also specify the saturation limits externally as block input
ports.

Programmatic Use

Block Parameter: LimitOutput

Type: string, character vector

Values: "off", "on"

Default: "off"

Source — Source for output saturation limits
internal (default) | external

Use this parameter to specify how to supply the upper and lower saturation limits of
the block output.

internal: Specify the output saturation limits using the Upper
limit and Lower limit parameters.
external: Specify the output saturation limits externally using block input ports.
The additional input ports up and
lo appear on the block. You can use the input ports
to implement the upper and lower output saturation limits determined by
logic or other calculations in the Simulink model and passed to the block.

Programmatic Use

Block Parameter:
SatLimitsSource

Type: string, character vector

Values:
"internal", "external"

Default:
"internal"

Upper limit — Upper saturation limit for block output
`Inf` (default) | scalar

Specify the upper limit for the block output. The block output is held at the Upper saturation limit whenever the weighted sum of the proportional, integral, and derivative actions exceeds that value.

Dependencies

To enable this parameter, select Limit output.

Programmatic Use

Block Parameter: UpperSaturationLimit

Type: scalar

Default: Inf

Lower limit — Lower saturation limit for block output
`-Inf` (default) | scalar

Specify the lower limit for the block output. The block output is held at the Lower saturation limit whenever the weighted sum of the proportional, integral, and derivative actions goes below that value.

Dependencies

To enable this parameter, select Limit output.

Programmatic Use

Block Parameter: LowerSaturationLimit

Type: scalar

Default: -Inf

Ignore saturation when linearizing — Force linearization to ignore output limits
`off` (default) | `on`

Force Simulink and Simulink
Control Design linearization commands to ignore block output limits specified in the Upper limit and Lower limit parameters. Ignoring output limits allows you to linearize a model around an operating point even if that operating point causes the block to exceed the output limits.

Dependencies

To enable this parameter, select the Limit output
parameter.

Programmatic Use

Block Parameter: LinearizeAsGain

Type: string, character vector

Values: "off", "on"

Default: "off"

Anti-windup method — Integrator anti-windup method
`none` (default) | `back-calculation` | `clamping`

When you select Limit output and the weighted sum of the
controller components exceeds the specified output limits, the block output holds at the
specified limit. However, the integrator output can continue to grow (integrator
windup), increasing the difference between the block output and the sum of the block
components. In other words, the internal signals in the block can be unbounded even if
the output appears bounded by saturation limits. Without a mechanism to prevent
integrator windup, two results are possible:

If the sign of the input signal never changes, the integrator continues to
integrate until it overflows. The overflow value is the maximum or minimum
value for the data type of the integrator output.
If the sign of the input signal changes once the weighted sum has grown
beyond the output limits, it can take a long time to unwind the integrator
and return the weighted sum within the block saturation limit.

In either case, controller performance can suffer. To combat the effects of windup
without an anti-windup mechanism, it may be necessary to detune the controller (for
example, by reducing the controller gains), resulting in a sluggish controller. To avoid
this problem, activate an anti-windup mechanism using this parameter.

none

Do not use an anti-windup mechanism.

back-calculation

Unwind the integrator when the block output saturates by feeding back to
the integrator the difference between the saturated and unsaturated control
signal. The following diagram represents the back-calculation feedback
circuit for a continuous-time controller. To see the actual feedback circuit
for your controller configuration, right-click on the block and select > .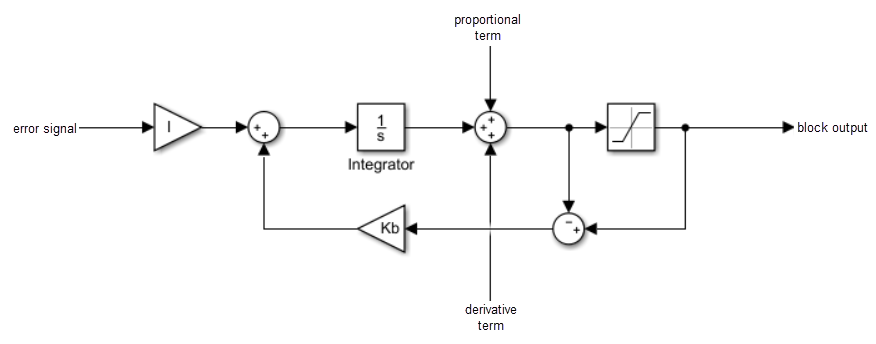

Use the Back-calculation coefficient (Kb) parameter
to specify the gain of the anti-windup feedback circuit. It is usually
satisfactory to set Kb = I, or for controllers with
derivative action, Kb = sqrt(I*D). Back-calculation can
be effective for plants with relatively large dead time
[1].

clamping

Integration stops when the sum of the block components exceeds the output
limits and the integrator output and block input have the same sign.
Integration resumes when the sum of the block components exceeds the output
limits and the integrator output and block input have opposite sign.
Clamping is sometimes referred to as conditional integration.

Clamping can be useful for plants with relatively small dead times, but
can yield a poor transient response for large dead times
[1].

Dependencies

To enable this parameter, select the Limit output
parameter.

Programmatic Use

Block Parameter:
AntiWindupMode

Type: string, character vector

Values:
"none",
"back-calculation","clamping"

Default:
"none"

Back-calculation coefficient (Kb) — Gain coefficient of anti-windup feedback loop
1 (default) | scalar

The back-calculation anti-windup method unwinds the integrator when the
block output saturates. It does so by feeding back to the integrator the difference
between the saturated and unsaturated control signal. Use the Back-calculation
coefficient (Kb) parameter to specify the gain of the anti-windup
feedback circuit. For more information, see the Anti-windup method
parameter.

Dependencies

To enable this parameter, select the Limit output parameter, and set the
Anti-windup method parameter to
back-calculation.

Programmatic Use

Block Parameter: Kb

Type: scalar

Default: 1

Integrator saturation

Limit Output — Limit integrator output to specified saturation limits
`off` (default) | `on`

Enable this parameter to limit the integrator output to be within a specified range. When the
integrator output reaches the limits, the integral action turns off to prevent integral
windup. Specify the saturation limits using the Lower limit and
Upper limit parameters.

Dependencies

To enable this parameter, set Controller to a controller type
that has integral action.

Programmatic Use

Block Parameter: LimitIntegratorOutput

Type: string, character vector

Values: "off", "on"

Default: "off"

Upper limit — Upper saturation limit for integrator
`Inf` (default) | scalar

Specify the upper limit for the integrator output. The integrator output is held at this value whenever it would otherwise exceed this value.

Dependencies

To enable this parameter, under Integrator saturation, select Limit output.

Programmatic Use

Block Parameter: UpperIntegratorSaturationLimit

Type: scalar

Default: Inf

Lower limit — Lower saturation limit for integrator
`-Inf` (default) | scalar

Specify the lower limit for the integrator output. The integrator output is held at this value whenever it would otherwise go below this value.

Dependencies

To enable this parameter, under Integrator saturation, select Limit output.

Programmatic Use

Block Parameter: LowerIntegratorSaturationLimit

Type: scalar

Default: -Inf

Data Types

The parameters in this tab are primarily of use in fixed-point code generation using Fixed-Point Designer™. They define how numeric quantities associated with the block are stored and processed when you generate code.

If you need to configure data types for fixed-point code generation, click Open Fixed-Point Tool and use that tool to configure the rest of the parameters in the tab. For information about using Fixed-Point Tool, see Autoscaling Data Objects Using the Fixed-Point Tool (Fixed-Point Designer).

After you use Fixed-Point Tool, you can use the parameters in this tab to make adjustments to fixed-point data-type settings if necessary. For each quantity associated with the block, you can specify:

Floating-point or fixed-point data type, including whether the data type is inherited from upstream values in the block.
The minimum and maximum values for the quantity, which determine how the quantity is scaled for fixed-point representation.

For assistance in selecting appropriate values, click to open the Data Type Assistant for the corresponding quantity. For more information, see Specify Data Types Using Data Type Assistant.

The specific quantities listed in the Data Types tab vary depending on how you configure the PID controller block. In general, you can configure data types for the following types of quantities:

Product output — Stores the result of a multiplication carried out under the block mask. For example, P product output stores the output of the gain block that multiplies the block input with the proportional gain P.
Parameter — Stores the value of a numeric block parameter, such as P, I, or D.
Block output — Stores the output of a block that resides under the PID controller block mask. For example, use Integrator output to specify the data type of the output of the block called Integrator. This block resides under the mask in the Integrator subsystem, and computes integrator term of the controller action.
Accumulator — Stores values associated with a sum block. For example,
SumI2 Accumulator sets the data type of the accumulator
associated with the sum block SumI2. This block resides under the mask in the Back
Calculation subsystem of the Anti-Windup subsystem.

In general, you can find the block associated with any listed parameter by looking under the
PID Controller block mask and examining its subsystems. You can also use the Model Explorer
to search under the mask for the listed parameter name, such as SumI2.
(See Model
Explorer.)

Matching Input and Internal Data Types

By default, all data types in the block are set to Inherit: Inherit via internal rule. With this setting, Simulink chooses data types to balance numerical accuracy, performance, and generated code size, while accounting for the properties of the embedded target hardware.

Under some conditions, incompatibility can occur between data types within the block. For
instance, in continuous time, the Integrator block under the mask can accept only signals of
type double. If the block input signal is a type that cannot be
converted to double, such as uint16,
the internal rules for type inheritance generate an error when you generate code.

To avoid such errors, you can use the Data Types settings to force a data type conversion. For
instance, you can explicitly set P product output, I product
output, and D product output to
double, ensuring that the signals reaching the
continuous-time integrators are of type double.

In general, it is not recommended to use the block in continuous time for code generation
applications. However, similar data type errors can occur in discrete time, if you
explicitly set some values to data types that are incompatible with downstream signal
constraints within the block. In such cases, use the Data Types settings to ensure that all
data types are internally compatible.

Fixed-Point Operational Parameters

Integer rounding mode — Rounding mode for fixed-point operations
`Floor` (default) | `Ceiling` | `Convergent` | `Nearest` | `Round` | `Simplest` | `Zero`

Specify the rounding mode for fixed-point operations. For more information, see Rounding (Fixed-Point Designer).

Block parameters always round to the nearest representable value. To control the
rounding of a block parameter, enter an expression using a MATLAB^® rounding function into the mask field.

Programmatic Use

Block Parameter:
RndMeth

Type: character vector

Values:

'Ceiling' | 'Convergent' | 'Floor' | 'Nearest' | 'Round' | 'Simplest' |

                        'Zero'

Default:
'Floor'

Saturate on integer overflow — Method of overflow action
`off` (default) | `on`

Specify whether overflows saturate or wrap.

off — Overflows wrap to the appropriate value that the data type can represent.

For example, the number 130 does not fit in a signed 8-bit integer and wraps to -126.
on — Overflows saturate to either the minimum or maximum value that the data type can represent.

For example, an overflow associated with a signed 8-bit integer can saturate to -128 or 127.

Tip

Consider selecting this check box when your model has a possible overflow and you want explicit saturation protection in the generated code.
Consider clearing this check box when you want to optimize efficiency of your generated code.

Clearing this check box also helps you to avoid overspecifying how a block handles out-of-range signals. For more information, see Troubleshoot Signal Range Errors.
When you select this check box, saturation applies to every internal operation on the block, not just the output or result.
In general, the code generation process can detect when overflow is not possible. In this case, the code generator does not produce saturation code.

Programmatic Use

Block Parameter: SaturateOnIntegerOverflow

Type: character vector

Values: 'off' | 'on'

Default: 'off'

Lock data type settings against changes by the fixed-point tools — Prevent fixed-point tools from overriding data types
`off` (default) | `on`

Select this parameter to prevent the fixed-point tools from overriding the data types you specify on this block. For more information, see Lock the Output Data Type Setting (Fixed-Point Designer).

Programmatic Use

Block Parameter: LockScale

Type: character vector

Values: 'off' | 'on'

Default: 'off'

State Attributes

The parameters in this tab are primarily of use in code generation.

State name (e.g., ‘position’) — Name for continuous-time filter and integrator states
`''` (default) | character vector

Assign a unique name to the state associated with the integrator or the filter, for continuous-time PID controllers. (For information about state names in a discrete-time PID controller, see the State name parameter.) The state name is used, for example:

For the corresponding variable in generated code
As part of the storage name when logging states during simulation
For the corresponding state in a linear model obtain by linearizing the block

A valid state name begins with an alphabetic or underscore character, followed by alphanumeric or underscore characters.

Dependencies

To enable this parameter, set Time domain to Continuous-time.

Programmatic Use

Parameter: IntegratorContinuousStateAttributes, FilterContinuousStateAttributes

Type: character vector

Default: ''

State name — Names for discrete-time filter and integrator states
empty string (default) | string | character vector

Assign a unique name to the state associated with the integrator or the filter, for discrete-time PID controllers. (For information about state names in a continuous-time PID controller, see the State name (e.g., ‘position’) parameter.)

A valid state name begins with an alphabetic or underscore character, followed by alphanumeric or underscore characters. The state name is used, for example:

For the corresponding variable in generated code
As part of the storage name when logging states during simulation
For the corresponding state in a linear model obtain by linearizing the block

For more information about the use of state names in code generation, see C Code Generation Configuration for Model Interface Elements (Simulink Coder).

Dependencies

To enable this parameter, set Time domain to Discrete-time.

Programmatic Use

Parameter: IntegratorStateIdentifier, FilterStateIdentifier

Type: string, character
vector

Default: ""

State name must resolve to Simulink signal object — Require that state name resolve to a signal object
`off` (default) | `on`

Select this parameter to require that the discrete-time integrator or filter state name resolves to a Simulink signal object.

Dependencies

To enable this parameter for the discrete-time integrator or filter state:

Set Time domain to Discrete-time.
Specify a value for the integrator or filter State name.
Set the model configuration parameter Signal resolution to a value other than None.

Programmatic Use

Block Parameter: IntegratorStateMustResolveToSignalObject, FilterStateMustResolveToSignalObject

Type: string, character vector

Values: "off", "on"

Default: "off"

Block Characteristics

Data Types	`double` \| `fixed point` \| `integer` \| `single`
Direct Feedthrough	`no`
Multidimensional Signals	`no`
Variable-Size Signals	`no`
Zero-Crossing Detection	`no`

References

[1] Visioli, A., “Modified
Anti-Windup Scheme for PID Controllers,” IEE Proceedings – Control Theory and
Applications, Vol. 150, Number 1, January 2003

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

For continuous-time PID controllers (Time domain set to Continuous-time):

Consider using Model Discretizer to map continuous-time blocks to
discrete equivalents that support code generation. To access Model Discretizer,
from your model, in the Apps tab, under Control
Systems, click Model Discretizer.
Not recommended for production code.

For discrete-time PID controllers (Time domain set to Discrete-time):

Depends on absolute time when placed inside a triggered subsystem hierarchy.
Generated code relies on memcpy or memset functions (string.h) under certain conditions.

HDL Code Generation
Generate Verilog and VHDL code for FPGA and ASIC designs using HDL Coder™.

HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.

HDL Architecture

This block has one default HDL architecture.

HDL Block Properties

ConstrainedOutputPipeline	Number of registers to place at the outputs by moving existing delays within your design. Distributed pipelining does not redistribute these registers. The default is `0`. For more details, see ConstrainedOutputPipeline (HDL Coder).
InputPipeline	Number of input pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is `0`. For more details, see InputPipeline (HDL Coder).
OutputPipeline	Number of output pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is `0`. For more details, see OutputPipeline (HDL Coder).

Restrictions

HDL code generation is supported for discrete-time PID controllers only (Time domain set to Discrete-time).
If the Integrator method is set to BackwardEuler or Trapezoidal, you cannot generate HDL code for the block under either of the following conditions:
- Limit output is selected and the Anti-Windup Method is anything other than none.
- Enable tracking mode is selected.
To generate HDL code:
- Use a discrete-time PID controller. On the Time
  domain section, specify .
- Leave the Use filtered derivative check
  box selected.
- Specify the initial conditions of the filter and integrator
  internally. On the Initialization tab,
  specify as
  internal.
  
  You can specify the filter coefficients internally and
  externally for HDL code generation. On the
  Main tab, for
  Source, you can use
  internal or
  external.
- Set to
  none.
- When you use double inputs, do not set
  to
  clamping.

PLC Code Generation
Generate Structured Text code using Simulink® PLC Coder™.

Fixed-Point Conversion
Design and simulate fixed-point systems using Fixed-Point Designer™.

Fixed-point code generation is supported for discrete-time PID controllers only (Time domain set to Discrete-time).

Version History

Introduced in R2009b

expand all

R2022b: Issues error when integrator and filter initial conditions lie outside saturation
limits

The block now issues an error when the integrator or filter initial condition value
lies outside the output saturation limits. In previous releases, the block did not issue
an error when these initial conditions had such values.

If this change impacts your model, update the PID integrator or filter initial
condition values such that they are within the output saturation limits.

R2021b: `ReferenceBlock` parameter returns different path

Starting in R2021b, the get_param function returns a different
value for the ReferenceBlock parameter. The
ReferenceBlock parameter is a property common to all Simulink blocks and gives the path of the library block to which a block links. The
PID Controller and Discrete PID Controller blocks now
link to 'slpidlib/PID Controller'. Previously, the blocks linked to
'pid_lib/PID Controller'.

This change does not affect any other functionality or workflows. You can still use
the previous path with the set_param function.

R2020b: `ReferenceBlock` parameter returns different path

Starting in R2020b, the get_param function returns a different
value for the ReferenceBlock parameter. The
ReferenceBlock parameter is a property common to all Simulink blocks and gives the path of the library block to which a block links. The
PID Controller and Discrete PID Controller blocks now
link to 'pid_lib/PID Controller'. Previously, the blocks linked to
'simulink/Continuous/PID Controller'.

This change does not affect any other functionality or workflows. You can still use the previous path with the set_param function.

Источник

Определение перерегулирования и времени переходного процесса в продукте Acsocad

Определение перерегулирования и времени переходного процесса в продукте MATLAB Simulink

Оценка показателей качества нескорректированной системы

8. Проведение синтеза последовательного корректирующего устройства методом Соколова

9. Построение лах и лфх скорректированной разомкнутой системы в Matlab

Description

Control Configuration

PID Gain Tuning

Examples

Ports

Input

Port_1( u ) — Error signal input scalar | vector

P — Proportional gain scalar | vector

Dependencies

I — Integral gain scalar | vector

Dependencies

I*Ts — Integral gain multiplied by sample time scalar | vector

Dependencies

D — Derivative gain scalar | vector

Dependencies

N — Filter coefficient scalar | vector

Dependencies

Reset — External reset trigger scalar

Dependencies

I0 — Integrator initial condition scalar | vector

Dependencies

D0 — Filter initial condition scalar | vector

Dependencies

up — Output saturation upper limit scalar | vector

Dependencies

lo — Output saturation lower limit scalar | vector

Dependencies

TR — Tracking signal scalar | vector

Dependencies

TDTI — Discrete-integrator time scalar

Dependencies

Output

Port_1( y ) — Controller output scalar | vector

Parameters

Controller — Controller type PID (default) | PI | PD | P | I

Programmatic Use

Form — Controller structure Parallel (default) | Ideal

Programmatic Use

Time domain — Specify discrete-time or continuous-time controller Discrete-time (default) | Continuous-time

Programmatic Use

PID Controller is inside a conditionally executed subsystem — Enable the discrete-integrator time port off (default) | on

Dependencies

Programmatic Use

Sample time (-1 for inherited) — Discrete interval between samples –1 (default) | positive scalar

Dependencies

Programmatic Use

Integrator method — Method for computing integral in discrete-time controller Forward Euler (default) | Backward Euler | Trapezoidal

Dependencies

Programmatic Use

Filter method — Method for computing derivative in discrete-time controller Forward Euler (default) | Backward Euler | Trapezoidal

Dependencies

Programmatic Use

Main

Source — Source for controller gains and filter coefficient internal (default) | external

Programmatic Use

Proportional (P) — Proportional gain 1 (default) | scalar | vector

Dependencies

Programmatic Use

Integral (I) — Integral gain 1 (default) | scalar | vector

Dependencies

Programmatic Use

Integral (I*Ts) — Integral gain multiplied by sample time 1 (default) | scalar | vector

Dependencies

Programmatic Use

Use I*Ts — Use integral gain multiplied by sample time off (default) | on

Dependencies

Programmatic Use

Derivative (D) — Derivative gain 0 (default) | scalar | vector

Dependencies

Programmatic Use

Use filtered derivative — Apply filter to derivative term on (default) | off

Dependencies

Programmatic Use

Filter coefficient (N) — Derivative filter coefficient 100 (default) | scalar | vector

Dependencies

Port_1( u ) — Error signal input
scalar | vector

P — Proportional gain
scalar | vector

I — Integral gain
scalar | vector

**I*T_s** — Integral gain multiplied by sample time
scalar | vector

D — Derivative gain
scalar | vector

N — Filter coefficient
scalar | vector

Reset — External reset trigger
scalar

I₀ — Integrator initial condition
scalar | vector

D₀ — Filter initial condition
scalar | vector

up — Output saturation upper limit
scalar | vector

lo — Output saturation lower limit
scalar | vector

TR — Tracking signal
scalar | vector

T_DTI — Discrete-integrator time
scalar

Port_1( y ) — Controller output
scalar | vector

Controller — Controller type
`PID` (default) | `PI` | `PD` | `P` | `I`

Form — Controller structure
`Parallel` (default) | `Ideal`

Time domain — Specify discrete-time or continuous-time controller
`Discrete-time` (default) | `Continuous-time`

PID Controller is inside a conditionally executed subsystem — Enable the discrete-integrator time port
`off` (default) | `on`

Sample time (-1 for inherited) — Discrete interval between samples
–1 (default) | positive scalar

Integrator method — Method for computing integral in discrete-time controller
`Forward Euler` (default) | `Backward Euler` | `Trapezoidal`

Filter method — Method for computing derivative in discrete-time controller
`Forward Euler` (default) | `Backward Euler` | `Trapezoidal`

Source — Source for controller gains and filter coefficient
internal (default) | external

Proportional (P) — Proportional gain
1 (default) | scalar | vector

Integral (I) — Integral gain
1 (default) | scalar | vector

**Integral (I*Ts)** — Integral gain multiplied by sample time
1 (default) | scalar | vector

**Use I*Ts** — Use integral gain multiplied by sample time
`off` (default) | `on`

Derivative (D) — Derivative gain
0 (default) | scalar | vector

Use filtered derivative — Apply filter to derivative term
`on` (default) | `off`

Filter coefficient (N) — Derivative filter coefficient
100 (default) | scalar | vector

Select tuning method — Tool for automatic tuning of controller coefficients
`Transfer Function Based (PID Tuner App)` (default) | `Frequency Response Based`

Enable zero-crossing detection — Detect zero crossings on reset and on entering or leaving a saturation state
`on` (default) | `off`

Source — Source for integrator and derivative initial conditions
`internal` (default) | `external`

Integrator — Integrator initial condition
0 (default) | scalar | vector

Filter — Filter initial condition
0 (default) | scalar | vector

Differentiator — Initial condition for unfiltered derivative
0 (default) | scalar | vector

Initial condition setting — Location at which initial condition is applied
`Auto` (default) | `Output`

External reset — Trigger for resetting integrator and filter values
`none` (default) | `rising` | `falling` | `either` | `level`

Ignore reset when linearizing — Force linearization to ignore reset
`off` (default) | `on`

Enable tracking mode — Activate signal tracking
`off` (default) | `on`

Tracking coefficient (Kt) — Gain of signal-tracking feedback loop
1 (default) | scalar

Limit Output — Limit block output to specified saturation values
`off` (default) | `on`

Source — Source for output saturation limits
internal (default) | external

Upper limit — Upper saturation limit for block output
`Inf` (default) | scalar

Lower limit — Lower saturation limit for block output
`-Inf` (default) | scalar

Ignore saturation when linearizing — Force linearization to ignore output limits
`off` (default) | `on`

Anti-windup method — Integrator anti-windup method
`none` (default) | `back-calculation` | `clamping`

Back-calculation coefficient (Kb) — Gain coefficient of anti-windup feedback loop
1 (default) | scalar

Limit Output — Limit integrator output to specified saturation limits
`off` (default) | `on`

Upper limit — Upper saturation limit for integrator
`Inf` (default) | scalar

Lower limit — Lower saturation limit for integrator
`-Inf` (default) | scalar

Integer rounding mode — Rounding mode for fixed-point operations
`Floor` (default) | `Ceiling` | `Convergent` | `Nearest` | `Round` | `Simplest` | `Zero`

Saturate on integer overflow — Method of overflow action
`off` (default) | `on`

Lock data type settings against changes by the fixed-point tools — Prevent fixed-point tools from overriding data types
`off` (default) | `on`