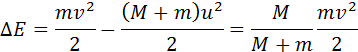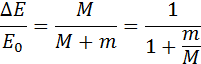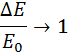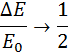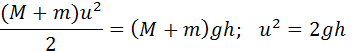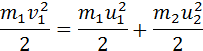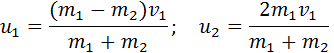§5. Задачи на столкновения и законы сохранения импульса и энергии
В физике под столкновениями понимают процессы взаимодействия между телами (частицами) в широком смысле слова, а не только в буквальном – как соприкосновение тел. Сталкивающиеся тела на большом расстоянии являются свободными. Проходя друг мимо друга, тела взаимодействуют между собой, в результате могут происходить различные процессы – тела могут соединиться в одно тело (абсолютно неупругий удар), могут возникать новые тела и, наконец, может иметь место упругое столкновение, при котором тела после некоторого сближения вновь расходятся без изменения своего внутреннего состояния. Столкновения, сопровождающиеся изменением внутреннего состояния тел, называются неупругими. Тела (частицы), участвующие в столкновении, характеризуются (до и после столкновения) импульсами, энергиями. Процесс столкновения сводится к изменению этих величин в результате взаимодействия. Законы сохранения энергии и импульса позволяют достаточно просто устанавливать соотношения между различными физическими величинами при столкновении тел. Особенно ценным здесь является то обстоятельство, что зачастую законы сохранения могут быть использованы даже в тех случаях, когда действующие силы не известны. Так обстоит дело, например, в физике элементарных частиц.
Происходящие в обычных условиях столкновения макроскопических тел почти всегда бывают в той или иной степени неупругими – уже хотя бы потому, что они сопровождаются некоторым нагреванием тел, т. е. переходом части их кинетической энергии в тепло. Тем не менее, в физике понятие об упругих столкновениях играет важную роль – с такими столкновениями часто приходится иметь дело в физическом эксперименте в области атомных явлений, да и обычные столкновения можно часто с достаточной степенью точности считать упругими.
Сохранение импульса тел (частиц) при столкновении обусловлено тем, что совокупность тел, участвующих в столкновении, составляет либо изолированную систему, т. е. на тела, входящие в систему, не действуют внешние силы, либо замкнутую: внешние силы отличны от нуля, а сумма внешних сил равна нулю. Несколько сложнее обстоит дело с применением закона сохранения энергии при столкновениях. Обращение к сохранению энергии требует порой учёта различных форм внутренней энергии.
Можно сказать, что действие законов сохранения импульса и энергии в процессах столкновения подтверждено широким спектром опытных данных.
Переходя к характерным примерам, отметим, что исследование столкновений традиционно проводится как в лабораторной системе отсчёта (ЛСО), т. е. в инерциальной системе отсчёта, связанной с лабораторией, где проводится опыт, так и в системе центра масс, с которой Вы познакомитесь в следующих Заданиях. Напомним также, что центральным ударом шаров (шайб), называют удар, при котором скорости шаров (шайб) направлены вдоль прямой, проходящей через их центры.
Неупругие столкновения
Частица массой `m` с кинетической энергией `K` сталкивается с неподвижной частицей массой `M`. Найдите приращение `Q` внутренней энергии системы частиц в результате абсолютно неупругого столкновения («слипания»).
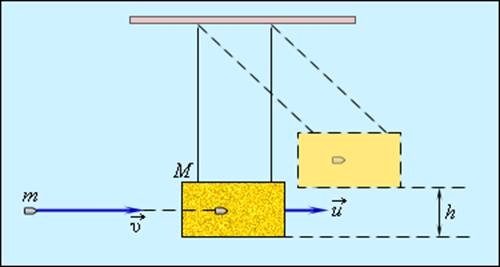
Рассмотрим абсолютно неупругий удар двух тел в ЛСО. Налетающая частица движется до столкновения в положительном направлении оси `Ox` со скоростью `vec v`, кинетическая энергия частицы `K = (mv^2)/2`. В результате абсолютно неупругого удара (слипания) частицы движутся с одинаковой скоростью `vec u`. По закону сохранения импульса
`mv = (m + M) u`.
По закону сохранения энергии
`(mv^2)/2 = ((m + M)u^2)/2 + Q`.
Из приведённых соотношений находим
`Q = M/(m + M) K`.
Отметим, что в предельных случаях
`Q = K`,
`m < < M`,
`Q = M/m K < < K`,
`m > > M`.
Как видим, при неупругом столкновении лёгкой частицы с массивной (например, электрона с атомом) происходит почти полный переход её кинетической энергии во внутреннюю энергию массивной частицы.
При равенстве масс `(m = M)` `Q = K/2`.
Отсюда следует, например, что при столкновении двух одинаковых автомобилей, один из которых неподвижен, а другой движется по направлению к нему, половина кинетической энергии идёт на разрушение.
Упругие столкновения
На гладкой горизонтальной поверхности лежит гладкий шар массой `M`. На него налетает гладкий шар того же радиуса массой `m`, движущийся со скоростью `vec v`. Происходит упругий центральный удар шаров. Найдите скорости `vecv_1` и `vecv_2` шаров после соударения. При каком условии налетающий шар будет двигаться после соударения в прежнем направлении?
Задачу рассмотрим в ЛСО, ось `Ox` которой направим по линии центров шаров в момент соударения. Внешние силы, действующие на шары в процессе соударения, это силы тяжести и силы нормальной реакции опоры. Их сумма равна нулю. Следовательно, импульс системы шаров в процессе взаимодействия не изменяется. По закону сохранения импульса
`m vec v = m vecv_1 + M vecv_2`.
Переходя к проекциям на ось `Ox`, получаем
`mv = mv_(1x) + Mv_2`,
здесь учтено, что направление скорости налетающего шара после соударения не известно. По закону сохранения энергии
`(mv^2)/2 = (mv_(1x)^2)/2 + (Mv_2^2)/2`.
Полученные соотношения перепишем в виде
`m(v – v_(1x)) = Mv_2`,
`m(v^2 – v_(1x)^2) = Mv_2^2`.
Разделив второе равенство на первое `(v != v_(1x))`, приходим к линейной системе `v_2 = v + v_(1x)`, `m(v – v_(1x)) = Mv_2`, решение которой имеет вид
`v_(1x) = (m – M)/(m + M) v`,
`v_2 = (2m)/(m + M) v`.
Налетающий шар будет двигаться после соударения в прежнем направлении `(v_(1x) > 0)` при `m > M`, т. е. если масса налетающего шара больше массы покоящегося шара.
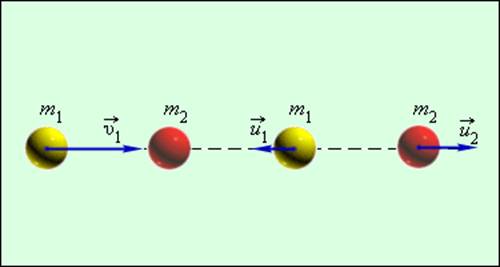
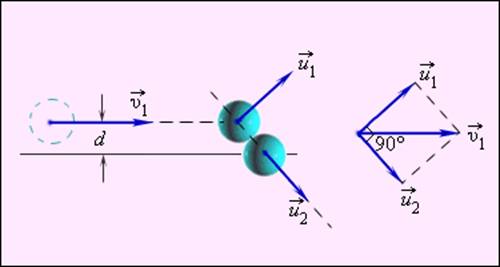
Две гладкие упругие круглые шайбы движутся поступательно по гладкой горизонтальной поверхности. Скорости `vecv_1` и `vecv_2` шайб непосредственно перед соударением известны и показаны на рис. 11. Найдите скорости `vecv_(1)^’` и `vecv_(2)^’` шайб после абсолютно упругого нецентрального соударения. Массы шайб `m_1` и `m_2`.
Задачу рассмотрим в ИСО, оси координат `Ox` и `Oy` которой лежат в горизонтальной плоскости, при этом ось `Ox` направлена по линии центров шайб в момент соударения (рис. 11).
В течение времени соударения на систему шайб действуют только вертикальные внешние силы: это силы тяжести и силы нормальной реакции. Их сумма равна нулю. Тогда импульс системы шайб в процессе взаимодействия сохраняется:
`vecp_1 + vecp_2 = vecp_(1)^’ + vecp_(2)^’`,
здесь `vecp_1 = m_1 vecv_1`, `vecp_2 = m_2 vecv_2`, `vecp_(1)^’= m_1 vecv_(1)^’`, `vecp_(2)^’ = m_2 vecv_(2)^’` – импульсы шайб до и после соударения.
Так как шайбы идеально гладкие, то в процессе соударения внутренние силы -силы упругого взаимодействия – направлены только по оси `Ox`. Эти силы не изменяют `y`-составляющие импульсов шайб. Тогда из `p_(1y) = p_(1y)^’`, `p_(2y) = p_(2y)^’` находим `y`-составляющие скоростей шайб после соударения:
`v_(1y)^’ = v_(1y)`, `v_(2y)^’ = v_(2y)`,
т. е. в проекции на ось `Oy` скорости шайб в результате соударения не изменились.
Найдём `x`-составляющие скоростей шайб после упругого соударения. При таком соударении сохраняется кинетическая энергия
`(m_1 (v_(1x)^2 + v_(1y)^2))/2 + (m_2 (v_(2x)^2 + v_(2y)^2))/2 = (m_1 ((v_(1x)^’)^2 + (v_(1y)^’)^2))/2 + (m_2 ((v_(2x)^’)^2 + (v_(2y)^’)^2))/2`.
С учётом равенства `y`-составляющих скоростей шайб до и после соударения последнее равенство принимает вид:
`(m_1 v_(1x)^2)/2 + (m_2 v_(2x)^2)/2 = (m_1 (v_(1x)^’)^2)/2 + (m_2 (v_(2x)^’)^2)/2`.
Обратимся к закону сохранения импульса и перейдём к проекциям импульсов шайб на ось `Ox`:
`m_1 v_(1x) + m_2 v_(2x) = m_1 v_(1x)^’ + m_2 v_(2x)^’`.
Таким образом, исходная задача сведена к задаче об абсолютно упругом центральном ударе: именно такой вид приняли бы законы сохранения энергии и импульса, если бы скорости шайб были направлены по линии центров. Полученную нелинейную систему уравнений можно свести к линейной. Для этого следует (как и в предыдущей задаче) в обоих уравнениях по одну сторону знака равенства объединить слагаемые, относящиеся к первой шайбе, а по другую – ко второй, и разделить `(v_(1x) != v_(1x)^’)` полученные соотношения. Это приводит к линейному уравнению
`v_(1x) + v_(1x)^’ = v_(2x) + v_(2x)^’`.
Решая систему из двух последних уравнений, находим
`v_(1x)^’ = ((m_1 – m_2) v_(1x) + 2m_2 v_(2x))/(m_1 + m_2)`,
`v_(2x)^’ = (2m_1 v_(1x) + (m_2 – m_1) v_(2x))/(m_1 + m_2)`.
Полученные соотношения для `v_(1x)^’`, `v_(1y)^’` и `v_(2x)^’`, `v_(2y)^’` решают вопрос о проекциях и величинах скоростей шайб после соударения
`v_1^’ = sqrt((v_(1x)^’)^2 + (v_(1y)^’)^2)`, `v_2^’ = sqrt((v_(2x)^’)^2 + (v_(2y)^’)^2)`,
а также об углах `alpha_1` и `alpha_2`, которые векторы скорости `vecv_(1)^’` и `vecv_(2)^’` образуют с положительным направлением оси `Ox`,
`bbb”tg” alpha_1 = (v_(1y)^’)/(v_(1x)^’)`, `bbb”tg” alpha_2 = (v_(2y)^’)/(v_(2x)^’)`.
Построенное в общем виде решение задач упругого центрального и нецентрального соударений открывает дорогу к анализу целого ряда задач, для которых рассмотренная модель соответствует характеру взаимодействия тел (частиц). Приведём пример.
Гладкая круглая шайба массой `m_1` движется со скоростью `vec v` вдоль хорды, расстояние до которой от центра гладкого тонкого однородного обруча равно `R//2` (рис. 12). Обруч массой `m_2` и радиусом `R` лежит на гладком горизонтальном столе. Через какое время `tau` после первого удара шайба окажется на минимальном расстоянии от центра движущегося обруча? Каково это расстояние? Удар считайте абсолютно упругим.
Воспользуемся результатами, полученными в предыдущем примере. В ЛСО, ось `Ox` которой направлена по линии центров шайбы и обруча в момент соударения, проекции скоростей шайбы и центра обруча на ось `Ox` после соударения равны соответственно
`v_(1x)^’ = ((m_1 – m_2)v_(1x) + 2m_2 v_(2x))/(m_1 + m_2) = ((m_1 – m_2)v_(1x))/(m_1 + m_2)`,
`v_(2x)^’ = (2m_1 v_(1x) + (m_2 – m_1)v_(2x))/(m_1 + m_2) = (2m_1 v_(1x))/(m_1 + m_2)`,
здесь `v_(1x) = vcos pi/6` – проекция скорости шайбы на ось `Ox` до соударения, `v_(2x) = 0` – обруч до соударения покоился.
Из этих соотношений следует, что в системе отсчёта, связанной с обручем, проекция скорости шайбы на линию центров после соударения
`v_(1xsf”отн”) = v_(1x)^’ – v_(2x)^’ =- v_(1x) =- vcos pi/6`
просто изменила знак, а перпендикулярная линии центров составляющая, как было показано, в рассматриваемом соударении не изменяется. Следовательно, в системе, связанной с обручем, шайба отразится по закону «угол падения равен углу отражения», и минимальное расстояние от шайбы до центра обруча снова будет равно `R//2`. Искомое время
`tau = (R cos^(2) pi/6)/|v_(1xsf”отн”)| = cos pi/6 R/v = sqrt3/2 R/v`.
|
|
Макеты страниц
Законы сохранения энергии и импульса часто позволяют гораздо проще получить ответы на некоторые вопросы, связанные с движением тел, чем непосредственное применение законов динамики. Разумеется, информация, получаемая с помощью законов сохранения, не является такой исчерпывающей, как при использовании законов динамики, но зато и получается она гораздо более легким путем. Особенно ценным здесь является то обстоятельство, что зачастую законы сохранения могут быть использованы даже в тех случаях, когда действующие силы неизвестны. Так обстоит дело, например, в физике элементарных частиц.
Законы сохранения энергии и импульса фактически являются единственным средством теоретического изучения процессов столкновения тел, когда характер действующих при столкновении сил неизвестен. Под столкновениями в физике понимают самые разнообразные процессы взаимодействия между телами при условии, что на бесконечно большом расстоянии друг от друга тела являются свободными. Когда тела проходят одно мимо другого, они взаимодействуют между собой, и результаты такого взаимодействия могут быть самыми разнообразными: тела могут соединиться вместе в одно тело (абсолютно неупругий удар), в результате соударения могут возникнуть новые тела, может случиться и так, что после взаимодействия тела вновь расходятся без изменения своего внутреннего состояния (абсолютно упругий удар). Столкновения макроскопических тел всегда в той или иной степени являются неупругими, однако в области физики атомных явлений и процессов с элементарными частицами понятие об упругом ударе играет важную роль, так как благодаря дискретному характеру энергетического спектра сталкивающихся частиц их внутреннее состояние либо не меняется вообще (упругий удар), либо скачком изменяется на конечную величину.
Неупругие столкновения. Рассмотрим абсолютно неупругий удар двух тел, при котором они соединяются вместе и движутся дальше как одно тело. Слипание вместе пластилиновых шаров, застревание пули в деревянном бруске, захват нейтрона атомным ядром — все это примеры абсолютно неупругого удара. Если сталкивающиеся тела образуют замкнутую систему, в которой действуют только внутренние силы, то полный импульс системы остается неизменным. Это позволяет легко определить скорость тела, образовавшегося в результате неупругого соударения двух тел.
Обозначим скорости тел с массами 





получаем

Легко видеть, что определяемая формулой (1) скорость 
Приведенная масса. При неупругом ударе кинетическая энергия поступательного движения сталкивающихся тел убывает, частично
превращаясь во внутреннюю энергию. Кинетическая энергия поступательного движения тел системы до удара

после удара

Подставляя в (2) скорость и из (1) и составляя разность кинетических энергий до и после удара, найдем

где

— так называемая приведенная масса двух тел. По существу (2) есть кинетическая энергия поступательного движения системы как целого, которая в замкнутой системе не меняется, ибо остается неизменной скорость центра масс. Поэтому (3) можно рассматривать как кинетическую энергию относительного движения сталкивающихся частиц, которая при неупругом столкновении превращается в другие виды энергии, например в теплоту.
Упругие столкновения. В отличие от неупругого, при абсолютно упругом ударе сохраняется не только импульс, но и механическая энергия, так как внутреннее состояние сталкивающихся частиц после удара остается таким же, каким оно было до удара. Так как частицы до и после столкновения являются свободными, то потенциальная энергия отсутствует, и сохранение механической энергии означает сохранение кинетической энергии сталкивающихся частиц.
При изучении закономерностей упругого столкновения будем для простоты считать, что одна из частиц (массы 





Начнем с некоторых простых частных случаев. Прежде всего рассмотрим «лобовое» столкновение частиц, например шаров, при
котором скорость 


Если массы шаров одинаковы 



Все описанные закономерности легко наблюдать на опыте, изучая столкновения движущихся на воздушной подушке тележек, снабженных упругими пружинными бамперами.
Передача энергии при ударе. Рассматривая изменение кинетической энергии шаров в результате удара, можно убедиться, что в случае равных масс происходит полный обмен энергией, в то время как при большой разнице в массах снаряд при столкновении может передать мишени лишь малую часть своей энергии. В самом деле, пусть, например, снаряд много легче мишени: Тогда, пренебрегая в знаменателе формулы (7) для 




Аналогичный результат получится и в случае, если снаряд значительно тяжелее мишени 
В действительности лобовой удар — это большая редкость. Его относительно легко осуществить разве что при игре в бильярд, а при столкновении молекул, атомов и элементарных частиц подавляющее число ударов являются нецентральными.
Если частица налетает на неподвижную частицу такой же массы, то при нецентральном упругом ударе частицы разлетаются под прямым углом друг к другу. Действительно, законы сохранения импульса и энергии (5) и (6) при 

Первое из этих равенств означает, что векторы скоростей 



Рис. 129. Векторы 
Однако законов сохранения энергии и импульса недостаточно для определения направления векторов 

Система центра масс. В общем случае частиц с разными массами применение законов сохранения к изучению процесса столкновения удобно интерпретировать геометрически. Для этого перейдем из лабораторной инерциальной системы отсчета, в которой частица-мишень до столкновения покоится, в другую инерциальную систему отсчета, в которой центр масс сталкивающихся частиц покоится как до столкновения, так и после. Эта система отсчета движется относительно лабораторной с такой же скоростью, как и центр масс:

так как мишень до столкновения в лабораторной системе отсчета покоится 
В системе центра масс движутся обе частицы — как снаряд, так и мишень. Их импульсы равны по модулю и противоположны по направлению, так что полный импульс сталкивающихся частиц в этой системе отсчета равен нулю.
В силу закона сохранения импульса импульсы обеих частиц остаются равными по модулю и противоположными по направлению
т. е. когда снаряд легче мишени. Так как точка В лежит при этом внутри окружности, то угол рассеяния снаряда 


Рис. 132. Максимальный угол рассеяния 

Видно, что в этом случае угол рассеяния частицы-снаряда 



Например, при упругом рассеянии дейтронов на неподвижных протонах, когда отношение 
Угол разлета. Наряду с углом рассеяния 



Рис. 133. В случае 

На рис. 133 такое построение выполнено для случая 



Полученные с помощью законов сохранения закономерности процессов столкновений остаются в силе и для тех случаев, когда рассматриваемая система сталкивающихся частиц, строго говоря, не является замкнутой. Необходимо лишь, чтобы внешние силы были малы по сравнению с внутренними силами, действующими во время
столкновения. Тогда импульсом внешних сил за время столкновения можно пренебречь. Например, магнитное поле в камере Вильсона существенно искривляет траектории заряженных частиц до и после столкновения, однако во время столкновения действием магнитного поля можно пренебречь.
Обратимость упругих столкновений. Упругие столкновения частиц, в частности столкновения молекул, обладают замечательным свойством обратимости, присущим всем консервативным системам. Представим себе, что процесс упругого соударения заснят на кинопленку. При просмотре фильма мы увидим, что частицы («молекулы») сначала сталкиваются, а затем разлетаются. Пустим теперь кинопленку в проекторе «задом наперед», т. е. в обратном направлении. Мы увидим, как частицы сходятся по траекториям, по которым они на самом деле разлетались, а затем, столкнувшись, разлетаются по траекториям, по которым они сходились. Здесь все будет происходить по тем же законам, что и в настоящем столкновении. Если заранее не знать, что пленка пущена вспять, т. е. время «обращено», то определить это с помощью законов физики не удастся. Особенно наглядно это проявляется на рисунках, где упругое столкновение изображено в системе центра масс, например на рис. 130.
Отбор нужных решений. Как уже отмечалось, применение законов сохранения энергии и импульса к процессам столкновений позволяет получить ответы на некоторые вопросы даже в тех случаях, когда неизвестен закон, описывающий силы взаимодействия между частицами. Это возможно потому, что уравнения законов сохранения фактически отражают не динамику происходящих процессов, а лишь баланс некоторых физических величин, т. е. своего рода «бухгалтерию», учитывающую «доходы» и «расходы». Поэтому при интерпретации полученных из законов сохранения результатов, как правило, необходим тщательный отбор решений, имеющих физический смысл, т. е. соответствующих именно тем процессам, которые фигурируют в условии задачи. Дело в том, что одни и те же уравнения законов сохранения могут соответствовать разным физическим процессам, и поскольку этим уравнениям «невдомек», какой именно из этих процессов нас интересует, то они и «выдают» ответы для всех мыслимых случаев. Обратите внимание на это обстоятельство при разборе приводимых ниже задач.
Задачи
1. Столкновение альфа-частицы с протоном. Во сколько раз уменьшится скорость альфа-частицы после центрального упругого удара о неподвижный протон, масса которого 

Решение. При нахождении интересующего нас отношения скоростей нет необходимости в детальном описании самого процесса столкновения. Скорость альфа-частицы после того, как сталкивающиеся частицы разлетелись, может быть найдена с помощью законов сохранения. Условие задачи позволяет записать уравнения законов сохранения импульса и энергии в следующем виде:

где 



Для нахождения искомого отношения скоростей 




Оно имеет два корня: 


О физическом смысле корней уравнения. Строго говоря, оба корня квадратного уравнения (12) соответствуют еще и обратным процессам. Для корня 

Избежать появления корня 


и разделить его почленно на уравнение (10), записанное в виде

что допустимо при 

Теперь система линейных уравнений (10) и (13) имеет только один корень для 

2. Лобовой удар. В момент наибольшего сближения частиц при упругом лобовом столкновении их скорости одинаковы и равны V. Каковы скорости этих частиц после разлета, если до столкновения они двигались со скоростями 
Решение. Поскольку по условию задачи удар лобовой, то векторы 


Кинетическая энергия частиц имеет одно и то же значение только перед столкновением и после разлета. При сближении частиц кинетическая энергия частично превращается в потенциальную энергию их взаимодействия, которая при упругом столкновении затем снова превращается в кинетическую. Поэтому для закона сохранения энергии в данном случае можно написать лишь одно уравнение:

Обратим внимание на то, что в систему трех уравнений 





Поскольку 

В системе центра масс. К ответу можно прийти без утомительных алгебраических выкладок, если решать задачу в системе центра масс.
Уравнение (14) закона сохранения импульса фактически говорит о том, что скорость и представляет собой скорость движения центра масс частиц в лабораторной системе отсчета, а уравнение (15) — о том, что эта скорость остается такой же и после столкновения. Очевидно, что скорости частиц в системе центра масс до столкновения равны 





Обратим внимание на то, что при проведении рассуждений в системе центра масс нам не пришлось явно использовать значение отношения масс частиц у. Для ответа на соответствующий вопрос задачи его проще всего выразить через 
3. Столкновение автомобилей. Примером неупругого удара может служить столкновение автомобилей. Абсолютно неупругому удару соответствует случай, когда столкнувшиеся искореженные автомобили «сцепляются» друг с другом. Почему при лобовом столкновении тяжелого грузовика с легковым автомобилем гораздо большей опасности подвергаются пассажиры легкового автомобиля? Оцените, какие перегрузки испытывают пассажиры легкового автомобиля и водитель грузового.
Решение. Рассматривая такое столкновение, можно не учитывать взаимодействие автомобилей с покрытием дороги, так как силы сцепления колес с дорогой гораздо меньше сил, возникающих при деформации автомобилей. Другими словами, в этой задаче систему можно считать замкнутой, как если бы все это происходило на обледенелой дороге. Силы взаимодействия колес с дорогой определяют лишь время, в течение которого сцепившиеся автомобили продолжают двигаться до полной остановки. Но для ответа на вопросы задачи важно отнюдь не это время, а время, в течение которого выравниваются скорости сталкивающихся автомобилей.
Попробуем оценить это время. Предположим, что грузовик двигался со скоростью 




Дальнейшие рассуждения удобно проводить в системе отсчета, связанной с центром масс автомобилей, так как скорость центра масс за время удара 




В справедливости этих выражений можно убедиться, учитывая, что модули импульсов автомобилей в системе центра масс одинаковы. Если различие в массах велико, так что 


Отсюда видно, что ускорение у легкового автомобиля при ударе будет гораздо больше, чем у грузовика, так как скорости 




Роль привязных ремней. Еще большей опасности подвергаются пассажиры, когда привязные ремни не надеты. В этом случае пассажир не почувствует никакой силы, пока не ударится о приборный щиток или ветровое стекло. В результате ему придется остановиться не за 
• Вещество для замедления нейтронов в ядерных реакторах должно быть таким, чтобы его ядра не поглощали нейтронов. В частности, свинец и тяжелая вода почти не поглощают нейтроны. Почему же для замедления быстрых нейтронов используют дорогую тяжелую воду и не используют гораздо более дешевый свинец?
• Какие ограничения накладывают законы сохранения на угол рассеяния и на угол разлета при упругом столкновении движущейся частицы с неподвижной?
• Выполните построение векторов скоростей 



• Почему при решении задачи 2 в системе центра масс не появляются посторонние решения 
• При неупругом ударе, например при лобовом столкновении автомобилей, кинетическая энергия частично идет на совершение работы по их
деформации. Докажите, что при большом различии масс автомобилей эта «потерянная» энергия практически совпадает с первоначальной кинетической энергией легкого автомобиля.
Оглавление
- ПРЕДИСЛОВИЕ
- I. КИНЕМАТИКА
- § 1. Пространство. Время
- § 2. Механическое движение. Система отсчета
- § 3. Материальная точка. Поступательное движение
- § 4. Радиус-вектор. Перемещение
- § 5. Одновременные перемещения. Сложение перемещений
- § 6. Средняя скорость
- § 7. Скорость
- § 8. Ускорение
- § 9. Одномерное движение
- § 10. Неравномерное одномерное движение
- § 11. Движение по окружности
- § 12. Равнопеременное движение в пространстве
- § 13. Траектории
- § 14. Относительность механического движения
- II. ДИНАМИКА
- § 15. Инерция. Первый закон Ньютона
- § 16. Сила — мера взаимодействия
- § 17. Связь между силой и ускорением. Второй закон Ньютона
- § 18. Взаимодействие тел. Третий закон Ньютона
- § 19. Применение законов динамики
- § 20. Силы в природе. Трение
- § 21. Проявления сухого трения
- § 22. Силы тяготения
- § 23. Движение в поле тяготения
- § 24. Силы упругости и деформации
- § 25. Механическое состояние. Уравнение движения
- § 26. Принцип относительности Галилея
- § 27. Системы единиц
- § 28. Метод анализа размерностей
- III. ЗАКОНЫ СОХРАНЕНИЯ
- § 29. Импульс. Импульс силы
- § 30. Центр масс. Реактивное движение
- § 31. Механическая работа. Кинетическая энергия
- § 32. Потенциальная энергия
- § 33. Закон сохранения механической энергии
- § 34. Связь законов сохранения с симметрией пространства и времени
- § 35. Применение законов сохранения при решении задач
- § 36. Космическая динамика и законы сохранения
- § 37. Столкновения частиц
- § 38. Фазовая плоскость. Адиабатические инварианты
- § 39. Механическое равновесие
- § 40. Движение твердого тела
- IV. КОЛЕБАНИЯ И ВОЛНЫ
- § 41. Собственные колебания
- § 42. Затухающие колебания
- § 43. Собственные колебания в разных физических системах
- § 44. Вынужденные колебания. Резонанс
- § 45. Энергетические превращения при вынужденных колебаниях. Установление колебаний
- § 46. Волны
- § 47. Интерференция и дифракция волн. Эффект Доплера
- V. ДВИЖЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ
- § 49. Движение идеальной жидкости
- § 50. Вязкая жидкость. Обтекание тел
Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда действующие силы неизвестны. Примером такого рода задач является ударное взаимодействие тел.
С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц).
Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).
Примером абсолютно неупругого удара может служить попадание пули (или снаряда) в баллистический маятник. Маятник представляет собой ящик с песком массой M, подвешенный на веревках (рис. 1.21.1). Пуля массой m, летящая горизонтально со скоростью попадает в ящик и застревает в нем. По отклонению маятника можно определить скорость пули.
Обозначим скорость ящика с застрявшей в нем пулей через Тогда по закону сохранения импульса
При застревании пули в песке произошла потеря механической энергии:
Отношение M / (M + m) – доля кинетической энергии пули, перешедшая во внутреннюю энергию системы:
Эта формула применима не только к баллистическому маятнику, но и к любому неупругому соударению двух тел с разными массами.
При m << M
почти вся кинетическая энергия пули переходит во внутреннюю энергию. При m = M
во внутреннюю энергию переходит половина первоначальной кинетической энергии. Наконец, при неупругом соударении движущегося тела большой массы с неподвижным телом малой массы (m >> М) отношение
Дальнейшее движение маятника можно рассчитать с помощью закона сохранения механической энергии:
где h – максимальная высота подъема маятника. Из этих соотношений следует:
Измеряя на опыте высоту h подъема маятника, можно определить скорость пули υ.
|
|
|
Рисунок 1.21.1. Баллистический маятник |
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.
Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.
При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.
Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя (рис. 1.21.2).
Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров.
|
|
|
Рисунок 1.21.2. Абсолютно упругий центральный удар шаров |
В общем случае массы m1 и m2 соударяющихся шаров могут быть неодинаковыми. По закону сохранения механической энергии
Здесь υ1 – скорость первого шара до столкновения, скорость второго шара υ2 = 0, u1 и u2 – скорости шаров после столкновения. Закон сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, записывается в виде:
Мы получили систему из двух уравнений. Эту систему можно решить и найти неизвестные скорости u1 и u2 шаров после столкновения:
В частном случае, когда оба шара имеют одинаковые массы (m1 = m2), первый шар после соударения останавливается (u1 = 0), а второй движется со скоростью u2 = υ1, т. е. шары обмениваются скоростями (и, следовательно, импульсами).
Если бы до соударения второй шар также имел ненулевую скорость (υ2 ≠ 0), то эту задачу можно было бы легко свести к предыдущей с помощью перехода в новую систему отсчета, которая движется равномерно и прямолинейно со скоростью υ2 относительно «неподвижной» системы. В этой системе второй шар до соударения покоится, а первый по закону сложения скоростей имеет скорость υ1‘ = υ1 – υ2. Определив по приведенным выше формулам скорости u1 и u2 шаров после соударения в новой системе, нужно сделать обратный переход к «неподвижной» системе.
Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения.
 |
|
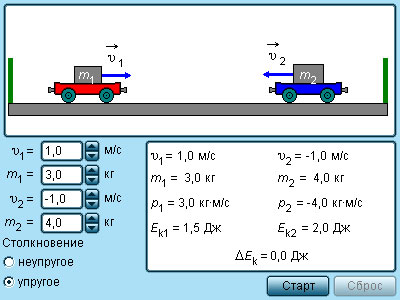
Модель. Упругие и неупругие соударения. |
Центральный (лобовой) удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой.
Частным случаем нецентрального упругого удара может служить соударение двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров (рис. 1.21.3).
|
|
|
Рисунок 1.21.3. Нецентральное упругое соударение шаров одинаковой массы. d – прицельное расстояние |
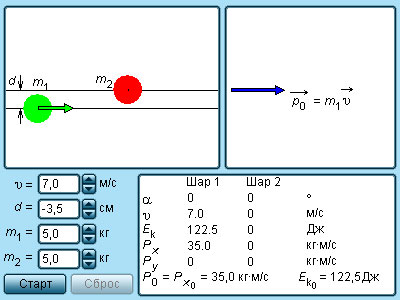
После нецентрального соударения шары разлетаются под некоторым углом друг к другу. Для определения скоростей и
после удара нужно знать положение линии центров в момент удара или прицельное расстояние d (рис. 1.21.3), т. е. расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скорости
налетающего шара. Если массы шаров одинаковы, то векторы скоростей
и
шаров после упругого соударения всегда направлены перпендикулярно друг к другу. Это легко показать, применяя законы сохранения импульса и энергии. При m1 = m2 = m эти законы принимают вид:
Первое из этих равенств означает, что векторы скоростей ,
и
образуют треугольник (диаграмма импульсов), а второе – что для этого треугольника справедлива теорема Пифагора, т. е. он прямоугольный. Угол между катетами
и
равен 90°.
 |
|
Модель. Соударения упругих шаров. |
Процесс упругого
взаимодействия осуществляется в газах
(столкновение молекул), ядерных реакциях
(например, столкновение нейтрона с
протоном).
Упругим называют
столкновение, в результате которого
внутреннее состояние взаимодействующих
частиц не меняется.
Большинство упругих
столкновений, за исключением ядерных
реакций высоких энергий, относятся к
медленным (нерелятивистским) процессам.
Для расчета процесса упругого столкновения
двух частиц применяют закон сохранения
импульса и закон сохранения энергии.
Для изолированной системы двух
взаимодействующих частиц закон сохранения
импульса запишем в виде
,
(31)
где р1
= m1v1,
p2 =
m2v2
–
импульсы частиц до взаимодействия (m1,
m2 и
v1,
v2
–
массы и скорости частиц до взаимодействия);
= m1u1,
= m2u2
–
импульсы этих же частиц после взаимодействия
(u1,
u2
–
скорости частиц после взаимодействия).
Закон сохранения энергии упругого
столкновения двух частиц
(32)
1.16.2. Лабораторная система отсчета
Применяя закон
сохранения центра масс (инерции) к
системе двух частиц с учетом формул
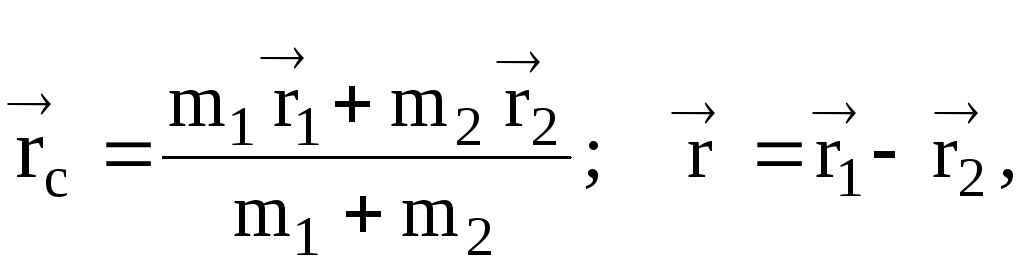
где
–
радиус-вектор центра масс;
,
–
радиус-векторы частиц в выбранной
системе отсчета, имеем
(34)
Скорости частиц
в ЛС можно выразить через скорость их
центра инерции
и
скорости их относительного движенияи
соответственно, до и после столкновения.
Дифференцируя выражение (34) по времени
и учитывая закон сохранения центра
инерции (масс),
находим векторы скорости частиц до
взаимодействия
(35)
и векторы скорости
частиц после взаимодействия
(36)
Формулы (35) и (36)
учитывают закон сохранения импульса
для взаимодействующих частиц.
1.16.3. Система центра инерции
В системе центра
инерции (СЦИ)
=
0. Векторы импульсов взаимодействующих
частиц в этой системе можно записать в
виде
где
(37)
приведенная
масса двух частиц.
Подставив полученные
значения импульсов в формулу (37), получим:

Рис. 18
Из формулы (38) видно, что
относительная скорость частиц до
взаимодействия равна относительной
скорости частиц после взаимодействия
(v = v*), т.е.
в результате столкновения частиц
скорость относительного движения
изменяет только свое направление, а по
абсолютному значению остается неизменной
(рис. 3.34). Угол
–
называют углом рассеяния в СЦИ, и по
величине он может быть любым. Если
рассматриваемые частицы движутся
навстречу друг другу с равными по
величине, но противоположно направленными
векторами импульсов
,
то суммарный импульс системы из двух
частиц равен нулю, т. е.
(39)
Поэтому при упругом
и лобовом столкновение двух частиц
(бильярдные шары) они «отражаются» друг
от друга и удаляются в противоположных
направлениях с теми же по величине
скоростями.
Замечание: условие
(39) выполняется и в случае неупругого
столкновения частиц. Следовательно,
как при упругих, так и неупругих
столкновениях в СЦИ импульсы не зависят
от угла.
Если же столкновение
не лобовое (рис. 18), то скорости частиц
после взаимодействия остаются неизменными
по величине, но направление векторов
скоростей (импульсов) частиц после
столкновения составляет некоторый угол
с их первоначальным направлением (рис.
18). При упругом взаимодействии величины
импульсов не изменяются, т. е.
.
Таким образом, в
СЦИ процесс взаимодействия характеризуется
высокой степенью симметрии и поэтому
анализ движения в ней осуществить проще,
чем в любой другой системе отсчета
(например, в экспериментах на накопительных
кольцах частицы движутся навстречу
друг другу с равными по величине, но
противоположно направленными импульсами).
Рис. 19
Если процесс столкновения
частиц является упругим, центральным
и происходит, например, вдоль оси Х (рис.
19), то для нахождения величин скоростей
частиц после взаимодействия воспользуемся
законом сохранения импульса в проекциях
на ось Х
(30)
или
(31)
и законом сохранения
энергии в виде
,
(32)
так как
,
векторы скорости всех частиц параллельны
оси Х, то vy
= 0, vz=
0 ()
и, следовательно,.
Формулы (31) и (32) преобразуем к виду
(33)
(34)
Решая совместно
выражения (33) и (34), имеем
(35)
где
,
–
соответствующие проекции относительных
скоростей на ось Х двух частиц до и после
столкновения.
Вывод:
относительная скорость двух частиц до
столкновения в точности равна их
относительной скорости после столкновения.
Такой вывод справедлив для любого
лобового упругого удара независимо от
того, какие массы имеют частицы.
Выражая последовательно
u2x и
u1x
из формулы (35) и подставив их значения
в выражение (33), находим скорости частиц
после взаимодействия:
,
(36)
.
(37)
Рассмотрим некоторые
частные случаи:
1. Если массы
взаимодействующих частиц равны (m1
= m2),
то u1x =
v2x,
u2x
= v1x,
т. е. частицы обмениваются скоростями.
2. Вторая частица
до столкновения покоится (v2
= 0): а) если
массы взаимодействующих частиц равны
(m1 =
m2),
то u1x =
0 и u2x =
v1x,
т. е. первое тело останавливается после
столкновения, а вторая частица начинает
двига-ться со скоростью первой, какую
она имела до столкновения; б) если m1
> m2,
то первая частица продолжает двигаться
в том же направлении, что и до удара, но
с меньшей скоростью (u2
< v1),
скорость второй частицы после удара
увеличится, т. е. u2
> u1;
в) если m1 <
m2,
то первая частица после столкновения
изменит направление скорости (импульса)
на противоположное, вторая частица
начинает движение в том же направлении,
в каком двигалась первая частица до
столкновения; г) если m1
<< m2
(случай упругого взаимодействия частицы
с массивной неподвижной стенкой), то u1
=
v1,
u2 =
0, т. е. направление скорости налетающей
частицы после соударения со стенкой
изменится на противоположное, а величина
останется неизменной.