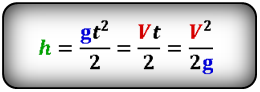1. Формулы скорости, высоты, времени в условиях свободного падения при начальной скорости равной нулю
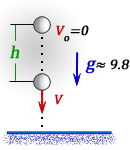
h – раcстояние пройденное телом за время t
V – скорость тела в момент времени t
t – время падения за которое тело пролетело расстояние или опустилось на высоту h
g ≈ 9,8 м/с2 – ускорение свободного падения
Формула скорости тела в определенный момент времени или на определенной высоте (V):

Формула высоты, на которую опустилось тело или расстояния, которое пролетело тело при падении (h):
Формула времени свободного падения тела вертикально вниз (t):
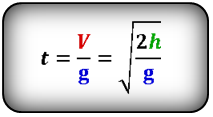
2. Формулы координаты тела, если направление оси OY совпадает с направлением скорости падующего тела V
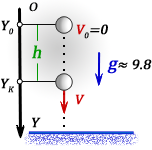
h – раcстояние пройденное телом за время t
V – скорость тела в момент времени t
t – время падения за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 – ускорение свободного падения
Yo , Yк – начальная и конечная координаты тела на оси OY
Формулы конечной координаты тела (Yк):

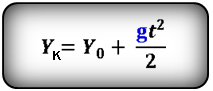
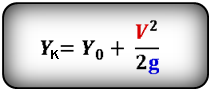
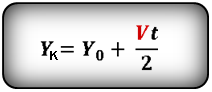
3. Формулы координаты тела, если направление оси OY не совпадает с направлением скорости V
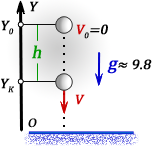
h – раcстояние пройденное телом за время t
V – скорость тела в момент времени t
t – время падения за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 – ускорение свободного падения
Yo , Yк – начальная и конечная координаты тела на оси OY
Формулы конечной координаты тела (Yк):
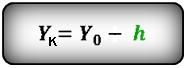
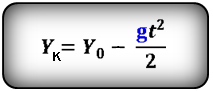
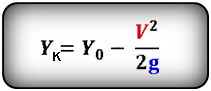
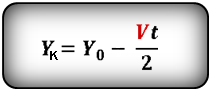
- Подробности
-
Опубликовано: 20 июля 2015
-
Обновлено: 13 августа 2021
Скорость, время и высота свободного падения
- Главная
- /
- Физика
- /
- Скорость, время и высота свободного падения
Чтобы посчитать скорость свободного падения, а также время или расстояние (высоту) свободного падения, воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Скорость свободного падения
Если известно время падения
Ускорение свободного падения g =
Время падения
t =
Расстояние h =
0
Скорость свободного падения
V =
0
/
Округление ответа:
Если известно расстояние (высота падения)
Ускорение свободного падения g =
Расстояние h =
Время падения
t =
0
Скорость свободного падения
V =
0
/
Округление ответа:
Расстояние и время свободного падения
Ускорение свободного падения g =
Скорость свободного падения
V =/
Расстояние h =
0
Время падения
t =
0
Округление ответа:
Просто введите данные, и получите ответ.
Стоит обратить внимание, на то, что данный калькулятор не учитывает сопротивление воздуха (атмосферы) и других сил способных повлиять на скорость падения тела, кроме силы тяжести.
Теория
Ускорение свободного падения
Ускорение свободного падения (g) – ускорение, которое придаёт падающему телу сила тяжести. У каждого небесного тела своё значение ускорения свободного падения, например, у планеты Земля оно составляет g = 9,80665 м/с².
Для небесных тел солнечной системы ускорение свободного падения имеет следующие значения:
- Земля – 9,80665 м/с²
- Луна – 1,62 м/с²
- Меркурий – 3,7 м/с²
- Венера – 8,87 м/с²
- Марс – 3,711 м/с²
- Сатурн – 10,44 м/с²
- Юпитер – 24,79 м/с²
- Нептун – 11,15 м/с²
- Уран – 8,87 м/с²
- Плутон – 0,617 м/с²
- Ио – 1,796 м/с²
- Европа – 1,315 м/с²
- Ганимед – 1,428 м/с²
- Каллисто – 1,235 м/с²
- Солнце – 274,0 м/с²
Как найти скорость свободного падения
Скорость свободного падения V можно рассчитать, зная расстояние (высоту) падения h или время падения t.
Зная время падения:
Формула
V = g⋅t
Пример
Для примера, рассчитаем с какой скоростью врежется в землю монета, брошенная из окна небоскрёба, если известно, что она упала за 5 секунд:
V = 9.8 ⋅ 5 = 49 м/с
Монетка ударилась об землю на скорости 49 м/с
Зная высоту падения:
Формула
V = √2⋅h⋅g
Пример
Для примера, определим скорость при ударе об землю ядра скинутого с 100 метровой вышки:
V = √2 ⋅ 100 ⋅ 9.8 = √1960 ≈ 44 м/с
Ядро ударится об землю на скорости 44 м/с
Время свободного падения
Время свободного падения – время, которое потребуется телу для того чтоб упасть на землю под действием силы тяжести. Чтобы рассчитать время свободного падения t необходимо знать высоту падения h или скорость в конце падения V.
Зная высоту падения:
Формула
t = √2h⁄g
Пример
Посчитаем чему будет равно время свободного падения t тела упавшего с высоты h = 100 метров:
t = √2⋅100⁄9.8 = √20.4 ≈ 4.5 с
Время свободного падения данного тела составит 4.5 секунды.
Зная скорость в конце падения:
Формула
t = V⁄g
Пример
Если тело после падения ударилось об землю со скоростью V = 50 м/с, то сколько секунд оно падало?
t = 50 ÷ 9.8 = 5.1 с
Время падения данного тела составило 5.1 секунды.
Высота свободного падения
Высота падения – высота с которой сбросили тело, численно равная расстоянию, которое пролетает тело за время падения. Чтобы рассчитать высоту падения h необходимо знать время падения t или скорость в конце падения V.
Зная время падения:
Формула
h = gt²⁄2
Пример
Для примера определим с какой высоты сбросили тело, если известно, что время его падения составило t = 5с:
h = 9.8 ⋅ 5² ÷ 2 = 122.5 м
Тело сбросили с высоты в 122.5 метров.
Зная скорость в конце падения:
Формула
h = V²⁄2g
Пример
Если тело после падения ударилось об землю со скоростью V = 60 м/с, то с какой высоты оно упало?
h = 60² ÷ 2⋅9.8 = 3600 ÷ 19.6 = 183.67 м
Тело упало с высоты в 183.67 метра.
См. также
Свободное падение тела — это его равнопеременное движение, которое происходит под действием силы тяжести. В этот момент другие силы, которые могут воздействовать на тело либо отсутствуют, либо настолько малы, что их влияние не учитывается. Например, когда парашютист прыгает из самолета, первые несколько секунд после прыжка он падает в свободном состоянии. Этот короткий отрезок времени характеризуется ощущением невесомости, сходным с тедж.м, что испытывают космонавты на борту космического корабля.
История открытия явления
О свободном падении тела ученые узнали еще в Средневековье: Альберт Саксонский и Николай Орем изучали это явление, но некоторые их выводы были ошибочными. Например, они утверждали, что скорость падающего тяжелого предмета возрастает прямо пропорционально пройденному расстоянию. В 1545 году поправку этой ошибки сделал испанский ученый Д. Сото, установивший факт, что скорость падающего тела увеличивается пропорционально времени, которое проходит от начала падения этого предмета.

В 1590 г. итальянский физик Галилео Галилей сформулировал закон, который устанавливает четкую зависимость пройденного падающим предметом пути от времени. Также ученым было доказано, что при отсутствии воздушного сопротивления все предметы на Земле падают с одинаковым ускорением, хотя до его открытия было принято считать, что тяжелые предметы падают быстрее.
Была открыта новая величина — ускорение свободного падения, которое состоит из двух составляющих: гравитационного и центробежного ускорений. Обозначается ускорение свободного падения буквой g и имеет различное значение для разных точек земного шара: от 9,78 м/с2 (показатель для экватора) до 9,83 м/с2 (значение ускорения на полюсах). На точность показателей влияют долгота, широта, время суток и некоторые другие факторы.
Стандартное значение g принято считать равным 9,80665 м/с2. В физических расчетах, которые не требуют соблюдения высокой точности, значение ускорения принимают за 9,81 м/с2. Для облегчения расчетов допускается принимать значение g равным 10 м/с2.
Для того чтобы продемонстрировать, как предмет падает в соответствии с открытием Галилея, ученые устраивают такой опыт: в длинную стеклянную трубку помещают предметы с различной массой, из трубки выкачивают воздух. После этого трубку переворачивают, все предметы под действием силы тяжести падают одновременно на дно трубки, независимо от их массы.
Когда эти же предметы помещены в какую-либо среду, одновременно с силой тяжести на них действует сила сопротивления, поэтому предметы в зависимости от своей массы, формы и плотности будут падать в разное время.
Формулы для расчетов
Существуют формулы, с помощью которых можно рассчитывать различные показатели, связанные со свободным падением. В них используются такие условные обозначения:
- u — конечная скорость, с которой перемещается исследуемое тело, м/с;
- h — высота, с которой перемещается исследуемое тело, м;
- t — время перемещения исследуемого тела, с;
- g — ускорение (постоянная величина, равная 9,8 м/с2).
Формула для определения расстояния, пройденного падающим предметом при известной конечной скорости и времени падения: h = ut /2.
Формула для расчета расстояния, пройденного падающим предметом по постоянной величине g и времени: h = gt 2/2.
Формула для определения скорости падающего предмета в конце падения при известном времени падения: u = gt .
Формула для расчета скорости предмета в конце падения, если известна высота, с которой падает исследуемый предмет: u = √2 gh.

Интересные факты
Если не углубляться в научные знания, бытовое определение свободного перемещения подразумевает передвижение какого-либо тела в земной атмосфере, когда на него не воздействуют никакие посторонние факторы, кроме сопротивления окружающего воздуха и силы тяжести.
В различное время добровольцы соревнуются между собой, пытаясь установить личный рекорд. В 1962 г. испытатель-парашютист из СССР Евгений Андреев установил рекорд, который был занесен в Книгу рекордов Гиннеса: при прыжке с парашютом в свободном падении он преодолел расстояние в 24500 м, во время прыжка не был использован тормозной парашют.
В 1960 г. американец Д. Киттингер совершил парашютный прыжок с высоты 31 тыс. м, но с использованием парашютно-тормозной установки.
В 2005 г. была зафиксирована рекордная скорость при свободном падении — 553 км/ч, а через семь лет установлен новый рекорд — эта скорость была увеличена до 1342 км/ч. Этот рекорд принадлежит австрийскому парашютисту Феликсу Баумгартнеру, который известен во всем мире своими опасными трюками.
Видео
Посмотрите интересное и познавательное видео, которое расскажет вам о скорости падения тел.
Время свободного падения — характерное время, которое потребуется телу для коллапса под действием силы тяготения, если никакие другие силы не противодействуют коллапсу. Играет важную роль при определении временных шкал ряда астрофизических процессов, таких как звездообразование, вспышки сверхновых звёзд.
Вывод формул[править | править код]
Падение на точечный источник гравитации[править | править код]
Несложно вывести формулу для времени свободного падения, применяя третий закон Кеплера к движению объекта по вырожденной эллиптической орбите. Рассмотрим точку массы 





Для того чтобы пояснить, почему большая полуось равна 






Если бы падающее тело совершило полный оборот по орбите, то движение началось бы на расстоянии 




.
Заметим, что 




Падение на сферически-симметричное распределение массы[править | править код]
Рассмотрим случай, когда 

,
где объём сферы равен 
Предположим, что единственной действующей силой является сила тяготения. Тогда, как было показано ещё Ньютоном и может быть получено при применении формулы Остроградского-Гаусса, ускорение в точке на расстоянии 



в последней формуле величины выражены в системе СИ.
Примечания[править | править код]
- ↑ Stellar Structure and Evolution Kippenhahn, Rudolf; Weigert, Alfred. Springer-Verlag, 1994, 3rd Ed. p.257 ISBN 3-540-58013-1
- Galactic dynamics Binney, James; Tremaine, Scott. Princeton University Press, 1987.
Что такое свободное падение? Это падение тел на Землю при отсутствии сопротивления воздуха. Иначе говоря – падение в пустоте. Конечно, отсутствие сопротивления воздуха – это вакуум, который нельзя встретить на Земле в нормальных условиях. Поэтому мы не будем брать силу сопротивления воздуха во внимание, считая ее настолько малой, что ей можно пренебречь.
Ускорение свободного падения
Проводя свои знаменитые опыты на Пизанской башне Галилео Галилей выяснил, что все тела, независимо от их массы, падают на Землю одинаково. То есть, для всех тел ускорение свободного падения одинаково. По легенде, ученый тогда сбрасывал с башни шары разной массы.
Ускорение свободного падения – ускорение, с которым все тела падают на Землю.
Ускорение свободного падения приблизительно равно 9,81 мс2 и обозначается буквой g. Иногда, когда точность принципиально не важна, ускорение свободного падения округляют до 10 мс2.
Земля – не идеальный шар, и в различных точках земной поверхности, в зависимости от координат и высоты над уровнем моря, значение g варьируется. Так, самое большое ускорение свободного падения – на полюсах (≈9,83 мс2), а самое малое – на экваторе (≈9,78 мс2).
Свободное падение тела
Рассмотрим простой пример свободного падения. Пусть некоторое тело падает с высоты h с нулевой начальной скоростью. Допустим мы подняли рояль на высоту h и спокойно отпустили его.
Свободное падение – прямолинейное движение с постоянным ускорением. Направим ось координат от точки начального положения тела к Земле. Применяя формулы кинематики для прямолинейного равноускоренного движения, можно записать.
h=v0+gt22.
Так как начальна скорость равна нулю, перепишем:
h=gt22.
Отсюда находится выражение для времени падения тела с высоты h:
t=2hg.
Принимая во внимание, что v=gt, найдем скорость тела в момент падения, то есть максимальную скорость:
v=2hg·g=2hg.
Движение тела, брошенного вертикально вверх
Аналогично можно рассмотреть движение тела, брошенного вертикально вверх с определенной начальной скоростью. Например, мы бросаем вверх мячик.
Пусть ось координат направлена вертикально вверх из точки бросания тела. На сей раз тело движется равнозамедленно, теряя скорость. В наивысшей точки скорость тела равна нулю. Применяя формулы кинематики, можно записать:
v=v0-gt.
Подставив v=0, найдем время подъема тела на максимальную высоту:
t=v0g.
Время падения совпадает со временем подъема, и тело вернется на Землю через t=2v0g.
Максимальная высота подъема тела, брошенного вертикально:
h=v022g.
Взглянем на рисунок ниже. На нем приведены графики скоростей тел для трех случаев движения с ускорением a=-g. Рассмотрим каждый из них, предварительно уточнив, что в данном примере все числа округлены, а ускорение свободного падения принято равным 10мс2.
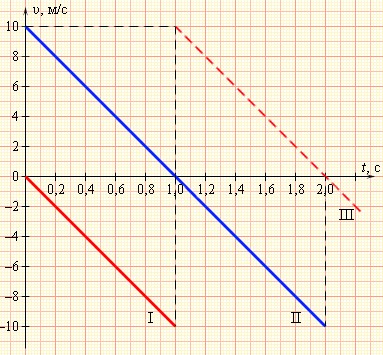
Первый график – это падение тела с некоторой высоты без начальной скорости. Время падения tп=1с. Из формул и из графика легко получить, что высота, с которой падало тело, равна h=5м.
Второй график – движение тела, брошенного вертикально вверх с начальной скоростью v0=10 мс. Максимальная высота подъема h=5м. Время подъема и время падения tп=1с.
Третий график является продолжением первого. Падающее тело отскакивает от поверхности и его скорость резко меняет знак на противоположный. Дальнейшее движение тела можно рассматривать по второму графику.
Движение тела, брошенного под углом к горизонту
С задачей о свободном падении тела тесно связана задача о движении тела, брошенного под определенным углом к горизонту. Так, движение по параболической траектории можно представить как сумму двух независимых движений относительно вертикальной и горизонтальной осей.
Вдоль оси OY тело движется равноускоренно с ускорением g, начальная скорость этого движения – v0y. Движение вдоль оси OX – равномерное и прямолинейное, с начальной скоростью v0x.
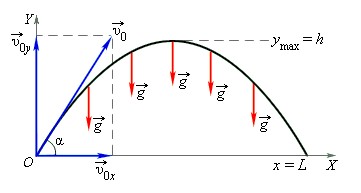
Условия для движения вдоль оси ОХ:
x0=0; v0x=v0cosα; ax=0.
Условия для движения вдоль оси OY:
y0=0; v0y=v0sinα; ay=-g.
Приведем формулы для движения тела, брошенного под углом к горизонту.
Время полета тела:
t=2v0sinαg.
Дальность полета тела:
L=v02sin2αg.
Максимальная дальность полета достигается при угле α=45°.
Lmax=v02g.
Максимальная высота подъема:
h=v02sin2α2g.
Отметим, что в реальных условиях движение тела, брошенного под углом к горизонту, может проходить по траектории, отличной от параболической вследствие сопротивления воздуха и ветра. Изучением движения тел, брошенных в пространстве, занимается специальная наука – баллистика.