Время, скорость, расстояние

О чем эта статья:
Расстояние
Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.
Расстояние — это длина от одного пункта до другого.
- Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.
Расстояние обозначается латинской буквой s.
Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).
Формула пути
Чтобы найти расстояние, нужно умножить скорость на время движения:
s = v × t
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.
Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.
Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.
Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
Время
Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.
Время — это продолжительность каких-то действий, событий.
- Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.
Время движения обозначается латинской буквой t.
Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.
Формула времени
Чтобы найти время, нужно разделить расстояние на скорость:
t = s : v
Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.
Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров в минуту на 15 минут, мы определим расстояние от дома до магазина:
s = v × t = 50 × 15 = 750 (м)
Ответ: мы прошли 750 метров.
Если известно время и расстояние, то можно найти скорость: v = s : t.
Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).
100 м : 25 с = 4 м/с
Так мы узнали, что скорость движения первого школьника 4 метра в секунду.
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
Значит, скорость движения второго школьника составляет 2 метра в секунду.
Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.
Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.
Ответ: первый школьник добежал быстрее.
Если известны скорость и расстояние, то можно найти время: t = s : v.
Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:
t = s : v = 500 : 100 = 5 (мин)
Ответ: от школы до стадиона мы дойдем за 5 минут.
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.
Перемещение и путь при равноускоренном прямолинейном движении
теория по физике 🧲 кинематика
Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.

При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:

Пример №1. По графику определить перемещение тела в момент времени t=3 с.

Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:

Извлекаем из графика необходимые данные:
- Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
- Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).
Подставляем известные данные в формулу:
Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.
Варианты записи формулы перемещения
Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:
В итоге получается формула:

Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».
Если начальная скорость равна 0 (v0 = 0), эта формула принимает
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:

Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.

Перемещение при разгоне и торможении тела
Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают ( а ↑↑ v ). Если векторы имеют противоположное направление ( а ↑↓ v ), движение следует описывать в два этапа:
Этап торможения
Время торможения равно разности полного времени движения и времени второго этапа:
Когда тело тормозит, через некоторое время t1оно останавливается. Поэтому скорость в момент времени t1 равна 0:
При торможении перемещение s1 равно:

Этап разгона
Время разгона равно разности полного времени движения и времени первого этапа:
Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t2 равна:
При разгоне перемещение s2 равно:

При этом модуль перемещения в течение всего времени движения равен:
Полный путь (обозначим его l), пройденный телом за оба этапа, равен:
Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с 2 . Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.
В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:

Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:
Подставляем выраженные величины в формулу:

Перемещение в n-ную секунду прямолинейного равноускоренного движения
Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:

За первую секунду тело переместится на расстояние, равное:

За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:

За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:

Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:

Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:
Формула перемещения за n-ную секунду

Пример №4. Автомобиль разгоняется с ускорением 3 м/с 2. Найти его перемещение за 6 секунду.
Подставляем известные данные в формулу и получаем:

Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:

где t — время одного промежутка, а n — порядковый номер этого промежутка.
Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с 2 . Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.
Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.
Подставляем известные данные в формулу:

Проекция и график перемещения
Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ ( v ↑↑OX), а вектора скорости и ускорения сонаправлены ( v ↑↑ a ), принимает следующий вид:

График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно ( v ↓↑ a ), принимает следующий вид:

Определение направления знака проекции ускорения по графику его перемещения:
- Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
- Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.
Пример №6. Определить ускорение тела по графику его перемещения.

Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:

Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:

График пути
График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.

В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:
- 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
- 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.

Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.
Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.

При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:

Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

 Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t – «>– 3t 2 (все величины выражены в СИ).
Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t – «>– 3t 2 (все величины выражены в СИ).
Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
Решение
Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.
Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:
x ( t ) = x 0 + v 0 t + a t 2 2 . .
Теперь мы можем выделить кинематические характеристики движения тела:
Перемещение тела определяется формулой:
s = v 0 t + a t 2 2 . .
Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:
x ( t ) = v 0 t + a t 2 2 . . = 5 t − 3 t 2
Кинетическая энергия тела определяется формулой:
Скорость при прямолинейном равноускоренном движении равна:
v = v 0 + a t = 5 − 6 t
Поэтому кинетическая энергия тела равна:
E k = m ( 5 − 6 t ) 2 2 . . = 0 , 2 2 . . ( 5 − 6 t ) 2 = 0 , 1 ( 5 − 6 t ) 2
Следовательно, правильная последовательность цифр в ответе будет: 34.
pазбирался: Алиса Никитина | обсудить разбор | оценить
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
pазбирался: Алиса Никитина | обсудить разбор | оценить
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
- Охарактеризовать движение тела на различных участках графика.
- Выделить участки движения, над которыми нужно работать по условию задачи.
- Записать исходные данные.
- Записать формулу определения искомой величины.
- Произвести вычисления.
Решение
Весь график можно поделить на 3 участка:
- От t1 = 0 c до t2 = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
- От t1 = 10 c до t2 = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
- От t1 = 30 c до t2 = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
- От t1 = 20 c до t2 = 30 с — с равномерным движением.
- От t1 = 30 c до t2 = 50 с — с равнозамедленным движением.
- Для первого участка. Начальный момент времени t1 = 20 c. Конечный момент времени t2 = 30 с. Скорость (определяем по графику) — 10 м/с.
- Для второго участка. Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Записываем формулу искомой величины:
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s1и s2, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить
Примеры решения задач
Пример 1. По заданному закону движения S =10 + 20t — 5t 2 ([S] = м; [t] = с) определить вид движения, начальную скорость и касательное ускорение точки, время до остановки.
(Рекомендуется обойтись без расчетов, использовать метод сравнения заданного уравнения с уравнениями различных видов движений в общем виде.)
 Решение
Решение
1. Вид движения: равнопеременное
2. При сравнении уравнений очевидно, что
- начальный путь, пройденный до начала отсчета – 10 м;
- начальная скорость 20 м/с;
- постоянное касательное ускорение at/2 = 5 м/с ; at= — 10 м/с .
- ускорение отрицательное, следовательно, движение замедленное (равнозамедленное), ускорение направлено в сторону, противоположную направлению скорости движения.
3. Можно определить время, при котором скорость точки будет равна нулю:
v = S’ = 20 — 2 • 5t; v = 20 – 10t = 0; t = 20/10 = 2 c.
Примечание. Если при равнопеременном движении скорость растет, значит, ускорение — положительная величина, график пути — вогнутая парабола. При торможении скорость падает, ускорение (замедление) — отрицательная величина, график пути — выпуклая парабола (рис. 10.4).
Пример 2. Точка движется по желобу из точки А в точку D (рис. 10.5).
 Как изменятся касательное и нормальное ускорения при прохождении точки через В и С?
Как изменятся касательное и нормальное ускорения при прохождении точки через В и С?
Скорость движения считать постоянной. Радиус участка АВ = 10 м, радиус участка ВС= 5 м.
Решение
1. Рассмотрим участок АВ. Касательное ускорение равно нулю (v = const).
Нормальное ускорение (ап = v 2 /r) при переходе через точку В увеличивается в 2 раза, оно меняет направление, т. к. центр дуги АВ не совпадает с центром дуги ВС.
2. На участке ВС:
— касательное ускорение равно нулю: at = 0;
— нормальное ускорение при переходе через точку С меняется: до точки С движение вращательное, после точки С движение становится прямолинейным, нормальное напряжение на прямолинейном участке равно нулю.
3. На участке CD полное ускорение равно нулю.

Пример 3. По заданному графику скорости найти путь, пройденный за время движения (рис. 10.6).
Решение
1. По графику следует рассмотреть три участка движения. Первый участок — разгон из состояния покоя (равноускоренное движение).

Второй участок — равномерное движение: v = 8 м/с; a2 = 0.
Третий участок — торможение до остановки (равнозамедленное движение).

2. Путь, пройденный за время движения, будет равен:

Пример 4. Тело, имевшее начальную скорость 36 км/ч, прошло 50 м до остановки. Считая движение равнозамедленным, определить время торможения.
Решение
1. Записываем уравнение скорости для равнозамедленного движения:
Определяем начальную скорость в м/с: vо = 36*1000/3600 = 10 м/с.
Выразим ускорение (замедление) из уравнения скорости: a = — v0/t
2. Записываем уравнение пути: S = vot/2 + at 2 /2. После подстановки получим: S = vot/2
3. Определяем время до полной остановки (время торможения):


Пример 5. Точка движется прямолинейно согласно уравнению s = 20t – 5t 2 (s — м, t — с). Построить графики расстояний, скорости и ускорения для первых 4 с движения. Определить путь, пройденный точкой за 4 с, и описать движение точки.
Решение
1. Точка движется прямолинейно по уравнению s = 20t – 5t 2 следовательно, скорость точки u = ds/d/t = 20 — 10t и ускорение a = at = dv/dt = —10 м/с 2 . Значит, движение точки равнопеременное (a = at = —10 м/c 2 = const) с начальной скоростью v0 = 20 м/с.
2. Составим зависимость числовых значений s и v для первых 4 с движения

3. По приведенным числовым значениям построим графики расстояний (рис. а), скорости (рис. б) и ускорения (рис. в), выбрав масштабы для изображения по осям ординат расстояний s, скорости v и ускорения а, а также одинаковый для всех графиков масштаб времени по оси абсцисс. Например, если расстояние s = 5 м изображать на графике длиной отрезка ls = 10 мм, то 5м = μs*10мм, где коэффициент пропорциональности μs и есть масштаб по оси Os : μs = 5/10 = 0,5 м/мм (0,5 м в 1 мм); если модуль скорости v = 10 м/с изображать на графике длиной lv =10 мм, то 10 м/c = μv * 10 мм и масштаб по оси Ov μv = 1 м/(с-мм) (1 м/с в 1 мм); если модуль ускорения а = 10 м/с 2 изображать отрезком la = 10 мм, то, аналогично предыдущему, масштаб по оси Оа μa = 1 м/(с 2 -мм) (1 м/с 2 в 1 мм); и наконец, изображая промежуток времени Δt = 1 с отрезком μt = 10 мм, получим на всех графиках масштаб по осям Ot μt = 0,1 с/мм (0,1 с в 1 мм).
4. Из рассмотрения графиков следует, что в течение времени от 0 до 2 с точка движется равнозамедленно (скорость v и ускорение в течение этого промежутка времени имеют разные знаки, значит, их векторы направлены в противоположные стороны); в период времени от 2 до 4 с точка движется равноускоренно (скорость v и ускорение имеют одинаковые знаки, т. е. их векторы направлены в одну сторону).
За 4 с точка прошла путь so_4 = 40 м. Начав движение со скоростью v0 = 20 м/с, точка по прямой прошла 20 м, а затем вернулась в исходное положение, имея ту же скорость, но направленную в противоположную сторону.
Если условно принять ускорение свободного падения g = 10 мс 2 и пренебречь сопротивлением воздуха, то можно сказать, что графики описывают движение точки, брошенной вертикально вверх со скоростью а0 = 20 м/с.
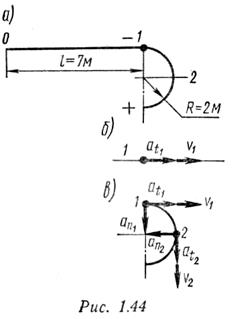 Пример 6. Точка движется по траектории, изображенной на рис. 1.44, а, согласно уравнению s = 0,2t 4 (s — в метрах, t — в секундах). Определить скорость и ускорение точки в положениях 1 и 2.
Пример 6. Точка движется по траектории, изображенной на рис. 1.44, а, согласно уравнению s = 0,2t 4 (s — в метрах, t — в секундах). Определить скорость и ускорение точки в положениях 1 и 2.
Решение
Время, необходимое для перемещения точки из положения 0 (начала отсчета) в положение 1, определим из уравнения движения, подставив частные значения расстояния и времени:

Уравнение изменения скорости

Скорость точки в положении 1

Уравнение изменения касательного ускорения

Касательное ускорение точки в положении 1

Нормальное ускорение точки на прямолинейном участке траектории равно нулю. Скорость и ускорение точки в конце этого участка траектории показаны на рис.1.44, б.
Определим скорость и ускорение точки в начале криволинейного участка траектории. Очевидно, что v1 = 11,5 м/с, аt1 = 14,2 м/с 2 .
Нормальное ускорение точки в начале криволинейного участка

Скорость и ускорение в начале криволинейного участка показаны на рис. 1.44, в (векторы at1 и aa1 изображены без соблюдения масштаба).
Положение 2 движущейся точки определяется пройденным путем, состоящим из прямолинейного участка 0 — 1 и дуги окружности 1 — 2, соответствующей центральному углу 90°:

Время, необходимое для перемещения точки из положения 0 в положение2,

Скорость точки в положении 2

Касательное ускорение точки в положении 2

Нормальное ускорение точки в положении 2

Ускорение точки в положении 2

Скорость и ускорения точки в положении 2 показаны на рис. 1.44, в (векторы at„ и аПг изображены без соблюдения масштаба).
 Пример 7. Точка движется по заданной траектории (рис. 1.45, а) согласно уравнению s = 5t 3 (s — в метрах, t — в секундах). Определить ускорение точки и угол α между ускорением и скоростью в момент t1, когда скорость точки v1 = 135 м/с.
Пример 7. Точка движется по заданной траектории (рис. 1.45, а) согласно уравнению s = 5t 3 (s — в метрах, t — в секундах). Определить ускорение точки и угол α между ускорением и скоростью в момент t1, когда скорость точки v1 = 135 м/с.
Решение
Уравнение изменения скорости

Время t1 определим из уравнения изменения скорости, подставив частные значения скорости и времени:

Определим положение точки на траектории в момент 3 с:

Дуга окружности длиной 135 м соответствует центральному углу

Уравнение изменения касательного ускорения
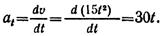
Касательное ускорение точки в момент tt

Нормальное ускорение точки в момент tt

Ускорение точки в момент tx

Скорость и ускорение точки в момент времени t1 показаны на рис. 1.45, б.
Как видно из рис. 1.45, б

Пример 8. В шахту глубиной H = 3000 м с поверхности земли без начальной скорости брошен предмет. Определить, через сколько секунд звук, возникающий в момент удара предмета о дно шахты, достигнет поверхности земли. Скорость звука 333 м/с.
Решение
Уравнение движения свободно падающего тела

Время, необходимое для перемещения предмета от поверхности земли до дна шахты, определим из уравнения движения:

Звук распространялся с постоянной скоростью 333 м/с. Уравнение распространения звука

Время достижения звуком поверхности земли

Тогда время с момента начала движения предмета до момента достижения звуком поверхности земли

Пример 9. По заданным уравнениям движения точки x = 2t 2 , y = 2t (x и у — в метрах, t — в секундах) найти уравнение траектории, а также скорость и ускорение точки в момент времени t = 2 с.
Решение
Для определения траектории точки нужно из уравнений движения исключить параметр t — время.
Выразим t через х из первого уравнения:

и подставим это значение во второе уравнение:

Траекторией точки является парабола, симметричная относительно оси х.
Чтобы найти скорость точки, нужно определить ее составляющие по координатным осям

Находим скорость точки

При t = 2 с получаем

Находим составляющие ускорения точки


Контрольные вопросы и задания
1. Запишите формулу ускорения при прямолинейном движении.
2. Запишите формулу ускорения (полного) при криволинейном движении.
3.  Тело скатывается по желобу (рис. 10.7). Какие параметры движения меняются при переходе через точку В и почему?
Тело скатывается по желобу (рис. 10.7). Какие параметры движения меняются при переходе через точку В и почему?
4. Параметры движения не меняются.

4. По заданному уравнению движения точки S = 25 + 1,5t + 6t 2 определите вид движения и без расчетов, используя законы движения точки, ответьте, чему равны начальная скорость и ускорение.
5. По заданному уравнению движения точки S = 22t — 4t 2 постройте графики скорости и касательного ускорения.
6. По графику скоростей точки определите путь, пройденный за время движения (рис. 10.8).
7. Точка движется по дуге. Охарактеризуй движение точки (рис. 10.9).
источники:
http://spadilo.ru/peremeshhenie-i-put-pri-ravnouskorennom-pryamolinejnom-dvizhenii/
http://mydocx.ru/12-105317.html
Онлайн калькулятор поможет рассчитать время торможения зная скорость автомобиля.
Например: тормозное время автомобиля движущегося со скоростью 60 километров в час равняется ~2.4 секунды.
Формула для расчета времени торможения по скорости автомобиля:
S – тормозной путь в метрах;
V – скорость в км/ч;
Kт – коэффициент торможения автомобиля;
Ksc – коэффициент сцепления автомобиля с дорогой;
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также
Как найти время торможения
Время торможения неразрывно связано с таким понятием, как «тормозной путь», то есть расстоянием, преодолеваемым транспортным средством от момента срабатывания тормозной системы до полной его остановки.

Инструкция
Непосредственно временем торможения считается время с момента обнаружения водителем препятствия и нажатия на тормозную педаль до полной остановки транспортного средства. Оно включает в себя время реакции водителя, время начала действия тормозной системы и время непосредственного торможения. Для его вычисления используйте формулу: t = V02 : a где V0– начальная скорость в м/сек и а – ускорение.
Время и протяженность тормозного пути зависит от многих факторов, важнейшими из которых являются скорость, состояние шин, проезжей части, массы транспортного средства и погодных условий. Не меньшее влияние на процесс торможения оказывает эффективность тормозной системы.
Максимальная тормозная сила зависит от нагрузки на колеса и от их сцепления с дорогой. Большей нагрузке соответствует большая тормозная сила. Признаком полностью блокированного колеса является так называемый юз, когда в результате резкого торможения о поверхность сухой дороги трется какой-то один участок шины. В результате этого образуются резиновые катыши, ускоряющие движение колеса, как подшипники. При таком торможении раздается характерный писк, возникают трудности с управлением, и автомобиль начинает уходить в сторону.
Сцепление напрямую зависит также от состояния дороги и изношенности колеса. Так, по сравнению с сухим асфальтом сцепление на мокром снижается в 2 раза, а во время гололеда – в 10 раз. Значительное уменьшение тормозной силы приводит к увеличению тормозного пути и, соответственно, времени до остановки. Как правило, одновременно с началом юза начинается занос задних колес. Исправить данную ситуацию можно с помощью рулевого колеса. Для выравнивания автомобиля отпустите педаль тормоза и выведите машину на чистый участок трассы или в крайнем случае, в сторону от нее. Единственно, что следует усвоить – все это придется проделывать за секунды и даже доли секунд.
Видео по теме
Обратите внимание
Грамотное торможение представляет собой максимальное использование сцепления колес с дорогой, умение в процессе ехать прямо, тормозить с помощью двигателя и переключения передач, а также умение остановиться, несмотря на отказ системы.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
4.1 Определение остановочного времени автомобиля с полной нагрузкой и без нагрузки
Остановочное время автомобиля определяется
по следующей формуле:
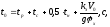 (4.1)
(4.1)
где 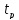 – время реакции водителя, с;
– время реакции водителя, с;
 – время срабатывания тормозной системы,
– время срабатывания тормозной системы,
с;
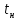 – время нарастания замедления, с;
– время нарастания замедления, с;
kэ – коэффициент
эффективности торможения;
V0– скорость автомобиля
непосредственно перед началом торможения,
м/с;
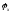 – коэффициент сцепления колес автомобиля
– коэффициент сцепления колес автомобиля
с поверхностью дороги;
g– ускорение свободного падения;
 принимаем равным 0,8 с;
принимаем равным 0,8 с;
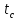 для автомобилей с гидравлическим
для автомобилей с гидравлическим
приводом тормозов 0,2 – 0,3 с, для автомобилей
с пневматическим приводом тормозов
0,6 – 0,8 с;
 рассчитывается по формуле:
рассчитывается по формуле:
 (4.2)
(4.2)
где G– вес автомобиля с данной
нагрузкой, Н;
b– расстояние от задней оси автомобиля
до центра тяжести, м;
hц– расстояние от центра
тяжести автомобиля до поверхности
дороги, м;
k1–скорость нарастания
тормозных сил, кН/с;
L– база автомобиля,
принимаем 3,77м.
Расстояние от задней оси автомобиля до
центра тяжести рассчитывается по
формуле:
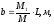 (4.3)
(4.3)
где М1 – масса
автомобиля, приходящаяся на переднюю
ось, кг;
М– масса всего автомобиля с данной
нагрузкой, кг;
k1 выбирается в
зависимости от типа тормозной системы:
для автомобилей с гидравлическим
приводом тормозов k1 =
15 – 30 кН/с;
kэ выбирается в
зависимости от типа автомобиля и его
весового состояния из следующей таблицы.
Таблица 4.1 – Значения коэффициентов
эффективности торможения
|
Тип |
Коэффициент |
|
|
без |
с |
|
|
Легковые |
1,10-1,15 |
1,15-1,20 |
|
Грузовые |
1,10-1,30 |
1,50-1,60 |
|
Грузовые |
1,40 |
1,60-1,80 |
При расчетах принимаем:
а) автомобиль до торможения двигается
с постоянной скоростью, равной 40 км/ч
(V0= 11,11 м/с);
б) коэффициент сцепления колес автомобиля
с поверхностью дороги
 = 0,6.
= 0,6.
в) коэффициент эффективности
торможения kэпринимаем
без нагрузки 1,2, с полнойц нагрузкой
1,5.
г) скорость нарастания тормозных сил
k1 =25кН/с.
Для автомобиля ГАЗ-3309с
полной нагрузкой:
По формуле (4.3) рассчитаем расстояние
от задней оси автомобиля до центра
тяжести:

 .
.
Время нарастания замедления рассчитаем
по формуле (4.2):
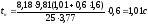 .
.
Остановочное время автомобиля определим
по формуле (4.1):
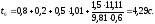
Для автомобиля ГАЗ-3309 без
нагрузки:
По формуле (4.3) рассчитаем расстояние
от задней оси автомобиля до центра
тяжести:

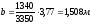 .
.
Время нарастания замедления рассчитаем
по формуле (4.2):
 .
.
Остановочное время автомобиля определим
по формуле (4.1):

4.2 Определение остановочного пути автомобиля с полной нагрузкой и без нагрузки
Определение
остановочного пути автомобиля производим
по следующей формуле:
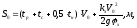 (4.3)
(4.3)
Для автомобиля ГАЗ-3309с
полной нагрузкой:
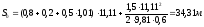
Для автомобиля ГАЗ-3309без нагрузки:
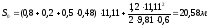
4.3 Определение замедления автомобиля с полной нагрузкой на уклоне и на подъеме
При торможении
автомобиля на уклоне или на подъеме
сила его инерции уравновешивается
алгебраической суммой тормозной
силы и силы сопротивления подъему. При
движении на подъем эти силы складываются,
а на уклоне – вычитаются:
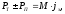 Н.
Н.
(4.4)
Отсюда замедление
автомобиля на уклоне или подъеме
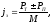 м/с2,
м/с2,
(4.5)
где РТ
–
тормозная сила, Н;
РП
–
сила сопротивления подъему, Н;
М-
масса автомобиля, кг.
Сила тяги и сила
сопротивления подъему рассчитываются
по следующим формулам:
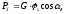 Н;
Н;
(4.6)
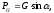 Н,
Н,
(4.7)
где
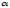
– угол
подъема (уклона) дороги;
G
–
вес автомобиля, Н;
 –
–
коэффициент сцепления колес автомобиля
с поверхностью дороги.
Конечная формула
для расчета замедления автомобиля на
уклоне и подъеме будет иметь следующий
вид:
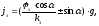 м/с2.
м/с2.
(4.8)
Замедление
автомобиля необходимо определять при
углах подъема (уклона)
 =
=
0,05 радиана.
Определение
замедления автомобиля с полной нагрузкой
на подъеме:
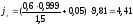 м/с2.
м/с2.
Определение
замедления автомобиля с полной нагрузкой
на уклоне:
 м/с2.
м/с2.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Известно, что грузовой автомобиль массой пять тысяч килограмм движется по горизонтальному пути со скоростью семьдесят два километра в час (20 метров в секунду).
Необходимо: определить силу и время торможения автомобиля, если тормозной путь составил пять метров.
Дано: m=5000 кг; v=20 м/сек; s=5 м
Найти: F-?; t-?
Решение
Исходя из того, что работа силы торможения численно равна изменению кинетической энергии движущегося автомобиля  , получаем формулу для определения силы торможения
, получаем формулу для определения силы торможения

Подставив в формулу численные значения, рассчитаем силу торможения грузового автомобиля
 н
н
Из формулы  , при условии, что vt=0:
, при условии, что vt=0:  , где
, где  , получаем формулу времени торможения
, получаем формулу времени торможения

Время торможения автомобиля
 сек
сек
Ответ: сила торможения автомобиля составила двести тысяч ньютон, время торможения равно половине секунды.

