Как найти время удара формула

Длительность удара

Задача 1. Оценить время упругого удара твердых тел, рассматривая столкновение стержня, налетающего торцом на неподвижную недеформируемую стенку (рис.).

Чаще всего в задачах считают, что упругий удар твердых тел происходит мгновенно, но совершенно очевидно, что это предположение является идеализацией. Столкновение реальных тел всегда занимает конечный промежуток времени $tau$. В самом деле, если бы изменение импульса тела при столкновении происходило мгновенно,

$F = frac{mDelta v}{t_{rightarrow infty}}$,

то сила взаимодействия тел при ударе была бы бесконечно большой, чего, естественно, не бывает.

От чего же может зависеть длительность столкновения?

Допустим, что мы рассматриваем отражение упругого тела от недеформируемой стенки. При столкновении кинетическая энергия тела в течение первой половины столкновения превращается в потенциальную энергию упругой деформации тела. В течение второй половины происходит обратное превращение энергии деформации в кинетическую энергию отскакивающего тела. Такая идея была заложена в задаче тестирования 2005 г. Решите эту задачу, для осмысления этого момента.

Задача 2. Две абсолютно упругие шайбы массами m₁ = m₂ = 240 г каждая скользят поступательно по гладкой горизонтальной поверхности навстречу друг другу со скоростями, модули которых v₁ = 21 м/с и v₂ = 9,0 м/с . Максимальное значение потенциальной энергии E упругой деформации шайб при их центральном столкновении равно … Дж.

Поэтому очевидно, что упругие свойства тела играют определенную роль при столкновении. Итак, можно ожидать, что длительность удара зависит от модуля Юнга материала тела Е, его плотности $rho$ и его геометрических размеров. Возможно, что длительность удара $tau$ зависит и от скорости v, с которой тело налетает на преграду. Нетрудно убедиться, что оценить время столкновения с помощью одних только соображений размерности не удастся. Действительно, если даже взять в качестве налетающего тела шар, размеры которого характеризуются только одним параметром — радиусом R, то из величин Е, $rho$, R и v можно составить бесчисленное множество выражений, имеющих размерность времени:

$tau = sqrt{frac{rho}{E}} cdot f(frac{rho v^2}{E})$, (1)

где $f$ — произвольная функция безразмерной величины $frac{rho v^2}{E}. Поэтому для нахождения $tau$ необходимо динамическое рассмотрение.

Проще всего такое рассмотрение провести для тела, имеющего форму длинного стержня. Пусть стержень, движущийся со скоростью $v$, налетает торцом на неподвижную стенку. При соприкосновении торцевого сечения стержня со стенкой скорости лежащих в этом сечении частиц стержня мгновенно обращаются в нуль. В следующий момент времени останавливаются частицы, расположенные в соседнем сечении, и т. д.

Участок стержня, частицы которого к данному моменту уже остановились, находится в деформированном состоянии. Другими словами, в этот момент времени деформированной оказывается та часть стержня, до которой дошла волна упругой деформации, распространяющаяся по стержню от места контакта с преградой. Эта волна деформации распространяется по стержню со скоростью звука $u$. Если считать, что стержень пришел в соприкосновение со стенкой в момент времени t = 0, то в момент времени t длина сжатой части стержня равна $ut$. Эта часть стержня на рис. а заштрихована.

В незаштрихованной части стержня скорости всех его частиц попрежнему равны $u$, а в сжатой (заштрихованной) части стержня все частицы покоятся. Первый этап процесса столкновения стержня со стенкой закончится в тот момент, когда весь стержень окажется деформированным, а скорости всех его частиц обратятся в нуль (рис. б).

В этот момент кинетическая энергия налетающего стержня целиком превращается в потенциальную энергию упругой деформации. Сразу после этого начинается второй этап столкновения, при котором стержень возвращается в недеформированное состояние. Этот процесс начинается у свободного конца стержня и, распространяясь по стержню со скоростью звука, постепенно приближается к преграде. На рис. в

стержень показан в тот момент, когда незаштрихованная часть уже не деформирована и все ее частицы имеют скорость $v$, направленную влево. Заштрихованный участок по-прежнему деформирован, и скорости всех его частиц равны нулю. Конец второго этапа столкновения наступит в тот момент, когда весь стержень окажется недеформированным, а все частицы стержня приобретут скорость $v$, направленную противоположно скорости стержня до удара. В этот момент правый конец стержня отделяется от преграды: недеформированный стержень отскакивает от стенки и движется в противоположную сторону с прежней по модулю скоростью (рис. г).

Энергия упругой деформации стержня при этом целиком переходит обратно в кинетическую энергию. Из изложенного ясно, что длительность столкновения τ равна времени прохождения фронта волны упругой деформации по стержню туда и обратно:

$tau = frac{2l}{u}$, (2)

где l — длина стержня. Определить скорость звука в стержне $u$ можно следующим образом.

Рассмотрим стержень в момент времени t (рис. а), когда волна деформации распространяется влево. Длина деформированной части стержня в этот момент равна $ut$. По отношению к недеформированному состоянию эта часть укоротилась на величину $vt$, равную расстоянию, пройденному к этому моменту еще недеформированной частью стержня. Поэтому относительная деформация этой части стержня равна $frac{v}{u}$.

На основании закона Гука

$frac{v}{u} = frac{1}{E} cdot frac{F}{S}$, (3)

где S — площадь поперечного сечения стержня, F — сила, действующая на стержень со стороны стенки, Е — модуль Юнга.

Поскольку относительная деформация $v/u$ одинакова во все моменты времени, пока стержень находится в контакте с преградой, то, как видно из формулы (3), сила F постоянна. Для нахождения этой силы применим закон сохранения импульса к остановившейся части стержня. До контакта с преградой рассматриваемая часть стержня имела импульс $rho Sut cdot v$, а в момент времени t ее импульс равен нулю. Поэтому

$rho Sut cdot v = Ft$. (4)

Подставляя отсюда силу F в формулу (3), получаем

$u = sqrt{frac{E}{rho}}$. (5)

Теперь выражение для времени $tau$.

Деформация столкновения стержня со стенкой (2) принимает вид

$tau = 2l cdot sqrt{frac{rho}{E}}$. (6)

Время столкновения $tau$ можно найти и иначе, воспользовавшись для этого законом сохранения энергии. Перед столкновением стержень недеформирован и вся его энергия — это кинетическая энергия поступательного движения $frac{1}{2}mv^2$. Спустя время $tau$/2 с начала столкновения скорости всех его частиц, как мы видели, обращаются в нуль, а весь стержень сказывается деформированным (рис. б). Длина стержня уменьшилась на величину $Delta l$ по сравнению с его недеформированным состоянием (рис. д).

В этот момент вся энергия стержня — это энергия его упругой деформации. Эту энергию можно записать в виде

$W = frac{1}{2}kDelta l^2$

где k — коэффициент пропорциональности между силой и деформацией: $F = kDelta l$.

Этот коэффициент с помощью закона Гука выражается через модуль Юнга E и размеры стержня:

$sigma = frac{F}{S} = frac{Delta l}{l}E, F = SEfrac{Delta l}{l}$ и $F = kDelta l$,

отсюда

$k = frac{ES}{l}$. (7)

Максимальная деформация $Delta l$ равна тому расстоянию, на которое перемещаются частицы левого конца стержня за время $tau$/2 (рис. д). Так как эти частицы двигались со скоростью $v$, то

$Delta l = frac{vtau}{2}$. (8)

Приравниваем кинетическую энергию стержня до удара и потенциальную энергию деформации. Учитывая, что масса стержня $m = rho Sl$, и используя соотношения (7) и (8), получаем

$frac{rho Slv^2}{2} = frac{ES}{2l} cdot (frac{vtau}{2})^2$,

откуда для $tau$ снова получаем формулу (6). Это время столкновения обычно очень мало.

Например, для стального стержня (E = 2 x 10¹¹ Па, $rho$ = 7,8 x 10³ кг/м³) длиной 28 см вычисление по формуле (6) дает $tau$ = 10^-4 с. Силу F, действующую на стенку во время удара, можно найти, подставляя скорость звука в стержне (5) в формулу (4):

$F = Svsqrt{rho E}$. (9)

Видно, что сила, действующая на стенку, пропорциональна скорости стержня перед ударом. Но для применимости приведенного решения необходимо, чтобы механическое напряжение стержня F/S не превосходило предела упругости материала, из которого изготовлен стержень. Например, для стали предел упругости (F/S)_max = 4 x 10⁸ Па. Поэтому максимальная скорость v стального стержня, при которой его соударение с преградой все еще можно считать упругим, оказывается согласно формуле (9) равной 10 м/с. Это соответствует скорости свободного падения тела с высоты всего лишь 5 м. Укажем для сравнения, что скорость звука в стали $u$ = 5000 м/с, т. е. $v << u$. Время столкновения стержня с неподвижной преградой (в отличие от силы) оказалось не зависящим от скорости стержня.

Этот результат, однако, не является универсальным, а связан со специфической формой рассматриваемого тела. Например, для упругого шара время столкновения со стенкой зависит от его скорости. Динамическое рассмотрение этого случая оказывается более сложным. Связано это с тем, что и площадь соприкосновения деформированного шара со стенкой, и действующая на шар сила в процессе столкновения не остаются постоянными.

Нижегородский Государственный
Технический Университет.

Лабораторная
работа по физике №1-21.

Механический
удар.

Цель работы: Ознакомиться с элементами
теории механического удара и
экспериментально определить время
удара
,
среднюю силу удара F,
коэффициент восстановления Е.

В работе изучаются основные характеристики
удара, ознакомляются с цифровыми
приборами для измерения временного
интервалов.

1. Теоретическая
часть.

Ударом называется изменения состояния
движения тела, вследствие кратковременного
взаимодействия его с другим телом. Во
время удара оба тела претерпевают
изменения формы (деформацию). Сущность
упругого удара заключается в том, что
кинетическая энергия относительного
движения соударяющихся тел, за короткое
время, преобразуется в энергию упругой
деформации или в той или иной степени
в энергию молекулярного движения. В
процессе удара происходит перераспределение
энергии между соударяющимися телами.

Пусть на плоскую поверхность массивной
пластины падает шар с некоторой скоростью
V₁
и
отскакивает от нее со скоростью V₂­­.

Рис.1.

Обозначим

– нормальные и тангенциальные составляющие
скоростей

и
,
а

и

– соответственно углы падения и отражения.
В идеальном случае при абсолютно упругом
ударе, нормальные составляющие скоростей
падения и отражения и их касательные
составляющие были бы равны;

.
При ударе всегда происходит частичная
потеря механической энергии. Отношение
как нормальных, так и тангенциальных
составляющих скорости после удара к
составляющим скорости до удара есть
физическая характеристика, зависящая
от природы сталкивающихся тел.

(1)

Эту характеристику Е называют
коэффициентом восстановления. Числовое
значение его лежит между 0 и 1.

2.
Определение средней силы удара,
начальной и конечной скоростей шарика
при ударе.

Экспериментальная установка состоит
из стального шарика А, подвешенного на
проводящих нитях, и неподвижного тела
В большей массы, с которым шарик
соударяется. Угол отклонения подвеса

измеряется по шкале. В момент удара на
шар массой m
действует сила тяжести со стороны Земли

,
сила реакции со стороны нити

и средняя сила удара

со стороны тела В (см. Рис.2.).

На
основании теоремы об изменении импульса
материальной точки:

(2)

где

и

– векторы скоростей шара до и после
удара;–
длительность
удара.

После проектирования уравнения (2) на
горизонтальную ось определим среднюю
силу удара:

(3)

Скорости шарика V₁
и V₂
определяются на основании закона
сохранения и превращения энергии.
Изменение механической энергии системы,
образованной шариком и неподвижным
телом В, в поле тяготения Земли определятся
суммарной работой всех внешних и
внутренних не потенциальных сил.
Поскольку внешняя сила

перпендикулярна перемещению и нить
нерастяжима, то эта сила работы не
совершает, внешняя сила

и внутренняя сила упругого взаимодействия

– потенциальны. Если эти силы много
больше других не потенциальных сил, то
полная механическая энергия выбранной
системы не меняется. Поэтому, уравнение
баланса энергии можно записать в виде:

(4)

Из чертежа (рис. 2) следует, что
,
тогда из уравнения (4) получим значения
начальной V₁
и конечной V₂
скоростей шарика:
(5)

где

и

– углы отклонения шара до и после
соударения.

3.
Метод
определения длительности удара.

В
данной работе длительность удара шарика
о плиту определяется частотомером Ч3-54
, функциональная схема которого
представлена на рисунке 3. С генератора
подается на вход системы управления СУ
импульсы с периодом Т. Когда в процессе
соударения металлической плиты В,
электрическая цепь, образованная СУ,
проводящими нитями подвеса шара, шаром,
плитой В и счетчиком импульсов С_ч,
оказывается замкнутой, и система
управления СУ пропускает на вход счетчика
С_ч импульсы электрического тока
только в интервале времени

, равном времени длительности удара.
Число импульсов, зарегистрированных
за время
,
равно
,
откуда
.

Чтобы определить длительность удара

,
необходимо число импульсов,
зарегистрированных счетчиком, умножить
на период импульсов, снимаемых с
генератора Г.

Измерительные
средства:

1). Частотомер
ЧЗ-34.

2). Шкала отсчета
углов.

Исходные
данные:

Масса шарика –

Длина нити –

Ускорение свободного
падения –

Приборные
погрешности.

1). Для частотомера
ЧЗ-34 :
t=

2). Для шкалы отсчёта
углов :
a=

Основные
формулы.

1).
По теореме об
изменении импульса материальной точки
:

,после
проектирования на ось Х
получаем F=.

2). По теореме об
изменении механической энергии системы
шар-Земля»
;

из рис.№1 получаем

;

откуда

3).
e=


–
коэффициент восстановления, причём
0<
e<1.

Таблица
№1.

a1,o	20	30	40	50	60
№ опыта	t,мкс	a2	t,мкс	a2	t,мкс	a2	t,мкс	a2	t,мкс	a2
1	58,43	13,5	51,06	19,5	49,72	24,0	48,86	29,5	44,12	36,0
2	57,66	13,5	52,72	20,0	50,08	24,5	46,61	30,5	44,95	36,5
3	56,33	14,5	53,39	19,5	49,75	23,5	46,39	29,5	44,65	36,5
4	57,41	14,0	52,8	19,0	50,6	24,0	46,92	30,5	43,71	37,0
5	58,78	13,5	53,67	19,0	48,61	23,5	46,67	28,5	44,39	36,5
6	57,19	13,5	52,53	18,5	49,62	23,5	47,5	30,5	44,98	35,5
7	56,78	14,0	51,86	18,5	47,11	24,0	46,28	30,5	44,48	36,5
8	58,21	14,0	52,51	20,5	49,73	24,0	47,46	30,5	44,21	37,0
9	59,72	13,5	51,11	19,5	50,47	24,0	46,23	29,5	45,15	35,5
10	58,22	13,5	50,46	20,0	48,85	24,0	46,66	30,5	44,36	36,5

Расчёты.

1).
V₁=.

2).
<V₂>=

3). <F>=;

4). e=.

Расчет погрешностей исходных данных.

1).

2).

3).

Расчет погрешностей прямых измерений.

Количество
повторений – 10 .

При Р=95% , коэффициенты
Стьюдента:

.

1).
<t>=57,77
мкс.

Dt=

e_t==

t=<t>t=(57,770,68)мкс,
Р=95%, e_t=1,18%.

2).

;
e_t==

t=<t>t=(52,210,76)мкс,
Р=95%, e_t=1,45%.

3).

;
e_t==

t=<t>t=(49,40,59)мкс,
Р=95%,
e_t=1,19%.

4).

;
e_t==

t=<t>t=(46,80,33)мкс,
Р=95%, e_t=0,7%.

5).

;
e_t==

t=<t>t=(44,50,33)мкс,
Р=95%, e_t=0,73%.

1).

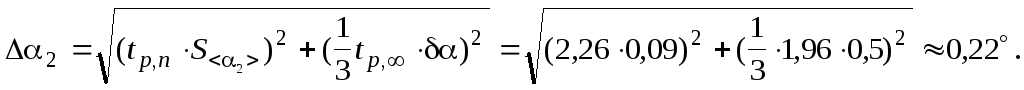
e_a==

a₂=<a₂>a=(13,50,22)⁰;
Р=95%, e_a=1,63%.

2).

;
e_a=

a₂=<a₂>a=(19,40,47)⁰;
Р=95%, e_a=2,45%.

3).

;
e_a=

a₂=<a₂>a=(23,90,24)⁰;
Р=95%, e_a=1%.

4).

;
e_a=

a₂=<a₂>a=(29,850,45)⁰;
Р=95%, e_a=1,52%.

5).

;
e_a=

a₂=<a₂>a=(36,30,39)⁰;
Р=95%,
e_a=1,07%.

Расчет погрешностей
косвенных измерений.

1).

V₁=
V₁±
DV₁=(0,86±0,0215)м/с;
P=95%;e=2,5.

2).

V₁=
V₁±
DV₁=(1,29±0,022)м/с;
P=95%;e=1,7

.

3).

V₁=
V₁±
DV₁=(1,7±0,022)м/с;
P=95%;e=1,3.

4).

V₁=
V₁±
DV₁=(2,1±0,021)м/с;
P=95%;e=1.

5).

V₁=
V₁±
DV₁=(2,48±0,022)м/с;
P=95%;e=0,9.

1).

V₂=<
V₂ > ±
DV₂=(0,6±0,01)м/с;
P=95%;e=1,7.

2).

V₂=<
V₂ > ±
DV₂=(0,84±0,02)м/с;
P=95%;e=2,4.

3).

V₂=<
V₂ > ±
DV₂=(1,04±0,01)м/с;
P=95%;e=1,1.

4).

V₂=<
V₂ > ±
DV₂=(1,28±0,02)м/с;
P=95%;e=1,5.

5).

V₂=<
V₂ > ±
DV₂=(1,53±0,02)м/с;
P=95%;e=1,1.

e_e

1).

e_e

e=e±De=0,7±0,021;
P=95%;
e_e=3.

2).

e_e

e=e±De=0,65±0,02;
P=95%;
e_e=3.

3).

e_e

e=e±De=0,61±0,01;
P=95%;
e_e=2.

4).

e_e

e=e±De=0,6±0,01;
P=95%;
e_e=2.

5).

e_e

e=e±De=0,62±0,006;
P=95%;
e_e=1.

e_F;

1).

F=<F>±DF=(478,74±14,4)H;
P=95%,
e_F=3.

2).

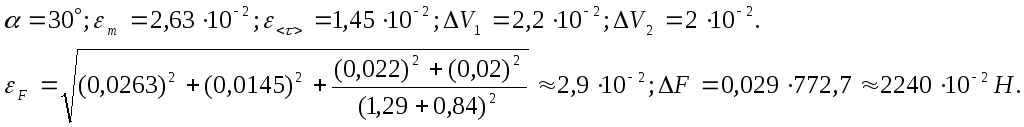
F=<F>±DF=(772,7±22,4)H;
P=95%,
e_F=2,9.

Соседние файлы в папке Отчёты 1 семестр

• #
• #
• #
• #
• #
• #

где t – время
в течении которого на тело действовала сила F,
изменившая импульс тела на величину DR.

    Применительно к удару в уравнении (14) F – средняя сила удара,

t – время
удара, т.е. время соприкосновения ударяющихся тел, DR=DmV, где m – масса одного из соударяющихся тел (второе тело
неподвижно), DV – изменение скорости этого тела, возникающее в результате
удара. Если бьющий шар после удара остается в покое, то DV=V, где V – скорость шара в
момент удара которая, согласно (10) равна

                      
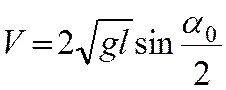                           (15)

Подставив (15) в (14) получаем окончательное выражение для
средней силы упругого удара

                          
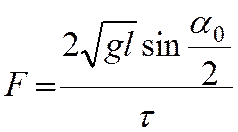                     (16)

ВЫПОЛНЕНИЕ
УПРАЖНЕНИЯ.

1.  Поместить на
нити подвеса шары одинаковой массы и отрегулировать их положение.

2.  Измерить время t соударения шаров не менее 10 раз.
Результаты занести в таблицу 2 и обработать.

3.  Определив длину
подвеса, массу одного шара и значение угла  по
формуле (16), рассчитать среднюю силу удара.

Упражнение 3: проверка закона сохранения импульса и
определение энергии остаточной деформации при неупругом ударе.

    Законы сохранения импульса и энергии при неупругом
ударе имеют вид

                     
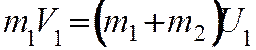                   (17)

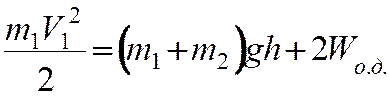                       (18)

где  – масса бьющего
пластилинового шара,

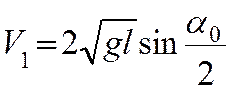 – его скорость в момент удара,

        – масса ударяемого
шара,

         – максимальная высота
подъема двух шаров после удара,

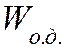         – энергия остаточной
деформации.

    Учитывая, что

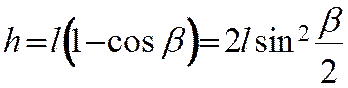
и принимая во внимание выражение (10), вместо (17) и (16)
запишем рабочие формулы

                      
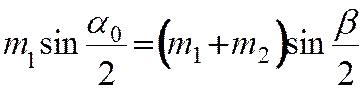                   (19)

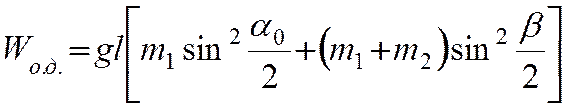              (20)

где b –
угол отклонения шаров после удара.

    Упражнение выполняется для одного удара на
пластилиновых шарах. Порядок выполнения такой же, как и в упражнении 1. Опыт
проделать не менее 5 раз.

Упражнение  №1

Проверка закона сохранения импульса и определение
коэффициента восстановления упругого удара.

=15⁰

Таблица  №1

№	(0)	(0)
1	0,25	8,5
2	0,1	9
3	0,25	8
4	0,25	8
5	0,2	8,25
6	0,3	8,5
7	0,2	9
8	0,25	8,5
9	0,15	9
10	0,15	8,5
(0)	0,280,174	8,70,653
(%)	62,255	7,507

;;

 –
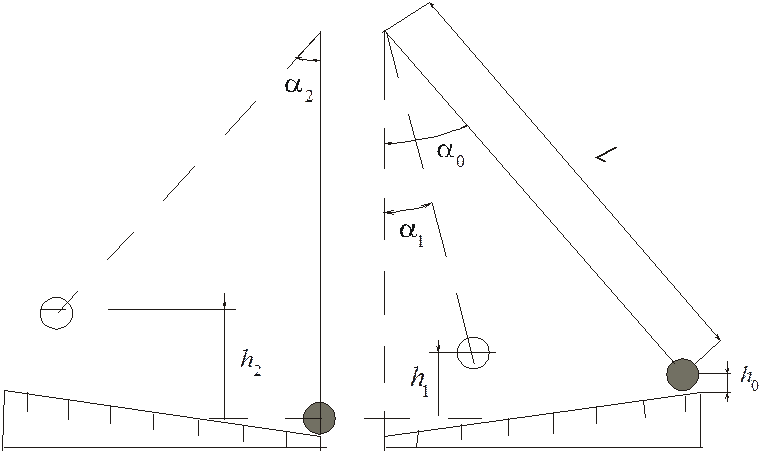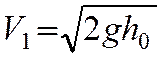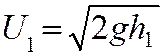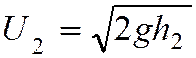
высота начального положения ударяющего (правого) шара (рис.2);

 –
высота, на которую поднимается ударяющий (правый) шар после соударения;

 –
высота, на которую поднимается ударяемый (левый) шар после соударения.

–
скорость правого шара в момент удара;

 и  – скорости шаров после удара.

      1|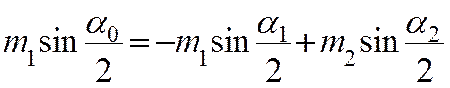

2|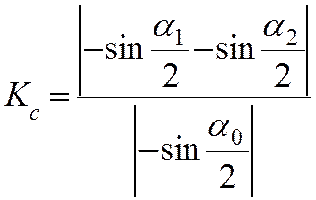     

3|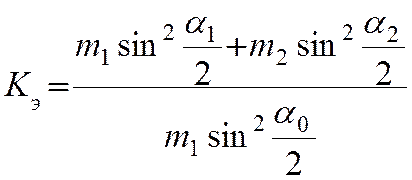         

1| 0,106*0.938=
–0.106*0,1395+ 0.172*0.935

0.099=0.14

2|К_с=|-0,1395+0.935|/|-0.938|=0.848

3|К_э=(0,106*0,01946025+0,172*0,874225)/(0,106*0,879844)=1,634

Вывод:

проверил закон
сохранения импульса и определил коэффициент восстановления упругого удара

Упражнение 2:определение времени упругого удара и
средней силы соударения шаров.

Таблица №2

№	t (мкс)
1	69
2	77
3	75
4	79
5	78
6	72
7	75
8	74
9	78
10	76
tср	75

l = 47 см = 0.47 см

1)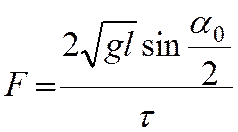=(2*(9,81*0,47)^1/2*0.938)/75=0.053
Н.

Вывод:

определил время
упругого удара и среднюю силу соударения шаров.

КОНТРОЛЬНЫЕ
ВОПРОСЫ.

1.  Внутренние и
внешние силы.

2.  Импульс. Закон
сохранения импульса (доказать).

3.  Типы удара
твердых тел.

4.  Количественные
характеристики удара твердых тел.

5.  Как изменяются
кинетическая энергия шаров и их относительная скорость при различных видах
удара: абсолютно упругом, неупругом и абсолютно неупругом (доказать).

6.  Вывести рабочие
формулы.

ЛИТЕРАТУРА

1. 
Сивухин Д.В. Общий курс физики. т.1, §§10-12,
18, 26, 28, М., 1979.

2. 
Матвеев А.Н. Механика и теория относительности, М., 1976.

3. 
Петровский И.И. Механика, Минск, 1973, гл.VI,
§§10-12.

4. 
Савельев И.В. Курс общей физика, т.1, §§22, 23, 30.

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание – внизу страницы.

1

Начнём с определения:

Удар — кратковременное взаимодействие тел, при котором происходит перераспределение кинетической энергии. Часто носит разрушительный для взаимодействующих тел характер.

Сила удара, как и любая другая сила, измеряется в Ньютонах (Н) и килограмм-силах (кгс).

Один Ньютон – это сила, благодаря которой тело массой 1 кг получает ускорение 1 м/с2. Одна кгс – это сила, которая сообщает телу массой 1 кг ускорение 1 g = 9,81 м/с2 (g – ускорение свободного падения). Поэтому 1 кгс = 9,81 Н.

Вес тела массой m определяется силой притяжения Р, с которой он давит на опору: P = mg.

Если масса Вашего тела 80 кг, то Ваш вес, определяемый силой тяжести или притяжением, P = 80 кгс. Но в просторечье говорят «мой вес 80 кг», и всем всё понятно.

Поэтому часто о силе удара тоже говорят, что он составляет сколько-то кг, а подразумевается кгс.

Согласно Второго закона динамики, силу удара спортсмена определяют по формуле:

F = V0 m k1 k2 / t

где V0 – скорость ударной массы в момент соударения, мс:

m – собственно ударная масса, кг.

k1 – коэффициент, учитывающий жесткость кинематической цепи звеньев тела и жёсткости мишени .

k2 – коэффициент, учитывающий форму ударного движения..

t – время взаимодействия (соударения) ударной поверхности и мишени.

Таким образом на величину силы удара спортсмена-единоборца влияют следующие факторы:

1. СКОРОСТЬ ДВИЖЕНИЯ УДАРНОЙ МАССЫ.

Спортсмены-ударники, стараются увеличивать силу удара конечностей, придавая им максимальное ускорение (взрывная сила), а также максимально быстро перемещая тело (быстрая сила). Ударная масса обратно пропорциональна скорости – с увеличением ударной массы уменьшается скорость ее перемещения и наоборот.

2. ВЕЛИЧИНА УДАРНОЙ МАССЫ. Чем выше весовая категория спортсмена-единоборца, тем больше его ударная масса. Вот почему бойцы при нанесении ударов стремятся увеличивать ударную массу используя максимально массу всех звеньев тела. Это необходимо для увеличения силы толчка или удара.

3. ЖЕСТКОСТЬ КИНЕМАТИЧЕСКОЙ ЦЕПИ. Чем больше жесткость соударяющихся тел, тем выше сила удара. По этому сила удара по мешку весом в 100 кг будет выше чем по мешку в 20кг. Понятно, что, ударив по воздушному шарику, какой-либо значительной величины мы вообще не получим.

В момент касания цели необходимо создать максимальную жесткость в кинематической цепи суставов тела (структура) путем кратковременной фиксации звеньев тела, участвующих в этом движении (структура тела). Это так же увеличит и ударную массу в момент контакта с мишенью.

Каждое движение выполняется по схеме «расслабление-напряжение». Фаза расслабления должна занимать 99% времени всего движения, именно за счет ее появляется «хлесткость» удара.

4. ФОРМА УДАРНОГО ДВИЖЕНИЯ. Классическая механика исходит из того, что при ударе кинетическая энергия ударной массы полностью переходит в кинетическую энергию ударяемого тела. Передача энергии улучшается в том случае, когда центры масс звеньев ударной цепи в момент удара находятся на одной линии. При этом, чем резче и акцентированней остановка ударной поверхности в конечной фазе удара, тем больший выброс энергии следует. Энергия удара зависит и от правильной координации движения то есть – от правильной техники исполнения удара.

5. ВРЕМЯ СОУДАРЕНИЯ обратно пропорционально силе удара и не зависит от конечной скорости ударной массы. Это время растет с увеличением масс соударяющихся тел и уменьшением жесткости суставных соединений (ослабление стутуры тела) .

Отсюда исходит важность правильного выстраивания структуры тела.

Оптимальное время контакта ударной поверхности с целью составляет 0,014-0,018 с, при увеличении времени до 0,3 с удар превращается в толчок.

Все пять указанных факторов связаны между собой “принципом одновременности окончания”. То есть, все движения, составляющие удар (вращение бедер, шаг, разгибание ударной или блокирующей конечности), а также концентрация физической силы в момент нанесения удара должны происходить и заканчиваться одновременно.

Но сила удара сама по себе еще не гарантирует эффективное поражение. Его поражающее воздействие зависит и от следующих дополнительных факторов:

– Подготовка ударной поверхности.

Сила удара так же зависит от подготовленности ударной поверхности. Чем выше сила удара, тем большей нагрузке подвергается тело бьющего бойца. По этому, подготовка к ударным нагрузкам (набивка) – важный этап обучения.

– Точность направления удара к поверхности тела.

Удары по прямой линии к оси вращения противника позволяют наиболее полно реализовать разрушительную силу удара.

– Восприимчивости уязвимого места.

Легче всего вывести противника из строя, воздействуя на его болевые точки (расположенные близко к поверхности тепа нервные центры, жизненно важные органы, оголения костей, сухожильные связки и прочее).

Подводя итог – если мы хотим сделать наши удары по настоящему грозным оружием – мы должны учитывать все факторы рассмотренные в статье.

Успехов в практике!