Электромагнитная индукция

Содержание
- Явление электромагнитной индукции
- Магнитный поток
- Закон электромагнитной индукции Фарадея
- Правило Ленца
- Самоиндукция
- Индуктивность
- Энергия магнитного поля
- Основные формулы раздела «Электромагнитная индукция»
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Опыты Фарадея
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ), площади поверхности ( S ), пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):


Обозначение – ( Phi ), единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции:

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла ( alpha ) магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из ( N ) витков, то ЭДС индукции:

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ( R ):

При движении проводника длиной ( l ) со скоростью ( v ) в постоянном однородном магнитном поле с индукцией ( vec{B} ) ЭДС электромагнитной индукции равна:

где ( alpha ) – угол между векторами ( vec{B} ) и ( vec{v} ).
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
- вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
- определить направление линий магнитной индукции внешнего магнитного поля;
- выяснить, как изменяется магнитный поток;
- определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
- по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.

Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции ( varepsilon_{is} ), возникающая в катушке с индуктивностью ( L ), по закону электромагнитной индукции равна:

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ( Phi ) через контур из этого проводника пропорционален модулю индукции ( vec{B} ) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:

Индуктивность – коэффициент пропорциональности ( L ) между силой тока ( I ) в контуре и магнитным потоком ( Phi ), создаваемым этим током:

Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:

Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:

Основные формулы раздела «Электромагнитная индукция»

Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
6. Решение проверить.
Электромагнитная индукция
3.2 (63.4%) 94 votes
Явление электромагнитной индукции заключается в том, что в результате изменения во времени магнитного потока, который пронизывает замкнутый проводящий контур, в контуре возникает электрический ток. Открыто это явление было физиком из Великобритании Максом Фарадеем в 1831 году.
Формула магнитного потока
Введем обозначения, необходимые нам для записи формулы. Для обозначения магнитного потока используем букву Ф, площади контура – S, модуля вектора магнитной индукции – B, α – это угол между вектором B→ и нормалью n→ к плоскости контура.
Магнитный поток, который проходит через площадь замкнутого проводящего контура, можно задать следующей формулой:
Φ=B·S·cos α,
Проиллюстрируем формулу.
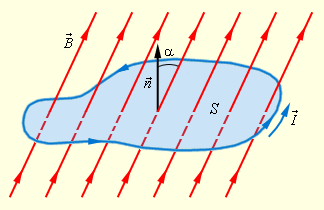
Рисунок 1.20.1. Магнитный поток через замкнутый контур. Направление нормали n→ и выбранное положительное направление l→ обхода контура связаны правилом правого буравчика.
За единицу магнитного потока в СИ принят 1 вебер (Вб). Магнитный поток, равный 1 Вб, может быть создан в плоском контуре площадью 1 м2 под воздействием магнитного поля с индукцией 1 Тл, которое пронизывает контур по направлению нормали.
1 Вб=1 Тл·м2
Закон Фарадея
Изменение магнитного потока приводит к тому, что в проводящем контуре возникает ЭДС индукции δинд. Она равна скорости, с которой происходит изменение магнитного потока через ограниченную контуром поверхность, взятой со знаком минус. Впервые экспериментально установил это Макс Фарадей. Он же записал свое наблюдение в виде формулы ЭДС индукции, которая теперь носит название Закона Фарадея:
Закон Фарадея:
δинд=-∆Φ∆t
Правило Ленца
Согласно результатам опытов, индукционный ток, который возникает в замкнутом контуре в результате изменения магнитного потока, всегда направлен определенным образом. Создаваемое индукционным током магнитное поле препятствует изменению вызвавшего этот индукционный ток магнитного потока. Ленц сформулировал это правило в 1833 году.
Проиллюстрируем правило Ленца рисунком, на котором изображен неподвижный замкнутый проводящий контур, помещенный в однородное магнитное поле. Модуль индукции увеличивается во времени.
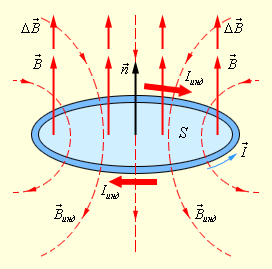
Рисунок 1.20.2. Правило Ленца
Здесь ∆Φ∆t>0, а δинд<0 < 0. Индукционный ток Iинд протекает навстречу выбранному положительному направлению l→ обхода контура.
Благодаря правилу Ленца мы можем обосновать тот факт, что в формуле электромагнитной индукции δинд и ∆Φ∆t противоположны по знакам.
Если задуматься о физическом смысле правила Ленца, то это частный случай Закона сохранения энергии.
Причины возникновения индукционного тока в движущихся и неподвижных проводниках
Причин, по которым может происходить изменение магнитного потока, пронизывающего замкнутый контур, две:
- Изменение магнитного потока вследствие перемещения всего контура или отдельных его частей в магнитном поле, которое не изменяется со временем;
- Изменение магнитного поля при неподвижном контуре.
Перейдем к рассмотрению этих случаев подробнее.
Перемещение контура или его частей в неизменном магнитном поле
При движении проводников и свободных носителей заряда в магнитном поле возникает ЭДС индукции. Объяснить возникновение δинд можно действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца здесь – это сторонняя сила.
На рисунке мы изобразили пример индукции, когда прямоугольный контур помещен в однородное магнитное поле B→ направленное перпендикулярно плоскости контура. Одна из сторон контура перемещается по двум другим сторонам с некоторой скоростью.
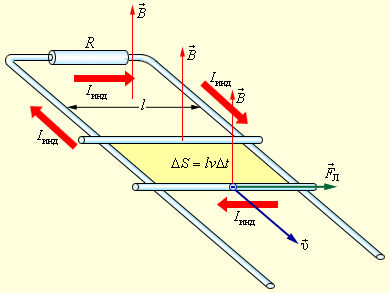
Рисунок 1.20.3. Возникновение ЭДС индукции в движущемся проводнике. Отражена составляющая силы Лоренца, которая действует на свободный электрон
На свободные заряды подвижной части контура воздействует сила Лоренца. Основная составляющая силы Лоренца в данном случае направлена вдоль проводника и связана с переносной скоростью зарядов υ→. Модуль этой сторонней силы равен:
FЛ=eυ→B.
Работа силы FЛ на пути l равна:
A=FЛ·l=eυBl.
По определению ЭДС:
δинд=Ae=υBl.
Значение сторонней силы для неподвижных частей контура равно нулю. Для соотношения δинд можно записать другой вариант формулы. Площадь контура с течением времени изменяется на ΔS=lυΔt. Соответственно, магнитный поток тоже будет с течением времени изменяться: ΔΦ=BlυΔt.
Следовательно,
δинд=∆Φ∆t.
Знаки в формуле, которая связывает δинд и ∆Φ∆t, можно установить в зависимости от того, какие направления нормали и направления контура будут выбраны. В случае выбора согласованных между собой по правилу правого буравчика направлений нормали n→ и положительного направления обхода контура l→ можно прийти к формуле Фарадея.
При условии, что сопротивление всей цепи – это R, то по ней будет протекать индукционный ток, который равен Iинд=δиндR. За время Δt на сопротивлении R выделится джоулево тепло:
∆Q=RIинд2∆t=υ2B2l2R∆t
Парадокса здесь нет. Мы просто не учли воздействие на систему еще одной силы. Объяснение заключается в том, что при протекании индукционного тока по проводнику, расположенному в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, которая связана с относительной скоростью движения зарядов вдоль проводника. Благодаря этой составляющей появляется сила Ампера FА→.
Для рассмотренного выше примера модуль силы Ампера равен FA =IBl. Направление силы Ампера таково, что она совершает отрицательную механическую работу Aмех. Вычислить эту механическую работу за определенный период времени можно по формуле:
Aмех=-Fυ∆t=-IBlυ∆t=-υ2B2l2R∆t
Проводник, перемещающийся в магнитном поле, испытывает магнитное торможение. Это приводит к тому, что полная работа силы Лоренца равна нулю. Джоулево тепло может выделяться либо за счет уменьшения кинетической энергии движущегося проводника, либо за счет энергии, которая поддерживает скорость перемещения проводника в пространстве.
Изменение магнитного поля при неподвижном контуре
Вихревое электрическое поле – это электрическое поле, которое вызывается изменяющимся магнитным полем.
В отличие от потенциального электрического поля работа вихревого электрического поля при перемещении единичного положительного заряда по замкнутому проводящему контуру равна δинд в неподвижном проводнике.
В неподвижном проводнике электроны могут приводиться в движение только под действием электрического поля. А возникновение δинд нельзя объяснить действием силы Лоренца.
Первым, кто ввел понятие вихревого электрического поля, был английский физик Джон Максвелл. Случилось это в 1861 году.
Фактически, явления индукции в подвижных и неподвижных проводниках протекают одинаково. Так что в этом случае мы тоже можем использовать формулу Фарадея. Отличия касаются физической причины возникновения индукционного тока: в движущихся проводниках δинд обусловлена силой Лоренца, в неподвижных – действием на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
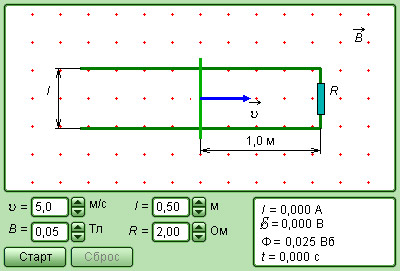
Рисунок 1.20.4. Модель электромагнитной индукции
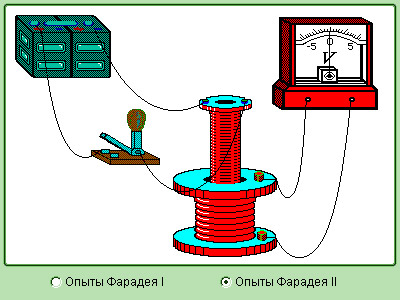
Рисунок 1.20.5. Модель опытов Фарадея
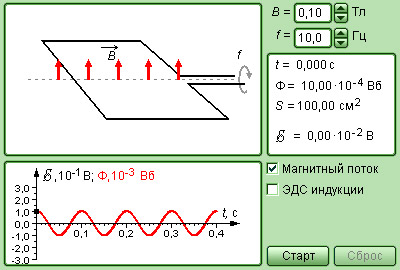
Рисунок 1.20.6. Модель генератора переменного тока
Магнитный поток наглядно истолковывается как число линий магнитной индукции, пронизывающих поверхность площадью S. Поэтому скорость изменения этого числа есть не что иное, как скорость изменения магнитного потока.
Если за малое время ∆t магнитный поток поменялся на ∆Ф, то скорость изменения магнитного потока равна ΔΦΔt. Поэтому утверждение, которое вытекает непосредственно из опыта, можно сформулировать так:
Сила индукционного тока пропорциональная скорости изменения магнитного потока через поверхность, ограниченную контуром:
Ii~ΔΦΔt
Известно, что в цепи появляется электрический ток в том случае, когда на свободные заряды проводника действуют сторонние силы. Работу этих сил при перемещении единичного положительного заряда вдоль замкнутого контура называют электродвижущей силой. Следовательно, при изменении магнитного потока через поверхность, ограниченную контуров, появляются сторонние силы, действие которых характеризуется ЭДС, называемой ЭДС индукции. Обозначают ее как εi.
Согласно закону Ома для замкнутой цепи:
Ii=εiR
Сопротивление проводника не зависит от изменения магнитного потока. Следовательно, сила индукционного тока пропорциональна скорости изменения магнитного потока только потому, что ЭДС индукции тоже пропорциональна этой скорости изменения потока.
Закон электромагнитной индукции
ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром.
εi=∣∣∣ΔΦΔt∣∣∣
Закон электромагнитной индукции формулируется именно для ЭДС, а не для силы тока. При такой формулировке закон выражает сущность явления, не зависящую от свойств проводников, в которых возникает индукционный ток.
Определение знака ЭДС индукции
На рисунке изображен замкнутый контур. Будем считать положительным направление обхода контура против часовой стрелки. Нормаль →n к контуру образует правый винт с направлением обхода.
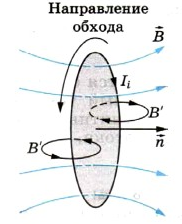
Пусть магнитная индукция →B внешнего магнитного поля направлена вдоль нормали к контуру и возрастает со временем. Тогда Φ>0 и ΔΦΔt>0. Согласно правилу Ленца индукционный ток создает магнитный поток Φ‘<0. Линии магнитной индукции B’ магнитного поля индукционного тока изображены черным цветом. Следовательно, индукционный ток Ii согласно правилу буравчика направлен по часовой стрелке (против направления положительного обхода) и ЭДС индукции отрицательна. Поэтому в законе электромагнитной индукции должен стоять знак «–», указывающий на то, что εi и ΔΦΔt имеют разные знаки:
εi=−ΔΦΔt
Пример №1. Магнитный поток через контур проводника сопротивлением 3∙10–2 Ом за 2 с изменился на 1,2∙10–2 Вб. Найдите силу тока в проводнике, если изменение потока происходило равномерно.
Известно, что:
Ii=εiR
εi=∣∣∣ΔΦΔt∣∣∣
Следовательно:
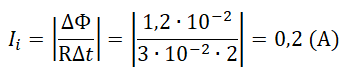
ЭДС индукции в движущихся проводниках
Электроны в неподвижном проводнике приводятся в движение электрическим полем, и это поле порождается переменным магнитным полем. Следовательно, изменяясь во времени, магнитное поле порождает электрическое поле. Но если проводник движется в постоянном во времени магнитном поле, то ЭДС индукции в проводнике обусловлена не вихревым электрическим полем, которое в этом случае не может возникнуть, а другой причиной.
При движении проводника его свободные заряды движутся вместе с ним. Поэтому на заряды со стороны магнитного поля действует сила Лоренца. Она и вызывает перемещение зарядов внутри проводника. ЭДС индукции, следовательно, имеет магнитное происхождение.
Вычислим ЭДС индукции, возникающую в проводнике, движущемся в однородном магнитном поле (см. рисунок). Пусть сторона контура MN длиной l скользит с постоянной скоростью →v вдоль сторон NC и MD, оставаясь все это время параллельной стороне CD. Вектор магнитной индукции →B однородного поля перпендикулярен проводнику и составляет угол α с направлением его скорости.
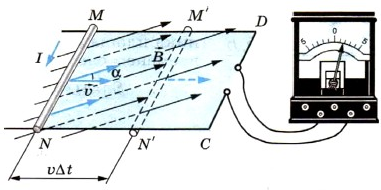
Сила, с которой магнитное поле действует на движущуюся заряженную частицу, равна по модулю:
FL=|q|vBsinα
Направлена эта сила вдоль проводника MN. Работа силы Лоренца на пути l положительна и составляет:
A=FLl=|q|vBlsinα
Внимание!
Формула выше определяет неполную работу силы Лоренца. Кроме силы Лоренца имеется составляющая силы Лоренца, направленная против скорости проводника →v. Такая составляющая тормозит проводник и совершает отрицательную работу. В результате полная работа силы Лоренца оказывается равной нулю.
Электродвижущая сила индукции в проводнике MN равна по определению отношению работы по перемещению заряда q к этому заряду:
εi=A|q|=vBlsinα
Эта формула справедлива для любого проводника длиной l, движущегося со скоростью →v в однородном магнитном поле.
В других проводниках контура ЭДС равна нулю, так как проводники неподвижны. Следовательно, ЭДС во всем контуре MNCD равна εi и остается неизменной, если скорость движения →v постоянна. Электрический ток при этом будет увеличиваться, так как при смещении проводника MN вправо уменьшается общее сопротивление контура.
С другой стороны, ЭДС индукции можно вычислить с помощью закона электромагнитной индукции. Магнитный поток через контур MNCD равен:
Φ=BScos(90°−α)=BSsinα
угол 90°−α представляет собой угол между векторами →B и нормалью →n к поверхности контура, а S — площадь контура MNCD. Если считать, что в начальный момент времени t=0 проводник MN находится на расстоянии NC от проводника CD, то при перемещении проводника площадь S изменяется со временем следующим образом:
S=l(NC−vt)
За время ∆t площадь контура меняется на ΔS=−lvΔt. Знак «минус» указывает на то, что она уменьшается. Изменение магнитного потока за это время равно:
ΔΦ=−BvlΔtsinα
Следовательно:
εi=−ΔΦΔt=Bvlsinα
Если весь контур MNCD движется в однородном магнитном поле, сохраняя свою ориентацию по отношению к вектору →B, то ЭДС индукции в контуре будет равна нулю, так как поток Φ через поверхность, ограниченную контуром, не меняется. Объяснить это можно так. При движении контура в проводниках MN и CD возникают силы, действующие на электроны в направлениях от N к M и от C к D. Суммарная работа этих сил при обходе контура по часовой стрелке или против нее равна нулю.
Пример №2. Проводник длиной 50 см движется в однородном магнитном поле со скоростью 4 м/с перпендикулярно силовым линиям. Найдите разность потенциалов, возникающую на концах проводника, если вектор магнитной индукции 8 мТл.
50 см = 0,5 м
8 мТл = 8∙10–3 Тл
Так как проводник движется перпендикулярно силовым линиям, то угол α равен 90 градусам, а синус прямого угла равен единице. Поэтому:
εi=Bvlsinα=8·10−3·4·0,5·1=16·10−3 (В)
Задание EF17754
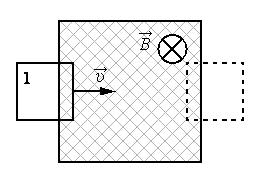 В заштрихованной области на рисунке действует однородное магнитное поле, направленное перпендикулярно плоскости рисунка, В = 0,1 Тл. Проволочную квадратную рамку сопротивлением R=10Ом и стороной l=10см перемещают в плоскости рисунка поступательно со скоростью υ=1м/с. Чему равен индукционный ток в рамке в состоянии 1?
В заштрихованной области на рисунке действует однородное магнитное поле, направленное перпендикулярно плоскости рисунка, В = 0,1 Тл. Проволочную квадратную рамку сопротивлением R=10Ом и стороной l=10см перемещают в плоскости рисунка поступательно со скоростью υ=1м/с. Чему равен индукционный ток в рамке в состоянии 1?
Ответ:
а) 1 мА
б) 5 мА
в) 10 мА
г) 20 мА
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать формулу для определения величины индукционного тока.
3.Записать закон электромагнитной индукции для движущихся проводников.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решения
Запишем исходные данные:
• Модуль вектора магнитной индукции однородного магнитного поля: B = 0,1 Тл.
• Сопротивление внутри квадратной проволочной рамки: R = 10 Ом.
• Сторона рамки: l = 10 см.
• Скорость перемещения рамки: v = 1 м/с.
10 см = 0,1 м
Индукционный ток, возникающий в рамке, определяется по формуле:
Ii=εiR
Закон электромагнитной индукции для движущихся проводников:
εi=vBlsinα
Отсюда индукционный ток равен:
Ii=vBlsinαR
На рисунке вектор магнитной индукции направлен в сторону от наблюдателя. Следовательно, угол между направлением движения рамки и вектором магнитной индукции равен 90 градусам. А синус прямого угла равен единице. Тогда:
Ii=vBlsin90°R=1·0,1·0,1·110=0,001 (А)=1 (мА)
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17970
При вращении в однородном магнитном поле плоскости металлического кольца из тонкой проволоки вокруг оси, перпендикулярной линиям поля, максимальная сила индукционного тока, возникающего в кольце, равна I1. Чему будет равна максимальная сила индукционного тока I2 в этом кольце при уменьшении скорости вращения кольца в 2 раза?
Ответ:
а) I2 = 2I1
б) I2 = I1
в) I2 = 0,5I1
г) I2 = 4I1
Алгоритм решения
1.Записать закон электромагнитной индукции.
2.Установить зависимость между величиной индукционного тока и скоростью вращения рамки.
3.Определить, как изменится величина индукционного тока в кольце при уменьшении скорости ее вращения.
Решение
Запишем формулу закона электромагнитной индукции:
εi=∣∣∣ΔΦΔt∣∣∣
Известно, что отношение изменения магнитного потока ко времени его изменения — это величина, характеризующая скорость этого изменения. Если кольцо в однородном магнитном поле вращать медленнее, то и магнитный поток начнет менять медленнее. Так как ЭДС индукции прямо пропорционально зависит от скорости изменения магнитного потока, то при уменьшении скорости вращения кольца в 2 раза она также уменьшится вдвое.
Также известно, что индукционный ток в рамке определяется формулой:
Ii=εiR
Видно, что индукционный ток и ЭДС индукции — прямо пропорциональные величины. Следовательно, при уменьшении ЭДС индукции вдвое сила индукционного тока тоже уменьшится в 2 раза. Отсюда следует, что I2 = 0,5I1.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18860
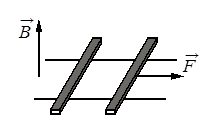 По горизонтально расположенным шероховатым рельсам с пренебрежимо малым сопротивлением могут скользить два одинаковых стержня массой m = 100 г и сопротивлением R = 0,1 Ом каждый. Расстояние между рельсами l = 10 см, а коэффициент трения между стержнями и рельсами μ = 0,1 Рельсы со стержнями находятся в однородном вертикальном магнитном поле с индукцией B = 1 Тл (см. рисунок). Под действием горизонтальной силы, действующей на первый стержень вдоль рельс, оба стержня движутся поступательно равномерно с разными скоростями. Какова скорость движения первого стержня относительно второго? Самоиндукцией контура пренебречь. Ответ записать в системе СИ.
По горизонтально расположенным шероховатым рельсам с пренебрежимо малым сопротивлением могут скользить два одинаковых стержня массой m = 100 г и сопротивлением R = 0,1 Ом каждый. Расстояние между рельсами l = 10 см, а коэффициент трения между стержнями и рельсами μ = 0,1 Рельсы со стержнями находятся в однородном вертикальном магнитном поле с индукцией B = 1 Тл (см. рисунок). Под действием горизонтальной силы, действующей на первый стержень вдоль рельс, оба стержня движутся поступательно равномерно с разными скоростями. Какова скорость движения первого стержня относительно второго? Самоиндукцией контура пренебречь. Ответ записать в системе СИ.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать закон электромагнитной индукции для двигающихся стержней.
3.Выполнить решение задачи в общем виде.
4.Подставить неизвестные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса стержней: m1=m2=m=100 г.
• Сопротивление стержней: R1=R2=R=0,1 Ом.
• Расстояние между рельсами: l = 10 см.
• Коэффициент трения между стержнями и рельсами: μ = 0,1.
• Модуль вектора магнитной индукции магнитного поля: B = 1 Тл.
• Угол между вектором магнитной индукцией и вектором скорости стержней: α = 90 градусов (синус прямого угла равен «1»).
100 г = 0,1 кг
10 см = 0,1 м
Когда под действием некой силы начинается двигаться первый стержень, магнитный поток, пронизывающий контур, образованные проводящими рельсами и двумя стержнями, меняется. Это приводит к возникновению в этом контуре электродвижущей силы, которую можно определить с помощью закона электромагнитной индукции для двигающихся стержней:
εi=vBlsinα
Причем v — это разность скоростей стержней (v2 – v1), которая характеризует скорость изменения площади проводящего контура.
Индукционный ток, возникающей в этом контуре, можно выразить, используя закон Ома:
εi=IRк
где Rк — сопротивление контура. Так как стержни соединяются последовательно, и их сопротивления равны R, а сопротивление рельсов ничтожно мало, сопротивление контура равно:
Rк=2R
Отсюда закон Ома принимает вид:
εi=2IR
Тогда ток в контуре равен:
I=εi2R=vBlsinα2R
С одной стороны на стержни действует сила Ампера, с другой — сила трения, возникающего между ними и рельсами. Так как стержни движутся равномерно, равнодействующая сил, приложенных к ним, равна нулю. Следовательно, сила трения и сила Ампера компенсируют друг друга (их модули равны):
Fтр=FА
μmg=BIlsinα
Подставим сюда выражение, полученное для силы тока в контуре:
μmg=BvBlsinα2Rlsinα=vB2l2sin2α2R
Отсюда скорость равна:
v=2μmgRB2l2sin2α
Так как синус угла равен «1»:
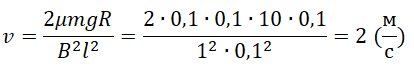
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5.5k
Магнитный поток, проходящий через площадь S равен:
Ф = BScosα;
где:
Ф ― величина магнитного потока [Вб],
S ― площадь контура [м2],
B ― индукция магнитного поля [Тл],
α ― угол между нормалью $overrightarrow{n}$ к площади контура и вектором индукции магнитного поля $overrightarrow{B}$.
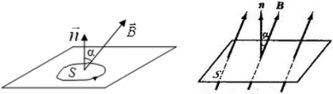
Если вектор индукции магнитного поля $overrightarrow{B}$ перпендикулярен площади контура, то магнитный поток равен:
Ф = BScos90° = BS;
Максимальное значение потока будет тогда, когда косинус будет максимальным (cosα = 1), то есть угол между вектором $overrightarrow{B}$ и вектором нормали к пластинке равен 0°, чему соответствует картинка 3. Наименьшее же значение потока будет тогда, когда косинус будет равен нулю (cosα = 0), то есть угол между нормалью к пластинке и вектором индукции равен 90°, чему соответствует картинка 4.
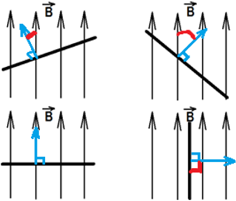
Электромагнитная индукция ― явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через контур. Если контур разомкнут, то на его концах наблюдается разносность потенциалов, равная ЭДС индукции.
ЭДС электромагнитной индукции возникает только тогда, когда изменяется магнитный поток.
Закон Фарадея об электромагнитной индукции и гласит, что индуцируемая ЭДС прямо пропорциональна скорости изменения магнитного потока:
$varepsilon_i = -frac{Delta text{Ф}}{Delta t}$
где:
$varepsilon_i $ ― ЭДС электромагнитной индукции [B],
$frac{Delta text{Ф}}{Delta t}$ ― скорость изменения магнитного потока [Вб/с],
∆Ф ― изменение магнитного потока [Вб],
∆t ― время, за которое происходит это изменение [c].
Кроме того, ЭДС индукции равна производной магнитного потока по времени:
$varepsilon_i = -text{Ф}_t’$
где:
- ― ЭДС электромагнитной индукции [B],
- ― производная магнитного потока по времени [Вб/с].
Задача 1
Замкнутый контур площадью S из тонкой проволоки помещён в магнитное поле. Плоскость контура перпендикулярна вектору магнитной индукции поля. В контуре возникают колебания тока с амплитудой iм = 35 мА, если магнитная индукция поля меняется с течением времени в соответствии с формулой B = acos (bt), где a = 6 · 10-3Тл, b = 3500 c-1. Электрическое сопротивление контура R = 1,2 Ом. Чему равна площадь контура?
Решение:
Обратите внимание на величины, данные в условии. Они здесь совсем не такие, к которым вы привыкли, потому что не дано значение магнитного поля, а дана зависимость магнитного поля от времени. Посмотрим, как это скажется на решении задачи.
Поскольку магнитное поле, а вместе с ним и поток меняются, то будет возникать ЭДС индукции, именно это ЭДС и вызовет электрический ток, поэтому запишем закон электромагнитной индукции.
По закону электромагнитной индукции $varepsilon_i = -frac{Delta text{Ф}}{Delta t}$
ЭДС — это изменение магнитного потока за время. Ничего в определении ЭДС не сказано про это самое время. Дело в том, что изменение какой-то величины за небольшой промежуток времени называется производной по времени. То есть наше ЭДС, которое является изменением магнитного потока за небольшой промежуток времени, это просто производная магнитного потока по времени $varepsilon_i = -text{Ф}_t’$
И это очень важный момент, без которого мы не сможем решить такого рода задачу.
Теперь посчитаем ЭДС индукции.
Напишем, чему равен магнитный поток Ф = BS = acos (bt) · S.
ЭДС индукции — это производная магнитного потока по времени. Теперь придётся вспомнить немного математики. Множители “a” и “S” перед косинусом не зависят от времени, поэтому производная их не трогает, а вот у косинуса в скобках стоит зависимость от времени, поэтому именно от косинуса производную и нужно взять.
Обратите внимание на полученную формулу магнитного потока. В ней стоит просто множитель aS перед сложной функцией косинуса
$text{Ф} underset{text{множитель}}{underbrace{aS}} ;; cdot ;; underset{text{сложная функция}}{underbrace{cos(bt)}}$.
Взяв производную от этой функции, получаем Ф´ = –abS · sin (bt). А теперь, раз мы знаем производную магнитного потока, значит, знаем и ЭДС индукции, потому что $varepsilon_i = -text{Ф}_t’$
Подставив сюда значение производной, получим $varepsilon_i = -text{Ф}_t’$ = abS · sin (bt).
Мы получили значение ЭДС. Кроме этого, мы знаем сопротивление и максимальную силу тока, поэтому запишем закон Ома.
По закону Ома $I = frac{varepsilon}{R}$ , подставив сюда значение ЭДС, получаем $I = frac{abScdot sin(bt)}{R}$.
Мы получили зависимость силы тока от времени.
Из-за синуса, который стоит в этой формуле, ток постоянно меняет свое значение, то он становится больше, то меньше, поскольку синус меняет своё значение от -1 до 1.
В условии дано максимальное значение силы тока, которое протекает по контуру. Когда эта величина будет максимальной? В тот момент, когда синус будет максимальным, то есть равный единице. Поэтому запишем sin (bt) = 1.
Максимальное значение тока будет в тот момент, когда будет максимальным значение ЭДС индукции, то есть когда, $I_{max} = frac{abS}{R}$.
Отсюда можно легко выразить площадь контура $S = frac{I_{max}R}{ab}$, подставив сюда все значения, получим $S = frac{I_{max}R}{ab} = frac{35cdot 10^{-3} Acdot 1,2text{Ом}}{6cdot 10^{-3}text{Тл} cdot 35000c^{-1}} = 0,002text{м}^2$
Ответ: 0,002
Как видно из формулы магнитного потока Ф = BScosα, изменение магнитного потока может быть вызвано разными факторами:
- увеличением или уменьшением модуля индукции магнитного поля (т. е. величины $frac{Delta B}{Delta t}$);
- изменением направления вектора магнитного поля (т. е. изменением угла α);
- деформацией контура, причем такой деформацией, при которой изменяется площадь контура (т. е. изменением величины $frac{Delta S}{Delta t}$ );
- изменением нескольких из этих величин одновременно.
Таким образом, изменение модуля или направление вектора магнитной индукции или площади контура неизбежно приводят к тому, что в контуре возникает электродвижущая сила.
Если нарисовать график зависимости магнитного потока, то он может выглядеть либо так: тогда поток не будет менятьсяи ЭДС не возникает.

Либо так, тогда будет меняться поток и возникать ЭДС:
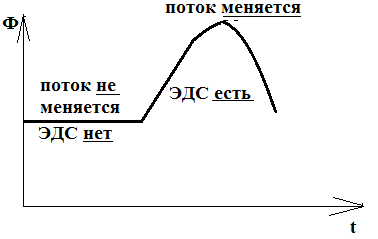
Знак «минус» перед скоростью изменения магнитного потока в формуле отражает правило Ленца: индуцированный ток всегда направлен так, чтобы магнитное поле, которое он создает, препятствовало изменению магнитного потока.
Если магнитный поток, проходящий через площадь контура, уменьшается, то магнитное поле индуцированных токов будет стремиться его увеличить.
Если поток увеличивается ― магнитное поле индуцированных токов будет стремиться его уменьшить.
Задача 2
Два проводящих кольца расположены относительно проводника с током в одной плоскости, как это показано на рисунке. В каком направлении будет индуцироваться ток в этих кольцах, если начать двигать их в направлении проводника?
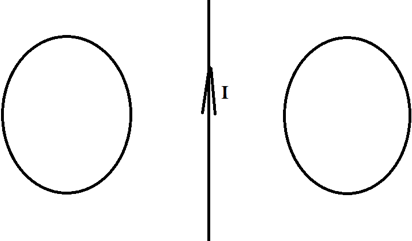
Решение:
Первым делом необходимо понять, как вообще может возникать индуцированный ток, если даже магнитного поля нет?
Его направление мы можем определить по правилу правого винта. Отметим это на рисунке.
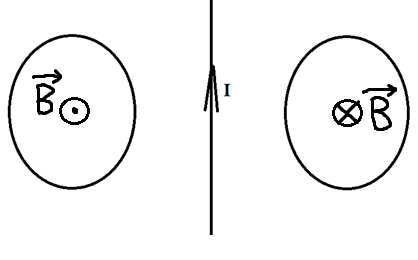
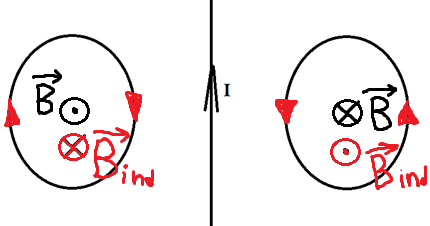
Теперь эти два проводника начинают двигать. Разве от этого меняется поток? Ведь площадь остаётся та же самая, угол между нормалью и вектором тоже не меняется. Однако, чем ближе к проводнику с током, тем сильней поле, а чем дальше от него, тем слабее! Поэтому, когда мы двигаем кольца к проводнику, мы увеличиваем поток, ведь ближе поле сильнее. Значит, будет появляться ток, а его направление можно определить по правилу Ленца. Что нам говорит правило Ленца?
Раз поток увеличивается, то по правилу Ленца ток будет индуцироваться так, чтобы уменьшить поток, то есть магнитное поле в левом кольце будет направлено от нас, а в правом ─ на нас. А значит, по правилу правого винта мы можем определить, что ток будет течь по часовой стрелке слева и против часовой стрелки справа.
Движение проводников
Если к концам проводника, движущегося в магнитном поле, подключить вольтметр, то прибор покажет наличие разности потенциалов на концах проводника. Таким образом, когда проводник перемещается в области с магнитным полем, в нем возникает электромагнитная движущая сила (ЭДС).
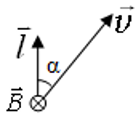
Согласно закону Лоренца, в проводнике, движущемся в магнитном поле, создается ЭДС $|varepsilon_i| = Blvsinalpha$;
где:
$varepsilon_i$― ЭДС электромагнитной индукции [B],
B ― индукция магнитного поля [Тл],
l ― длина проводника [м],
v ― скорость движения проводника [м/с],
α ― угол между направлением вектора скорости $overrightarrow{v}$ и длиной проводника $overrightarrow{l}$ , если вектор индукции магнитного поля $overrightarrow{B}$перпендикулярен проводнику и вектору скорости его движения: $overrightarrow{B} perp overrightarrow{v}, overrightarrow{B} perp overrightarrow{l}$
Используя силу Лоренца, можно получить это определение ЭДС. Сила Лоренца ― это проявленное действие магнитного поля на заряженную частицу.
В проводнике присутствует большое количество свободных зарядов (именно это отличает проводники от диэлектриков), и на каждый из зарядов действует сила Лоренца, перемещая их по проводнику так, что в одной его части скапливается отрицательный заряд, а в другой, соответственно, положительный. Это распределение зарядов и является физической основой для возникновения электродвижущей силы.
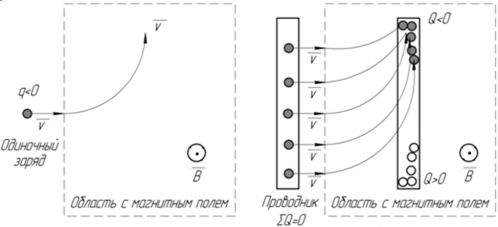
На рисунке показано как сила Лоренца, действующая на каждый из зарядов проводника, создаёт ЭДС в проводнике. Если одиночный отрицательный заряд попадает в магнитное поле, направленное от нас, то, согласно правилу левой руки, направление его движения изменяется так, как показано на рисунке. Если в область с таким же магнитным полем входит проводник, суммарный заряд которого равен нулю, но внутри которого находятся электроны, способные свободно перемещаться в проводнике, то электроны стекаются в один конец проводника. Так как электроны переместились в один конец проводника, то этот конец приобретает отрицательный заряд, а противоположный ему ― положительный. Таким образом, в проводнике возникает разность потенциалов и электродвижущая сила.
В некоторых случаях удобно решать задачи, используя определение ЭДС через закон Лоренца (обычно это задачи о движении прямолинейного проводника в поле), в других ― через закон Фарадея.
В проводнике, движущемся в магнитном поле, образуется разность потенциалов U = lvBsinα;
где:
U — разность потенциалов [В],
l — длина проводника [м],
v — скорость движения проводника $big[ frac{text{м}}{c} big]$
B — индукция магнитного поля [Тл],
α — угол между направлением скорости и длиной проводника.
В случае, если есть какой-то замкнутый контур, то ЭДС в нем возникает только тогда, когда меняется магнитный потокчерез этот контур. В случае же тонкого стержня, для которого нельзя применить понятия магнитного потока, потому что у него просто нет площади, ЭДС возникает при движении в постоянном магнитном поле.
В случае, если в задаче дана проводящая рамка или контур, для определения ЭДС (напряжения) используем формулу $varepsilon_i = – frac{Delta text{Ф}}{Delta t}$
В случае, если в задачи дан проводник, движущейся в поле, для определения ЭДС (напряжения) используем формулу $varepsilon$ =U= lvBsinα.
Задача 3
В заштрихованной области на рисунке действует однородное магнитное поле, перпендикулярное плоскости рисунка с индукцией В = 0,1 Тл. Квадратную проволочную рамку, сопротивление которой 10 Ом и длина стороны 10 см, перемещают в этом поле в плоскости рисунка поступательно равномерно с некоторой скоростью υ. При попадании рамки в магнитное поле в положении 1 в ней возникает индукционный ток, равный 1 мА. Какова скорость движения рамки?
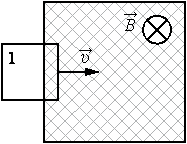
Решение:
Составим цепочку.
Зная силу тока и сопротивление, что можно найти? Мы сможем найти напряжение, то есть ЭДС, а ЭДС, уже можно легко связать со скоростью движения рамки.
Составим цепочку. Мы знаем магнитное поле (В), длину стороны (a), сопротивление (R) и силу тока (I), а найти нужно скорость(v).

Зная ток и сопротивление, что сразу можно найти? Напряжение, то есть ЭДС, которое мы сможем найти по закону Ома.
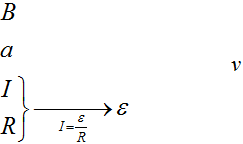
А связать ЭДС с индукцией поля, стороной рамки и скоростью движения очень легко, воспользовавшись той формулой, которую мы получили в прошлой задаче.
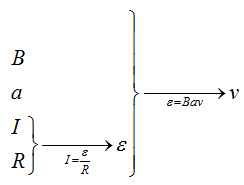
Пройдёмся вдоль этой цепочки.
Запишем закон Ома $I = frac{varepsilon}{R}$, подставив сюда формулу для ЭДС, которую мы получили в прошлой задаче, отбросив знак «минус» получим $I = frac{varepsilon}{R} = frac{Bav}{R}$отсюда выразим скорость, и, подставив все величины, получим $v = frac{IR}{Ba} = frac{1cdot 10^{-3} Acdot 10text{Ом}}{0,1 text{Тл} cdot 0,1 text{м}} = 1 frac{text{м}}{c}$
Ответ: 1
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
Зако́н электромагни́тной инду́кции Фараде́я является основным законом электродинамики, касающимся принципов работы трансформаторов, дросселей, многих видов электродвигателей и генераторов.[1] Закон гласит:
Для любого контура индуцированная электродвижущая сила (ЭДС) равна скорости изменения магнитного потока, проходящего через этот контур, взятой со знаком минус.[1]
или другими словами:
Генерируемая ЭДС пропорциональна скорости изменения магнитного потока.
При этом индукционный ток направлен таким образом, что его действие противоположно действию причины, вызвавшей этот ток (правило Ленца).[2]
История[править | править код]
Электромагнитная индукция была обнаружена независимо друг от друга Майклом Фарадеем и Джозефом Генри в 1831 году, однако Фарадей первым опубликовал результаты своих экспериментов[3][4].
В первой экспериментальной демонстрации электромагнитной индукции (август 1831) Фарадей обмотал двумя проводами противоположные стороны железного тора (конструкция похожа на современный трансформатор). Основываясь на своей оценке недавно обнаруженного свойства электромагнита, он ожидал, что при включении тока в одном проводе особого рода волна пройдёт сквозь тор и вызовет некоторое электрическое влияние на его противоположной стороне. Он подключил один провод к гальванометру и смотрел на него, когда другой провод подключал к батарее. В самом деле, он увидел кратковременный всплеск тока (который он назвал «волной электричества»), когда подключал провод к батарее, и другой такой же всплеск, когда отключал его.[5] В течение двух месяцев Фарадей нашёл несколько других проявлений электромагнитной индукции. Например, он увидел всплески тока, когда быстро вставлял магнит в катушку и вытаскивал его обратно, он генерировал постоянный ток во вращающемся вблизи магнита медном диске со скользящим электрическим проводом («диск Фарадея»)[6].

Фарадей объяснил электромагнитную индукцию с использованием концепции так называемых силовых линий. Однако, большинство учёных того времени отклонили его теоретические идеи, в основном потому, что они не были сформулированы математически.[7] Исключение составил Максвелл, который использовал идеи Фарадея в качестве основы для своей количественной электромагнитной теории.[7][8][9] В работах Максвелла аспект изменения во времени электромагнитной индукции выражен в виде дифференциальных уравнений. Оливер Хевисайд назвал это законом Фарадея, хотя он несколько отличается по форме от первоначального варианта закона Фарадея и не учитывает индуцирование ЭДС при движении. Версия Хевисайда является формой признанной сегодня группы уравнений, известных как уравнения Максвелла.
Эмилий Христианович Ленц сформулировал в 1834 году закон (правило Ленца), который описывает «поток через цепь» и даёт направление индуцированной ЭДС и тока в результате электромагнитной индукции.

Эксперимент Фарадея, показывающий индукцию между витками провода: жидкостная батарея (справа) даёт ток, который протекает через небольшую катушку (A), создавая магнитное поле. Когда катушки неподвижны, ток не индуцируется. Но когда маленькая катушка вставляется или извлекается из большой катушки (B), магнитный поток через катушку изменяется, вызывая ток, который регистрируется гальванометром (G).[10]
Закон Фарадея как два различных явления[править | править код]
Некоторые физики отмечают, что закон Фарадея в одном уравнении описывает два разных явления: двигательную ЭДС, генерируемую действием магнитной силы на движущийся провод, и трансформаторную ЭДС, генерируемую действием электрической силы вследствие изменения магнитного поля. Джеймс Клерк Максвелл обратил внимание на этот факт в своей работе О физических силовых линиях в 1861 году. Во второй половине части II этого труда Максвелл даёт отдельное физическое объяснение для каждого из этих двух явлений. Ссылка на эти два аспекта электромагнитной индукции имеется в некоторых современных учебниках.[11] Как пишет Ричард Фейнман:[12]
Таким образом, «правило потока» о том, что ЭДС в цепи равна скорости изменения магнитного потока через контур, применяется независимо от причины изменения потока: то ли потому что поле изменяется, то ли потому что цепь движется (или и то, и другое)…. В нашем объяснении правила мы использовали два совершенно различных закона для двух случаев –
для «движущейся цепи» и
для «меняющегося поля».
Мы не знаем никакого аналогичного положения в физике, когда такие простые и точные общие принципы требовали бы для своего реального понимания анализа с точки зрения двух различных явлений.
Отражение этой очевидной дихотомии было одним из основных путей, которые привели Эйнштейна к разработке специальной теории относительности:
Известно, что электродинамика Максвелла — как её обычно понимают в настоящее время — при применении к движущимся телам приводит к асимметрии, которая, как кажется, не присуща этому явлению. Возьмем, к примеру, электродинамическое взаимодействие магнита и проводника. Наблюдаемое явление зависит только от относительного движения проводника и магнита, тогда как обычное мнение рисует резкое различие между этими двумя случаями, в которых либо одно, либо другое тело находится в движении. Ибо, если магнит находится в движении, а проводник покоится, в окрестности магнита возникает электрическое поле с определенной плотностью энергии, создавая ток там, где расположен проводник. Но если магнит покоится, а проводник движется, то в окрестности магнита никакое электрическое поле не возникает. В проводнике, однако, мы находим электродвижущую силу, для которой не существует соответствующей энергии самой по себе, но которая вызывает — предполагая равенство относительного движения в двух обсуждаемых случаях — электрические токи по тому же направлению и той же интенсивности, как в первом случае.
Примеры подобного рода вместе с неудачной попыткой обнаружить какое-либо движение Земли относительно «светоносной среды» предполагают, что явления электродинамики, а также механики не обладают свойствами, соответствующими идее абсолютного покоя.
— Альберт Эйнштейн, К электродинамике движущихся тел[13]
В общем случае объяснение появления двигательной ЭДС с помощью действия магнитной силы на заряды в движущемся проводе или в изменяющем свою площадь контуре является неудовлетворительным. Действительно, заряды в проводе или в контуре могут вообще отсутствовать, исчезнет ли тогда сам эффект электромагнитной индукции в этом случае? Данная ситуация анализируется в статье, в которой при записи интегральных уравнений электромагнитного поля в четырёхмерном ковариантном виде вместо частной производной по времени в законе Фарадея появляется полная производная по времени от магнитного потока через контур. [14] Таким образом, электромагнитная индукция возникает либо при изменении со временем магнитного поля, либо при изменении площади контура. С физической точки зрения лучше говорить не об ЭДС индукции, а об индуцированной напряжённости электрического поля 










Поток через поверхность и ЭДС в контуре[править | править код]

Определение поверхностного интеграла предполагает, что поверхность Σ поделена на мелкие элементы. Каждый элемент связан с вектором dS, величина которого равна площади элемента, а направление — по нормали к элементу во внешнюю сторону.
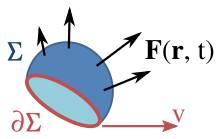
Векторное поле F(r, t) определено во всём пространстве, а поверхность Σ ограничена кривой ∂Σ, движущейся со скоростью v. По этой поверхности производится интегрирование поля.
Закон электромагнитной индукции Фарадея использует понятие магнитного потока ΦB через поверхность Σ, который определён через поверхностный интеграл:
где dS — площадь элемента поверхности Σ(t), B — магнитное поле, а B·dS — скалярное произведение B и dS. Предполагается, что поверхность имеет «устье», очерченное замкнутой кривой, обозначенной ∂Σ(t). Закон индукции Фарадея утверждает, что когда поток изменяется, то при перемещении единичного положительного пробного заряда по замкнутой кривой ∂Σ возникает ЭДС 
где 
Для плотно намотанной катушки индуктивности, содержащей N витков, каждый с одинаковым магнитным потоком ΦB, закон индукции Фарадея утверждает, что:
где N — число витков провода, ΦB — магнитный поток в веберах на один виток.
Выбираемый путь ∂Σ(t) для нахождения ЭДС должен удовлетворять двум основным требованиям: (i) путь должен быть замкнутым, и (ii) путь должен охватывать относительное движение частей контура (источник происхождения t-зависимости в ∂Σ(t)). К требованиям не относится то, что путь должен совпадать с линией тока, но, конечно, ЭДС, которая находится по закону потока, будет считаться по выбранному пути. Если путь не совпадает с линией тока, то подсчитанная ЭДС, возможно, будет не та ЭДС, которая вызывает ток.
Пример 1: пространственно меняющееся магнитное поле[править | править код]
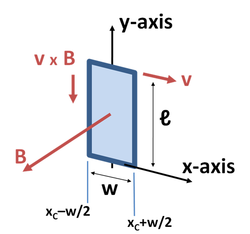
Рис. 3. Замкнутый прямоугольный провод движется вдоль оси x со скоростью v в магнитном поле, которое изменяется вдоль x.
Рассмотрим случай на рисунке 3, на котором прямоугольная замкнутая проволочная петля, расположенная в плоскости xy, перемещается в направлении оси x со скоростью v. Центр петли xC удовлетворяет условию v = dxC / dt. Петля имеет длину ℓ в направлении оси y и ширину w в направлении оси x. Зависящее от времени пространственно меняющееся магнитное поле B(x) показано в направлении z. Магнитное поле на левой стороне равно B(xC − w / 2), а на правой стороне B(xC + w / 2). Электродвижущую силу можно найти либо с помощью закона Лоренца, либо, что эквивалентно, используя вышеизложенный закон индукции Фарадея.
Закон Лоренца[править | править код]
Заряд q в проводнике на левой стороне петли испытывает силу Лоренца q v × B k = −q v B(xC − w / 2) j (j, k — единичные векторы в направлениях y и z; см. векторное произведение векторов), что вызывает ЭДС (работу на единицу заряда) v ℓ B(xC − w / 2) по всей длине левой стороны петли. На правой стороне петля аналогичное рассуждение показывает, что ЭДС равна v ℓ B(xC + w / 2). Две противоположные друг другу ЭДС толкают положительный заряд по направлению к нижней части петли. В случае, когда поле B возрастает вдоль х, сила на правой стороне будет больше, а ток будет течь по часовой стрелке. Используя правило правой руки, мы получаем, что поле B, создаваемое током, противоположно приложенному полю.[15] ЭДС, вызывающая ток, должна увеличиваться по направлению против часовой стрелки (в отличие от тока). Складывая ЭДС в направлении против часовой стрелки вдоль петли мы находим:
Закон Фарадея[править | править код]
В любой точке петли магнитный поток через неё равен:
Выбор знака определяется по принципу, имеет ли нормаль к поверхности в данной точке то же направление, что и B, или противоположное. Если нормаль к поверхности имеет то же направление, что и поле B наведённого тока, этот знак отрицательный. Производная по времени от потока (найденная с помощью методов дифференцирования сложной функции или по правилу Лейбница дифференцирования интеграла) равна:
(где v = dxC / dt является скоростью движения петли в направлении оси х), что приводит к:
как и в предыдущем случае.
Эквивалентность этих двух подходов является общеизвестной, и в зависимости от решаемой задачи более практичным может оказаться либо тот, либо другой метод.
Пример 2: проводник, движущийся в постоянном магнитном поле[править | править код]
Рис. 4. Два проводника замкнутые на проводящие обода образуют «рамку» вращающуюся с угловой скоростью ω в радиальном, направленном наружу магнитном поле B фиксированной величины. Ток подается щётками, касающимися верхнего и нижнего дисков с проводящими ободами.
На рис. 4 показан шпиндель, образованный двумя дисками с проводящими ободами, и проводники, расположенные вертикально между этими ободами. ток скользящими контактами подается на проводящие обода. Эта конструкция вращается в магнитном поле, которое направлено радиально наружу и имеет одно и то же значение в любом направлении. то есть мгновенная скорость проводников, ток в них и магнитная индукция, образуют правую тройку, что заставляет проводники вращаться.
Сила Лоренца[править | править код]
В этом случае на проводники действует Сила Ампера, а на единичный заряд в проводнике Сила Лоренца — поток вектора магнитной индукции B , ток в проводниках, соединяющих проводящие обода, направлен нормально к вектору магнитной индукции, тогда сила, действующая на заряд в проводнике, будет равна
где v = скорости движущегося заряда[16]
Следовательно, сила действующая на проводники
где l — длина проводников
Здесь мы использовали B как некую данность, на самом деле она зависит от геометрических размеров ободов конструкции, и это значение можно вычислить, используя Закон Био — Савара — Лапласа . Данный эффект используется и в другом устройстве, называемом Рельсотрон
Закон Фарадея[править | править код]
Интуитивно привлекательный, но ошибочный подход к использованию правила потока выражает поток через цепь по формуле ΦB = B w ℓ, где w — ширина движущейся петли.
Ошибочность такого подхода в том, что это не рамка в обычном понимании этого слова. Прямоугольник на рисунке образован отдельными проводниками, замкнутыми на обод. Как видно на рисунке, ток по обоим проводникам течет в одном направлении, то есть здесь отсутствует понятие «замкнутый контур»
Наиболее простое и понятное объяснение этому эффекту дает понятие сила Ампера. То есть вертикальный проводник может быть вообще один, чтобы не вводить в заблуждение. Или же проводник конечной толщины может быть расположен на оси, соединяющей обода. Диаметр проводника должен быть конечным и отличаться от нуля, чтобы момент силы Ампера был ненулевой.
Уравнение Фарадея — Максвелла[править | править код]

Рис. 6. Иллюстрация теоремы Кельвина-Стокса с помощью поверхности Σ, её границы ∂Σ и ориентации n , установленной правилом правой руки.
Переменное магнитное поле создаёт электрическое поле, описываемое уравнением Фарадея — Максвелла:
где:
обозначает ротор.
- E — электрическое поле.
- B — плотность магнитного потока.
Это уравнение присутствует в современной системе уравнений Максвелла, часто его называют законом Фарадея. Однако, поскольку оно содержит только частные производные по времени, его применение ограничено ситуациями, когда заряд покоится в переменном по времени магнитном поле. Оно не учитывает[уточнить] электромагнитную индукцию в случаях, когда заряженная частица движется в магнитном поле.
В другом виде закон Фарадея может быть записан через интегральную форму теоремы Кельвина-Стокса:[17]
Для выполнения интегрирования требуется независимая от времени поверхность Σ (рассматриваемая в данном контексте как часть интерпретации частных производных). Как показано на рис. 6:
- Σ — поверхность, ограниченная замкнутым контуром ∂Σ, причём, как Σ, так и ∂Σ являются фиксированными, не зависящими от времени,
- E — электрическое поле,
- dℓ — бесконечно малый элемент контура ∂Σ,
- B — магнитное поле,
- dA — бесконечно малый элемент вектора поверхности Σ.
Элементы dℓ и dA имеют неопределённые знаки. Чтобы установить правильные знаки, используется правило правой руки, как описано в статье о теореме Кельвина-Стокса. Для плоской поверхности Σ положительное направление элемента пути dℓ кривой ∂Σ определяется правилом правой руки, по которому на это направление указывают четыре пальца правой руки, когда большой палец указывает в направлении нормали n к поверхности Σ.
Интеграл по ∂Σ называется интеграл по пути или криволинейным интегралом. Поверхностный интеграл в правой части уравнения Фарадея-Максвелла является явным выражением для магнитного потока ΦB через Σ. Обратите внимание, что ненулевой интеграл по пути для E отличается от поведения электрического поля, создаваемого зарядами. Генерируемое зарядом E-поле может быть выражено как градиент скалярного поля, которое является решением уравнения Пуассона и имеет нулевой интеграл по пути.
Интегральное уравнение справедливо для любого пути ∂Σ в пространстве и любой поверхности Σ, для которой этот путь является границей.
Рис. 7. Площадь заметания элемента вектора dℓ кривой ∂Σ за время dt при движении со скоростью v.
Используя[18]
и принимая во внимание 


Добавляя член 
что и является законом Фарадея. Таким образом, закон Фарадея и уравнения Фарадея-Максвелла физически эквивалентны.
Рис. 7 показывает интерпретацию вклада магнитной силы в ЭДС в левой части уравнения. Площадь, заметаемая сегментом dℓ кривой ∂Σ за время dt при движении со скоростью v, равна:
так что изменение магнитного потока ΔΦB через часть поверхности, ограниченной ∂Σ за время dt, равно:
и если сложить эти ΔΦB-вклады вокруг петли для всех сегментов dℓ, мы получим суммарный вклад магнитной силы в закон Фарадея. То есть этот термин связан с двигательной ЭДС.
Пример 3: точка зрения движущегося наблюдателя[править | править код]
Возвращаясь к примеру на рис. 3, в движущейся системе отсчета выявляется тесная связь между E– и B-полями, а также между двигательной и индуцированной ЭДС.[19] Представьте себе наблюдателя, движущегося вместе с петлёй. Наблюдатель вычисляет ЭДС в петле с использованием как закона Лоренца, так и с использованием закона электромагнитной индукции Фарадея. Поскольку этот наблюдатель движется с петлей, он не видит никакого движения петли, то есть нулевую величину v × B. Однако, поскольку поле B меняется в точке x, движущийся наблюдатель видит изменяющееся во времени магнитного поля, а именно:
где k — единичный вектор в направлении z.[20]
Закон Лоренца[править | править код]
Уравнение Фарадея-Максвелла говорит, что движущийся наблюдатель видит электрическое поле Ey в направлении оси y, определяемое по формуле:
Применяя правило дифференцирования сложной функции:
Решение для Ey с точностью до постоянной, которая ничего не добавляет в интеграл по петле:
Используя закон Лоренца, в котором имеется только компонента электрического поля, наблюдатель может вычислить ЭДС по петле за время t по формуле:
и мы видим, что точно такой же результат найден для неподвижного наблюдателя, который видит, что центр масс xC сдвинулся на величину xC + v t. Однако, движущийся наблюдатель получил результат под впечатлением, что в законе Лоренца действовала только электрическая составляющая, тогда как неподвижный наблюдатель думал, что действовала только магнитная составляющая.
Закон индукции Фарадея[править | править код]
Для применения закона индукции Фарадея рассмотрим наблюдателя, движущегося вместе с точкой xC. Он видит изменение магнитного потока, но петля ему кажется неподвижной: центр петли xC фиксирован, потому что наблюдатель движется вместе с петлей. Тогда поток:
где знак минуса возникает из-за того, что нормаль к поверхности имеет направление, противоположное приложенному полю B. Из закона индукции Фарадея ЭДС равна:
и мы видим тот же результат. Производная по времени используется при интегрировании, поскольку пределы интегрирования не зависят от времени. Опять же, для преобразования производной по времени в производную по x используются методы дифференцирования сложной функции.
Неподвижный наблюдатель видит ЭДС как двигательную , тогда как движущийся наблюдатель думает, что это индуцированная ЭДС.[21]
Электрический генератор[править | править код]
Рис. 8. Электрический генератор на основе диска Фарадея. Диск вращается с угловой скоростью ω, при этом проводник, расположенный вдоль радиуса, движется в статическом магнитном поле B. Магнитная сила Лоренца v × B создаёт ток вдоль проводника по направлению к ободу, затем цепь замыкается через нижнюю щётку и ось поддержки диска. Таким образом, вследствие механического движения генерируется ток.
Явление возникновения ЭДС, порождённой по закону индукции Фарадея из-за относительного движения контура и магнитного поля, лежит в основе работы электрических генераторов. Если постоянный магнит перемещается относительно проводника или наоборот, проводник перемещается относительно магнита, то возникает электродвижущая сила. Если проводник подключён к электрической нагрузке, то через неё будет течь ток, и следовательно, механическая энергия движения будет превращаться в электрическую энергию. Например, дисковый генератор построен по тому же принципу, как изображено на рис. 4. Другой реализацией этой идеи является диск Фарадея, показанный в упрощённом виде на рис. 8. Обратите внимание, что и анализ рис. 5, и прямое применение закона силы Лоренца показывают, что твёрдый проводящий диск работает одинаковым образом.
В примере диска Фарадея диск вращается в однородном магнитном поле, перпендикулярном диску, в результате чего возникает ток в радиальном плече благодаря силе Лоренца. Интересно понять, как получается, что чтобы управлять этим током, необходима механическая работа. Когда генерируемый ток течёт через проводящий обод, по закону Ампера этот ток создаёт магнитное поле (на рис. 8 оно подписано «индуцированное B» — Induced B). Обод, таким образом, становится электромагнитом, который сопротивляется вращению диска (пример правила Ленца). В дальней части рисунка обратный ток течёт от вращающегося плеча через дальнюю сторону обода к нижней щётке. Поле В, создаваемое этим обратным током, противоположно приложенному полю, вызывая сокращение потока через дальнюю сторону цепи, в противовес увеличению потока, вызванного вращением. На ближней стороне рисунка обратный ток течёт от вращающегося плеча через ближнюю сторону обода к нижней щётке. Индуцированное поле B увеличивает поток по эту сторону цепи, в противовес снижению потока, вызванного вращением. Таким образом, обе стороны цепи генерируют ЭДС, препятствующую вращению. Энергия, необходимая для поддержания движения диска в противовес этой реактивной силе, в точности равна вырабатываемой электрической энергии (плюс энергия на компенсацию потерь из-за трения, из-за выделения тепла Джоуля и прочее). Такое поведение является общим для всех генераторов преобразования механической энергии в электрическую.
Хотя закон Фарадея описывает работу любых электрических генераторов, детальный механизм в разных случаях может отличаться. Когда магнит вращается вокруг неподвижного проводника, меняющееся магнитное поле создаёт электрическое поле, как описано в уравнении Максвелла-Фарадея, и это электрическое поле толкает заряды через проводник. Этот случай называется индуцированной ЭДС. С другой стороны, когда магнит неподвижен, а проводник вращается, на движущиеся заряды воздействует магнитная сила (как описывается законом Лоренца), и эта магнитная сила толкает заряды через проводник. Этот случай называется двигательной ЭДС.[11]
Электродвигатель[править | править код]
Электрический генератор может работать в «обратном направлении» и становиться двигателем. Рассмотрим, например, диск Фарадея. Предположим, постоянный ток течёт через проводящее радиальное плечо от какого-либо напряжения. Тогда по закону силы Лоренца на этот движущийся заряд воздействует сила в магнитном поле B, которая будет вращать диск в направлении, определённым правилом левой руки. При отсутствии эффектов, вызывающих диссипативные потери, таких как трение или тепло Джоуля, диск будет вращаться с такой скоростью, чтобы d ΦB / dt было равно напряжению, вызывающему ток.
Электрический трансформатор[править | править код]
ЭДС, предсказанная законом Фарадея, является также причиной работы электрических трансформаторов. Когда электрический ток в проволочной петле изменяется, меняющийся ток создаёт переменное магнитное поле. Второй провод в доступном для него магнитном поле будет испытывать эти изменения магнитного поля как изменения связанного с ним магнитного потока d ΦB / d t. Электродвижущая сила, возникающая во второй петле, называется индуцированной ЭДС или ЭДС трансформатора. Если два конца этой петли связать через электрическую нагрузку, то через неё потечёт ток.
Электромагнитные расходомеры[править | править код]
Закон Фарадея используется для измерения расхода электропроводящих жидкостей и суспензий. Такие приборы называются магнитными расходомерам. Наведённое напряжение ℇ, генерируемое в магнитном поле B за счет проводящей жидкости, движущейся со скоростью v, определяется по формуле:
где ℓ — расстояние между электродами в магнитном расходомере.
Паразитная индукция и тепловые потери[править | править код]
В любом металлическом объекте, движущемся по отношению к статическому магнитному полю, будут возникать индукционные токи, как и в любом неподвижном металлическом предмете по отношению к движущемуся магнитному полю. Эти энергетические потоки в сердечниках трансформаторов нежелательны, из-за них в слое металла течёт электрический ток, который нагревает металл.
В соответствии с правилом Ленца вихревые токи протекают внутри проводника по таким путям и направлениям, чтобы своим действием возможно сильнее противится причине, которая их вызывает. Вследствие этого при движении в магнитном поле на хорошие проводники действует тормозящая сила, вызываемая взаимодействием вихревых токов с магнитным полем. Этот эффект используется в ряде приборов для демпфирования колебаний их подвижных частей.
Есть ряд методов, используемых для борьбы с этими нежелательными индуктивными эффектами.
- Электромагниты в электрических двигателях, генераторах и трансформаторах не делают из сплошного металла, а используют тонкие листы жести, называемые «ламинатами». Эти тонкие пластины уменьшают паразитные вихревые токи, как будет описано ниже.
- Катушки индуктивности в электронике обычно используют магнитные сердечники. Чтобы минимизировать паразитный ток, их делают из смеси металлического порошка со связующим наполнителем, и они имеют различную форму. Связующий материал предотвращает прохождение паразитных токов через порошковый металл.
Расслоение электромагнита[править | править код]

Вихревые токи возникают, когда сплошная масса металла вращается в магнитном поле, так как внешняя часть металла пересекает больше силовых линий, чем внутренняя, следовательно, индуцированная электродвижущая сила неравномерна и стремится создать токи между точками с наибольшим и наименьшим потенциалами. Вихревые токи потребляют значительное количество энергии, и часто приводят к вредному повышению температуры.[22]

На этом примере показаны всего пять ламинатов или пластин для демонстрации расщепление вихревых токов. На практике число пластин или перфорация составляет от 40 до 66 на дюйм, что приводит к снижению потерь на вихревых токах примерно до одного процента. Хотя пластины могут быть отделены друг от друга изоляцией, но поскольку возникающие напряжения чрезвычайно низки, то естественной ржавчины или оксидного покрытия пластин достаточно, чтобы предотвратить ток через пластины.[22]

Это ротор от двигателя постоянного тока диаметром примерно 20 мм, используемого в проигрывателях компакт-дисков. Обратите внимание, для снижения паразитных индуктивных потерь сделано расслоение полюса электромагнита на части.
Паразитные потери в катушках индуктивности[править | править код]

На этой иллюстрации сплошной медный стержень катушки индуктивности во вращающемся якоре просто проходит под кончиком полюса N магнита. Обратите внимание на неравномерное распределение силовых линий через стержень. Магнитное поле имеет большую концентрацию и, следовательно, сильнее на левом краю медного стержня (a, b), тогда как слабее по правому краю (c, d). Поскольку два края стержня будут двигаться с одинаковой скоростью, это различие в напряженности поля через стержень создаст вихри тока внутри медного стержня.[23]
Это одна из причин, по которой устройства с высоким напряжением, как правило, более эффективны, чем низковольтные устройства. Высоковольтные устройства имеют множество небольших витков провода в двигателях, генераторах и трансформаторах. Эти многочисленные небольшие витки провода в электромагните разбивают вихревые потоки, а в пределах больших, толстых катушек индуктивности низкого напряжения образуется вихревые токи большей величины.
См. также[править | править код]
|
|
Примечания[править | править код]
- ↑ 1 2 Sadiku, M. N. O. Elements of Electromagnetics (англ.). — fourth. — New York (USA)/Oxford (UK): Oxford University Press, 2007. — P. 386. — ISBN 0-19-530048-3.
- ↑ Калашников, 1956, с. 208.
- ↑ Ulaby, Fawwaz. Fundamentals of applied electromagnetics (неопр.). — 5th. — Pearson:Prentice Hall, 2007. — С. 255. — ISBN 0-13-241326-4. Архивировано 8 мая 2020 года.
- ↑ Joseph Henry. Distinguished Members Gallery, National Academy of Sciences. Архивировано 4 марта 2012 года.
- ↑ Michael Faraday, by L. Pearce Williams, p. 182-3
- ↑ Michael Faraday, by L. Pearce Williams, p. 191-5
- ↑ 1 2 Michael Faraday, by L. Pearce Williams, p. 510
- ↑ Maxwell, James Clerk (1904), A Treatise on Electricity and Magnetism, Vol. II, Third Edition. Oxford University Press, pp. 178-9 and 189.
- ↑ «Archives Biographies: Michael Faraday», The Institution of Engineering and Technology. Дата обращения: 1 сентября 2011. Архивировано 29 сентября 2011 года.
- ↑ Poyser, Arthur William (1892), Magnetism and electricity: A manual for students in advanced classes Архивная копия от 2 февраля 2017 на Wayback Machine. London and New York; Longmans, Green, & Co., p. 285, fig. 248
- ↑ 1 2 Griffiths, David J. Introduction to Electrodynamics (неопр.). — Third. — Upper Saddle River NJ: Prentice Hall, 1999. — С. 301—303. — ISBN 0-13-805326-X. Архивировано 29 октября 2019 года.
- ↑ Richard Phillips Feynman, Leighton R B & Sands M L. The Feynman Lectures on Physics (неопр.). — San Francisco: Pearson/Addison-Wesley, 2006. — С. Vol. II, pp. 17—2. — ISBN 0805390499.
- ↑ A. Einstein, On the Electrodynamics of Moving Bodies Архивная копия от 17 июля 2013 на Wayback Machine
- ↑ Fedosin, S. G. On the Covariant Representation of Integral Equations of the Electromagnetic Field (англ.) // Progress In Electromagnetics Research C : journal. — 2019. — Vol. 96. — P. 109—122. — doi:10.2528/PIERC19062902. — Bibcode: 2019arXiv191111138F. — arXiv:1911.11138. // О ковариантном представлении интегральных уравнений электромагнитного поля Архивная копия от 22 мая 2021 на Wayback Machine.
- ↑ В-поле наведенного тока ведет к снижению магнитного потока, в то время как движение цикла имеет тенденцию к увеличению (так как В (х) возрастает по мере цикла движений). Эти противоположные действия — пример принципа Ле Шателье в форме закона Ленца.
- ↑ Chapter 5, Electromagnetic Induction, http://services.eng.uts.edu.au/cempe/subjects_JGZ/ems/ems_ch5_nt.pdf Архивная копия от 22 августа 2011 на Wayback Machine
- ↑ Roger F Harrington. Introduction to electromagnetic engineering (англ.). — Mineola, NY: Dover Publications, 2003. — P. 56. — ISBN 0486432416.
- ↑ K. Simonyi, Theoretische Elektrotechnik, 5th edition, VEB Deutscher Verlag der Wissenschaften, Berlin 1973, equation 20, page 47
- ↑ В этом примере предполагается, что скорости движения намного меньше скорости света, поэтому корректировкой поля, связанной с преобразованиями Лоренца, можно пренебречь.
- ↑ Единственным способом определения этого является измерение x от xC в движущемся контуре, скажем ξ = x — xC (t). Тогда за время t движущийся наблюдатель увидит поле B (ξ, t), тогда как неподвижный наблюдатель увидит в той же точке поле B [ ξ + xC (t) ] = B (ξ + xC0 + v t) при xC0 = xC (t = 0).
- ↑ Peter Alan Davidson. An Introduction to Magnetohydrodynamics (неопр.). — Cambridge UK: Cambridge University Press, 2001. — С. 44. — ISBN 0521794870.
- ↑ 1 2 Images and reference text are from the public domain book: Hawkins Electrical Guide, Volume 1, Chapter 19: Theory of the Armature, pp. 272—273, Copyright 1917 by Theo. Audel & Co., Printed in the United States
- ↑ Images and reference text are from the public domain book: Hawkins Electrical Guide, Volume 1, Chapter 19: Theory of the Armature, pp. 270—271, Copyright 1917 by Theo. Audel & Co., Printed in the United States
Ссылки[править | править код]
- A simple interactive Java tutorial on electromagnetic induction
- R. Vega Induction: Faraday’s law and Lenz’s law — Highly animated lecture
- Notes from Physics and Astronomy HyperPhysics at Georgia State University
- Faraday’s Law for EMC Engineers
- Maxwell, James Clerk (1881), A treatise on electricity and magnetism, Vol. II, Chapter III, § 530, p. 178. Oxford, UK: Clarendon Press. ISBN 0-486-60637-6.
- Tankersley and Mosca: Introducing Faraday’s law.
Литература[править | править код]
- Калашников С.Г. Электричество. — М.: Гостехтеориздат, 1956. — 664 с.



![{mathcal {E}}=vell [B(x_{C}+w/2)-B(x_{C}-w/2)] .](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a72f01b482f885963a3c5d5e39df3c721ec3f06)


![{displaystyle {frac {dPhi _{B}}{dt}}=(-){frac {d}{dx_{C}}}left[int _{0}^{ell }dy int _{x_{C}-w/2}^{x_{C}+w/2}dxB(x)right]{frac {dx_{C}}{dt}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/41ddaf1f754720997a3191b66d98a1752c1b851b)
![{displaystyle qquad =(-)vell [B(x_{C}+w/2)-B(x_{C}-w/2)] ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76e1acfab9bb49d651723d4b11eb53fb6669d6f8)
![{mathcal {E}}=-{frac {dPhi _{B}}{dt}}=vell [B(x_{C}+w/2)-B(x_{C}-w/2)] ,](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc2b9c4abd6d355ecf587b1a94e9613ad83002aa)
















![{mathcal {E}}=-ell [E_{y}(x_{C}+w/2, t)-E_{y}(x_{C}-w/2, t)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/28c3c17ff369123ebc572ae50480462b519144ee)
![{displaystyle qquad =vell [B(x_{C}+w/2+vt)-B(x_{C}-w/2+vt)] ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88871cfa10f1af14169555c17bbdf81634b6ee30)



![{displaystyle qquad =vell [B(x_{C}+w/2+vt)-B(x_{C}-w/2+vt)] ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c42af51b0ed885f240fbf8eb2d439a65ac7a5779)


