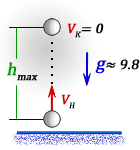
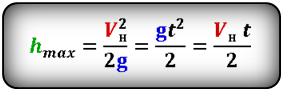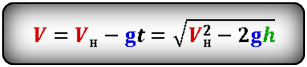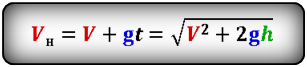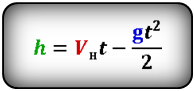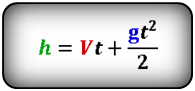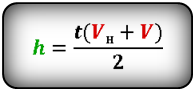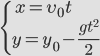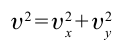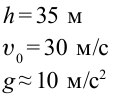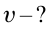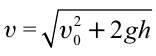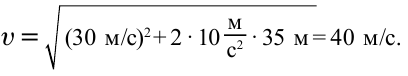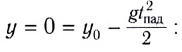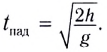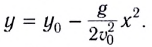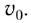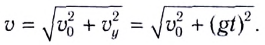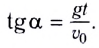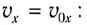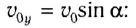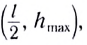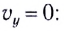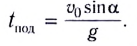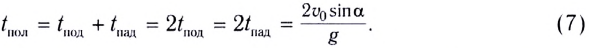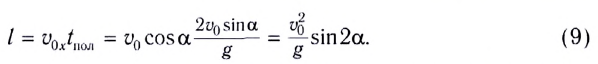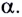1. Формулы максимальной высоты и времени за которое тело поднялось на максимальную высоту
h max
– максимальная высота достигнутая телом за время t
Vк – конечная скорость тела на пике, равная нулю
Vн – начальная скорость тела
t – время подъема тела на максимальную высоту h
g ≈ 9,8 м/с2 – ускорение свободного падения
Формула максимальной высоты (h max):
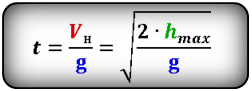
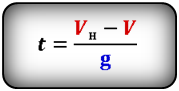
Формула времени за которое тело достигло максимальную высоту (t):
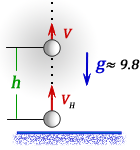
2. Формулы скорости, высоты и времени тела брошенного вертикально вверх под воздействием силы тяжести
h – расстояние пройденное телом за время t
Vн – начальная скорость тела
V – скорость тела в момент времени t
t – время подъема за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 – ускорение свободного падения
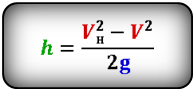
Формула скорости тела в момент времени t (V):
Формула начальной скорости тела (Vн):
Формулы высоты тела в момент времени t (h):
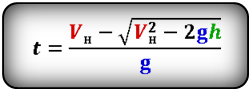
Формулы времени, за которое тело достигло высоту h (t):
- Подробности
-
Опубликовано: 04 августа 2015
-
Обновлено: 13 августа 2021
Движение тела, брошенного вертикально вверх
Тело, брошенное вертикально вверх, движется равномерно замедленно с начальной скоростью u0 и ускорением
a = -g.
Перемещение тела за время t представляет собой высоту подъема h.
Для этого движения справедливы формулы:
Если:
u0 — начальная скорость движения тела ,
u — скорость падения тела спустя время t,
g — ускорение свободного падения, 9.81 (м/с²),
h — высота на которую поднимется тело за время t,
t — время,
То, движение тела, брошенного вертикально вверх описывается следующими формулами:
Высота подъема тела за некоторое время, зная конечную скорость
[ h = frac{u_0 + u}{2} t ]
Высота подъема тела за некоторое время, зная ускорение свободного падения
[ h = u_0 t – frac{g t^2}{2} ]
Скорость тела через некоторое время, зная ускорение свободного падения
[ u = u_0 – gt ]
Скорость тела на некоторой высоте, зная ускорение свободного падения
[ u = sqrt{ u_0^2 – 2gh} ]
Максимальная высота подъема тела, зная первоначальную скорость и ускорение свободного падения
Тело, брошенное вертикально вверх, достигает максимальной высоты в тот момент, когда его скорость обращается в ноль. Поднявшись на максимальную высоту тело начинает свободное падение вниз.
[ h_{max} = frac{u_0^2}{2g} ]
Время подъема на максимальную высоту подъема тела, зная первоначальную скорость и ускорение свободного падения
[ t_{hmax} = frac{u_0}{g} ]
Примечание к статье: Движение тела, брошенного вертикально вверх
- Сопротивление воздуха в данных формулах не учитывается.
- Ускорение свободного падения имеет приведенное значение (9.81 (м/с²)) вблизи земной поверхности. Значение g на других расстояниях от поверхности Земли изменяется!
Движение тела, брошенного вертикально вверх |
стр. 409 |
|---|
- Это движение в плоскости, поэтому для описания движения необходимо 2 координаты.
- Считаем, что движение происходит вблизи поверхности Земли, поэтому ускорение тела – ускорение свободного падения (a = g).
Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли (g) – вдоль вертикальной оси (y), вдоль оси х движение равномерное и прямолинейное.
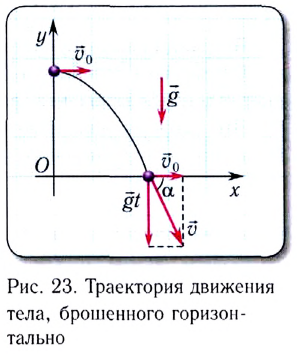
Движение тела, брошенного горизонтально.
Выразим проекции скорости и координаты через модули векторов.
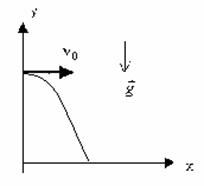
Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y:
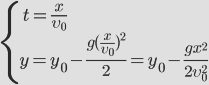
Движение тела, брошенного под углом к горизонту.
Порядок решения задачи аналогичен предыдущей.
Решим задачу для случая х0=0 и y0=0.
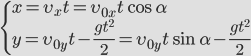
Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории):
.
Мы получили квадратичную зависимость между координатами. Значит траектория – парабола.
Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0.
Время полета:


Зная время полета, найдем максимальное расстояние, которое пролетит тело:
Дальность полета:
Из этой формулы следует, что:
– максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 450;
– на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т.н. навесная и настильная баллистические траектории.
Используя то, что парабола – это симметричная кривая, найдем максимальную высоту, которой может достичь тело.
Время, за которое тело долетит до середины, равно: 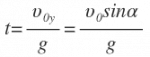
Время подъема:
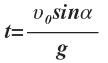
Тогда:
Максимальная высота:
Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна
Угол, под которым направлен вектор скорости в любой момент времени:
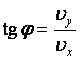
Движение горизонтально брошенного тела:
Рассмотрим движение шара, движущегося прямолинейно по поверхности стола с высотой
При достаточно малом сопротивлении воздуха, которым можно пренебречь, тело будет двигаться в горизонтальном направлении равномерно со скоростью 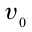
в горизонтальном направлении в любой момент времени 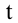
Проекции скорости тела на оси 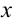
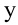
В вертикальном же направлении, двигаясь равноускоренно без начальной скорости, тело будет свободно падать с высоты 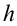
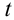
Из соотношений (1.21) и (1.22) уравнение траектории движения горизонтально брошенного тела на плоскости 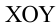
Выражение (1.24) является уравнением параболы. Значит, горизонтально брошенное тело будет двигаться по параболической линии. Время полета тела, брошенного горизонтально с высоты 
В этом случае формула для расчета длины полета тела будет иметь вид:
Горизонтально брошенное тело, одновременно двигаясь в горизонтальном направлении равномерно и в вертикальном направлении равноускоренно, свободно падает. К концу движения (после истечения времени 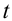
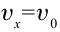
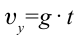
или
Перемещение и траектория тела при криволинейном движении неравны между собой. Модуль вектора и направление движения горизонтально брошенного тела на протяжении движения меняются непрерывно.
Образец решения задачи:
Тело брошено горизонтально на высоте 35 м со скоростью 30м/с. Найти скорость тела при падении на землю.
Дано:
Найти:
Формула:
Решение:
Ответ: 40 м/c.
Движение тела, брошенного горизонтально и под углом к горизонту
Если материальная точка участвует одновременно в нескольких движениях, то такое движение называют сложным.
Примером сложного движения является движение под действием силы тяжести в том случае, если падающему телу сообщена начальная скорость, непараллельная вектору ускорения свободного падения.
Рассмотрим движение тела, брошенного горизонтально со скоростью 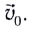
Это сложное движение можно представить в виде суммы двух независимых движений — равномерного с постоянной скоростью 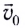
Движение тела в горизонтальном направлении будет описываться уравнением
а в вертикальном — уравнением
Здесь 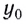
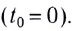
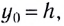
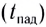
условия
Для получения уравнения траектории движения у(х) необходимо исключить время из уравнений движения (1) и (2). Из уравнения (1) выражаем время t и подставляем в уравнение (2). Получаем
Это уравнение параболы, ветви которой направлены вниз, так как коэффициент перед множителем 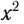
Скорость вдоль направления оси Ох остается неизменной и равной
Вдоль оси Оу движение равноускоренное. В начальный момент времени вертикальная составляющая скорости равна нулю 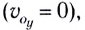
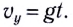
Угол между начальной скоростью 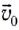
В приведенных формулах сопротивление воздуха не учитывается.
Рассмотрим теперь движение тела, брошенного со скоростью 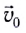
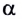
Это сложное движение можно представить в виде суммы двух независимых движений — равномерного в горизонтальном направлении со скоростью
и равноускоренного в вертикальном направлении с ускорением 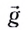
скоростью
В том случае, если система координат выбрана так, что начальные координаты 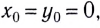
Как и при движении тела, брошенного горизонтально, траектория представляет собой параболу, ветви которой направлены вниз, поскольку коэффициент перед 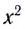
где l — дальность полета тела, 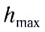
Модули горизонтальной 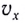
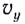
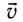
Мгновенную скорость 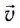
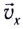
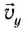
Время подъема тела можно найти из условия
Если сопротивление воздуха при движении не учитывается, то время подъема равно времени падения: 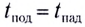
Таким образом, время полета тела можно найти как
Определив вертикальную составляющую скорости 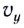
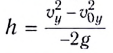
Максимальная высота подъема тела 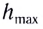
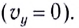
Дальность полета l — расстояние, пройденное телом за время полета 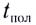
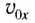
Таким образом, дальность полета определяется модулем начальной скорости 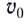
Заметим, что согласно формуле (9) при неизменном модуле начальной скорости тела максимальная дальность 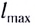
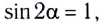
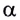
- Движение тела, брошенного под углом к горизонту
- Принцип относительности Галилея
- Движение в гравитационном поле
- Зависимость веса тела от вида движения
- Вертикальное движение тел в физик
- Неравномерное движение по окружности
- Равномерное движение по окружности
- Взаимная передача вращательного и поступательного движения
Движение тела, брошенного под углом к горизонту, теория и онлайн калькуляторы
Движение тела, брошенного под углом к горизонту
Начальные условия. Движение тела, брошенного под углом к горизонту
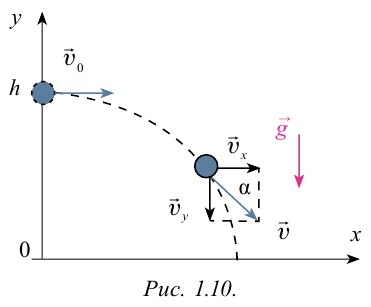
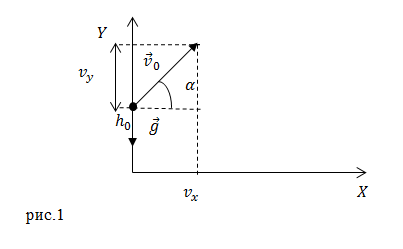
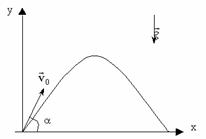
Рассмотрим движение тела в поле тяжести Земли, сопротивление воздуха учитывать не будем. Пусть начальная скорость брошенного тела направлена под углом к горизонту $alpha $ (рис.1). Тело брошено с высоты ${y=h}_0$; $x_0=0$.
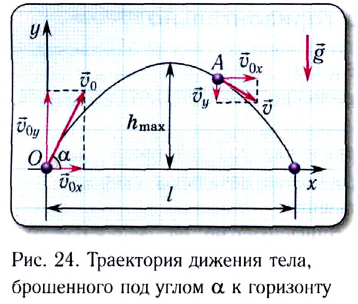
Тогда в начальный момент времени тело имеет горизонтальную ($v_x$) и вертикальную ($v_y$) составляющие скорости. Проекции скорости на оси координат при $t=0$ равны:
[left{ begin{array}{c}
v_{0x}=v_0{cos alpha , } \
v_{0y}=v_0{sin alpha . } end{array}
right.left(1right).]
Ускорение тела равно ускорению свободного паления и все время направлено вниз:
[overline{a}=overline{g}left(2right).]
Значит, проекция ускорения на ось X равна нулю, а на ось Y равна $a_y=g.$
Так как по оси X составляющая ускорения равна нулю, то скорость движения тела в этом направлении является постоянной величиной и равна проекции начальной скорости на ось X (см.(1)). Движение тела по оси X равномерное.
При ситуации, изображенной на рис.1 тело по оси Y будет двигаться сначала вверх, а затем виз. При этом ускорение движения тела в обоих случаях равно ускорению $overline{g}.$ На прохождение пути вверх от произвольной высоты ${y=h}_0$ до максимальной высоты подъема ($h$) тело тратит столько же времени, сколько на падение вниз от $h$ до ${y=h}_0$. Следовательно, точки симметричные относительно вершины подъема тела лежат на одинаковой высоте. Получается, что траектория движения тела симметрична относительно точки-вершины подъема – и это парабола.
Скорость движения тела, брошенного под углом к горизонту можно выразить формулой:
[overline{v}left(tright)={overline{v}}_0+overline{g}t left(3right),]
где ${overline{v}}_0$ – скорость тела в момент броска. Формулу (3) можно рассматривать как результат сложения скоростей двух независимых движений по прямым линиям, в которых участвует тело.
Выражения для проекции скорости на оси принимают вид:
[left{ begin{array}{c}
v_x=v_0{cos alpha , } \
v_y=v_0{sin alpha -gt } end{array}
left(4right).right.]
Уравнение для перемещения тела при движении в поле тяжести:
[overline{s}left(tright)={overline{s}}_0+{overline{v}}_0t+frac{overline{g}t^2}{2}left(5right),]
где ${overline{s}}_0$ – смещение тела в начальный момент времени.
Проектируя уравнение (5) на оси координат X и Y, получим:
[left{ begin{array}{c}
x=v_0{cos left(alpha right)cdot t, } \
y={h_0+v}_0{sin left(alpha right)cdot t-frac{gt^2}{2} } end{array}
left(6right).right.]
Тело, двигаясь вверх, имеет по оси Y сначала равнозамедленное перемещение, после того, как тело достигает вершины, движение по оси Y становится равноускоренным.
Траектория движения материальной точки получается, задана уравнением:
[y=h+x tg alpha -frac{gx^2}{2v^2_0{cos}^2alpha }left(7right).]
По форме уравнения (7) видно, что траекторией движения является парабола.
Время подъема и полета тела, брошенного под углом к горизонту
Время, затрачиваемое телом для того, чтобы достигнуть максимальной высоты подъема получают из системы уравнений (4). . В вершине траектории тело имеет только горизонтальную составляющую, $v_y=0.$ Время подъема ($t_p$) равно:
[t_p=frac{v_0{sin alpha }}{g}left(8right).]
Общее время движения тела (время полета ($t_{pol}))$находим из второго уравнения системы (6), зная, что при падении тела на Землю $y=0$, имеем:
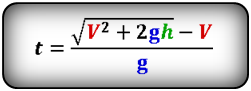
[t_{pol}=frac{v_0{sin alpha +sqrt{v^2_0{sin}^2alpha +2gh} }}{g}left(9right).]
Дальность полета и высота подъема тела, брошенного под углом к горизонту
Для нахождения горизонтальной дальности полета тела ($s$) при заданных нами условиях в уравнение координаты $x$ системы уравнений (6) следует подставить время полета ($t_{pol}$) (9). При $h=0,$ дальность полета равна:
[s=frac{v^2_0{sin left(2alpha right) }}{g}left(10right).]
Из выражения (9) следует, что при заданной скорости бросания дальность полета максимальна при $alpha =frac{pi }{4}$.
Максимальную высоту подъема тела ($h_{max}$) находят из второго уравнения системы (6), подставляя в него время подъема ($t_p$) (8):
[h_{max}=h+frac{{v_0}^2{{sin}^2 б }}{2g}left(11right).]
Выражение (11) показывает, что максимальная высота подъема тела прямо пропорциональна квадрату скорости бросания и увеличивается при росте угла бросания.
Примеры задач с решением
Пример 1
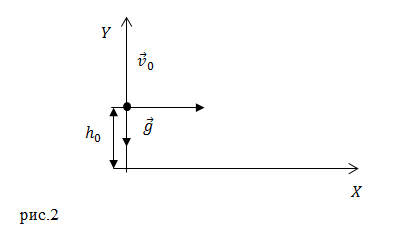
Задание. Во сколько раз изменится время полета тела, которое бросили с высоты $h$ в горизонтальном направлении, если скорость бросания тела увеличили в $n$ раз?
Решение. Найдем формулу для вычисления времени полета тела, если его бросили горизонтально (рис.2).
В качестве основы для решения задачи используем выражение для равноускоренного движения тела в поле тяжести:
[overline{s}={overline{s}}_0+{overline{v}}_0t+frac{overline{g}t^2}{2}left(1.1right).]
Используя рис.2 запишем проекции уравнения (1.1) на оси координат:
[left{ begin{array}{c}
X:x=v_0t;; \
Y:y=h_0-frac{gt^2}{2} end{array}
right.left(1.2right).]
Во время падения тела на землю $y=0,$ используем этот факт и выразим время полета из второго уравнения системы (1.2), имеем:
[0=h_0-frac{g{t_{pol}}^2}{2}to t_{pol}=sqrt{frac{2h_0}{g}} left(1.3right).]
Как мы видим, время полета тела не зависит от его начальной скорости, следовательно, при увеличении начальной скорости в $n$ раз время полета тела не изменится.
Ответ. Не изменится.
Пример 2
Задание. Как изменится дальность полета тела в предыдущей задаче, если начальную скорость увеличить в $n$ раз?
Решение. Дальность полета – это расстояние, которое пройдет тело по горизонтальной оси. Это означает, что нам потребуется уравнение:
[x=v_0t (2.1)]
из системы (1.2) первого примера. Подставив вместо $t,$ время полета, найденное в (1.3), мы получим дальность полета ($s_{pol}$):
[s_{pol}=v_0t_{pol}=v_0sqrt{frac{2h_0}{g}} left(2.2right).]
Из формулы (2.2) мы видит, что при заданных условиях движения дальность полета прямо пропорциональна скорости бросания тела, следовательно, во сколько раз увеличим начальную скорость, во столько раз увеличится дальность полета тела.
Ответ. Дальность полета тела увеличится в $n$ раз.
Читать дальше: закон сообщающихся сосудов.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!