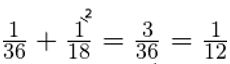Приветствую читателей статьи и подписчиков канала Тесты_математика!
Помните школьные задачи про трубы? Труба А наливает, а труба В выливает воду.
Сегодня предлагаю одну из задач, предлагаемых на ЕГЭ, с условием о наполнении воды в бассейн.
Как известно, в этих задачах, кроме времени наполнения водой того или иного бассейна , есть разные трубы.
Это трубы, их бывает несколько, по которым вода наливается с различной скоростью.
Это трубы или одна труба, через которые вода выливается, или сливается.
В это задаче 2 трубы, в одну наливается воды, через другую трубу – сливается. Предлагается узнать время наполнения бассейна , если открыты сразу 2 трубы.
Задача.
Бассейн можно заполнить за 3 часа, а слить воду за 5 часов . Сколько нужно времени для наполнения бассейна , если не закрывать сливное отверстие
Не торопитесь утверждать, что задача очень простая. Вот такие задачи с трубами часто ставят в тупик учащихся.
Ответьте на три вопроса:
1) Будет ли наливаться вода при двух открытых одновременно кранах.?
2) Почему не будет наливаться, если ответ такой?
3) За сколько часов нальётся полный бассейн при двух открытых кранах?
Ответы или 1 ответ можно писать в комментариях.
Так же можно выбрать верный ответ в тесте.
Форма теста.
В галерее рисунков полное решение задачи и ответ. Переходите по стрелкам. Если не желаете смотреть ответ, и решение, можете сразу писать ответ или способ решение в комментариях.
Подпишитесь! Будем рады видеть вас в нашей семье подписчиков!
Спасибо за прочтение статьи, решение задачи или теста!
Подпишитесь на канал, Тесты_математика!
чтобы не пропустить новые публикации!
#задачи , #егэ , #математика , #обучение , #задачи на логику
Для решения задач на совместную работу используются уравнения и системы уравнений. Применение уравнений для решения задач в 4 классе является дискуссионым, однако часто без них никак.
Задачи на совместную работу многообразны. Это могут быть и бригады рабочих, выполняющие одну и ту же работу, и трубы, наполняющие бассейн и выводящие из него воду, землекопы, копающие траншеи и пр.
Принципы решения задач на совместную работу схожи с принципами решения задач на движение. В задачах на движение путь – это произведение скорости на время.
В задачах на совместную работу аналогом пройденного пути выступает объём сделанной работы, который вычисляется как скорость производства чего бы то ни было (скорость наполнения воды в бассейне, копания канавы и пр.), умноженная на время.
В задачах на движение скорости двух объектов, движущихся навстречу друг другу, складываются, а в случае, когда один объект догоняет другой, то скорость сближения определяется как разность скоростей двух объектов.
Аналогично в задачах на совместную работу скорости выполнения работ – если это работа в одно направлении, складываются, и вычитаются, если это работы в противоположном направлении. Например, если две трубы заполняют бассейн с определённой скоростью, то для вычисления времени, за который бассейн будет заполнен двумя трубами, надо сложить скорости заполнения каждой из труб – этот случай аналогичен движению объектов навстречу друг другу (у них одна цель, т.е. они делают одну и ту же работу).
Если же у нас из одной трубы в бассейн втекает объём воды с определённой скоростью, а из другой трубы вытекает с другой (меньшей) скоростью, то для нахождения времени заполнения бассейна нам надо из скорости первой трубы вычесть скорость второй трубы. Это аналогично случаю, когда более быстрый объект догоняет более медленный. У них разные цели – один хочет оторваться от преследования, второй хочет его догнать, и их скорости вычитаются. Точно так же у двух труб разные цели – одна хочет бассейн наполнить, а вторая опустошить.
Рассмотрим конкретные примеры.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Задача 1
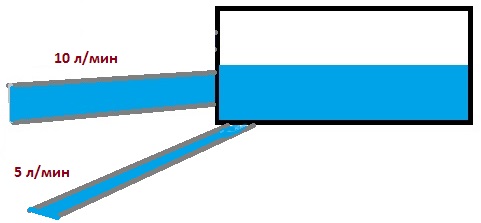
2 трубы наполняют бассейн. Одна со скоростью 5 литров в минуту, вторая со скоростью 10 литров в минуту. Объём бассейна 300 литров. За какое время две трубы наполнят бассейн?
Решение
Две трубы делают одну и ту же работу, поэтому для нахождения суммарной скорость их работы надо сложить скорость наполнения бассейна первой трубой со скоростью наполнения второй трубой.
V = 5 + 10 = 15 л/мин.
Объём бассейна нам известен – 300 л. Следовательно, для того, чтобы найти, за какое время он будет наполнен, надо объём бассейна разделить на скорость наполнения, которую мы только что нашли.
t = 300 / 15 = 20 минут.
Ответ: бассейн наполнится за 20 минут
Задача 2
В изначально пустой бассейн объёмом 400 литров поступает вода из трубы со скоростью 30 литров в минуту. Из второй трубы меньшего диаметра вода вытекает из бассейна со скоростью 20 литров в минуту. За какое время наполнится бассейн?
Решение
В данном случае трубы выполняют противоположную работу, поэтому для нахождения итоговой скорости работы надо из большей скорости вычесть меньшую скорость.
V = 30 – 20 = 10 л/мин
10 л/мин – это итоговая скорость наполнения бассейна. Если у нас за одну минуту в бассейн вылилось 30 литров воды, и за эту же минуту 20 литров вытекло из него, то осталось всего 10 литров – это и есть скорость наполнения.
Время заполнения бассейна водой мы находим аналогично первой задаче:
t = 400/10 = 40 мин.
Ответ: бассейн заполнится за 40 минут
Задача 3
Первая бригада может выполнить задание за 36 ч, а вторая бригада может выполнить то же задание за 18 ч. За сколько часов это задание выполнят две бригады при совместной работе?
Решение. 1 способ – с помощью дробей
В старших классах такая задача решается просто с помощью дробей.
Примем всю работу за единицу, тогда за 1 ч первая бригада выполняет 1/36 работы, а вторая бригада за 1 час сделает 1/18 работы. При совместной работе за 1 ч две бригады выполняют всей работы, поэтому всю работу они выполнят
всей работы. Таким образом, если за 1 час выполняется 1/12 всей работы, то вся работа целиком будет сделана за 12 часов.
Ответ: 12 часов
Решение. 2 способ – по действиям без дробей
Если первая бригада всю работу делает за 36 часов, то мы можем представить, что работа состоит из 36 частей, каждая из которых равна 1 часу.
1. Определим, какую часть работы делает за 1 час первая бригада.
Для этого разделим общее количество частей, из которых состоит работа, на то время, за которое первая бригада делает всю работу
36:36 = 1 часть
2. Определим, какую часть работы делает за 1 час вторая бригада.
Делаем как в первом действии
36:18 = 2 части.
3. Найдём, сколько частей работы делают за один час две бригады в месте
2 + 1 = 3 части
4. Найдём, за какое время обе бригады сделают всю работу.
Для этого общее количество частей (36) разделим на суммарную скорость работы двух бригад, т.е. 3 части в час.
36:3 = 12 часов.
Как видим, при решении вторым способом мы получили тот же ответ, что и при решении с помощью дробей.
Ответ: 12 часов
Одна труба может наполнить бассейн водой за 12 часов, а другая – за 20 часов. За какое время бассейн будет наполнен водой, если две трубы будут работать одновременно?
Решение
В 4-м классе дети дробей ещё не знают, поэтому задачу надо решать через части.
Итак, нам надо всю работу обозначить каким-то количеством частей, и далее, исходя из этого, определить скорость работы труб в частях.
Наиболее простой способ определения количества частей – перемножить 12 на 20 и получить 240 частей. В этом случае скорость работы первой трубы – 20 частей в час (12 – это 1/20 от 240), а скорость второй трубы – 12 частей в час (20 – это 1/12 от 240).
Суммарная скорость работы двух труб: 20+12 = 32 части в час.
Чтобы найти время, за которое наполнится бассейн, надо 240 поделить на 32. Дробных чисел дети в 4-м классе ещё не знают, поэтому поделим нацело 240 на 32 и найдём частное и остаток:
240:32 = 7 остаток 16.
16 – это половина от 32
Суммарная скорость двух труб – 32 части в час, значит 16 частей бассейна заполняются за полчаса, то есть 30 минут.
Ответ – 7 часов 30 минут.
Общее количество частей можно определить не путём перемножения времени работы первой трубы на время работы второй, а путём нахождения наименьшего общего кратного (НОК) этих двух чисел.
Для 12 и 20 НОК равен 60. 60 – наименьшее число, которое без остатка делится и на 12 и на 20.
Таким образом, если вся работа – 60 частей, то
скорость первой трубы – 60:12 = 5 частей в час
скорость второй трубы – 60:2- = 3 части в час.
Суммарная скорость двух труб: 5+3 = 8 частей в час.
Теперь для нахождения времени заполнения бассейна нам надо 60 поделить на 8.
60:8 = 7 остаток 4.
Суммарная скорость двух труб – 8 частей в час, значит 4 части бассейна заполняются за полчаса, то есть 30 минут.
Таким образом, общее время наполнения бассейна – 7 часов 30 минут. Мы получили то же самое время, что и в первом способе, когда у нас вся работа состояла из 240 частей.
Ответ: 7 часов 30 минут
Задача 5
За пять недель пират Ерёма
Способен выпить бочку рома
А у пирата, у Емели
Ушло б на это две недели.
За сколько дней прикончат ром
Пираты, действуя вдвоём?
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Решение
Эту задачу можно решить через дроби. 5 недель – это 35 дней, 2 недели – 14 дней, далее нужно 1/35 (скорость выпивания бочки в день пирата Ерёмы) сложить с 1/14 (скорость Емели), привести дроби к общему знаменателю, получить суммарную скорость в 1/10, и, соответственно, ответ в 10 дней.
Но можно решить эту задачу и без использования дробей.
Аналогично предыдущей задачи про бассейн, выразим всю работу в частях, при этом так, чтобы это число делилось без остатка и на 35 и на 14.
Наименьшее число, которое делится без остатка и на 35 и на 14 – это 70. (Если мы испытываем сложности с нахождением минимального числа, то всегда можно перемножить 35 на 14 и получить 490).
Итак, всю бочку рома мы приняли равной в 70 частей. Акцентирую ваше внимание, что мы вместо 70 могли бы взять любое другое количество частей – это не повлияло бы на логику решения задачи, но, т.к. в 4-м классе дети не умеют работать с дробными числами, то мы берём то число частей, которое без остатка делится на скорость работы всех работников, которые есть в условии задачи. В нашем случае работники – это два пирата, работа которых заключается в выпивании рома.
Таким образом, если Ерёма выпивает всю бочку за 35 дней, то его скорость это
70:35 = 2 части в день
Скорость Емели, который ту же бочку выпивает за 14 дней:
70:14 = 5 частей в день.
Суммарная скорость выпивания рома Ерёмы и Емели – 5 + 2 = 7 частей в день.
Таким образом, если весть объём рома – это 70 частей, а оба пирата за день выпивают 10 частей, то весь ром они выпьют за
70:7 = 10 дней.
Ответ: 10 дней.
Задача 6
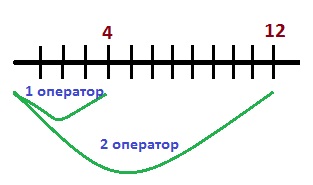
Два оператора могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 4 ч, а второй 12 ч, то они выполнят всю работу. За какое время может набрать весь текст каждый оператор, работая отдельно?
Решение
введём обозначения
x – объём текста, который в час печатает первый оператор
y – объём текста, который в час печатает второй оператор
С одной стороны, весь объём работы можно выразить как
8x + 8y (два оператора набирают текст за 8 часов).
С другой стороны, этот же объём работы:
4x + 12y
Т.к. это одинаковые объёмы работы, то составим уравнение:
8x + 8y = 4x + 12y
8x – 4x = 12y – 8y
4x = 4y
x = y
Отсюда делаем вывод, что операторы работают с одинаковой скоростью.
Рассмотрим случай, когда первый оператор будет работать 4 ч, а второй 12 ч.
Вот схема их работы:
Первые 4 часа оба оператора работают вместе, и за это время они сделают половину всей работы (т.к. работая вместе 8 часов, они сделают всю работу).
После 4 часов работы первый оператор прекращает работать и продолжает работать второй оператор. Всего он по условию задачи работает 12 часов – то есть ещё 8 часов после того, как прошли первые 4 часа.
И если за первые 4 часа сделана половина работы, то оставшиеся 8 часов работы второго оператора – это вторая половина работы.
То есть второй оператор половину работы делает за 8 часов, и, следовательно, всю работу он сделает за 16 часов. Как мы уже выяснили ранее, скорости работы операторов равны, поэтому первый оператор также всю работу выполнит за 16 часов.
Ответ: и первый и второй оператор всю работу по отдельности выполнят за 16 часов.
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Задача 7
Первая труба наполняет резервуар объемом 180 литров, а вторая труба наполняет резервуар объемом 120 литров. При этом известно, что одна из труб пропускает на 1 литр воды в минуту меньше, чем другая. Необходимо определить, сколько литров в минуту пропускает первая труба, если резервуары полностью заполняются за одинаковое время.
Решение
Как мы уже говорили в начале этого урока, принципы решения задач на совместную работу схожи с принципами решения задач на движение.
Рассматриваемая задача схожа с задачами на движение, в которых один объект догоняет другой. Напомню, что в таких задачах, если у нас известно первоначальное расстояние между двумя объектами, и скорости этих объектов, то время, за которое второй объект догонит первый, рассчитывается как первоначальное расстояние, поделённое на скорость сближения объектов, где скорость сближения – разница между скоростью догоняющего объекта и догоняемого.
В этой задаче про два резервуара известно, что они наполняются за одинаковое время, хотя их объёмы разные. То есть скорость наполнения первого, более большого резервуара, очевидно выше, чем скорость наполнения второго, меньшего по объему. Разница между скоростями наполнения известна – 1 литр в минуту.
Таким образом, если проводить аналогии с задачами на движение, где один объект догоняет второй, мы можем сказать, что скорость догона в нашем случае – это тот самый 1 литр в минуту, а первоначальное расстояние между объектами – это разница в объёмах двух резервуаров, то есть 180-120 = 60 л. И чтобы найти, за какое время один объект догонит другой – то есть в нашем случае, когда они полностью заполнятся, надо разницу в объёмах разделить на разницу в скоростях заполнения.
То есть 60/60 = 1 час.
1 час равен 60 минутам.
По условию задачи нам надо определить, сколько литров в минуту пропускает первая труба.
Для этого объём первого резервуара надо поделить на время, за которое он полностью заполняется.
То есть 180 литров /60 минут = 3 литра в минуту.
Ответ: скорость первой трубы – 3 литра в минуту.
Мы понимаем, что приведённые при решении этой задачи рассуждения могут показаться неочевидными. Для того, чтобы вы могли убедиться, что данная методика является верной, проиллюстрируем её на примере с меньшими цифрами.
Пусть у нас есть два бака, один объёмом 15 литров, второй объёмом 18 литров. Первый наполняется со скоростью 5 литров в минуту, а второй – со скоростью 6 литров в минуту.
Несложно подсчитать, что время заполнения у них будет одинаковое – 3 минуты (15:5 = 3, 18:6 = 3).
Эти же три минуты можно получить по другому:
Разница в объёмах баков – 3 литра (18- 15 = 3). Разница в скоростях наполнения – 1 литр в минуту (6 – 5 = 1).
Соответственно, время, за которое второй, более объёмный бак, “догонит” первый, меньший по объёму, составляет 3:1 = 3 минуты.
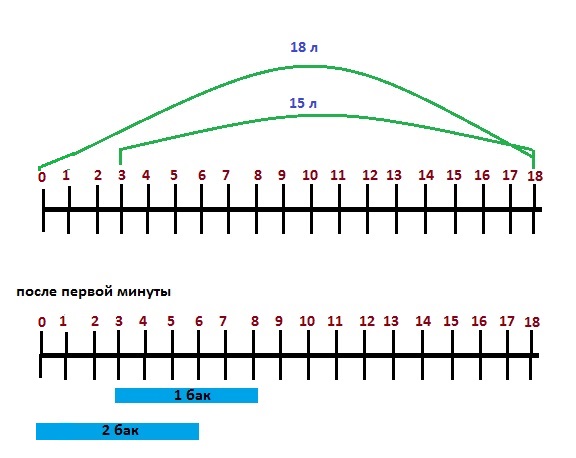
Проиллюстрируем это на рисунке.
На горизонтальной шкале отложим объём – от нуля до 18 литров.
Для первого бака, который объёмом 15 литров, отсчёт будем вести от отметки в 3 л и до 18 л. То есть как будто бы его объём тоже 18 литров, но на три литра он уже заполнен, и осталось заполнить 15 литров.
Таким образом отметка в 3 литра – это первоначальное “расстояние” между двумя баками.
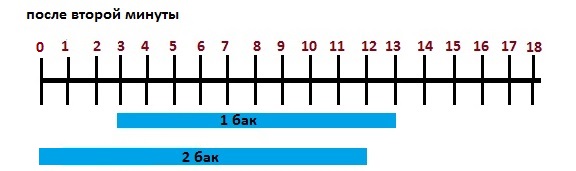
После первой минуты первый бак заполнился на 5 литров, и мы рисуем синюю полоску от отметки 3 л до отметки 8 л. Второй бак заполнился на 6 литров, и мы рисуем синюю полоску от 0 до 6 л. Таким образом, за первую минуту разница в объёмах воды в двух баках (“расстояние” между ними) сократилось с первоначальных 3 литров до 2 литров.
После второй минуты первый бак заполнился ещё на 5 литров (итого за 2 минуты на 10 литров), и мы рисуем синюю полоску от отметки 3 литра до отметки 13 литров. Второй бак заполнился ещё на 6 литров (итого на 12 литров за 2 минуты), и мы рисуем синюю полоску от отметки 0 до 12 литров. Разница в объёмах воды в баках сократилась с 2 литров до 1 литра.
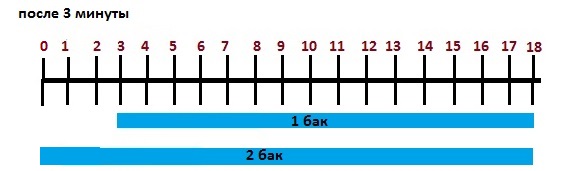
После третьей минуты первый бак заполнился ещё на 5 литров (итого за 3 минуты на 15 литров), и мы рисуем синюю полоску от отметки 3 литра до финальной отметки 18 литров. Второй бак заполнился ещё на 6 литров (итого на 18 литров за 3 минуты), и мы рисуем синюю полоску от отметки 0 до 18 литров. Разница в объёмах воды в баках сократилась с 1 литров до нуля. Оба бака заполнились полностью.
Таким образом, из данного рисунка следует, с каждой минутой разница в объёмах воды в баках сокращается ровно на величину, равную разнице скоростей наполнения баков.
Поэтому применённая нами формула для решения этой задачи, согласно которой время наполнения – это разница в объёмах резервуаров, делённая на разницу скоростей, является рабочей.
Badrossss
Профи
(571),
закрыт
8 лет назад
ДАНО: бассейн и 4 трубы, наполняющие его. Если включить 1 и 4 трубы, то бассейн заполнится за 20 минут, если 2,3,4 за 15 минут и если 1,2,3 за 12 минут. Вопрос: за сколько времени заполнится бассейн, если подключить все трубы.
Дополнен 10 лет назад
Я приводил время общее-сколько бассейнов может наполниться за 1 час.
Дополнен 10 лет назад
Дополнение для приведения производительности в один масштаб-3 бассейна, 4 и 5 за 1 час, соответственно.
Дивергент
Высший разум
(1537974)
10 лет назад
Проще пареной репы. За 10 минут. Причем тут масштаб.. .
2/(1/20+1/15+1/12)=2/(1/5)=2*5=10 минут. Всего и делов!
BadrossssПрофи (571)
10 лет назад
Что такое “2” и поясните ход решения.
Дивергент
Высший разум
(1537974)
Не хочу. Слишком простая задача. Решается в уме. Сейчас пеньковатые набегут, разъяснят тебе, как уравнения складывать, а мне некогда.
Спасибо всем за ответы, и хотя результат у всех верный, что-то с решениями не всё понятно. Nasos решил подбором – повезло, Ироха намудрила с единицами, я тоже не смогла понять, единица – это что – скорость, бассейн, часть бассейна? ОлегТ решил задачу более понятно, однако, наполнять 4 бассейна вместо одного – зачем? А задача эта для 7 класса, когда учащиеся учатся решать задачи с помощью простой системы из двух уравнений. Приведу своё решение этим способом.
Пусть х ч – это время, за которое первая труба наполнит весь бассейн, а у ч – время, за которое вторая труба наполнит весь бассейн. Значит, в первом случае первая труба наполнит четверть бассейна за время х/4 ч, а потом вторая труба наполнит три четверти бассейна за время 3у/4 ч, а в итоге это займёт 5 часов. Вот и получаем первое уравнение.
х/4+3у/4=5 (1)
Точно также рассуждаем про второй вариант наполнения бассейна, и получаем второе уравнение.
3х/4+у/4=7 (2)
Чтобы избавиться от дробей, домножим первое уравнение на 4, а второе на 7, получаем:
х+3у=20 (1)
3х+у=28 (2)
Теперь из первого уравнения выразим х и подставим во второе.
х=20-3у
3*(20-3у)+у=28
60-9у+у=28
8у=32
у=4 (ч) – время наполнения бассейна второй трубой.
Для проверки найдём х.
х=20-3*4
х=8 (ч) – время наполнения бассейна первой трубой.
А теперь проверка. Первая труба наполнит четверть бассейна за 8/4=2 ч. Вторая труба наполнит 3/4 за (3/4)*4=3 ч. Всего 2+3=5 ч. Сходится.
Также со вторым вариантом.
(3/4)*8+(1/4)*4=6+1=7 ч. Сходится.
Ответ: вторая труба наполнит бассейн за 4 часа.
Определите за сколько часов бассейн может быть наполнен
Определите, за сколько часов бассейн может быть наполнен
3. Воспользовавшись моделью, построенной в примере 1, определите, за сколько часов бассейн может быть наполнен через первую трубу, если через вторую он заполняется за 24 часа, а через первую и вторую вместе — за 8 часов. 4. У садовника имеется 32 м провода, которым он хочет обозначить на земле границу клумбы. Форму клумбы ему надо выбрать из следующих вариантов: Хватит ли садовнику имеющегося провода, чтобы обозначить границу каждой из представленных клумб? 12.
Слайд 12 из презентации ««Информационные модели» 7 класс». Размер архива с презентацией 1061 КБ.
Информатика 7 класс
«Рисование в Paint» – Прямые, кривые и разные фигуры. Инструменты выделения. Учимся рисовать. Что вы узнали о рисовании в программе Paint. Оформление фотографий. Коллаж. Метод последовательных укрупнений. Метод вспомогательных построений. Создание и действия с текстом. Инструменты свободного рисования и их свойства.
««Информационные модели» 7 класс» – Информационные модели. Определите сказку, для которой следующий граф определяет отношения. Ярусная диаграмма, характеризующая размеры выручки кафе. Вычислительные таблицы. Найдите истинные высказывания. Приведите пример двух классов. По сравнению с 2004 годом в 2005 году резко возросло число ограблений. Линия, выходящая из некоторой вершины и входящая в нее же. Математические модели. Графики и диаграммы.
«Устройства ввода информации в компьютер» – Мышь и трекбол. Звуковая карта и микрофон. Устройства ввода информации. Клавиши управления курсором. Специальные клавиши. Клавиатура. Манипуляторы. Координатные устройства ввода. Сканер. Цифровой блок. Алфавитно-цифровые клавиши. Устройства ввода. Джойстик. Разрешающая способность. Функциональные клавиши. Цифровые камеры. Оптические мыши. Сенсорная панель. Клавиши редактирования.
«Модели на графах» – Корень. Файловая структура. Дороги между пятью населенными пунктами. Схема дорог. Семантическая сеть. Иерархия. Задача. Взвешенный граф. Цепь. Информационные модели на графах. Связь между графом и таблицей. Граф. Схема дорог, связывающих города. Ориентированный граф. Ход рассуждения. Состав графа. Дороги. Неориентированный граф. Дерево.
«Таблицы и диаграммы Word» – Оглавление: Основные параметры: Тип диаграммы; Заголовок диаграммы; Рамка; Координатная сетка. Удаление ячеек и таблиц. Форматирование диаграмм. В окне Образец щелкните нужные стороны схемы. Добавление заливки к таблице. Методическая разработка урока по информатике. Диаграмма. Добавление границ к таблице. Создание таблицы. Удаление Диаграмм. Таблицы и диаграммы в Microsoft Word. Создание Диаграмм.
«Файловая система диска» – Папка. 2 знака. Вид представления объектов. Диск. Значок. Путь к файлу. Компьютерный ринг. Файлы. Три логических диска. Крупные значки. Какая папка находится непосредственно в корневом каталоге диска. Операционная система. Файловая система. Точный размер. Приз. Текстовый документ. Файл. Объект. Последовательность имен папок. Найдите ошибку в файловой структуре. Совокупность данных. Логический диск.
Всего в теме «Информатика 7 класс» 26 презентаций
Одна труба заполняет бассейн за 12 часов, а вторая за 16 часов. Бассейн должен быть заполнен на 3/4. Какую часть бассейна останентся заполнить после 4
часов их одновременной работы?
4*(t2+6+t2)*t2 значит t1=12
1/12- производительность 1го
1/16- производ-ть 2го
1/12+1/16=4/48+3/48=7/48- совместная производительность
7/48*4=7/12 заполнили за 4 часа
3/4-7/12=9/12-7/12=2/12=1/6 остается заполнить до 3/4
Другие вопросы из категории
каждого вещества надо взять чтобы приготовить 340 грамм состава??=
часть дргой, то разгрузка баржы будет выполнена за 9 часов. За сколько часов может разгрузить баржу каждый кран , работая в отдельности? РЕШИТЕ ПОЖАЛУЙСТА НЕ МОГУ ПОНЯТЬ!
Из двух городов ,расстояние между которыми 7 400 км,вылетели одновременно навстречу друг другу два самолёта и
встретелись через 4 ч.Скорость одного самолёта 950 км/ч.Определи скорость второго самолёта. Очень срочно. Пожалуйста. Заранее спасибо.
Читайте также
работы? Какая часть бассейна остается незаполненной?
Ч? 2)КАКУЮ ЧАСТЬ БАССЕЙНА НАПОЛНЯТ ЗА 1 Ч ДВЕ ТРУБЫ ВМЕСТЕ ? 3)ЗА СКОЛЬКО ЧАСОВ НАПОЛНИТСЯ ВЕСЬ БАССЕЙН ,ЕСЛИ ОТКРЫТЬ ОБЕ ТРУБЫ ОДНОВРЕМЕННО? №658 Б)Одна дригадаможет выполнить работу за 6 дней ,а другая -за 12 дней.За сколько дней две бригады выполнят ту же работу вместе?
если третью ,то за 16 часов.Открыли все три трубы.Какая часть бассейна будет заполнена через час?
2 задача (Старинная задача)Работник сделал в первый день 1/4 всей работы ,во второй -3/20,в третий-0,3.В четвёртый день он закончил работу и получил за это 2 руб .40 коп.Сколько денег он заработал за четыре дня??
3.укажите два числа,каждое из которых больше 9/11,но меньше 10/11.
4.При каких натуральных значениях( y )выполняется неравенство:2y/19 5-9 класс математика ответов 2
При включении 1-ой трубы бассейн наливается за 10 ч.
При включении 2-ой – наливается за 15 ч.
Нужно найти, за сколько часов нальется через одну лишь 3-юю трубу.
По идее за 12 часов, подсказал мне старший брат, но я ни черта не понял.
Разьясните и обьясните все пожалуйста)
часов.открыли все три трубы.какая часть бассейна будет заполнена через час?
Решение задач на совместную работу
Главная > Решение
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Тема. Задачи на совместную работу (бассейн)
Ребята! Здравствуйте! Ознакомьтесь с основными понятиями по данной теме и разберите предложенные задачи. Советую Вам сначала попробовать самостоятельно составить математическую модель к задаче, затем проверить решение. Если возникнут вопросы по решению, можно их задать и получить консультацию по адресу:
1) Обычно объём работы принимают за единицу. В задачах с бассейнами и трубами объём бассейна принимают за единицу. Но можно также обозначить любой буквой (произвольной постоянной).
2) Производительность работы – это количество работы, выполненной за единицу времени.
Например, если одна труба наполняет бассейн за 5 часов, то за
1 час она наполнит 
часть задания.
3) При решении задач, связанных с выполнением (индивидуально или совместно) определенного объема работы, используют формулу
где А — количество всей работы, намеченной к выполнению (по смыслу задачи часто А принимают за единицу), t — время выполнения всего количества работы, P — производительность труда, т. е. количество работы, выполняемой в единицу времени.
Если весь объем работы, принятый за единицу, выполняется одним субъектом за t 1 , а вторым — за t 2 единиц времени, то производительность труда при их совместном выполнении того же объема работы равна
Решение задач на совместную работу
Пример 1. Две трубы вместе наполняют бассейн за 3 ч. Одна первая труба может наполнить бассейна на 8 ч быстрее, чем одна вторая труба. За сколько часов может наполнить бассейн одна первая труба?
Решение. Типовая задача на работу. Пусть 1-я труба наполняет бассейн за х(ч), а 2-я за – у(ч). Тогда + – объем, наполняемый обеими трубами вместе за 1ч. Так как две трубы наполняют бассейн за 3 ч, то за 1ч они наполнят объема бассейна. Уравнение + = ; по условию у – х = 8. Из системы х = 4; у = 12.
Замечание. Чтобы вместо дробно – рациональных уравнений получить линейные за неизвестную величину иногда рациональнее принять производительность.
Пример 2. Бассейн наполняется четырьмя трубами за 4 часа. Первая, вторая и четвертая заполняют за 6 часов. Вторая, третья и четвертая – за 5 часов. За сколько часов заполняют бассейн первая и третья трубы?
Решение. Пусть x, y, z, u – производительности 1-й, 2-й, 3-й и 4-й труб.(Если за неизвестное принять время выполнения всего объема работы, то уравнения получатся сложнее). Тогда получаем систему уравнений
Вычитая из 1-го уравнения 2-е, получаем z = ; из 1-го 3-е, что – х = .
Общая производительность 1 и 3 труб z + x = .
Тогда искомое время = 7,5 ч
Пример 3. Две трубы, работая совместно, наполняют бассейн за 6 часов. За какое время наполняет бассейн каждая труба, если известно, что в течение часа из первой трубы вытекает па 50% больше воды, чем из второй?
Решение. Пусть х л воды в час вытекает из первой трубы (производительность 1трубы), у л воды в час вытекает из второй трубы (производительность 2трубы), тогда за 1 час обе трубы наполнят ( х + у ) л или бассейна.
В течение часа из первой трубы вытекает на 50% больше воды, чем из второй, то есть х = 1,5 у .
Тогда .
Таким образом, за 1 час первая труба наполняет 
бассейна. То есть первая труба наполнит весь бассейн за 10 часов, а вторая – за 15 часов.
Ответ: 10 ч, 15 ч.
Пример 4. Три насоса, качающие воду для поливки, начали работать одновременно. Первый и третий насосы закончили работу одновременно, а второй – через 2 ч после начала работы. В результате первый насос выкачал 9 м 3 воды, а второй и третий вместе 28 м 3 . Какое количество воды выкачивает за час каждый насос, если известно, что третий насос за час выкачивает на 3 м 3 больше, чем первый, и что три насоса, работая вместе, выкачивают за час 14 м 3 ?
Одна труба заполняет бассейн за 12 часов, а вторая за 16 часов. Бассейн должен быть заполнен на 3/4. Какую часть бассейна останентся заполнить после 4
часов их одновременной работы?
4*(t2+6+t2)*t2 значит t1=12
1/12- производительность 1го
1/16- производ-ть 2го
1/12+1/16=4/48+3/48=7/48- совместная производительность
7/48*4=7/12 заполнили за 4 часа
3/4-7/12=9/12-7/12=2/12=1/6 остается заполнить до 3/4
Другие вопросы из категории
каждого вещества надо взять чтобы приготовить 340 грамм состава??=
часть дргой, то разгрузка баржы будет выполнена за 9 часов. За сколько часов может разгрузить баржу каждый кран , работая в отдельности? РЕШИТЕ ПОЖАЛУЙСТА НЕ МОГУ ПОНЯТЬ!
Из двух городов ,расстояние между которыми 7 400 км,вылетели одновременно навстречу друг другу два самолёта и
встретелись через 4 ч.Скорость одного самолёта 950 км/ч.Определи скорость второго самолёта. Очень срочно. Пожалуйста. Заранее спасибо.
Читайте также
работы? Какая часть бассейна остается незаполненной?
Ч? 2)КАКУЮ ЧАСТЬ БАССЕЙНА НАПОЛНЯТ ЗА 1 Ч ДВЕ ТРУБЫ ВМЕСТЕ ? 3)ЗА СКОЛЬКО ЧАСОВ НАПОЛНИТСЯ ВЕСЬ БАССЕЙН ,ЕСЛИ ОТКРЫТЬ ОБЕ ТРУБЫ ОДНОВРЕМЕННО? №658 Б)Одна дригадаможет выполнить работу за 6 дней ,а другая -за 12 дней.За сколько дней две бригады выполнят ту же работу вместе?
если третью ,то за 16 часов.Открыли все три трубы.Какая часть бассейна будет заполнена через час?
2 задача (Старинная задача)Работник сделал в первый день 1/4 всей работы ,во второй -3/20,в третий-0,3.В четвёртый день он закончил работу и получил за это 2 руб .40 коп.Сколько денег он заработал за четыре дня??
3.укажите два числа,каждое из которых больше 9/11,но меньше 10/11.
4.При каких натуральных значениях( y )выполняется неравенство:2y/19 5-9 класс математика ответов 2
При включении 1-ой трубы бассейн наливается за 10 ч.
При включении 2-ой – наливается за 15 ч.
Нужно найти, за сколько часов нальется через одну лишь 3-юю трубу.
По идее за 12 часов, подсказал мне старший брат, но я ни черта не понял.
Разьясните и обьясните все пожалуйста)
часов.открыли все три трубы.какая часть бассейна будет заполнена через час?