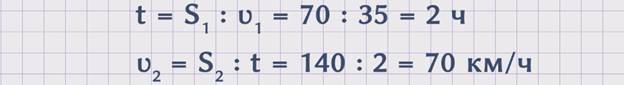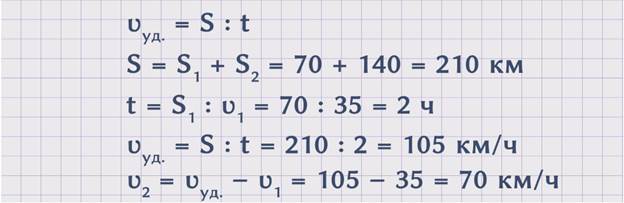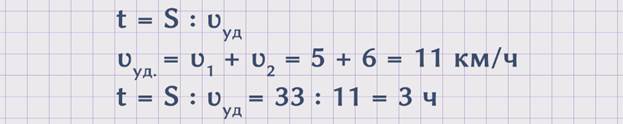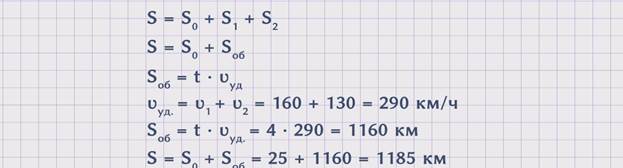Рассказываем, как решать задачи на движение в противоположном направлении. Приводим алгоритм решения задач и примеры. Задачи для решения.
Суть задач на движение в противоположных направлениях
Задачи на движение в противоположных направлениях – это задачи на нахождение скорости, времени и расстояния по заданным параметрам. При условии движения объектов в противоположных направлениях.
Например: Из одного города одновременно в противоположных направлениях выехали мотоцикл и автобус. Через 4 ч расстояние между ними было 572 км. Скорость мотоцикла 96 км/ч. С какой скоростью ехал автобус?
Алгоритм решения задач
Алгоритм решения задач на движение в противоположных направлениях:
- Составляем краткую запись.
- Решаем задачу.
- Выписываем полный ответ.
Способы решения задач
Примеры решения задачи
Базовые знания: Как рассчитать время, скорость, расстояние?
Тип 1
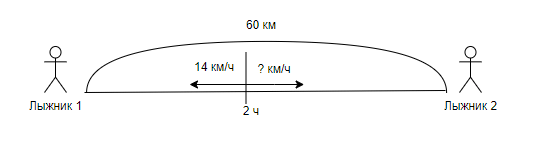
Задача 1. С одной лыжной базы одновременно в противоположных направлениях вышли два лыжника. Через 2 ч расстояние между ними было 60 км. Чему равна скорость второго лыжника, если скорость первого 14 км/ч?
Краткая запись:
Решение:
- 14х2=28 (км) – прошел 1 лыжник;
- 60-28=32 (км) – прошел 2 лыжник;
- 32:2=16 (км/ч) – скорость 2 лыжника.
Ответ: 16 км/ч скорость второго лыжника.
Тип 2
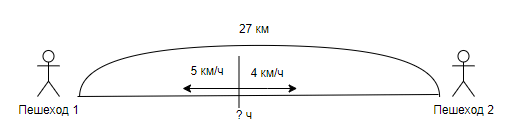
Задача 2. Из одного посёлка вышли в одно и то же время в противоположных направлениях два пешехода. Скорость одного из них 5 км/ч, а скорость другого 4 км/ч. Через сколько часов расстояние между ними будет 27 км?
Краткая запись:
Решение:
- 5+4=9 (км/ч) – общая скорость;
- 27:9=3 (ч) – в пути пешеходы.
Ответ: через 3 часа расстояние между пешеходами будет 27 км.
Тип 3
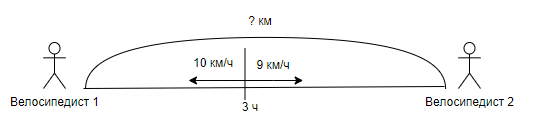
Задача 3. Из одного города одновременно в противоположных направлениях выехали два велосипедиста. Скорость одного велосипедиста 10 км/ч, а другого – 9 км/ч. Какое расстояние будет между ними через 3 ч?
Краткая запись:
Решение:
- 10х3=30 (км) – проехал 1 велосипедист;
- 9х3=27 (км) – проехал 2 велосипедист;
- 30+27=57 (км) – расстояние проехали оба велосипедиста вместе.
Ответ: 57 км – расстояние между ними через 3 ч.
Задачи для самостоятельного решения
Тип 1
- Из одного города одновременно в противоположных направлениях выехали два автобуса. Через 3 ч расстояние между ними было 243 км. Чему равна скорость первого автобуса, если скорость второго 45 км/ч?
- С одной крыши одновременно в противоположных направлениях полетели два воробья. Через 18 с расстояние между ними было 396 м. Найди скорость одного из воробьёв, если скорость другого 10 м/с.
- С одного цветка одновременно в противоположных направлениях полетели две златоглазки. Через 7 с расстояние между ними было 826 см. Найди скорость одной из златоглазок, если скорость другой 60 см/с.
- Автомобиль и мотоцикл выехали одновременно в противоположных направлениях из одного города. Скорость автомобиля 60 км/ч. Через 3 ч расстояние между ними было 390 км. Чему равна скорость мотоцикла?
- От стойбища одновременно в противоположных направлениях побежали два оленя. Через 19 с расстояние между ними было 722 м. Найди скорость одного из оленей, если скорость другого 20 м/с.
Тип 2
- От одной лыжной базы в одно и то же время в противоположных направлениях вышли два лыжника. Скорость одного из них 12 км/ч, а другого – 13 км/ч. Через сколько часов лыжники будут находиться на расстоянии 150 км друг от друга?
- От одной пристани одновременно в противоположных направлениях отплыли две вёсельные лодки со скоростью 8 и 5 км/ч. Через какое время расстояние между ними будет 39 км?
- От одного дома одновременно в противоположных направлениях побежали две кошки со скоростью 4 и 8 м/с. Через какое время расстояние между ними будет 60 м?
- От одного камня побежали одновременно в противоположных направлениях две ящерицы. Скорость одной ящерицы 8 м/с, другой – 7 м/с. Через какое время расстояние между ними будет 375 м?
- От одного места два бегемота побежали одновременно в противоположных направлениях. Скорость одного бегемота 11 м/с, а другого – 12 м/с. Через какое время расстояние между ними будет 368 м?
Тип 3
- Из одного трамвайного депо одновременно в противоположных направлениях выехали два трамвая со скоростью 610 и 598 м/мин. Какое расстояние будет между ними через 12 мин?
- От одной льдины одновременно в противоположных направлениях поплыли два пингвина со скоростью 6 и 7 м/с. Какое расстояние будет между ними через 30 с?
- От одного камня одновременно в противоположных направлениях поползли две морские звезды со скоростью 15 и 14 см/мин. Какое расстояние будет между ними через 9 мин?
- Из одного улья одновременно в противоположных направлениях вылетели две пчелы со скоростью 2 и 3 м/с. Какое расстояние будет между ними через 45 с?
- Из одной мастерской одновременно в противоположных направлениях выехали два трактора со скоростью 456 и 387 м/мин. Какое расстояние будет между ними через 6 мин?
Задачи на движение в противоположных направлениях
Рассмотрим задачи, в которых речь идёт о движении в противоположных направлениях. В таких задачах два каких-нибудь объекта движутся в противоположных направлениях, отдаляясь друг от друга. Задачи на движение в противоположных направлениях можно решать двумя способами.
Задача 1. Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго — 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение: Из условия задачи известны скорость каждого автомобиля и время, которое автомобили были в пути. Значит, можно найти расстояние, которое проехал каждый автомобиль, для этого нужно скорость умножить на время:
1) 100 · 4 = 400 (км) — проехал первый автомобиль,
2) 70 · 4 = 280 (км) — проехал второй автомобиль.
Найдя сумму полученных результатов, узнаем расстояние между автомобилями через 4 часа:
400 + 280 = 680 (км).
Данную задачу можно решить и другим способом. Каждый час расстояние между автомобилями увеличивалось на 170 километров (100 + 70), 170 км/ч — это скорость удаления автомобилей. За 4 часа они проедут расстояние:
170 · 4 = 680 (км).
Таким образом, задачу на движение в противоположных направлениях можно решить двумя способами:
| 1-й способ: | 2-й способ: |
|---|---|
| 1) 100 · 4 = 400 (км) | 1) 100 + 70 = 170 (км/ч) |
| 2) 70 · 4 = 280 (км) | 2) 170 · 4 = 680 (км) |
| 3) 400 + 280 = 680 (км) |
Ответ: Через 4 часа между автомобилями будет 680 км.
Задача 2. Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два пешехода. Первый пешеход шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между пешеходами будет через 5 часов?
Решение: Сначала можно определить сколько километров прошёл каждый из пешеходов за 5 часов, для этого скорость пешеходов умножим на 5:
1) 4 · 5 = 20 (км) — прошёл первый пешеход,
2) 5 · 5 = 25 (км) — прошёл второй пешеход.
Затем можно найти общий путь, пройденный двумя пешеходами за 5 часов:
20 + 25 = 45 (км).
Теперь можно найти расстояние между пешеходами, прибавив к пути, пройденному пешеходами, расстояние между населёнными пунктами:
45 + 40 = 85 (км).
У данной задачи есть и второй вариант решения. Можно сначала найти скорость удаления пешеходов:
4 + 5 = 9 (км/ч).
Затем найти пройденное расстояние, умножив скорость удаления (9 км/ч) на время движения пешеходов (5 ч):
9 · 5 = 45 (км).
А теперь, для нахождения расстояния между пешеходами, сложить пройденное расстояние (45 км) с расстоянием между населёнными пунктами:
45 + 40 = 85 (км).
Таким образом, данная задача имеет два варианта решения:
| 1-й способ: | 2-й способ: |
|---|---|
| 1) 4 · 5 = 20 (км) | 1) 4 + 5 = 9 (км/ч) |
| 2) 5 · 5 = 25 (км) | 2) 9 · 5 = 45 (км) |
| 3) 20 + 25 = 45 (км) | 3) 45 + 40 = 85 (км) |
| 4) 45 + 40 = 85 (км) |
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.
— простые задачи на скорость, время и расстояние;
— задачи на встречное и противоположное движение;
— задачи на движение в одном направлении (на сближение и удаление);
— решение задач на движение по реке.
Скорость, время и расстояние: определения, обозначения, формулы
скорость = расстояние: время — формула нахождения скорости;
время = расстояние: скорость — формула нахождения времени;
расстояние = скорость · время — формула нахождения расстояния.
Скорость – это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Пример обозначения: 7 км/ч (читается: семь километров в час).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным.
На сайте представлены калькуляторы онлайн, с помощью которых можно перевести скорость, время и расстояние в другие единицы измерения:
1.Конвертер единиц измерения скорости
2.Конвертер единиц измерения времени
3.Конвертер единиц измерения расстояния (длины)
Примеры простых задач.
Задача 1.
Автомобиль проехал 180 км за 2 часа. Чему равна скорость автомобиля?
Решение: 180:2=90 (км/ч.)
Ответ: Скорость автомобиля равна 90 км/ч.
Задача 2.
Автобус проехал путь в 240 км со скоростью 80 км/ч. Сколько времени ехал автобус?
Решение: 240:80=3 (ч.)
Ответ: Автобус проехал 3 часа.
Задача 3.
Грузовик ехал 5 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Решение: 70 · 3 = 350 (км)
Ответ: Грузовик за 5 часов проехал 350 км.
Задачи на встречное движение
В таких задачах два объекта движутся навстречу друг другу.
Задачи на встречное движение можно решать двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние. Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Задача 4.
Из двух пунктов навстречу друг другу одновременно выехали два поезда и встретились через 3 часа. Первый поезд ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся пункты?
Решение:
Первый способ. Найти расстояние, которое проехал каждый автобус, и сложить полученные данные:
80*3=240 (км) – проехал 1й автобус, 70*3=210 (км) – проехал 2й поезд,
240+210=450 (км) – проехали два поезда.
Второй способ. Найти скорость сближения поездов, то есть на сколько сокращалось расстояние между ними каждый час; а затем найти расстояние:
80+70=150 (км/ч), 150*3=450 (км).
Ответ: города находятся на расстоянии 450 км.
Задача 5.
Из двух городов навстречу друг другу одновременно выехали два автобуса. Первый автобус ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. Какое расстояние будет между ними через 2 часа, если расстояние между городами 450 км?
Решение:
Первый способ. Определить, сколько километров проехал каждый автобус и найти расстояние, которое осталось проехать:
80*2=160 (км)-проехал 1й автобус, 70*2=140 (км)-проехал 2й автобус,
160+140=300 (км)-проехали два автобуса, 450-300=150 (км)-осталось проехать.
Второй способ. Найти скорость сближения автобусов и умножить ее на время в пути.
80*70=150 (км/ч) – скорость сближения; 150*2=300 (км) – проехали два автобуса; 450-300=150 (км) – осталось проехать.
Ответ: Через 2часа расстояние между автобусами будет 150 км.
Задачи на движение в противоположных направлениях
В таких задачах два объекта движутся в противоположных направлениях, отдаляясь друг от друга. В таком типе задачи используется скорость удаления. Задачи на движение в противоположных направлениях также можно решить двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость удаления объектов (как сумму их скоростей), общие время и расстояние. Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Задача 6.
Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго – 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение:
Первый способ. Определить расстояние, которое проехал каждый автомобиль и найти сумму полученных результатов:
1) 100 · 4 = 400 (км) – проехал первый автомобиль
2) 70 · 4 = 280 (км) – проехал второй автомобиль
400 + 280 = 680 (км)
Второй способ. Найти скорость удаления, то есть значение увеличения расстояния между автомобилями за каждый час, а затем скорость удаления умножить на время в пути.
100 + 70= 170 км/ч – это скорость удаления автомобилей.
170 · 4 = 680 (км)
Ответ: Через 4 часа между автомобилями будет 680 км.
Задача 7.
Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два туриста. Первый турист шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между туристами будет через 5 часов?
Решение:
Первый способ. Определить сколько километров прошёл каждый из туристов за 5 часов, сложить полученные результаты, а затем к полученному расстоянию прибавить расстояние между населенными пунктами.
1) 4 · 5 = 20 (км) – прошёл первый турист;
2) 5 · 5 = 25 (км) – прошёл второй турист;
3) 20 + 25 = 45 (км);
4) 45 + 40 = 85 (км).
Второй способ. Найти скорость удаления пешеходов, затем найти пройденное расстояние, к полученному результату прибавить расстоянием между населёнными пунктами.
4 + 5 = 9 (км/ч);
9 · 5 = 45 (км);
45 + 40 = 85 (км);
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.
Задачи на движение в одном направлении
В таких задачах два объекта движутся в одном направлении с разной скоростью, при этом они сближаются друг с другом или отдаляются друг от друга. Соответственно находится скорость сближения или скорость удаления объектов.
Формула нахождения скорости сближения или удаления двух объектов, которые движутся в одном направлении: из большей скорости вычесть меньшую.
Задача 8.
Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?,
Решение:
Задачу можно решить с помощью уравнения.
В этом случае скорость первого автомобиля 40 км/час, время в пути на 4 часа больше, чем время второго автомобиля (или t+4). Скорость второго автомобиля 60 км/час, время в пути – t. Расстояние оба автомобиля проехали одинаковое. Поэтому можно составить уравнение: 40*(t+4)=60*t. Отсюда получаем t=8 (часов) – время в пути второго автомобиля, за которое он догонит первый.
Решение задачи без использования уравнения.
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на: 40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит, каждый час расстояние между автомобилями будет сокращаться на разность их скоростей: 60 — 40 = 20 (км/ч) – это скорость сближения.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся: 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 9.
Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов: 5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого: 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.
Задача 10.
Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение:
1) 80 — 40 = 40 (км/ч) — скорость удаления автомобилей друг от друга.
2) 40 · 3 = 120 (км) – расстояние между ними через 3 часа./
3) 200 : 40 = 5 (ч) – время, через которое расстояние между автомобилями станет 200 км.
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.
Задачи на движение по реке
Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.
Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки. Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Задача 11.
Лодка движется по реке. За сколько часов она преодолеет расстояние 120 км, если ее собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Решение:
1) лодка движется по течению реки.
27 + 3 = 30 (км/ч) – скорость лодки по течению реки.
120 : 30 = 4 (ч) – проплывет путь.
2) лодка движется против течения реки.
27 — 3 = 24 (км/ч) — скорость лодки против течения реки
120 : 24 = 5 (ч) – проплывет путь.
Ответ:
1) При движении по течению реки лодка потратит 4 часа на путь.
2) При движении против течения реки лодка потратит 5 часов на путь.
Итак, для решения задач на движение:
- Основная формула:S=ν*t;
- Нужно сделать чертеж, который поможет определить тип задачи.
- Все цифры нужно привести в единые единицы измерения: длина и время
Заключение.
Решая много задач по данной теме, ученик обязательно научится быстро ориентироваться в понятиях «скорость», «время» и «расстояние» и быстро решать задачи всех типов.
Весь курс начальной школы (за 1-4 классы) в краткой форме на сайте edu.intmag24.ru. С помощью курса можно быстро повторить основные моменты и правила по предметам: русский язык, математика, окружающий мир.
Для решения более сложных задач на движение посмотрите, как составлять схемы и таблицы данных для наглядного представления и структурирования данных.
Содержание:
- § 1 Движение в противоположных направлениях
- § 2 Решение задач
- § 3 Краткие итоги по теме урока
§ 1 Движение в противоположных направлениях
В этом уроке мы познакомимся с задачами на движение в противоположных направлениях.
При решении любой задачи на движение мы сталкиваемся с такими понятиями, как «скорость», «время» и «расстояние».
Скорость – это расстояние, которое преодолевает объект за единицу времени. Измеряется скорость в км/ч, м/сек и т.д. Обозначается латинской буквой ʋ.
Время – это время, за которое объект преодолевает определенное расстояние. Измеряется время в секундах, минутах, часах и т.д. Обозначается латинской буквой t.
Расстояние – это путь, который преодолевает объект за определенное время. Измеряется расстояние в километрах, метрах, дециметрах и т.д. Обозначается латинской буквой S.
В задачах на движение эти понятия взаимосвязаны. Так, чтобы найти скорость, необходимо расстояние разделить на время: ʋ = S : t. Чтобы найти время, надо расстояние разделить на скорость: t = S : ʋ. А чтобы найти расстояние, скорость умножают на время: S = ʋ · t.
При решении задач на движение в противоположных направлениях, используют еще одно понятие «скорость удаления».
Скорость удаления – это расстояние, на которое удаляются объекты за единицу времени. Обозначается ʋуд..
Чтобы найти скорость удаления, зная скорости объектов, надо найти сумму этих скоростей: ʋуд. = ʋ1 + ʋ2. Чтобы найти скорость удаления, зная время и расстояние, необходимо расстояние разделить на время: ʋуд. = S : t.
§ 2 Решение задач
Рассмотрим взаимосвязь понятий «скорость», «время» и «расстояние» при решении задач на движение в противоположных направлениях.
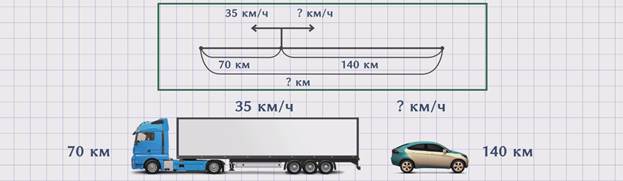
ЗАДАЧА 1. Грузовой и легковой автомобили отправились от автостанции в разных направлениях. За одно и то же время грузовик проехал 70 км, а легковой автомобиль – 140 км. С какой скоростью двигался легковой автомобиль, если скорость грузовика – 35 км/ч?
Изобразим движение грузового и легкового автомобиля на схеме.
Скорость грузового автомобиля обозначим буквой ʋ1 = 35 км/ч. Скорость легкового автомобиля обозначим буквой ʋ2 = ? км/ч. Время в пути обозначим буквой t. Расстояние, которое проехал грузовой автомобиль – буквой S1 = 70 км. Расстояние, которое проехал легковой автомобиль – S2 = 140 км.
Разберем первый вариант.
Поскольку, чтобы найти неизвестную скорость, необходимо знать расстояние, которое проехал легковой автомобиль, а оно известно и равно 140 км, и знать время движения, которое не указано в условиях задачи, то необходимо найти это время.Из условия задачи нам известно расстояние, которое проехал грузовой автомобиль S1 = 70 км и скорость грузового автомобиля ʋ1 = 35 км/ч. Используя эти данные, мы можем найти время. t = S1 : ʋ1 = 70 : 35 = 2 часа. Зная время и расстояние, которое проехал легковой автомобиль, мы сможем узнать скорость легкового автомобиля, так как ʋ2 = S2 : t = 140 : 2 = 70 км/ч. Получили, что скорость легкового автомобиля равна 70 км/ч.
Рассмотрим второй вариант.
Поскольку, чтобы найти неизвестную скорость, необходимо знать скорость грузового автомобиля, из условий задачи она известна, и скорость удаления, которая не оговаривается условиями задачи, то надо найти скорость удаления. Чтобы найти скорость удаления автомобилей, можно расстояние, которое проехали оба автомобиля, разделить на время. ʋуд. = S : t . Расстояние, которое проехали оба автомобиля, равно сумме расстояний S1 и S2. S = S1 + S2 = 70 + 140 = 210 км. Время можно узнать, разделив расстояние, которое проехал грузовой автомобиль, на его скорость. t = S1 : ʋ1 = 70 : 35 = 2 часа. Значит, ʋуд. = S : t = 210 : 2 = 105 км/ч. Теперь, зная скорость удаления, можем найти скорость легкового автомобиля. ʋ2 = ʋсбл. – ʋ1 = 105 – 35 = 70 км/ч. Получили, что скорость легкового автомобиля равна 70 км/ч.
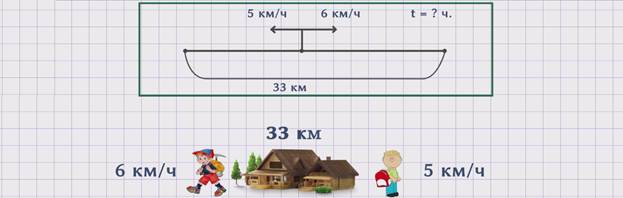
ЗАДАЧА 2. Два человека в одно и то же время вышли из поселка в разных направлениях. Один двигался со скоростью 6 км/ч, скорость другого была 5 км/ч. Сколько часов понадобится, чтобы расстояние между ними стало 33 км?
Изобразим движение людей на схеме.
Скорость первого человека обозначим буквой ʋ1 = 5 км/ч. Скорость второго человека обозначим буквой ʋ2 = 6 км/ч. Расстояние, которое они прошли, обозначим буквой S = 33 км. Время – буквой t = ? часов.
Чтобы ответить на поставленный вопрос задачи, необходимо знать расстояние и скорость удаления, так как t = S : ʋуд.. Поскольку расстояние нам известно из условия задачи, надо найти скорость удаления. ʋуд. = ʋ1 + ʋ2 = 5 + 6 = 11 км/ч. Теперь зная скорость удаления, можем найти неизвестное время. t = S : ʋуд = 33 : 11 = 3 ч. Получаем, что понадобилось 3 часа, чтобы расстояние между людьми стало 33 км.
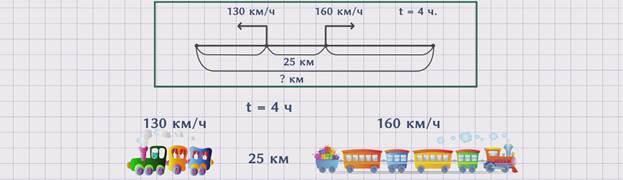
ЗАДАЧА 3. Два поезда одновременно начали движение в противоположных направления с разных станций, расстояние между которыми составляет 25 км. Один двигался со скоростью 160 км/ч. На каком расстоянии друг от друга поезда будут через 4 часа, если скорость другого поезда – 130 км/ч?
Покажем движение поездов на схеме.
Скорость первого поезда обозначим буквой ʋ1 = 130 км /ч. Скорость второго поезда обозначим ʋ2 = 160 км/ч. Расстояние между станциями обозначим буквой Sм = 25 км. Время – буквой t = 4 часа. А искомое расстояние – буквой S = ? км.
Чтобы ответить на вопрос задачи, необходимо знать расстояние между станциями, расстояние, которое проехал первый поезд, и расстояние, которое проехал второй поезд, так как S = Sм + S1 + S2. Расстояние между станциями известно из условия задачи, а расстояния S1 и S2 нет, но их можно найти, используя другие данные задачи. Однако искомое расстояние можно найти более рациональным путем, а именно сложив расстояние между станциями и общее расстояние, которое проехали оба поезда, так как S = Sм + Sоб.. Поскольку расстояние между станциями известно из условия задачи, надо найти общее расстояние. Для этого необходимо время умножить на скорость удаления. Sоб = t · ʋуд. А скорость удаления равна сумме скоростей поездов. ʋуд. = ʋ1 + ʋ2 = 160 + 130 = 290 км/ч. Теперь можем найти общее расстояние Sоб = t · ʋуд.= 4 · 290 = 1160 км.Зная общее расстояние, можем найти искомое расстояние. S = Sм + Sоб = 25 + 1160 = 1185 км. Получили, что через 4 часа расстояние между поездами будет составлять 1185 км.
§ 3 Краткие итоги по теме урока
При решении задач на движение в противоположных направлениях, следует помнить, что в задачах такого типа выполняются следующие условия:
1)объекты начинают свое движение одновременно в противоположных направлениях, а значит, находятся в пути одинаковое количество времени; время обозначается латинской буквой t = S : ʋуд;
2)расстояние S – это сумма всех расстояний, оговоренных условиями задачи;
S = S1 + S2 + Sмили S = ʋуд. · t;
3)объекты удаляются с определенной скоростью – скоростью удаления, обозначающейся латинской буквой ʋуд. = S : t или ʋуд = ʋ1 + ʋ2, соответственно
ʋ1 = S1 : t и ʋ2 = S2 : t.
Список использованной литературы:
- Петерсон Л.Г. Математика. 4 класс. Часть 2. / Л.Г. Петерсон. – М.: Ювента, 2014. – 96 с.: ил.
- Математика. 4 класс. Методические рекомендации к учебнику математики «Учусь учиться» для 4 класса / Л.Г. Петерсон . – М.: Ювента, 2014. – 280 с.: ил.
- Зак С.М. Все задания к учебнику математики для 4 класса Л.Г. Петерсон и комплекту самостоятельных и контрольных работ. ФГОС. – М.: ЮНВЕС, 2014.
- CD-ROM. Математика. 4 класс. Сценарии уроков к учебнику к 2 части Петерсон Л.Г. – М.: Ювент, 2013.
Использованные изображения:
Памятка «Учимся решать задач на движение»
В задачах на движение рассматриваются три взаимосвязанные величины:
S – расстояние (пройденный путь),
t – время движения и
V – скорость – расстояние, пройденное за единицу времени.
Расстояние – это произведение скорости на время движения
S = V ● t
Скорость – это частное от деления расстояния на время движения
V = S : t
Время – это частное от деления расстояния на скорость движения
t = S : V
Задачи на встречное движение
Скорость сближения – это сумма скоростей, движущихся навстречу друг другу тел. V сближ. = 1V + 2V
Пример 1. Два велосипедиста одновременно выехали навстречу друг другу из двух посёлков и встретились через 3 часа. Первый велосипедист ехал со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии находятся посёлки?
Схема к задаче:
Решение:
S = V ● t
V сближ. = 1V + 2V
1 способ:
1) 12 • 3 = 36 (км) – проехал первый велосипедист до встречи
2) 14 • 3 = 42 (км) – проехал второй велосипедист до встречи
3) 36 + 42 = 78 (км)
2 способ:
1) 12 + 14 = 26 (км/ч) – скорость сближения
2) 26 • 3 = 78 (км)
Ответ: расстояние между посёлками 78 км.
Пример 2. Из двух городов навстречу друг другу выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через, сколько часов машины встретятся, если расстояние между городами 280 км?
Схема к задаче:

Решение:
V сближ. = 1V + 2V
t = S : V
1) 80 + 60 = 140 (км/ч) – скорость сближения
2) 280 : 140 = 2 (ч)
Ответ: машины встретятся через 2 часа.
Пример 3. Из двух городов, расстояние между которыми 340 км, выехали одновременно навстречу друг другу две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если встретились они через 2 часа?
Схема к задаче:
Решение:
V = S : t
2V = V сближ. – 1V
1) 340 : 2 = 170 (км/ч) – скорость сближения
2) 170 – 80 = 90 (км/ч)
Ответ: 90 км/ч. скорость второй машины
Задачи на движение в противоположных направлениях
Скорость удаления – это расстояние, которое проходят тела за 1 ч при движении в противоположных направлениях.
V удал. = 1V + 2V
Пример 1. Два лыжника одновременно вышли из пункта А в противоположных направлениях. Первый лыжник шёл со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии друг от друга они будут через 3 ч?
Схема к задаче:
Решение:
S = V ● t
1 способ
1)12 • 3 = 36 (км) – расстояние, которое прошёл первый лыжник за 3 ч
2)14 • 3 = 42 (км) – расстояние, которое прошёл второй лыжник за 3 ч
3)36 + 42 = 78 (км)
2 способ
V удал. = 1V + 2V
S = V ● t
1)12 + 14 = 26 (км/ч) – скорость удаления
2)26 • 3 = 78 (км)
Ответ: через 3 ч они будут друг от друга на расстоянии 78 км.
Пример 2. Из города в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через сколько часов расстояние между машинами будет 280 км?
Схема к задаче:
Решение:
V удал. = 1V + 2V
t = S : V
1) 80 + 60 = 140 (км/ч) – скорость удаления
2) 280 : 140 = 2 (ч)
Ответ: через 2 часа расстояние между машинами будет 280 км
Пример 3. Из города одновременно в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если через 2 часа расстояние между ними было 340 км?
Схема к задаче:
Решение:
V = S : t
2V = V удал. – 1V
1) 340 : 2 = 170 (км/ч) – скорость удаления машин
2) 170 – 80 = 90 (км/ч)
Ответ: скорость второй машины 90 км/ч.