Как найти время зная равноускоренное движение

«Формула времени. Решение задач»

Скорость, время и расстояние — физические величины, взаимосвязаны процессом движения. Виды движений: 1) равномерное (прямолинейное, криволинейное и по окружности), 2) равноускоренное (с постоянным ускорением), 3) гармоническое. Для каждого вида движения своя формула времени.

Время обозначается как t. Единица измерения времени – с (секунды).

Самая простая формула при равномерном прямолинейном движении. Время, необходимое для прохождения пути равняется частному от деления пути на скорость равномерного прямолинейного движения: t = S / v.

При равноускоренном движении время равняется частному от деления разницы конечной и начальной скорости на ускорение: t = (v — v₀) / a  или частному от деления пути на разность конечной и начальной скорости: t = S / (v — v₀).

Решение задач через формулу времени

Задача № 1.

Конькобежец может развивать скорость до 13 м/с. За какое время он пробежит дистанцию длиной 2,6 км?

 Ответ: 200 с.

---

Задача № 2.

Двигаясь с ускорением 5 м/с² скорость космической ракеты увеличилась на 100 м/с. За какое время произошло такое изменение скорости?

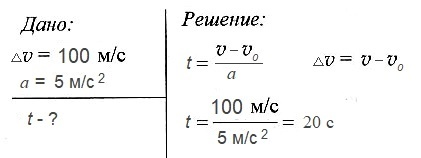 Ответ: 20 с.

---

Задача № 3.

Пункты А и В находятся на берегу реки на некотором расстоянии друг от друга. Моторная лодка проходит расстояние АВ вниз по течению реки за время t₁ = 3 ч, а плот то же расстояние – за время t₀ =12 ч. Какое время t₂ затратит моторная лодка на обратный путь?

Решение. Обозначим расстояние между пунктами А и В через L, скорость моторной лодки относительно воды через v_л , а скорость течения через v_т. Тогда t₀ = L / v_т ,  t₁ = L / (v_л +  v_т) ,  t₂ = L / (v_л —  v_т) . Исключая из записанной системы уравнений L, v_л и  v_т
находим 

Ответ: 6 ч.

---

Конспект урока «Формула времени. Решение задач».

Следующая тема: «».

Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется (увеличивается или уменьшается) на одну и ту же величину за равные промежутки времени.

Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. То есть, показывает, на какую величину изменяется скорость за единицу времени.

Примеры равноускоренного движения:

• разгон самолета перед взлетом;
• падающая с крыши сосулька;
• торможение лыжника на горном склоне;
• разгоняющийся на склоне сноубордист;
• свободное падение в результате прыжка с парашютом;
• камень брошенный под углом к горизонту;

Равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.

Равноускоренное движение: формулы

Формула для скорости при равноускоренном движении:

где: V_к — конечная скорость тела,
V_н — начальная скорость тела,
a=const — ускорение (a>0 при ускорении, a<0 при замедлении)
t — время.

Формула для ускорения при равноускоренном движении:

Во время движения тела ускорение остается постоянным.

Задача 1

Кирилл ехал на велосипеде со скоростью 6 м/с, затем начал разгоняться на горке. Чему будет равна его скорость через 10 секунд, если ускорение равно 0,5 м/с?
Решение. Vн=6м/с, ускорение a=0,5м/с, время разгона t=10 секунд.
Получаем: Vн= 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10с Кирилл разгонится до скорости 11 м/с.

Формула расстояния при равноускоренном движении

• Если известны  время, скорость начальная и скорость конечная

• Если известны время, скорость начальная и ускорение

где: S — путь, пройденный за время t,
Vн — начальная скорость,
Vк — конечная скорость,
a — ускорение тела,
t — время.

В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:

где S — путь, пройденный за время t ,
V0 — начальная скорость,
V — скорость в момент времени t,
a — ускорение тела.

Задача 2

Таксист получил заказ и начал движение с ускорением 0,1 м/с2. На каком расстоянии от начала движения его скорость станет равной 15м/с?
Решение. Так как таксист начал движение, начальная скорость равна нулю (Vн=0), Vк=15м/с, ускорение a=0,1м/с2.
Получаем: ​
S = 15^2 — 0^2 =1125 м.
Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.

Перемещение при равноускоренном движении

Важно напомнить разницу между путем и перемещением тела.

• Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Путь — всегда положительное значение.
• Перемещение — вектор, соединяющий начальное и конечное положение тела. Проекция перемещения может принимать отрицательное значение.

Например, если путник прошел в одну сторону расстояние S1, а обратно — S2, то: путь тела равен S1 + S2, а перемещение равно S1 − S2. В некоторых задачах путь и перемещение могут совпадать, но не всегда.

Равноускоренное движение: графически

График зависимости ускорения от времени:
Во время движения тела ускорение остается постоянным.

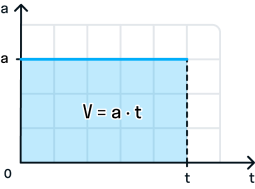
Взаимосвязь скорости, времени и расстояния:
На рисунке показан график,  в котором скорость равномерно увеличивается.
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени.

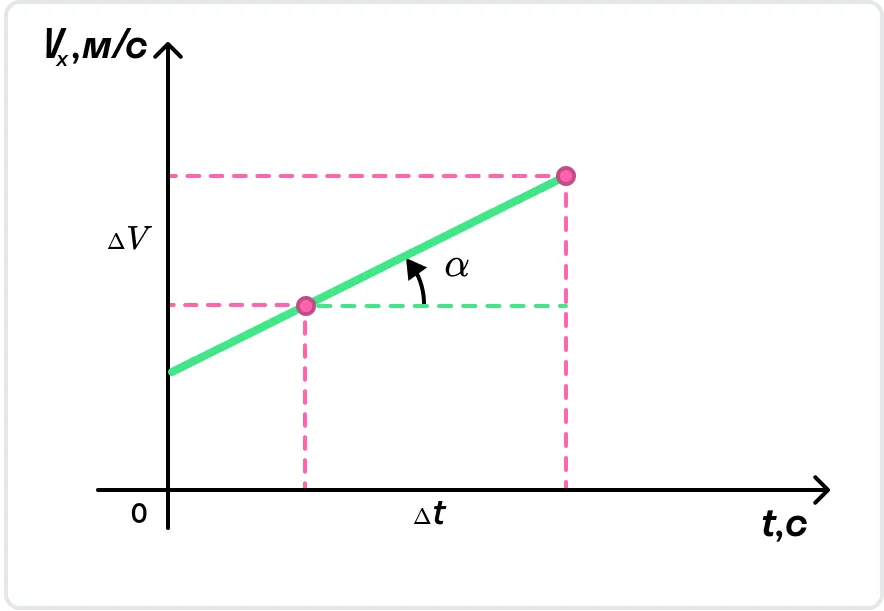
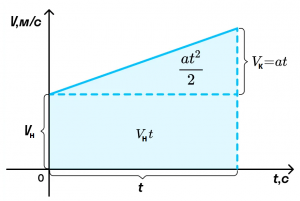
Из графика скорости получим формулу пути при равноускоренном движении тела.

Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника V_нt и треугольника at²/2. Получим: S = V_нt + at²/2.​

Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.

Задача 3

Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2с после начала движения из начала координат.

Дано:
Vн = 3 м/с, начальная координата (t) равна нулю,
Vк = 15м/с, 
a —  скорость лыжника увеличивается, поэтому ускорение — положительное число,
S = 36м — путь с горы,
t — 2с.

Решение:
Найдем ускорение из формулы пути при равноускоренном движении: 2аS = V_к²−V_н² 
Получим:  а = (V_к²−V_н² )/2S = (225-9)/(2*36) = 3 м/с2.
Составим уравнение движения лыжника исходя из формулы: S = V_нt + at²/2.
Получаем: x(t) =  3t + 1,5t² 
По уравнению определим координату лыжника в момент времени t = 2с:
Получаем: x(2) =  3*2 + 1,5*2² =6+6=12 м.

Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.

Для того, чтобы проверить правильность решения задач на равноускоренное движение, воспользуйтесь калькулятором равноускоренного движения.

Для того, чтобы перевести единицы измерения, воспользуйтесь конвертерами единиц измерения:

• Конвертер единиц измерения расстояния (длины)
• Конвертер единиц измерения скорости
• Конвертер единиц измерения времени

Равноускоренное движение: формулы, примеры

Равноускоренное движение

Равноускоренное движение – это движение, при котором вектор ускорения не меняется по модулю и направлению. Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение – частный случай равноускоренного движения с ускорением, равным нулю.

Рассмотрим случай свободного падения (тело брошено под уголом к горизонту) более подробно. Такое движение можно представить в виде суммы движений относительно вертикальной и горизонтальной осей.

В любой точке траектории на тело действует ускорение свободного падения g → , которое не меняется по величине и всегда направлено в одну сторону.

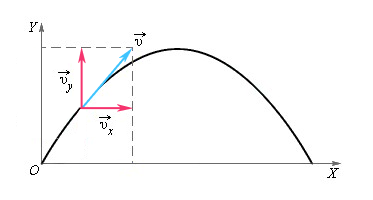
Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y – равноускоренное и прямолинейное. Будем рассматривать проекции векторов скорости и ускорения на оси.

Формулы для равноускоренного движения

Формула для скорости при равноускоренном движении:

Здесь v 0 – начальная скорость тела, a = c o n s t – ускорение.

Покажем на графике, что при равноускоренном движении зависимость v ( t ) имеет вид прямой линии.

​​​​​​​

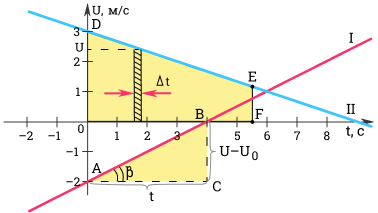
Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC.

a = v – v 0 t = B C A C

Чем больше угол β , тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.

Для первого графика: v 0 = – 2 м с ; a = 0 , 5 м с 2 .

Для второго графика: v 0 = 3 м с ; a = – 1 3 м с 2 .

По данному графику можно также вычислить перемещение тела за время t . Как это сделать?

Выделим на графике малый отрезок времени ∆ t . Будем считать, что он настолько мал, что движение за время ∆ t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆ t . Тогда, перемещение ∆ s за время ∆ t будет равно ∆ s = v ∆ t .

Разобьем все время t на бесконечно малые промежутки ∆ t . Перемещение s за время t равно площади трапеции O D E F .

s = O D + E F 2 O F = v 0 + v 2 t = 2 v 0 + ( v – v 0 ) 2 t .

Мы знаем, что v – v 0 = a t , поэтому окончательная формула для перемещения тела примет вид:

s = v 0 t + a t 2 2

Для того, чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение. Изменение координаты в зависимости от времени выражает закон равноускоренного движения.

Закон равноускоренного движения

y = y 0 + v 0 t + a t 2 2 .

Еще одна распространенная задача кинематики, которая возникает при анализе равноускоренного движения – нахождение координаты при заданных значениях начальной и конечной скоростей и ускорения.

Исключая из записанных выше уравнений t и решая их, получаем:

s = v 2 – v 0 2 2 a .

По известным начальной скорости, ускорению и перемещению можно найти конечную скорость тела:

v = v 0 2 + 2 a s .

При v 0 = 0 s = v 2 2 a и v = 2 a s

Величины v , v 0 , a , y 0 , s , входящие в выражения, являются алгебраическими величинами. В зависимости от характера движения и направления координатных осей в условиях конкретной задачи они могут принимать как положительные, так и отрицательные значения.

Время, скорость, расстояние

О чем эта статья:

Расстояние

Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.

Расстояние — это длина от одного пункта до другого.

• Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.

Расстояние обозначается латинской буквой s.

Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).

Формула пути

Чтобы найти расстояние, нужно умножить скорость на время движения:

s = v × t

Скорость

Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.

Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.

Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.

Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.

Формула скорости

Чтобы найти скорость, нужно разделить путь на время:

v = s : t

Показатели скорости чаще всего выражаются в м/сек или км/час.

Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.

Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.

Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.

Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.

Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.

Время

Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.

Время — это продолжительность каких-то действий, событий.

• Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.

Время движения обозначается латинской буквой t.

Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.

Формула времени

Чтобы найти время, нужно разделить расстояние на скорость:

t = s : v

Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.

Взаимосвязь скорости, времени, расстояния

Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.

Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?

Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров в минуту на 15 минут, мы определим расстояние от дома до магазина:

s = v × t = 50 × 15 = 750 (м)

Ответ: мы прошли 750 метров.

Если известно время и расстояние, то можно найти скорость: v = s : t.

Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?

Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.

Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:

Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).

В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).

100 м : 25 с = 4 м/с

Так мы узнали, что скорость движения первого школьника 4 метра в секунду.

Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:

Значит, скорость движения второго школьника составляет 2 метра в секунду.

Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.

Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.

Ответ: первый школьник добежал быстрее.

Если известны скорость и расстояние, то можно найти время: t = s : v.

Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?

Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?

Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:

t = s : v = 500 : 100 = 5 (мин)

Ответ: от школы до стадиона мы дойдем за 5 минут.

Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.

Формулы равномерного и равноускоренного движения

Равномерное движение

Формула скорости движения при равномерном движении: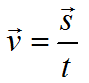

v=const
a=0
v — скорость, м/с
s — перемещение, м
t — время, с
Формула перемещения при равномерном движении: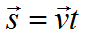

Координата вычисляются через кинематическое уравнение равномерного прямолинейного движения по формуле: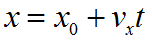

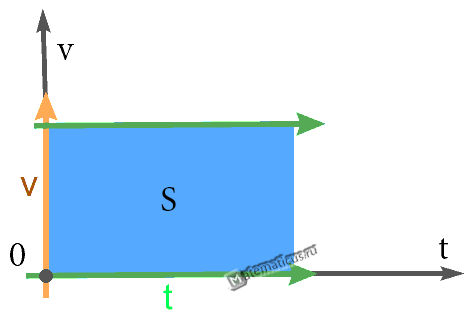
График — Равномерного прямолинейного движения

Равноускоренное движение

Формула скорости при равноускоренном движении: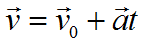

a=const
v₀ — начальная скорость, м/с
a — ускорение, м/с 2
Формула для нахождения перемещения при равноускоренном движении: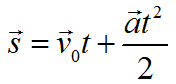

или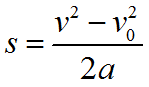

Уравнение равноускоренного движения в проекции на оси координат: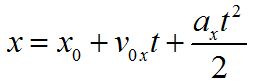

Формула для определения ускорения при равноускоренном прямолинейном движении: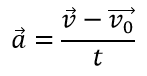

v₀ — начальная скорость, м/с
v — мгновенная скорость, м/с
Формула для определения средней скорости движения: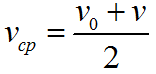

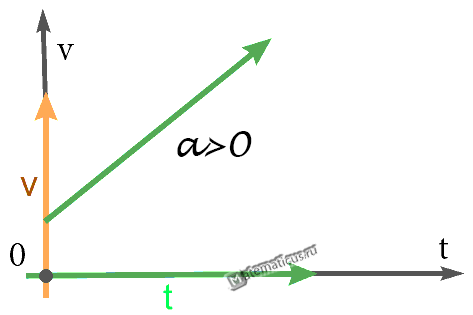
График — Равноускоренное движение при a>0

Равнозамедленное движение

Формула скорости при равнозамедленном движении: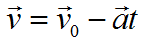

Формула перемещения при равнозамедленном движении: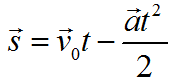

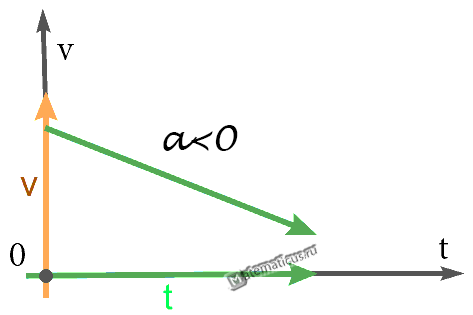
График — Равнозамедленное движение при a 2
Формула для вычисления скорости при свободном падении тела: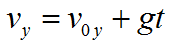

Формула для вычисления перемещения при свободном падении тела: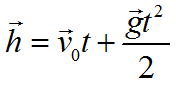


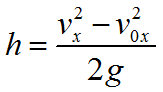
Формула координаты при свободном падении тела: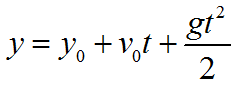

Формула высоты с которой тело свободно падает: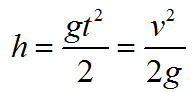

Формула для определения скорости тела в конце свободного падения: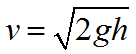

Время свободного падения тела равно: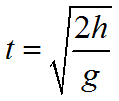

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.7 / 5. Количество оценок: 45

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/vremya-skorost-rasstoyanie

[/spoiler]

Общая характеристика

Скорость, время и расстояние являются физическими показателями, взаимосвязанными между собой процессом движения. На практике и теории известно равномерное и равноускоренное движение тел. Первый случай описывает постоянство времени, а второй — его изменение.

Основные понятия

Однозначное и конкретное определение тяжело сформулировать, но существуют разные концепции современной философской мысли в математике и физике. Течение времени является естественным процессом. Оно уходит, меняется все вокруг, совершаются разные события в мире, поэтому для физической меры характерен контекст событий.

Чтобы измерить время, нужно знать общие повторяющиеся события с одинаковым периодом. Это может быть смена дня, ночи или времени года. Чтобы определить единицу измерения времени (метр, час, секунда), ученые обращались к древнейшим источникам познаний.

Год состоит из двенадцати месяцев или четырех сезонов. Такое количество раз в весенний, летний, зимний и осенний периоды главный спутник Земли меняет свои фазы.

По мере развития прогресса измерение t модифицировалось, появлялись новые солнечные, водные, песчаные, огненные, механические, электронные и молекулярные измерители времени — часы.

Время включено в семь основных физических величин международной системы единиц СИ. Этот показатель используют для остальных составляющих. Четкое понимание t помогает проведению экспериментов и в обычной жизни.

Основной целью навигации и астрономии было измерение t. С 1000 по 1960 год секундное измерение воспринималось как 1/86400 дней. С 1970 г. это понятие видоизменилось, поскольку стала учитываться периодичность земной орбиты.

Самые точные мерила —швейцарские часы FOCS, измеряющие t с погрешностью хода в одну секунду за 30 млн лет.

Физическая величина отражает свойство материальных процессов, имеет определенную продолжительность, следует друг за другом. Взаимосвязан этот показатель с материей, движением, так как является формой его существования.

Длительность физического процесса, происходящего в определенной точке, устанавливают с помощью часов, расположенных в ней. Здесь используется прямое сравнение, уравнивается длительность процессов. Измерение продолжительности сводится к фиксированию начала и окончанию процесса на шкале. Когда говорят о фиксации показаний часов во время начала и завершения процесса, это не относится к фактическому месту их нахождения.

Теория относительности Эйнштейна меняет понимание времени, утверждая, что прогресс его не универсален и зависит от того, кто его изменяет. В такой картине реальности часы тикают с разной скоростью в зависимости от того, кто их носит.

Принимая большое ускорение или располагаясь рядом с сильными силами гравитации (вблизи черной дыры), можно изменить скорость течения времени, остановить его или возвратить. Для человека, находящегося внутри черной дыры, пространство и время кажутся взаимозаменяемыми, поэтому спуск в нее неизбежен, как и течение t вне этой области. Относительность уравнивает время и пространство.

Древняя система исчисления

До существования нашей эры люди привязывали отсчет времени к движению небесных тел или событий, связанных с ними. Древние народы искали основу для построения своей системы исчисления. В Вавилоне это было число 60, благодаря ему окружность содержит 360°, градус равен 60 минутам, а каждая из них состоит из 60 секунд.

Год представлялся окружностью в 360 градусов. Когда-то минимальной мерой исчисления был час. Жители Древнего Вавилона оказались сильны в математике, поэтому производили важные расчеты и решали задачи. Вводилась наименьшая единица времени. 60 минут составляют час, а в минуте столько же секунд.

Объяснение того, что сутки составляют 24 часа, а день делится пополам и равен 12 часам, выявили египтяне. Самой большой единицей измерения является индуистское и буддистское понятие Кальпа. Величина равна 4,32 млрд лет, что совпадает с возрастом планеты. Если перевести век Брахмы в обычные годы, получится 311 трлн и 40 млрд лет.

Первыми старинными часами являются солнечные мерила. Действие их основывается на изменении длины теней предметов по мере движения Солнца по небу. Такие часы внешне представляли собой длинный шест, воткнутый в землю. Затем возникли водяные, песчаные и огненные часы. Работа таких механизмов не привязывалась к движению Солнца, Луны либо звезд.

Первые механические мерила начали производиться мастерами Китая в 725 г. Жители Европы в Средние века устанавливали на башнях соборов часы, которые имели только одну часовую стрелку. Карманные измерители возникли в середине XVII века, а наручные намного позже.

В соответствии с международной системой измерения определение одной секунды привязано к периоду электромагнитного излучения, начинающемуся при переходе между тонкими уровнями основного состояния атома цезия-133. Одна секунда составляет 919 263 770 периодов.

Показатели физики

Не существует определенной концепции или класса времени. Показатель непрерывности процессов можно вычислить по формуле, проанализировать на графике или диаграмме.

Определения и концепции расчета

Термодинамика гласит, что время не вернуть. Его ход зависит от движения системы отсчета и может быть мгновенным.

Существует понятие «релятивистское замедление времени»: если часы находятся в неподвижной системе, то в движущемся теле все процессы замедлены. Этап старения для двух братьев-близнецов может пройти по-разному, если одного отправить в космос, а другого оставить на Земле. Человек в космосе не постареет, поскольку там изменяется масса его тела, а также замедляется гравитационное время. В условиях притяжения меняется ход часов. Чем сильнее поле гравитации, тем больше замедление. Между объектами, имеющими массу, создается взаимодействие.

Периодическая цепь событий рассчитывается неодинаково в зависимости от показателей. Зависимые величины:

• время;
• скорость;
• расстояние.

Секунда — стандартная единица, характеризующая время. Его определение в физике представляется как продолжительный показатель. Время через расстояние и скорость вычисляется по формуле t=S/V. Стандартная расшифровка:

• S — расстояние;
• V — конечная скорость (километровое значение);
• t — время.

Когда скорость измеряется в км/ч, то и время выражается в часах. В любой системе события развиваются одновременно.

Формула времени при равноускоренном движении выглядит как t = (V — V0)/a или t = S/(V — V0), где V0 — начальная скорость, a — ускорение. Таблица показателей:

Вид движения	Скорость (V)	Перемещение (S)	Время (t)
Равномерное	V = знак постоянства (const)	S = Vt	t = S/V
Равноускоренное	V = V0+at	S = V0t+at2/2	t = V-V0/a

Атом изотопа цезия за секунду совершает 9192631770 собственных квантовых переходов. В зависимости от его расположения секунда имеет разные значения.

Решение задач

Понять действие формул времени при равномерном движении или равноускоренном можно, решив задачу. Многие сайты предлагают онлайн-калькулятор для удобного подсчета. В соответствующие графы достаточно ввести основные данные, после чего программа рассчитает все самостоятельно.

Задача 1. Автомобиль ехал со скоростью 200 км/ч и проехал всего 80 км. Требуется определить время движения машины. Условные обозначения:

• V — скорость;
• S — расстояние;
• t — время.

Показатели нужно перевести из километров в метры, из часов в секунды: 1 км = 1 тыс. м, 1 час = 3600 секунд. Получаем S = 80000 м, V= 200000/3600 = 55,55 м/с. Находим скорость по формуле: V= S/t = 80000/55,55 = 1440,14 сек.

t = 1440

14/3600 = 0,4 часа.

Ответ: автомобиль пройдет 0,4 ч.

При неравномерном движении путь, пройденный телом, равен произведению средней скорости на время, в течение которого тело перемещалось.

Задача 2. Движение точки задано уравнением: х = 2t — 0,03t2. Нужно определить, в какой период скорость точки сближения сравняется с нулевой отметкой. Коэффициенты равны 2м/с, 0,03 м/с2.

Условия задачи содержат функцию x (t). Скорость можно вычислить по формуле V = dx/dt = 2 — 0,06t Приравниваем скорость к 0, находим t:

2 — 0,06t = 0

t = 2/0,06 = 33,33 сек.

Необходимо определить зависимость модуля ускорения от времени: A (t)= dv/dt = -0,06.

Задача 3. Самолет для взлета набирает 350 км/ч. Нужно определить время разгона, если скорость достигается в конце взлетной полосы длиной в 2 км. Движение считается равноускоренным.

При равноускоренном движении формула выглядит как S = V0t+at2/2. При этом V= V0+at. Разгон самолета начинается с состояния покоя, то есть V0 = 0.

S = at2/2

V=at.

S = (V/t)*(t2/2) = Vt/2.

S = 2000 м

V=350 км/ч = 97,2 м/с.

t= 2S/V = 2*2000/97,2 = 41,15.

Благодаря вычислению известно, что разгон самолета длится 41,15 сек.

Задача 4. Скорость конькобежца составляет 15 м/с. Нужно вычислить время, за которое он пробежит путь 3 км.

V= 15 м/с.

S = 3 км (3000 м).

t = S/V = 3000/15 = 200

Ответ: за 200 секунд конькобежец пробежит 3 км.

Современная наука распределяет известные представления о времени в разные концепции — относительную и вещественную. По мнению относительной, в природе не существует временных рамок, а понятие времени является отношением между событиями. Время — проявление свойств физических тел и изменений, оно статично, как и пространство.