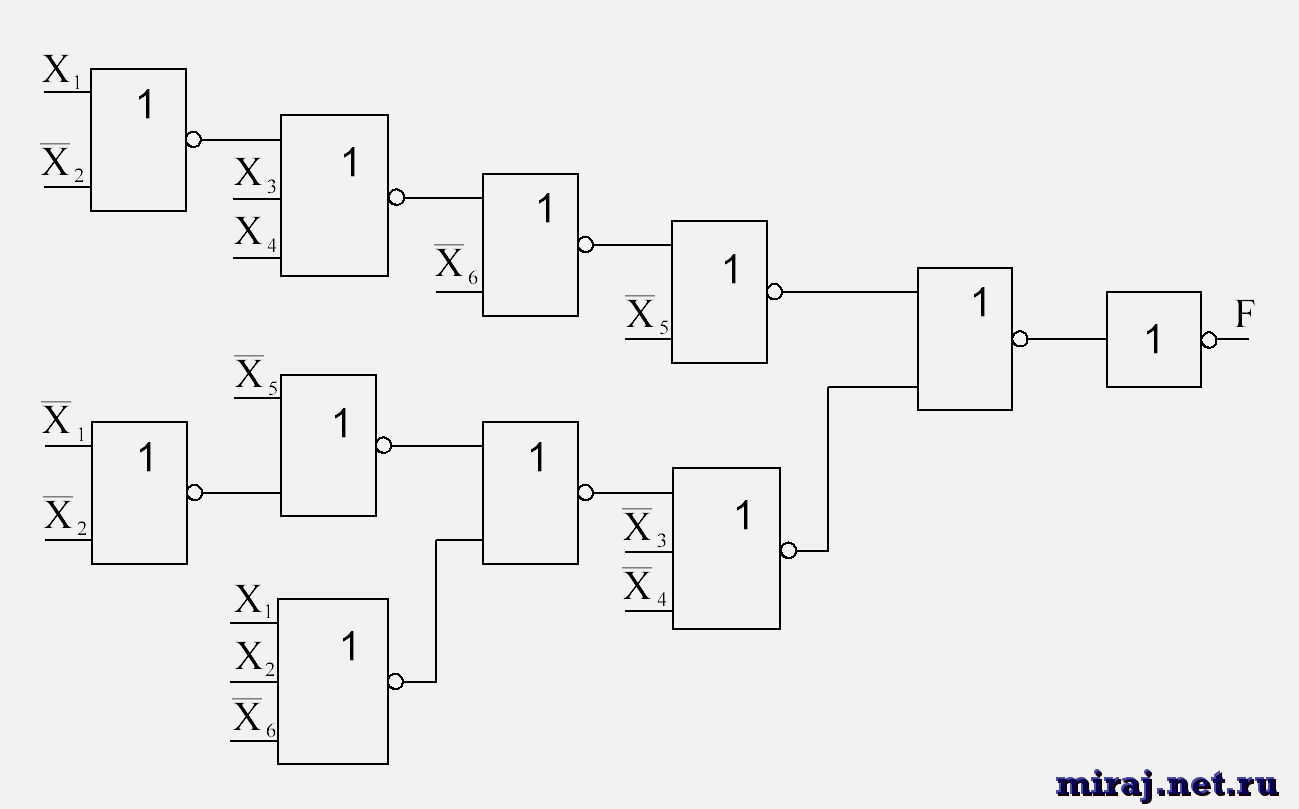Как найти все базисы системы функций

Как найти все базисы системы функций

Определение. Полная система функций называется Базисом пространства булевых функций, если любое собственное подмножество данной системы функций уже не является полным.

Другими словами, базис – это минимальная (но не по количеству, а в смысле отношения включения) полная система булевых функций.

Примеры. Система функций — полная, но не базис, так как полными являются ее подмножества и (последнее вытекает из равенств и ). Множества и уже являются базисами. Они носят названия конъюнктивного и дизъюнктивного базиса Буля, соответственно. Нетрудно показать, что базисом является также множество — базис Жегалкина.

подпись: x y 0 0 1 1 0 1 0 1 1 0 0 1 1 1 0 0 Рассмотрим две новые функции: (стрелка Пирса) и (штрих Шеффера), которые определяются таблицей значений, приведенной справа. Легко видеть также, что справедливы следующие представления этих функций:

==;

==.

Несложно проверить, что каждая из этих функций не принадлежит ни одному из основных замкнутых классов K0, K1, KS, KM, KL. Таким образом, одноэлементные множества {} и {} также являются базисами (базис Пирса и базис Шеффера).

Теорема. Всякий базис пространства булевых функций содержит не более четырёх функций.

Доказательство. Очевидно, что в базисе не более 5 функций – по одной функции для каждого из пяти основных замкнутых классов (не принадлежащей данному классу). Если какая-то функция в базисе не принадлежит сразу нескольким классам, то в базисе меньше пяти функций. Четырёх функций для базиса достаточно по следующей причине. В базисе обязательно имеется функция F(X1, X2, …, Xn), не сохраняющая константу 0, т. е. такая, что F(0, 0, …, 0) = 1. Существует две возможности: либо F(1, 1, … , 1) = 0, т. е. F(X1, X2,…, Xn) не сохраняет также константу 1; либо F(1, 1, … , 1) = 1 и тогда эта функция не может быть самодвойственной (для неё ). В любом случае этой функции достаточно на 2 класса.

Замечание. Оценку 4 (количества функций в базисе) в общем случае нельзя уменьшить, так как существуют базисы из четырёх функций, например, (см. пункт 3). Рассмотренные выше примеры показывают, что существуют также базисы, состоящие из одной, двух и трёх функций.

Пример. Рассмотрим функций S =. Покажем, что она является полной, и найдем все базисы, которые можно составить из функций данной совокупности. Для этого заполним следующую таблицу (впрочем, полнота S Следует уже из того, что S Содержит конъюнктивный базис Буля: ).

подпись: k0 k1 ks km kl 1. 0 + + + 2. + + 3. xy + + + 4. + 5. + + Чтобы найти все базисы, пронумеруем функции и отождествляя их с номерами запишем условие полноты в виде конъюнктивной формы. Для того, чтобы система функций была полной, необходимо и достаточно, чтобы для каждого из пяти основных замкнутых классов нашлась функция, которая данному классу не принадлежит (теорема Поста). Для класса K0 (см. таблицу) это может быть функция 2, 4 или 5; для класса K1 – 1 или 2 и т. д.. В результате получим:

Преобразуем полученную конъюнктивную форму в дизъюнктивную. В процессе преобразования будем формулу упрощать, пользуясь законами:

, .

Применив первый закон, сразу получим:

.

Далее, раскрывая скобки и упрощая согласно второму закону, окончательно получим:

.

Дальше дизъюнктивная форма не упрощается. Это означает, что имеется четыре базиса: 1) {1, 3, 5}; 2) {2, 3}; 3) {2, 4}; 4) {1, 4} (здесь цифры – номера функций).

Замечание. Метод, состоящий в записи конъюнктивной формы и её преобразовании в дизъюнкцию, который выше применялся для нахождения всех базисов данной совокупности функций, носит название Метода Петрика.

< Предыдущая   Следующая >
Источник

Количество
различных булевых функций зависит от
количества переменных и значности
логики. В двузначной логике это количество
равно

,
где n
– число переменных булевых функций.

В таблице 4 приведены
функции от двух переменных. Перечислим
их:


–
константа «0»;


–
конъюнкция;


–
левая коимпликация;


–
сохраняющая x1;


–
правая коимпликация;


–
функция, сохраняющая
x2;


–
сложение по модулю
2, или функция нечетности, или
неэквивалентности;


–
дизъюнкция;


–
функция Вебба;


–
эквивалентность,
или функция четности, или равнозначности;


–
отрицание, инверсия;


–
правая импликация
(«из x2
следует x1»,
«если x2,
то x1»);


–
отрицание, инверсия;


–
левая импликация;


–
функция Шеффера;


–
константа «1».

Различных
булевых функций от двух переменных –
16, от трех переменных – 256 и т.д., но все
ли они необходимы при составлении
логических выражений. Возникает вопрос,
можно ли использовать ограниченные
совокупности булевых функций для
представления логического высказывания
любой сложности. Из каких функций эти
совокупности должны состоять? Скажем,
что такие совокупности функций называются
системами и базисами булевых функций.

Определение.
Системой булевых функций называется
такая их совокупность, с помощью которой
можно построить любое логическое
выражение, а возможность строить любые
логические выражения называется полнотой
системы.

Базисом
булевых функций называется такая
система булевых функций, из которой
невозможно удалить ни одной функции
без потери этой системой полноты.

Для решения вопроса
о том, какая совокупность функций
является системой или базисом булевых
функций применяется критерий полноты.

1.6.
КРИТЕРИЙ ПОЛНОТЫ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ
ПОСТА-ЯБЛОНСКОГО

Система S булевых
функций fi является
полной тогда и только тогда, когда среди
булевых функций

найдется

  • хотя
    бы одна

    ,
    не сохраняющая 0 (не принадлежащая
    классу К0);

  • хотя
    бы одна

    ,
    не сохраняющая 1 (не принадлежащая
    классу К1);

  • хотя
    бы одна

    нелинейная (не принадлежащая классу
    КЛ);

  • хотя
    бы одна
    несамодвойственная
    (не принадлежащая классу КС);

  • хотя
    бы одна

    немонотонная
    (не принадлежащая классу КМ);

Приведем определения
свойств булевых функций, принадлежащих
пяти вышеперечисленным классам булевых
функций.

К
лассом
К0 булевых функций
называется множество

таких, что
.

В
двузначной логике P2 таких функций
ровно половина, т.е.

,
так же, как и принадлежащих К1.

Классом
К1 булевых функций
называют множество

таких, что
.

Классом
КЛ линейных
булевых функций называют множество
функций

таких, что

,

где

– коэффициенты, определяемые для

,


–
сумма по модулю 2,


–
полином Жегалкина.

Классом
КС самодвойственных
булевых функций, называются такие
,
для которых на противоположных наборах
переменных

и

значения функций также противоположны
.

Число
самодвойственных функций от n-переменных

(n–1, так как противоположных пар
входных наборов в 2 раза меньше, чем

).

Классом КМ
монотонных БФ называется множество
таких

,
у которых значения функции на сравниваемых
наборах

при том, что сравниваемые наборы k
и l
являются склеиваемыми


.

Определим, является
ли полной система, состоящая из функции

.

#

0

0

0

1

0

0

1

0


0

1

0

0

0

1

1

0

1

0

0

0

1

0

1

0

1

1

0

0

1

1

1

0

K0:

K1:

KЛ:

Определим
неопределенные коэффициенты, начиная
с c0
на нулевом наборе.

можно определить
на наборе (100), когда полином сокращается
до

из-за значений x2
 и x3,
равных 0.

Аналогично поступим
при определении

и

.

Проверим соответствие
значений полинома с вычисленными
коэффициентами значениям функции на
всех остальных наборах (или для
доказательства принадлежности к

– нелинейным функциям – до первого
несоответствия).

КС:
самодвойственность определяется по
таблицам истинности, где противоположные
наборы расположены симметрично середине
таблицы:

(000)↔
(111) , (001) ↔ (110) , (101) ↔ (010) и т.д.

Значения
функции также должны быть противоположны
относительно середины:

на наборах (000) и
(111) свойство самодвойственности
выполняется.

на наборах (011) и
(100) свойство самодвойственности не
выполняется

.

КМ:
для определения монотонности воспользуемся
графом функции # (геометрической
интерпретацией булевых функций)



0 111
уровень
3

(
3
единицы)

1






10 0
0 101
0 011
уровень 2

(

2
единицы)

1

00 0
0 010 0
001
уровень 1

(

1
единица)

1 000
уровень 0

(0 единиц в

двоичном

наборе)

Распределение
вершин графа по уровням с одинаковым
количеством единиц позволяет увидеть,
что сравниваемые наборы находятся на
соседних уровнях. Например, (001) и (011)
или (101) и (111) и связаны между собой ребрами
(0_1) и (1_1) соответственно. Не сравнимыми
будут наборы противоположные или с
несмежных уровней ((010) и (101) или (000) и
(011)).

Монотонные
наборы: # (100) ≤ # (101),

# (110) ≤ # (111) и т.д.

Наличие хотя бы
одной пары немонотонных наборов
обозначает немонотонность функции. То
есть

.

Итак,

не принадлежит ни к одному классу булевых
функций, и, следовательно, сама составляет
базис булевых функций { # }.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Булев базис

На чтение 2 мин. Просмотров 1.9k. Опубликовано 02.04.2021

Система в полном исполнении называется базисом. Минимальные возможности представлены в виде функций. Булев базис – это структура, состоящая из набора элементарных действий. Это функции, которые будут описаны ниже. Полностью информировано пространство, в котором применяются все свойства. Каждая система имеет свою структуру и состав.

Содержание

  1. Система характеристик
  2. Логическая схема
  3. Законы булевых функций

Система характеристик

Базис булевых функций – полная система характеристик и признаков. Без нарушений и изъянов существуют выражения. Не исключается ни единая функция. Распространенный базис представляет собой полную систему. В ней содержатся элементарные функции. Местоимения И, ИЛИ И НЕ – это основные операции. Логические действия предусмотрены законами математики.

Логическая схема

Необходимо построить в булевом базисе логическую схему, которая будет завершающим этапом явления. Она описывает законы. Приводятся примеры базиса множества булевых функций.

булев базис

Существует сочетательный закон. Это ассоциативное понятие, которое применятся в математике. Правила гласят, что итоговый исход будет результатом последовательного выполнения действий. Это одноименные операции логистических данных. Не происходит зависимости от х1(х2х3) = (х1х2)х3; х1 + (х2 + х3) = (х1 + х2) + х3.

Базисы в булевой алгебре применяются часто. Алгебраические операции становятся примером правильных решений. Предусмотрен базис полной системы булевых функций. Это две элементарные функции. Они относятся к основному положению.

Законы булевых функций

Распределительный закон подразумевает под собой дистрибутив. Здесь операции выполняются последовательно с логическим пониманием цепи. Местами меняются значения. Пример х1 (х2 + х3) = х1х2 + х1х3, х1 + х2 х3 = (х1 + х2) (х1 + х3).

Есть другой коммутативный закон, который позволяет перемещать значения. Исходные данные не зависит от изменения мест множителей. Слагаемые будут измены.

х1 х2 = х2 х1; х1 + х2 = х2 + х1.

булев базис

Следующим законом является – двойственность. По понятиям де Моргана. Здесь происходит инверсия дизъюнкции. Так, логические операции при сложении становятся эквивалентны конъюнкции. Это умножение.

Правило диктует свои значения, которые являются примером для учеников. Они используют данные варианты. Согласно законам действует положение, при котором исходная ФАЛ (f(x1, x2) = x1 + x2) будет равна двойственному значению. Базис системы булевых функций представлен переменными.

Источник

Тема: Полнота системы булевых функций. Графы.. Читаем, комментируем, решаем ДЗ.

Системы булевых функций. Базис Жегалкина

Конечное множество булевых функций
$ mathcal{F} = { f_1, f_2, dots f_n }$ называют
системой булевых функций. Систему булевых функций называют полной, если
любая булева функция может быть выражена в виде формулы над этой системой (другими
словами, если она представима через функции данной системы).

Другой распространённой полной системой булевых функций является базис Жегалкина:

$ mathcal{F}_{mbox{Ж}} = { oplus, cdot, 1 }$, включающий исключающее или, коньюнкцию
и константу 1. Можно доказать, что любая булева функция представима в виде так называемого
полинома Жегалкина:

где
$ a_j in {0, 1}$. В частном случае, полином Жегалкина имеет линейный вид:

Булева функция, представимая в виде линейного полинома Жегалкина, называется линейной.

Существует простой способ выражения любой булевой функции над базисом Жегалкина. Этот
способ носит название метода неопределённых коэффициентов. Рассмотрим этот метод на
примере:

Рассмотрим функцию
$ f(x_1, x_2, x_3) = (0 0 1 1 1 0 0 1) $. В общем виде полином
Жегалкина для этой функции имеет вид:

Вычислим все коэффициенты начиная с $ a_0$, последовательно подставляя в полином известные
значения функции $ f$:

Таким образом, функция имеет вид:

Теорема Поста

Существует метод проверки полноты системы, называемый теоремой Поста. Она основывается на
выделении пяти классов Поста булевых функций:

класс функций сохраняющих 0

$ f in T_0 Leftrightarrow f(0, 0, dots 0) = 0$,

класс функций сохраняющих 1

$ f in T_1 Leftrightarrow f(1, 1, dots 1) = 1$,

класс самодвойственных функций

$ f in S Leftrightarrow (forallalpha)(f(overline{alpha}) = overline{f(alpha)})$,

класс монотонных функций

$ f in M Leftrightarrow (forall alpha, beta)(alphaleqslant beta Rightarrow f(alpha) leqslant f(beta))$, где подразумевается
стандартный порядок булевой алгебры (при котором существуют и несравнимые элементы!),

класс линейных функций

$ f = sumlimits_{i in overline{1, n}} a_i x_i oplus a_0$, т.е. функция представима в виде полинома Жегалкина первой степени.

Можно доказать, что все эти классы являются замкнутыми, т.е. любая комбинация
функций из одного класса остаётся в том же классе.

Теорема (Поста): система булевых функций полна тогда и только тогда, когда она
целиком не лежит ни в одном из классов Поста.

Рассмотрим пример:
$ f(x_1, x_2, x_3) = x_1 (overline{x_1} vert x_3) (overline{x_1} oplusoverline{x_3}) rightarrow (x_2 sim x_3), w = (1 1 1 0 0 1 1 0)$. Необходимо проверить полноту
системы $ {f, w}$.

Функция $ f$ принимает следующие значения:
$ f = (1 1 1 1 1 1 0 1)$. Проверка принадлежности
первых четырёх классов поста может быть проведена очень быстро. Для проверки линейности
построим представление данных функций в виде полинома Жегалкина:

Поучается, что
$ f = x_1 x_2 x_3 oplus x_1 x_2 oplus 1$ нелинена.

Поучается, что
$ w = x_1 x_2 x_3 oplus x_1 x_2 oplus x_2 x_3 oplus x_1 x_3 oplus x_1oplus 1$ нелинена.

Принадлежность классам Поста обощим в таблице:

Система функций $ {f, w}$ является полной, более того, полной является уже система $ { w}$.

Выразим стандартный базис
$ { wedge, overline{phantom{x}}}$ через функцию $ w$. Воспользуемся тем,
что $ w$ не сохраняет ни 0, ни 1, значит:

$ w$ — нелинейна, выразим коньюнкцию из полинома Жегалкина этой функции. Можно получить,
что
$ w(x_1, x_2, 0) = x_1 x_2 oplus x_1 oplus 1$. Тогда

откуда
$ x y = overline{w(x, overline{y}, 0)}$.

Схемы из функциональных элементов

Часто для формального задания булевых функций используется схемы из функциональных
элементов (СФЭ) — графы специального вида, основу которых составляют собственно
функциональные элементы, т.е. булевы функции, принимающие на вход переменные и выдающие
результат.

На рисунке 1 изображены функциональные элементы для стандартных булевых
функций. С их помощью, к примеру, функция исключающего или может быть реализована
следующим образом (рисунок 2):

Рис. 1:
Функциональные элементы для стандартных функций

includegraphics[width=5cm]{schema_std.eps}

Рис. 2:
СФЭ для функции исключающего или

includegraphics[width=8cm]{schema_xor.eps}

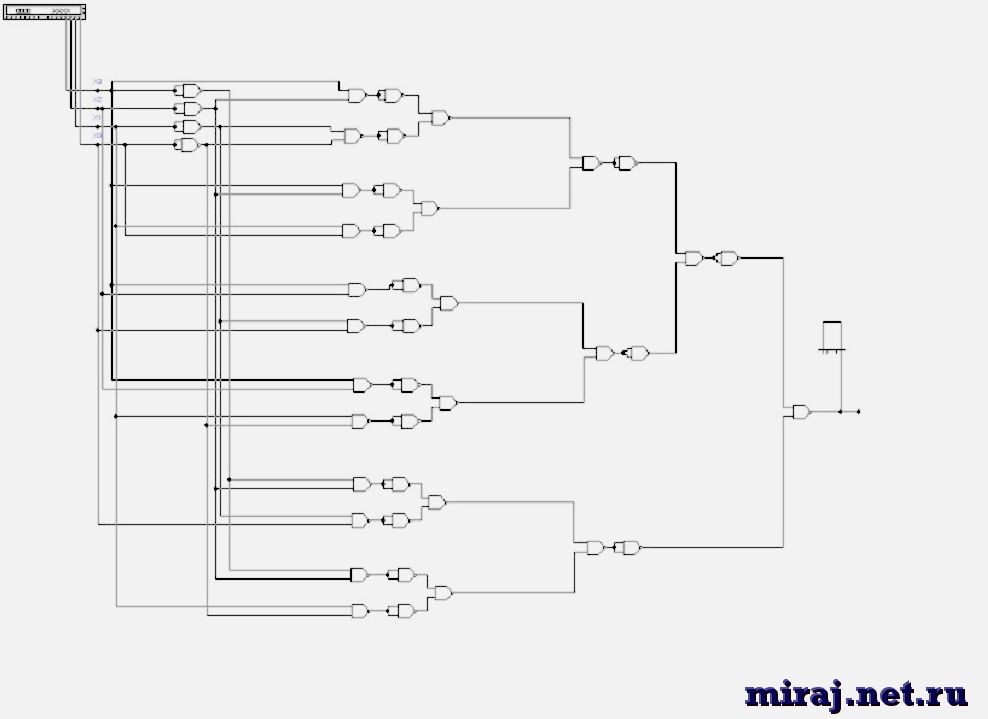
Аналогичным образом могут быть построены схемы для булевых функций любой сложности. В
электронике часто используются схемы, выполняющие сложение битовых переменных. Такие схемы
называются сумматорами. Таблица истинности для булевых функций сложения двух
$ x_1 +x_2 = y_1 y_2$ и трёх
$ x_1 + x_2 + x_3 = y_1 y_2$ однобитовых (булевых) переменных
содержит два столбца результата (результат имеет большее число разрядов, чем аргументы),
т.е. мы имеем две булевых функции для каждой из операций сложения:

СФЭ для сумматора сложения трёх переменных представлен на рисунке
3. Удобство использования этого сумматора таково, что на его основе
можно стоить сумматоры для сложнения сколь угодно больших чисел. Например, на рисунке
4 проказан сумматор для сложения двух трёхразрядных переменных

$ x_1 x_2 x_3 + y_1 y_2 y_3 = z_1 z_2 z_3 z_4$:

Рис. 3:
СФЭ сумматора

includegraphics[width=8cm]{schema_sum3.eps}

Рис. 4:
СФЭ для сумматора трёхразрядных переменных

includegraphics[width=8cm]{schema_sum_many.eps}

Графы

В теории графов выделяют два вида графов: неориентированные и
ориентированные.

Неориентированные графы

Неориентированным графом называют пару $ (V, E)$, где $ V$ — конечное множество
вершин, а $ E$ — множество рёбер такое, что
$ E subseteq { {v, w} vert v, win V And v neq w }$. Важно, что рёбра могут соединять какие-то две
вершины. Вершины можно представить в виде точек на плоскости, а дуги — линиями, их
соединяющими. При этом для нас представляют интерес не координаты точек или длина и форма
линий, а связь между дугами и вершинами.

На рисунке 5 показаны примеры неориентированных графов. Граф (а)
определяется как:

А вот в графе (в) все вершины соедины с каким-либо ребром:

Рис. 5:
Примеры неориентированных графов

includegraphics[width=13cm]{graph_examples.eps}

Можно легко получить число возможных графов для заданного числа вершин $ vert Vvert =n$. Максимальное число рёбер в таком графе — число неупорядоченных пар из $ n$,
т.е.
$ C_n^2 = frac{n (n - 1)}{2}$. Тогда общее число неориентированных графов равно
мощности множества подмножеств всех рёбер, т.е.
$ 2^{frac{n (n - 1)}{2}}$.

Для каждой вершины вводится понятие степени:

т.е. число рёбер, соединённых с вершиной.

Цепью в графе называют произвольную конечную или бесконечную последовательность
вершин, в которой каждая последующая соединена ребром с предыдущей. Для конечной цепи
число рёбер в ней называют длиной. Цепь называется простой, если все её
вершины, кроме, быть может, первой и последней, попарно различны и все её рёбра попарно
различны. Простая цепь ненулевой длины, начало и конец которой совпадают, называется
циклом. Неориентированный граф, не имеющий циклов называют ацикличным. На
рисунке 6 показаны цепь, простая цепь и цикл.

Рис. 6:
Цепь, простая цепь и цикл

includegraphics[width=13cm]{graph_chain.eps}

Подграфом
$ mathcal{G}' = (V', E')$ графа
$ mathcal{G} = (V, E)$ называют такой граф, что:

$ V' subseteq V And E' subseteq E$. Так как
$ mathcal{G}'$ — граф, в нём не могут быть только
вершины, соединённые с ребрами. Подграф называется остовным, если $ V = V'$.

Неориентированный граф называется связным, если в нём любые две вершины соединены
цепью. Максимальный связный подграф — компонента связности этого графа (или
просто компонента). Компоненты не имеют ни общих вершин, ни общих рёбер.

Для двух вершин можно ввести бинарное отношение достижимости: $ u v$ выполняется,
когда вершины $ u$ и $ v$ можно соединить цепью. Можно доказать, что это отношение является
отношением эквивалентности. Тогда граф может быть факторизован, и элементами
фактор-множества будут являться компоненты данного графа. На рисунке
7 показан пример графа из нескольких компонент связности.

Рис. 7:
Компоненты неориентированного графа

includegraphics[width=7cm]{graph_com.eps}

Особый интерес представляют особые виды графов. Ациклический связный граф называется
деревом. Обычно в дереве одна из вершин выделяется в качестве корня. Более
общим случаем дерева является лес: граф, состоящий из двух и более деревьев
(ациклический граф). Вершины, степень которых равна 1 и не являющиеся корнем, называют
листьями. Граф, состоящий только из корня и листьев, называют кустом. На
рисунке 8 показаны дерево, куст и лес.

Рис. 8:
Дерево, куст и лес

includegraphics[width=10cm]{graph_tree.eps}

Помимо перечисления множеств $ V$ и $ E$, неориентированные графы можно представлять в виде
матрицы смежности: матрица имеет квадратный и симметрический вид, размером
$ ntimes n$, где $ n$ — число вершин. Элементы матрицы равны:

Для графа на рисунке 5, (а) матрица смежности будет иметь
вид:

Другой матрицей, представляющей для нас интерес, является матрица
достижимости, размер которой также
$ ntimes n$. Элементы матрицы равны:

В том же примере матрица достижимости отличается от матрицы смежности:

Оринтированные графы

Ориентированный граф отличается наличием направления на дугах, соединяющих
вершины. Ориентированный граф определяется как пара $ (V, E)$, где $ V$ — множество
вершин, как в неориентированном графе, а
$ E subseteq V times V$ — множество
дуг. Каждая дуга — упорядоченная пара вершин, стрелка на которой направлена от первой
вершины ко второй. Отметим также, что в случае неориентированного графа возможны
петли, т.е. дуги вида $ (v, v)$. На рисунке 9 показан пример
ориентированного графа. Для него множество вершин и дуг равно:

Рис. 9:
Пример ориентированного графа

includegraphics[width=7cm]{ograph_example.eps}

Число ориентированных графов для заданного числа вершин больше, чем
неориентированных. Всего между $ n$ вершинами можно провести $ n^2$ дуг (число упорядоченных
пар). Значит число графов будет равно мощности множества подмножеств всех дуг: $ 2^{n^2}$.

Для ориентированных графов степень вершины состоит из двух частей:

полустепень захода

$ dg^{-}(v) = vert{ v vert (w, v) in E}vert$ — число дуг, входящих в вершину;

полустепень исхода

$ dg^{+}(v) = vert{ v vert (v, w) in E}vert$ — число дуг, исходящих
из вершины.

Например, для вершины “Оля” на рисунке 9 полустепень захода равна
3, а полустепень исхода — 1.

Аналогом цепи в ориентированных графах является путь — при этом движение возможно
только в направлении стрелок. Также определяется и простой путь, а аналог цикла
называется контуром.

В ориентированных графах определяется три вида связности:

связность

Ориентированный граф называется связным (просто связным, связным
односторонне), если
$ (forall v, u in V)(v Rightarrow^* u vee u Rightarrow^* v)$,
т.е. существует путь нулевой или большей длины из $ u$ в $ v$ или из $ v$ в $ u$.

сильная связность

Ориентированный граф называется сильно связным (связным
двусторонне), если
$ (forall v, u in V)(v Rightarrow^* u And u Rightarrow^* v)$,
т.е. существуют пути нулевой или большей длины из $ u$ в $ v$ и из $ v$ в $ u$.

слабая связность

Ориентированный граф называется слабо связным, если
соответствующий ему неориентированный граф (стереть все стрелочки и удалить петли) связен.

На рисунке 10 показаны связный, сильно и слабо связные подграфы
исходных графов.

Рис. 10:
Связность в ориентированных графах

includegraphics[width=12cm]{ograph_conn.eps}

Ориентированное дерево определяется следующим образом:

  1. $ dg^-(v) leqslant 1$ для всех вершин;

  2. $ dg^-(v) = 0$ для единственной вершины, называемой корнем;

  3. в графе нет контуров.

Куст и лес определяются аналогично. Граф более общего вида, не имеющий контуров,
называется сетью.

Ориентированные графы также могут задаваться матрицей смежности. В этом случае элементы
матрицы равны:

Такая матрица уже не является в общем случае симметричной. Для графа на рисунке
9 матрица будет равна:

Аналогично определяется и матрица достижимости. Для нашего примера такая матрица будет
равна:

Источник

Добавить комментарий