Найти целые решения системы неравенств
В алгебре часто требуется не просто решить систему неравенств, но выбрать из полученного множества решений решения, удовлетворяющие некоторым дополнительным условиям.
Найти целые решения системы неравенств — одно из заданий такого рода.
1) Найти целые решения системы неравенств:
Неизвестные переносим в одну сторону, известные — в другую с противоположным знаком:
После упрощения разделим обе части каждого неравенства на
Отмечаем решения неравенств на числовых прямых. Решением системы является пересечение решений (то есть та часть, где штриховка есть на обеих прямых).
Оба неравенства строгие, поэтому -4 и 2 изображаются выколотыми точками и в решение не входят:
Из промежутка (-4;2) выбираем целые решения.
Ответ: -3; -2; -1; 0; 1.
2) Какие целые решения имеет система неравенств?
Переносим неизвестные в одну сторону, известные — в другую с противоположным знаком
Упрощаем и делим обе части на число, стоящее перед иксом. Первое неравенство делим на положительное число, поэтому знак неравенства не меняется, второе — на отрицательное число, поэтому знак неравенства изменяется на противоположный:
Отмечаем решения неравенств на числовых прямых. Первое неравенство нестрогое, поэтому -2 изображаем закрашенной точкой. Второе неравенство нестрогое, соответственно, 5 изображается выколотой точкой:
Целые решения на промежутке [-2;5) — это -2; -1; 0; 1; 2; 3; 4.
Ответ: -2; -1; 0; 1; 2; 3; 4.
В некоторых примерах не требуется перечислять целые решения, нужно лишь указать их количество.
3) Сколько целых решений имеет система неравенств?
Переносим неизвестные в одну сторону, известные — в другую:
Обе части первого неравенства делим на отрицательное число, поэтому знак неравенства изменяется на противоположный. Обе части второго неравенства делим на положительное число, знак неравенства при этом не меняется:
Решение неравенств отмечаем на числовых прямых. Оба неравенства нестрогие, поэтому -3,5 и 1,7 изображаем закрашенными точками:
Решением системы является промежуток [-3,5; 1,7]. Целые числа, которые входят в данный промежуток — это -3; -2; -1; 0; 1. Всего их 5.
Ответ: 5.
4) Сколько целых чисел являются решениями системы неравенств?
Неизвестные — в одну сторону, известные — в другую с противоположным знаком:
При делении обеих частей неравенства на положительное число знак неравенства не изменяется, при делении на отрицательное число — меняется на противоположный:
Решение неравенств отмечаем на числовых прямых.
Множество решений системы состоит из единственного элемента — {2}. 2 — целое число, следовательно, решением данной системы является одно целое число.
Ответ: 1.
При решении неравенств вы должны свободно владеть понятием числового неравенства, знать, что такое решение неравенства, что значит решить неравенство, помнить свойства неравенств. То же относится и к системам числовых неравенств. Все эти сведения вы можете найти в любом пособии для поступающих в вузы.
Напомним свойства числовых неравенств.
1. Если а > b , то b < а; наоборот, если а < b, то b > а.
2. Если а > b и b > c, то а > c. Точно так же, если а < b и b < c, то а < c.
3. Если а > b, то а + c > b+ c (и а – c > b – c). Если же а < b, то а + c < b+ c (и а – c < b – c). Т. е. к обеим частям неравенства можно прибавлять (или из них вычесть) одну и ту же величину.
4. Если а > b и c > d, то а + c > b + d; точно так же, если а < b и c < d, то а + c < b + d, т. е. два неравенства одинакового смысла можно почленно складывать.
Замечание.
Два неравенства одинакового смысла нельзя почленно вычитать друг из друга, так как результат может быть верным, но может быть и неверным. Например, если из неравенства 11 > 9 почленно вычесть неравенство 3 > 2, то получим верное неравенство 8 > 7. Если из неравенства 11 > 9 почленно вычесть неравенство 7 > 2, то полученное неравенство будет неверным.
5. Если а > b и c < d, то а – c > b – d; если а < b и c > d, то а – c < b – d, т.е. из одного неравенства можно почленно вычесть другое неравенство противоположного смысла, оставляя знак того неравенства, из которого вычиталось другое.
6. Если а > b и m – положительное число, то m а > m b и 
Если же а > b и n – отрицательное число, то n а < n b и 
7. Если а > b и c > d , где а, b, c, d > 0, то а c > b d и если а < b и c < d, где а, b, c, d > 0, то аc < bd, т.е. неравенства одного смысла на множестве положительных чисел можно почленно перемножать.
Следствие. Если а > b, где а, b > 0, то а2 > b2, и если а < b, то а2 < b2, т.е. на множестве положительных чисел обе части неравенства можно возводить в квадрат.
8. Если а > b, где а, b > 0, то 

Виды неравенств и способы их решения
1. Линейные неравенства и системы неравенств
Пример 1. Решить неравенство 
Решение:

Ответ: х < – 2.
Пример 2. Решить систему неравенств 
Решение:

Ответ: (– 2; 0].
Пример 3. Найти наименьшее целое решение системы неравенств
Решение:
Ответ:
2. Квадратные неравенства
Пример 4. Решить неравенство х2 > 4.
Решение:
х2 > 4 (х – 2)∙(х + 2) > 0.
Решаем методом интервалов.
Ответ:
3. Неравенства высших степеней
Пример 5. Решить неравенство (х + 3)∙(х2 – 2х + 1) > 0.
Решение:

Ответ: 
Пример 6. Найти середину отрезка, который является решением неравенства 4х2 – 24х + 24 < 4у2, где 
Решение:
Область определения неравенства: 
С учётом области определения 4х2 – 24х + 24 < 4у2 будет равносильно неравенству
Решаем методом интервалов.
Решение неравенства: 
Середина отрезка: 
Ответ: 
4. Рациональные неравенства
Пример 7. Найти все целые решения, удовлетворяющие неравенству 
Решение:

Методом интервалов:
Решение неравенства: 
Целые числа, принадлежащие полученным полуинтервалам: – 6; – 5; – 4; 1.
Ответ: – 6; – 5; – 4; 1.
5. Иррациональные неравенства
Помните! Начинать решение иррациональных неравенств нужно с нахождения области определения.
Пример 8. Решить неравенство 
Решение:
Область определения: 
Так как арифметический корень не может быть отрицательным числом, то 
Ответ: 
Пример 9. Найти все целые решения неравенства 
Решение:
Область определения 



Целыми числами из этого отрезка будут 2; 3; 4.
Ответ: 2; 3; 4.
Пример 10. Решить неравенство 
Решение:
Область определения: 
Преобразуем неравенство: 


Ответ: 
Пример 11. Решить неравенство 
Решение:
Раскрываем знак модуля.
Объединим решения систем 1) и 2): 
Ответ: 
6. Показательные, логарифмические неравенства и системы неравенств
Пример 12. Решите неравенство 
Решение:

Ответ: 
Пример 13. Решите неравенство 
Решение:

Ответ: 
Пример 14. Решите неравенство 
Решение:
Ответ: 
Пример 15. Решите неравенство 
Решение:
Ответ: 
Задания для самостоятельного решения
Базовый уровень
Целые неравенства и системы неравенств
1) Решите неравенство 2х – 5 ≤ 3 + х.
2) Решите неравенство – 5х > 0,25.
3) Решите неравенство 
4) Решите неравенство 2 – 5х ≥ – 3х.
5) Решите неравенство х + 2 < 5x – 2(x – 3).
6) Решите неравенство
.
7) Решите неравенство (х – 3) (х + 2) > 0.
8) Решить систему неравенств 
9) Найдите целочисленные решения системы неравенств 
10) Решить систему неравенств 
11) Решить систему неравенств 
12) Найти наименьшее целое решение неравенства 
13) Решите неравенство 
14) Решите неравенство 
15) Решите неравенство 
16) Решите неравенство 
17) Найдите решение неравенства 

18) Решить систему неравенств 
19) Найти все целые решения системы 
Рациональные неравенства и системы неравенств
20) Решите неравенство 
21) Решите неравенство 
22) Определите число целых решений неравенства 
23) Определите число целых решений неравенства 
24) Решите неравенство 
25) Решите неравенство 2x<16 .
26) Решите неравенство 
27) Решите неравенство 
28) Решите неравенство 
29) Найдите сумму целых решений неравенства 
30) Решите неравенство 
31) Решите неравенство 
Иррациональные неравенства
32) Решите неравенство 
33) Решите неравенство
34) Решите неравенство 
Показательные, логарифмические неравенства и системы неравенств
35) Решите неравенство 
36) Решите неравенство 
37) Решите неравенство 
38) Решите неравенство 
39) Решите неравенство 
40) Решите неравенство 49∙7х < 73х + 3.
41) Найдите все целые решения неравенства 
42) Решите неравенство 
43) Решите неравенство 
44) Решите неравенство 7x+1-7x<42 .
45) Решите неравенство log3(2x2+x-1)>log32 .
46) Решите неравенство log0,5(2x+3)>0 .
47) Решите неравенство 
48) Решите неравенство 
49) Решите неравенство 
50) Решите неравенство logx+112>logx+12 .
51) Решите неравенство logx9<2.
52) Решите неравенство 
Повышенный уровень
53) Решите неравенство |x-3|>2x.
54) Решите неравенство 2│х + 1| > х + 4.
55) Найдите наибольшее целое решение неравенства 
56) Решить систему неравенств 
57) Решить систему неравенств 
58) Решите неравенство 
59) Решите неравенство 25•2x-10x+5x>25 .
60) Решите неравенство 
Ответы
1) х ≤ 8; 2) х < – 0,05; 3) х ≥ 5; 4) х ≤ 1; 5) х > –2; 6) х < 11; 7) 




20) (0; 2); 21) (0; 1,5); 22) 3; 23) 6; 24) (–1; 1,5); 25) х < 4; 26)
; 29) – 10; 30) (0; + ∞); 31)









.
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Указатель — Разделы — Обозначения — Автор — О проекте
Вспомогательная страница к разделу ☞ МОДУЛЯРНАЯ АРИФМЕТИКА. Плохо обработанные заметки, и не уверен, что скоро вернусь к ним…
Найти двузначные натуральные числа, удовлетворяющие уравнению $ 17, x+ 20, y+45, z =4111 $.
Решение. Выражаем $ x_<> $: $$ x=241-y-2,z+frac<14-3,y-11,z> <17> . $$ Полагаем $$ 17, t_1 =14-3,y-11,z quad iff quad 17, t_1 + 3,y+11,z=14 . $$ Выражаем $ y_<> $: $$ y=4-3,z-5,t_1+frac<2-2,z-2,t_1> <3> . $$ Полагаем $$ 3, t_2=2-2,z-2,t_1 quad iff quad 3, t_2+2,z+2,t_1=2 . $$ Выражаем $ z_<> $: $$ z=1-t_1-t_2-frac <2> . $$ Полагаем $$ t_2=2,t_3 . $$ Теперь выражаем неизвестные $ x,y,z_<> $: $$ z=1-t_1-3,t_3, y=1-2, t_1 +11, t_3, x=238+5, t_1- 5, t_3 . $$ При любых значениях параметров $ subset mathbb Z $ последние формулы дадут решение уравнения. Для того, чтобы удовлетворить дополнительным ограничениям на решения, параметры должны подчиняться условиям: $$ 9 t_3>-18 , $$ (здесь мы снова воспользовались целочисленностью параметра). Умножим теперь первое неравенство на $ 2_<> $ и прибавим ко второму: $$-84 ☞ ЗДЕСЬ схеме. Если это уравнение разрешимо в целых числах, то множество его решений записывается в виде соотношений $$ x_1=beta_<11>t_1+dots+beta_<1,n-1>t_ + gamma_1,dots x_n=beta_t_1+dots+beta_t_ + gamma_n, $$ при некоторых фиксированных целочисленных $ <beta_>, <gamma_j>$ и произвольном выборе целочисленных параметров $ t_1,dots,t_ $. Подставляем полученные соотношения в оставшиеся уравнения системы, переписываем их в новую систему — относительно новых неизвестных $ t_1,dots,t_ $. Число уравнений и число неизвестных уменьшились на единицу. Продолжаем процесс.
Пример. Решить систему линейных уравнений в целых числах $$ left< begin x_1& & – x_3 & +4,x_4 &=3, \ 2,x_1 &- x_2 & & & =3, \ 3,x_1 &-2,x_2 & & -x_4 & =1. end right. $$
Решение. Из второго уравнения выражаем $ x_ <2>$: $$x_2=-3+2, x_1=t_1 quad Rightarrow quad x_1=frac<3+t_1>2=1+frac2 . $$ Обозначим $$t_2=frac2 quad Rightarrow quad x_1=1+t_2, quad Rightarrow quad x_2=-1+2,t_2 . $$ Подставляем в третье: $$ x_4=4-t_2 , $$ теперь все получившиеся выражения для $ x_1,x_2,x_4 $ подставляем в первое уравнение: $$ x_3=14-3,t_2 . $$
Ответ. $ x_1 = 1+t_2, x_2 =-1+2,t_2, x_3=14-3,t_2, x_4=4-t_2 $ при $ t_2 in mathbb Z $.
Решим теперь более сложный пример.
Пример. Решить систему линейных уравнений в целых числах $$ left< begin 5,x_1& + 7, x_2 & +8,x_3 &=11, \ 2,x_1 &- 3,x_2 & +6,x_3 & =5. end right. $$
Решение. Имеем из первого уравнения: $$ x_1=frac<11-7,x_2-8,x_3><5>=2-x_2-x_3+frac<1-2,x_2-3,x_3> <5>quad Rightarrow quad t_1=frac<1-2,x_2-3,x_3> <5> . $$ Далее, $$ 2,x_2+3,x_3+5,t_1=1 quad Rightarrow quad x_2=frac<1-3,x_3-5,t_1><2>=-x_3-2,t_1+ frac<1-x_3-t_1> <2>quad Rightarrow quad t_2=frac<1-x_3-t_1> <2> . $$ Получаем выражение для $ x_ <3>$: $$ x_3=1-t_1-2,t_2 , $$ подставляем его в выражение для $ x_ <2>$: $$ x_2=-x_3-2,t_1+t_2=-t_1=3,t_2-1 . $$ Теперь $$ x_1=2-x_2-x_3+t_1=2+3,t_1-t_2 . $$ Все три получившиеся формулы подставляем во второе уравнение системы: $$ 3,t_1-23,t_2=-8 . $$ Решаем это уравнение в той же технике, получаем: $$t_1=23,u_2+5, t_2=3, u_2+1 . $$ И возвращаемся к выражениям для $ x_1,x_2,x_3 $.
Ответ. $ x_1=16+66, u_2, x_2=-3-14, u_2, x_3=-6-29, u_2 $ при $ u_2 in mathbb Z $.
Если бы мы решали предыдущую систему в рациональных или вещественных числах, то получили бы аналогичный вид решения: $$ x_1=x_<10>+66, t, x_2=x_<20>-14, t, x_3=x_<30>-29, t quad npu quad t in mathbb R . $$ Можно проверить, что сомножители при $ t_<> $ — это величины миноров системы уравнений, т.е. $$ left| begin a_ <12>& a_ <13>\ a_ <22>& a_ <23>end right| , quad -left| begin a_ <11>& a_ <13>\ a_ <21>& a_ <23>end right| , quad left| begin a_ <11>& a_ <12>\ a_ <21>& a_ <22>end right| $$ соответственно. См. упражнение ☞ ЗДЕСЬ. Геометрически: направляющий вектор прямой, соответствующей пересечению двух плоскостей, всегда можно выбрать целочисленным. Таким образом, если система имеет целочисленное решение, то вхождения параметра в формулы, описывающие все множество этих решений, можно оценить с помощью методов линейной алгебры (см. теорию ☞ ЗДЕСЬ ). Проблема заключается в поиске хотя бы одного частного целочисленного решения $ x_<10>,x_<20>,x_ <30>$. Вот оно может и не существовать. К примеру, система $$ left< begin 2,x_1& + x_2 & -x_3 &=1, \ x_1 &+ 2,x_2 & + x_3 & =1 end right. $$ не имеет решений в $ mathbb Z_<> $.
Решение системы линейных уравнений в целых числах возможно еще симплекс-методом, но с этим я еще не разбирался. И следующий результат тоже выкладываю в надежде когда-нибудь разобраться…
Теорема [Минковский]. Рассмотрим систему вещественных линейных неравенств относительно неизвестных $ x_<1>,dots,x_n $ $$ left< begin a_<11>x_1 &+a_<12>x_2&+ ldots&+a_<1n>x_n &le b_1,\ a_<21>x_1 &+a_<22>x_2&+ ldots&+a_<2n>x_n &le b_2,\ dots & & & dots & \ a_x_1 &+a_x_2&+ ldots&+a_x_n & le b_n. end right. $$ при $ b_1>0,b_2>0,dots,b_n>0 $. Пусть определитель коэффициентов левых ее частей отличен от нуля: $$ det [a_]_^n ne 0 . $$ Тогда система имеет целочисленное решение если произведение правых ее частей не меньше абсолютной величины этого определителя: $$ prod_^n b_j ge left| det [a_]_^n right| . $$
math4school.ru
Уравнения в целых числах
Немного теории
Уравнения в целых числах – это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами. Решениями такого уравнения являются все целочисленные (иногда натуральные или рациональные) наборы значений неизвестных переменных, удовлетворяющих этому уравнению. Такие уравнения ещё называют диофантовыми, в честь древнегреческого математика Диофанта Александрийского, который исследовал некоторые типы таких уравнений ещё до нашей эры.
Современной постановкой диофантовых задач мы обязаны французскому математику Ферма. Именно он поставил перед европейскими математиками вопрос о решении неопределённых уравнений только в целых числах. Наиболее известное уравнение в целых числах – великая теорема Ферма: уравнение
не имеет ненулевых рациональных решений для всех натуральных n > 2.
Теоретический интерес к уравнениям в целых числах достаточно велик, так как эти уравнения тесно связаны со многими проблемами теории чисел.
В 1970 году ленинградский математик Юрий Владимирович Матиясевич доказал, что общего способа, позволяющего за конечное число шагов решать в целых числах произвольные диофантовы уравнения, не существует и быть не может. Поэтому следует для разных типов уравнений выбирать собственные методы решения.
При решении уравнений в целых и натуральных числах можно условно выделить следующие методы:
способ перебора вариантов;
применение алгоритма Евклида;
представление чисел в виде непрерывных (цепных) дробей;
разложения на множители;
решение уравнений в целых числах как квадратных (или иных) относительно какой-либо переменной;
метод бесконечного спуска.
Задачи с решениями
1. Решить в целых числах уравнение x 2 – xy – 2y 2 = 7.
Запишем уравнение в виде (x – 2y)(x + y) = 7.
Так как х, у – целые числа, то находим решения исходного уравнения, как решения следующих четырёх систем:
1) x – 2y = 7, x + y = 1;
2) x – 2y = 1, x + y = 7;
3) x – 2y = –7, x + y = –1;
4) x – 2y = –1, x + y = –7.
Решив эти системы, получаем решения уравнения: (3; –2), (5; 2), (–3; 2) и (–5; –2).
Ответ: (3; –2), (5; 2), (–3; 2), (–5; –2).
2. Решить в целых числах уравнение:
а) 20х + 12у = 2013;
в) 201х – 1999у = 12.
а) Поскольку при любых целых значениях х и у левая часть уравнения делится на два, а правая является нечётным числом, то уравнение не имеет решений в целых числах.
Ответ: решений нет.
б) Подберём сначала некоторое конкретное решение. В данном случае, это просто, например,
Поскольку числа 5 и 7 взаимно простые, то
Значит, общее решение:
х = 1 + 7k, у = 2 – 5k,
где k – произвольное целое число.
Ответ: (1+7k; 2–5k), где k – целое число.
в) Найти некоторое конкретное решение подбором в данном случае достаточно сложно. Воспользуемся алгоритмом Евклида для чисел 1999 и 201:
НОД(1999, 201) = НОД(201, 190) = НОД(190, 11) = НОД(11, 3) = НОД(3 , 2) = НОД(2, 1) = 1.
Запишем этот процесс в обратном порядке:
1 = 2 – 1 = 2 – (3 – 2) = 2·2 – 3 = 2· (11 – 3·3) – 3 = 2·11 – 7·3 = 2·11 – 7(190 – 11·17) =
= 121·11 – 7·190 = 121(201 – 190) – 7·190 = 121·201 – 128·190 =
= 121·201 – 128(1999 – 9·201) = 1273·201 – 128·1999.
Значит, пара (1273, 128) является решением уравнения 201х – 1999у = 1. Тогда пара чисел
x0 = 1273·12 = 15276, y0 = 128·12 = 1536
является решением уравнения 201х – 1999у = 12.
Общее решение этого уравнения запишется в виде
х = 15276 + 1999k, у = 1536 + 201k, где k – целое число,
или, после переобозначения (используем, что 15276 = 1283 + 7·1999, 1536 = 129 + 7·201),
х = 1283 + 1999n, у = 129 + 201n, где n – целое число.
Ответ: (1283+1999n, 129+201n), где n – целое число.
3. Решить в целых числах уравнение:
а) x 3 + y 3 = 3333333;
б) x 3 + y 3 = 4(x 2 y + xy 2 + 1).
а) Так как x 3 и y 3 при делении на 9 могут давать только остатки 0, 1 и 8 (смотрите таблицу в разделе «Делимость целых чисел и остатки»), то x 3 + y 3 может давать только остатки 0, 1, 2, 7 и 8. Но число 3333333 при делении на 9 даёт остаток 3. Поэтому исходное уравнение не имеет решений в целых числах.
Ответ: целочисленных решений нет.
б) Перепишем исходное уравнение в виде (x + y) 3 = 7(x 2 y + xy 2 ) + 4. Так как кубы целых чисел при делении на 7 дают остатки 0, 1 и 6, но не 4, то уравнение не имеет решений в целых числах.
Ответ: целочисленных решений нет.
а) в простых числах уравнение х 2 – 7х – 144 = у 2 – 25у;
б) в целых числах уравнение x + y = x 2 – xy + y 2 .
а) Решим данное уравнение как квадратное относительно переменной у. Получим
у = х + 9 или у = 16 – х.
Поскольку при нечётном х число х + 9 является чётным, то единственной парой простых чисел, которая удовлетворяет первому равенству, является (2; 11).
Так как х, у – простые, то из равенства у = 16 – х имеем
С помощью перебора вариантов находим остальные решения: (3; 13), (5; 11), (11; 5), (13; 3).
Ответ: (2; 11), (3; 13), (5; 11), (11; 5), (13; 3).
б) Рассмотрим данное уравнение как квадратное уравнение относительно x:
x 2 – (y + 1)x + y 2 – y = 0.
Дискриминант этого уравнения равен –3y 2 + 6y + 1. Он положителен лишь для следующих значений у: 0, 1, 2. Для каждого из этих значений из исходного уравнения получаем квадратное уравнение относительно х, которое легко решается.
Ответ: (0; 0), (0; 1), (1; 0), (1; 2), (2; 1), (2; 2).
5. Существует ли бесконечное число троек целых чисел x, y, z таких, что x 2 + y 2 + z 2 = x 3 + y 3 + z 3 ?
Попробуем подбирать такие тройки, где у = –z. Тогда y 3 и z 3 будут всегда взаимно уничтожаться, и наше уравнение будет иметь вид
Чтобы пара целых чисел (x; y) удовлетворяла этому условию, достаточно, чтобы число x–1 было удвоенным квадратом целого числа. Таких чисел бесконечно много, а именно, это все числа вида 2n 2 +1. Подставляя в x 2 (x–1) = 2y 2 такое число, после несложных преобразований получаем:
y = xn = n(2n 2 +1) = 2n 3 +n.
Все тройки, полученные таким образом, имеют вид (2n 2 +1; 2n 3 +n; –2n 3 – n).
6. Найдите такие целые числа x, y, z, u, что x 2 + y 2 + z 2 + u 2 = 2xyzu.
Число x 2 + y 2 + z 2 + u 2 чётно, поэтому среди чисел x, y, z, u чётное число нечётных чисел.
Если все четыре числа x, y, z, u нечётны, то x 2 + y 2 + z 2 + u 2 делится на 4, но при этом 2xyzu не делится на 4 – несоответствие.
Если ровно два из чисел x, y, z, u нечётны, то x 2 + y 2 + z 2 + u 2 не делится на 4, а 2xyzu делится на 4 – опять несоответствие.
Поэтому все числа x, y, z, u чётны. Тогда можно записать, что
и исходное уравнение примет вид
Теперь заметим, что (2k + 1) 2 = 4k(k + 1) + 1 при делении на 8 даёт остаток 1. Поэтому если все числа x1, y1, z1, u1 нечётны, то x1 2 + y1 2 + z1 2 + u1 2 не делится на 8. А если ровно два из этих чисел нечётно, то x1 2 + y1 2 + z1 2 + u1 2 не делится даже на 4. Значит,
и мы получаем уравнение
Снова повторив те же самые рассуждения, получим, что x, y, z, u делятся на 2 n при всех натуральных n, что возможно лишь при x = y = z = u = 0.
7. Докажите, что уравнение
(х – у) 3 + (y – z) 3 + (z – x) 3 = 30
не имеет решений в целых числах.
Воспользуемся следующим тождеством:
(х – у) 3 + (y – z) 3 + (z – x) 3 = 3(х – у)(y – z)(z – x).
Тогда исходное уравнение можно записать в виде
(х – у)(y – z)(z – x) = 10.
Обозначим a = x – y, b = y – z, c = z – x и запишем полученное равенство в виде
Кроме того очевидно, a + b + c = 0. Легко убедиться, что с точностью до перестановки из равенства abc = 10 следует, что числа |a|, |b|, |c| равны либо 1, 2, 5, либо 1, 1, 10. Но во всех этих случаях при любом выборе знаков a, b, c сумма a + b + c отлична от нуля. Таким образом, исходное уравнение не имеет решений в целых числах.
8. Решить в целых числах уравнение 1! + 2! + . . . + х! = у 2 .
если х = 1, то у 2 = 1,
если х = 3, то у 2 = 9.
Этим случаям соответствуют следующие пары чисел:
Заметим, что при х = 2 имеем 1! + 2! = 3, при х = 4 имеем 1! + 2! + 3! + 4! = 33 и ни 3, ни 33 не являются квадратами целых чисел. Если же х > 5, то, так как
5! + 6! + . . . + х! = 10n,
можем записать, что
1! + 2! + 3! + 4! + 5! + . . . + х! = 33 + 10n.
Так как 33 + 10n – число, оканчивающееся цифрой 3, то оно не является квадратом целого числа.
Ответ: (1; 1), (1; –1), (3; 3), (3; –3).
9. Решите следующую систему уравнений в натуральных числах:
a 3 – b 3 – c 3 = 3abc, a 2 = 2(b + c).
3abc > 0, то a 3 > b 3 + c 3 ;
таким образом имеем
b 2 2 + х = у 4 + у 3 + у 2 + у.
Разложив на множители обе части данного уравнения, получим:
х(х + 1) = у(у + 1)(у 2 + 1),
х(х + 1) = (у 2 + у)(у 2 + 1)
Такое равенство возможно, если левая и правая части равны нулю, или представляют собой произведение двух последовательных целых чисел. Поэтому, приравнивая к нулю те или иные множители, получим 4 пары искомых значений переменных:
Произведение (у 2 + у)(у 2 + 1) можно рассматривать как произведение двух последовательных целых чисел, отличных от нуля, только при у = 2. Поэтому х(х + 1) = 30, откуда х5 = 5, х6 = –6. Значит, существуют ещё две пары целых чисел, удовлетворяющих исходному уравнению:
Ответ: (0; 0), (0; –1), (–1; 0), (–1; –1), (5; 2), (–6; 2.)
Задачи без решений
1. Решить в целых числах уравнение:
б) х 2 + у 2 = х + у + 2.
2. Решить в целых числах уравнение:
а) х 3 + 21у 2 + 5 = 0;
б) 15х 2 – 7у 2 = 9.
3. Решить в натуральных числах уравнение:
4. Доказать, что уравнение х 3 + 3у 3 + 9z 3 = 9xyz в рациональных числах имеет единственное решение
5. Доказать, что уравнение х 2 + 5 = у 3 в целых числах не имеет решений.
Найти целые решения системы неравенств
В алгебре часто требуется не просто решить систему неравенств, но выбрать из полученного множества решений решения, удовлетворяющие некоторым дополнительным условиям.
Найти целые решения системы неравенств — одно из заданий такого рода.
1) Найти целые решения системы неравенств:
7x – 5\ 5 – x
Неизвестные переносим в одну сторону, известные — в другую с противоположным знаком:
– 5 – 3\ – x + 6x
После упрощения разделим обе части каждого неравенства на b» href=»http://www.algebraclass.ru/axb/» target=»_blank»>число, стоящее перед иксом. При делении на положительное число знак неравенства не меняется:
– 8___left| <:2 >0> right.\ 5x 0> right. end right.]” title=”Rendered by QuickLaTeX.com”/>
– 4\ x
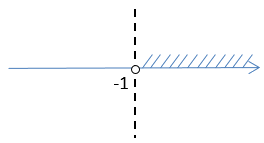
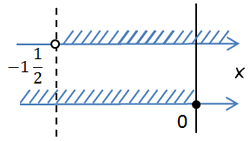
Отмечаем решения неравенств на числовых прямых. Решением системы является пересечение решений (то есть та часть, где штриховка есть на обеих прямых).
Оба неравенства строгие, поэтому -4 и 2 изображаются выколотыми точками и в решение не входят:
Из промежутка (-4;2) выбираем целые решения.
Ответ: -3; -2; -1; 0; 1.
2) Какие целые решения имеет система неравенств?
17 – 4x end right.]” title=”Rendered by QuickLaTeX.com”/>
Переносим неизвестные в одну сторону, известные — в другую с противоположным знаком
17 – 37 end right.]” title=”Rendered by QuickLaTeX.com”/>
Упрощаем и делим обе части на число, стоящее перед иксом. Первое неравенство делим на положительное число, поэтому знак неравенства не меняется, второе — на отрицательное число, поэтому знак неравенства изменяется на противоположный:
0> right.\ – 4x > – 20___left| <:( – 4)
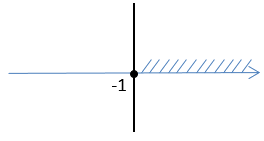
Отмечаем решения неравенств на числовых прямых. Первое неравенство нестрогое, поэтому -2 изображаем закрашенной точкой. Второе неравенство нестрогое, соответственно, 5 изображается выколотой точкой:
Целые решения на промежутке [-2;5) — это -2; -1; 0; 1; 2; 3; 4.
Ответ: -2; -1; 0; 1; 2; 3; 4.
В некоторых примерах не требуется перечислять целые решения, нужно лишь указать их количество.
3) Сколько целых решений имеет система неравенств?
Переносим неизвестные в одну сторону, известные — в другую:
0> right. end right.]” title=”Rendered by QuickLaTeX.com”/>
Обе части первого неравенства делим на отрицательное число, поэтому знак неравенства изменяется на противоположный. Обе части второго неравенства делим на положительное число, знак неравенства при этом не меняется:
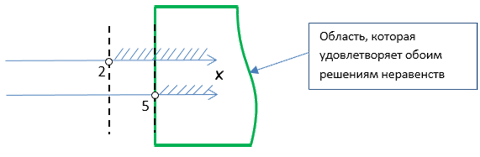
Решение неравенств отмечаем на числовых прямых. Оба неравенства нестрогие, поэтому -3,5 и 1,7 изображаем закрашенными точками:
Решением системы является промежуток [-3,5; 1,7]. Целые числа, которые входят в данный промежуток — это -3; -2; -1; 0; 1. Всего их 5.
4) Сколько целых чисел являются решениями системы неравенств?
Неизвестные — в одну сторону, известные — в другую с противоположным знаком:
0> right. end right.]” title=”Rendered by QuickLaTeX.com”/>
При делении обеих частей неравенства на положительное число знак неравенства не изменяется, при делении на отрицательное число — меняется на противоположный:
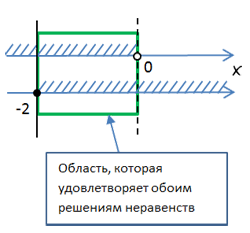
Решение неравенств отмечаем на числовых прямых.
Множество решений системы состоит из единственного элемента — <2>. 2 — целое число, следовательно, решением данной системы является одно целое число.
[spoiler title=”источники:”]
http://math4school.ru/uravnenija_v_celih_chislah.html
[/spoiler]
Сколько целых решений имеет неравенство -18
Для того, чтобы определить сколько целых решений имеет неравенство — 18 < х < 174 выполним следующие действия.
Алгоритм решения задачи
- вспомним определение целого числа;
- выясним входят ли концы отрезка в решение неравенства;
- найдем число отрицательных решений неравенства;
- найдем число положительных решений неравенства;
- найдем количество целых решений неравенства.
Определение целого числа
Давайте вспомним определение целого числа в математике.
Натуральные числа, противоположные им числа и 0 называются целыми числами.
Теперь выясним входят ли концы отрезка в решение неравенства.
Знаки в заданном неравенстве — 18 < х < 174 строгие и при изображении этих точек на координатной прямой они будут выколотыми и не будут являться решением неравенства.
Найдем количество целых решений неравенства — 18 < х < 174
Чтобы посчитать число целых решений неравенства можно поступить двумя способами:
1) выписать все целые числа удовлетворяющие неравенству и сосчитать их;
2) методом логических рассуждений вычислить число отрицательных решений, число положительных решений и не забыть про ноль.
Давайте решим наше задание вторым способом.
Рассмотрим отрезок (- 18; 0). На нем целых чисел, удовлетворяющих нашему неравенству будет 17 (так как -18 не входит и число 0 мы посчитаем отдельно).
0 будем считать за 1 решение неравенства.
Рассмотрим отрезок (0; 174). На нем целых чисел, удовлетворяющих неравенству 173.
Сложим число всех найденных решений на каждом из рассмотренных отрезков и получим:
Что значит найти целые решения системы неравенств. Найти целые цешения системы неравенств. Соблюдение вашей конфиденциальности на уровне компании
В алгебре часто требуется не просто решить систему неравенств, но выбрать из полученного множества решений решения, удовлетворяющие некоторым дополнительным условиям.
Найти целые решения системы неравенств — одно из заданий такого рода.
1) Найти целые решения системы неравенств:
Неизвестные переносим в одну сторону, известные — в другую с противоположным знаком:
Title=»Rendered by QuickLaTeX.com»>
После упрощения разделим обе части каждого неравенства на . При делении на положительное число знак неравенства не меняется:
Title=»Rendered by QuickLaTeX.com»>
Title=»Rendered by QuickLaTeX.com»>
Отмечаем решения неравенств на числовых прямых. является пересечение решений (то есть та часть, где штриховка есть на обеих прямых).
Оба неравенства строгие, поэтому -4 и 2 изображаются выколотыми точками и в решение не входят:
Из промежутка (-4;2) выбираем целые решения.
Ответ: -3; -2; -1; 0; 1.
2) Какие целые решения имеет система неравенств?
Title=»Rendered by QuickLaTeX.com»>
Переносим неизвестные в одну сторону, известные — в другую с противоположным знаком
Title=»Rendered by QuickLaTeX.com»>
Упрощаем и делим обе части на число, стоящее перед иксом. Первое неравенство делим на положительное число, поэтому знак неравенства не меняется, второе — на отрицательное число, поэтому знак неравенства изменяется на противоположный:
Title=»Rendered by QuickLaTeX.com»>
Отмечаем решения неравенств на числовых прямых. Первое неравенство нестрогое, поэтому -2 изображаем закрашенной точкой. Второе неравенство нестрогое, соответственно, 5 изображается выколотой точкой:
Целые решения на промежутке [-2;5) — это -2; -1; 0; 1; 2; 3; 4.
Ответ: -2; -1; 0; 1; 2; 3; 4.
В некоторых примерах не требуется перечислять целые решения, нужно лишь указать их количество.
3) Сколько целых решений имеет система неравенств?
Переносим неизвестные в одну сторону, известные — в другую:
Title=»Rendered by QuickLaTeX.com»>
Обе части первого неравенства делим на отрицательное число, поэтому знак неравенства изменяется на противоположный. Обе части второго неравенства делим на положительное число, знак неравенства при этом не меняется:
Решение неравенств отмечаем на числовых прямых. Оба неравенства нестрогие, поэтому -3,5 и 1,7 изображаем закрашенными точками:
Решением системы является промежуток [-3,5; 1,7]. Целые числа, которые входят в данный промежуток — это -3; -2; -1; 0; 1. Всего их 5.
4) Сколько целых чисел являются решениями системы неравенств?
Неравенство это выражение с, ≤, или ≥. Например, 3x — 5 Решить неравенство означает найти все значения переменных, при которых это неравенство верно. Каждое из этих чисел является решением неравенства, а множество всех таких решений является его множеством решений . Неравенства, которые имеют то же множество решений, называются эквивалентными неравенствами .
Линейные неравенства
Принципы решения неравенств
Для любых вещественных чисел a, b, и c :
Принцип прибавления неравенств : Если a Принцип умножения для неравенств : Если a 0 верно, тогда ac Если a bc также верно.
Подобные утверждения также применяются для a ≤ b.
Когда обе стороны неравенства умножаются на отрицательное число, необходимо полностью изменить знак неравенства.
Неравенства первого уровня, как в примере 1 (ниже), называются линейными неравенствами .
Пример 1 Решите каждое из следующих неравенств. Затем изобразите множество решений.
a) 3x — 5 b) 13 — 7x ≥ 10x — 4
Решение
Любое число, меньше чем 11/5, является решением.
Множество решений есть Чтобы сделать проверку, мы можем нарисовать график y 1 = 3x — 5 и y 2 = 6 — 2x. Тогда отсюда видно, что для x
Множеством решений есть , или (-∞, 1]. График множества решений изображён ниже.
Двойные неравенства
Когда два неравенства соединены словом и , или , тогда формируется двойное неравенство . Двойное неравенство, как
-3 и 2x + 5 ≤ 7
называется соединённым , потому что в нём использовано и . Запись -3 Двойные неравенства могут быть решены с использованием принципов прибавления и умножения неравенств.
Пример 2 Решите -3 Решение У нас есть
Множество решений или x > 3>. Мы можем также написать решение с использованием обозначения интервала и символ для объединения или включения обоих множеств: (-∞ -1] (3, ∞). График множества решений изображен ниже.
Для проверки, нарисуем y 1 = 2x — 5, y 2 = -7, и y 3 = 1. Заметьте, что для или x > 3>, y 1 ≤ y 2 или y 1 > y 3 .
Неравенства с абсолютным значением (модулем)
Неравенства иногда содержат модули. Следующие свойства используются для их решения.
Для а > 0 и алгебраического выражения x:
|x| |x| > a эквивалентно x или x > a.
Подобные утверждения и для |x| ≤ a и |x| ≥ a.
Например,
|x| |y| ≥ 1 эквивалентно y ≤ -1 или y ≥ 1;
и |2x + 3| ≤ 4 эквивалентно -4 ≤ 2x + 3 ≤ 4.
Пример 4 Решите каждое из следующих неравенств. Постройте график множества решений.
a) |3x + 2| b) |5 — 2x| ≥ 1
Решение
a) |3x + 2|
Множеством решением есть
b) |5 — 2x| ≥ 1
Множеством решением есть или x ≥ 3>, или (-∞, 2] .
Весь выше прописанный алгоритм записывается так:
3 · x + 12 ≤ 0 ; 3 · x ≤ − 12 ; x ≤ − 4 .
Ответ: x ≤ − 4 или (− ∞ , − 4 ] .
Указать все имеющиеся решения неравенства − 2 , 7 · z > 0 .
Решение
Из условия видим, что коэффициент a при z равняется — 2 , 7 , а b в явном виде отсутствует или равняется нулю. Первый шаг алгоритма можно не использовать, а сразу переходить ко второму.
Производим деление обеих частей уравнения на число — 2 , 7 . Так как число отрицательное, необходимо поменять знак неравенства на противоположный. То есть получаем, что (− 2 , 7 · z) : (− 2 , 7) 0 ; z , ≥) :
Числовое неравенство вида b , ≥) верно, тогда исходное неравенство имеет решение при любом значении, а неверно тогда, когда исходное неравенство не имеет решений.
Решить неравенство 0 · x + 7 > 0 .
Решение
Данное линейное неравенство 0 · x + 7 > 0 может принимать любое значение x . Тогда получим неравенство вида 7 > 0 . Последнее неравенство считается верным, значит любое число может быть его решением.
Ответ : промежуток (− ∞ , + ∞) .
Найти решение неравенства 0 · x − 12 , 7 ≥ 0 .
Решение
При подстановке переменной x любого числа получим, что неравенство получит вид − 12 , 7 ≥ 0 . Оно является неверным. То есть 0 · x − 12 , 7 ≥ 0 не имеет решений.
Ответ: решений нет.
Рассмотрим решение линейных неравенств, где оба коэффициента равняется нулю.
Определить не имеющее решение неравенство из 0 · x + 0 > 0 и 0 · x + 0 ≥ 0 .
Решение
При подстановке любого числа вместо x получим два неравенства вида 0 > 0 и 0 ≥ 0 . Первое является неверным. Значит, 0 · x + 0 > 0 не имеет решений, а 0 · x + 0 ≥ 0 имеет бесконечное количество решений, то есть любое число.
Ответ : неравенство 0 · x + 0 > 0 не имеет решений, а 0 · x + 0 ≥ 0 имеет решения.
Данный метод рассматривается в школьном курсе математики. Метод интервалов способен разрешать различные виды неравенств, также и линейные.
Метод интервалов применяется для линейных неравенств при значении коэффициента x не равному 0 . Иначе придется вычислять при помощи другого метода.
Метод интервалов – это:
- введение функции y = a · x + b ;
- поиск нулей для разбивания области определения на промежутки;
- определение знаков для понятия их на промежутках.
Соберем алгоритм для решения линейных уравнений a · x + b , ≥) при a ≠ 0 с помощью метода интервалов:
- нахождение нулей функции y = a · x + b , чтобы решить уравнение вида a · x + b = 0 . Если a ≠ 0 , тогда решением будет единственный корень, который примет обозначение х 0 ;
- построение координатной прямой с изображением точки с координатой х 0 , при строгом неравенстве точка обозначается выколотой, при нестрогом – закрашенной;
- определение знаков функции y = a · x + b на промежутках, для этого необходимо находить значения функции в точках на промежутке;
- решение неравенства со знаками > или ≥ на координатной прямой добавляется штриховка над положительным промежутком, 0 .
Решение
Из алгоритма следует, что для начала нужно найти корень уравнения − 3 · x + 12 = 0 . Получаем, что − 3 · x = − 12 , x = 4 . Необходимо изобразить координатную прямую, где отмечаем точку 4 . Она будет выколотой, так как неравенство является строгим. Рассмотрим чертеж, приведенный ниже.
Нужно определить знаки на промежутках. Чтобы определить его на промежутке (− ∞ , 4) , необходимо произвести вычисление функции y = − 3 · x + 12 при х = 3 . Отсюда получим, что − 3 · 3 + 12 = 3 > 0 . Знак на промежутке является положительным.
Определяем знак из промежутка (4 , + ∞) , тогда подставляем значение х = 5 . Имеем, что − 3 · 5 + 12 = − 3 , причем штриховка выполняется над положительным промежутком. Рассмотрим чертеж, приведенный ниже.
Из чертежа видно, что искомое решение имеет вид (− ∞ , 4) или x 0 и 0 , 5 · x − 1 ≥ 0 . Их решениями будут значения x 2 и x ≥ 2 . Для этого изобразим график линейной функции y = 0 , 5 · x − 1 , приведенный ниже.
- решением неравенства 0 , 5 · x − 1 0 считается промежуток, гре функция располагается выше О х;
- решением 0 , 5 · x − 1 ≥ 0 считается промежуток, где график выше О х или совпадает.
Смысл графического решения неравенств заключается в нахождении промежутков, которое необходимо изображать на графике. В данном случае получаем, что левая часть имеет y = a · x + b , а правая – y = 0 , причем совпадает с О х.
Построение графика функции y = a · x + b производится:
- во время решения неравенства a · x + b 0 производится определение промежутка, где график изображается выше О х;
- во время решения неравенства a · x + b ≥ 0 производится определение промежутка, где график находится выше О х или совпадает.
Решить неравенство — 5 · x — 3 > 0 при помощи графика.
Решение
Необходимо построить график линейной функции — 5 · x — 3 > 0 . Данная прямая является убывающей, потому как коэффициент при x является отрицательным. Для определения координат точки его пересечения с О х — 5 · x — 3 > 0 получим значение — 3 5 . Изобразим графически.
Решение неравенства со знаком > , тогда необходимо обратить внимание на промежуток выше О х. Выделим красным цветом необходимую часть плоскости и получим, что
Необходимый промежуток является частью О х красного цвета. Значит, открытый числовой луч — ∞ , — 3 5 будет решением неравенства. Если бы по условию имели нестрогое неравенство, тогда значение точки — 3 5 также являлось бы решением неравенства. И совпадало бы с О х.
Ответ : — ∞ , — 3 5 или x 0 , 7 · (x − 1) + 3 ≤ 4 · x − 2 + x , x — 3 5 — 2 · x + 1 > 2 7 · x .
Неравенства, приведенные выше, всегда приводятся к виду линейного уравнения. После чего раскрываются скобки и приводятся подобные слагаемые, переносятся из разных частей, меняя знак на противоположный.
При сведении неравенства 5 − 2 · x > 0 к линейному, представляем его таким образом, чтобы оно имело вид − 2 · x + 5 > 0 , а для приведения второго получаем, что 7 · (x − 1) + 3 ≤ 4 · x − 2 + x . Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:
7 · x − 7 + 3 ≤ 4 · x − 2 + x 7 · x − 4 ≤ 5 · x − 2 7 · x − 4 − 5 · x + 2 ≤ 0 2 · x − 2 ≤ 0
Это приводит решение к линейному неравенству.
Эти неравенства рассматриваются как линейные, так как имеют такой же принцип решения, после чего возможно приведение их к элементарным неравенствам.
Для решения такого вида неравенства такого вида необходимо свести его к линейному. Это следует делать таким образом:
- раскрыть скобки;
- слева собрать переменные, а справа числа;
- привести подобные слагаемые;
- разделить обе части на коэффициент при x .
Решить неравенство 5 · (x + 3) + x ≤ 6 · (x − 3) + 1 .
Решение
Производим раскрытие скобок, тогда получим неравенство вида 5 · x + 15 + x ≤ 6 · x − 18 + 1 . После приведения подобных слагаемых имеем, что 6 · x + 15 ≤ 6 · x − 17 . После перенесения слагаемых с левой в правую, получим, что 6 · x + 15 − 6 · x + 17 ≤ 0 . Отсюда имеет неравенство вида 32 ≤ 0 из полученного при вычислении 0 · x + 32 ≤ 0 . Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.
Ответ : нет решений.
Стоит отметить, что имеется множество неравенств другого вида, которые могут сводится к линейному или неравенству вида, показанного выше. Например, 5 2 · x − 1 ≥ 1 является показательным уравнением, которое сводится к решению линейного вида 2 · x − 1 ≥ 0 . Эти случаи будут рассмотрены при решении неравенств данного вида.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Решение целых и дробно рациональных неравенств
Продолжаем разбирать способы решения неравенств, имеющих в составе одну переменную. Мы уже изучили линейные и квадратные неравенства, которые представляют из себя частные случаи рациональных неравенств. В этой статье мы уточним, неравенства какого типа относятся к рациональным, расскажем, на какие виды они делятся (целые и дробные). После этого покажем, как правильно их решать, приведем нужные алгоритмы и разберем конкретные задачи.
Понятие рациональных равенств
Когда в школе изучают тему решения неравенств, то сразу берут рациональные неравенства. На них приобретаются и оттачиваются навыки работы с этим видом выражений. Сформулируем определение данного понятия:
Рациональное неравенство представляет из себя такое неравенство с переменными, которое содержит в обоих частях рациональные выражения.
Отметим, что определение никак не затрагивает вопрос количества переменных, значит, их может быть сколь угодно много. Следовательно, возможны рациональные неравенства с 1 , 2 , 3 и более переменными. Чаще всего приходится иметь дело с выражениями, содержащими всего одну переменную, реже две, а неравенства с большим количеством переменных обычно в рамках школьного курса не рассматривают вовсе.
Таким образом, мы можем узнать рациональное неравенство, посмотрев на его запись. И с правой, и с левой стороны у него должны быть расположены рациональные выражения. Приведем примеры:
x > 4 x 3 + 2 · y ≤ 5 · ( y − 1 ) · ( x 2 + 1 ) 2 · x x — 1 ≥ 1 + 1 1 + 3 x + 3 · x 2
А вот неравенство вида 5 + x + 1 < x · y · z не относится к рациональным, поскольку слева у него есть переменная под знаком корня.
Все рациональные неравенства делятся на целые и дробные.
Целое рациональное равенство состоит из целых рациональных выражений (в обеих частях).
Дробно рациональное равенство – это такое равенство, которое содержит дробное выражение в одной или обеих своих частях.
Например, неравенства вида 1 + x — 1 1 3 2 2 + 2 3 + 2 11 — 2 · 1 3 · x — 1 > 4 — x 4 и 1 — 2 3 5 — y > 1 x 2 — y 2 являются дробно рациональными, а 0 , 5 · x ≤ 3 · ( 2 − 5 · y ) и 1 : x + 3 > 0 – целыми.
Мы разобрали, что из себя представляют рациональные неравенства, и выделили их основные типы. Можем переходить дальше, к обзору способов их решения.
Как решать целые неравенства
Допустим, что нам требуется найти решения целого рационального неравенства r ( x ) < s ( x ) , которое включает в себя только одну переменную x . При этом r ( x ) и s ( x ) представляют собой любые целые рациональные числа или выражения, а знак неравенства может отличаться. Чтобы решить это задание, нам нужно преобразовать его и получить равносильное равенство.
Начнем с перенесения выражения из правой части в левую. Получим следующее:
вида r ( x ) − s ( x ) < 0 ( ≤ , > , ≥ )
Мы знаем, что r ( x ) − s ( x ) будет целым значением, а любое целое выражение допустимо преобразовать в многочлен. Преобразуем r ( x ) − s ( x ) в h ( x ) . Это выражение будет тождественно равным многочленом. Учитывая, что у r ( x ) − s ( x ) и h ( x ) область допустимых значений x одинакова, мы можем перейти к неравенствам h ( x ) < 0 ( ≤ , > , ≥ ) , которое будет равносильно исходному.
Зачастую такого простого преобразования будет достаточно для решения неравенства, поскольку в итоге может получиться линейное или квадратное неравенство, значение которого вычислить несложно. Разберем такие задачи.
Условие: решите целое рациональное неравенство x · ( x + 3 ) + 2 · x ≤ ( x + 1 ) 2 + 1 .
Решение
Начнем с переноса выражения из правой части в левую с противоположным знаком.
x · ( x + 3 ) + 2 · x − ( x + 1 ) 2 − 1 ≤ 0
Теперь, когда мы выполнили все действия с многочленами слева, можно переходить к линейному неравенству 3 · x − 2 ≤ 0 , равносильному тому, что было дано в условии. Решить его несложно:
Ответ: x ≤ 2 3 .
Условие: найдите решение неравенства ( x 2 + 1 ) 2 − 3 · x 2 > ( x 2 − x ) · ( x 2 + x ) .
Решение
Переносим выражение из левой части в правую и выполняем дальнейшие преобразования с помощью формул сокращенного умножения.
( x 2 + 1 ) 2 − 3 · x 2 − ( x 2 − x ) · ( x 2 + x ) > 0 x 4 + 2 · x 2 + 1 − 3 · x 2 − x 4 + x 2 > 0 1 > 0
В итоге наших преобразований мы получили неравенство, которое будет верным при любых значениях x , следовательно, решением исходного неравенства может быть любое действительное число.
Ответ: любое действительно число.
Условие: решите неравенство x + 6 + 2 · x 3 − 2 · x · ( x 2 + x − 5 ) > 0 .
Решение
Из правой части мы ничего переносить не будем, поскольку там 0 . Начнем сразу с преобразования левой части в многочлен:
x + 6 + 2 · x 3 − 2 · x 3 − 2 · x 2 + 10 · x > 0 − 2 · x 2 + 11 · x + 6 > 0 .
Мы вывели квадратное неравенство, равносильное исходному, которое легко решить несколькими методами. Применим графический способ.
Начнем с вычисления корней квадратного трехчлена − 2 · x 2 + 11 · x + 6 :
D = 11 2 — 4 · ( — 2 ) · 6 = 169 x 1 = — 11 + 169 2 · — 2 , x 2 = — 11 — 169 2 · — 2 x 1 = — 0 , 5 , x 2 = 6
Теперь на схеме отметим все необходимые нули. Поскольку старший коэффициент меньше нуля, ветви параболы на графике будут смотреть вниз.
Нам будет нужна область параболы, расположенная над осью абсцисс, поскольку в неравенстве у нас стоит знак > . Нужный интервал равен ( − 0 , 5 , 6 ) , следовательно, эта область значений и будет нужным нам решением.
Ответ: ( − 0 , 5 , 6 ) .
Бывают и более сложные случаи, когда слева получается многочлен третьей или более высокой степени. Чтобы решить такое неравенство, рекомендуется использовать метод интервалов. Сначала мы вычисляем все корни многочлена h ( x ) , что чаще всего делается с помощью разложения многочлена на множители.
Условие: вычислите ( x 2 + 2 ) · ( x + 4 ) < 14 − 9 · x .
Решение
Начнем, как всегда, с переноса выражения в левую часть, после чего нужно будет выполнить раскрытие скобок и приведение подобных слагаемых.
( x 2 + 2 ) · ( x + 4 ) − 14 + 9 · x < 0 x 3 + 4 · x 2 + 2 · x + 8 − 14 + 9 · x < 0 x 3 + 4 · x 2 + 11 · x − 6 < 0
В итоге преобразований у нас получилось равносильное исходному равенство, слева у которого стоит многочлен третьей степени. Применим метод интервалов для его решения.
Сначала вычисляем корни многочлена, для чего нам надо решить кубическое уравнение x 3 + 4 · x 2 + 11 · x − 6 = 0 . Имеет ли оно рациональные корни? Они могут быть лишь в числе делителей свободного члена, т.е. среди чисел ± 1 , ± 2 , ± 3 , ± 6 . Подставим их по очереди в исходное уравнение и выясним, что числа 1 , 2 и 3 будут его корнями.
Значит, многочлен x 3 + 4 · x 2 + 11 · x − 6 может быть описан в виде произведения ( x − 1 ) · ( x − 2 ) · ( x − 3 ) , и неравенство x 3 + 4 · x 2 + 11 · x − 6 < 0 может быть представлено как ( x − 1 ) · ( x − 2 ) · ( x − 3 ) < 0 . С неравенством такого вида нам потом будет легче определить знаки на промежутках.
Далее выполняем оставшиеся шаги интервального метода: рисуем числовую прямую и точки на ней с координатами 1 , 2 , 3 . Они разбивают прямую на 4 промежутка, в которых нужно определить знаки. Заштрихуем промежутки с минусом, поскольку исходное неравенство имеет знак < .
Нам осталось только записать готовый ответ: ( − ∞ , 1 ) ∪ ( 2 , 3 ) .
Ответ: ( − ∞ , 1 ) ∪ ( 2 , 3 ) .
В некоторых случаях выполнять переход от неравенства r ( x ) − s ( x ) < 0 ( ≤ , > , ≥ ) к h ( x ) < 0 ( ≤ , > , ≥ ) , где h ( x ) – многочлен в степени выше 2 , нецелесообразно. Это распространяется на те случаи, когда представить r ( x ) − s ( x ) как произведение линейных двучленов и квадратных трехчленов проще, чем разложить h ( x ) на отдельные множители. Разберем такую задачу.
Условие: найдите решение неравенства ( x 2 − 2 · x − 1 ) · ( x 2 − 19 ) ≥ 2 · x · ( x 2 − 2 · x − 1 ) .
Решение
Данное неравенство относится к целым. Если мы перенесем выражение из правой части влево, раскроем скобки и выполним приведение слагаемых, то получим x 4 − 4 · x 3 − 16 · x 2 + 40 · x + 19 ≥ 0 .
Решить такое неравенство непросто, поскольку придется искать корни многочлена четвертой степени. Оно не имеет ни одного рационального корня (так, 1 , − 1 , 19 или − 19 не подходят), а искать другие корни сложно. Значит, воспользоваться этим способом мы не можем.
Но есть и другие способы решения. Если мы перенесем выражения из правой части исходного неравенства в левую, то сможем выполнить вынесение за скобки общего множителя x 2 − 2 · x − 1:
( x 2 − 2 · x − 1 ) · ( x 2 − 19 ) − 2 · x · ( x 2 − 2 · x − 1 ) ≥ 0 ( x 2 − 2 · x − 1 ) · ( x 2 − 2 · x − 19 ) ≥ 0 .
Мы получили неравенство, равносильное исходному, и его решение даст нам искомый ответ. Найдем нули выражения в левой части, для чего решим квадратные уравнения x 2 − 2 · x − 1 = 0 и x 2 − 2 · x − 19 = 0 . Их корни – 1 ± 2 , 1 ± 2 5 . Переходим к равенству x — 1 + 2 · x — 1 — 2 · x — 1 + 2 5 · x — 1 — 2 5 ≥ 0 , которое можно решить методом интервалов:
Согласно рисунку, ответом будет — ∞ , 1 — 2 5 ∪ 1 — 2 5 , 1 + 2 ∪ 1 + 2 5 , + ∞ .
Ответ: — ∞ , 1 — 2 5 ∪ 1 — 2 5 , 1 + 2 ∪ 1 + 2 5 , + ∞ .
Добавим, что иногда нет возможности найти все корни многочлена h ( x ) , следовательно, мы не можем представить его в виде произведения линейных двучленов и квадратных трехчленов. Тогда решить неравенство вида h ( x ) < 0 ( ≤ , > , ≥ ) мы не можем, значит, решить исходное рациональное неравенство тоже нельзя.
Как решать дробно рациональные неравенства
Допустим, надо решить дробно рационально неравенств вида r ( x ) < s ( x ) ( ≤ , > , ≥ ) , где r ( x ) и s ( x ) являются рациональными выражениями, x – переменной. Хотя бы одно из указанных выражений будет дробным. Алгоритм решения в этом случае будет таким:
- Определяем область допустимых значений переменной x .
- Переносим выражение из правой части неравенства налево, а получившееся выражение r ( x ) − s ( x ) представляем в виде дроби. При этом где p ( x ) и q ( x ) будут целыми выражениями, которые являются произведениями линейных двучленов, неразложимых квадратных трехчленов, а также степеней с натуральным показателем.
- Далее решаем полученное неравенство методом интервалов.
- Последним шагом является исключение точек, полученных в ходе решения, из области допустимых значений переменной x , которую мы определили в начале.
Это и есть алгоритм решения дробно рационального неравенства. Большая часть его понятна, небольшие пояснения требуются только для п. 2 . Мы перенесли выражение из правой части налево и получили r ( x ) − s ( x ) < 0 ( ≤ , > , ≥ ) , а как потом привести его к виду p ( x ) q ( x ) < 0 ( ≤ , > , ≥ ) ?
Сначала определим, всегда ли можно выполнить данное преобразование. Теоретически, такая возможность имеется всегда, поскольку в рациональную дробь можно преобразовать любое рациональное выражение. Здесь же у нас есть дробь с многочленами в числителе и знаменателе. Вспомним основную теорему алгебры и теорему Безу и определим, что любой многочлен n -ной степени, содержащий одну переменную, может быть преобразован в произведение линейных двучленов. Следовательно, в теории мы всегда можем преобразовать выражение таким образом.
На практике разложение многочленов на множители зачастую оказывается довольно трудной задачей, особенно если степень выше 4 . Если мы не сможем выполнить разложение, то не сможем и решить данное неравенство, однако в рамках школьного курса такие проблемы обычно не изучаются.
Далее нам надо решить, будет ли полученное неравенство p ( x ) q ( x ) < 0 ( ≤ , > , ≥ ) равносильным по отношению к r ( x ) − s ( x ) < 0 ( ≤ , > , ≥ ) и к исходному. Есть вероятность, что оно может оказаться и неравносильным.
Равносильность неравенства будет обеспечена тогда, когда область допустимых значений p ( x ) q ( x ) совпадет с областью значений выражения r ( x ) − s ( x ) . Тогда последний пункт инструкции по решению дробно рациональных неравенств выполнять не нужно.
Но область значений для p ( x ) q ( x ) может оказаться шире, чем у r ( x ) − s ( x ) , например, за счет сокращения дробей. Примером может быть переход от x · x — 1 3 x — 1 2 · x + 3 к x · x — 1 x + 3 . Либо это может происходить при приведении подобных слагаемых, например, здесь:
x + 5 x — 2 2 · x — x + 5 x — 2 2 · x + 1 x + 3 к 1 x + 3
Для таких случаев и добавлен последний шаг алгоритма. Выполнив его, вы избавитесь от посторонних значений переменной, которые возникают из-за расширения области допустимых значений. Возьмем несколько примеров, чтобы было более понятно, о чем идет речь.
Условие: найдите решения рационального равенства x x + 1 · x — 3 + 4 x — 3 2 ≥ — 3 · x x — 3 2 · x + 1 .
Решение
Действуем по алгоритму, указанному выше. Сначала определяем область допустимых значений. В данном случае она определяется системой неравенств x + 1 · x — 3 ≠ 0 x — 3 2 ≠ 0 x — 3 2 · ( x + 1 ) ≠ 0 , решением которой будет множество ( − ∞ , − 1 ) ∪ ( − 1 , 3 ) ∪ ( 3 , + ∞ ) .
Далее нам надо сделать так, чтобы в правой части неравенства получился 0 . Выполняем перенос выражения из правой части влево с противоположным знаком и получаем неравенство, равносильное исходному:
x x + 1 · x — 3 + 4 ( x — 3 ) 2 + 3 · x ( x — 3 ) 2 · ( x + 1 ) ≥ 0
После этого нам нужно преобразовать его так, чтобы было удобно применить метод интервалов. Первым делом приводим алгебраические дроби к наименьшему общему знаменателю ( x − 3 ) 2 · ( x + 1 ) :
x x + 1 · x — 3 + 4 ( x — 3 ) 2 + 3 · x ( x — 3 ) 2 · ( x + 1 ) = = x · x — 3 + 4 · x + 1 + 3 · x x — 3 2 · x + 1 = x 2 + 4 · x + 4 ( x — 3 ) 2 · ( x + 1 )
Сворачиваем выражение в числителе, применяя формулу квадрата суммы:
x 2 + 4 · x + 4 x — 3 2 · x + 1 = x + 2 2 x — 3 2 · x + 1
Областью допустимых значений получившегося выражения является ( − ∞ , − 1 ) ∪ ( − 1 , 3 ) ∪ ( 3 , + ∞ ) . Мы видим, что она аналогична той, что была определена для исходного равенства. Заключаем, что неравенство x + 2 2 x — 3 2 · x + 1 ≥ 0 является равносильным исходному, значит, последний шаг алгоритма нам не нужен.
Используем метод интервалов:
Видим решение ∪ ( − 1 , 3 ) ∪ ( 3 , + ∞ ) , которое и будет решением исходного рационального неравенства x x + 1 · x — 3 + 4 x — 3 2 ≥ — 3 · x ( x — 3 ) 2 · ( x + 1 ) .
Ответ: ∪ ( − 1 , 3 ) ∪ ( 3 , + ∞ ) .
Условие: вычислите решение x + 3 x — 1 — 3 x x + 2 + 2 x — 1 > 1 x + 1 + 2 · x + 2 x 2 — 1 .
Решение
Определяем область допустимых значений. В случае с этим неравенством она будет равна всем действительным числам, кроме − 2 , − 1 , 0 и 1 .
Переносим выражения из правой части в левую:
x + 3 x — 1 — 3 x x + 2 + 2 x — 1 — 1 x + 1 — 2 · x + 2 x 2 — 1 > 0
Далее выполняем преобразование левой части. Сначала преобразуем первую дробь:
x + 3 x — 1 — 3 x x + 2 = x + 3 — x — 3 x x + 2 = 0 x x + 2 = 0 x + 2 = 0
Учитывая получившийся результат, запишем:
x + 3 x — 1 — 3 x x + 2 + 2 x — 1 — 1 x + 1 — 2 · x + 2 x 2 — 1 = = 0 + 2 x — 1 — 1 x + 1 — 2 · x + 2 x 2 — 1 = = 2 x — 1 — 1 x + 1 — 2 · x + 2 x 2 — 1 = = 2 x — 1 — 1 x + 1 — 2 · x + 2 ( x + 1 ) · x — 1 = = — x — 1 ( x + 1 ) · x — 1 = — x + 1 ( x + 1 ) · x — 1 = — 1 x — 1
Для выражения — 1 x — 1 областью допустимых значений будет множество всех действительных чисел, за исключением единицы. Мы видим, что область значений расширилась: в нее были добавлены − 2 , − 1 и 0 . Значит, нам нужно выполнить последний шаг алгоритма.
Поскольку мы пришли к неравенству — 1 x — 1 > 0 , можем записать равносильное ему 1 x — 1 < 0 . С помощью метода интервалов вычислим решение и получим ( − ∞ , 1 ) .
Исключаем точки, которые не входят в область допустимых значений исходного равенства. Нам надо исключить из ( − ∞ , 1 ) числа − 2 , − 1 и 0 . Таким образом, решением рационального неравенства x + 3 x — 1 — 3 x x + 2 + 2 x — 1 > 1 x + 1 + 2 · x + 2 x 2 — 1 будут значения ( − ∞ , − 2 ) ∪ ( − 2 , − 1 ) ∪ ( − 1 , 0 ) ∪ ( 0 , 1 ) .
Ответ: ( − ∞ , − 2 ) ∪ ( − 2 , − 1 ) ∪ ( − 1 , 0 ) ∪ ( 0 , 1 ) .
В заключение приведем еще один пример задачи, в котором окончательный ответ зависит от области допустимых значений.
Условие: найдите решение неравенства 5 + 3 x 2 x 3 + 1 x 2 — x + 1 — x 2 — 1 x — 1 ≥ 0 .
Решение
Область допустимых значений неравенства, заданного в условии, определяет система x 2 ≠ 0 x 2 — x + 1 ≠ 0 x — 1 ≠ 0 x 3 + 1 x 2 — x + 1 — x 2 — 1 x — 1 ≠ 0 .
Решений у этой системы нет, поскольку
x 3 + 1 x 2 — x + 1 — x 2 — 1 x — 1 = = ( x + 1 ) · x 2 — x + 1 x 2 — x + 1 — ( x — 1 ) · x + 1 x — 1 = = x + 1 — ( x + 1 ) = 0
Значит, исходное равенство 5 + 3 x 2 x 3 + 1 x 2 — x + 1 — x 2 — 1 x — 1 ≥ 0 не имеет решения, поскольку нет таких значений переменной, при которой оно имело бы смысл.
Прежде чем перейти к разбору темы «Как решать
систему линейных неравенств» обязательно внимательно изучите
урок «Как решать неравенства».
Потренируйтесь в решении неравенств, тогда с системами неравенств у вас не возникнет трудностей.
Важно!
Системой неравенств называют два или более неравенства, которые объединены фигурной скобкой.
Рассмотрим пример системы неравенств.
Как видно на примере выше, систему неравенств легко определить по фигурной скобке.
Как решить систему неравенств
Запомните!
Чтобы решить систему неравенств нужно:
- решить отдельно каждое неравенство;
- сравнить полученные решения каждого неравенства и получить общий ответ системы.
Вернемся к нашему примеру системы неравенств.
Так как оба неравенства в системе уже решены и представляют собою готовый ответ, то
сразу переходим к поиску общего решения всей системы.
Для этого проведем две числовые оси (для каждого из неравенств свою). На осях заштрихуем результат решения неравенств.
Важно!
Числовые оси с решениями нужно располагать друг под другом.
Числа на осях отмечают в порядке возрастания. То есть число «2» будет
находиться левее «5».
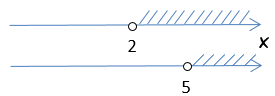
|
После того как мы построили числовые оси с решениями неравенств, необходимо провести через отмеченные
на осях числа перпендикулярные прямые.
Запомните!
При проведении прямых через точки на осях соблюдают следующие правила:
- если точка не входит в область решения («пустая» точка), то рисуют
пунктирную линию;
- если точка входит в область решения («заполненная» точка), то рисуют
сплошную линию.
Проведем прямые через числовые точки на осях.
Для определения ответа найдем те области решения, которые удовлетворяют ответам обоим неравенствам.
Другими словами, те области, где в обоих случаях области решений заштрихованы.
Исходя из полученного анализа, мы получаем, что решением системы неравенств будет
«x > 5». Запишем полученный ответ.
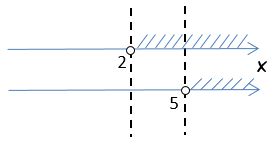
|
Ответ: x > 5
Рассмотрим другой пример системы неравенств.
Так как неравенства в системе снова представляют собой готовые ответы — сразу перейдем к поиску общего
решения системы неравенств.
Нарисуем числовые оси для каждого неравенства и отметим на них решения. Проведем
через каждое отмеченное число на осях прямую по правилам, описанным выше.
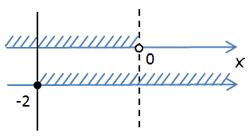
|
Выберем те области решений, которые удовлетворяют обоим неравенствам.
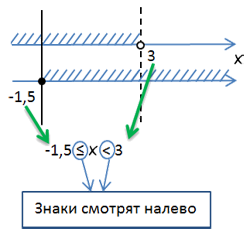
Как видно на рисунке выше, область решений, которая подходит для обоих неравенств, находится между числами
«−2» и «0».
Когда область решений находится между двумя числами, принято записывать ответ с помощью двойного неравенства.

|
Ответ: −2 ≤ x < 0
Запомните!
Запись двойного неравенства используют, когда интервал решения системы неравенств лежит между числами.
Знаки сравнения («<» или «≤») в двойном
неравенстве всегда смотрят влево.
Числа записываются в том же порядке, что они расположены на оси.
Другие примеры решения систем неравенств
В отличии от примеров выше, как правило, в системах неравенств перед поиском общего решения всей системы необходимо
предварительно решить каждое из неравенств.
Рассмотрим и решим систему, где неравенства требуют предварительного решения.
Решим линейные неравенства по правилам, описанным в уроке
«Решение линейных неравенств». Затем найдем общий
ответ системы.
| 5(x + 1) − x > 2x + 2 | |
| 4(x + 1) − 2 ≤ 2(2x + 1) − x |
| 5x + 5 − x > 2x + 2 | |
| 4x + 4 − 2 ≤ 4x + 2 − x |
| 5x − x + 5 > 2x + 2 | |
| 4x + 4 − 2 ≤ 4x + 2 − x |
| 4x + 5 > 2x + 2 | |
| 4x + 2 ≤ 3x + 2 |
| 4x − 2x > 2 − 5 | |
| 4x − 3x ≤ 2 − 2 |
|
|
Ответ: −1 < x ≤ 0
При решении систем неравенств, в которых есть неравенства, содержащие пропорцию, используем
правило пропорции.
| 5(x + 1) ≤ 3(x + 3) + 1 | |
| ≤ |
| 5x + 5 ≤ 3x + 9 + 1 | |
| (2x − 1) · 2 ≤ (x + 1) · 7 |
| 5x − 3x ≤ 10 − 5 | |
| 4x − 2 ≤ 7x + 7 |
| 2x ≤ 5 | (:2) | |
| − 3x ≤ 9 | (:−3) |
| 2x (:2) ≤ 5 (:2) | |
| − 3x (:−3) ≥ 9 (:−3) |
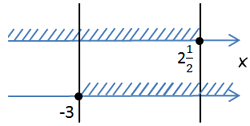
|
Ответ: −3 ≤ x ≤ 2
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий: