Как найти все циклы эйлера - Сайт, где вы сможете решить свои вопросы

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 10 августа 2021 года; проверки требуют 4 правки.

Граф Кёнигсбергских мостов. Этот граф не является полуэйлеровым, поэтому решения не существует

Каждая вершина этого графа имеет чётную степень, поэтому этот граф — эйлеров. Обход рёбер в алфавитном порядке даёт эйлеров цикл

Эйлеров путь (эйлерова цепь) в графе — это путь, проходящий по всем рёбрам графа и притом только по одному разу. (ср. Гамильтонов путь)

Эйлеров цикл — эйлеров путь, являющийся циклом, то есть замкнутый путь, проходящий через каждое ребро графа ровно по одному разу.

Полуэйлеров граф — граф, в котором существует эйлеров путь.

Эйлеров граф — граф, в котором существует эйлеров цикл.

Существование эйлерова цикла и эйлерова пути[править | править код]

В неориентированном графе[править | править код]

Согласно теореме, доказанной Эйлером, эйлеров цикл существует тогда и только тогда, когда граф связный или будет являться связным, если удалить из него все изолированные вершины, и в нём отсутствуют вершины нечётной степени.

Эйлеров путь в графе существует тогда и только тогда, когда граф связный и содержит не более двух вершин нечётной степени.^[1]^[2] Ввиду леммы о рукопожатиях, число вершин с нечётной степенью должно быть чётным. А значит эйлеров путь существует только тогда, когда это число равно нулю или двум. Причём, когда оно равно нулю, эйлеров путь вырождается в эйлеров цикл.

В ориентированном графе[править | править код]

Ориентированный граф G=(V,A) содержит эйлеров цикл тогда и только тогда, когда он сильно связан или среди его компонент сильной связности только одна содержит ребра (а все остальные являются изолированными вершинами) и для каждой вершины графа её входящая степень равна её исходящей степени , то есть в вершину входит столько же ребер, сколько из неё и выходит: .

Так как эйлеров цикл является частным случаем эйлерова пути, то очевидно, что ориентированный граф G=(V,A) содержит эйлеров путь тогда и только тогда, когда он содержит либо эйлеров цикл, либо эйлеров путь, не являющийся циклом. Ориентированный граф G=(V,A) содержит эйлеров путь, не являющийся циклом, тогда и только тогда, когда он слабо связен и существуют две вершины pin V и qin V (начальная и конечная вершины пути соответственно) такие, что их полустепени захода и полустепени исхода связаны равенствами и , а все остальные вершины имеют одинаковые полустепени исхода и захода: ^[3].

Поиск эйлерова пути в графе[править | править код]

Можно всегда свести задачу поиска эйлерова пути к задаче поиска эйлерова цикла. Действительно, предположим, что эйлерова цикла не существует, а эйлеров путь существует. Тогда в графе будет ровно 2 вершины нечётной степени. Соединим эти вершины ребром, и получим граф, в котором все вершины чётной степени, и эйлеров цикл в нём существует. Найдём в этом графе эйлеров цикл (алгоритмом, описанным ниже), а затем удалим из ответа несуществующее ребро.

Поиск эйлерова цикла в графе[править | править код]

Алгоритм Флёри[править | править код]

Основной источник: M. Fleury. Deux problèmes de Géométrie de situation (фр.) // Journal de mathématiques élémentaires [et spéciales]. — Paris: C. Delagrave, 1883. — Vol. 2, livr. 2nd ser.. — P. 257–261.

Алгоритм был предложен Флёри в 1883 году.

Пусть задан граф G=(V,E) . Начинаем с некоторой вершины pin V и каждый раз вычеркиваем пройденное ребро. Не проходим по ребру, если удаление этого ребра приводит к разбиению графа на две связные компоненты (не считая изолированных вершин), т.е. необходимо проверять, является ли ребро мостом или нет.

Этот алгоритм неэффективен: время работы оригинального алгоритма O(|E|²). Если использовать более эффективный алгоритм для поиска мостов^[4], то время выполнения можно снизить до ${displaystyle O(|E|(log |E|)^{3}log log |E|)}$ , однако это всё равно медленнее, чем другие алгоритмы.

Алгоритм может быть распространен на ориентированные графы.

Алгоритм на основе циклов[править | править код]

Будем рассматривать самый общий случай — случай ориентированного мультиграфа, возможно, с петлями. Также мы предполагаем, что эйлеров цикл в графе существует (и состоит хотя бы из одной вершины). Для поиска эйлерова цикла воспользуемся тем, что эйлеров цикл — это объединение всех простых циклов графа. Следовательно, наша задача — эффективно найти все циклы и эффективно объединить их в один.

Реализовать это можно, например, так, рекурсивно:

procedure find_all_cycles (v)
var массив cycles
1. пока есть цикл, проходящий через v, находим его
    добавляем все вершины найденного цикла в массив cycles (сохраняя порядок обхода)
    удаляем цикл из графа
2. идем по элементам массива cycles
    каждый элемент cycles[i] добавляем к ответу
    из каждого элемента рекурсивно вызываем себя: find_all_cycles (cycles[i])

Достаточно вызвать эту процедуру из любой вершины графа, и она найдёт все циклы в графе, удалит их из графа и объединит их в один эйлеров цикл.

Для поиска цикла на шаге 1 используем поиск в глубину.

Сложность полученного алгоритма — O(|E|), то есть линейная относительно количества рёбер в данном графе.

Примечания[править | править код]

↑ Эйлеровы пути. Дата обращения: 26 ноября 2008. Архивировано из оригинала 5 января 2009 года.
↑ В. Алексеев, В. Таланов, Курс “Графы и алгоритмы”, Лекция № 2 “Маршруты, связность, расстояния”: Маршруты и связность в орграфах // Интуит.ру, 27.09.2006
↑ Кристофидес Н. Теория графов. Алгоритмический подход (глава 9.5) — М.: Мир, 1978.
↑ Mikkel Thorup. Near-optimal fully[sic]-dynamic graph connectivity // Proceeding STOC ’00 Proceedings of the thirty-second annual ACM symposium on Theory of computing. — Portland: Association for Computing Machinery, 2000. — 21–23 5. — С. 343–350. — doi:10.1145/335305.335345.

См. также[править | править код]

Гамильтонов цикл
Граф (математика)
Задача о ходе коня
Дискретная математика
Проблема семи мостов Кёнигсберга
Список объектов, названных в честь Леонарда Эйлера

Ссылки[править | править код]

Реализация алгоритма поиска эйлерова цикла (краткие описания и программы на C++)
Реализация алгоритма поиска эйлерова цикла на codenet.ru
Теория графов и комбинаторика
Графы. Циклы и разрезы (ДИСКРЕТНАЯ МАТЕМАТИКА: АЛГОРИТМЫ, Визуализаторы)
Е. Гик. «Шахматы и математика» Конь-хамелеон
Weisstein, Eric W. Eulerian Circuit (англ.) на сайте Wolfram MathWorld.

Источник

Эйлеров путь и цикл

Эйлеров путь(цепь) проходит через каждое ребро графа ровно по одному разу.

Эйлеров цикл — это замкнутый путь, проходящий через каждое ребро графа ровно по одному разу.

Алгоритм поиска Эйлеров цикла

Сервис использует алгоритм поиска Эйлеров цикла на основе циклов.

Кроме того, перед поиском цикла проверяется его существование, для этого происходит поиск степени вершин.

Более подробно вы можете узнать об этом алгоритме
в Википедии.

Реализацию алгоритма на языке C++ вы можете найти в нашем репозитории на GitHub: Реализация поиска Эйлерового цикла в Graphoffline.

Алгоритм поиска Эйлервой цепи

Для поиска Эйлеров пути мы добавляем псевдо ребро соединяющие начальную и конечную вершину Эйлерова пути.

Начальная и конечная вершина для неориентированного графа будет иметь нечётные степени.

Для ориентированного графа начальная вершина имеет полустепень исхода на единицу больше полустепени захода. Для конечной вершины полустепень исхода на единицу меньше полустепени захода.

Как использовать

Создайте граф.
Выберите пункт меню Алгоритмы -> “Найти Эйлеров цикл” для поиска Эйлеров цикл.

Выберите пункт меню Алгоритмы -> “Найти Эйлерову цепь” для поиска Эйлеровой цепи.

Источник

import java.util.ArrayList;

import java.util.Arrays;

import java.util.List;

// Класс для хранения ребра Graph

class Edge

{

int source, dest;

public Edge(int source, int dest)

{

this.source = source;

this.dest = dest;

}

// Класс для представления graphического объекта

class Graph

{

// Список списков для представления списка смежности

List<List<Integer>> adjList;

// Конструктор

Graph(List<Edge> edges, int n)

{

adjList = new ArrayList<>();

for (int i = 0; i < n; i++) {

adjList.add(new ArrayList<>());

}

// добавляем ребра в неориентированный graph

for (Edge edge: edges)

{

adjList.get(edge.source).add(edge.dest);

adjList.get(edge.dest).add(edge.source);

}

class Main

{

// Вспомогательная функция для обхода DFS на Graphе

public static void DFS(Graph graph, int v, boolean[] discovered)

{

// помечаем текущий узел как обнаруженный

discovered[v] = true;

// делаем для каждого ребра (v, u)

for (int u: graph.adjList.get(v))

{

// если `u` еще не обнаружен

if (!discovered[u]) {

DFS(graph, u, discovered);

}

// Функция для проверки, все ли вершины с ненулевой степенью в Graph

// принадлежат одному связанному компоненту

public static boolean isConnected(Graph graph, int n)

{

// чтобы отслеживать, посещена ли вершина или нет

boolean[] visited = new boolean[n];

// запускаем поиск в глубину с первой вершины с ненулевой степенью

for (int i = 0; i < n; i++)

{

if (graph.adjList.get(i).size() > 0)

{

DFS(graph, i, visited);

break;

}

// если один вызов DFS не может посетить все вершины с ненулевой степенью,

// graph содержит более одной компоненты связности

for (int i = 0; i < n; i++)

{

if (!visited[i] && graph.adjList.get(i).size() > 0) {

return false;

}

return true;

}

// Вспомогательная функция для возврата общего количества вершин в Graph

// с нечетной степенью

public static int countOddVertices(Graph graph)

{

int count = 0;

for (List<Integer> list: graph.adjList)

{

if ((list.size() & 1) == 1) {

count++;

}

return count;

}

public static void main(String[] args)

{

// Список ребер Graph согласно приведенной выше диаграмме

List<Edge> edges = Arrays.asList(new Edge(0, 1), new Edge(0, 3),

new Edge(1, 2), new Edge(1, 3), new Edge(1, 4),

new Edge(2, 3), new Edge(3, 4));

// общее количество узлов в Graph (от 0 до 4)

int n = 5;

// создаем неориентированный graph из заданных ребер

Graph graph = new Graph(edges, n);

// проверяем, все ли вершины с ненулевой степенью принадлежат

// одиночный связный компонент

boolean is_connected = isConnected(graph, n);

// находим общее количество вершин с нечетной степенью

int odd = countOddVertices(graph);

// Эйлеров путь существует, если все вершины не нулевой степени соединены,

// и ноль или две вершины имеют нечетную степень

if (is_connected && (odd == 0 || odd == 2))

{

System.out.println(“The graph has an Eulerian path”);

// Связный graph имеет эйлеров цикл, если каждая вершина имеет

// четная степень

if (odd == 0) {

System.out.println(“The graph has an Eulerian cycle”);

}

// В Graph есть эйлеров путь, но нет эйлерова цикла

else {

System.out.println(“The Graph is Semi–Eulerian”);

}

else {

System.out.println(“The Graph is not Eulerian”);

}

Источник

I have implemented an algorithm to find an Euler cycle for a given starting vertex in an undirected graph (using DFS and removing visited edges), but it always returns only one path. How do I modify the algorithm to search for all possible Euler cycles for a vertex?

Here is relevant code:

typedef int Graph[200][200]; // adjacency matrix
int v, e; // vertex count, edge count

......

void DFS(Graph &G, int x) {
    int i;
    Push(x);
    for (i = 0; i < v; i++)
        if (G[i][x] > 0) {
            G[i][x] = 0;
            G[x][i] = 0;
            DFS(G, i);
            break;
    }

}

Jacob

77.3k24 gold badges146 silver badges228 bronze badges

asked May 16, 2011 at 20:41

After the recursive call, you should reinsert the edges you deleted before, and get rid of the break.

void DFS(Graph &G, int x) 
{
    int i;
    Push(x);
    for (i = 0; i < v; i++)
        if (G[i][x] > 0) 
        {
            G[i][x] *= -1;
            G[x][i] *= -1;
            DFS(G, i);
            G[i][x] *= -1;
            G[x][i] *= -1;
        }

}

All you need now is a way to figure out when you’ve generated a full cycle so you can print it and move on to the next. That happens when you’ve eliminated every edge of your graph.

answered May 16, 2011 at 21:07

IVladIVlad

43k13 gold badges110 silver badges178 bronze badges

You want to loop through all vertex.

answered May 16, 2011 at 20:51

MicromegaMicromega

12.5k7 gold badges35 silver badges72 bronze badges

Источник

Эйлеров цикл: определение, условие существования, алгоритм нахождения

Эйлеров
путь (эйлерова цепь) в графе — это путь,
проходящий по всем рёбрам графа и притом
только по одному разу.

Эйлеров
цикл — это эйлеров путь, являющийся
циклом, то есть замкнутый путь, проходящий
через каждое ребро графа ровно по одному
разу.

Условие
существования:

В
неориентированном графе эйлеров цикл
существует тогда и только тогда, когда
граф связный или будет являться связным,
если удалить из него все изолированные
вершины, и в нём отсутствуют вершины
нечётной степени.

В
ориентированном графе эйлеров цикл
существует тогда и только тогда, когда
он сильно связан (то есть из любой
вершины графа существует ориентированный
путь в любую другую) или среди его
компонент сильной связности только
одна содержит ребра (а все остальные
являются изолированными вершинами) и
для каждой вершины графа её входящая
степень любой вершины равна её выходной
степени.

Алгоритм
нахождения:

Для
поиска эйлерова цикла воспользуемся
тем, что эйлеров цикл — это объединение
всех простых циклов графа. Следовательно,
задача — эффективно найти все циклы
и эффективно объединить их в один.

Реализовать
это можно, например, так, рекурсивно:

procedure
FindEulerPath (V)

1.
перебрать все рёбра, выходящие из
вершины V; каждое такое ребро удаляем
из графа, и вызываем FindEulerPath из второго
конца этого ребра;

2.
добавляем вершину V в ответ.

Сложность
полученного алгоритма — O(M), то есть
линейная относительно количества рёбер
М в данном графе.

Гамильтонов цикл: определение, алгоритм нахождения на основе динамического программирования

Гамильтонов
цикл – цикл проходящий через каждую
вершину графа ровно один раз. Граф
который имеет гамильтонов цикл называется
гамильтонов граф.

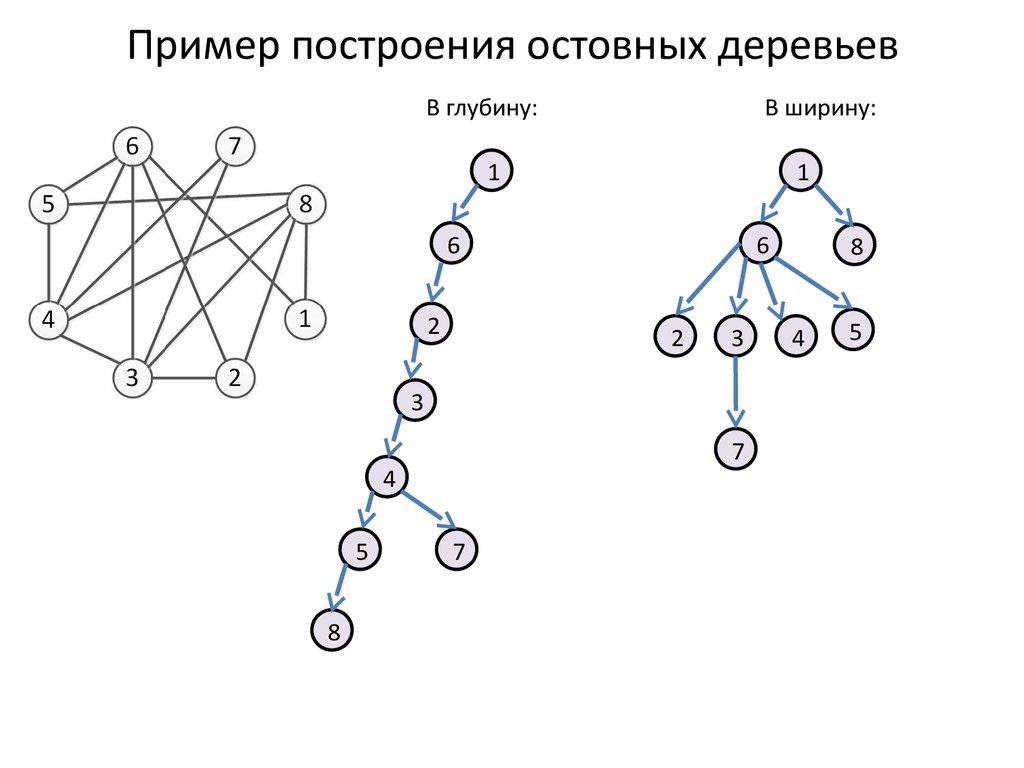
Деревья: остовное дерево, алгоритм Крускала

Остовное
дерево — ациклический связный подграф
данного связного неориентированного
графа, в который входят все его вершины.

Понятие
остовный лес неоднозначно, под ним
могут понимать один из следующих
подграфов:

любой
ациклический подграф, в который входят
все вершины графа, но не обязательно
связный;
в
несвязном графе — подграф, состоящий
из объединения остовных деревьев для
каждой его компоненты связности.

Остовное
дерево также иногда называют покрывающим
деревом, остовом или скелетом графа.
Ударение в слове «остовный» у разных
авторов указывается на первый (от слова
о́стов) или на второй слог.

П
ример
минимального остовного дерева.

Свойства

Любое
остовное дерево в графе с n вершинами
содержит ровно n-1 ребро.

Число
остовных деревьев в полном графе на n
вершинах равно n^{n-2}; это утверждение
называется формулой Кэли

Число
остовных деревьев в полном двудольном
графе Km.n
равно mn-1*nm-1

В
общем случае, число остовных деревьев
в произвольном графе может быть вычислено
при помощи так называемой матричной
теоремы о деревьях.

Остовное
дерево может быть построено практически
любым алгоритмом обхода графа, например
поиском в глубину или поиском в ширину.
Оно состоит из всех пар рёбер u,v), таких,
что алгоритм, просматривая вершину u,
обнаруживает в её списке смежности
новую, не обнаруженную ранее вершину
v.

Остовные
деревья, построенные при обходе графа
алгоритмом Дейкстры, начиная из вершины
s, обладают тем свойством, что кратчайший
путь в графе из s до любой другой вершины
— это (единственный) путь из s до этой
вершины в построенном остовном дереве.

Существует
также несколько параллельных и
распределённых алгоритмов нахождения
остовного дерева. Как практический
пример распределённого алгоритма можно
привести протокол STP.

Если
каждому ребру графа присвоен вес (длина,
стоимость и т. п.), то нахождением
оптимального остовного дерева, которое
минимизирует сумму весов входящих в
него рёбер, занимаются многочисленные
алгоритмы нахождения минимального
остовного дерева.

Задача
о нахождении остовного дерева, в котором
степень каждой вершины не превышает
некоторой наперёд заданной константы
k, является NP-полной/

Алгоритм
Краскала (англ. Kruskal’s algorithm) — алгоритм
поиска минимального остовного дерева
(англ. minimum spanning tree, MST) во взвешенном
неориентированном связном графе.

Будем
последовательно строить подграф F графа
G (“растущий лес”), пытаясь на каждом
шаге достроить F до некоторого MST. Начнем
с того, что включим в F все вершины графа
G. Теперь будем обходить множество E(G)
в порядке неубывания весов ребер. Если
очередное ребро e соединяет вершины
одной компоненты связности F, то
добавление его в остов приведет к
возникновению цикла в этой компоненте
связности. В таком случае, очевидно, e
не может быть включено в F. Иначе e
соединяет разные компоненты связности
F, тогда существует ⟨S,T⟩
разрез такой, что одна из компонент
связности составляет одну его часть,
а оставшаяся часть графа — вторую.
Тогда e — минимальное ребро, пересекающее
этот разрез. Значит, из леммы о безопасном
ребре следует, что e является безопасным,
поэтому добавим это ребро в F. На последнем
шаге ребро соединит две оставшиеся
компоненты связности, полученный
подграф будет минимальным остовным
деревом графа G. Для проверки возможности
добавления ребра используется система
непересекающихся множеств.

Соседние файлы в предмете Государственный экзамен

Источник

Существование эйлерова цикла и эйлерова пути[править | править код]

В неориентированном графе[править | править код]

В ориентированном графе[править | править код]

Поиск эйлерова пути в графе[править | править код]

Поиск эйлерова цикла в графе[править | править код]

Алгоритм Флёри[править | править код]

Алгоритм на основе циклов[править | править код]

Примечания[править | править код]

См. также[править | править код]

Ссылки[править | править код]

Эйлеров путь и цикл

Алгоритм поиска Эйлеров цикла

Алгоритм поиска Эйлервой цепи

Как использовать

Эйлеров цикл: определение, условие существования, алгоритм нахождения

Гамильтонов цикл: определение, алгоритм нахождения на основе динамического программирования

Деревья: остовное дерево, алгоритм Крускала

Вам также может понравиться

Как найти где воевала часть

Как в пульте найти телевизор dexp

Как найти видео по стоп кадру

Добавить комментарий Отменить ответ