The following is a demo implementation in C# (and Java, see end of answer) based on depth first search.
An outer loop scans all nodes of the graph and starts a search from every node. Node neighbours (according to the list of edges) are added to the cycle path. Recursion ends if no more non-visited neighbours can be added. A new cycle is found if the path is longer than two nodes and the next neighbour is the start of the path. To avoid duplicate cycles, the cycles are normalized by rotating the smallest node to the start. Cycles in inverted ordering are also taken into account.
This is just a naive implementation.
The classical paper is: Donald B. Johnson. Finding all the elementary circuits of a directed graph. SIAM J. Comput., 4(1):77–84, 1975.
A recent survey of modern algorithms can be found here
using System;
using System.Collections.Generic;
namespace akCyclesInUndirectedGraphs
{
class Program
{
// Graph modelled as list of edges
static int[,] graph =
{
{1, 2}, {1, 3}, {1, 4}, {2, 3},
{3, 4}, {2, 6}, {4, 6}, {7, 8},
{8, 9}, {9, 7}
};
static List<int[]> cycles = new List<int[]>();
static void Main(string[] args)
{
for (int i = 0; i < graph.GetLength(0); i++)
for (int j = 0; j < graph.GetLength(1); j++)
{
findNewCycles(new int[] {graph[i, j]});
}
foreach (int[] cy in cycles)
{
string s = "" + cy[0];
for (int i = 1; i < cy.Length; i++)
s += "," + cy[i];
Console.WriteLine(s);
}
}
static void findNewCycles(int[] path)
{
int n = path[0];
int x;
int[] sub = new int[path.Length + 1];
for (int i = 0; i < graph.GetLength(0); i++)
for (int y = 0; y <= 1; y++)
if (graph[i, y] == n)
// edge referes to our current node
{
x = graph[i, (y + 1) % 2];
if (!visited(x, path))
// neighbor node not on path yet
{
sub[0] = x;
Array.Copy(path, 0, sub, 1, path.Length);
// explore extended path
findNewCycles(sub);
}
else if ((path.Length > 2) && (x == path[path.Length - 1]))
// cycle found
{
int[] p = normalize(path);
int[] inv = invert(p);
if (isNew(p) && isNew(inv))
cycles.Add(p);
}
}
}
static bool equals(int[] a, int[] b)
{
bool ret = (a[0] == b[0]) && (a.Length == b.Length);
for (int i = 1; ret && (i < a.Length); i++)
if (a[i] != b[i])
{
ret = false;
}
return ret;
}
static int[] invert(int[] path)
{
int[] p = new int[path.Length];
for (int i = 0; i < path.Length; i++)
p[i] = path[path.Length - 1 - i];
return normalize(p);
}
// rotate cycle path such that it begins with the smallest node
static int[] normalize(int[] path)
{
int[] p = new int[path.Length];
int x = smallest(path);
int n;
Array.Copy(path, 0, p, 0, path.Length);
while (p[0] != x)
{
n = p[0];
Array.Copy(p, 1, p, 0, p.Length - 1);
p[p.Length - 1] = n;
}
return p;
}
static bool isNew(int[] path)
{
bool ret = true;
foreach(int[] p in cycles)
if (equals(p, path))
{
ret = false;
break;
}
return ret;
}
static int smallest(int[] path)
{
int min = path[0];
foreach (int p in path)
if (p < min)
min = p;
return min;
}
static bool visited(int n, int[] path)
{
bool ret = false;
foreach (int p in path)
if (p == n)
{
ret = true;
break;
}
return ret;
}
}
}
The cycles for the demo graph:
1,3,2
1,4,3,2
1,4,6,2
1,3,4,6,2
1,4,6,2,3
1,4,3
2,6,4,3
7,9,8
The algorithm coded in Java:
import java.util.ArrayList;
import java.util.List;
public class GraphCycleFinder {
// Graph modeled as list of edges
static int[][] graph =
{
{1, 2}, {1, 3}, {1, 4}, {2, 3},
{3, 4}, {2, 6}, {4, 6}, {7, 8},
{8, 9}, {9, 7}
};
static List<int[]> cycles = new ArrayList<int[]>();
/**
* @param args
*/
public static void main(String[] args) {
for (int i = 0; i < graph.length; i++)
for (int j = 0; j < graph[i].length; j++)
{
findNewCycles(new int[] {graph[i][j]});
}
for (int[] cy : cycles)
{
String s = "" + cy[0];
for (int i = 1; i < cy.length; i++)
{
s += "," + cy[i];
}
o(s);
}
}
static void findNewCycles(int[] path)
{
int n = path[0];
int x;
int[] sub = new int[path.length + 1];
for (int i = 0; i < graph.length; i++)
for (int y = 0; y <= 1; y++)
if (graph[i][y] == n)
// edge refers to our current node
{
x = graph[i][(y + 1) % 2];
if (!visited(x, path))
// neighbor node not on path yet
{
sub[0] = x;
System.arraycopy(path, 0, sub, 1, path.length);
// explore extended path
findNewCycles(sub);
}
else if ((path.length > 2) && (x == path[path.length - 1]))
// cycle found
{
int[] p = normalize(path);
int[] inv = invert(p);
if (isNew(p) && isNew(inv))
{
cycles.add(p);
}
}
}
}
// check of both arrays have same lengths and contents
static Boolean equals(int[] a, int[] b)
{
Boolean ret = (a[0] == b[0]) && (a.length == b.length);
for (int i = 1; ret && (i < a.length); i++)
{
if (a[i] != b[i])
{
ret = false;
}
}
return ret;
}
// create a path array with reversed order
static int[] invert(int[] path)
{
int[] p = new int[path.length];
for (int i = 0; i < path.length; i++)
{
p[i] = path[path.length - 1 - i];
}
return normalize(p);
}
// rotate cycle path such that it begins with the smallest node
static int[] normalize(int[] path)
{
int[] p = new int[path.length];
int x = smallest(path);
int n;
System.arraycopy(path, 0, p, 0, path.length);
while (p[0] != x)
{
n = p[0];
System.arraycopy(p, 1, p, 0, p.length - 1);
p[p.length - 1] = n;
}
return p;
}
// compare path against known cycles
// return true, iff path is not a known cycle
static Boolean isNew(int[] path)
{
Boolean ret = true;
for(int[] p : cycles)
{
if (equals(p, path))
{
ret = false;
break;
}
}
return ret;
}
static void o(String s)
{
System.out.println(s);
}
// return the int of the array which is the smallest
static int smallest(int[] path)
{
int min = path[0];
for (int p : path)
{
if (p < min)
{
min = p;
}
}
return min;
}
// check if vertex n is contained in path
static Boolean visited(int n, int[] path)
{
Boolean ret = false;
for (int p : path)
{
if (p == n)
{
ret = true;
break;
}
}
return ret;
}
}
Графы
Как хранить графы?
Граф — $G=(V, E)$.
-
матрица смежности:
+ $O(1)$ на проверку $(i, j) in E$
— Размер $Theta(|V|^2)$
— $Theta(|V|^2)$ на обход всех рёбер -
список смежности
+ Размер $O(|V| + |E|)$
+ Обход $O(|V| + |E|)$
— $O(|V|)$ на проверку $(i, j) in E$ -
матрица инцидентности (почти не используется)
+ подходит для мультиграфов
Поиск в глубину
def Explore(v):
visited[v] = true
previsit(v)
for u : (v, u) in E # O(E)
if not visited[u]
Explore(v) # O(V) вызовов Explore
postvisit(v)
def DFS(G):
for i = 1 to |V|:
visited[i] = False
for v = 1 to |V|: # O(V)
if not visited[v]:
Explore(v)
Итого: $O(|V| + |E|)$ для списков смежности, и $O(|V|^2)$ для матриц смежности.
Компоненты связности в неориентированном графе
Как решить задачу с помощью $DFS$‘a?
Заведём массив, который содержит компоненты вершин. То есть для каждой вершины мы храним, в какой компоненте она находится.
def CC(G):
for v = 1 to |V|:
CC[v] = 0
global counter = 0
for v = 1 to |V|:
counter += 1
if CC[v] == 0:
Explore(v)
def previsit:
CC[v] = counter
Поиск циклов в неориентированном графе
$DFS$ позволяет нам построить дерево по графу. Соответственно, если в процедуре Explore вершина $v$ уже была посещена, это означает существование цикла.
Чтобы вернуть цикл, добавим в массив сначала вершину $v$, а потом будем возвращаться вверх по стеку вызовов, добавлять просматриваемую вершину и так до тех пор пока не не встретим вершину $v$.
Утверждение. В графе есть цикл $Leftrightarrow$ в обходе $DFS$ есть обратное ребро.
Док-во. Если в графе есть цикл, рассмотрим цикл. Там возьмём первую вершину. Все остальные вершины рассмотрим тот же самый $Explore$, но одно ребро мы пройти не сможем (количество рёбер в дереве меньше чем вершин, а в цикле их столько же, то есть одно ребро останется), оно и смотрит наверх.
Обратно очевидно, если есть обратное ребро, то вот он цикл.
Поиск в глубину в ориентированном графе
Поиск циклов
см. картинку
- рёбра обхода
- прямые рёбра
- перекрёстные рёбра
- обратные рёбра
Утверждение. В орграфе есть цикл $Leftrightarrow$ в обходе есть обратное ребро.
Будем записывать время заходи и исхода из вершин.
global counter = 1 # time
previsit(v):
pre[v] = counter
counter += 1
postvisit(v):
post[v] = counter
counter += 1
Утверждение. Для $forall (u, v) in E$ отрезки на числовой прямой $[ pre[v], post[v] ]$ и $[ pre[u], post[u] ]$ либо не пересекаются, либо один содержит другой. То есть не может быть такой картинки:
v *------------*
*----------* u
Рассмотрим различные соотношения отрезков для ребра $(u, v)$.
-
Ребро дерева / прямое ребро
u *------------* v *-----* -
Обратное ребро
v *------------* u *-----* -
Перекрёстное ребро. Обратное положение невозможно.
v *------* *-------* u
Таким образом, если мы найдём обратное ребро, мы найдём цикл.
Топологическая сортировка (всегда для ациклических графов)
Топологическая сортировка — это такой порядок вершин что: $forall (u,v) in E: T[i] < T[v]$.
По сути мы уже решили эту задачу, используя время выхода из вершин.
Утверждение. Вершина с максимальным $post$ — это вершина, которая ни от чего не зависит. Это исток (source, в неё не входит никакие рёбра).
Следствие. вершины в порядке убывания $post$ — это топологическая сортировка. (По индукции будем убирать вершину с максимальным post, и искать следующую с максимальным).
Рассмотрим алгоритм поиска всех элементарных циклов в неориентированном графе. В этой статье будет приведено описание алгоритма и его реализация на языке программирования C#.
Циклом в графе называется такая конечная цепь, которая начинается и заканчивается в одной вершине. Цикл обозначается последовательностью вершин, которые он содержит, например: (3-5-6-7-3).
Кстати, про цепи, а именно про поиск элементарных цепей в графе мы недавно писали.
Цикл называется элементарным, если все вершины, входящие в него, различны (за исключением начальной и конечной).
Давайте рассмотрим пример. Пусть дан такой граф:
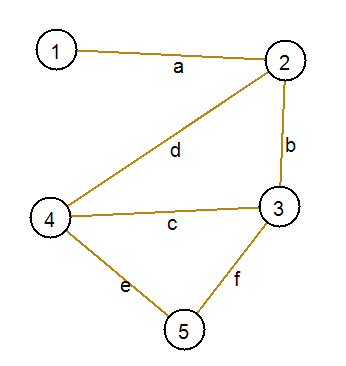
Перечислим все элементарные циклы в нем: 2-3-4-2, 2-3-5-4-2, 3-2-4-3, 3-2-4-5-3, 3-4-5-3, 4-3-2-4, 4-3-5-4, 4-2-3-5-4, 5-4-3-5, 5-4-2-3-5.
Допустим граф задается, как G = (V, E), где V – множество вершин графа, а E – множество ребер этого графа. Вершины и ребра представим объектами таких классов:
|
//вершина class Vertex { public int x, y; public Vertex(int x, int y) { this.x = x; this.y = y; } } |
, где x, y – координаты центра вершины на плоскости.
|
//ребро class Edge { public int v1, v2; public Edge(int v1, int v2) { this.v1 = v1; this.v2 = v2; } } |
, где v1, v2 – номера вершин, которые соединяет данное ребро.
Важно! Нумерация вершин начинается с нуля!
Множества вершин и ребер графа будем хранить в списках List<>:
|
List<Vertex> V; List<Edge> E; |
Для поиска всех элементарных циклов в неориентированном графе будем использовать модификацию рекурсивного алгоритма “поиск в глубину” (DFS). DFS (Depth-first search) — это один из алгоритмов для обхода графа. Обязательно почитайте про него подробнее здесь.
Модифицируем алгоритм DFS в DFScycle. Прототип функции DFScycle будет таким:
|
DFScycle(int u, int endV, List<Edge> E, int[] color, int unavailableEdge, List<int> cycle) |
, где u – номер вершины, в которой мы находимся в данный момент, endV – номер конечной вершины цикла, Е – список ребер, color[] – массив, в котором хранятся цвета вершин, unavailableEdge — см. ниже, cycle – список, в который заносится последовательность вершин искомого цикла.
В конечном итоге будем преобразовывать последовательность номеров вершин цикла из списка cycle в строку вида: «2-6-7-2». Хранить всю совокупность элементарных циклов будем в списке строк:
|
List<string> catalogCycles; |
Рассмотрим работу алгоритма DFScycle. В начальный момент времени все вершины графа окрашены в белый цвет. Необходимо выполнить следующее:
Перебираем все вершины, любая из них может иметь элементарный цикл. На каждой итерации перекрашиваем все вершины в белый цвет (обозначим его 1, а черный цвет будем обозначать 2). Добавляем в список вершин цикла cycle текущую вершину.
Теперь поговорим про параметр unavailableEdge. Вершину, для которой ищем цикл, перекрашивать в черный цвет не будем, иначе программа не сможет в нее вернуться, поскольку эта вершина окажется недоступной. Поэтому введем переменную unavailableEdge, в которую будем передавать номер последнего ребра, по которому осуществлялся переход между вершинами, соответственно это ребро на следующем шаге окажется недоступным для перехода. В действительности это необходимо только на первом уровне рекурсии, чтобы избежать некорректной работы алгоритма и вывода, например, ошибочного результата поиска 1-2-1 при наличии такого графа:
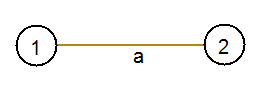
Вызовем процедуру DFScycle(…).
|
private void cyclesSearch() { int[] color = new int[V.Count]; for (int i = 0; i < V.Count; i++) { for (int k = 0; k < V.Count; k++) color[k] = 1; List<int> cycle = new List<int>(); //поскольку в C# нумерация элементов начинается с нуля, то для //удобочитаемости результатов поиска в список добавляем номер i + 1 cycle.Add(i + 1); DFScycle(i, i, E, color, –1, cycle); } } |
Процедура DFScycle(int u, int endV, List<Edge> E, int[] color, int unavailableEdge, List<int> cycle).
- ЕСЛИ номер вершины u не равен endV, то мы не достигли конца элементарного цикла, поэтому перекрашиваем вершину u в черный цвет. ИНАЧЕ ЕСЛИ число вершин в списке cycle больше или равно двум – конец цикла достигнут: добавляем цикл cycle в список catalogCycles и выполняем возврат из функции.
- Для всякой вершины w, смежной с вершиной u и окрашенной в белый цвет, рекурсивно выполняем процедуру DFScycle(w, endV, E, color, unavailableE, cycleNEW), предварительно добавив вершину w в список cycleNEW. Возвращаем вершине w белый цвет (возможно через нее проходят другие циклы, поэтому не будем исключать ее из рассмотрения).
Примечание 1. Поскольку алгоритм обходит граф во все стороны, то выходит, что он обходит цикл в обе стороны, в итоге программа находит одинаковые циклы вида: 1-3-4-1, 1-4-3-1. Получаются своеобразные палиндромы. В реализации функции DFScycle присутствует механизм исключения таких палиндромов из списка результатов поиска.
Примечание 2. Поскольку в языке C# списки List передаются по ссылке (а не по значению), то для корректной работы алгоритма необходимо создавать копию списка cycle cycleNEW и передавать ее [копию] в новый вызов функции DFScycle().
Реализация процедуры DFScycle на языке программирования C#:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
private void DFScycle(int u, int endV, List<Edge> E, int[] color, int unavailableEdge, List<int> cycle) { //если u == endV, то эту вершину перекрашивать не нужно, иначе мы в нее не вернемся, а вернуться необходимо if (u != endV) color[u] = 2; else if (cycle.Count >= 2) { cycle.Reverse(); string s = cycle[0].ToString(); for (int i = 1; i < cycle.Count; i++) s += “-“ + cycle[i].ToString(); bool flag = false; //есть ли палиндром для этого цикла графа в List<string> catalogCycles? for (int i = 0; i < catalogCycles.Count; i++) if (catalogCycles[i].ToString() == s) { flag = true; break; } if (!flag) { cycle.Reverse(); s = cycle[0].ToString(); for (int i = 1; i < cycle.Count; i++) s += “-“ + cycle[i].ToString(); catalogCycles.Add(s); } return; } for (int w = 0; w < E.Count; w++) { if (w == unavailableEdge) continue; if (color[E[w].v2] == 1 && E[w].v1 == u) { List<int> cycleNEW = new List<int>(cycle); cycleNEW.Add(E[w].v2 + 1); DFScycle(E[w].v2, endV, E, color, w, cycleNEW); color[E[w].v2] = 1; } else if (color[E[w].v1] == 1 && E[w].v2 == u) { List<int> cycleNEW = new List<int>(cycle); cycleNEW.Add(E[w].v1 + 1); DFScycle(E[w].v1, endV, E, color, w, cycleNEW); color[E[w].v1] = 1; } } } |
Результатом выполнения этой процедуры поиска элементарных циклов для графа, рассмотренного выше, будет такая последовательность циклов:

Скачать код процедуры DFScycle
Графы
Как хранить графы?
Граф — $G=(V, E)$.
-
матрица смежности:
+ $O(1)$ на проверку $(i, j) in E$
— Размер $Theta(|V|^2)$
— $Theta(|V|^2)$ на обход всех рёбер -
список смежности
+ Размер $O(|V| + |E|)$
+ Обход $O(|V| + |E|)$
— $O(|V|)$ на проверку $(i, j) in E$ -
матрица инцидентности (почти не используется)
+ подходит для мультиграфов
Поиск в глубину
def Explore(v): visited[v] = true previsit(v) for u : (v, u) in E # O(E) if not visited[u] Explore(v) # O(V) вызовов Explore postvisit(v)
def DFS(G): for i = 1 to |V|: visited[i] = False for v = 1 to |V|: # O(V) if not visited[v]: Explore(v)
Итого: $O(|V| + |E|)$ для списков смежности, и $O(|V|^2)$ для матриц смежности.
Компоненты связности в неориентированном графе
Как решить задачу с помощью $DFS$’a?
Заведём массив, который содержит компоненты вершин. То есть для каждой вершины мы храним, в какой компоненте она находится.
def CC(G): for v = 1 to |V|: CC[v] = 0 global counter = 0 for v = 1 to |V|: counter += 1 if CC[v] == 0: Explore(v)
def previsit: CC[v] = counter
Поиск циклов в неориентированном графе
$DFS$ позволяет нам построить дерево по графу. Соответственно, если в процедуре Explore вершина $v$ уже была посещена, это означает существование цикла.
Чтобы вернуть цикл, добавим в массив сначала вершину $v$, а потом будем возвращаться вверх по стеку вызовов, добавлять просматриваемую вершину и так до тех пор пока не не встретим вершину $v$.
Утверждение. В графе есть цикл $Leftrightarrow$ в обходе $DFS$ есть обратное ребро.
Док-во. Если в графе есть цикл, рассмотрим цикл. Там возьмём первую вершину. Все остальные вершины рассмотрим тот же самый $Explore$, но одно ребро мы пройти не сможем (количество рёбер в дереве меньше чем вершин, а в цикле их столько же, то есть одно ребро останется), оно и смотрит наверх.
Обратно очевидно, если есть обратное ребро, то вот он цикл.
Поиск в глубину в ориентированном графе
Поиск циклов
см. картинку
- рёбра обхода
- прямые рёбра
- перекрёстные рёбра
- обратные рёбра
Утверждение. В орграфе есть цикл $Leftrightarrow$ в обходе есть обратное ребро.
Будем записывать время заходи и исхода из вершин.
global counter = 1 # time previsit(v): pre[v] = counter counter += 1 postvisit(v): post[v] = counter counter += 1
Утверждение. Для $forall (u, v) in E$ отрезки на числовой прямой $[ pre[v], post[v] ]$ и $[ pre[u], post[u] ]$ либо не пересекаются, либо один содержит другой. То есть не может быть такой картинки:
v *------------*
*----------* u
Рассмотрим различные соотношения отрезков для ребра $(u, v)$.
-
Ребро дерева / прямое ребро
u *------------* v *-----* -
Обратное ребро
v *------------* u *-----* -
Перекрёстное ребро. Обратное положение невозможно.
Таким образом, если мы найдём обратное ребро, мы найдём цикл.
Топологическая сортировка (всегда для ациклических графов)
Топологическая сортировка — это такой порядок вершин что: $forall (u,v) in E: T[i] < T[v]$.
По сути мы уже решили эту задачу, используя время выхода из вершин.
Утверждение. Вершина с максимальным $post$ — это вершина, которая ни от чего не зависит. Это исток (source, в неё не входит никакие рёбра).
Следствие. вершины в порядке убывания $post$ — это топологическая сортировка. (По индукции будем убирать вершину с максимальным post, и искать следующую с максимальным).
Обходите граф в глубину. Стеком вершин назовем маршрут от начальной вершины до текущей вершины, по которому мы до неё добрались. Заведите множество вершин V, которые вы уже посетили. Для каждой вершины помните, из какой вершины вы в неё пришли (словарь P) при обходе. Если при обходе вы видите в числе соседей вершины уже посещённую вершину K, которая не входит в текущий стек вершин, то “разматывайте” путь от K до изначальной вершины, используя информацию из словаря P, это в совокупности со стеком вершин даст цикл. А если K входит в стек вершин, то циклом будет часть стека от K до вершины стека.
Дополнение не совсем в тему. Есть элегантный алгоритм, который для числа n определяет, входит ли вершина в цикл с повторами длины n. Но так как цикл с повторами, а граф неориентированный, то циклы вида A-B-A-B-A-… тожу будут учитываться. Видимо, можно придумать способ вычесть их количество из полученного числа циклов. Так я и собирался делать, но потом понял, что ничего этого не нужно и задача решается простым обходом в глубину.
UPD. Оказалось, что мой ответ неправильный. Правильные мысли описаны в научной статье.
