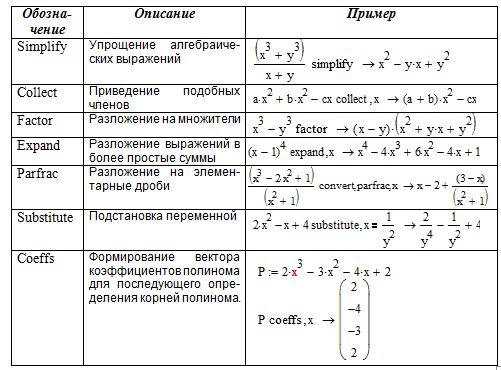
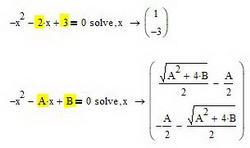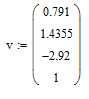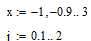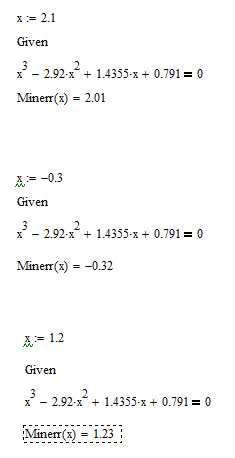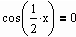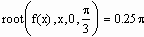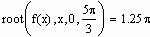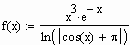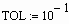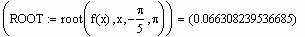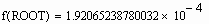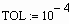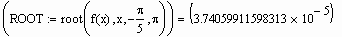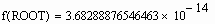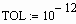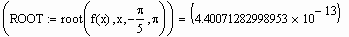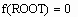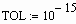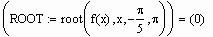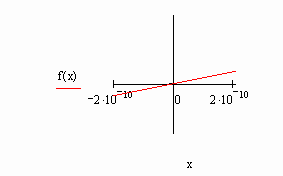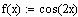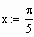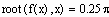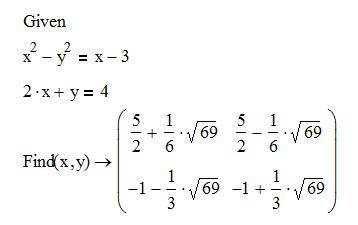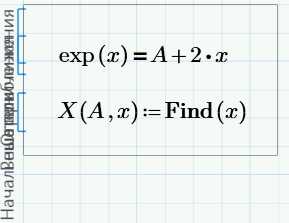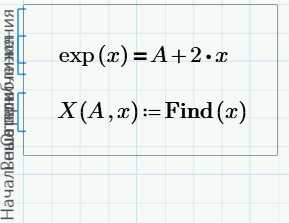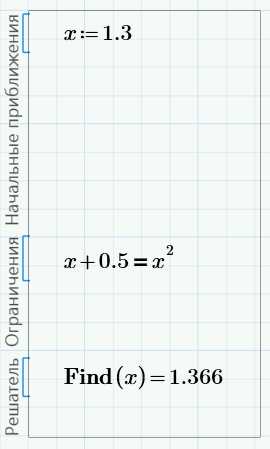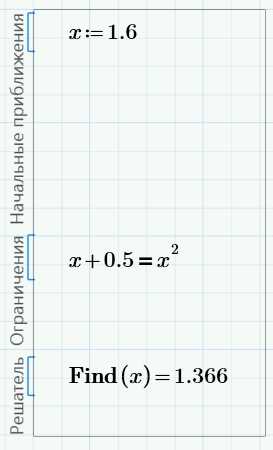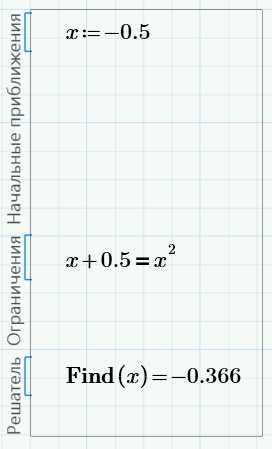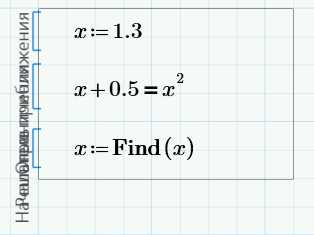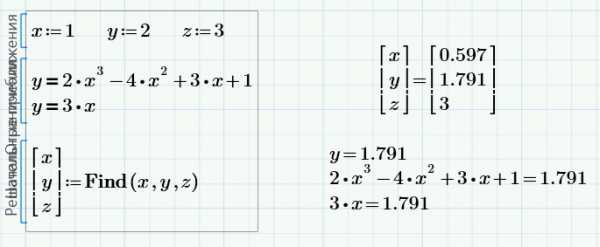Для решения уравнений в Mathcad можно воспользоваться двумя способами:
- Метод Given – Find
- Метод Solve
Использование метода Given – Find:
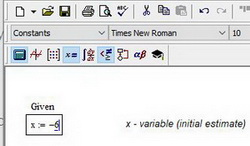
Это наиболее распространенный способ решения обычных алгебраических уравнений. Он достаточно прост. В рабочем поле записываем слово Given. Это служебное слово. Оно подключает определенные программные модули mathcad для обработки исходных данных, необходимых для решения уравнения численными методами.
Затем указывается начальное приближение для искомой переменной. Это нужно для увеличения скорости и точности решения уравнения. Если начальное приближение не задать, то mathcad по умолчанию примет его равным нулю
Рис. 1. Ввод данных в поле mathcad
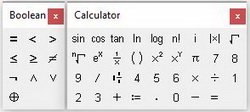
Далее вводится уравнение. Его можно записать в явном или неявном виде. Само уравнение набирается с клавиатуры вручную с использованием панели Calculator. Из этой панели можно взять основные математические операции: дроби, тригонометрию, факториалы и прочее. Уравнение нужно записывать с использованием логического символа “ровно”. На панели Boolean он выделен жирным шрифтом (см. рис. 2)
Рис. 2. Панели Boolean и Calculator
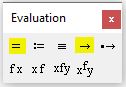
После уравнения вводится функция Find(x) (где х – переменная). Это функция, которая возвращает результат. Значение функции Find(x) можно присвоить какой-либо переменной с помощью символа “:=” и использовать ее далее в расчетах
Для получения результата, после Find(x) следует поставить символ “→” либо “=” из панели Evaluation (см. рис. 3). Причем, если вы используете символ “→“, то mathcad определит все корни уравнения и сформирует матрицу результатов. Но если вы используете символ “=“, то mathcad выведет единственный корень, который был наиболее близок к начальному приближению. Так что, если вы не знаете сколько корней имеет уравнение, то лучше использовать стрелочку
Рис. 3. Панель “Evaluation”
В зависимости от сложности уравнения через определенное время MathCad выведет результат. На рис.4 можно рассмотреть синтаксис и различие результатов выводимых mathcad. Обратите внимание, что выводимые результаты одного и того же уравнения различны
Рис. 4. Результат численного решения уравнения
Mathcad позволяет решать уравния в символьном виде. Например, если мы заменим все числовые константы на неизвестные параметры и решим уравнение относительно x, то результат выведется в символьном виде (см. рис. 5). Причем, обратите внимание, что в данном случае нам не нужно вводить начальное приближение и мы должны использовать символ “→” для вывода результата
Рис. 5. Результат символьного решения уравнения
Использование метода Solve:
Этот метод отличается от выше рассмотренного синтаксисом. На свободном поле вводим уравнение с использованием логического символа “ровно” из панели Boolean. После ввода уравнения, не смещая курсор ввода, на панели Symbolic нажимаем кнопку solve (см. рис. 6)
Рис. 6. Панель Symbolic
Затем ставим запятую и вводим переменную, относительно которой нужно решить уравнение (в нашем случае это x). Нажимаем Enter на клавиатуре и смотрим результат (см. рис. 7)
Рис. 7. Результат решения уравнения методом Solve
Обратите внимание, что метод подходит как для численного так и для символьного представления результатов
Как показывает моя личная инженерная практика, иногда не удается решить уравнения с помощью Given – Find, но получается в Solve. При этом, к сожалению, метод Solve не очень удобен для далнейшего использования результатов решения уравнения
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Поволжский
государственный технологический
университет
Кафедра
радиотехники и связи
Отчет
по практике
Вариант
№ 1
Нахождение корней
уравнения в MathCad
Выполнила:
студентка группы ИТС-11
Блинова
Е.В.
Проверил:
аспирант кафедры РТиС
Чернов
А.А.
Йошкар-Ола
2010
Цель
работы: нахождение
корней уравнения в программе MathCad
с использованием встроенных функций
root,
polyroots,
символьного решения.
|
№ |
Интервал |
Уравнение |
|
1 |
[-1; |
x3-2,92x2+1,4355x+0,791=0 |
І
-
Запускаем
программу MathCad -
Записываем
функцию f(x)=
x3-2,92x2+1,4355x+0,791 -
Интервал
для нахождения корней определяется
шагом в 0.1 т.е.
-
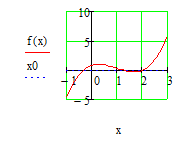
Строим
график функции f(x)=
x3-2,92x2+1,4355x+0,791
и x0=0.
Форматируем график. Нажимаем на пустом
месте в поле графика, вызываем контекстное
меню (пкм) во вкладке «Формат» ставим
галочку в поле «Линии сетки» и «Стиль
осей: пересекающиеся»
-
Далее,
на графике определяем точки пересечения
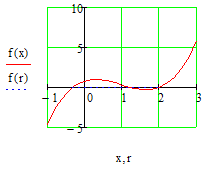
кривой заданной функцией f(x)
и х0. Мы видим, что таких точек всего 3.
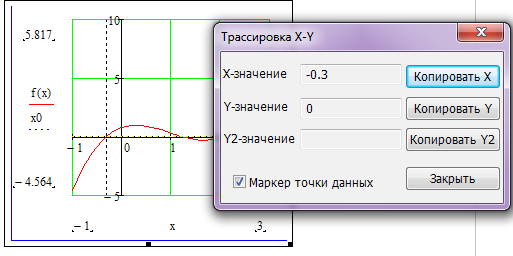
Точное значение х1, х2, х3 мы сможем узнать
вызвав контекстное меню в поле
«Трассировка». Получим значения: -0.3;
1.2;2.1 соответственно.
-
Вычислить
значение корней с помощью формул: root
(f(x1),x1), root (f(x2),x2), root (f(x3),x3)
II
-
Найдем
корни заданного в варианте уравнения
вторым способом. -
Создаем
вектор из коэффициентов уравнения,
используя панель управления Матрица.
Задав один столбец и четыре строки для
коэффициентов уравнения.
Вектор
из коэффициентов уравнения будет иметь
следующий вид
-
С
помощью встроенной функции r:=polyroots(v)
найдем корни уравнения и представим
их в виде вектора rT,
транспонированного по отношению к r,
то есть преобразованного из столбца в
строку.
-
Создаем
циклы для переменной х
и количества найденных корней:
-
Строим
график для функции f(x)
и f(r)
III
-
Найдем
корни уравнения 3 способом. -
Приравниваем
левую часть уравнения к нулю с помощью
логического знака «=» (Ctrl+=) -
Выделяем
переменную х и в главном меню выбираем
Символика/Переменная/Решить -
Найдены
корни уравнения запишутся в виде
вектора:
IV
4
способ нахождения приближенного значения
решения уравнения использованием
функции minerr(
x1,…).
-
Записываем
чему равно х. -
Вводим
ключевое слово given
(дано), с которого начинается блок
решений. -
Записывем
уравнение, используя знак логического
равенства между правой и левой частью
уравнения. -
Обращаемся
к функции minerr(
x).
Корень будет найден.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
11.03.2016149.05 Кб501.docx
- #
- #
Определить все корни уравнения в маткаде
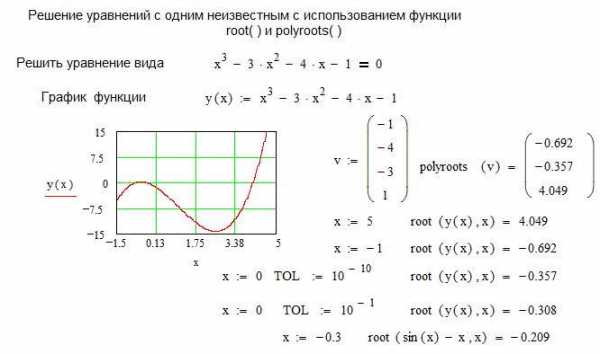
Для решения одного уравнения с одним неизвестным используется функция root. Аргументами этой функции являются выражение и переменная, входящая в выражение. Ищется значение переменной, при котором выражение обращается в ноль. Функция возвращает значение переменной, которое обращает выражение в ноль.
| root( f(z), z) | Возвращает значение z, при котором выражение или функция f(z) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр. |
Первый аргумент есть либо функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения.
Второй аргумент — имя переменной, которое используется в выражении. Это та переменная, варьируя которую Mathcad будет пытаться обратить выражение в ноль. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.
Рассмотрим пример, как найти a — решение уравнения e x = x 3 . Для этого выполните следующие шаги:
- Определите начальное значение переменной x. Введите x:3. Выбор начального приближения влияет на корень, возвращаемый Mathcad (если выражение имеет несколько корней).
- Определите выражение, которое должно быть обращено в ноль. Для этого перепишите уравнение e x = x 3 в виде x 3 – e x = 0. Левая часть этого выражения и является вторым аргументом функции root
- Определите переменную a как корень уравнения. Для этого введите a:root(x^3[Space]-e^x[Space],x).
- Напечатайте a=, чтобы увидеть значение корня.
При использовании функции root имейте в виду следующее:
- Удостоверьтесь, что переменной присвоено начальное значение до начала использования функции root.
- Для выражения с несколькими корнями, например x 2 – 1 = 0, начальное значение определяет корень, который будет найден Mathcad. На Рисунке 1 приведен пример, в котором функция root возвращает различные значения, каждое из которых зависит от начального приближения.
- Mathcad позволяет находить как комплексные, так и вещественные корни. Для поиска комплексного корня следует взять в качестве начального приближения комплексное число.
- Задача решения уравнения вида f(x) = g(x) эквивалентна задаче поиска корня выражения f(x) – g(x) =0. Для этого функция root может быть использована следующим образом:
Функция root предназначена для решения одного уравнения с одним неизвестным. Для решения систем уравнений используйте методику, описанную в следующем разделе “Системы уравнений”. Для символьного решения уравнений или нахождения точного численного решения уравнения в терминах элементарных функций выберите Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.
Рисунок 1: Использование графика и функции root для поиска корней уравнения.
Что делать, когда функция root не сходится
Mathcad в функции root использует для поиска корня метод секущей. Начальное значение, присвоенное переменной x, становится первым приближением к искомому корню. Когда значение выражения f(x) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным, и функция root возвращает результат.
Если после многих итераций Mathcad не может найти подходящего приближения, то появляется сообщение об ошибке “отсутствует сходимость”. Эта ошибка может быть вызвана следующими причинами:
- Уравнение не имеет корней.
- Корни уравнения расположены далеко от начального приближения.
- Выражение имеет локальные максимумы или минимумы между начальным приближением и корнями.
- Выражение имеет разрывы между начальным приближением и корнями.
- Выражение имеет комплексный корень, но начальное приближение было вещественным (или наоборот).
Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x)=0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее функция root будет сходиться к точному значению. roots;using plots to find
Некоторые советы по использованию функции root
В этом разделе приведены несколько советов по использованию функции root:
- Для изменения точности, с которой функция root ищет корень, можно изменить значение встроенной переменной TOL. Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, функция root будет сходиться медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке рабочего документа, используйте определение вида TOL := 0.01. Чтобы изменить значение TOL для всего рабочего документа, выберите из меню Математика команду Встроенные переменные и введите подходящее значение в поле TOL. Нажав “OK”, выберите из меню Математика команду Пересчитать всё, чтобы обновить все вычисления в рабочем документе с использованием нового значения переменной TOL.
- Если уравнение имеет несколько корней, пробуйте использовать различные начальные приближения, чтобы найти их. Использование графика функции полезно для нахождения числа корней выражения, их расположения и определения подходящих начальных приближений. Рисунок 1 показывает пример. Если два корня расположены близко друг от друга, можно уменьшить TOL, чтобы различить их.
- Если f(x) имеет малый наклон около искомого корня, функция может сходиться к значению r, отстоящему от корня достаточно далеко . В таких случаях для нахождения более точного значения корня необходимо уменьшить значение TOL. Другой вариант заключается в замене уравнения f(x)=0 на g(x)=0, где
Решение уравнений с параметром
Предположим, что нужно решать уравнение многократно при изменении одного из параметров этого уравнения. Например, пусть требуется решить уравнение для нескольких различных значений параметра a. Самый простой способ состоит в определении функции
Чтобы решить уравнение для конкретного значения параметра a, присвойте значение параметру a и начальное значение переменной x как аргументам этой функции. Затем найдите искомое значение корня, вводя выражение f(a,x)=.
Рисунок 2 показывает пример того, как такая функция может использоваться для нахождения корней исследуемого уравнения при различных значениях параметра. Обратите внимание, что, хотя начальное значение x непосредственно входит в определение функции, нет необходимости определять его в другом месте рабочего документа.
Рисунок 2: Определение функции пользователя с функцией root.
Нахождение корней полинома
Для нахождения корней выражения, имеющего вид
лучше использовать функцию polyroots, нежели root. В отличие от функции root, функция polyroots не требует начального приближения. Кроме того, функция polyroots возвращает сразу все корни, как вещественные, так и комплексные. На Рисунках 3 и 4 приведены примеры использования функции polyroots.
| polyroots(v) | Возвращает корни полинома степени . Коэффициенты полинома находятся в векторе v длины n+1. Возвращает вектор длины n, состоящий из корней полинома. |
Функция polyroots всегда возвращает значения корней полинома, найденные численно. Чтобы находить корни символьно, используйте команду Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.
Рисунок 3: Использование функции polyroots для решения задачи, изображенной на Рисунке 1.
Рисунок 4: Использование функции polyroots для поиска корней полинома.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Решение уравнений в MathCad
Для решения уравнений в Mathcad можно воспользоваться двумя способами:
Использование метода Given – Find:
Это наиболее распространенный способ решения обычных алгебраических уравнений. Он достаточно прост. В рабочем поле записываем слово Given. Это служебное слово. Оно подключает определенные программные модули mathcad для обработки исходных данных, необходимых для решения уравнения численными методами.
Затем указывается начальное приближение для искомой переменной. Это нужно для увеличения скорости и точности решения уравнения. Если начальное приближение не задать, то mathcad по умолчанию примет его равным нулю
Рис. 1. Ввод данных в поле mathcad
Далее вводится уравнение. Его можно записать в явном или неявном виде. Само уравнение набирается с клавиатуры вручную с использованием панели Calculator. Из этой панели можно взять основные математические операции: дроби, тригонометрию, факториалы и прочее. Уравнение нужно записывать с использованием логического символа “ровно”. На панели Boolean он выделен жирным шрифтом (см. рис. 2)
Рис. 2. Панели Boolean и Calculator
После уравнения вводится функция Find(x) (где х – переменная). Это функция, которая возвращает результат. Значение функции Find(x) можно присвоить какой-либо переменной с помощью символа “:=” и использовать ее далее в расчетах
Для получения результата, после Find(x) следует поставить символ “→” либо “=” из панели Evaluation (см. рис. 3). Причем, если вы используете символ “→“, то mathcad определит все корни уравнения и сформирует матрицу результатов. Но если вы используете символ “=“, то mathcad выведет единственный корень, который был наиболее близок к начальному приближению. Так что, если вы не знаете сколько корней имеет уравнение, то лучше использовать стрелочку
Рис. 3. Панель “Evaluation”
В зависимости от сложности уравнения через определенное время MathCad выведет результат. На рис.4 можно рассмотреть синтаксис и различие результатов выводимых mathcad. Обратите внимание, что выводимые результаты одного и того же уравнения различны
Рис. 4. Результат численного решения уравнения
Mathcad позволяет решать уравния в символьном виде. Например, если мы заменим все числовые константы на неизвестные параметры и решим уравнение относительно x, то результат выведется в символьном виде (см. рис. 5). Причем, обратите внимание, что в данном случае нам не нужно вводить начальное приближение и мы должны использовать символ “→” для вывода результата
Рис. 5. Результат символьного решения уравнения
Использование метода Solve:
Этот метод отличается от выше рассмотренного синтаксисом. На свободном поле вводим уравнение с использованием логического символа “ровно” из панели Boolean. После ввода уравнения, не смещая курсор ввода, на панели Symbolic нажимаем кнопку solve (см. рис. 6)
Рис. 6. Панель Symbolic
Затем ставим запятую и вводим переменную, относительно которой нужно решить уравнение (в нашем случае это x). Нажимаем Enter на клавиатуре и смотрим результат (см. рис. 7)
Рис. 7. Результат решения уравнения методом Solve
Обратите внимание, что метод подходит как для численного так и для символьного представления результатов
Как показывает моя личная инженерная практика, иногда не удается решить уравнения с помощью Given – Find, но получается в Solve. При этом, к сожалению, метод Solve не очень удобен для далнейшего использования результатов решения уравнения
Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.
Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.
Нахождение корней уравнения в MathCad
Дата добавления: 2015-07-23 ; просмотров: 17986 ; Нарушение авторских прав
Цель работы:нахождение корней уравнения в программе MathCad с использованием встроенных функций root,polyroots, символьного решения.
Указания к выполнению лабораторной работы:
IНахождение корней уравнения в программе MathCad с использованием встроенной функции root
1. Запустить программу MathCad .
2. Записать на рабочем листе MathCad вид функции f(х), для которой необходимо найти на заданном интервале корни.
3. Создать цикл из точек интервала, на котором определяются корни, и вычислить в этих точках функцию f(х). Построить график функции f(х) и график функции х0=0 (т.е. ось х).
4. Определить точки пересечения двух кривых f(х) и х0, которые будут приближением к корням уравнения.
4.1. Использовать для определения на графике значений корней в контекстном меню (рис.17, a) опцию Trace (рис. 17,б), установить флажок в окне Track Data Poіnt.
4.2. Подвести курсор мыши к точкам пересечения кривых, координаты точек пересечения кривых, т.е. корни, будут представлены в окнах Х-Value и У- Value, а на графике отобразится вертикальная прямая.
5. Задать для независимой переменной х начальное приближение, которое выбирается как значение точки пересечения кривых f(х) и х0. Обратиться ко встроенной в MathCad функции root(f(x), x) (функция root возвращает значение независимой переменной х, для которой f(х) равняется 0) и найти корень х1.
6. Найти второй (х2) и третий (х3) корни уравнения f(х)=0 (уравнение третьей степени имеет не больше трех действительных корней), задав для них соответственно их начальные значения как координаты точек пересечения кривых f(х) и х0 и использовав функцию root.
Рисунок 17 – Диалоговые окна для определения координат точек пересечения кривых
ІІ Нахождение корней уравнения в программе MathCad с использованием встроенной функции polyroots, которая возвращает вектор, имеющий все корни уравнения, коэффициенты уравнения при этом задаются вектором.
1. Записать на рабочем листе MathCad вид функции f(х), для которой необходимо найти на заданном интервале корни.
2. Записать как вектор v все коэффициенты уравнения, расположить их в порядке увеличения степеней.
3. Найти корни, обратившись ко встроенной функции r:=polyroots(v), результат будет получено относительно трансформированного вектора r T .
4. Для интервала нахождения корня и количества элементов вектора r T создать соответствующие циклы и вычислить значение функции в точках цикла.
5. Построить график функции в точках цикла, а также в найденных точках корней, в которых функция будет иметь значения, равные нулю.
ІІІ Нахождение корней уравнения в программе MathCad с использованием символьных решений уравнений.
1. Ввести левую часть уравнения.
2. Ввести знак равенства с использованием панели управления Evaluatіon (Выражения) или с помощью нажатия клавиш Ctrl + =.
3. За знаком равенства ввести правую часть уравнения.
4. Выделить переменную, относительно которой решается уравнение.
5. Выбрать команду Symbolіc/Varіable/Solve.
По окончанию решения корни уравнения выводятся в виде вектора.
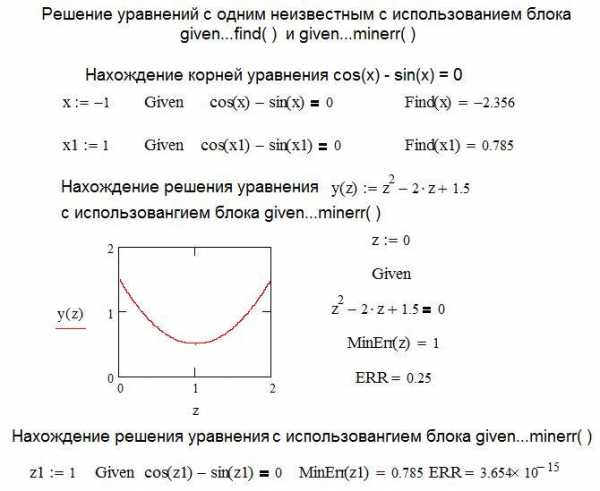
ІV Найти приближенное решение с использованием функции mіnerr(x1. ).
1. Задать приближение последовательно для первого корня х:=1.
2. Ввести ключевое слово gіven (дано), из которого начинается блок решений.
3. Записать уравнение, используя знак логического равенства между правой и левой частями уравнения.
4. Обратиться к функции mіnerr( x). Корень будет найдено.
Таблица 1.1 – Варианты заданий к лабораторной работе № 1
| № варианта | Интервал нахождения корней | Уравнение |
| [-1; 3] | x 3 -2,92x 2 +1,4355x+0,791=0 | |
| [-2; 3] | x 3 -2,56x 2 -1,325x+4,395=0 | |
| [-3,5; 2,5] | x 3 +2,84x 2 -5,606x-14,766=0 | |
| [-2,5; 2,5] | x 3 +1,41x 2 -5,472x-7,38=0 |
| [-1,6; 1,1] | x 3 +0,85x 2 -0,432x+0,044=0 |
| [-1,6; 1,6] | x 3 -0,12x 2 -1,478x+0,192=0 |
| [-1,6; 0,8] | x 3 +0,77x 2 -0,251x-0,017=0 |
| [-1,4; 1] | x 3 +0,88x 2 -0,3999x-0,0376=0 |
| [-1,4; 2,5] | x 3 +0,78x 2 -0,827x-0,1467=0 |
| [-2,6; 1,4] | x 3 +2,28x 2 -1,9347x-3,90757=0 |
| [-2,6; 3,2] | x 3 -0,805x 2 -7x+2,77=0 |
| [-3; 3] | x 3 -0,345x 2 -5,569x+3,15=0 |
| [-2; 3,4] | x 3 -3,335x 2 -1,679x+8,05=0 |
| [-1; 2,8] | x 3 -2,5x 2 +0,0099x+0,517=0 |
| [-1,2; 3] | x 3 -3x 2 +0,569x+1,599=0 |
| [-2,5; 2,5] | x 3 -2,2x 2 +0,82x+0,23=0 |
| [-1,2; 4,6] | x 3 -5x 2 +0,903x+6,77=0 |
| [-1; 7,4] | x 3 -7,5x 2 +0,499x+4,12=0 |
| [-1.6; 9] | x 3 -7,8x 2 +0,899x+8,1=0 |
| [-3,4; 2] | x 3 +2x 2 -4,9x-3,22=0 |
| [-3,4; 1,2] | x 3 +3x 2 -0,939x-1,801=0 |
| [-4,6; 3,0] | x 3 +5,3x 2 +0,6799x-13,17=0 |
| [-2,4; 8,2] | x 3 -6,2x 2 -12,999x+11,1=0 |
| [-3,2; 2,7] | x 3 -0,34x 2 -4,339x-0,09=0 |
| [-1; 3] | x 3 -1,5x 2 +0,129x+0,07=0 |
| [-1; 3] | x 3 -5,5x 2 +2,79x+0,11=0 |
| [-1; 3] | x 3 -5,7x 2 -6,219x-2,03=0 |
| [-1; 3] | x 3 -3,78x 2 -7,459x-4,13=0 |
| [-1; 3] | x 3 -5x 2 -9,9119x+0,01=0 |
| [-1; 3] | x 3 -7x 2 -1,339x-7,55=0 |
Пример
І Для уравнения найти корни на интервале [-1, 1], шаг изменения переменной х равен 0.1.
1 Записать цикл из точек интервала х:=-1, -0.9..1.
2 Записать функции и х0=0.
3 Построить графики для этих функций.
4 Определить на графике точки пересечения кривых и х0=0.
5 Задать как приближение значения точек пересечения х1, х2, х3. В примере х1=-0.9, х2=0.2, х3= 0.7.
6 Вычислить значение корней с помощью формул: root (f(x1),x1), root (f(x2),x2), root (f(x3),x3). Полученные значения корней такие: х1=-0.92, х2=0.21, х3= 0.721 (рис. 18).
Рисунок 18 – Результат нахождения корней с использованием функции root
II Для уравнения найти корни на интервале [-1.1, 7.1] , шаг изменения переменной х равен 0.1.
1. Создать вектор из коэффициентов уравнения, используя панель управления Matrix (Матрица) (рис.19) и задав один столбец и четыре строки для коэффициентов уравнения.
Рисунок 19 – Диалоговое окно для определения вектора из коэффициентов уравнения
Вектор из коэффициентов уравнения будет иметь следующий вид
2. С помощью встроенной функции r:=polyroots(v) найти корни уравнения и представить их в виде вектора r T , транспонированного по отношению к r, то есть преобразованного из столбца в строку.
3. Создать циклы для переменной х и количества найденных корней:
4. Построить графики для функции и определить функцию в точках корней. В точках корней значения функции равны нулю.
5. Определить значения корней на графике (рис. 20).
Рисунок 20 – Результат нахождения корней с использованием функции polyroots
III Для уравнения найти корни с использованием символьных решений уравнений.
1. Записать левую часть уравнения
.
2. Поставить логический знак «=» и в правой части записать 0.
3. Выделить переменную х.
4. Обратиться в главном меню MathCad к команде Symbolic/Variable/ Solve.
Найдены корни уравнения запишутся в виде вектора:
IV Найти приближенное решение вышеприведенного уравнения с использованием функции minerr( x1,…).
1. Задать приближение последовательно для первого корня х:=1.
2. Ввести ключевое слово given (дано), с которого начинается блок решений.
3. Записать уравнение, используя знак логического равенства между правой и левой частью уравнения.
4. Обратиться к функции minerr( x). Корень будет найдено.
5. Аналогические действия выполнить для двух других корней уравнения, поскольку уравнения третьей степени имеет не больше трех корней.
Контрольные вопросы
1 Какие встроенные функции позволяют находить корни уравнения?
2 Как выполняется символьное нахождение корней уравнений?
Лабораторная работа №3
Действия с матрицами в MathCad
Цель работы:выполнение действий с матрицами в программе MathCad .
Указания к выполнению лабораторной работы:
1. Запустить программу MathCad .
2. Создать матрицы , , , , , из коэффициентов a, b, c, m, k, n в соответствии с вариантом задания.
3. Выполнить действия с матрицами в соответствии с вариантом задания.
4. Найти ранг матрицы А.
5. В символьном виде выполнить транспонирование матрицы В, инвертирование матрицы А.
6. Найти обратную матрицу К. Найти детерминант матрицы А.
Таблица 2.1 – Варианты заданий к лабораторной работе № 2
| Номер варианта | Значение элементов матриц | Действия с матрицами |
| a=1; b=0.5; c=-1; m=2; k=-2.1;n=-0.8 | 1) A+A×M; 2) B×C; 3) M 3 ; 4)D+m×K; 5)A×D+D×M; 6)K -2 | |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 | |
| a=-1; b=5; c=1.3; m=0.9; k=0.1;n=-0.5 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 | |
| a=1; b=0.5; c=1; m=0.2; k=0.27 ;n=0.7 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 | |
| a=3; b=2.1; c=0.91; m=1.2; k=1; n=3 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 | |
| a=4; b=-0.5; c=-1; m=3.2; k=1.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 | |
| a=1; b=2.5; c=0.3; m=1; k=-2.1;n=-0.8 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 | |
| a=2; b=0.5; c=-1.1; m=2; k=1.9 ;n=-3.8 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 | |
| a=3; b=-2.5; c=4; m=3; k=-2.1;n=0.8 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 | |
| a=3.1; b=1.5; c=2.1; m=3.2; k=1.1;n=-1.6 | 1) A+A×M; 2) B×C; 3) M 3 ; 4)D+m×K; 5)A×D+D×M; 6)K -2 | |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 | |
| a=-1; b=5; c=1.3; m=0.9; k=0.1;n=-0.5 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 | |
| a=1; b=0.5; c=1; m=0.2; k=0.27 ;n=0.7 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 | |
| a=3; b=2.1; c=0.91; m=1.2; k=1; n=3 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 | |
| a=4; b=-0.5; c=-1; m=3.2; k=1.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 | |
| a=1; b=2.5; c=0.3; m=1; k=-2.1;n=-0.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 |
Продолжение табл. 2.1
| a=2; b=0.5; c=-1.1; m=2; k=1.9 ;n=-3.8 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 |
| a=3; b=-2.5; c=4; m=3; k=-2.1;n=0.8 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 |
| a=3.1; b=1.5; c=2.1; m=3.2; k=1.1;n=-1.6 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 |
| a=1; b=0.5; c=-1; m=2; k=-2.1;n=-0.8 | 1) A+A×M; 2) B×C; 3) M 3 ; 4)D+m×K; 5)A×D+D×M; 6)K -2 |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 |
| a=-1; b=5; c=1.3; m=0.9; k=0.1;n=-0.5 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 |
| a=1; b=0.5; c=1; m=0.2; k=0.27 ;n=0.7 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 |
| a=3; b=2.1; c=0.91; m=1.2; k=1; n=3 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 |
| a=4; b=-0.5; c=-1; m=3.2; k=1.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 |
| a=1; b=2.5; c=0.3; m=1; k=-2.1;n=-0.8 | 1) A+A×M; 2) B×C; 3) M 3 ; 4)D+m×K; 5)A×D+D×M; 6)K -2 |
| a=2; b=0.5; c=-1.1; m=2; k=1.9 ;n=-3.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 |
| a=3; b=-2.5; c=4; m=3; k=-2.1;n=0.8 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 |
| a=3.1; b=1.5; c=2.1; m=3.2; k=1.1;n=-1.6 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 |
Пример
Выполнить действия с матрицами, создав их из заданных коэффициентов a=1, b=2, c= 3, m=4, k=5, n=6. Матрицы имеют следующий вид:
1. Создать матрицы.
1.1. Выбрать панель управления Matrіx (Матрица).
1.2. Определить число строк и столбцов для каждой матрицы (рис.21).
Рисунок 21 – Диалоговое окно для определения размера матрицы
1.3. Матрицы в примере имеют такие размеры: А – (3´3), В – (3´2), С(2´2), М(1´2), К(3´3).
1.4. Заполнить матрицы соответствующими параметрами (рис. 29).
2 Выполнить следующие действия с матрицами:
1) А+n·K; 2)A·B; 3) A 2 ; 4) A·D; 5)D·M; 6) D-1.
3 Найти ранг матрицы А (ранг матрицы -наибольший порядок минора этой матрицы, который отличный от нуля): rank(A).
4 В символьном виде выполнить транспонирование матрицы В, т.е. заменить местами строки и столбцы матрицы В.
4.1 Выделить матрицу В.
4.2 Обратиться в главном меню к команде Symbolіc / Matrіx/Transpose (рис. 28).
5 В символьном виде выполнить инвертирование матрицы А (т.е. найти матрицу, которая будет обратной к матрице А) .
5.1 Выделить матрицу A.
5.2 Обратиться в главном меню к команде Symbolіc/Matrіx/Іnvert (рис.28).
6 В символьном виде найти обратную матрицу К.
6.1 Выделить матрицу К.
6.2 Обратиться в главном меню к команде Symbolіc / Matrіx/Іnvert (рис.28).
7 В символьном виде найти детерминант (определитель) матрицы А.
7.1 Выделить матрицу A.
7.2 Обратиться в главном меню к команде Symbolіc/Matrіx/Determіnant (рис.22).
Рисунок 22 – Меню Symbolic для работы с матрицами в символьном виде
Рисунок 23 – Результаты вычисления матриц
Контрольные вопросы
1 Як можно создать матрицу и вектор?
2 Какие действия выполняются с матрицами?
3 Как определяются элементы матрицы?
Лабораторная работа №4
Нахождение решений системы линейных уравнений в MathCad
Цель работы:нахождение решений системы линейных уравнений в программе MathCad .
Указания к выполнению лабораторной работы:
I Найти решение системы линейных уравнений с использованием функции soln.
1 Запустить программу MathCad.
2 Создать матрицу А из коэффициентов при неизвестных.
3 Создать вектор b из свободных членов.
4 Обратиться к встроенной программе решения линейных уравнений soln и записать soln1:=А -1 ×b.
5 Получить решение линейного уравнения у векторному виде
.
IIНайти решение системы линейных уравнений с использованием так званого «блоку решений».
1 Задать начальные значения переменным, которые есть в уравнении.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать уравнение, используя знак логического равенства между правой и левой частью уравнения из панели управления Evaluation (Выражения).
4 Ввести ключевое слово find (найти), которым заканчивается блок решений.
IIIНайти решение вышеприведенной системы уравнений с использованием функции lsolve.
1Создать матрицу А из коэффициентов при неизвестных.
2 Создать вектор b из свободных членов.
4 Обратиться к встроенной программе решения линейных уравнений lsolve и записать lsolve(А,b).
5 Получить результат решения линейного уравнения в векторном виде
.
IVНайти приближенное решение с использованием функции minerr(x1,…).
1 Задать приближение последовательно для значений переменной х1, х2,… хn.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать систему уравнений, используя знак логического равенства между правой и левой частями каждого уравнения.
4 Обратиться к функции minerr( x1,x2. ). Значения неизвестных будут найдены.
Таблица 3.1 – Варианты заданий к лабораторной работе № 3
| № варианта | Коэффициенты при неизвестных | Свободные члени | ||
| a11 а21 а31 а41 | а12 а22 а23 а24 | а13 а23 а33 а34 | а14 а24 а34 а44 | в1 в2 в3 в4 |
| 0,12 | -0,43 | 0,14 | 0,64 | -0,17 |
| -0,07 | 0,34 | -0,72 | 0,32 | 0,62 |
| 1,18 | -0,08 | -0,25 | 0,43 | 1,12 |
| 1,17 | 0,53 | -0,84 | -0,53 | 1,15 |
| 0,12 | -0,43 | 0,14 | 0,64 | -0,17 |
| -0,07 | 0,34 | -0,72 | 0,32 | 0,62 |
| 1,18 | -0,08 | -0,25 | 0,43 | 1,12 |
| 1,17 | 0,53 | -0,84 | -0,53 | 1,15 |
| 3,7 | 5,6 | 9,5 | ||
| 3,36 | 31,1 | 1,5 | ||
| 7,93 | 4,2 | 6,3 | 4,4 | |
| 42,7 | 3,7 | 6,2 | ||
| 1,3 | 1,6 | 2,2 | ||
| 4,4 | 6,7 | 2,5 | ||
| 2,8 | 0,73 | 67,8 | ||
| 3,4 | ||||
| 5,3 | 1,6 | 5,5 | 3,3 | |
| 4,1 | 6,4 | 3,9 | ||
| 2,1 | 3,3 | 2,04 | 4,9 | |
| 3,1 | ||||
| 0,2 | ||||
| 8,3 | 5,3 | |||
| 2,6 | 6,1 | 4,1 | ||
| 0,93 | 3,8 | |||
| 34,7 | ||||
| 3,6 | ||||
| 3,4 | 4,2 | |||
| 44,7 | ||||
| 5,1 | 0,2 | |||
| 3,4 | 5,34 | |||
| 2,7 | 6,7 | |||
| 3,3 | ||||
| 2,5 | 1,3 | |||
| 5,2 | 0,78 | |||
| 6,11 | 4,2 | |||
| 6,78 | 3,76 | |||
| 2,3 | ||||
| 3,4 | 2,5 | |||
| 0,2 | ||||
| 1,25 | ||||
| 3,3 | 8,2 | |||
| 1,2 | ||||
| 1,3 | ||||
| 5,9 | ||||
| 6,6 | ||||
| 3,3 | 2,1 | |||
| 4,8 | ||||
| 0,4 | ||||
| 0,2 | ||||
| 1,3 | 1,5 | 2,22 | 3,2 | |
| 3,4 | 5,55 | 1,3 | ||
| 3,3 | 2,2 | 6,77 | ||
| 4,9 | 3,6 | 6,88 | ||
| 0,4 | ||||
| 0,3 | ||||
| 3,3 | 7,6 | 5,5 | ||
| 5,4 | ||||
| 9,2 | ||||
| 3,2 | ||||
| 0,44 | ||||
| 0,67 |
| 3,35 | 5,3 | |||
| 4,22 | 6,7 | 3,5 | ||
| 2,8 | 3,8 | 2,9 | ||
| 2,34 | 3,44 | |||
| 5,23 | ||||
| 13,4 | 6,33 | 5,1 | 2,11 | 3,33 |
| 4,66 | 6,1 | 3,33 | 5,44 | 0,11 |
| 2,22 | 2,55 | 6,33 | 4,44 | |
| 2,98 | 3,78 | 6,11 | 3,33 |
Пример
I Найти решение системы уравнений с использованием функции soln
1 Создать матрицу А
А:= .
2 Создать вектор b
b:= .
3 Найти решение системы, используя функцию soln
.
4 Результат решения
II Найти решение вышеприведенной системы уравнений с использованием так званого «блоку решений»
1 Задать начальные значения переменным, которые присутствуют в уравнении
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать уравнение, используя знак логического равенства между правой и левой частями уравнения из панели управления Evaluation (Выражения).
4 Ввести ключевое слово find (найти), которым заканчивается блок решений.
5 Результат решения
IIIНайти решение вышеприведенной системы уравнений с использованием функции lsolve.
1 Создать матрицу А
.
2 Создать вектор b
.
3 Найти решение системы, используя функцию lsolve:
IVНайти решение вышеприведенной системы уравнений с использованием функции minerr (x,у,z).
1 Задать начальные условия для неизвестных, например, x=1,у=1,z=1.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать уравнения, используя знак логического равенства между правой и левой частью уравнения из панели.
4 Обратиться к функции minerr (x,у,z). Решение системы уравнений будет найдено.
Контрольные вопросы
1 Какие встроенные функции позволяют найти решение системы линейных уравнений?
2 В каком виде представляются результаты решения системы линейных уравнений?
Лабораторная работа №5
Нахождение решений системы нелинейных уравнений в MathCad
Цель работы: нахождение решений системы нелинейных уравнений в программе MathCad .
Указания к выполнению лабораторной работы:
І Найти решение системы нелинейных уравнений с использованием так называемого “блока решений”.
1 Задать начальные значения переменным, которые есть в уравнении.
2 Ввести ключевое слово gіven (дано), из которого начинается блок решений.
3 Записать уравнение, используя знак логического равенства между правой и левой частями уравнения из панели управления.
4 Ввести ключевое слово fіnd (найти), которым заканчивается блок решений.
ІІ. Найти приближенное решение с использованием функции mіnerr(x1. ).
1 Задать приближение последовательно для значений переменной х1, х2. хn.
2 Ввести ключевое слово gіven (дано), из которого начинается блок решений.
3 Записать систему уравнений, используя знак логического равенства между правой и левой частями каждого уравнения.
4 Обратиться к функции mіnerr( x1,x2. ). Значение неизвестных будет найдено.
Таблица 4.1 – Варианты задания к лабораторной работе №4
| № варианта | Система уравнений | № варианта | Система уравнений |
Пример
Найти решение системы нелинейных уравнений с использованием так называемого «блока решений».
1 Задать начальные значения переменным, которые есть в уравнении
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать уравнения, используя знак логического равенства между правой и левой частью уравнения из панели управления
4 Ввести ключевое слово find (найти), которым заканчивается блок решений.
5 Результат решения
IIНайти приближенное решение с использованием функции minerr(x1,…).
1 Задать приближения последовательно для значений переменной х=1, y=1.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать систему уравнений, используя знак логического равенства между правой и лево частью каждого уравнения.
4 Обратится к функции minerr( x,y.). Значение неизвестных будет найдено.
Контрольные вопросы
1 Какие встроенные функции позволяют найти решение системы нелинейных уравнений?
2 В каком виде представляются результаты решения системы нелинейных уравнений?
3 Нужно ли задавать начальные приближения при решении системы нелинейных уравнений?
Лабораторная работа № 6
Символьные действия математического анализа в MathCad
Цель работы:определение неопределенных и определенных интегралов и производных в программе MathCad с использованием символьных операций.
Указания к выполнению лабораторной работы:
1 Запустить программу MathCad.
2 Записать на рабочем листе в соответствии с номером варианта формулы для определения неопределенных интегралов, определенных интегралов, производных первого порядка. От производных первого порядка определить производные второго, третьего порядков.
3 Применить последовательно к каждой функции команды меню Symbolic/Simplify, отметив последовательно каждую из функций.
Таблица 5.1 – Варианты задания к лабораторной работе №5
| Номер варианта | Неопределенные интегралы | Определенные интегралы | Производные |
Продолжение табл. 5.1
Продолжение табл. 5.1
Примеры
1 Найти неопределенный интеграл .
Результат :
2 Найти определенный интеграл .
Результат .
3 Найти производные первого порядка .
Результат .
4 Найти производные высокого порядка .
Результат
Контрольные вопросы
1 Как найти в символьном виде определенные и неопределенные интегралы?
2 Можно ли применять символьные операции к интегралам по области, к трехмерным интегралам, к контурным интегралам?
3 Можно ли в символьному виде найти производные высоких порядков?
| | | следующая лекция ==> | |
| Задание 3. | | | Лабораторная работа № 1 |
Не нашли то, что искали? Google вам в помощь!
[spoiler title=”источники:”]
http://student-engineer.pro/mathcadold/equat/
http://life-prog.ru/2_59715_nahozhdenie-korney-uravneniya-v-mathcad.html
[/spoiler]
Численное решение уравнений в MathCAD
Все задачи, с которыми вам приходилось сталкиваться в школе или изучать в университете, решались символьно. То есть вы тем или иным образом преобразовывали и упрощали выражения, использовали какие-то стандартные формулы и методы, умножали, делили, сокращали — и в результате приходили к какому-то аналитически несложному результату. Так, например, при решении квадратного уравнения вы использовали формулы Виета; пытаясь найти корни кубического уравнения, вы разлагали выражение на линейные множители (или, в крайнем случае, использовали формулу Кардано), для бикубических уравнений прибегали к замене. В общем, для того, чтобы решить даже очень несложное нелинейное уравнение, от вас требовалось знание великого множества разнообразных формул и подходов. Но, увы, как бы вы хорошо ни ориентировались во всех этих методах и подходах, зачастую это мало вам помогало, так как использование большинства из них крайне трудоемко и подходит для решения очень немногих (специально подобранных) уравнений. На практике же, как правило, приходится работать с уравнениями, включающими разнородные функции (что, как правило, автоматически означает невозможность символьного решения) или с очень неудобными коэффициентами. Справиться со многими из них привычным преобразованием или заменами никак не получится. Что же делать?
Естественно, если вам попадется такое “нерешаемое” уравнение, вы попытаетесь просто подобрать корни. Для этого вы будете подставлять какие-то значения переменной (выбор которых, скорее всего, в основном будет определяться вашей интуицией) в надежде на то, что какое-то из них обратит уравнение в нуль. К сожалению, и такой способ весьма малоэффективен на практике: подставив десяток-другой значений, вы почти наверняка предпочтете удовлетвориться мыслью о том, что данное уравнение не имеет решений вовсе, чем продолжать эту чрезвычайно неинтересную работу.
Но если у вас есть компьютер с системой MathCAD, то никаких проблем с поиском решения не будет вне зависимости от сложности уравнения. Конечно, аналитическое решение компьютер вряд ли найдет даже для очень простых уравнений (в этом пока человек значительно превосходит машину), но зато ввиду колоссальной по сравнению с человеческой скоростью обработки данных очень эффективными становятся так называемые численные методы.
В основе всех численных методов решения уравнений лежит принцип подбора. Но, в отличие от подбора возможных корней человеком, в численных методах этот процесс является строго направленным. Основным понятием численных методов является итерация. Итерация — это буквально повторение, то есть все численные методы построены на принципе повторения одного и того же действия или последовательности действий, результатом которых является большее или меньшее приближение некоторого рабочего значения переменной к корню. Поэтому численные методы решения уравнений называются еще итерационными. Число необходимых итераций определяется скоростью сходимости алгоритма (эффективностью). Эффективность различных численных алгоритмов может различаться весьма значительно, но это не значит, что всегда стоит избирать из них наиболее быстрый: чем выше скорость сходимости к решению, тем, как правило, чувствительность алгоритма к различного рода трудностям (многочисленным экстремумам, разрывам или недифференцируемости в некоторых точках) выше. Поэтому очень важно иметь представление (хотя бы самое поверхностное) о том, какие принципы лежат в основе работы той или иной функции: это поможет выбрать наиболее подходящий в рамках данной задачи алгоритм и тем самым избежать лишних ошибок и проблем.
Немного о выборе типа алгоритма. В общем случае, конечно, гораздо лучше получить решение в результате символьных преобразований, так как при этом можно найти сразу все корни (при использовании встроенных функций MathCAD — только один), причем без какой-либо погрешности. Но, увы, аналитическое решение имеет относительно небольшое количество задач, а символьный процессор MathCAD сможет справиться вообще с мизерным процентом уравнений. Так что применение численных методов — это печальная необходимость. Но особо огорчаться по этому поводу не стоит: все недостатки численных алгоритмов MathCAD можно легко преодолеть.
Для численного поиска решений алгебраических уравнений с одним неизвестным в MathCAD существует специальная встроенная функция root (корень). Функция эта может использоваться с различными начальными условиями, при этом реализуются разные численные алгоритмы. Так, если определена только одна точка приближения к корню, поиск решений будет осуществляться так называемым методом секущих. Если же задан интервал, на котором предположительно локализовано решение, то поиск его будет осуществлен с применением метода деления пополам (или метода Больцано).
Если необходимо найти корень некоторого уравнения, причем известен интервал, в котором находится корень, проще всего использовать функцию root с 4 аргументами: root(f(x), x, a, b), где f ( x ) — функция, определяющая уравнение, x — переменная, a и b — границы интервала локализации. Обязательным условием является то, что значения функции на концах интервала должны быть противоположных знаков.
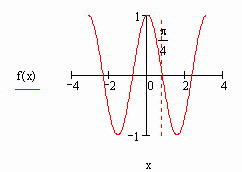
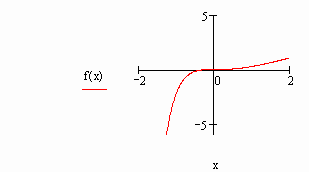
Попробуем протестировать функцию root и для этого найдем корни какого-нибудь уравнения, точное решение которого очевидно. К примеру, возьмем уравнение
все корни которого имеют вид p × N/4 (N=1, 2, …). Попробуем найти первое положительное решение. Очевидно, что таковым будет x=p /4 (что очень хорошо видно на графике).
Посмотрим, однако, найдет ли этот корень функция root. Интервал локализации определим от 0 до p /3:
MathCAD не подвел на этот раз: решение найдено в точности. Попробуем решить это уравнение с другим интервалом локализации:
Полученный результат отличается от первого решения, хотя корень х =0.25 (находится в данном интервале. Все дело в том, что в этом же промежутке находится еще 4 корня, и заранее предсказать, какой именно из них будет выдан в качестве ответа, совершенно невозможно. Поэтому следует ввести еще одно ограничение для применения функции root в рассматриваемой интерпретации: на промежутке должен быть локализован только один корень. В тех случаях, когда определить границы такой локализации невозможно, следует применять функцию root с одной точкой приближения (то есть перейти от метода Больцано к методу секущих). Хотя практически всегда определить нужный промежуток можно и чисто визуально, предварительно задав график. Вообще, строить график всегда желательно, когда вы используете численные методы: это самый надежный способ избежать ошибок и не потерять корни. Другой вопрос, что в случае систем уравнений это может помочь очень мало (так как сделать какие-то более или менее точные выводы по двум пересекающимся поверхностям совершенно невозможно).
Очень важной характеристикой решения является его точность. В MathCAD можно регулировать величину погрешности решения, изменяя значение специальной системной переменной TOL (от английского tolerance — точность). Строго говоря, TOL — это параметр, определяющий условие прекращения итераций. То есть цикл численного алгоритма остановит свою работу и выдаст последнее значение x, если f ( x ) примет значение, меньшее, чем TOL. Изменить величину этой встроенной переменной можно либо при помощи команды Math/Options/Built-in variables/TOL (Математические/Опции/Системные переменные/TOL), либо выполнив соответствующее присваивание непосредственно слева или сверху функции численного решения. Посмотрим, как влияет изменение величины TOL (по умолчанию равной 10 -3 ) на точность поиска корня. Пусть дана следующая функция:
Для того чтобы определить существование у нее нулей, а также, при их наличии, приблизительные границы интервала локализации корней, построим график:
Один корень вполне очевиден — это 0. Посмотрим, однако, сможет ли найти его функция root. Попробуем провести такой расчет при различных значениях TOL:
Для такой невысокой точности результат получился на удивление неплохим (значение функции в точке, определенной как корень, на 3 порядка меньше TOL — условия остановки цикла алгоритма). Но все равно 0.066 — это довольно далеко от настоящего значения корня. А то, что значение f ( x ) в этой точке весьма близко к нулю, совсем неудивительно: это связано с особенностью поведения функции в окрестности 0, где она буквально “скользит” по оси X .
Увеличим точность:
При уменьшении TOL на три порядка приблизительно во столько же порядков увеличилась и точность решения (что вполне закономерно). Новое значение корня может удовлетворить большинству требований к точности, возникающих на практике. Но все же мы попытаемся получить максимально точное решение. Для этого еще более уменьшим значение TOL:
Значение корня уже крайне близко к нулю. Попробуем задать высшую точность, возможную в MathCAD (TOL=10 -15 ):
Только в этом предельном случае наконец удалось получить правильное решение. Проанализируем, с чем были связаны трудности в поиске нуля этой функции (как вы помните, решения для косинуса находились очень просто и без применения условия особой точности). Для этого построим график, на котором ясно видно прохождение кривой через точку корня. Сделать это проще всего можно при помощи инструмента ZOOM, который позволяет увеличивать отдельные фрагменты графика.
Более 30 раз пришлось повторить операцию с этим инструментом, пока наконец кривая перестала сливаться с осью X ! В результате получился следующий график:
Теперь совсем несложно понять причину возникших трудностей: просто кривая в окрестности 0 слишком близко подходит к оси X . А, как вы помните, корень считается найденным, когда значение функции в некоторой точке меньше TOL. В случае же рассматриваемой функции для стандартной точности (10 -3 ) такие точки появятся на относительно большом расстоянии от точки решения. Поэтому результат получается неверным. Но, с другой стороны, утверждать, что решение в рассмотренных выше случаях находилось ошибочное, совершенно некорректно. Ведь по условию в точке корня значение функции должно быть меньше TOL. Для большинства численных методов это основное, а в случае метода бисекции (схожий с ним алгоритм лежит в основе работы функции root с четырьмя аргументами) — единственное условие определения некоторой точки x как корня. Условие же это при всех значениях точности было выполнено, причем TOL и f ( x ) отличались на несколько порядков. Просто, строго говоря, получаемые значения корней следует округлять до порядка, равного порядку продекларированной точности (ведь значение функции не может быть точнее входных данных). Если бы мы это сделали, то во всех случаях, в том числе и при TOL=10 -1, ответ получился бы верным (хотя, надо признать, в случае TOL=10 -1 это было бы, скорее, счастливое совпадение).
Из всего вышесказанного можно сделать вывод: нахождение корня функцией root совсем не означает его действительного существования. Очень даже возможна такая ситуация, когда кривая функции очень близко подходит к оси Х, но при этом не пересекает ее. Если же установленный уровень точности окажется больше того расстояния, на которое она приближается к оси, то точку, в которой это сближение происходит, MathCAD определит как корень.
Что же делать, чтобы избежать таких ошибок? Во-первых, всегда строить график. В системе MathCAD это делается предельно быстро и просто, а неприятностей позволяет избежать очень многих. Во-вторых, если вы видите, что график как бы скользит по оси Х (очень неясная ситуация: возможно и пересечение в 2-х точках, и касание в одной, и отсутствие общих точек вообще), попробуйте увеличить точность по максимуму: в большинстве случаев этого бывает вполне достаточно. И в-третьих, если сомнения все равно остаются, используйте инструмент ZOOM в области предполагаемого расположения корня. Пожалуй, способ этот самый надежный: ведь увеличение можно производить практически до бесконечности.
Найти решение уравнения в MathCAD можно применяя другую форму встроенной функции root, имеющую только 2 аргумента (имя функции и переменной). При использовании этого варианта выше или правее самой функции root следует задать начальное приближение для x:
Определить величину начального приближения можно либо чисто интуитивно, либо (лучше) построив график.
Вы можете задать резонный вопрос: если существует весьма верный и простой метод бисекции, зачем использовать другие, менее надежные (как будет показано далее) методы? Тут все дело вот в чем: во-первых, не всегда существованию корня сопутствует интервал с различными по знаку значениями функции в точках его границ (есть возможность простого касания); во-вторых, метод бисекции не очень удобно использовать при программном поиске всех корней уравнения сканированием некоторой широкой области; в-третьих, ввиду того, что построенные при помощи компьютерных программ графики отражают вид функции довольно искаженно, определение при их помощи интервала локализации корня нельзя считать абсолютно надежным.
Однако можно утверждать, что лучше воздержаться от использования метода секущих (то есть функции root в варианте с начальным приближением) в случае периодических функций (особенно сложного вида), очень осторожно следует применять ее при наличии локальных экстремумов (и ни в коем случае не определять начальное приближение вблизи таких точек, а также точек перегиба) и точек разрыва. Также следует учитывать поведение функции на бесконечности. Поэтому во всех сложных случаях куда лучше применять метод бисекции.
Дмитрий Гурский, Юрий Стрельченко, dot@omen.ru
Компьютерная газета. Статья была опубликована в номере 07 за 2003 год в рубрике soft :: текст
Уравнение и системы уравнений в математическом пакете Mathcad в символьном виде решаются с использованием специального оператора символьного решения solve в сочетании со знаком символьного равенства, который может быть также введен с рабочей панели “Символика”. Например:
Аналогичные действия при решении уравнений в Mathcad можно выполнить, используя меню “Символика”. Для этого необходимо записать вычисляемое выражение. Затем выделить переменную, относительно которой решается уравнение, войти в меню Символика, Переменная, Разрешить. Например:
В случае, если необходимо упростить полученный результат, используется знак равенства [=]. Например:
При решении некоторых уравнений, результат включает большое количество символов. Mathcad сохраняет его в буфере, а на дисплей выводитcя сообщение: “
This array has more elements than can be displayed at one time. Try using the “submatrix” function” – “Этот массив содержит больше элементов, чем может быть отображено одновременно. Попытайтесь использовать функцию “submatrix””. В этом случае рекомендуется использовать численное решение. Или, в случае необходимости, символьное решение может быть выведено и отображено на дисплее.
Символьное решение может быть получено с использованием блока given … find. В этом случае при записи уравнения для связи его левой и правой части использует символ логического равенства “=” с панели инструментов Boolean, например:
Аналогичным способом решаются системы уравнений в символьном виде. Ниже приводятся примеры решения систем уравнений в символьном виде различными способами. При использовании оператора символьного решения
solve в сочетании со знаком символьного равенства система уравнений должна быть задана в виде вектора, который вводится вместо левого маркера оператора solve, а перечень переменных, относительно которых решается система, вместо правого маркера. Например:
Пример использования блока given…find для решения системы уравнений:
allmathcad.com
Уравнения с одним неизвестным в Mathcad
Простейший способ найти корень уравнения с одним неизвестным в Mathcad обеспечит функция root ( ). Аргументами функции root ( ) являются вид функции определяющей решаемое уравнение и имя переменой, относительно которой ищется решение — root (f(x),x) Если уравнение в Mathcad содержит несколько корней, то функция обеспечивает нахождение единственного корня, ближайшего к заданному начальному значению для искомой переменной. Точность вычислений может быть увеличена или уменьшена посредством задания значения переменной
TOL, равной по умолчанию 10-3 и определённой в меню Math, Options (Математика, Опции). Установленное значение TOL также оказывает влияние на точность вычислений.
В случае, если решаемое уравнение в Mathcad представлено полиномом, то все его решения могут быть получены с помощью функции polyroots (v). В качестве аргументов этой функции выступает вектор коэффициентов полинома –v, а результат представляется в виде вектора корней полинома. На листинге представлен пример нахождения корней уравнений с использованием функций root ( ) и polyroots ( ).
Другим способом решения уравнений в Mathcad является применение специального вычислительного блока, начинающегося с ключевого слова given с использованием функций find( ) и minerr ( ).
Блок имеет следующую структуру:
Начальное значение искомой переменной
given
Решаемое уравнение
Выражение с использованием функции find( ) или minerr ( )
Нахождение корней уравнения в Mathcad с использованием блока given…find ( ) в чем – то аналогично использованию функции root ( ). В Mathcad задается начальное значение для искомой переменной, после находится решение, ближайшее к заданному начальному условию. Использовании блока given…minerr ( ) имеет существенные особенности. Решение будет найдено в любом случае, даже при его отсутствии. Дело в том, что ищется не решение системы, а минимальная невязка уравнений. На листинге рассмотрена функция, заведомо не имеющая действительных корней и при использовании блока
given…minerr ( ) найдено решение, значение, которое наиболее приближено к оси х, то есть обеспечивает минималь-ную невязку. Значение невязки (ошибки) показывает системная переменная ERR.
allmathcad.com
Решение системы уравнений в Mathcad
Первоначально рассмотрим СЛАУ в Mathcad. Для их решения может использоваться блок given …find() или специальная функция lsolve(). Применение блока given …find() предопределяет необходимость задания начальных значений искомых переменных. Далее после ключевого слова given описывается СЛАУ и с помощью find() находится решение. Следует указать, что в том случае, когда
СЛАУ в Mathcad имеет бесконечное множество решений блок given …find() дает конкретный результат, что несомненно следует отнести к недостаткам. В случае отсутствия решения будет выдано сообщение “Matrix is singular. Cannot compute its inversу – Матрица сингулярная. Нельзя вычислить эту инверсию”.
Применение функции lsolve( ) позволяет избежать этого недостатка. Функция lsolve(M,b) имеет два аргумента. M – матрица коэффициентов при неизвестных, b – вектор свободных членов. На листинге приведен пример решения СЛАУ.
Пример решения СЛАУ:

given…find() и given…minerr () для решения систем нелинейных уравнений.
allmathcad.com
Урок 24. Решение уравнений в Mathcad – использование функций
Решение уравнений является важным для решения практических задач. Поэтому уделим уравнениям еще один урок.
Блок решения в функции
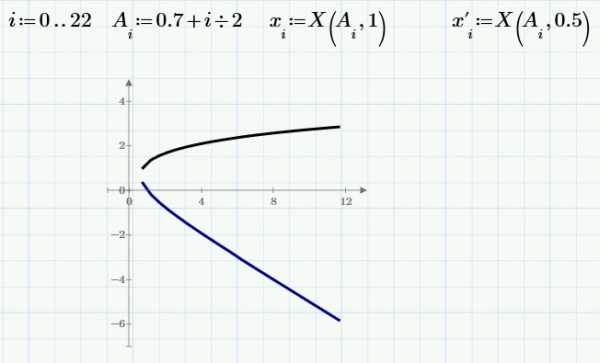
Если Вы хотите исследовать изобразить на графике поведение уравнения в зависимости от значения определенного параметра, Вам, возможно, придется решить систему уравнений много раз. Вы можете сделать это, используя блок решения в функции. Покажем на примере: предположим, мы хотим исследовать поведение решения следующего уравнения в зависимости от различных значения параметра
A:
Блоку решения не нужно ни значение параметра, ни начальное приближение, поскольку решение есть функция этих двух значений. Эти значения мы будем задавать при вызове функции.
Функцию можно использовать сколько угодно раз:
Использовать функцию можно с диапазоном переменных:
Такая техника решения не самая надежная. Если хотя бы одно решение не может быть найдено, Вы не получите и решений для других параметров (это произойдет, если задать
A<0.7). Поэтому лучше заранее проверить свою функцию.
Сообщения об ошибке можно избежать, написав маленькую программу:
Если блок решения выдает сообщение об ошибке, на выходе получим значение NaN (Not a Number – «Не Число»), которое просто не отображается на графике:
Построим две ветки уравнения с использованием этого приема:
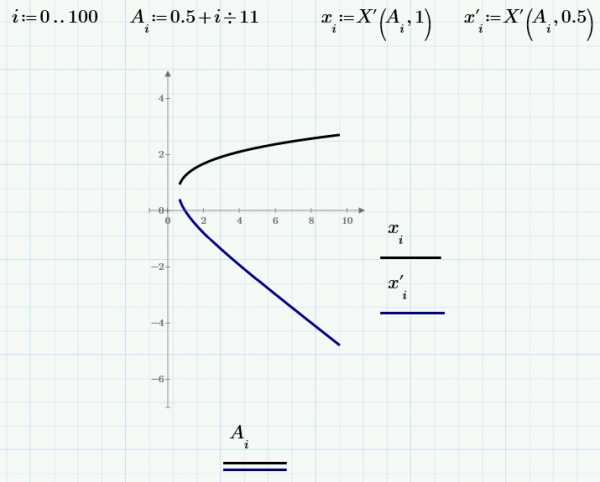
Когда переменных много
Расчеты часто содержат несколько переменных, но Вам, возможно, придется использовать лишь некоторые из них. В качестве примера рассмотрим систему восьми уравнений, где нам нужно получить только значения X и Y. Начальные приближения следует задать для всех переменных:
Решение представляет собой вектор из восьми элементов, но нам нужны лишь элементы с индексами 0 и 1.
Минимизация ошибки
Find() – не единственный решатель в Mathcad. Еще один полезным решателем является Minnerr(), находящий решения, которые минимизируют ошибку в системе уравнений. Рассмотрим пример: есть набор данных, которые мы хотим аппроксимировать уравнением Бейтмена:
Мы хотим подобрать три константы в уравнении Бейтмена таким образом, чтобы ошибка приближения была минимальна. У нас есть семь уравнений (по одной для каждого эксперимента) и три константы, так что в системе избыток данных. Minerr() может обработать эту проблему:
Замечания:
- Три константы являются переменными для этой системы.
- Переменные не могут иметь счетных индексов.
- У параметров (t и c) могут быть счетные индексы.
Возможно, Вам хотелось бы использовать цикл
for для семи уравнений, но в блоке решений этого сделать нельзя.
Для полностью определенных систем (с одинаковым числом независимых уравнений и неизвестных) функция Minerr() дает тот же ответ, что и Find().
Резюме
В этом уроке мы определили способы расширенного использования блоков решения:
- Вы можете определить вывод блока решения как функцию. Таким образом в блок решения можно передавать параметры и начальные приближения.
- Если при вычислении точек для графика хотя бы одно решение не будет найдено, то график не будет построен. Этой ошибки можно избежать, написав небольшую программу с использованием “try/on error”, которая выводит NaN (Not a Number – Не Число), если результат отсутствует.
- Для двух и более неизвестных (и уравнений) вывод блока решения является вектором. Если нужен один или два элемента этого вектора, их можно вывести, используя подстрочные индексы.
- Вместо функции Find() можно использовать Minerr() – она минимизирует ошибку для заданного набора ограничений, в том числе, если данные избыточны. Minerr() часто может дать приближенный результат, когда Find() выдает ошибку.
Другие интересные материалы
sapr-journal.ru
2. Решение уравнений в Mathcad
2.1. Численное решение уравнения
Для простейших уравнений
вида f(x) = 0
решение в Mathcad находится с помощью
функции root
root(
f(х1,
x2,
…),
х1,
a,
b
)
Возвращает значение х1,
принадлежащее отрезку [a,
b],
при котором выражение или функция f(х)
обращается в 0. Оба
аргумента этой функции должны быть
скалярами. Функция возвращает скаляр.
Аргументы:
f(х1,
x2,
…)
— функция,
определенная где-либо в рабочем документе,
или выражение. Выражение должно возвращать
скалярные значения.
х1
— — имя переменной,
которая используется в выражении. Этой
переменной перед использованием функции
root
необходимо присвоить
числовое значение. Mathcad использует его
как начальное приближение при поиске
корня.
a,
b
– необязательны, если
используются, то должны быть вещественными
числами, причем a
< b.
Наиболее распространен
графический способ
определения начальных приближений.
Принимая во внимание, что действительные
корни уравнения f(x)
= 0 — это точки пересечения графика функции
f(x)
с осью абсцисс, достаточно построить
график функции f(x)
и отметить точки пересечения f(x)
с осью Ох,
или отметить на оси Ох
отрезки, содержащие по одному корню.
Построение графиков часто удается
сильно упростить, заменив уравнение
f(x)
= 0 равносильным
ему уравнением:
|
, |
где функции
f1(x)
и f2(x)
— более простые, чем функция
f(x).
Тогда, построив графики функций у
=
f1(x)
и у
= f2(x),
искомые корни получим как абсциссы
точек пересечения этих графиков.
Пример.
Графически отделить
корни уравнения:
Уравнение (1) удобно
переписать в виде равенства:
lg x=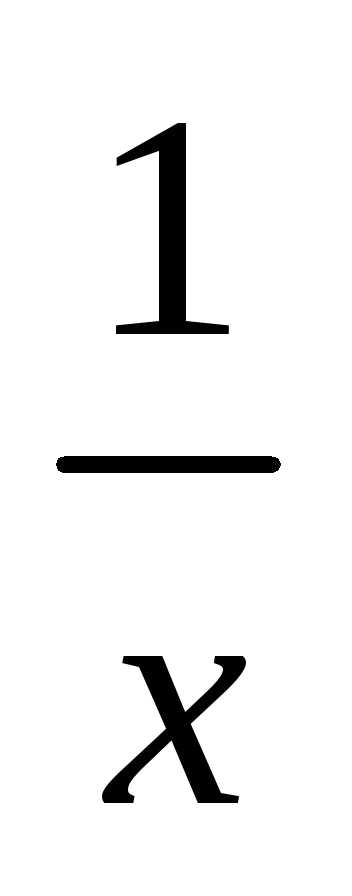
Отсюда ясно, что корни
уравнения (1) могут быть найдены как
абсциссы точек пересечения логарифмической
кривой y
= lg x и
гиперболы y
=
Построив эти кривые, приближенно найдем
единственный корень
уравнения (1) или определим его содержащий
отрезок [2, 3].
Упражнение 1.
Построить график
функции f(x)
(Таблица 1) и приблизительно
определить один из корней уравнения.
Решить уравнение f(x)=
0 с
помощью встроенной функции Mathcad root.
Таблица 1
Варианты упражнения 1
-
x3
+ x2
-2sin(x)
=05x
— 8ln(x) = 8x2
+ x — cos(3x) = 1x2
— sin(4x) = 03x
— 2ln(x) = 52x
-2,2x =0x2
— 2x -sin(3x) =1x
— sin(x)
-0.25
= 03x —
ex
= 03x
— 2ln(x) = 5ex
+ e-3x
= 4x
+4sin(x) = 22.7x
— 1.5ln(x) = 2.8x3
+ x2
-2sin(x)
=0ex
-6x =3
studfiles.net
Решение уравнений в MathCad – использование функций
Одной из самых важных математических задач является решение уравнений. Поэтому нам стоит остановиться на них еще подробнее.
Блок решения в функциях
Если вам нужно просмотреть на графике действие уравнения, относительно определенных параметров, вам, судя по всему, придется решить данное уравнение огромное количество раз. Давайте обратимся к визуальному примеру. Попробуем просмотреть поведение решения уравнений в зависимости от разных значений параметра А.
Блок решения не нуждается в значениях параметров, изначальных приближениях. Решением будет считаться функция двух указанных значений. Их мы будем оформлять во время вызова функций.
Каждая функция может быть использованной неограниченное количество раз.
Так, можно воспользоваться функцией с диапазонами переменных.
Данная методика решения задач не считается самой проверенной и надежной. Если хотя бы одно решение не удастся найти, пользователь не сможет перейти к решению остальных параметров. Вот почему нужно быть максимально уверенным в правильности заданных функций.
Чтобы избежать появления ошибок, достаточно написать небольшую программу.
Когда блок решения начинает выдавать ошибки, мы получим значение NaN (Not a Number – «Не Число». Впрочем, на графике мы его не увидим.
Теперь разработаем две ветки уравнения при использовании данного опционала:
Что делать в случаях, когда переменных много
Бывают расчеты, в которых вмещено несколько переменных. Вполне возможно, что когда-то с ними столкнетесь и вы. Для примера мы возьмем систему, которая состоит из восьми уравнений. Нам понадобится получить только X и Y. Сначала же зададим всем переменным начальное приближение.
Решение становится вектором из восьми пунктов. Нам потребуются исключительно те элементы, которые вмещают индексы 0 и 1.
Устранение ошибки
Теперь давайте на примере просмотрим набор данных, которые будут аппроксимированны в соответствии с уравнениями Бейтмена.
Сейчас мы собираемся разработать три константы при помощи уравнения Бейтмена таким образом, чтобы актуальная ошибка приближения была минимизирована. Что мы имеем? Систему из семи уравнений. Каждая из них соответствует отдельному эксперименту. Также у нас есть три константы, а, следовательно, система пострадала от преизбытка данных. Опция Minerr () станет оптимальным инструментом для обработки данной проблемы.
Константы – это переменные нашей системы. Переменные не имеют математических индексов. Параметры имеют индексы счетного типа.
archicad-autocad.com
Урок 23. Нелинейные уравнения в Mathcad
Mathcad может решать системы линейных и нелинейных уравнений с помощью встроенных алгоритмов. На самом деле, «решать» — не совсем верное определение того, что делает программа. Лучше рассуждать так: Вы задаете приближенное значение, затем программа уточняет эту оценку. Поэтому, используя такую технологию решения, нужно знать, что Вы делаете. Вы должны понимать, как ведет себя функция, которую исследуете. Иначе Вы можете быть разочарованы.
Изучение «решения» начнем с уравнений с одной переменной. В этом случае поведение уравнения можно понять, построив график. Позже мы рассмотрим системы уравнений.
Уравнения с одной переменной
Уравнение, которое мы рассмотрим, достаточно простое:
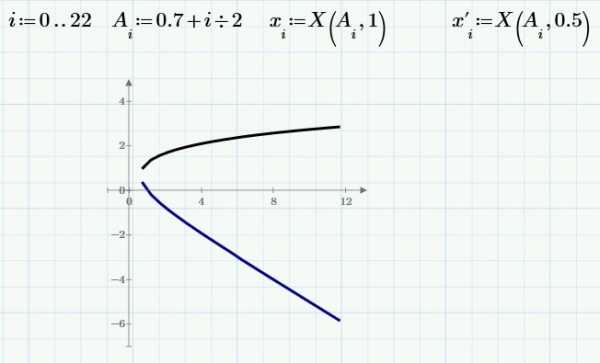
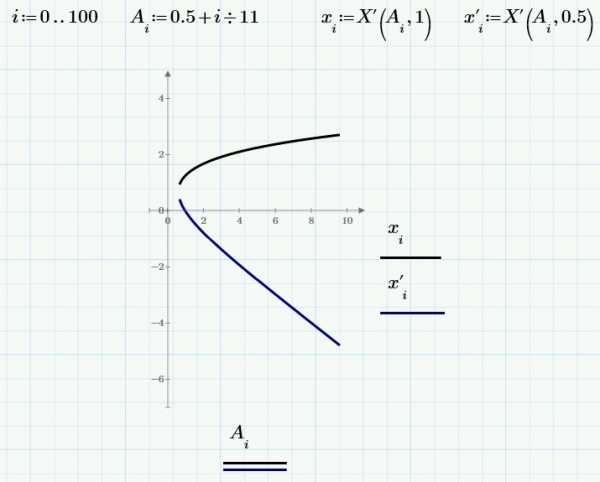
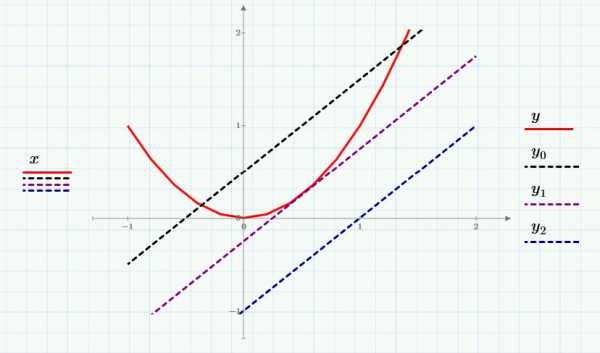
Рассмотрим это уравнение как пересечение прямой линии (левая часть) и парабола (правая часть). Построим графики трех прямых линий и посмотрим, что произошло:
Первая (самая верхняя) линия дважды пересекается с параболой около точек x=-0.3 и x=1.3. У второй линии – одно пересечение (или два близко расположенных) возле точки x=0.5. Пересечений с третьей прямой (самой нижней) нет.
Решения
Сначала рассмотрим самую верхнюю линию. Чтобы получить решение, нам нужен Блок решения (вкладка Математика –> Области –> Блок решения). Заполним блок для решения первого уравнения:
Здесь есть три области для различных записей:
— начальные приближения;
— ограничения;
— решатель.
В области ограничений мы записали уравнение, которое хотим решить. В первой области мы задали приближенное решение этого уравнения. Функция Find(), которую мы записали в последней области – это решатель.
Как видно, решение 1.366 – это правое пересечение прямой и параболы. Начальное приближение не критично – можно ввести 1.6, щелкнуть мышью вне блока и получить тот же результат:
Изменим начальное приближение на значение, близкое к левому пересечению, скажем, -0.5. Решение изменится на -0.366:
Измените начальное приближение обратно на 1.3.
Теперь поменяем константу 0.5 в уравнении на -0.25. Решение изменится на 0.5:
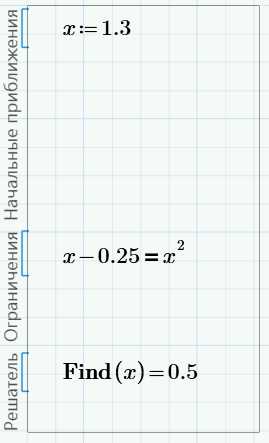
Этот же ответ мы будем получать для любого значения начального приближения – это единственное решение.
Наконец, изменим константу в уравнении на -1 (последнее уравнение). Щелкнем вне блока и получим сообщение об ошибке:
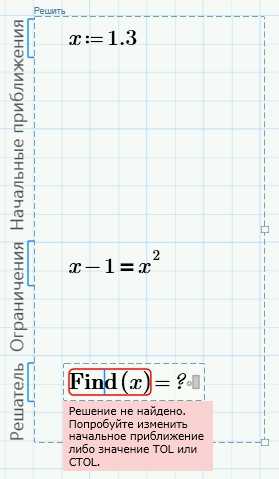
Решения нет. Изменим константу обратно на 0.5.
Вывод решения
Переменные в блоке решений локальны. Вы не можете использовать их значения вне блока. Вернемся к уравнению, где приближенное значение задано 1.3. Мы решили уравнение, чтобы найти более точное решение x=1.366. Однако если мы попробуем вывести значение x, мы получим вектор, которые определили для нашего графика.
Если Вы хотите использовать результат решения в дальнейших вычислениях, нужно присвоить функцию решателя переменной:
Тогда получим верный результат:
Решение систем уравнений
Для примера решим систему трех уравнений: два линейных и одно кубическое. Здесь три неизвестных – начальное приближение даем для всех трех:
Все три ответа можно вывести в вектор:
Удалите последнее из трех уравнений. Решение все равно будет найдено, с учетом двух оставшихся уравнений:
Однако, такое решение может быть не тем, которое Вам нужно.
Обратите внимание еще на некоторые детали. В блоке решения используются два вида знака «равно»: знак присваивания для начальных приближений и для решателя Find, и знак булева равенства в уравнении. Эта разница очень важна. Еще один момент – щелкните по слову Find в области решателя, откройте вкладку Математика. В строке Обозначения должно быть отмечено «Ключевое». Некоторые другие ключевые слова мы рассмотрим в последующих уроках.
Растворимость вещества
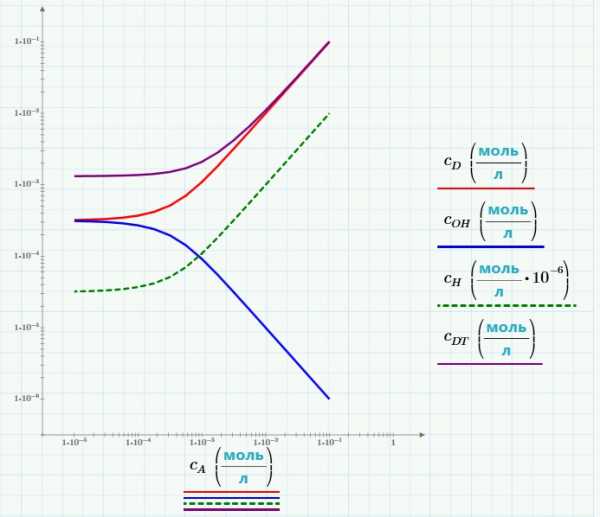
Рассмотрим растворение вещества DOH. Это двухстадийный процесс: сначала растворяется твердая фаза, затем растворенные части диссоциируют на D и OH. Малую растворимость можно повысить, добавив небольшое количество сильной кислоты HA. Она диссоциирует, и ионы водорода вступают в реакцию с гидроксильной группой:
Как зависит общая растворимость D от количества добавленной кислоты? Концентрацию будем считать в моль/л. Концентрация насыщения нерастворенной кислоты:
Начнем с концентрации кислоты:
Константы равновесия реакции:
Блок решения начинается с трех неизвестных и их начальных приближений:
Решение:
Общая концентрация вещества:
Расчет для построения графика (подробнее о таких расчетах поговорим в следующем уроке):
График показывает концентрацию как функцию от количества добавленной кислоты. Концентрация ионов водорода на порядки меньше, чем концентрации других элементов. Поэтому мы изменили масштаб в миллион раз, чтобы показать этот график в тех же осях:
Если концентрация кислоты мала, решение содержит низкую концентрацию DOH, которая диссоциирует только частично. При увеличении концентрации кислоты, все больше и больше вещества диссоциирует.
Резюме
- Если есть уравнение или система уравнений, Вы можете дать приближенное решение, а Mathcad улучшит эту оценку. Такой способ используется в Блоке решения.
- Первая часть блока решения – начальные приближения, т.е. Ваши оценки. Здесь используется знак присваивания «:=». Эти значения могут быть помещены и до блока.
- В области «Ограничения» (уравнения) нужно использовать булево равенство [Ctrl+=]. Это единственный знак, по обе стороны от которого могут быть выражения.
- Блок решения заканчивается функцией для решения. Мы рассмотрели Find(), которая содержит неизвестные, которые нужно найти.
- Чтобы использовать результат решения в дальнейших расчетах, присвойте Find() переменной. Это может быть как одна переменная, так и вектор.
- Для решения системы нелинейных уравнений нужно быть внимательным. Число уравнений должно быть равно числу неизвестных. Кроме того, приближенные значения должны быть как можно ближе к решению.
- Если решение не было найдено, не спешите обвинять Mathcad. Нелинейные уравнения являются головной болью для любого языка программирования. Попробуйте понять поведение Ваших уравнений, прежде чем приступать – часто уравнения могут не иметь решения.
Другие интересные материалы
sapr-journal.ru