Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.
Паросочетания
Задача. Пусть есть (n) мальчиков и (m) девочек. Про каждого мальчика и про каждую девочку известно, с кем они не против танцевать. Нужно составить как можно больше пар, в которых партнёры хотят танцевать друг с другом.
Формализуем эту задачу, представив мальчиков и девочек как вершины в двудольном графе, рёбрами которого будет отношение «могут танцевать вместе».
Паросочетанием (M) называется набор попарно несмежных рёбер графа (иными словами, любой вершине графа должно быть инцидентно не более одного ребра из (M)).
Все вершины, у которых есть смежное ребро из паросочетания (т.е. которые имеют степень ровно один в подграфе, образованном (M)), назовём насыщенными этим паросочетанием.
Мощностью паросочетания назовём количество рёбер в нём. Наибольшим (максимальным) паросочетанием назовём паросочетание, мощность которого максимальна среди всех возможных паросочетаний в данном графе, а совершенным — где все вершины левой доли им насыщенны.
Паросочетания можно искать в любых графах, однако этот алгоритм неприятно кодить, и он работает за (O(n^3)), так что сегодня мы сфокусируемся только на двудольных графах. Будем в дальнейшем обозначать левую долю графа как (L), а правую долю как (R).
Цепью длины (k) назовём некоторый простой путь (т.е. не содержащий повторяющихся вершин или рёбер), содержащий ровно (k) рёбер.
Чередующейся цепью относительно некоторого паросочетания назовём простой путь длины (k) в которой рёбра поочередно принадлежат/не принадлежат паросочетанию.
Увеличивающей цепью относительно некоторого паросочетания назовём чередующуюся цепь, у которой начальная и конечная вершины не принадлежат паросочетанию.

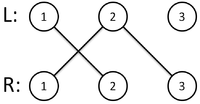
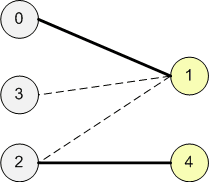
Здесь красными помечены вершины паросочетания, а в графе есть увеличивающая цепь: (1 to 8 to 4 to 6 to 3 to 7).
Зачем нужны увеличивающие цепи? Оказывается, можно с их помощью увеличивать паросочетание на единицу (отсюда и название). Можно взять такой путь и провести чередование — убрать из паросочетания все рёбра, принадлежащие цепи, и, наоборот, добавить все остальные. Всего в увеличивающей цепи нечетное число рёбер, а первое и последнее были не в паросочетании. Значит, мощность паросочетания увеличилась ровно на единицу.
В примере добавятся синие рёбра ((1, 8)), ((3, 7)) и ((4, 6)), а удалятся красные ((3, 6)) и ((4, 8)). С ребром ((2, 5)) ничего не случится — оно не в увеличивающей цепи. Таким образом, размер паросочетания увеличится на единицу.
Алгоритм Куна в этом и заключается — будем искать увеличивающую цепь, пока ищется, и проводить чередование в ней. Увеличивающие цепи удобны тем, что их легко искать: можно просто запустить поиск пути из произвольной свободной вершины из левой доли в какую-нибудь свободную вершину правой доли в том же графе, но в котором из правой доли можно идти только по рёбрам паросочетания (то есть у вершин правой доли будет либо одно ребро, либо ноль). Это можно делать как угодно (для упражнения автор рекомендует явно строить такой граф, искать путь и явно проводить чередования), однако устоялась эффективная реализация в виде dfs на 20 строчек кода, приведённая ниже.
const int maxn;
vector<int> g[maxn]; // будем хранить только рёбра из левой доли в правую
int mt[maxn]; // с какой вершиной сматчена вершина правой доли (-1, если ни с какой)
bool used[maxn]; // вспомогательный массив для поиска пути dfs-ом
// dfs возвращает, можно ли найти путь из вершины v
// в какую-нибудь вершину правой доли
// если можно, то ещё и проводит чередование
bool dfs(int v) {
if (used[v])
return false;
used[v] = true;
for (int u : g[v]) {
// если вершина свободна, то можно сразу с ней соединиться
// если она занята, то с ней можно соединиться только тогда,
// когда из её текущей пары можно найти какую-нибудь другую вершину
if (mt[u] == -1 || dfs(mt[u])) {
mt[u] = v;
return true;
}
}
return false;
}
// где-то в main:
memset(mt, -1, sizeof mt);
for (int i = 0; i < n; i++) {
memset(used, 0, sizeof mt);
if (dfs(i))
cnt++;
}Корректность
Для доказательства алгоритма нам будет достаточно ещё доказать, что если увеличивающие цепи уже не ищутся, то паросочетание в принципе нельзя увеличить.
Теорема (Бержа). Паросочетание без увеличивающих цепей является максимальным.
Доказательство проведём от противного: пусть есть два паросочетания вершин (|A| leq |B|), и для (A) нет увеличивающих путей, и покажем, как найти этот путь и увеличить (A) на единицу.
Раскрасим ребра из паросочетания, соответствующего (A) в красный цвет, (B) — в синий, а ребра из обоих паросочетаний — в пурпурный. Рассмотрим граф из только красных и синих ребер. Любая компонента связности в нём представляет собой либо путь, либо цикл, состоящий из чередующихся красных и синих ребер. В любом цикле будет равное число красных и синих рёбер, а так как всего синих рёбер больше, то должен существовать путь, начинающийся и оканчивающийся синим ребром — он и будет увеличивающей цепью для (A), а значит (A) не оптимальное, и мы получили противоречие.
Скорость работы
Такой алгоритм ровно (n) раз ищет увеличивающий путь, каждый раз просматривая не более (m) рёбер, а значит работает за (O(nm)).
Что примечательно, его можно не бояться запускать на ограничениях и побольше ((n, m approx 10^4)), потому что для него есть мощные неасимптотические оптимизации:
-
Eго можно жадно инициализировать (просто заранее пройтись по вершинам левой доли и сматчить их со свободной вершиной правой, если она есть).
-
Можно не заполнять нулями на каждой итерации массив
used, а использовать следующий трюк: хранить в нём вместо булева флага версию последнего изменения, а конкретно – номер итерации, на которой это значение сталоtrue. Если этот номер меньше текущего номера итерации, то мы можем воспринимать это значение какfalse. В каком-то смысле это позволяет эмулировать очищение массива за константу. -
Очень часто граф приходит из какой-то другой задачи, природа которой накладывает ограничения на его вид. Например, в задачах на решетках (когда есть двумерный массив, и соседние клетки связаны друг с другом) граф двудольный, но степень каждой вершины маленькая, и граф имеет очень специфичную структуру, и на нём алгоритм Куна работает быстрее, чем ожидается из формулы (n times m). Контрпримеры в таких задачах на самом деле почти всегда можно сгенерировать, но авторы редко так заморачиваются.
Вообще говоря, увлекаться ускорением алгоритма Куна не стоит — существует более асимптотически быстрый алгоритм. Задача нахождения максимального паросочетания — частный случай задачи о максимальном потоке, и если применить алгоритм Диница к двудольным графам с единичной пропускной способностью, то выясняется, что работать он будет за (O(m sqrt n)).
Покрытие путями DAG-а
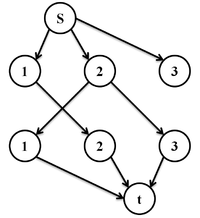
Сводить задачи к поиску максимального паросочетания обычно не очень трудно, но в некоторых случаях самому додуматься сложно. Разберём одну такую известную задачу. Дан ориентированный ациклический граф (G) (англ. directed acyclic graph). Требуется покрыть его наименьшим числом путей, то есть найти наименьшее множество простых путей, где каждая вершина принадлежит ровно одному пути.
Построим соответствующие изначальному графу (G) два двудольных графа (H) и (overline{H}) следующим образом:
- В каждой доле графа (H) будет по (n) вершин. Обозначим их через (a_i) и (b_i) соответственно.
- Для каждого ребра ((i, j)) исходного графа (G) проведём соответствующее ребро ((a_i, b_j)) в графе (H).
- Теперь из графа (H) сделаем граф (overline{H}), добавив обратное ребро ((b_i, a_i)) для каждого (i).
Если мы рассмотрим любой путь (v_1, v_2, ldots, v_k) в исходном графе (G), то в графе (overline{H}) ему будет соответствовать путь (a_{v_1}, b_{v_2}, a_{v_2}, b_{v_3}, ldots, a_{v_{k-1}}, b_{v_k}). Обратное тоже верно: любой путь, начинающийся в левой доле (overline{H}) и заканчивающийся в правой будет соответствовать какому-то пути в (G).
Итак, есть взаимно однозначное соответствие между путями в (G) и путями (overline{H}), идущими из левой доли в правую. Заметим, что любой такой путь в (overline{H}) — это паросочетание в (H) (напомним, это (overline{H}) без обратных рёбер). Получается, любому пути из (G) можно поставить в соответствие паросочетание в (H), и наоборот. Более того, непересекающимся путям в (G) соответствуют непересекающиеся паросочетания в (H).
Заметим, что если есть (p) непересекающихся путей, покрывающих все (n) вершин графа, то они вместе содержат (r = n – p) рёбер. Отсюда получаем, что чтобы минимизировать число путей (p), мы должны максимизировать число рёбер (r) в них.
Мы теперь можем свести задачу к нахождению максимального паросочетания в двудольном графе (H). После нахождения этого паросочетания мы должны преобразовать его в набор путей в (G). Это делается тривиальным алгоритмом: возьмем (a_1), посмотрим, с какой (b_k) она соединена, посмотрим на (a_k) и так далее. Некоторые вершины могут остаться ненасыщенными — в таком случае в ответ надо добавить пути нулевой длины из каждой из этих вершин.
Лемма Холла
Лемма Холла (или: теорема о свадьбах) — очень удобный критерий в задачах, где нужно проверить, что паросочетание существует, но при этом не требуется строить его явно.
Лемма Холла. Полное паросочетание существует тогда и только тогда, когда любая группа вершин левой доли соединена с не меньшим количеством вершин правой доли.
Доказательство. В одну сторону понятно — если совершенное паросочетание есть, то для любого подмножества вершин левой доли можно взять вершины правой, соединенные с ним паросочетанием.
В другую сложнее — нужно воспользоваться индукцией. Будем доказывать, что если паросочетание не полное, то можно в таком графе найти увеличивающую цепь, и с её помощью увеличить паросочетание на единицу.
База индукции: одна вершина из (L), которая по условию соединена с хотя бы одной вершиной из (R).
Индукционный переход: пусть после (k < n) шагов построено паросочетание (M). Докажем, что в (M) можно добавить вершину (v) из (L), не насыщенную паросочетанием.
Рассмотрим множество вершин (H) — все вершины, достижимые из (x), если можно ходить из правой доли в левую только по рёбрам паросочетания, а из левой в правую — по любым (мы такой граф по сути строим, когда ищем увеличивающую цепь в алгоритме Куна)
Тогда в (H) найдется вершина (y) из (R), не насыщенная паросочетанием. Иначе, если такой вершины нет, то получается, что если рассмотреть вершины (H_L) (вершины левой доли, насыщенные паросочетанием), то для них не будет выполнено условие, что (|H_L| leq |N(H_L)|) (здесь (N(X)) — множество вершин, соединенным паросочетанием с (X)).
Тогда должен существовать путь из (x) в (y), и он будет увеличивающим для паросочетания (M), потому что из (R) в (L) мы всегда шли только по ребрам паросочетания. Проведя чередование вдоль этого пути, получим большее паросочетание, следовательно предположение индукции верно.
Минимальное вершинное покрытие
Задача. Дан граф. Назовем вершинным покрытием такое множество вершин, что каждое ребро графа инцидентно хотя бы одной вершине из множества. Необходимо найти вершинное покрытие наименьшего размера.
Следует заметить, что в общем случае это очень сложная задача, но для двудольных графов она имеет достаточно простое решение.
Теорема. (mid V_{min} mid le mid M mid), где (V_{min}) — минимальное вершинное покрытие, а (M) — максимальное паросочетание.
Доказательство. (mid V_{min} mid ge mid M mid), поскольку (M) — множество независимых ребер. Теперь приведем алгоритм, который строит вершинное покрытие размера (mid M mid). Очевидно, оно будет минимальным.
Алгоритм. Мысленно ориентируем ребра графа: ребра из (M) проведем из правой доли в левую, остальные — из левой в правую, после чего запустим обход в глубину из всех вершин левой доли, не включенных в (M).

Заметим, что граф разбился на несколько множеств: (L^+, L^-, R^+, R^-), где “плюсовые” множества — это множества посещенных в процессе обхода вершин. В графе такого вида не бывает ребер (L^+ rightarrow R^-), (L^- leftarrow R^+) по очевидным соображениям. Ребер (L^+ leftarrow R^-) не бывает, потому что в противном случае паросочетание (M) не максимальное — его можно дополнить ребрами такого типа.
[
L^- cup R^+ = V_{min}
]
Понятно, что данное множество покроет все ребра. Осталось выяснить, почему (L^- cup R^+). Это верно потому, что (L^- cup R^+) покрывает все ребра (M) ровно один раз (ведь ребра (L^- rightarrow R^+) не принадлежат (M)), а также потому, что в нем нет вершин, не принадлежащих (M) (для (L^-) это справедливо по определению, для (R^+) можно провести доказательство от противного с использованием чередующихся цепей).
Упражнение. Подумайте, как это можно применить к решению задачи о нахождении максимального независимого множества.
Для ноулайферов: матроиды
С весьма большой вероятностью матроиды вам никогда не пригодятся в школьных олимпиадах, однако, если вам совсем нечего делать, можете про них почитать.
Математика вообще занимается тем, что обобщает всякие объекты и старается формулировать все теоремы максимально абстрактно. Так, концепцию хороших подмножеств (паросочетаний) обобщает понятие матроида. Практическое применение — жадный алгоритм Радо-Эдмондса, который нужен для обоснования большого числа жадников, где нужно набрать какое-то подмножество минимального / максимального веса. Сам алгоритм максимально простой: давайте отсортируем эти объекты по весу и будем добавлять их в таком порядке в наше хорошее множество, если оно после добавления остается хорошим.
Применимо к паросочетаниям: пусть у вершин левой доли есть вес, и нам нужно набрать максимальное паросочетание минимального веса. Тогда выясняется, что можно просто отсортировать вершины левой доли по весу и пытаться в таком порядке добавлять их в паросочетание стандартным алгоритмом Куна.
В теории графов паросочетание, или независимое множество рёбер в графе, — это набор попарно несмежных рёбер.
Определение[править | править код]
Пусть дан граф G = (V,E), паросочетание M в G — это множество попарно несмежных рёбер, то есть рёбер, не имеющих общих вершин, т.е. 
Связанные определения[править | править код]
Максимальное паросочетание — это такое паросочетание M в графе G, которое не содержится ни в каком другом паросочетании этого графа, то есть к нему невозможно добавить ни одно ребро, которое бы являлось несмежным ко всем рёбрам паросочетания. Другими словами, паросочетание M графа G является максимальным, если любое ребро в G имеет непустое пересечение, по крайней мере, с одним ребром из M. Ниже приведены примеры максимальных паросочетаний (красные рёбра) в трёх графах[1].
Наибольшее паросочетание (или максимальное по размеру паросочетание[2])— это такое паросочетание, которое содержит максимальное количество рёбер.
Число паросочетания[3]


Некоторые авторы используют термин «максимальное паросочетание» для наибольшего паросочетания[4][5][6][7].
Совершенным паросочетанием (или 1-фактором) называется паросочетание, в котором участвуют все вершины графа. То есть любая вершина графа инцидентна ровно одному ребру, входящему в паросочетание. Фигура (b) на рисунке выше является примером такого паросочетания. Любое совершенное паросочетание является наибольшим и максимальным. Совершенное паросочетание является также рёберным покрытием минимального размера. В общем случае 


Почти совершенным паросочетанием называется паросочетание, в котором не участвует ровно одна вершина. Это может произойти, если граф имеет нечётное число вершин. На рисунке выше паросочетание в графе (c) является почти совершенным. Если для любой вершины в графе существует почти совершенное паросочетание, не содержащее именно эту вершину, граф называется факторно-критическим.
Пусть задано паросочетание M.
- чередующийся путь — это путь, в котором рёбра поочерёдно принадлежат паросочетанию и не принадлежат ему.
- пополняющий путь (или увеличивающий путь) — это чередующийся путь, начинающийся и кончающийся свободными вершинами (то есть не участвующими в паросочетании).
Лемма Бержа утверждает, что паросочетание является наибольшим в том и только в том случае, если не существует пополняющего пути.
Свойства[править | править код]
- Число совершенных паросочетаний в двудольном графе равно перманенту его матрицы смежности.
- В любом графе без изолированных вершин число паросочетания и число рёберного покрытия в сумме дают число вершин[8].
- В частности, если существует совершенное паросочетание, то оба числа равны |V| / 2.
- Если A и B — два максимальных паросочетания, то |A| ≤ 2|B| и |B| ≤ 2|A|. Чтобы это увидеть, заметьте, что каждое ребро из B A может быть сопряжено максимум двум рёбрам из A B поскольку A — паросочетание. Однако каждое ребро A B сопряжено с ребром B A ввиду того, что B — максимальное. Следовательно,
- Далее мы имеем
- В частности, отсюда вытекает, что любое максимальное паросочетание является 2-аппроксимацией наибольшего паросочетания, а также 2-аппроксимацией минимального максимального паросочетания. Это неравенство точное. Например, если G — путь с тремя рёбрами и 4 вершинами, минимальный размер максимального паросочетания равен 1, а размер наибольшего паросочетания равен 2.
Многочлен паросочетаний[править | править код]
Производящая функция числа k-рёберных паросочетаний в графе называется многочлен паросочетаний.
Пусть G — граф и mk — число k-рёберных паросочетаний.
Полиномом паросочетаний графа G будет
Есть другое определение полинома паросочетаний
,
где n — число вершин в графе.
Оба определения имеют свои области применения.
Алгоритмы и вычислительная сложность[править | править код]
Наибольшее паросочетание в двудольном графе[править | править код]
Задачи нахождения паросочетания часто возникают при работе с двудольными графами. Поиск наибольшего паросочетания в двудольном графе[9]

Алгоритм пополняющего пути получает его, находя пополняющий путь из каждой вершины 

- Установи
.
- Пока имеются расширяющие пополняющие пути
:
, где
– симметрическая разность множеств.
Пополняющий путь – это путь вида 



Лемма: Для любого графа 

















Лемма: Для любого графа 
















является изолированной вершиной или
является циклом четной длины или
является путем четной длины или
является путем нечетной длины
Вершины в 



, а 





Найти дополняющий путь можно следующим образом:
- Даны
двудольный граф и паросочетание
.
- Создай
, где
- Поиск дополняющего пути сводится к поиску в
из свободной вершины
в свободную вершину
.
Поскольку пополняющий путь может быть найден за 












Во взвешенном двудольном графе[править | править код]
Во взвешенном двудольном графе каждому ребру приписывается вес. Паросочетание максимального веса в двудольном графе[9] определяется как паросочетание, для которого сумма весов рёбер паросочетания имеет максимальное значение. Если граф не является полным двудольным, отсутствующие рёбра добавляются с нулевым весом. Задача поиска такого паросочетания известна как задача о назначениях. Замечательный венгерский алгоритм решает задачу о назначениях и был одним из первых алгоритмов комбинаторной оптимизации. Задача может быть решена с помощью модифицированного поиска кратчайшего пути в алгоритме пополняющего пути.
Если используется алгоритм Беллмана — Форда, время работы будет 

[13]
Наибольшие паросочетания[править | править код]
Имеется алгоритм полиномиального времени для нахождения наибольшего паросочетания или паросочетания максимального веса в графе, не являющемся двудольным. Следуя Джеку Эдмондсу[en] его называют методом путей, деревьев и цветов или просто алгоритмом Эдмондса для паросочетаний. Алгоритм использует двунаправленные дуги[en].
Обобщение той же техники может быть использовано для поиска максимального независимого множества в графах без клешней. Алгоритм Эдмодса был впоследствии улучшен до времени работы 
Другой (рандомизированный) алгоритм, разработанный Муча и Санковсим (Mucha, Sankowski)[10], основанный на быстром произведении матриц, даёт сложность 
Максимальные паросочетания[править | править код]
Максимальное паросочетание можно найти простым жадным алгоритмом.
Cамым большим максимальным паросочетанием является наибольшее паросочетание, которое может быть найдено за полиномиальное время. Pеализация с использованием псевдокода:
- Дан граф
.
- Установи
.
- Пока множество
не пустое:
- Выбери
.
- Установи
.
- Установи
.
- Выбери
- Выведи
.
Однако неизвестно никакого полиномиального по времени алгоритма для нахождения наименьшего максимального паросочетания, то есть максимального паросочетания, содержащего наименьшее возможное число рёбер.
Заметим, что наибольшее паросочетание из k рёбер является рёберным доминирующим множеством с k рёбрами. И обратно, если задано минимальное рёберное доминирующее множество с k рёбрами, мы можем построить наибольшее паросочетание с k рёбрами за полиномиальное время. Таким образом, задача нахождения минимального по размеру максимального паросочетания эквивалентна задаче нахождения минимального рёберного доминирующего множества[15]. Обе эти задачи оптимизации известны как NP-трудные, а их распознавательные версии являются классическими примерами NP-полных задач[16]. Обе задачи могут быть аппроксимированы с коэффициентом 2 с полиномиальным временм — просто находим произвольное максимальное паросочетание M[17].
Задачи перечисления[править | править код]
Число паросочетаний в графе известно как индекс Хосойи. Вычисление этого числа является #P-полной задачей. Задача остаётся #P-полной в специальном случае перечисления совершенных паросочетаний в двудольном графе, поскольку вычисление перманента случайной 0-1 матрицы (другая #P-полная задача) — это то же самое, что вычисление числа совершенных паросочетаний в двудольном графе, имеющем заданную матрицу в качестве матрицы смежности. Существует, однако, рандомизированная аппроксимационная схема полиномиального времени для вычисления числа паросочетаний в двудольном графе[18]. Замечательная теорема Кастелейна[en], утверждающая, что число совершенных паросочетаний в планарном графе может быть вычислено в точности за полиномиальное время с помощью алгоритма FKT.
Число совершенных паросочетаний в полном графе Kn (с чётным n) задаётся двойным факториалом (n − 1)!![19]. Число паросочетаний в полном графе без ограничения, чтобы паросочетание было совершенным, задаётся телефонными номерами[en][20].
Нахождение всех рёбер, паросочетаемых рёбер[править | править код]
Одной из основных задач в теории паросочетаний является поиск всех рёбер, которые могут быть расширены до наибольшего паросочетания. Лучший детерминированный алгоритм решения этой задачи работает за время 
Существует рандомизированный алгоритм, решающий задачу за время 
В случае двудольного графа можно найти наибольшее паросочетание и использовать его для нахождения всех максимально-паросочетаемых рёбер за линейное время[23];
что даст в результате 


В случае, если одно из наибольших паросочетаний известно заранее[24], общее время работы алгоритма будет 
Характеристики и замечания[править | править код]
Теорема Кёнига утверждает, что в двудольных графах размер наибольшего паросочетания равно размеру наименьшего вершинного покрытия. Из этого следует, что для двудольных графов задачи нахождения наименьшего вершинного покрытия, наибольшего независимого множества, и максимальной вершинной биклики могут быть решены за полиномиальное время.
Теорема Холла (или теорема о свадьбах) обеспечивает характеризацию двудольных графов, имеющих совершенные паросочетания, а теорема Татта даёт характеризацию произвольных графов.
Совершенное паросочетание порождает остовный 1-регулярный подграф, то есть 1-фактор. В общем случае остовный k-регулярный подграф — это k-фактор.
Приложения[править | править код]
Структурная формула Кекуле ароматических соединений состоит из совершенных паросочетаний их углеродного скелета, показывая местоположение двойных связей в химической структуре. Эти структуры названы в честь Фридриха Августа Кекуле, который показал, что бензол (в терминах теории графов — это цикл из 6 вершин) может быть представлен в виде такой структуры[25].
Индекс Хосойи — это число непустых паросочетаний плюс единица. Он применяется в вычислительной и математической химии для исследования органических соединений.
См. также[править | править код]
- Рёберная раскраска
- Независимое множество
- Декомпозиция Далмейджа-Мендельсона
- Устойчивое паросочетание
- Оптимальное паросочетание[en]
- Кососимметический граф[en]
- Словарь терминов теории графов
Примечания[править | править код]
- ↑ 1 2 Станислав Окулов. Дискретная математика. Теория и практика решения задач по информатике. Учебное пособие. — Litres, 2014-02-07. — С. 186. — 428 с. — ISBN 9785457534674.
- ↑ Alan Gibbons, Algorithmic Graph Theory, Cambridge University Press, 1985, Chapter 5.
- ↑
Евстигнеев В.А.,Касьянов В.Н. Series-parallel poset // Словарь по графам в информатике / Под редакцией проф. Виктора Николаевича Касьянова. — Новосибирск: ООО «Сибирское Научное Издательство», 2009. — Т. 17. — (Конструирование и оптимизация программ). — ISBN 978-591124-036-3. - ↑ Фуад Алескеров, Элла Хабина, Дмитрий Шварц. Бинарные отношения, графы и коллективные решения. — Litres, 2016-01-28. — С. 22. — 343 с. — ISBN 9785457966925.
- ↑ Рубчинский А. А. Дискретные математические модели. Начальные понятия и стандартные задачи. — Directmedia, 2014-08-06. — С. 136. — 269 с. — ISBN 9785445838029.
- ↑ Леонид Гладков, Владимир Курейчик, Виктор Курейчик. Генетические алгоритмы. — Litres, 2016-01-28. — С. 276. — 367 с. — ISBN 9785457965997.
- ↑ Леонид Гладков, Владимир Курейчик, Виктор Курейчик, Павел Сороколетов. Биоинспирированные методы в оптимизации. — Litres, 2016-01-28. — С. 330. — 381 с. — ISBN 9785457967472.
- ↑ Tibor Gallai. Über extreme Punkt- und Kantenmengen // Ann. Univ. Sci. Budapest. Eötvös Sect. Math.. — 1959. — Т. 2. — С. 133–138.
- ↑ 1 2 Douglas Brent West. Introduction to Graph Theory. — 2nd. — Prentice Hall, 1999. — ISBN 0-13-014400-2.
- ↑ 1 2 M. Mucha, P. Sankowski. Maximum Matchings via Gaussian Elimination // Proc. 45th IEEE Symp. Foundations of Computer Science. — 2004. — С. 248–255.
- ↑ Bala G. Chandran, Dorit S. Hochbaum. Practical and theoretical improvements for bipartite matching using the pseudoflow algorithm. — 2011. — arXiv:1105.1569..
- ↑ M. Fredman, R. Tarjan. Fibonacci heaps and their uses in improved network optimization algorithms // Journal of the ACM. — 1987. — Т. 34, вып. 3. — С. 596–615.
- ↑ Rainer Burkard, Mauro Dell’Amico, Silvano Martello. Assignment Problems. — Philadelphia: SIAM, Society for Industrial and Applied Mathematics, 2009. — С. 77—79, 98. глава 4.1.3 Historical notes, books, and surveys, глава 4.4.3 Efficient implementations
- ↑
Silvio Micali, Vijay Vazirani. Analgorithm for finding maximum matching in general graphs // Proc. 21st IEEE Symp. Foundations of Computer Science. — 1980. — С. 17–27. — doi:10.1109/SFCS.1980.12.
- ↑ Yannakakis Mihalis, Gavril Fanica. Edge dominating sets in graphs // SIAM Journal on Applied Mathematics. — 1980. — Т. 38, вып. 3. — С. 364–372. — doi:10.1137/0138030.
- ↑
Michael R. Garey, David S. Johnson. Computers and Intractability: A Guide to the Theory of NP-Completeness. — W.H. Freeman, 1979. — ISBN 0-7167-1045-5.. Рёберное доминирующее множество обсуждается при рассмотрении задач нахождения доминирующих множеств, задачи GT2 в приложении A1.1. Минимальное по размеру максимальное паросочетание — это задача GT10 в приложении A1.1. - ↑ Giorgio Ausiello, Pierluigi Crescenzi, Giorgio Gambosi, Viggo Kann, Alberto Marchetti-Spaccamela, Marco Protasi. Complexity and Approximation: Combinatorial Optimization Problems and Their Approximability Properties. — Springer, 2003. Минимальное доминирующее рёберное множество — это задача GT3 в приложении B (страница 370). Минимальное по размеру максимальное паросочетание — это задача GT10 в приложении B (страница 374). См. также Minimum Edge Dominating Set Архивная копия от 5 сентября 2013 на Wayback Machine и Minimum Maximal Matching Архивная копия от 6 марта 2014 на Wayback Machine в web compendium Архивная копия от 2 октября 2013 на Wayback Machine.
- ↑ Ivona Bezáková, Daniel Štefankovič, Vijay V. Vazirani, Eric Vigoda. Accelerating Simulated Annealing for the Permanent and Combinatorial Counting Problems // SIAM Journal on Computing. — 2008. — Т. 37, вып. 5. — С. 1429–1454. — doi:10.1137/050644033.
- ↑
David Callan. A combinatorial survey of identities for the double factorial. — 2009. — arXiv:0906.1317. - ↑
Extremal problems for topological indices in combinatorial chemistry // Journal of Computational Biology. — 2005. — Т. 12, вып. 7. — С. 1004–1013. — doi:10.1089/cmb.2005.12.1004. - ↑ Marcelo H.de Carvalho, Joseph Cheriyan. An
algorithm for ear decompositions of matching-covered graphs // Proc. ACM/SIAM Symposium on Discrete Algorithms (SODA). — 2005. — С. 415–423.
- ↑ Michael O. Rabin, Vijay V. Vazirani. Maximum matchings in general graphs through randomization // J. of Algorithms. — 1989. — Т. 10. — С. 557–567.
- ↑
Tamir Tassa. Finding all maximally-matchable edges in a bipartite graph // Theoretical Computer Science. — 2012. — Т. 423. — С. 50–58. — doi:10.1016/j.tcs.2011.12.071. - ↑
Aris Gionis, Arnon Mazza, Tamir Tassa. k-Anonymization revisited // International Conference on Data Engineering (ICDE). — 2008. — С. 744–753. - ↑ Смотрите, например, Nenad Trinajstić, Douglas J. Klein, Milan Randić. On some solved and unsolved problems of chemical graph theory. — 1986. — Т. 30, вып. S20. — С. 699–742. — doi:10.1002/qua.560300762.
Литература для дальнейшего чтения[править | править код]
- László Lovász, Michael D. Plummer. Matching Theory. — North-Holland, 1986. — ISBN 0-444-87916-1.
- Introduction to Algorithms. — second. — MIT Press and McGraw–Hill, 2001. — ISBN 0-262-53196-8.
- S. J. Cyvin, Ivan Gutman. Kekule Structures in Benzenoid Hydrocarbons. — Springer-Verlag, 1988.
- Marek Karpinski, Wojciech Rytter. Fast Parallel Algorithms for Graph Matching Problems. — Oxford University Press, 1998. — ISBN 978-0-19-850162-6.
Ссылки[править | править код]
- Пример решения задачи на YouTube Архивная копия от 22 марта 2016 на Wayback Machine
- Алгоритм поиска наибольшего паросочетания в двудольном графе Архивная копия от 7 января 2012 на Wayback Machine
- A graph library with Hopcroft-Karp and Push-Relabel-based maximum cardinality matching implementation Архивная копия от 25 октября 2005 на Wayback Machine
Содержание
- 1 Идея алгоритма
- 2 Корректность алгоритма
- 3 Оценка производительности
- 4 Псевдокод
- 5 См. также
- 6 Источники информации
Идея алгоритма
Пусть дан неориентированный двудольный граф и требуется найти максимальное паросочетание в нём. Обозначим доли исходного графа как
и . Построим граф следующим образом:
(т.е. добавим новый исток и сток );
.
|
|
|
Изначально текущее паросочетание пусто. На каждом шаге алгоритма будем поддерживать следующий инвариант: в текущее найденное паросочетание входят те и только те ребра, которые направлены из в .
- Ищем в графе путь из в поиском в глубину.
- Если путь найден, перезаписываем текущее паросочетание. Далее инвертируем все рёбра на пути (ребро становится ребром ) и удаляем и ребра, покрывающие вершины, принадлежащие текущему паросочетанию.
- Если путь не был найден, значит текущее паросочетание является максимальным, и алгоритм завершает работу. Иначе переходим к пункту 1.
Корректность алгоритма
Обозначим как путь из в без первого и последнего ребра. Пусть он
является дополняющей цепью для исходного графа , и пусть также существование дополняющей цепи в графе приводит к существованию пути . Тогда из теоремы: если мы на каком-то шаге можем найти новый путь, т.е дополняющую цепь, то мы увеличиваем текущее паросочетание. Если путь найти мы уже не можем, значит дополняющих цепей в графе нет и текущее паросочетание — искомое. Осталось доказать что сделанное предположение действительно верно.
Т. к. — путь в двудольном графе, начинающийся в и заканчивающийся в , то он нечетной длины. Вершины в нем не повторяются (т.к. это путь в дереве поиска в глубину). Рассмотрим текущее паросочетание. Согласно поддерживаемому инварианту -ребра в паросочетании, а -ребра — нет. В таком случае ребра пути можно пронумеровать так, чтобы нечетные ребра были свободными, а четные — покрытыми ребрами текущего паросочетания. Заметим, что путь может начинаться и заканчиваться только в свободной вершине, т. к. из ведут ребра только в свободные вершины и только из свободных вершин ведут ребра в . Итак, теперь ясно, что — дополняющая цепь для графа .
Обратно, пусть существует дополняющая цепь в графе . В одной из ориентаций она начинается в какой-то свободной вершине и заканчивается в свободной вершине , далее будем рассматривать именно эту ориентацию. Ребра поочередно то не лежат, то лежат в паросочетании, значит в нашей ориентации эти ребра поочередно ориентированы то , то . Заметим что эта ориентация совпадает с ориентацией ребер на пути, а значит в нашем ориентированом графе существует путь из свободной вершины в свободную вершину . Нo каждая свободная вершина из связана ребром с в графе , аналогично каждая свободная вершина из связана ребром с . Не сложно заметить, что, в таком случае, достижим из , а значит в процессе поиска в глубину будет найден некий путь и соответствующий ему .
Утверждение доказано.
Оценка производительности
Поиск в глубину запускается от вершины не более чем раз, т.к. из ведет ровно ребер, и при каждом запуске одно из них инвертируется. Сам поиск работает за , каждая инвертация и перезапись паросочетания так же занимает времени. Тогда все время алгоритма ограничено .
Псевдокод
- — массив вершин , инцидентные в текущем паросочетании,
- — массив вершин , инцидентные в текущем паросочетании,
- — массив, где помечаются посещенные вершины.
Максимальное паросочетание — такие ребра , что .
Поиск в глубину, одновременно инвертирующий ребра:
bool dfs(x):
if vis[x]
return false
vis[x] = true
for
if py[y] == -1
py[y] = x
px[x] = y
return true
else
if dfs(py[y])
py[y] = x
px[x] = y
return true
return false
Инициализация и внешний цикл:
func fordFulkerson():
fill(px, -1)
fill(py, -1)
isPath = true
while isPath
isPath = false
fill(vis, false)
for
if px[x] == -1
if dfs(x)
isPath = true
См. также
- Теорема о максимальном паросочетании и дополняющих цепях
- Алгоритм Форда-Фалкерсона, реализация с помощью поиска в глубину
Источники информации
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн — “Алгоритмы: построение и анализ”, 2-е издание, стр. 758 – 761.
Поиск максимального паросочетания
Пусть дан неориентированный граф G = (V, Е). Паросочетанием (matching)
называется подмножество ребер М є Е, такое что для всех вершин v е V в М
содержится не более одного ребра, инцидентного v.
Максимальным паросочетанием называется паросочетание максимальной мощности, т.е. такое паросочетание М, что для любого паросочетания М’: |М| >= |М’|.
Ограничимся рассмотрением задачи поиска максимальных паросочетаний в двудольных графах. Мы предполагаем, что множество вершин можно разбить на два подмножества V = L U R, где L и R не пересекаются, и все
ребра из Е проходят между L и R. Далее мы предполагаем, что каждая вершина из V имеет по крайней мере одно инцидентное ребро.
С помощью метода Форда-Фалкерсона можно найти максимальное паросочетание в неориентированном двудольном графе G = (V,E) за время, полиномиально зависящее от |V| и |Е|. Определим для заданного двудольного графа G соответствующую
транспортную сеть G’ = (V’, Е’) следующим образом. Возьмем в качестве источника s и стока t новые вершины, не входящие в V, и пусть V’ = V U {s, t}. Если
разбиение вершин в графе G задано как V = L U R, ориентированными ребрами G будут ребра Е, направленные из L в R, а также |V| новых ребер. Чтобы завершить построение, присвоим каждому ребру Е’ единичную пропускную способность.
Ниже показан двудольный граф и соответствующая ему транспортная сеть. Выделенные ребра обеспечивают максимальный поток и определяют максимальное паросочетание
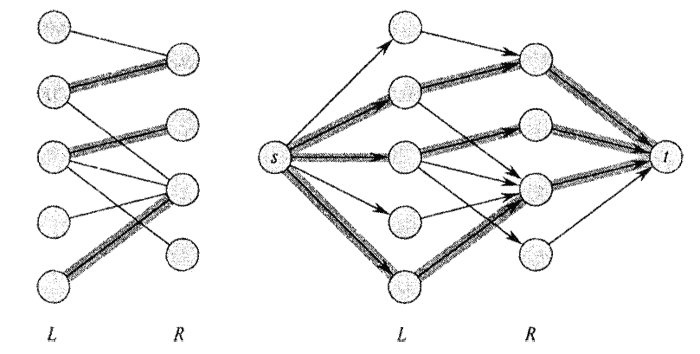
Формальное описание [вверх]
Matching(G)
1. Проверить, является ли граф двудольным.
2. Если граф двудольный, то перейти к пункт 2.1., иначе
вывести сообщение о том, что граф недвудольный и завершить работу.
2.1. Разбить граф на 2 части.
2.2. Создать 2 вершини, связать стартовую со своеми вершинами
из первой части графа, конечную - со всеми вершинами
из второй части графа.
2.3. Модернизировать полученную сеть, изменяя пропускную способность
в обратну сторону графа на отрицательные значения.
2.4. Найти максимальный поток с помощью алгоритма Форда-Фалкерсона.
2.5. Считать рёбра между двумя частями графа
с потоком равным 1 рёбрами паросочитаний.
2.6. Подсчитать количество рёбер в паросочитании.
Оценка сложности [вверх]
Поскольку любое паросочетание в двудольном графе имеет мощность не более min(L, R) = О (V), величина максимального потока в G составляет О (V).
Поэтому максимальное паросочетание в двудольном графе можно найти за время O(V*E’) = O(V*E), поскольку |Е’| = o(Е).
Пример [вверх]
Рассмотрим схему сведения двудольного графа к некоторой сети. На рисунке показан исходный двудольный граф G.
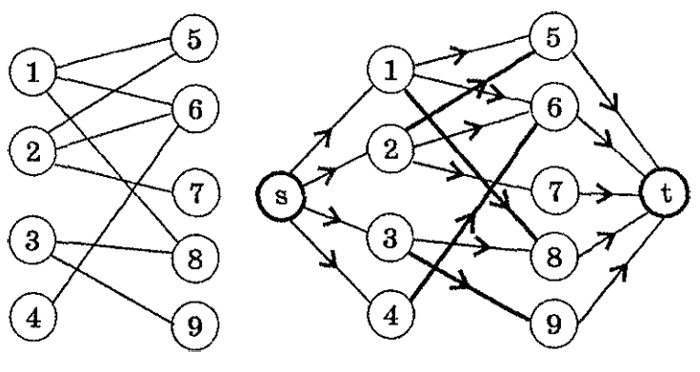
Построим сеть S(G) с источником s и стоком t следующим образом:
* источник s соединим дугами с вершинами из множества X;
* вершины из множества Y соединим дугами со стоком t;
* направление на ребрах исходного графа будет от вершин из X к вершинам из Y;
* пропускная способность всех дуг C[i,j] = 1.
Найдем максимальный поток из s в t для построенной сети. Он существует. Насыщенные дуги потока (они выделены «жирными» линиями на рисунке) соответствуют ребрам наибольшего паросочетания исходного графа. Найденное наибольшее паросочетание не единственное.
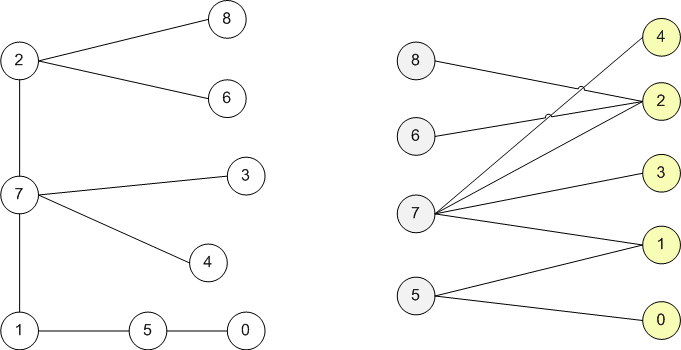
Найдём в исходном графе (слева) две доли и запомним их. Таким образом мы получим двудольный граф.
Добавим вершину-исток и вершину-сток. Соеденим исток и сток с разными долями графа.
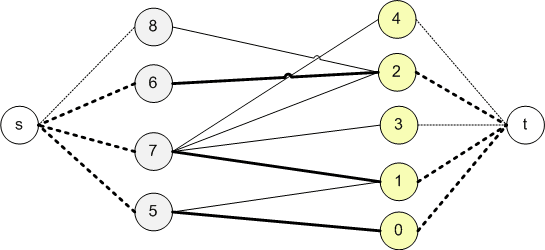
Для всех рёбер пропускная способность равна 1. Найдём максимальный поток из истока в сток.
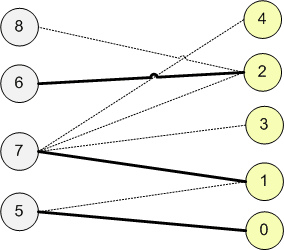
Рёбра первоначального графа, через которые поток равен 1, будут рёбрами максимального паросочетания. В данном случае максимальное паросочетание состоит из 2 рёбер: (0;1) и (2;4).
Найдём в исходном графе (слева) две доли и запомним их. Таким образом мы получим двудольный граф.
Добавим вершину-исток и вершину-сток. Соеденим исток и сток с разными долями графа.
Для всех рёбер установим пропускную способность равную 1. Найдём максимальный поток из истока в сток.
Рёбра первоначального графа, через которые поток равен 1, будут рёбрами максимального паросочетания. В данном случае максимальное паросочетание состоит из 2 рёбер: (0;1) и (2;4).
[вверх]
Находим паросочетание максимальной мощности – наибольшее паросочетание с максимально возможным числом ребер из графа
Перед вами третья статья из серии о задачах паросочетаний графов. В первой статье я рассказал о том, что такое паросочетание графов, и изложил сопутствующие концепции. Во второй статье были представлены решения для задачи нахождения наибольшего паросочетания; в завершение читателям была предложена задача нахождения паросочетания максимальной мощности.
Предположим, у вас есть набор X (например, соискатели рабочих мест), не пересекающийся с множеством Y (например, рабочие места), и двудольный граф G, соединяющий вершины двух наборов (пары «соискатель — рабочее место», где соискатель обладает достаточной квалификацией для выполнения работы). Паросочетание M в графе G представляет подмножество ребер в G, где никакие два ребра не совпадают (не имеют общей вершины). Наибольшее паросочетание представляет собой то, к которому нельзя добавить больше ребер в графе. Паросочетание максимальной мощности — это наибольшее паросочетание с максимально возможным числом ребер из графа. На рисунке 1 показаны примеры паросочетаний графов.
 |
| Рисунок 1. Примеры паросочетания в графе |
В нашем примере «соискатели — рабочие места» нужно найти паросочетание максимальной мощности, чтобы максимально задействовать соискателей и заполнить рабочие места.
Тестовые данные
Чтобы продемонстрировать и испытать решение для паросочетания максимальной мощности, будут использованы те же тестовые данные, что и в предыдущих статьях. Воспользуйтесь программным кодом листинга 1, чтобы создать малый набор данных для проверки правильности решения.
Используйте программный код листинга 2, чтобы создать большой набор тестовых данных (~1000000 ребер) для тестирования производительности решения.
Если вы используете SQL Server 2016 или более новую версию, обязательно создайте пустой столбчатый индекс columnstore для оптимизации с оператором Window Aggregate пакетного режима:
CREATE NONCLUSTERED COLUMNSTORE INDEX idx_cs_dummy ON dbo.G (x) WHERE x = 'yes' AND x = 'no';
Алгоритм поиска паросочетания максимальной мощности
В алгоритме поиска паросочетания максимальной мощности используется увеличивающийся путь (разновидность чередующегося пути). Напомню, что при паросочетании M в графе G чередующийся путь, или M-чередующийся путь в G, — это путь, состоящий из ребер в G, которые меняются от присутствующих в паросочетании к отсутствующим в паросочетании. Увеличивающийся путь — это чередующийся путь, который начинается и заканчивается на свободных вершинах. На рисунке 2 показаны типы путей.
 |
| Рисунок 2. Типы путей |
Ниже приводится алгоритм поиска паросочетания максимальной мощности M в G.
- Начните с любого паросочетания M в G (пустого или непустого).
- Повторяйте шаги, пока верно следующее утверждение:
— задать M = M ⊕ P (симметрическая разность M и P), где P = M-чередующийся путь в G;
— если увеличивающийся путь не обнаружен, прервать.
Подробные сведения об этом алгоритме, а также его обоснование и оценку сложности можно найти в лекции по паросочетанию в двудольном графе (http://math.mit.edu/~goemans/18433 S07/matching-notes.pdf).
На рисунке 3 показано применение этого алгоритма с малым набором тестовых данных, начиная с пустого паросочетания.
 |
| Рисунок 3. Алгоритм поиска максимума паросочетаний |
Обратите внимание, что мощность паросочетания увеличивается на единицу на каждом шаге. Это означает, что, если отправной точкой является паросочетание с мощностью n (0 для пустого паросочетания в качестве отправной точки) и мощность паросочетания максимальной мощности — m, алгоритм совершит m — n итераций увеличения.
В предыдущей статье были представлены различные решения для поиска наибольшего паросочетания. В большинстве представленных решений среднее время поиска каждого ребра в наибольшем паросочетании значительно меньше времени поиска увеличивающегося пути и применения приращения. Поэтому полезно начинать с наибольшего паросочетания в качестве отправной точки для поиска паросочетания максимальной мощности.
Решения для наибольшего паросочетания
Напомню, что в Решении 5 для поиска наибольшего паросочетания было создано паросочетание большей мощности, чем во всех других решениях. Поэтому воспользуемся этим решения для поиска наибольшего паросочетания, которое послужит отправной точкой для поиска паросочетания максимальной мощности.
Если это еще не сделано, сначала выполните следующий программный код для создания пустого индекса columnstore, чтобы обеспечить оптимизацию с использованием оператора Window Aggregate пакетного режима:
CREATE NONCLUSTERED COLUMNSTORE INDEX idx_cs_dummy ON dbo.G (x) WHERE x = 'yes' AND x = 'no';
Затем выполните программный код листинга 3 для создания процедуры MaximalMatching, которая реализует Решение 5 из предыдущей статьи.
Процедура MaximalMatching заполняет таблицу M наибольшим паросочетанием в G.
Алгоритм поиска увеличивающегося пути
Для паросочетания M в двудольном графе G, которое соединяет вершины из набора X с вершинами из набора Y, в этом разделе описан алгоритм поиска M-увеличивающегося пути в G. Алгоритм создает остаточный направленный граф G’. Сформируйте остаточный граф следующим образом:
- добавьте исходную вершину s и создайте направленные ребра, указывающие из s ко всем свободным вершинам x (вершины x, не совпадающие ни с одной из вершин в M);
- добавьте целевую вершину t и создайте направленные ребра из всех свободных вершин y (вершины y, которые не принадлежат никаким ребрам в M), указывающие на t;
- для каждого ребра в M создайте направленное ребро в G’, указывающее из y в x;
- для каждого ребра в G, которое отсутствует в M, создайте направленное ребро в G’, указывающее из x в y.
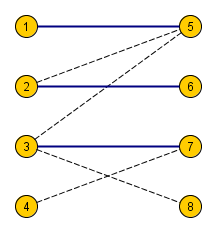
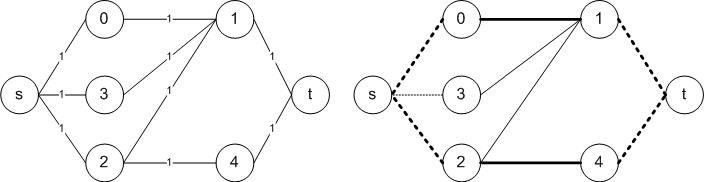
Примените алгоритм поиска преимущественно в глубину (depth-first search, DFS) или поиска в ширину (breadth-first search, BFS), чтобы найти кратчайший путь между s и t. Этот путь, без первого и последнего ребер из s в t, является M-увеличивающимся путем в G. На рисунке 4 дано графическое представление этого алгоритма. Слева находится некоторое паросочетание M в графе G. В центре — остаточный граф G’, созданный из M и G на основе приведенных выше инструкций. Справа — выделенный кратчайший путь из s к t: s->D->3->B->1->A->2->t. После удаления первого и последнего ребра в пути вы получите D->3->B->1->A->2, что является M-увеличивающимся путем в G. Наша цель — вернуть увеличивающийся путь как подмножество вершин из G: {(D, 3), (B, 3), (B, 1), (A, 1), (A, 2)}.
 |
| Рисунок 4. Нахождение увеличивающегося пути |
Реализация алгоритма поиска увеличивающегося пути
В нашем решении для паросочетания максимальной мощности применяется последовательность приращений, каждое из которых устанавливает M равной симметрической разности M и увеличивающегося пути в M. По этой причине удобно реализовать решение поиска увеличивающегося пути как многооператорной, определенной пользователем функции (с именем AugmentingPath), которая возвращает табличную переменную @P с набором ребер, формирующих путь. Функция реализует следующие действия.
- Пытается идентифицировать увеличивающийся путь размера 1 и записать его в @P. Это любое ребро в G со свободной x и свободной y. Если такой путь обнаружен, возврат.
- Если увеличивающегося пути размера 1 не существует, функция ищет все потенциальные начала для более длинных увеличивающихся путей (свободные вершины x из G, соединенные с соответствующими вершинами y) и записывает их в табличную переменную @X. Если ни одно не обнаружено, увеличивающегося пути не существует, возврат.
- Повторяет, пока увеличивающийся путь не обнаружен:
— Добавляет в табличную переменную @Y отдельные соответствующие вершины y из G, которые имеют родительскую вершину в @X из предыдущей итерации и которых еще нет в @Y. Использует MIN (x) для y в качестве родителя, поскольку в конечном итоге нам нужен только один увеличивающийся путь. В случае нескольких родительских x не имеет значения, из которого мы идем к y. Все обработанные «родители» находятся в @X, поэтому не приходится повторно посещать пути в последующих итерациях. Если таких вершин y не обнаружено, увеличивающийся путь не существует, возврат.
— Если существуют новые вершины y, функция ищет соответствующие вершины x в M. Они должны существовать и быть отдельными (поскольку соединенные вершины y с предыдущего уровня сопоставлены).
— Добавьте к @P любое ребро со свободной y и x из текущего уровня в @X. Если такая вершина существует, мы обнаружили увеличивающийся путь.
- Если вы пришли к этому шагу, увеличивающийся путь должен существовать и его длина больше чем один сегмент. Сконструируйте путь из @P, @X и @Y.
Запустите программный код листинга 4, чтобы создать полную функцию AugmentingPath.
Обратите внимание, что в действительности это решение не строит остаточный граф G’, но воспринимает его как виртуальный. Опущена часть с источником s и приемником t; они полезны на концептуальном уровне. Решение начинается со свободными вершинами x и завершается со свободными вершинами y, а прерывается, если обнаружить увеличивающийся путь не удается.
Используйте следующий программный код для проверки функции (сначала с малым набором тестовых данных):
SELECT * FROM dbo.AugmentingPath ();
Если выполнить этот программный код с пустым M, то будет получен путь с одной вершиной. Вы можете вручную заполнить M любым начальным паросочетанием, а затем запустить функцию, чтобы убедиться в ее успешном выполнении.
Реализация алгоритма поиска паросочетания максимальной мощности
Как отмечалось выше, алгоритм поиска паросочетания максимальной мощности имеет следующий вид.
- Начать с любого паросочетания M в G (пустого или не пустого).
- Повторять, пока верно следующее условие:
— задать M = M ⊕ P (симметрическая разность M и P), где P = M-увеличивающийся путь в G;
— если увеличивающийся путь не обнаружен, прервать.
В нашем решении используется наибольшее паросочетание в качестве отправной точки после выполнения подготовленной ранее процедуры MaximalMatching.
Затем в цикле с условием, которое всегда истинно (например, WHILE 1 = 1), реализуются два шага.
- Предложение MERGE, которое задает M значение симметрической разности M и результата функции AugmentingPath. Эта инструкция определяет M как цель, а функция AugmentingPath (с псевдонимом P) как источник. Предикат объединения — M.x = P.x AND M.y = P.y. Если обнаружено паросочетание, целевая строка удаляется; если паросочетание не обнаружено, исходная строка вставляется в цель.
- Если число строк, на которые воздействует инструкция MERGE, равно 0, то операция завершена, поэтому происходит выход из цикла.
В листинге 5 приводится реализация этого решения с несколькими дополнительными строками программного кода для измерения времени выполнения каждой из двух основных частей: поиска наибольшего паросочетания и применения оставшихся приращений.
Этот программный код в основном прост, но может возникнуть вопрос относительно цели пустого оператора в действии UPDATE в предложении MERGE, поскольку на практике оно никогда не активируется:
WHEN MATCHED AND 0 = 1 THEN UPDATE SET x = 'Thanks, Paul White!', y = 1759
Без этого предложения в результате ошибки инструкция MERGE может привести к сбою из-за нарушения промежуточного повторяющегося ключа, если производится внутренняя обработка вставок перед удалениями. Решение Пола Уайта состоит в добавлении предложения с действием UPDATE. В результате оптимизатор выдает широкий (для каждого индекса) план обновления с разбиением, сортировкой и свертыванием, что исключает промежуточные повторяющиеся ключи. Более подробно об этом рассказано в его журнале (http://sqlblog.com/blogs/paul_white/archive/2012/12/10/merge-bug-with-filtered-indexes.aspx).
Запуск этого решения с малым набором тестовых данных приводит к выходным данным, показанным на экране 1.
 |
| Экран 1. Результат работы кода листинга 5 с малым набором тестовых данных |
Запуск этого решения с большим набором тестовых данных приводит к выходным данным (сокращенно), как на экране 2.
 |
| Экран 2. Результат работы кода листинга 5 с большим набором тестовых данных |
Как оказалось, процедура MaximalMatching обнаружила наибольшее паросочетание, которое также является паросочетанием максимальной мощности. Это идеальный случай, поэтому на первом проходе не удалось найти увеличивающийся путь, и цикл был прерван.
Итак, в этой серии статей мы рассмотрели задачи паросочетаний графов, начиная с изложения принципов и описания сопутствующих концепций, с последующим представлением решений для наибольшего паросочетания и, наконец, решения для паросочетания максимальной мощности. Я лишь поверхностно коснулся этого предмета. Существует множество связанных задач с дополнительными уровнями сложности, в том числе с учетом весов (например, приоритета) и т. д. Если вы хотите более подробно рассмотреть эту тему, обратите внимание на такие вопросы, как паросочетание графов (https://en.wikipedia.org/wiki/Matching_ (graph_theory)) и потоки в сетях (https://en.wikipedia.org/wiki/Flow_network). Я надеюсь, что по мере совершенствования функциональности графов в SQL продукт будет дополнен инструментарием, который сделает более эффективным решение подобных задач.
Листинг 1. Создание малого набора тестовых данных
SET NOCOUNT ON;
USE tempdb;
-- Очистка
DROP TABLE IF EXISTS dbo.M, dbo.G, dbo.X, dbo.Y;
GO
-- Набор X, например Applicants
CREATE TABLE dbo.X
(
x VARCHAR(10) NOT NULL CONSTRAINT PK_X PRIMARY KEY,
moreonx VARCHAR(20) NOT NULL
);
INSERT INTO dbo.X(x, moreonx) VALUES
('A', 'Applicant A'),
('B', 'Applicant B'),
('C', 'Applicant C'),
('D', 'Applicant D');
-- Набор Y, например Jobs
CREATE TABLE dbo.Y
(
y INT NOT NULL CONSTRAINT PK_Y PRIMARY KEY,
moreony VARCHAR(20) NOT NULL
);
INSERT INTO dbo.Y(y, moreony) VALUES
(1, 'Job 1'),
(2, 'Job 2'),
(3, 'Job 3'),
(4, ‘Job 4’);
-- Граф G = (X, Y, E), например возможные соединения «соискатель-рабочее место»
CREATE TABLE dbo.G
(
x VARCHAR(10) NOT NULL
CONSTRAINT FK_G_X FOREIGN KEY REFERENCES dbo.X,
y INT NOT NULL
CONSTRAINT FK_G_Y FOREIGN KEY REFERENCES dbo.Y,
CONSTRAINT PK_G PRIMARY KEY (x, y)
);
INSERT INTO dbo.G(x, y) VALUES
('A', 1),
('A', 2),
('B', 1),
('B', 3),
('C', 3),
(‘C’, 4),
(‘D’, 3);
GO
-- M является паросочетанием в G
CREATE TABLE dbo.M
(
x VARCHAR(10) NOT NULL
CONSTRAINT UQ_M_x UNIQUE,
y INT NOT NULL
CONSTRAINT UQ_M_y UNIQUE,
CONSTRAINT PK_M PRIMARY KEY (x, y),
CONSTRAINT FK_M_G FOREIGN KEY (x, y) REFERENCES dbo.G(x, y)
);
Листинг 2. Создание большого набора данных
-- Очистка
SET NOCOUNT ON;
USE tempdb;
DROP TABLE IF EXISTS dbo.M, dbo.G, dbo.X, dbo.Y;
DROP FUNCTION IF EXISTS dbo.GetNums;
GO
-- Вспомогательная функция dbo.GetNums
CREATE FUNCTION dbo.GetNums(@low AS BIGINT, @high AS BIGINT) RETURNS TABLE
AS
RETURN
WITH
L0 AS (SELECT c FROM (SELECT 1 UNION ALL SELECT 1) AS D(c)),
L1 AS (SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B),
L2 AS (SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B),
L3 AS (SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B),
L4 AS (SELECT 1 AS c FROM L3 AS A CROSS JOIN L3 AS B),
L5 AS (SELECT 1 AS c FROM L4 AS A CROSS JOIN L4 AS B),
Nums AS (SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L5)
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums
ORDER BY rownum;
GO
CREATE TABLE dbo.X
(
x VARCHAR(10) NOT NULL CONSTRAINT PK_X PRIMARY KEY,
moreonx VARCHAR(20) NOT NULL
);
CREATE TABLE dbo.Y
(
y INT NOT NULL CONSTRAINT PK_Y PRIMARY KEY,
moreony VARCHAR(20) NOT NULL
);
CREATE TABLE dbo.G
(
x VARCHAR(10) NOT NULL
CONSTRAINT FK_G_X FOREIGN KEY REFERENCES dbo.X,
y INT NOT NULL
CONSTRAINT FK_G_Y FOREIGN KEY REFERENCES dbo.Y,
CONSTRAINT PK_G PRIMARY KEY (x, y)
);
CREATE TABLE dbo.M
(
x VARCHAR(10) NOT NULL
CONSTRAINT UQ_M_x UNIQUE,
y INT NOT NULL
CONSTRAINT UQ_M_y UNIQUE,
CONSTRAINT PK_M PRIMARY KEY (x, y),
CONSTRAINT FK_M_G FOREIGN KEY (x, y) REFERENCES dbo.G(x, y)
);
GO
DECLARE @n AS INT = 10000000; -- ~ общее количество строк
SET @n = SQRT(@n * 2); -- количество членов арифметической последовательности
INSERT INTO dbo.X(x, moreonx)
SELECT
RIGHT('000000000' + CAST(N.n AS VARCHAR(10)), 10) AS x,
'Applicant ' + RIGHT('000000000' + CAST(N.n AS VARCHAR(10)), 10) AS moreonx
FROM dbo.GetNums(1, @n) AS N;
INSERT INTO dbo.Y(y, moreony)
SELECT
N.n AS y,
'Job ' + CAST(N.n AS VARCHAR(10)) AS moreonx
FROM dbo.GetNums(1, @n) AS N;
INSERT INTO dbo.G WITH (TABLOCK) (x, y)
SELECT RIGHT('000000000' + CAST(X.n AS VARCHAR(10)), 10) AS x, Y.n AS y
FROM dbo.GetNums(1, @n) AS X
CROSS APPLY (SELECT TOP (@n - X.n + 1) n
FROM dbo.GetNums(1, @n)
ORDER BY NEWID()) AS Y;
Листинг 3. Создание процедуры MaximalMatching
CREATE OR ALTER PROC dbo.MaximalMatching AS SET NOCOUNT, XACT_ABORT ON; DECLARE @n AS BIGINT, @x AS VARCHAR(10), @y AS INT; TRUNCATE TABLE dbo.M; CREATE TABLE #G ( n BIGINT NOT NULL, x VARCHAR(10) NOT NULL, y INT NOT NULL, INDEX idx_n_y CLUSTERED(n, y) ); WITH C AS ( SELECT x, y, COUNT(*) OVER(PARTITION BY x) AS cnt FROM dbo.G ) INSERT INTO #G (n, x, y) SELECT DENSE_RANK() OVER(ORDER BY cnt, x) AS n, x, y FROM C; SELECT TOP (1) @n = n, @x = x, @y = y FROM #G ORDER BY n, y; WHILE @@ROWCOUNT > 0 BEGIN INSERT INTO dbo.M(x, y) VALUES(@x, @y); SELECT TOP (1) @n = n, @x = x, @y = y FROM #G AS G WHERE n > @n AND NOT EXISTS ( SELECT * FROM dbo.M WHERE M.y = G.y ) ORDER BY n, y; END; DROP TABLE #G; GO
Листинг 4. Создание полной функции AugmentingPath
CREATE OR ALTER FUNCTION dbo.AugmentingPath() RETURNS @P TABLE ( x VARCHAR(10) NOT NULL, y INT NOT NULL, PRIMARY KEY (x, y) ) AS BEGIN DECLARE @i AS INT = 0, -- Уровень итерации @pathfound AS INT = 0; -- Флаг, указывающий на обнаружение увеличивающегося пути -- Набор вершин x, рассматриваемый на каждой итерации -- Имеет родителя y, который ведет к x DECLARE @X AS TABLE ( x VARCHAR(10) NOT NULL PRIMARY KEY, parent_y INT NULL, i INT NOT NULL ); -- Набор вершин y, обрабатываемый на каждой итерации -- Имеет родителя x, который ведет к y DECLARE @Y AS TABLE ( y INT NOT NULL PRIMARY KEY, parent_x VARCHAR(10) NOT NULL, i INT NOT NULL ); -- Попытайтесь найти увеличивающийся путь размера 1 -- An edge from G with a free x and a free y Ребро из G с свободной x и свободной y -- («свободной» означает несовпадающей с любой вершиной в M) INSERT INTO @P(x, y) SELECT TOP (1) x, y FROM dbo.G WHERE NOT EXISTS ( SELECT * FROM dbo.M WHERE M.x = G.x ) AND NOT EXISTS ( SELECT * FROM dbo.M WHERE M.y = G.y ); IF @@ROWCOUNT > 0 RETURN; -- Если увеличивающийся путь размером 1 не обнаружен, инициализировать @X -- с отдельными свободными вершинами x из G -- Мы уже знаем, что если они существуют, то указывают на сопоставленные вершины y INSERT INTO @X(x, parent_y, i) SELECT DISTINCT x, NULL AS parent_y, @i AS i FROM dbo.G WHERE NOT EXISTS ( SELECT * FROM dbo.M WHERE M.x = G.x ); IF @@ROWCOUNT = 0 RETURN; -- Пока увеличивающийся путь не обнаружен WHILE @pathfound = 0 BEGIN SET @i += 1; -- Добавьте к @Y раздельные сопоставленные вершины y из G, которые имеют -- родительскую вершину x в @X из предшествующей итерации -- и которых еще нет в y -- Используйте MIN(x) для y как родителя, поскольку в конечном итоге нам нужен -- только один (любой) увеличивающийся путь, поэтому в случае нескольких -- родительских x не имеет значения, из которого мы пришли к y -- все обработанные «родители» содержатся в @X, поэтому мы избегаем -- повторных обращений на последующих итерациях INSERT INTO @Y(y, parent_x, i) SELECT G.y, MIN(G.x) AS parent_x, @i AS i FROM dbo.G INNER JOIN @X AS X ON G.x = X.x AND X.i = @i - 1 WHERE NOT EXISTS ( SELECT * FROM @Y AS Y WHERE Y.y = G.y ) GROUP BY G.y; IF @@ROWCOUNT = 0 RETURN; -- Если существуют новые вершины y, ищите соответствующие вершины x в M -- Они должны существовать и должны отличаться -- (поскольку соединенные вершины y с предыдущего уровня сопоставлены) INSERT INTO @X(x, parent_y, i) SELECT M.x, Y.y AS parent_y, @i AS i FROM dbo.M INNER JOIN @Y AS Y ON M.y = Y.y AND Y.i = @i; -- Добавьте к @P любое ребро из G с свободной y -- и x из текущего уровня в @X -- Если такая вершина существует, мы обнаружили увеличивающийся путь INSERT INTO @P(x, y) SELECT TOP (1) G.x, G.y FROM dbo.G INNER JOIN @X AS X ON G.x = X.x AND X.i = @i WHERE NOT EXISTS ( SELECT * FROM dbo.M WHERE M.y = G.y ); IF @@ROWCOUNT > 0 SET @pathfound = 1; END; -- Если пришли сюда, увеличивающийся путь должен существовать, и его длина больше одного сегмента -- Сконструируйте путь из @P, @X и @Y WHILE @i > 0 BEGIN SET @i -= 1; INSERT INTO @P(x, y) SELECT X.x, X.parent_y AS y FROM @P AS P INNER JOIN @X AS X ON P.x = X.x AND X.i = @i + 1 INSERT INTO @P(x, y) SELECT Y.parent_x AS x, Y.y AS y FROM @P AS P INNER JOIN @Y AS Y ON P.y = Y.y AND Y.i = @i + 1 END; RETURN; END; GO
Листинг 5. Код поиска паросочетания максимальной мощности
DECLARE @i AS INT = 0, @dt AS DATETIME2 = SYSDATETIME(), @cnt AS INT; -- Начинаем с поиска наибольшего паросочетания EXEC dbo.MaximalMatching; SET @cnt = (SELECT COUNT(*) FROM dbo.M); PRINT 'Maximal matching with ' + CAST(@cnt AS VARCHAR(10)) + ' matches found in ' + CAST(DATEDIFF(second, @dt, SYSDATETIME()) AS VARCHAR(10)) + ' seconds.'; SET @dt = SYSDATETIME(); -- Для приращения пути, обнаруженного на последнем проходе, ищем другое и выполняем приращение, -- то есть задаем M = M ⊕ P (симметрическая разность) WHILE 1 = 1 BEGIN MERGE INTO dbo.M USING dbo.AugmentingPath() AS P ON M.x = P.x AND M.y = P.y -- Ниже добавление для обхода ошибки (благодарность Полу Уайту) WHEN MATCHED AND 0 = 1 THEN UPDATE SET x = 'Thanks, Paul White!', y = 1759 WHEN MATCHED THEN DELETE WHEN NOT MATCHED THEN INSERT(x, y) VALUES(P.x, P.y); IF @@ROWCOUNT = 0 BREAK; SET @i += 1; END; PRINT 'Processed ' + CAST(@i AS VARCHAR(10)) + ' augmenting paths in ' + CAST(DATEDIFF(second, @dt, SYSDATETIME()) AS VARCHAR(10)) + ‘ more seconds.’; -- Возвращается паросочетание максимальной мощности SELECT x, y FROM dbo.M;