Как найти все маршруты в графе

Как найти все маршруты в графе

Блок-схема алгоритма Дейкстры.

Алгори́тм Де́йкстры (англ. Dijkstra’s algorithm) — алгоритм на графах, изобретённый нидерландским учёным Эдсгером Дейкстрой в 1959 году. Находит кратчайшие пути от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса. Алгоритм широко применяется в программировании, например, его используют протоколы маршрутизации OSPF и IS-IS.

Формулировка задачи[править | править код]

Примеры[править | править код]

Вариант 1. Дана сеть автомобильных дорог, соединяющих города Московской области. Некоторые дороги односторонние. Найти кратчайшие пути от города А до каждого города области (если двигаться можно только по дорогам).

Вариант 2. Имеется некоторое количество авиарейсов между городами мира, для каждого известна стоимость. Стоимость перелёта из A в B может быть не равна стоимости перелёта из B в A. Найти маршрут минимальной стоимости (возможно, с пересадками) от Копенгагена до Барнаула.

Формальное определение[править | править код]

Дан взвешенный ориентированный[1] граф G(V,E) без дуг отрицательного веса[2]. Найти кратчайшие пути от некоторой вершины a графа G до всех остальных вершин этого графа.

Неформальное объяснение[править | править код]

Dijkstra Animation.gif

Каждой вершине из V сопоставим метку — минимальное известное расстояние от этой вершины до a.

Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки.

Работа алгоритма завершается, когда все вершины посещены.

Инициализация.

Метка самой вершины a полагается равной 0, метки остальных вершин — бесконечности.

Это отражает то, что расстояния от a до других вершин пока неизвестны.

Все вершины графа помечаются как непосещённые.

Шаг алгоритма.

Если все вершины посещены, алгоритм завершается.

В противном случае, из ещё не посещённых вершин выбирается вершина u, имеющая минимальную метку.

Мы рассматриваем всевозможные маршруты, в которых u является предпоследним пунктом. Вершины, в которые ведут рёбра из u, назовём соседями этой вершины. Для каждого соседа вершины u, кроме отмеченных как посещённые, рассмотрим новую длину пути, равную сумме значений текущей метки u и длины ребра, соединяющего u с этим соседом.

Если полученное значение длины меньше значения метки соседа, заменим значение метки полученным значением длины. Рассмотрев всех соседей, пометим вершину u как посещённую и повторим шаг алгоритма.

Пример[править | править код]

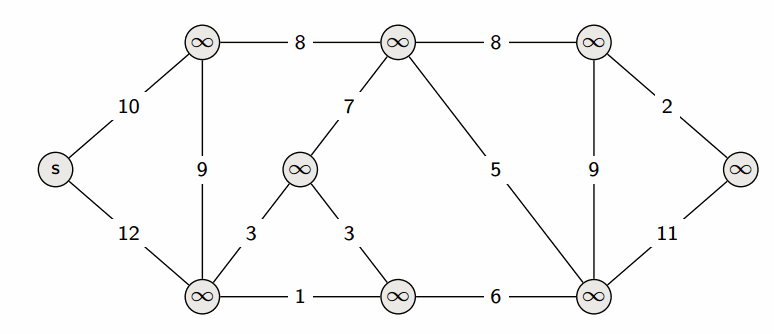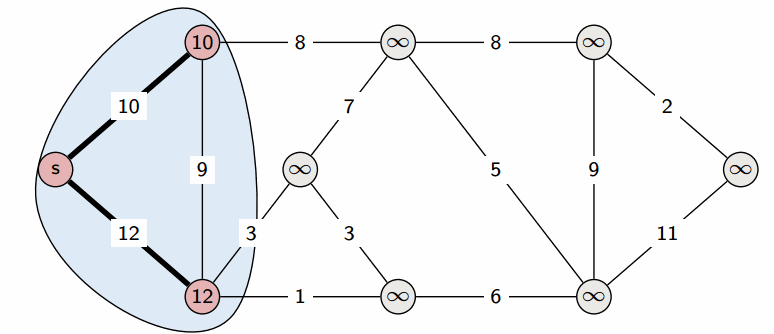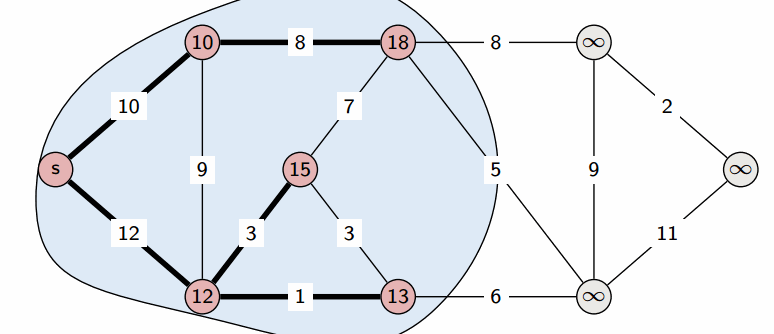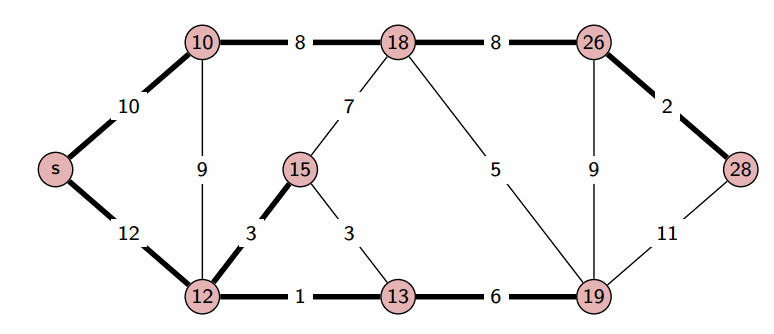
Рассмотрим выполнение алгоритма на примере графа, показанного на рисунке.

Пусть требуется найти кратчайшие расстояния от 1-й вершины до всех остальных.

Dijkstra graph0.PNG

Кружками обозначены вершины, линиями — пути между ними (рёбра графа).

В кружках обозначены номера вершин, над рёбрами обозначен их вес — длина пути.

Рядом с каждой вершиной красным обозначена метка — длина кратчайшего пути в эту вершину из вершины 1.

Dijkstra graph1.PNG

Первый шаг.

Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6.

Dijkstra graph2.PNG

Первый по очереди сосед вершины 1 — вершина 2, потому что длина пути до неё минимальна.

Длина пути в неё через вершину 1 равна сумме значения метки вершины 1 и длины ребра, идущего из 1-й в 2-ю, то есть 0 + 7 = 7.

Это меньше текущей метки вершины 2, бесконечности, поэтому новая метка 2-й вершины равна 7.

Dijkstra graph3.PNG

Аналогичную операцию проделываем с двумя другими соседями 1-й вершины — 3-й и 6-й.

Dijkstra graph5.PNG

Все соседи вершины 1 проверены.

Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит.

Вычеркнем её из графа, чтобы отметить, что эта вершина посещена.

Dijkstra graph6.PNG

Второй шаг.

Снова находим «ближайшую» из непосещённых вершин. Это вершина 2 с меткой 7.

Dijkstra graph7.PNG

Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю вершину. Соседями вершины 2 являются вершины 1, 3 и 4.

Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем.

Следующий сосед — вершина 3, так как имеет минимальную метку.

Если идти в неё через 2, то длина такого пути будет равна 17 (7 + 10 = 17). Но текущая метка третьей вершины равна 9, а это меньше 17, поэтому метка не меняется.

Dijkstra graph9.PNG

Ещё один сосед вершины 2 — вершина 4.

Если идти в неё через 2-ю, то длина такого пути будет равна сумме кратчайшего расстояния до 2-й вершины и расстояния между вершинами 2 и 4, то есть 22 (7 + 15 = 22).

Поскольку 22<infty , устанавливаем метку вершины 4 равной 22.

Dijkstra graph8.PNG

Все соседи вершины 2 просмотрены, замораживаем расстояние до неё и помечаем её как посещённую.

Dijkstra graph10.PNG

Третий шаг.

Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим такие результаты:

Dijkstra graph11.PNG

Дальнейшие шаги.

Повторяем шаг алгоритма для оставшихся вершин. Это будут вершины 6, 4 и 5, соответственно порядку.

Dijkstra graph12.PNG
Dijkstra graph13.PNG
Dijkstra graph14.PNG

Завершение выполнения алгоритма.

Алгоритм заканчивает работу, когда все вершины посещены.

Результат работы алгоритма виден на последнем рисунке: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.

Если в какой-то момент все непосещённые вершины помечены бесконечностью, то это значит, что до этих вершин нельзя добраться (то есть граф несвязный). Тогда алгоритм может быть завершён досрочно.

Алгоритм[править | править код]

Обозначения[править | править код]

Код реализации алгоритма[править | править код]

Ниже приведён код реализации алгоритма на языке программирования Java. Данный вариант реализации не является лучшим, но наглядно показывает возможную реализацию алгоритма:

class Dijkstra {
	double[] dist = new double[GV()];
	Edge[] pred = new Edge[GV()];
	public Dijkstra(WeightedDigraph G, int s) {
		boolean[] marked = new boolean[GV()];
		for (int v = 0; v <GV(); v++)
			dist[v] = Double.POSITIVE_INFINITY;
		MinPQplus<Double, Integer> pq;
		pq = new MinPQplus<Double, Integer>(); \Priority Queue
		dist[s] = 0.0;
		pq.put(dist[s], s);
		while (!pq.isEmpty()) {
			int v = pq.delMin();
				if (marked[v]) continue;
			marked(v) = true;
			for (Edge e  (v)) {
				int w = e.to();
				if (dist[w]> dist[v] + e.weight()) {
					dist[w] = dist[v] + e.weight();
					pred[w] = e;
					pq.insert(dist[w], w);
				}
			}
		}
	}
}

Псевдокод[править | править код]

Присвоим

d[a]gets 0, p[a]gets 0

Для всех uin V отличных от a присвоим d[u]gets infty .

Пока exists vnotin U. Пусть vnotin U — вершина с минимальным d[v] занесём v в U

Для всех unotin U таких, что vuin E

если d[u]>d[v]+w[vu] то

изменим d[u]gets d[v]+w[vu]

изменим {displaystyle p[u]gets (p[v],u)}

Описание[править | править код]

В простейшей реализации для хранения чисел d[i] можно использовать массив чисел, а для хранения принадлежности элемента множеству U — массив булевых переменных.

В начале алгоритма расстояние для начальной вершины полагается равным нулю, а все остальные расстояния заполняются большим положительным числом (бо́льшим максимального возможного пути в графе). Массив флагов заполняется нулями. Затем запускается основной цикл.

На каждом шаге цикла мы ищем вершину v с минимальным расстоянием и флагом равным нулю. Затем мы устанавливаем в ней флаг в 1 и проверяем все соседние с ней вершины u. Если в них (в u) расстояние больше, чем сумма расстояния до текущей вершины и длины ребра, то уменьшаем его.
Цикл завершается, когда флаги всех вершин становятся равны 1, либо когда у всех вершин c флагом 0 d[i]=infty . Последний случай возможен тогда и только тогда, когда граф G несвязный.

Доказательство корректности[править | править код]

Пусть {displaystyle l(v)} — длина кратчайшего пути из вершины a в вершину v. Докажем по индукции, что в момент посещения любой вершины z выполняется равенство {displaystyle d(z)=l(z)}.

База. Первой посещается вершина a. В этот момент {displaystyle d(a)=l(a)=0}.

Шаг. Пусть мы выбрали для посещения вершину zneq a. Докажем, что в этот момент {displaystyle d(z)=l(z)}. Для начала отметим, что для любой вершины v всегда выполняется d(v)geq l(v) (алгоритм не может найти путь короче, чем кратчайший из всех существующих). Пусть P — кратчайший путь из a в z. Вершина z находится на P и не посещена. Поэтому множество непосещённых вершин на P непусто. Пусть y — первая непосещённая вершина на P, x — предшествующая ей (следовательно, посещённая). Поскольку путь P кратчайший, его часть, ведущая из a через x в y, тоже кратчайшая, следовательно {displaystyle l(y)=l(x)+w(xy)}.

По предположению индукции, в момент посещения вершины x выполнялось {displaystyle d(x)=l(x)}, следовательно, вершина y тогда получила метку не больше чем {displaystyle d(x)+w(xy)=l(x)+w(xy)=l(y)}. Следовательно, {displaystyle d(y)=l(y)}. Если {displaystyle z=y}, то индукционный переход доказан. Иначе, поскольку сейчас выбрана вершина z, а не y, метка z минимальна среди непосещённых, то есть d(z)leq d(y)=l(y)leq l(z). Комбинируя это с d(z)geq l(z), имеем {displaystyle d(z)=l(z)}, что и требовалось доказать.

Поскольку алгоритм заканчивает работу, когда все вершины посещены, в этот момент {displaystyle d=l} для всех вершин.

Сложность алгоритма[править | править код]

Сложность алгоритма Дейкстры зависит от способа нахождения вершины v, а также способа хранения множества непосещённых вершин и способа обновления меток. Обозначим через n количество вершин, а через m — количество рёбер в графе G.

скрытые константы в асимптотических оценках трудоёмкости велики и использование фибоначчиевых куч редко оказывается целесообразным: обычные двоичные (d-ичные[en]) кучи на практике эффективнее.

Альтернативами им служат толстые кучи, тонкие кучи и кучи Бродала[en], обладающие теми же асимптотическими оценками, но меньшими константами[4].

См. также[править | править код]

  • Очередь с приоритетом (программирование)
  • Минимальное остовное дерево
  • Остовное дерево
  • Задача о кратчайшем пути
  • Алгоритм Борувки
  • Алгоритм Краскала
  • Алгоритм обратного удаления
  • Алгоритм Прима

Примечания[править | править код]

  1. ↑ Частными случаями ориентированного графа являются неориентированный и смешанный («частично ориентированный») графы.
  2. ↑ Для графа с отрицательными весами применяется более общий алгоритм — Алгоритм Дейкстры с потенциалами
  3. ↑ Владимир Алексеев, Владимир Таланов, Курс «Структуры данных и модели вычислений», Лекция № 7: Биномиальные и фибоначчиевы кучи // 26.09.2006, Интуит.ру
  4. ↑ Владимир Алексеев, Владимир Таланов, Курс «Структуры данных и модели вычислений», Лекция № 8: Тонкие кучи // 26.09.2006, Интуит.ру

Литература[править | править код]

  • Dijkstra E. W. A note on two problems in connexion with graphs (англ.) // Numerische Mathematik / F. Brezzi — Springer Science+Business Media, 1959. — Vol. 1, 1, Iss. 1, 1. — P. 269—271, 269—271. — ISSN 0029-599X; 0945-3245 — doi:10.1007/BF01386390
  • Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1.
  • Левитин А. В. Глава 9. Жадные методы: Алгоритм Дейкстры // Алгоритмы. Введение в разработку и анализ — М.: Вильямс, 2006. — С. 189—195. — 576 с. — ISBN 978-5-8459-0987-9

Ссылки[править | править код]

  • C. Анисимов. Как построить кратчайший маршрут между двумя точками.
  • Реализация простейшего варианта алгоритма Дейкстры на e-maxx.ru
  • Реализация варианта алгоритма Дейкстры для разреженных графов на e-maxx.ru
  • Реализация варианта алгоритма Дейкстры с корневой эвристикой
  • Алгоритм Дейкстры. Код программы на Python
  • Пример на YouTube
  • Dijkstra’s algorithm — реализация алгоритма на разных языках на Rosetta Code[en].
Источник

Алгоритм Дейкстры (англ. Dijkstra’s algorithm) находит кратчайшие пути от заданной вершины $s$ до всех остальных в графе без ребер отрицательного веса.

Существует два основных варианта алгоритма, время работы которых составляет $O(n^2)$ и $O(m log n)$, где $n$ — число вершин, а $m$ — число ребер.

#Основная идея

Заведём массив $d$, в котором для каждой вершины $v$ будем хранить текущую длину $d_v$ кратчайшего пути из $s$ в $v$. Изначально $d_s = 0$, а для всех остальных вершин расстояние равно бесконечности (или любому числу, которое заведомо больше максимально возможного расстояния).

Во время работы алгоритма мы будем постепенно обновлять этот массив, находя более оптимальные пути к вершинам и уменьшая расстояние до них. Когда мы узнаем, что найденный путь до какой-то вершины $v$ оптимальный, мы будем помечать эту вершину, поставив единицу ($a_v=1$) в специальном массиве $a$, изначально заполненном нулями.

Сам алгоритм состоит из $n$ итераций, на каждой из которых выбирается вершина $v$ с наименьшей величиной $d_v$ среди ещё не помеченных:

$$
v = argmin_{u | a_u=0} d_u
$$

(Заметим, что на первой итерации выбрана будет стартовая вершина $s$.)

Выбранная вершина отмечается в массиве $a$, после чего из из вершины $v$ производятся релаксации: просматриваем все исходящие рёбра $(v,u)$ и для каждой такой вершины $u$ пытаемся улучшить значение $d_u$, выполнив присвоение

$$
d_u = min (d_u, d_v + w)
$$

где $w$ — длина ребра $(v, u)$.

На этом текущая итерация заканчивается, и алгоритм переходит к следующей: снова выбирается вершина с наименьшей величиной $d$, из неё производятся релаксации, и так далее. После $n$ итераций, все вершины графа станут помеченными, и алгоритм завершает свою работу.

#Корректность

Обозначим за $l_v$ расстояние от вершины $s$ до $v$. Нам нужно показать, что в конце алгоритма $d_v = l_v$ для всех вершин (за исключением недостижимых вершин — для них все расстояния останутся бесконечными).

Для начала отметим, что для любой вершины $v$ всегда выполняется $d_v ge l_v$: алгоритм не может найти путь короче, чем кратчайший из всех существующих (ввиду того, что мы не делали ничего кроме релаксаций).

Доказательство корректности самого алгоритма основывается на следующем утверждении.

Утверждение. После того, как какая-либо вершина $v$ становится помеченной, текущее расстояние до неё $d_v$ уже является кратчайшим, и, соответственно, больше меняться не будет.

Доказательство будем производить по индукции. Для первой итерации его справедливость очевидна — для вершины $s$ имеем $d_s=0$, что и является длиной кратчайшего пути до неё.

Пусть теперь это утверждение выполнено для всех предыдущих итераций — то есть всех уже помеченных вершин. Докажем, что оно не нарушается после выполнения текущей итерации, то есть что для выбранной вершины $v$ длина кратчайшего пути до неё $l_v$ действительно равна $d_v$.

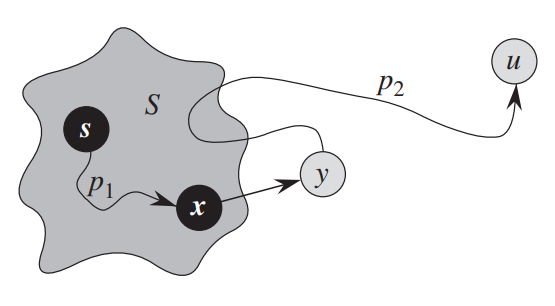
Рассмотрим любой кратчайший путь до вершины $v$. Обозначим первую непомеченную вершину на этом пути за $y$, а предшествующую ей помеченную за $x$ (они будут существовать, потому что вершина $s$ помечена, а вершина $v$ — нет). Обозначим вес ребра $(x, y)$ за $w$.

Так как $x$ помечена, то, по предположению индукции, $d_x = l_x$. Раз $(x,y)$ находится на кратчайшем пути, то $l_y=l_x+w$, что в точности равно $d_y=d_x+w$: мы в какой-то момент проводили релаксацию из уже помеченный вершины $x$.

Теперь, может ли быть такое, что $y ne v$? Нет, потому что мы на каждой итерации выбираем вершину с наименьшим $d_v$, а любой вершины дальше $y$ на пути расстояние от $s$ будет больше. Соответственно, $v = y$, и $d_v = d_y = l_y = l_v$, что и требовалось доказать.

#Время работы и реализация

Единственное вариативное место в алгоритме, от которого зависит его сложность — как конкретно искать $v$ с минимальным $d_v$.

#Для плотных графов

Если $m approx n^2$, то на каждой итерации можно просто пройтись по всему массиву и найти $argmin d_v$.

const int maxn = 1e5, inf = 1e9;
vector< pair<int, int> > g[maxn];
int n;

vector<int> dijkstra(int s) {
    vector<int> d(n, inf), a(n, 0);
    d[s] = 0;
    for (int i = 0; i < n; i++) {
        // находим вершину с минимальным d[v] из ещё не помеченных
        int v = -1;
        for (int u = 0; u < n; u++)
            if (!a[u] && (v == -1 || d[u] < d[v]))
                v = u;
        // помечаем её и проводим релаксации вдоль всех исходящих ребер
        a[v] = true;
        for (auto [u, w] : g[v])
            d[u] = min(d[u], d[v] + w);
    }
    return d;
}

Асимптотика такого алгоритма составит $O(n^2)$: на каждой итерации мы находим аргминимум за $O(n)$ и проводим $O(n)$ релаксаций.

Заметим также, что мы можем делать не $n$ итераций а чуть меньше. Во-первых, последнюю итерацию можно никогда не делать (оттуда ничего уже не прорелаксируешь). Во-вторых, можно сразу завершаться, когда мы доходим до недостижимых вершин ($d_v = infty$).

#Для разреженных графов

Если $m approx n$, то минимум можно искать быстрее. Вместо линейного прохода заведем структуру, в которую можно добавлять элементы и искать минимум — например std::set так умеет.

Будем поддерживать в этой структуре пары $(d_v, v)$, при релаксации удаляя старый $(d_u, u)$ и добавляя новый $(d_v + w, u)$, а при нахождении оптимального $v$ просто беря минимум (первый элемент).

Поддерживать массив $a$ нам теперь не нужно: сама структура для нахождения минимума будет играть роль множества ещё не рассмотренных вершин.

vector<int> dijkstra(int s) {
    vector<int> d(n, inf);
    d[root] = 0;
    set< pair<int, int> > q;
    q.insert({0, s});
    while (!q.empty()) {
        int v = q.begin()->second;
        q.erase(q.begin());
        for (auto [u, w] : g[v]) {
            if (d[u] > d[v] + w) {
                q.erase({d[u], u});
                d[u] = d[v] + w;
                q.insert({d[u], u});
            }
        }
    }
    return d;
}

Для каждого ребра нужно сделать два запроса в двоичное дерево, хранящее $O(n)$ элементов, за $O(log n)$ каждый, поэтому асимптотика такого алгоритма составит $O(m log n)$. Заметим, что в случае полных графов это будет равно $O(n^2 log n)$, так что про предыдущий алгоритм забывать не стоит.

#С кучей

Вместо двоичного дерева «правильнее» использовать более специализированную структуру, которая поддерживает именно добавление элементов и нахождение минимума: кучу. Удалять произвольные элементы в ней немного сложнее, поэтому вместо этого будем просто игнорировать все повторные вершины.

vector<int> dijkstra(int s) {
    vector<int> d(n, inf);
    d[root] = 0;
    // объявим очередь с приоритетами для *минимума* (по умолчанию ищется максимум)
    using pair<int, int> Pair;
    priority_queue<Pair, vector<Pair>, greater<Pair>> q;
    q.push({0, s});
    while (!q.empty()) {
        auto [cur_d, v] = q.top();
        q.pop();
        if (cur_d > d[v])
            continue;
        for (auto [u, w] : g[v]) {
            if (d[u] > d[v] + w) {
                d[u] = d[v] + w;
                q.push({d[u], u});
            }
        }
    }
}

На практике вариант с priority_queue немного быстрее.

Помимо обычной двоичной кучи, можно использовать и другие. С теоретической точки зрения, особенно интересна Фибоначчиева куча: у неё все почти все операции кроме работают за $O(1)$, но удаление элементов — за $O(log n)$. Это позволяет облегчить релаксирование до $O(1)$ за счет увеличения времени извлечения минимума до $O(log n)$, что приводит к асимптотике $O(n log n + m)$ вместо $O(m log n)$.

#Восстановление путей

Часто нужно знать не только длины кратчайших путей, но и получить сами пути.

Для этого можно создать массив $p$, в котором в ячейке $p_v$ будет хранится родитель вершины $v$ — вершина, из которой произошла последняя релаксация по ребру $(p_v, v)$.

Обновлять его можно параллельно с массивом $d$. Например, в последней реализации:

if (d[u] > d[v] + w) {
    d[u] = d[v] + w;
    p[u] = v; // <-- кратчайший путь в u идет через ребро (v, u)
    q.push({d[u], u});
}

Для восстановления пути нужно просто пройтись по предкам вершины $v$:

void print_path(int v) {
    while (v != s) {
        cout << v << endl;
        v = p[v];
    }
    cout << s << endl;
}

Обратим внимание, что код распечатает путь в обратном порядке.

Источник

%saved0% Граф — это (упрощенно) множество точек, называемых вершинами, соединенных какими-то линиями, называемыми рёбрами (необязательно все вершины соединены). Можно представлять себе как города, соединенные дорогами.

Любое клетчатое поле можно представить в виде графа. Вершинами будут являться клетки, а ребрами — смежные стороны клеток.

Наглядное представление о работе перечисленных далее алгоритмов можно получить благодаря визуализатору PathFinding.js.

Поиск в ширину (BFS, Breadth-First Search)

Алгоритм был разработан независимо Муром и Ли для разных приложений (поиск пути в лабиринте и разводка проводников соответственно) в 1959 и 1961 годах. Этот алгоритм можно сравнить с поджиганием соседних вершин графа: сначала мы зажигаем одну вершину (ту, из которой начинаем путь), а затем огонь за один элементарный промежуток времени перекидывается на все соседние с ней не горящие вершины. В последствие то же происходит со всеми подожженными вершинами. Таким образом, огонь распространяется «в ширину». В результате его работы будет найден кратчайший путь до нужной клетки.

Алгоритм Дейкстры (Dijkstra)

Этот алгоритм назван по имени создателя и был разработан в 1959 году. В процессе выполнения алгоритм проверит каждую из вершин графа, и найдет кратчайший путь до исходной вершины. Стандартная реализация работает на взвешенном графе — графе, у которого каждый путь имеет вес, т.е. «стоимость», которую надо будет «заплатить», чтобы перейти по этому ребру. При этом в стандартной реализации веса неотрицательны. На клетчатом поле вес каждого ребра графа принимается одинаковым (например, единицей).

А* (А «со звездочкой»)

Впервые описан в 1968 году Питером Хартом, Нильсом Нильсоном и Бертрамом Рафаэлем. Данный алгоритм является расширением алгоритма Дейкстры, ускорение работы достигается за счет эвристики — при рассмотрении каждой отдельной вершины переход делается в ту соседнюю вершину, предположительный путь из которой до искомой вершины самый короткий. При этом существует множество различных методов подсчета длины предполагаемого пути из вершины. Результатом работы также будет кратчайший путь. О реализации алгоритма читайте в здесь.

Поиск по первому наилучшему совпадению (Best-First Search)

Усовершенствованная версия алгоритма поиска в ширину, отличающаяся от оригинала тем, что в первую очередь развертываются узлы, путь из которых до конечной вершины предположительно короче. Т.е. за счет эвристики делает для BFS то же, что A* делает для алгоритма Дейкстры.

IDA* (A* с итеративным углублением)

Расшифровывается как Iterative Deeping A*. Является измененной версией A*, использующей меньше памяти за счет меньшего количества развертываемых узлов. Работает быстрее A* в случае удачного выбора эвристики. Результат работы — кратчайший путь.

Jump Point Search

Самый молодой из перечисленных алгоритмов был представлен в 2011 году. Представляет собой усовершенствованный A*. JPS ускоряет поиск пути, «перепрыгивая» многие места, которые должны быть просмотрены. В отличие от подобных алгоритмов JPS не требует предварительной обработки и дополнительных затрат памяти.

Материалы по более интересным алгоритмам мы обозревали в подборке материалов по продвинутым алгоритмам и структурам данных.

Источник

Привет, сегодня поговорим про алгоритм поиска путей в графе, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
алгоритм поиска путей в графе , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.

Задание

Найти все возможные пути между двумя вершинами в графе не пеpесекающиеся по:
а) pебpам
б) веpшинам.

Ввод

Входящими данными является матрица смежности, составленная по такому правилу: C[i,j]=1, если в графе есть ребро (Ai,Aj) и C[i,j]=0 иначе.

Решение     [вверх]

Для построения всех возможных путей между двух вершин, воспользуемся поиском в глубину, который будет модифицирован.

Для поиска маршрута, не пересекающимся по вершинам, необходимо запоминать пройденные вершины и не совершать повторный проход по ним. Поиск текущего пути считается завершенным при достижении финишной вершины или невозможности добавления еще одного ребра в маршрут . Об этом говорит сайт https://intellect.icu . В любом случае после завершение построения текущего маршрута, мы возвращаемся на 1 шаг назад и пытаемся построить другой маршрут.

Для поиска маршрута, не пересекающимся по ребрам, необходимо создать массив-индикатор использования каждого ребра. Если ребро не было использовано, то метка для него истинна, иначе – ложная. Во время поиска маршрута прежде чем перейти к вершине мы проверяем, было ли использовано текущее ребро. Если не было, то мы добавляем его в маршрут и рекурсивно вызываем поиск для следующей вершины. При достижении “тупика” нахождении финишной вершины мы делаем шаг назад, считая последнее ребро в маршруте непройденным.

Формальное описание

Way()
1. Создать матрицу смежности для графа.
2. Прочитать номера стартовой и финишной вершины графа.
3. Инициализировать метки о использовании.
4. Добавить стартовую вершину в путь.
5. Найти все маршруты, не пересекающиеся по ребрам (пп.5.1-5.5):
   5.1. Если поиск вызван не со стартовой вершины, то считать последнее 
        ребро маршрута пройденным.
   5.2. Найти вершину, инцидентную данной.
   5.3. Если ребро, которое ведет к инцидентной вершине не было 
        использовано, то добавить вершину в путь, то считать ей 
        текущей и перейти к 5.1.
   5.4. Если финишная вершина достигнута, то вывести путь.
   5.5. Считать последнее ребро маршрута непройденным.
6. Найти все маршруты, не пересекающиеся по вершинам (пп.6.1-6.5):
   6.1. Присвоить текущей вершине номер шага.
   6.2. Найти вершину, инцидентную данной.
   6.3. Если инцидентная вершина не была использована, то считать ее 
        текущей, запомнить предыдущую вершину и перейти к п.6.1.
   6.4. Если финишная вершина достигнута, то вывести путь.
   6.5. Считать последнюю вершину маршрута непройденной.

Напиши свое отношение про алгоритм поиска путей в графе. Это меня вдохновит писать для тебя всё больше и больше интересного. Спасибо Надеюсь, что теперь ты понял что такое алгоритм поиска путей в графе
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Алгоритмы и теория алгоритмов

Из статьи мы узнали кратко, но емко про алгоритм поиска путей в графе

Источник
Задача:
Задан ациклический граф и две вершины и . Необходимо посчитать количество путей из вершины в вершину по рёбрам графа .

Содержание

  • 1 Решение задачи
    • 1.1 Перебор всех возможных путей
    • 1.2 Метод динамического программирования
    • 1.3 Псевдокод
  • 2 Пример работы
  • 3 См. также
  • 4 Источники информации

Решение задачи

Перебор всех возможных путей

Небольшая модификация алгоритма обхода в глубину. Запустим обход в глубину от вершины . При каждом посещении вершины проверим, не является ли она искомой вершиной . Если это так, то ответ увеличивается на единицу и обход прекращается. В противном случае производится запуск обхода в глубину для всех вершин, в которые есть ребро из , причем он производится независимо от того, были эти вершины посещены ранее, или нет.

Функция принимает граф в виде списка смежности, начальную вершину и конечную вершину . 

countPaths(g, v, t)
    if v == t
        return 1
    else
        s = 0
        for to in g[v]
            s += countPaths(g, to, t)
        return s

Время работы данного алгоритма в худшем случае , где — число путей в графе из в . Например, на следующем графе данный алгоритм будет иметь время работы . Если же использовать метод динамического программирования, речь о котором пойдет ниже, то асимптотику можно улучшить до .

Пример графа, на котором алгоритм имеет время работы [math]O(2^{n/2})[/math]

Метод динамического программирования

Пусть — число путей от вершины до вершины .
Тогда зависит только от вершин, ребра из которых входят в . Тогда таких , что есть ребро из в . Мы свели нашу задачу к меньшим подзадачам, причем мы также знаем, что . Это позволяет решить задачу методом динамического программирования.

Псевдокод

Пусть — стартовая вершина, а — конечная, для нее и посчитаем ответ. Будем поддерживать массив , где — число путей из вершины до вершины и массив , где , если ответ для вершины уже посчитан, и в противном случае. Изначально для всех вершин , кроме , а . Функция будет возвращать ответ для вершины . Удобнее всего это реализовать в виде рекурсивной функции с запоминанием. В этом случае значения массива будут вычисляться по мере необходимости и не будут считаться лишний раз: 

count(g, v)
    if w[v]
        return d[v]
    else
        sum = 0
        w[v] = true
        for c in g[v]
            sum += count(g, c)
        d[v] = sum
        return sum

countPaths(g, s, t)
    d[s] = 1
    w[s] = true
    answer = count(t)
    return answer

Значение функции считается для каждой вершины один раз, а внутри нее рассматриваются все такие ребра . Всего таких ребер для всех вершин в графе , следовательно, время работы алгоритма в худшем случае оценивается как , где — число вершин графа, — число ребер.

Пример работы

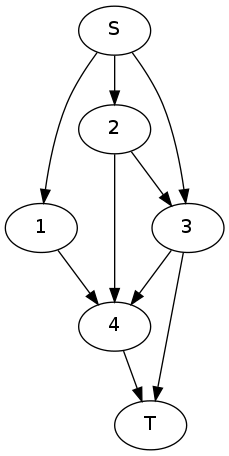
Рассмотрим пример работы алгоритма на следующем графе:

Count-path-graph-example.png

Изначально массивы и инициализированы следующим образом:

вершина S 1 2 3 4 T
w true false false false false false
d 1 0 0 0 0 0

Сначала функция будет вызвана от вершины . Ответ для нее еще не посчитан (), следовательно будет вызвана от вершин и . Для вершины ответ также не посчитан (), следовательно будет вызвана уже для вершин и . А вот для них ответ мы уже можем узнать: для он равен , так как это — единственная вершина, ребро из которой входит в нее. Непосредственно для ответ нам также известен. На текущий момент таблица будет выглядеть следующим образом:

вершина S 1 2 3 4 T
w true false true false false false
d 1 0 1 0 0 0

Теперь мы знаем значения для вершин и , что позволяет вычислить . Также обновим значения в массиве : .

вершина S 1 2 3 4 T
w true false true true false false
d 1 0 1 2 0 0

В самом начале для вычисления нам требовались значения и . Теперь нам известно значение , поэтому проследим за тем, как будет вычисляться . , но , следовательно значения и мы уже знаем, и нам необходимо вызвать . Ответ для этой вершины равен , так как это единственная вершина, ребро из которой входит в . Обновим соответствующие значения массивов и :

вершина S 1 2 3 4 T
w true true true true false false
d 1 1 1 2 0 0

Теперь нам известны все три значения, требующиеся для вычисления ответа для вершины . :

вершина S 1 2 3 4 T
w true true true true true false
d 1 1 1 2 4 0

Наконец, вычислим и обновим таблицы и :

вершина S 1 2 3 4 T
w true true true true true true
d 1 1 1 2 4 6

Этот алгоритм позволяет вычислить количество путей от какой-либо вершины не только до , но и для любой вершины, лежащей на любом из путей от до . Для этого достаточно взять значение в соответствующей ячейке .

См. также

  • Динамическое программирование
  • Кратчайший путь в ациклическом графе
  • Задача о расстановке знаков в выражении
  • Задача о порядке перемножения матриц

Источники информации

  • Акулич И.Л. Глава 4. Задачи динамического программирования // Математическое программирование в примерах и задачах. — М.: Высшая школа, 1986. — 319 с. — ISBN 5-06-002663-9..
Источник

Добавить комментарий