Как найти все матрицы перестановочные с матрицей

В принципе все уже изложено в предыдущих разделах. Однако описанная схема может быть достаточно трудоемкой из-за того, что некоторые вычисления будут несколько раз повторяться. Покажем, как этих повторений можно избежать.

Пусть задана СЛАУ Ax = b. Запишем ее расширенную матрицу (A | b). Каждому элементарному преобразованию строк расширенной матрицы соответствует аналогичное преобразование уравнений в исходной СЛАУ:

а) умножение i-й строки матрицы на число λ ≠ 0 означает умножение i-го уравнения СЛАУ на это же число;

б) перестановке i-й и k-й строк в матрице отвечает перестановка i-го и k-го уравнений СЛАУ;

в) добавление к i-й строке матрицы ее k-й строки равнозначно замене i-го уравнения его суммой с k-м уравнением СЛАУ.

Указанные преобразования СЛАУ не изменяют множество решений этой СЛАУ. Поэтому приведение расширенной матрицы системы к ступенчатому виду с помощью элементарных преобразований ее строк означает сведение самой СЛАУ к эквивалентной системе, имеющей ступенчатую матрицу.

Итак, сначала приводим расширенную матрицу (A | b) заданной СЛАУ с помощью элемен-тарных преобразований строк к ступенчатому виду (A’ | b’). При этих преобразованиях ранги матриц не меняются, поэтому Rg(A | b) = Rg(A’ | b’), а Rg A = Rg A’. Ранги матриц A’ и (A’ | b’) равны количеству их ненулевых строк. Если эти ранги равны, то по теореме 13.1 Кронекера — Капелли СЛАУ совместна, а в противоположном случае — несовместна.

Приведение расширенной матрицы СЛАУ к ступенчатому виду преследует две цели: во-первых, позволяет проверить, является ли система совместной; во-вторых, если СЛАУ совместна, мы ее сводим к более простому виду.

Предположим, что, решаемая система совместна. В матрице A’ ступенчатого вида выбираем базисный минор и фиксируем соответствующие ему базисные и свободные неизвестные (см. 12.3). В матрице (A’| b’) ступенчатого вида отбрасываем нулевые строки (им соответствуют тривиальные уравнения) и по получившейся матрице восстанавливаем СЛАУ. В уравнениях этой СЛАУ слагаемые со свободными неизвестными переносим в правые части и получаем систему, матрица которой является верхней треугольной и невырожденной, так как ее определитель совпадает с базисным минором матрицы A’. Последовательно исключая неизвестные, выражаем базисные неизвестные через свободные. Свободные неизвестные обозначаем как произвольные постоянные и записываем общее решение СЛАУ в виде линейной комбинации столбцов, выделяя в правых частях полученных выражений в отдельные столбцы: а) свободные члены; б) коэффициенты при каждой произвольной постоянной. В этой записи столбец свободных членов есть частное решение СЛАУ, а столбцы при произвольных постоянных образуют нормальную фундаментальную систему решений однородной СЛАУ, соответствующей заданной неоднородной системе.

Если исходная СЛАУ является однородной, то изложенный метод решения чуть упрощается, поскольку в расширенной матрице последний столбец является всегда нулевым и не меняется при элементарных преобразованиях строк. Имея это в виду, его опускают, т.е. все преобразования проводят с матрицей системы.

Пример 14.1. Решим однородную СЛАУ

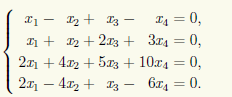
Чтобы найти общее решение, запишем матрицу системы и преобразуем ее при помощи эле-ментарных преобразований строк к ступенчатому виду:

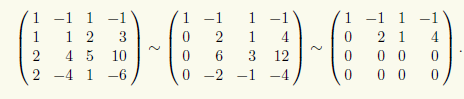
Базисный минор в преобразованной матрице стоит вверху слева и имеет второй порядок.
Это значит, что ранг r матрицы системы равен двум, фундаментальная система решений со
стоит из n — r = 4 — 2 = 2 решений, а сама СЛАУ эквивалентна следующей системе, которая соответствует преобразованной матрице:

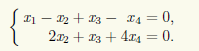
Базисными неизвестными являются х₁ и х₂, а свободными — х₃и х₄. Выражаем базисные неизвестные через свободные:

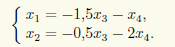
Вводим обозначения x₃ = c₁, x₄ = c₂ и записываем общее решение СЛАУ:

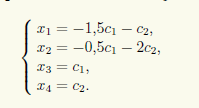
Используя матричную форму записи, получаем

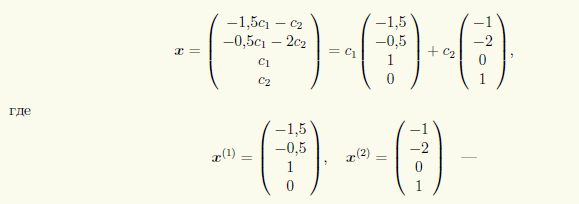
нормальная фундаментальная система решений, а c₁, c₂ — произвольные постоянные.

Пример 14.2. Решим неоднородную СЛАУ

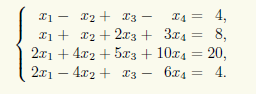
Преобразуем расширенную матрицу этой СЛАУ при помощи элементарных преобразований строк к ступенчатому виду:

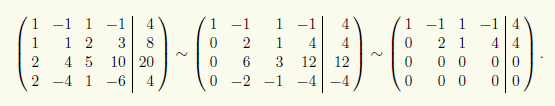
Теперь видно, что для преобразованной матрицы минор М_1,2^1,2 является базисным. Поэтому Rg A = Rg(A | b) = 2 = r, и, согласно теореме 13.1 Кронекера — Капелли, СЛАУ совместна. Кроме того, СЛАУ свелась к эквивалентной системе

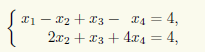
которая соответствует преобразованной матрице. Однако можно продолжить преобразования в матрице, упрощая базисные столбцы (1-й и 2-й) с помощью элементарных преобразований строк так, чтобы в каждом из них остался один ненулевой элемент, причем нулевые строки можно отбросить:

По этой матрице восстанавливаем систему

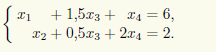
Перенося свободные неизвестные x₃, x₄ в правые части уравнений, получаем

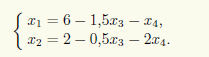
Для свободных неизвестных положим x₃ = c₁, x₄ = c₂, и тогда

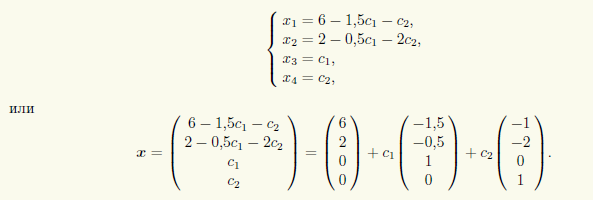
Полученное общее решение очень наглядно: 1-й столбец — частное решение неоднородной СЛАУ, а два последних — нормальная фундаментальная система решений соответствующей однородной СЛАУ (ср. пример 14.1).

Пример 14.3. Решим неоднородную СЛАУ

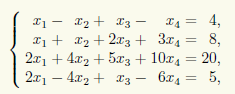
отличающуюся от системы из примера 14.2 лишь одним коэффициентом.

Преобразуем расширенную матрицу этой СЛАУ при помощи элементарных преобразований строк к ступенчатому виду:

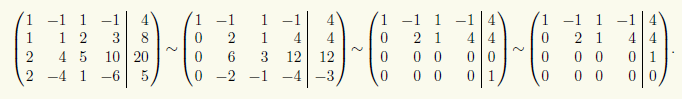
Теперь видно, что в преобразованной матрице минор М_1,2^1,2 является базисным для матрицы системы, а минор М_1,2,5^1,2,5 — для расширенной матрицы. Поэтому Rg A = 2, Rg(A | b) = 3 и, согласно теореме 13.1 Кронекера — Капелли, СЛАУ несовместна. Впрочем, несовместность очевидна и так, потому что последней матрице соответствует СЛАУ, в которой третье уравнение имеет вид: 0x₁ + 0x₂ + 0x₃ + 0x₄ = 1.

Пример 14.4. Найдем все матрицы, перестановочные с матрицей

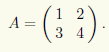
Обозначим искомые матрицы через X. Условие перестановочности означает выполнение ма-тричного равенства AX = XA. Чтобы существовало произведение в левой части этого равенства, матрица X должна иметь две строки, а чтобы существовало произведение в правой части — два столбца. Следовательно, X — квадратная матрица второго порядка, т.е.

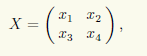
и для ее нахождения требуется решить матричное уравнение

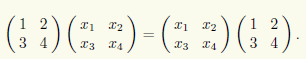
Перемножая матрицы в этом уравнении и приравнивая элементы, стоящие на одинаковых местах в получающихся матрицах, приходим к равносильной системе четырех уравнений

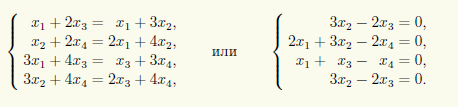
Эта система имеет простой вид, и мы можем отойти от общей схемы решения однородных СЛАУ, продемонстрированной в примере 14.1. Легко увидеть, что если из второго уравнения вычесть удвоенное третье, то получится такое же уравнение, как первое и последнее. Поэтому первые два уравнения в этой системе можно отбросить и тогда

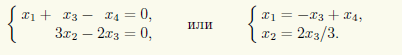
Итак, x₃, x₄ — свободные, а x₁, x₂ — базисные неизвестные. Для свободных неизвестных положим x₃ = c₁, x₄ = c₂ и тогда получим ответ в виде

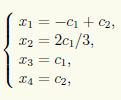
или в матричной форме

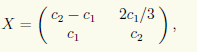
где c₁, c₂ ∈ R — произвольные постоянные. Если фиксировать для c₁, c₂ конкретные значения, то из множества всех перестановочных с A матриц будет выделена одна. Например, при c₁ = 0 и с₂ = 0 получается нулевая матрица, а при c₁ = 0 и с₂ = 1 — единичная.

google.com/+ВикторЦекунов

Репетитор по математике, физике (Минск): Виктор Иванович.

Высшая математика и физика для студентов.
Профессиональный репетитор окажет помощь в решении задач, подготовит к экзаменам. Занятия в Серебрянке, индивидуально. (90 мин)
= 20 $.
Тел: +375(29) 127 61 86.___________________________________________________________________________

Оказываю
платные услуги: решение задач по высшей математике. Оплата WebMoney.
Заказы направляйте сюда: Платные услуги
___________________________________________________________________________
   
     2.1. Арифметика целых чисел.

    
2.2. Матрицы и определители.

     2.3.
Системы линейных уравнений.

     2.4.
Множества и отображения.

     2.5.
Комплексные числа.

    
2.6. Группы.

    
2.7. Кольца.

    
2.8. Алгебраические уравнения.

     2.9.
Элементы теории полей.

    
2.10. Линейные пространства.

    
2.11. Линейные операторы.

    
2.12. Квадратичные формы.

    
2.13. Тензоры.

     2.1. Арифметика целых чисел.

2.1-1.
Используя
алгоритм Евклида сократить дробь: 169/448.

Решение:
Применяя
алгоритм Евклида, получаем равенства (в правой части равенств после плюса стоят
остатки):
448 = 169∙2 + 110,
169 = 110∙1 + 59,
110 = 59∙1 + 51,
59 = 51∙1 + 8,
51 = 8∙6 + 3,
8 = 3∙2 + 2,
3 = 2∙1 + 1,
2 = 1∙2.
Так как последний отличный от нуля остаток равен 1, то наибольший общий
делитель чисел 448 и 169
НОД(448, 169) = 1.
Это означает, что числа 448 и 169 – взаимно простые. Следовательно, дробь
169/448 несократима.

2.1-2.
Используя
алгоритм Евклида сократить дроби: 490/1372; 92400/13960

Решение:
1)  Дробь 490/1372:
Применяя алгоритм Евклида, получаем равенства (в правой части равенств после
плюса стоят остатки):
1372 = 490∙2 + 392,
490 = 392∙1 + 98,
392 = 98∙4.
Так как последний отличный от нуля остаток равен 98, то наибольший общий
делитель чисел 1372 и 490
НОД(1372, 490) = 98.
Сокращаем дробь на 98
(490:98)/(1372:98) = 5/14.

2) Дробь 92400/139600:
Применяя алгоритм Евклида, получаем равенства (в правой части равенств после
плюса стоят остатки):
139600 = 92400∙1 + 47200,
92400 = 47200∙1 + 45200,
47200 = 45200∙1 + 2000,
45200 = 2000∙22 + 1200,
2000 = 1200∙1 + 800,
1200 = 800∙1 + 400,
800 = 400∙2.
Так как последний отличный от нуля остаток равен 400, то наибольший общий
делитель чисел 139600 и 92400
НОД(139600, 92400) = 400.

Сокращаем
дробь на 400
(92400:400)/(139600:400) = 231/349.
Ответ:  490/1372 = 5/14;    92400/139600 = 231/349.

2.1-3.
Найти
наименьшее натуральное число x, удовлетворяющее условиям:
 
x = 6mod13
 
x = 33mod37
 
x = 19mod23
 
x = 14mod36

Решение:
 x = 6 mod13
 
x = 33 mod37
 
x = 19 mod23
 
x = 14 mod36
 
x є N
 
x(min) – ?
Прежде
всего, уясним
x = 6 mod13  означает:
x/13
даёт в остатке 6 или иначе (x-6)/13 делится без остатка.

Имеем систему сравнений вида

x = aᵢ modnᵢ      i=1,2,3,4,
где
a₁=6 , a₂=33 ,
a₃=19 ,
a₄=14 ,
n₁=13 ,
n₂=37 ,
n₃=23 ,
n₄=36.
Т.к. n₁, n₂, n₃, n₄
попарно взаимно простые, то согласно китайской теореме об остатках данная
система сравнений имеет единственное решение относительно x є Zn,
n = n₁n₂n₃n₄=
13·37·23·36=398268.
(Zn –
кольцо классов вычетов целых чисел по модулю n).    

Решение будем искать по методу Гаусса:

x = (a₁N₁M₁ + a₂N₂M₂ + a₃N₃M₃ + a₄N₄M₄) modn,            (1)
где
N₁=n/n₁=398268/13=30636,
N₂=n/n₂=398268/37=10764,
N₃=n/n₃=398268/23=17316,
N₄=n/n₄=398268/36=11063,
Mᵢ = Nᵢ⁻¹ modnᵢ.    i=1,2,3,4.
Mᵢ –
мультипликативно обратный к Nᵢ элемент по модулю nᵢ.

Вычислим

M₁.
M₁ =
30636⁻¹ mod13 или
30636M₁ mod13=1,
30636 mod13·M₁ mod13=1,
8·M₁ mod13=1,
отсюда
8M₁
может принимать значения 14, 27, 40, …
Т.к. 40 делится на 8, то из уравнения
8M₁ = 40
находим
M₁=40/8=5.
 

Вычислим

M₂.
M₂ =
10764⁻¹ mod37 или
10764M₂ mod37=1,
10764 mod37·M₂ mod37=1,
34·M₂ mod37=1,
отсюда
34M₂
может принимать значения 38, 75, 112, 149, 186, 223, 260, 297, 334, 371, 408,
…
Т.к. 408 делится на 34, то из уравнения
34M₂ =
408 находим
M₂=408/34=12.

Вычислим

M₃.
M₃ =
17316⁻¹ mod23 или
17316M₃ mod23=1,
17316 mod23·M₃ mod23=1,
20·M₃ mod23=1,
отсюда
20M₃
может принимать значения 24, 47, 70, 93, 116, 139, 162, 185, 208, 231,
254, 277, 300, …
Т.к. 300 делится на 20, то из уравнения
20M₃ =
300 находим
M₃=300/20=15.

Вычислим

M₄.
M₄ =
11063⁻¹ mod36 или
11063M₄ mod36=1,
11063 mod36·M₄ mod36=1,
11·M₄ mod36=1,
отсюда
11M₄
может принимать значения 37, 73, 109, 145, 181, 217, 253, …
Т.к. 253 делится на 11, то из уравнения
11M₄ =
253 находим
M₄=253/11=23.Подставим
всё в (1)
x = (6·30636·5 + 33·10764·12 + 19·17316·15 + 14·11063·23) mod398268 =
= 13678970 mod398268 = 137858.
Ответ: x = 137858.
________________________________________________________________________________________________

     2.2. Матрицы и определители.

2.2-2.
Найдите все матрицы, перестановочные с матрицей 

Решение:
Пусть матрица перестановочна с матрицей А, т. е. выполняется равенство
АВ = ВА.                                               (1)
Вычислим произведения матриц: АВ и ВА.

Подставим в (1)

Равенство матриц означает равенство соответствующих элементов этих матриц.
Получаем систему уравнений:
{ a = a + 2b
{ b = b
{ 2a + c = c + 2d
{ 2b + d = d.
Отсюда получим: b = 0, a = d и матрица В примет вид

 , где а, с є R.

Ответ:

, где a, c є R.

2.2-3.
Известно, что А – квадратная матрица 4-го порядка, причем det A = 3.
Чему тогда равен
det 3A?

Решение:
n = 4
det A = 3
det 3A − ?
Сначала докажем общую формулу, затем решим эту задачу.

1. Пусть А − квадратная матрица порядка

n (a_ij є R), λ − общий множитель (λ є R).
Доказать:
det(λA) = λⁿdetA.                                                         (1)
Доказательство:
Матрицы А, λА и
определитель detA
матрицы А:
      
_                                           _                               _                                                 _
     
| a₁₁     a₁₂   …  
a₁_n-1     a₁_n    |                              | λa₁₁    λa₁₂   …   
λa₁_n-1    λa₁_n    |
     
| a₂₁     a₂₂   …  a₂_nn-1     a₂n  |                              | λa₂₁    λa₂₂   …    λa₂_n-1    λa₂_n    |
A = |
………………………………………..|                      λA = | ……………………………………..……… |
     
| a_n-1₁ a_n-1₂ … a_{n-1 n-1} a_n–1n |                              | λa_n-1₁ λa_n-1₂ … λa_{n-1 n-1} λa_n–1n |
     
| a_n₁     a_n₂ …   a_nn-1        a_nn |                              | λan₁    λa_n₂   …  λa_nn-1    λa_nn    |
      
‾                                           ‾                                ‾                                                 ‾
          
| a₁₁    a₁₂   …   
a₁_n-1   a₁_n     |
          
| a₂₁    a₂₂   …    a₂_n-1   a₂_n    |
detA = |
……………………………………….|
          
| a_n-1₁ a_n-1₂ … a_{n-1 n-1} a_n-1n |
          
| a_n₁     a_n₂  …    a_nn-1   a_nn   |.

Воспользуемся
свойством определителя:
общий множитель всех элементов произвольной строки (столбца) определителя можно
вынести за знак определителя.                                   (*)
Тогда для определителя матрицы λA, в силу свойства (*), применённого последовательно к
строкам с номерами 1, 2, … , n-1, n, имеем

                
|

λa₁₁    λa₁₂    …  
λa₁_n-1    λa₁_n     |       | a₁₁     a₁₂     …    
a₁_n-1     a₁_n     |
               
| λa₂₁    λa₂₂    …   λa₂_n-1    λa₂_n    |       | λa₂₁    λa₂₂    …    λa₂_n-1   λa₂n   |
det(λA) = |
……………………………………………… | = λ·| …………………………………………..… | =
               
| λa_n-1₁ λa_n-1₂ … λa_{n-1 n-1} λa_n-1n |       | λa_n-1₁ λa_n-1₂ … λa_{n-1 n–1} λa_n-1n |
               
| λa_n₁    λa_n₂    …   λa_nn-1   λa_nn    |       | λa_n₁     λa_n₂  …    λa_nn-1   λa_nn   |

       
|

a₁₁       a₁₂   …    
a₁_n-1      a₁_n     |                | a₁₁    a₁₂   
…   a₁_n-1    a₁_n    |
      
| a₂₁       a₂₂   …     a₂_n-1      a₂_n     |               | a₂₁    a₂₂    …   a₂_n-1     a₂_n    |
= λ²·|
……………………………………………….| = … = λⁿ·| ………………………………..…….  | = λⁿ·detA.
      
| λa_n-1₁ λa_n-1₂ … λa_{n-1 n-1} λa_n-1n |               | a_n-1₁ a_n-1₂ … a_{n-1 n-1} a_n-1n |
      
| λa_n₁     λa_n₂   …   λa_nn-1    λa_nn   |               | a_n₁     a_n₂   …    a_nn-1   a_nn  |

Итак, мы получили

det(λA) = λⁿ·detA и
формула (1) доказана!

2. Из формулы (1) при n = 4, det A = 3 получаем
det 3A = 3⁴·det A =
3⁴·3 = 3⁵= 243.
Ответ: det 3A = 3⁴·det A = 243.

________________________________________________________________________________________________

     2.3.
Системы линейных уравнений.

2.3-1.
Определите коэффициенты a, b, c, d многочлена f(x) = ax³ + bx² + cx + d, если известно, что f(-1) =
-9, f(0) =
-2, f(1) =
-3, f(2) =
0.

Решение:
Подставляя в f(x) = ax³ + bx² + cx + d
соответственно х = -1, 0, 1 и 2, получим систему уравнений
{ – a + b – c      + d = – 9

{                         d = – 2

{ a + b + c       + d = – 3

{ 8a + 4b + 2c + d = 0.
Решим данную систему уравнений методом Гаусса.
Составим расширенную матрицу данной системы и с помощью элементарных
преобразований строк приведём её к треугольному виду.
 _                    _                                                            _ _
| -1 1 -1 1 | -9 |                                                          | -1 1 -1  1 | -9 | (1. К 2-й строке + 1-ю
| 0  0  0  1 | -2 |                                                          | 8  4  2  1 | 0  |      строку, умноженную на 8;
| 1  1  1  1 | -3 | (переставим 2-ю и 4-ю строки) ~ | 1  1  1  1 | -3 |   2. К 3-й
строке + 1-ю
| 8  4  2  1 |  0 |                                                          | 0  0  0  1 | -2 |     строку)
 ‾                     ‾                                                           ‾ ‾
   
_                         _                                                           _                         _
  
| -1  1  -1  1 | -9   |                                                         | -1  1 -1 1  | -9    | (К 3-й строке + 2-ю
  
| 0  12 -6  9 | -72 |                                                         |  0  2   0  2 | -12  | строку, умноженную на
~ | 0   2   0  2 | -12 | (переставим 2-ю и 3-ю строки) ~ | 0 12  -6  9 | -72 | на -6)
  
| 0   0   0  1 |   -2 |                                                          | 0  0    0  1 | -2   |
   
‾                         ‾                                                           ‾                         ‾
   
_                       _
  
| -1 1 -1 1  | -9   |
  
| 0  2  0  2  | -12 |
~ | 0  0 -6 -3 |   0   |
  
| 0  0  0  1  |  -2  |
   
‾                        ‾
По последней матрице выпишем систему, равносильную исходной системе
{ – a + b – c + d = – 9

{ 2b + 2d = –
12
{ – 6c – 3d = 0
{ d = –
2.
Из 4-го уравнения имеем:  d = – 2.
Из 3-го уравнения имеем:  – 6c – 3(-2) = 0, отсюда с = 1.
Из 2-го уравнения имеем:  2b + 2(-2) = – 12, отсюда b = –
4.
Из 1-го уравнения имеем:  – a – 4 – 1 – 2 = – 9, отсюда a = 2.
Ответ:
a = 2, b = – 4, c = 1, d = – 2.

2.3-2. Дана система уравнений:

Как выглядит базисное решение этой системы?

Решение:
Перепишем
систему в виде
x₁ – 5x₂       +2x₄       = 4
      4x₂ – x₃               = -1                       (1)
      2x₂       +3x₄ – x₅ = 0
Выпишем расширенную матрицу системы (1) и, с помощью элементарных преобразований
строк, приведём её к ступенчатому виду
 _                                 _
|   1  -5   0   2   0  |  4   |
|   0   4  -1   0   0  | -1   | ~ ( к
2-й строке +3-ю строку, умноженную на (-2) ) ~
|_ 0   2   0   3  -1  |  0 _|
    _                                 _
   |   1  -5   0   2   0  |  4   |
~ |   0   0  -1  -6   2  | -1   | ~ (
поменяем местами 2-ю и 3-ю строки ) ~
   |_ 0   2   0   3  -1  |  0 _|
    _                                 _
  |   1  -5   0   2   0  |  4    |
~|   0   2   0   3  -1  |  0    |
  |_ 0   0  -1  -6   2  |  -1 _|

Соответствующая ступенчатая система имеет вид

x₁ – 5x₂     + 2x₄          = 4
      2x₂     + 3x₄  –   x₅ = 0
            –x₃ – 6x₄ + 2x₅ = -1
Неизвестные x₄ и x₅
объявим свободными и перепишем последнюю систему так:
x₁ – 5x₂     =  4 – 2x₄
      2x₂     = – 3x₄  + x₅
            x₃ = -6x₄+2x₅ + 1
Пусть x₄ = a, x₅ = b,  a и b є R.
Получаем
x₁ – 5x₂     =  4 – 2a
      2x₂     = -3a + b
            x₃ = -6a + 2b + 1
откуда
x₃ = 2b-6a+1,  x₂ = (b-3a)/2,  x₁ = (5b-19a+8)/2.
Таким образом, система (1) имеет бесконечное множество решений вида
(  (5b-19a+8)/2;
 (b-3a)/2;   2b-6a+1;  a;  b  ),
где  a, b –
произвольные действительные числа.
Других
решений система не имеет.
Ответ: (  (5b-19a+8)/2;
 (b-3a)/2;   2b-6a+1;  a;  b  ),    a, b є R.

2.3-3.
Объясните, как из матрицы:
(1 0 0 | 0)
(0 1 -1| 0)
(0 0 0 | 0)
получили такое решение:
       ( 0 )
X =  (с1)
       (с1).

Решение:

( 1 0 0 | 0 )                                                  {x₁ = 0                       {x₁ = 0
(0 1 -1 | 0 ) отсюда система уравнений  { x₂ – x₃ = 0
или        { x₂ = x₃ .
( 0 0 0 | 0 )
Обозначим x₃ = c₁ .
Тогда x₁ = 0,
x₂ = c₁ , x₃ = c₁ .
Или в виде матрицы-столбца
      
(0)
X = (c₁)
      (c₁).2.3-4.
Проверить, является ли система линейных уравнений

 

                             (1)

невырожденной, и решить её по формулам Крамера.

Решение:
1. Матрица А данной системы:

Вычислим определитель ∆ матрицы А:

 
= ( к 2-й строке прибавим 1-ю строку, умноженную на (-1) ) =

= (разложим определитель по 1-му столбцу) =

= 1·1( 3·(-1) – 1·2 ) = -3 – 2 =
-5.

Так как ∆ = -5 ≠ 0, то система уравнений невырожденная и имеет решение.
Найдём решение системы по формулам Крамера:
х₁ = ∆₁/∆, х₂ = ∆₂/∆, х₃ = ∆₃/∆.                                   (2)

2. Запишем определитель ∆₁ . Для этого в определитель ∆ вместо 1-го столбца
вставим столбец свободных членов системы (1):   
0,  1,  -3.
Имеем

 
= (к 3-й строке прибавим 2-ю строку, умноженную на 3) =

= (разложим определитель по 1-му столбцу) =

= 1·(-1)( (-1·2 – 7·(-1) ) = -(-2 +
7) = -5.

3. Запишем определитель ∆₂ . Для этого в определитель ∆ вместо 2-го столбца
вставим столбец свободных членов системы (1): 

0,  1,  -3.
Имеем

 
= ( к 2-й строке прибавим 1-ю строку, умноженную на (-1) ) =

 
= (разложим определитель по 1-му столбцу) =

 = 1·1( 1·(-1) – (-3)·2 ) = -1 + 6 =
5.

4. Запишем определитель ∆₃ . Для этого в определитель ∆ вместо 3-го столбца
вставим столбец свободных членов системы (1): 

0,  1,  -3.
Имеем

 
= ( к 2-й строке прибавим 1-ю строку, умноженную на (-1) ) =

= (разложим определитель по 1-му столбцу) =

= 1·1( 3·(-3) – 1·1 ) = -9 – 1 =
-10.

Тогда по формулам (2) имеем
х₁ = -5/(-5) = 1, х₂ = 5/(-5) = -1, х₃ = -10/(-5) = 2.
Ответ: х₁ = 1, х₂ = -1,
х₃ = 2.

________________________________________________________________________________________________

     2.5.
Комплексные числа.

2.5-1. Описать множество точек, изображающих на комплексной плоскости числа z,
удовлетворяющие условию |z+1-i| < |z-1+i|

Решение:
|z+1-i| < |z-1+i|
Подставим сюда z = x + iy
|x+iy+1-i| <
|x+iy-1+i| или
|x+1+i(y-1)|
< |x-1+i(y+1)|  или
√( (x+1)²+(y-1)² )
< √( (x-1)²+(y+1)² ).
Возведём обе части полученного неравенства в квадрат
(x+1)²+(y-1)²
< (x-1)²+(y+1)².
Раскроем скобки и, после упрощения, получим
y > x.
Рисуем прямую y = x (она
направлена под углом 45⁰ к оси OX ).
Полуплоскость выше прямой y = x и будет искомое множество точек.
Ответ: полуплоскость выше прямой y = x.
________________________________________________________________________________________________

     2.11. Линейные операторы.2.11-1.
Найти
матрицу оператора осевой симметрии относительно прямой x = – y.

Решение:
Пусть f –
оператор симметрии, М(x, y) – точка на плоскости, А – искомая матрица оператора f.
Оператор f
переводит точку М в точку М₁ :   f( М(x, y) ) = М₁ (-y, –x).
Для вектора  ОМ:   f( ОМ(x, y) ) =
ОМ₁ (-y, –x).
Пусть е₁(1;0) и е₂(0;1) – единичные и взаимно ортогональные векторы, образующие
базис (е₁ направлен по оси X, е₂ – по оси Y).
Тогда  f(
е₁(1;0) ) = (0;-1) = -е₂ ,   f( е₂(0;1) ) = (-1;0) = -е₁.
(0;-1) – первый столбец матрицы А.
(-1;0) – второй столбец матрицы А.
                       |‾  0   -1  ‾|
Матрица А = |                 |
                       |_ -1    0  _|

                  |‾ 0   -1 ‾|
Ответ: А = |              |
                  |_ -1   0 _|

2.11-2.
Найти собственные значения и собственные векторы матрицы
      
_           _
     
| 5  -1  1 |
A = | 0 
4  -1 |.
     
| 0  -1  4 |
      
‾           ‾
Решение:
1. Матрица А имеет порядок n = 3. Запишем характеристическое уравнение матрицы А:

              (1)

Разложим определитель по 1-му столбцу

= (
применим формулу: a² – b² = (a + b)(a – b) ) = (5 – λ)(4 – λ + 1) )(4 – λ – 1) = (5 – λ)(5 – λ)(3 – λ) =
= (5
– λ)²(3 –
λ).
Тогда уравнение (1) примет вид
(5 – λ)²(3 –
λ) = 0,
откуда находим корни λ₁ = 3, λ₂,₃ = 5, которые являются собственными значениями
матрицы А. Найдем соответствующие им собственные векторы.
Составляем систему для определения координат x₁ , x₂ , x₃
собственных векторов:
{ (5-λ)x₁ +
(-1)·x₂     + 1·x₃ = 0;

{               (4-λ)x₂ +
(-1)·x₃ = 0;                     
(2)
{                (-1)·x₂ +
(4-λ)x₃ = 0.


2. Подставляя λ = λ₁ = 3
в систему (2), имеем:
{ (5-3)x₁ +
(-1)·x₂     + 1·x₃ = 0         
{ 2x₁ – x₂ + x₃ = 0
{               (4-3)x₂ +
(-1)·x₃ = 0
или  {          x₂ – x₃ = 0
{                (-1)·x₂ +
(4-3)x₃ = 0        
{       – x₂ + x₃ = 0.

Решаем ее методом Гаусса. Выписываем расширенную матрицу
        
_               _
       
| 2  -1  1  0 |
A* = |
0  1 -1  0  |.
       
| 0  -1  1  0 |
        
‾               ‾
С помощью элементарных преобразований строк приведём матрицу А* к треугольному
виду.
        
_              _                                                                    _                _
        | 2  -1  1  0 | (к 3-й строке прибавим 2-ю строку)    | 2  -1  1  0  |
A* = |
0  1  -1  0 |                                                              ~ | 0   1  -1  0 |
       
| 0  -1  1  0 |                                                                 | 0   0   0  0  |.
        
‾               ‾                                                                   ‾                ‾
В полученной матрице все миноры 3-го порядка равны нулю. Вычисляем левый верхний
минор 2-го порядка
 _      _
| 2 -1 | = 2 ≠ 0. Получили не равный нулю минор 2-го порядка, значит ранг r = 2.
| 0  1 |
 ‾      ‾
По преобразованной матрице А* возвращаемся к системе уравнений
{ 2x₁ – x₂ + x₃ = 0
{         x₂  – x₃ = 0.

Так как r = 2,
то зависимых (базисных) переменных два, а свободное одно. Пусть x₃ –
свободное неизвестное, тогда
{ 2x₁ – x₂ = – x₃
{         x₂ = x₃.
Решая эту систему, находим общее решение: x₁ = 0,
x₂ = x₃.
Фундаментальная система решений состоит из одного решения, так как n – r = 3 –
2 = 1.
Множество собственных векторов, отвечающих собственному числу λ = 3,
имеет вид:
{0, x₃, x₃} = x₃{0,
1, 1}, где x₃ –
любое число (x₃ ≠ 0). Выберем из этого множества один вектор,
например, положив x₃ = 1:  Х₁ = {0, 1, 1}.
Итак, собственному числу λ = 3 соответствует собственный вектор Х₁ = {0, 1, 1}.

3. Подставляя λ = λ₂,₃ =
5 в систему (2), имеем:
{ (5-5)x₁ +
(-1)·x₂     + 1·x₃ = 0        
{ – x₂ + x₃ = 0
{               (4-5)x₂ +
(-1)·x₃ = 0
или { – x₂ – x₃ = 0
{                (-1)·x₂ +
(4-5)x₃ = 0       
{ – x₂ – x₃ = 0.

Решаем ее методом Гаусса. Выписываем расширенную матрицу
          
_                _
         
| 0  -1   1  0 |
A** = |
0  -1  -1  0 |.
         
| 0  -1  -1  0 |
          
‾                ‾
С помощью элементарных преобразований строк приведём матрицу А** к треугольному
виду.
          
_             _                                                                                                      _             _
         
| 0 -1  1 0 |(к 3-й строке прибавим 2-ю строку, умноженную на (-1))   | 0 -1  1 0
|
A** = |
0 -1 -1 0 |                                                                                                 ~ | 0 -1 -1 0 |
         
| 0 -1 -1 0 |                                                                                                    | 0  0  0  0 |
          
‾             ‾                                                                                                      ‾              ‾
                                                                                                     
_             _
(к 2-й строке прибавим 1-ю строку, умноженную на (-1))    | 0 -1 1  0 |
                                                                                                 
~ | 0  0 -2 0 |
                                                                                                    
| 0  0  0 0 |.
                                                                                                     
‾             ‾
В полученной матрице все миноры 3-го порядка равны нулю. Не равный нулю
базисный минор 2-го порядка
 _      _
| -1 1 | = 2 ≠ 0. Получили не равный нулю минор 2-го порядка, значит ранг r = 2.
| 0 -2 |
 ‾      ‾
По преобразованной матрице А** возвращаемся к системе уравнений
{ – x₂ + x₃ = 0
{       – 2x₃ = 0.

Отсюда получим x₂ = x₃ = 0.
Так как r = 2,
то зависимых (базисных) переменных два, а свободное одно. Так как базисный
минор стоит на пересечении 1-й и 2-й строки и 2-го и 3-го столбца, то x₂ и x₃ − базисные переменные, а x₁ ≠ 0 – свободная переменная, принимающая любое
значение. Общее решение:  x₁ , x₂ = x₃ = 0.
Фундаментальная система решений состоит из одного решения, так как
n – r = 3 –
2 = 1.
Множество собственных векторов, отвечающих собственному числу λ = 5,
имеет вид:
{x₁ , 0,
0} = x₁{1,
0, 0}, где x₁ ≠ 0.
Выберем из этого множества один вектор, например, положив x₁ = 1:  
Х₂ = {1, 0, 0}.
Итак, собственному числу λ = 5 соответствует собственный вектор Х₂ = {1, 0, 0}.
Легко видеть, что вектора Х₁ и Х₂ ортогональны (Х₁ _|_ Х₂), т.к. их скалярное
произведение равно нулю:  0·1 + 1·0 + 1·0 = 0.
Ответ: 
λ₁ = 3,  λ₂,₃ = 5;     Х₁ = {0; 1; 1},  Х₂ = {1; 0; 0}.

________________________________________________________________________________________________

     2.12. Квадратичные формы.

2.12-1. Как определить являются ли линейными преобразования каких-либо выражений?

Решение:
Пусть
выражение состоит из переменных
                Х₁,
Х₂, …, Хn.                               (1)
Пусть дано произвольное поле P. Переход от переменных (1) к переменным
                Y₁, Y₂, …, Yn                                 (2)
С помощью формул
                Х₁ = a₁₁Y₁+ a₁₂Y₂+ … a₁nYn
                Х₂ = a₂₁Y₁+ a₂₂Y₂+ … a₂nYn            (3)
               
……………………………………..
                Хn = an₁Y₁+ an₂Y₂+ … annYn,  
где аᵢᵧ –
произвольные элементы поля P, называется линейным преобразованием переменных над
полем P.________________________________________________________________________________________________

     
2.13. Тензоры.

2.13-1. Вычислить свертку Cijbkj+BmEikm

Решение:
Свёртка
выполняется по одинаковым индексам, конечный результат от них уже не зависит.
Свёртка (Cijbkj + Bmеikm) = С′ibk +

B′еik.
Свёртка Сii = С′
– константа.

Набор обобщающих
Примеров соответствует требованиям
«Семестрового плана» при изучении темы:
«Алгебра матриц».
Эти Примеры предназначены закрепить
навыки применения общих алгоритмов
решений, установленных в поясняющих
Примерах.

☺ ☻ ☺

Пример
1–788:Вычислить
произведение матриц: C=AB=.

Решение:

В таблице представлена
схема вычисления произведения матриц
AиB:

▫ для вычисления
столбца-1 матрицы Cнад матрицей размещаем столбец-1 матрицыB;

▫ для вычисления
столбца-2 матрицы Cнад матрицей размещаем столбец-2 матрицыB;

Столбец	3	2	Столбец	Столбец	4	5	Столбец
	3	-2	5		3	-2	2
	5	-4	7		5	-4	0

Использование
технологического шаблона в виде таблицы
позволит отработать алгоритм вычисления
произведения матриц и защитить от ошибок
в вычислениях. Проследим вычисление
столбца-1 матрицы C:
=,
=.

Ответ: C=.

Пример 2–790:
Вычислить
произведение матриц: C=AB=.

Решение:

В таблице представлена
схема вычисления произведения матриц
AиB:

▫ для вычисления
столбца-1 матрицы Cнад матрицей размещаем столбец-1 матрицыB;

▫ для вычисления
столбца-2 матрицы Cнад матрицей размещаем столбец-2 матрицыB;

▫ для вычисления
столбца-3 матрицы Cнад матрицей размещаем столбец-3 матрицыB;

Столбец	2	1	1	Столбец	Столбец	5	2	3	Столбец	Столбец	6	5	2	Столбец
	1	-3	2	1		1	-3	2	5		1	-3	2	-5
	3	-4	1	3		3	-4	1	10		3	-4	1	0
	2	-5	3	2		2	-5	3	9		2	-5	3	-7

Из
таблицы видим ответ. Проследим вычисление
столбца-1 матрицы C:

=,
=,
=.

Ответ:=.

Пример
3–792:Вычислить
произведение матриц: C=AB=.

Решение:

В таблице представлена
схема вычисления произведения матриц
AиB:

▫ для вычисления
столбца-1 матрицы Cнад матрицей размещаем столбец-1 матрицыB;

▫ для вычисления
столбца-2 матрицы Cнад матрицей размещаем столбец-2 матрицыB;

▫ для вычисления
столбца-3 матрицы Cнад матрицей размещаем столбец-3 матрицыB;

▫ для вычисления
столбца-4 матрицы Cнад матрицей размещаем столбец-4 матрицыB.

Столбец	7	5	3	2	Столбец	Столбец	8	7	4	1	Столбец
	2	-1	3	-4	10		2	-1	3	-4	17
	3	-2	4	-3	17		3	-2	4	-3	23
	5	-3	-2	1	16		5	-3	-2	1	12
	3	-3	-1	2	7		3	-3	-1	2	1

(продолжение
таблицы).

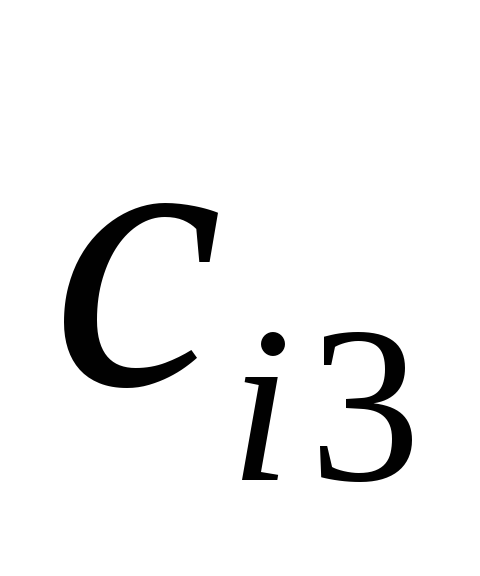
Столбец	6	4	5	1	Столбец	Столбец	9	5	6	2	Столбец
	2	-1	3	-4	19		2	-1	3	-4	23
	3	-2	4	-3	27		3	-2	4	-3	35
	5	-3	-2	1	9		5	-3	-2	1	20
	3	-3	-1	2	3		3	-3	-1	2	10

Из
таблицы видим ответ. Проследим вычисление
столбца-1 матрицы C:

=,
=,

=,
=.

Ответ: C=.

Пример
4–796:Вычислить
произведение матриц: C=ABD=.

Решение:

В
таблице представлена схема вычисления
произведения матриц AB=T.

Столбец	-28	38	Столбец	Столбец	93	–126	Столбец
	4	3	2		4	3	-6
	7	5	-6		7	5	21

В
таблице представлена схема вычисления
произведения матриц C=
T
D.

Столбец	7	2	Столбец	Столбец	3	1	Столбец
	2	-6	2		2	-6	0
	-6	21	0		-6	21	3

Ответ: C=.

Пример
5–799:Вычислить: C=A³,
еслиA
=.

Решение:

1)
Применим вычислительную схему:
C=
A³
=
AAA
=
=
TA.

В
таблице представлена схема вычисления
произведения матриц AA=T.

Столбец	1	3	Столбец	Столбец	-2	–4	Столбец
	1	-2	-5		1	-2	6
	3	-4	-9		3	-4	10

В
таблице представлена схема вычисления
произведения матриц C=
TA.

Столбец	1	3	Столбец	Столбец	-2	-4	Столбец
	-5	6	13		-5	6	-14
	-9	10	21		-9	10	-22

Ответ: C=.

Пример
6–801:
Вычислить: C=Aⁿ,
еслиA
=,
или C=
AAA…

Решение:

В
таблице представлена схема вычисления
произведения матриц AA=B=A².

Столбец	2	3	Столбец	Столбец	-1	–2	Столбец
	2	-1	1		2	-1	0
	3	-2	0		3	-2	1

В
таблице представлена схема вычисления
произведения матриц D=
BA=A³.

Столбец	2	3	Столбец	Столбец	-1	–2	Столбец
	1	0	2		1	0	–1
	0	1	3		0	1	–2

Сравним полученные
результаты умножений: A=A¹
=A³;
в то же времяA⁴
=
A³A.
Используя результат:A³
=A,
получаем равенствоA⁴
=
A².

Закономерность
очевидна: если
=– чётное, тоC=Aⁿ=,если=– нечётное, тоC=Aⁿ=.

Ответ: если
=– чётное, тоC=Aⁿ=,если=– нечётное, тоC=Aⁿ=.

Пример
7–805:
Вычислить: C
=Aⁿ,
еслиA
=,
или C=
AAA…

Решение:

В
таблице представлена схема вычисления
произведения матриц AA=T.

Столбец	λ	0	Столбец	Столбец	1	λ	Столбец
	λ	1	λ2		λ	1	2 λ
	0	λ	0		0	λ	λ2

В
таблице представлена схема вычисления
произведения матриц C=
TA.

Столбец	λ	0	Столбец	Столбец	1	λ	Столбец
	λ2	2 λ	λ3		λ2	2 λ	3λ2
	0	λ2	0		0	λ2	λ3

Анализируя
полученные результаты, замечаем
закономерность: C==.Для её доказательстваприменим
метод математической индукции: будем
считать, что утверждение C– верно. Тогда
вычислим выражение D=
=·:

В
таблице представлена схема вычисления
произведения матриц D=
CA.
с учётом принятого допущения о верности
C.

Столбец	λ	0	Столбец	Столбец	1	λ	Столбец
	λn	n·λn-1	λn+1		λn	n·λn-1	(n+1)·λn
	0	λn	0		0	λn	λn

Видим, что
утверждение: D=
=верно → значит полученная формула:
=– верна!

Ответ: C=.

Пример
8–810:
Доказать, что если для матрицAиBоба произведенияAB=C₁иBA=C₂существуют, причемAB=BA,
то матрицыAиBквадратные и имеют одинаковый порядок.

Решение:

Замечание:
предполагается, что умножение матриц
определено по правилу строка
– столбец:
количество столбцов в матрице A
равно количеству строк в матрице B.

1). Так как возможно
составить произведение AB,
то число строк матрицыBдолжно быть равным числу столбцов
матрицыA, это отражено
на схеме:

n

k

k

m

A

n

B

m

C1

•

═

2). Так как возможно
составить произведение BA,
то число строк матрицыAдолжно быть равным числу столбцов
матрицыB, это отражено
на схеме:

k

n

n

n

B

m

A

n

C2

•

═

3). Из представленных
схем следует: необходимо k=m.

4). Из условия:
следует→n= m. Имеем
окончательно: матрицыAиBквадратные и имеют
одинаковый порядок:
.

Ответ: доказано.

Пример
9–816:
Доказать, что если матрицыAиB– квадратные одного
порядка, причём=,
то всегда справедливо утверждение:

.

Решение:

1) Вспомним
формулу бинома Ньютона: ,
где a
и b
числа.
При получении формулы бинома Ньютона
были использованы свойства
элементов
a,b:
переместительное, сочетательное и
распределительное в операции умножения.

2) В общем
случае для любых двух матриц A
и B
операция умножения матриц обладает
свойствами: сочетательное и
распределительное. Дополнительное
условие для заданных матриц A
и B:
выполнение равенства
=
добавляет операции умножения свойство
переместительное для элементов:
A
и
B.

3)
Сравнивая свойства элементов a
и b
со свойствами элементов A
и
B,
находим их одинаковыми для совокупности
операций, используемых в формуле бинома
Ньютона → заданное утверждение
справедливо!

Ответ: доказано.

Пример
10–822:
Найти все матрицы, перестановочные с
матрицей:=.

Решение:

1) Пусть
имеем матрицу: ,
такую, что
=.
Учитывая правило умножения матриц,
легко заметить, что умножение этих
матриц возможно только в случае, если
матрица –
квадратная, причём той же размерности,
что матрица .

2) Примем:
=,
и запишем выражение =:

В
таблице представлена схема вычисления
произведения матриц T
=AB.

Столбец	a	b	Столбец	Столбец	c	d	Столбец
	1	2	a+2b		1	2	c+2d
	3	4	3a+4b		3	4	3c+4d

3)
Примем: =,
и запишем выражение =:

В
таблице представлена схема вычисления
произведения матриц C=BA.

Столбец	1	3	Столбец	Столбец	2	4	Столбец
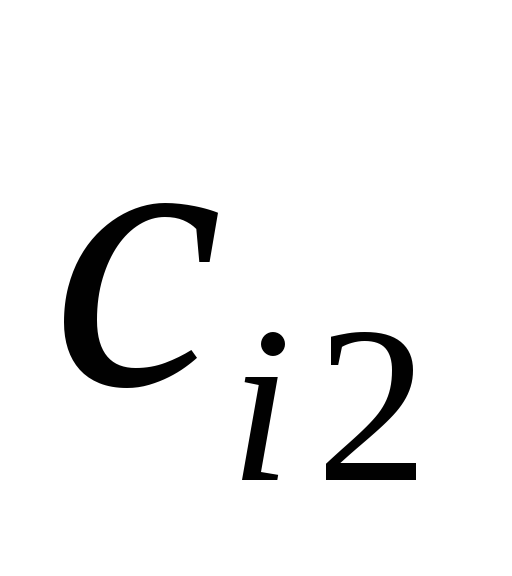
	a	c	a+3c		a	c	2a+4c
	b	d	b+3d		b	d	2b+4d

4)
Воспользуемся равенством: →
получаем уравнения для вычисления
матрицы :

a+2b=a+3c
→ 2b=3c;

3a+4b=
b+3d
→ a+b=d;

c+2d=2a+4c
→ 2d=2a+3c;

3c+4d=2b+4d
→ 3c=2b.

5)
Используя полученные уравнения, примем:
a
→ a;
b
→ 3b;
c
→ 2b;
d
→ 3b+a.
Используя принятые соотношения, получаем
все перестановочные с заданной матрицей
матрицы:

=
,
где a;
b
– любые числа.

Ответ:
=,
гдеa;b– любые числа.

Пример
11–826:
Найти все числаk,
умножение на которые невырожденной
матрицыAне изменяет
ее определителя.

Решение:

Замечание:
а) известно, что матрица
A
называется невырожденной,
если её определитель
не равен нулю: |A|
≠ 0;
поэтому значение числа k
существенно;

б) в
соответствии с правилом умножения
матрицы на число запишем: =
k·.

1). Имеем: |kA|=·|A|.

2). По условию:
|kA|=·|A|=|A|.
Следует:=1
→k=,
причем считаем 1 – комплексное число.
Известно:=+,k= 0,1, 2, … , (n–1).

Ответ:
=+,k= 0, 1, 2, … , (n–1).

Пример
12–828:Найти
значение многочлена: =от матрицы: A=.

Решение:

1) Вычислим матрицу
B=,
используя схему вычислений, представленную
таблицей:

Столбец	5	1	2	Столбец	Столбец	2	3	2	Столбец	Столбец	-3	-1	-1	Столбец
	5	2	-3	21		5	2	-3	10		5	2	-3	-14
	1	3	-1	6		1	3	-1	9		1	3	-1	–5
	2	2	-1	10		2	2	-1	8		2	2	-1	-7

2) Вычислим матрицу
C=,
используя схему вычислений, представленную
таблицей:

Столбец	5	1	2	Столбец	Столбец	2	3	2	Столбец	Столбец	-3	-1	-1	Столбец
	21	10	-14	87		21	10	-14	44		21	10	-14	-59
	6	9	-5	29		6	9	-5	29		6	9	-5	-22
	10	8	-7	44		10	8	-7	30		10	8	-7	-31

2) Запишем значение
многочлена: =от матрицы: A:

=–7+13–=.

Ответ:
==.

☻

Вопросы
для самопроверки:

1. Можно ли сложить матрицу с размерами
   (2х3) с матрицей с размерами (3х2)?

2. Можно ли умножить матрицу с размерами
   (2х3) на матрицу с размерами (2х3)?

3. Можно ли из одной матрицы
   вычесть другую? Каким условиям должны
   удовлетворять при этом матрицы? Какие
   размеры имеет матрица, являющаяся
   результатом этой операции?

4. Можно ли умножить матрицу A
   на матрицу A, если
   ?

5. Назовите свойства операции сложения
   матриц. Попробуйте их доказать.

6. Назовите свойства операции
   умножения матрицы на число. Попробуйте
   их доказать.

7. Назовите свойства операции умножения
   матриц. Попробуйте их доказать. Почему
   операция перемножения матриц не
   коммутативна?

< * * * * * >

Соседние файлы в папке ЛА и АГ пособие

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

§1. Основные определения. Линейные операции над матрицами.

Определение 1. Матрицей называется прямоугольная таблица из чисел, содержащая — строк и — столбцов. .

Определение 2.Числа И называются Порядками матрицы (или говорят, что матрица имеет размер )

Определение 3. Числа , входящие в состав данной матрицы, называются ее Элементами.

Определение 4. Матрицы называются Равными, если они имеют одинаковый порядок и все их соответствующие элементы равны.

Определение 5. Матрица называется Нулевой, если все ее элементы равны нулю.

Определение 6. Матрица называется Квадратной если число строк равно числу столбцов. В случае квадратной матрицы вводятся понятия Главной диагонали (это числа —) и Побочной диагонали (это числа —).

Определение 7. Квадратная матрица называется Диагональной, если все ее элементы, расположенные вне главной диагонали равны нулю.

Определение 8. Диагональная матрица называется Единичной , если все элементы стоящие на главной диагонали равны единице. , где если и .

Определение 9. Квадратная матрица называется Симметричной, если .

Определение 10. Треугольной называется квадратная матрица, все элементы которой расположенные ниже (выше) главной диагонали, равны нулю. Первую из этих матриц называют Верхней треугольной, а вторую — Нижней треугольной.

Линейные операции над матрицами.

1. Сложение матриц.

Определение 11. Суммой двух матриц и одних и тех же порядков И называется матрица Тех же порядков И , элементы которой равны

Для обозначения сложения используется запись

.

Из определения суммы матриц непосредственно вытекает, что операция сложения матриц обладает теми же свойствами, что и операция сложения вещественных чисел.

Свойства сложения:

1) (Коммутативность);

2) (ассоциативность);

3) ;(существование нейтрального элемента относительно операции)

4) .(существование противоположного элемента относительно операции)

Замечание 1. Множество матриц одинаковой размерности образует Абелеву группу.

Пример1. Даны матрицы: , , . Указать матрицы которые можно складывать? Найти их сумму.

► Матрицу можно сложить с матрицей , так как они имеют одинаковый порядок — , и нельзя их сложить с матрицей , так как она имеет порядок .

Так как при сложении матриц складываются соответствующие эле-

Менты, то

.◄

2. Умножение матрицы на число.

Определение 12. Произведением матрицы порядков И на вещественное число называется матрица Тех же порядков И , элементы которой равны

.

Для обозначения умножения матрицы на число используется запись .

Свойства умножения матрицы на число:

1) ;

2) ;

3) ;

Пример 2. Дана матрица: . Найти .

► Для того, чтобы умножить матрицу на число надо все элементы матрицы умножить на этот число. Имеем

.◄

Замечание 2. Разностью двух матриц и одних и тех же порядков И называется матрица тех же порядков И , Которая в сумме с матрицей дают матрицу . Для обозначения разности используется запись .

§2. Произведение матриц.

Определение 1. Произведением матрицы , имеющей порядки, соответственно равные И , на матрицу имеющую порядки, соответственно равные и называется матрица Имеющая порядки, соответственно равные И , элементы определяются формулой

.

Для обозначения произведения матрицы на матрицу используется запись

.

Из определения следует, что матрицу можно умножить не на всякую матрицу . Необходимо чтобы число столбцов матрицы было равно числу строк матрицы .

Формулу умножения можно сформулировать словесно. Элемент стоящий на пересечении Той строки иТого столбца матрицы равен сумме попарных произведений соответствующих элементов Той строки матрицы и соответствующих элементов Того столбца матрицы .

Пример 1. Даны матрицы: , . Указать порядок в котором матрицы можно перемножить? Найти произведение матриц.

►Так как матрица имеет порядок , а матрицей имеет порядок , то число столбцов матрицы равно числу строк матрицы , следовательно , существует. Число столбцов матрицы не равно числу строк матрицы , следовательно , не существует.

Произведение имеет порядок . Найдем его

.◄

Пример 2. Известно, что . Найти порядок матрицы .

►По правилу умножения матриц число столбцов матрицы равно числу строк матрицы , следовательно так как матрица имеет порядок , то есть число ее столбцов равно 5, то и число строк матрицы равно 5. Порядок матрицы равен порядку матрицы , то есть следовательно . Матрица Имеет порядок .◄

Пример 3. Даны матрицы: , .Найти элемент

если и элемент если .

►Элемент расположен на пересечении 2-ой строки и 3-го столбца, следовательно он получается перемножением 2-ой строки матрицы и 3-го столбца матрицы :

Элемент расположен на пересечении 2-ой строки и 3-го столбца, следовательно он получается перемножением 2-ой строки матрицы и 3-го столбца матрицы :

.

Очевидно , следовательно , то есть произведение матриц не коммутативно.◄

.

Лемма 1.

Свойства произведения матриц.

1) (ассоциативность);

2) , ;(дистрибутивность);

3)

4).

5) Произведение матриц всегда не коммутативно.

Замечание. Свойство коммутативности может выполняться для квадратных матриц одинакового порядка. Примеры показывают, что произведение квадратных матриц одинакового порядка вообще говоря не коммутативно. Матрицы для которых справедливо называются перестановочными. Важнейшая перестановочная матрица единичная.

Пример 4. Найти все матрицы перестановочные с матрицей если .

►Т. к. исходная матрица квадратная второго порядка, то и искомые матрицы квадратные второго порядка. Обозначим искомую матрицу.

Посчитаем , затем

Где — любые числа. Все перестановочные матрицы с исходной имеют вид: .◄

.

Степени квадратной матрицы.

Пусть квадратная матрица,

.

Лемма 2.

Для любой квадратной матрицы и для любого Справедливо

Многочлен от матрицы.

Пусть квадратная матрица и – многочлен. Значением многочлена при называется матрица

.

Пример 5. Найти , если: , .

►Согласно определению многочлена от матрицы

.◄

Пример 6. Найти .

►Возведем в квадрат

Пусть при возведении в -ую степень имеем .

Докажем, что при возведению -ую степень имеем

.

Используя известные формулы :

,

Имеем При возведении в -ую степень имеем .◄

§3. Транспонирование матриц

Пусть произвольная матрица. Матрица , полученная из матрицы заменой столбцов строками с теми же номерами, называется Транспонированной По отношению к

Свойства транспонирования матриц:

1)

2)

3)

4)

Матрицы называются Симметричными, если .

Пример 1. Найти , если , .

► . По свойствам транспонирования , по условию , поэтому , поэтому . ◄

Пример 2. Найти , если .

►По свойствам транспонирования , .◄

§4. Определители

Каждой квадратной матрице мы поставим в соответствие число называемое определителем.

Пусть есть квадратная матрица.

Если То — определитель первого порядка.

Если То — определитель второго порядка.

Теперь перейдем к выяснению понятия определитель любого порядка. Понятие определителя введем индуктивно, считая, что нами уже ведено понятие определителя -го порядка.

Определение 1. Определителем -го порядка, соответствующего матрице , назовем число равное

,

Где — минор элемента .

Определение 2. Минором Любого элемента матрицы называется определитель порядка , соответствующий той матрице которая получается вычеркиванием -й строки и –го столбца, обозначим его .

Определение 3. Алгебраическим дополнением к элементу квадратной матрицы называется число равное

Если у матрицы и у определителя вычеркнуть строк и столбцов, то элементы расположенные на их пересечении образуют определитель -го порядка . Элементы которые остаются от определителя после вычеркивания строк и столбцов образуют определитель, которые называют минором дополнительным к исходному . Каждый элемент матрицы является ее минором.

Лемма 1. (О разложении определителя по первому столбцу)

Лемма 2

При транспонировании матрицы определитель не меняется

Лемма 3

При перестановке двух рядом стоящих строк (столбцов) определителя, он меняет лишь знак.

Теорема 1.(О разложении определителя по произвольной строке (столбцу))

Определитель равен сумме произведений элементов произвольной строки (столбца) на их алгебраические дополнения.

. ()

Свойства определителей.

1) Если в определителе все элементы строки (столбца) являются суммами каких — либо слагаемых, то определитель равен сумме двух определителей, для первого определителя в соответствующей строке берется первое слагаемое, для второго — второе.

2) Общий множитель всех элементов произвольной строки (столбца) определителя можно вынести за знак определителя.

3) Если определитель содержит строку (столбец) нулей, он равен нулю.

4) Если определитель содержит две одинаковые строки (столбца), он равен нулю.

5) Если определитель содержит две пропорциональные строки (столбца), он равен нулю.

6) Если к какой-нибудь строке (столбцу) прибавить другую строку (столбец) умноженную на какое-нибудь число, то определитель при этом не изменится.

Теорема 2.(аннулирования)

Сумма произведений элементов какой-либо строки (столбца) определителя на соответствующие алгебраические дополнения элементов другой строки (столбца) равна нулю.

Теорема 3.(замещения)

Пусть задан определитель -го порядка и пусть кроме того задан упорядоченный набор чисел . Сумма произведений чисел на соответствующие алгебраические дополнения элементов другой строки (столбца) исходного определителя равна определителю полученному из исходного заменой этой строки (столбца) на строку (столбец) состоящую из чисел .

().

Теорема 4.(Лапласа)

При любом номере , и при любых фиксированных номерах строк для определителя -го порядка справедлива формула

.

Теорема 5.

Определитель от произведения квадратных матриц равен произведению определителей.

§5. Обратная матрица

Определение 1. Квадратная матрица называется невырожденной если ее определитель отличен от нуля.

Определение 2. Квадратная матрица называется обратной к квадратной матрице того же порядка, если

.

Лемма.(необходимое условие существования обратной матрицы)

Если квадратная матрица имеет обратную, то она невырожденная.

Теорема (существования и единственности)

Для любой невырожденной квадратной матрицы существует единственная ей обратная.

Свойства обратной матрицы

1) ;

2) ;

3) ;

4)

§6. Матричные уравнения

Определение. Матричным уравнением называется уравнение вида

(1)

Или

(2)

Где и известные матрицы, — неизвестная, нужных порядков.

Теорема.

Если невырожденная квадратная матрица Го порядка и число строк матрицы равно , то (1) имеет единственное решение.

Упражнение. Сформулировать и доказать теорему для (2).

§7. Решение систем линейных алгебраических уравнений.

Правило Крамера.

Определение 1. Система линейных алгебраических уравнений — это система уравнений вида:

(1)

Определение 2. Решением (1) называется упорядоченный набор чисел, который при подстановке в каждое уравнение системы обращает его в тождество.

Пусть — матрица системы, — столбец неизвестных, — столбец свободных членов,

, (2)

Тогда в том смысле, что если — решение (1) , то — решение (2) и наоборот.

Теорема (правило Крамера)

Если в системе линейных алгебраических уравнений число уравнений равно числу неизвестных и , то система имеет единственное решение, которое можно найти по формуле

,

Где определитель системы (матрицы ), Определитель получаемый из заменой Го столбца на столбец свободных членов.

Контрольные вопросы по теме 4

1.Что значит матрица имеет порядок ?

2. Какие матрицы называются равными?

3. Какая матрица называется квадратной?

4. Какая матрица называется симметричной?

5. Какая матрица называется диагональной?

6. Какая матрица называется единичной?

7.Какие матрицы можно складывать?

8.Какие операции над матрицами являются линейными?

9. Каковы свойства линейных операций над матрицами?

10.В каком случае можно умножить матицу на матрицу?

11. Каковы должны быть порядки матриц , чтобы существовало произведение ?

12.В каком случае существуют произведения И ?

13. Пусть существуют произведения И . Всегда ли ?

14. Какие матрицы называются перестоновочными?

15. Каковы свойства произведения матриц?

16. В каком случае существует произведение ?

17. Что называется нулевой степенью квадратной матрицы?

18 В каком случае квадратная матрица является корнем многочлена ?

19 Какая матрица называется транспонированной к данной?

20. Каковы свойства операции транспонирования