Здравствуйте!
Требуется найти все нормальные подгруппы в группе $%S_3$%.
Мы это решали, но мне кое-что непонятно. Попробую изложить. $%e$% и вся группа нормальны, это не очень интересно. Поскольку порядок группы равен $%6$%, а порядок нормальной подгруппы должен быть делителем порядка группы, то будем искать подгруппы размера $%2, 3$%. В нормальную группу должна входить $%e$%, значит, чтобы получить порядка $%2$%, нужно ещё что-то добавить к $%e$%. И вот тут мы взяли все подгруппы вида $%{e, (i j)}$%, то есть с транспозицией (вот тут у меня вопрос – почему мы добавили именно транспозицию к $%e$%?). Получились: $%{e, (12)}, {e, (13)}, {e, (23)}$%. Поскольку все эти транспозиции сопряжены, то сопряжением мы можем выйти из этих подгрупп, а значит, все три не являются нормальными. Далее подбираем порядка $%3$%. Получается группа из всех циклов длины $%3$%: $% {e, (123), (132)} $%. Поскольку все циклы длины $%3$% уже сюда входят, то сопряжением мы не выйдем за пределы группы, значит, она нормальна.
|
|
Подгруппы и нормальные подгруппы группы
|
|
14/02/20 |
Задача формулируется так: найти все подгруппы и нормальные подгруппы, например, Понятно, что задача легко решима перебором. Однако же, я полагаю, более пристальный взгляд в теорию групп позволит как-то упростить себе жизнь и найти заданные подгруппы в этом случае (и более сложных) легче. Например, если основываться на том, что я знаю, порядок всех подгрупп в Вот вопрос: как еще можно упростить процедуру поиска?
|
|
|
|
|
Aritaborian |
Re: Подгруппы и нормальные подгруппы группы
|
|
11/06/12 |
Прочтя обсуждение на Math.SE, пестрящее словами типа “in general a very difficult problem”, я сделал вывод, что лёгких путей здесь нет. Хотя отдельные лёгкие случаи встречаются.
|
|
|
|
|
artempalkin |
Re: Подгруппы и нормальные подгруппы группы
|
|
14/02/20 |
Aritaborian Забавно, что предлагают там в точности то, что использовал уже я Цитата: Finding all subgroups of large finite groups is in general a very difficult problem. Usually, I’d start with Lagrange’s theorem to find possible orders of subgroups. Next, you know that every subgroup has to contain the identity element. Then you can start to work out orders of elements contained in possible subgroups – again noting that orders of elements need to divide the order of the group. Ну вот, к примеру, возьмем
|
|
|
|
|
mihaild |
Re: Подгруппы и нормальные подгруппы группы
|
||
16/07/14 |
он войдет в другую подгруппу, только если она будет порядка 3 Тут сразу можно и остановиться – элемент второго порядка не может входить в подгруппу порядка 3. Учитывая, что любая подгруппа должна содержать нейтральный элемент остается проверить Меньше – подгруппа порядка 2 содержит элемент порядка 2 (а таких элементов всего 3), подгруппа же порядка 3 содержит два элемента порядка 3, а таких элементов во всей группе всего 2. С ростом
|
||
|
|
|||
|
artempalkin |
Re: Подгруппы и нормальные подгруппы группы
|
|
14/02/20 |
Тут сразу можно и остановиться – элемент второго порядка не может входить в подгруппу порядка 3. А, ну да, правильно, ведь все элементы группы порядка Получается, что, чтобы найти подгруппу, нужно: 1) с помощью теоремы Лагранжа определить порядок возможных подгрупп; К счастью нормальных подгрупп у Без проверки, основываясь на вашем сообщении, я предполагаю, что в То есть по сути осталось проверить, что наши подгруппы второго порядка (ну или точнее любой их представитель) НЕ являются нормальными подгруппами.
|
|
|
|
Модераторы: Модераторы Математики, Супермодераторы
I’m assuming you want to know more about group theory, so here is an answer to point you to some of the interesting things that you can learn if you are interested in computing with finite groups.
(i) If you have the conjugacy classes and there are not too many, then writing normal subgroups as unions of conjugacy classes is fast and easy. This is often the case when you only have access to a group through its character table, such as when the Suzuki and the sporadic simple groups were being discovered, and we wanted to understand some of their (non-simple) subgroups.
For a typical finite group given concretely as a permutation group, you use a special type of induction working along what is called a chief series, where you find a maximal chain of normal subgroups. It turns out there are some fairly easy ways to find these: for a solvable group, or any group G with an abelian quotient group, you can fairly easily and concretely find the derived subgroup, [G,G]. The quotient group is an abelian group, so every subgroup between the whole group and the derived subgroup is normal. You then take the derived subgroup of the derived subgroup, but now you only take subgroups that are normalized by G/[G,G]. The action of G/[G,G] is relatively plain and easy to understand, so these “invariant” subgroups are pretty easy to find. To finish the inductive step, you need to find the normal subgroups of G/[[G,G],[G,G]] that don’t contain [G,G], and this can be done by a slightly easier version of the general subgroup lattice algorithm using what is called the first cohomology group, or “derivations” (basically derivatives for groups, and related in a way to the derived subgroup). When you reach the point where the group is its own derived subgroup, a perfect group, then a second algorithm begins, that identifies the simple groups involved in the top of the group, and then constructs the solvable group below them. Sometimes you even have to repeat those last two steps, but not for groups of order less than 6024 ≈ 4.7e42 or so.
(ii) Often in mathematics, you want to use “induction”. A normal subgroup is one of the two main ways to do induction in group theory. Usually it is not necessary to find all normal subgroups, but rather a single (nice) chief series will do. Some groups only have a single chief series (a fair number of dihedral groups are like this), and so finding the chief series and finding all normal subgroups is the same question. You might try the symmetric group of degree 4 and order 24 as an example.
жение называется внутренним автоморфизмом группы G, порожденным элементом g.
94.Докажите, что внутренний автоморфизм группы является изоморфизмом группы на себя.
95.Во что переходит отражение треугольника относительно его высоты при всевозможных внутренних автоморфизмах группы симметрий треугольника?
96.Во что переходит вращение треугольника на 120◦ при всевозможных внутренних автоморфизмах группы симметрий треугольника?
97.Какие 2 элемента группы симметрий тетраэдра можно перевести друг в друга внутренним автоморфизмом,
акакие нельзя? Тот же вопрос для группы вращений тетраэдра.
98.Докажите, что порядки элементов ab и ba в любой группе равны.
Заметим, что при всяком внутреннем автоморфизме группы (как и при любом изоморфизме) каждая ее подгруппа переходит в подгруппу, вообще говоря, другую (например, отражения относительно одной высоты треугольника переходят в отражения относительно другой высоты). Однако некоторые «особенно симметричные» подгруппы остаются на месте при всех внутренних автоморфизмах (например, подгруппа вращений треугольника в группе симметрий треугольника). Такие подгруппы мы сейчас и рассмотрим.
§ 10. Нормальные подгруппы
О п р е д е л е н и е. Подгруппа некоторой группы называется нормальной подгруппой, если она переходит в себя при всех внутренних автоморфизмах группы. Иными словами, подгруппа N группы G называется нормальной подгруппой в G, если для любого элемента a из N и любого элемента g из G элемент gag−1 содержится в N.
Таким образом, подгруппа вращений является нормальной подгруппой в группе симметрий треугольника, а подгруппа отражений относительно высоты, опущенной из вершины A на сторону BC (состоящая из двух элементов), нормальной подгруппой группы симметрий треугольника не является.
34

99.Докажите, что в коммутативной группе всякая подгруппа является нормальной подгруппой.
100.Является ли нормальной подгруппой группы симметрий квадрата подгруппа центральных симметрий, состоящая из элементов {e, a} (примеры 3, 4, стр. 17–18)?
Те о р е м а 2. Подгруппа N группы G является нормальной подгруппой тогда и только тогда, когда левое
иправое разложения (см. § 8) группы G по подгруппе N совпадают *).
101.Доказать сформулированную теорему.
102.Пусть n — порядок группы G, m — порядок подгруппы H и m = n/2. Доказать, что H является нормальной подгруппой группы G.
103.Доказать, что пересечение (см. сноску на стр. 28) любого числа нормальных подгрупп некоторой группы G является нормальной подгруппой группы G.
104.Множество элементов группы G, перестановочных со всеми элементами группы, называется центром группы G. Доказать, что центр — подгруппа и, более того, нормальная подгруппа группы G.
105.Пусть N1 и N2 — нормальные подгруппы соответственно в группах G1 и G2. Доказать, что N1 × N2 — нормальная подгруппа в группе G1 × G2.
Следующий пример показывает, что нормальная подгруппа нормальной подгруппы группы G может не быть нормальной подгруппой самой группы G.
П р и м е р 11. Рассмотрим подгруппу группы симметрий квадрата, состоящую из отражений относительно диагоналей и центра (см. примеры 3, 4, стр. 17–18, подгруппа {e, a, d, f}). Эта подгруппа содержит половину элементов группы симметрий квадрата и является поэтому
нормальной подгруппой в ней (см. 102). Подгруппа {e, d}, состоящая из отражений относительно одной из диагоналей, содержит половину элементов подгруппы {e, a, d, f} и является, следовательно, нормальной подгруппой в ней. С другой стороны, подгруппа {e, d} не является нормальной подгруппой всей группы симметрий квадрата, так как при внутренних автоморфизмах d переходит в отражение
*) В этом случае получающееся разложение будет называться просто разложением по нормальной подгруппе.
35

E A B C
относительно другой диагонали: bdb−1 = f.
§ 11. Факторгруппы
Начнем с примера. Рассмотрим разложение группы симметрий квадрата по нормальной подгруппе, состоящей из центральных симметрий e и a (см. примеры 3, 4, стр. 17–18). Легко получить, что разложение нашей группы на 4 смежных класса имеет вид, указанный в табл. 2.
Та б л и ц а 2 Обозначим каждый смежный класс ка- кой-нибудь буквой, например, E, A, B, C.
|
e |
b |
d |
g |
Если умножить любой элемент из клас- |
|
|
a |
c |
f |
h |
||
|
са A на любой элемент из класса B, то |
|||||
результат оказывается в одном и том же классе C независимо от того, какие именно элементы классов A и B взяты. Из решения следующей задачи вытекает, что это не случайно.
106. Пусть есть разложение группы G по нормальной подгруппе N, и пусть элементы x1 и x2 лежат в одном смежном классе и элементы y1 и y2 также лежат в одном смежном классе. Доказать, что элементы x1y1 и x2y2 лежат в одном смежном классе.
Таким образом, взяв по представителю из двух смежных классов и перемножив их в определенном порядке, мы попадем в смежный класс, который не будет зависеть от того, каких именно представителей мы выбрали. Следовательно, при разложении группы по нормальной подгруппе N на множестве смежных классов можно определить бинарную операцию следующим образом: если A = xN, B = yN, то положим A · B = (xy)N. Результат задачи 105 показывает, что эта операция определена однозначно и не зависит от выбора элементов x и y, порождающих смежные классы A
иB. Так, в рассмотренном выше примере A · B = C.
Взадачах 107–109 речь идет о разложениях по нормальной подгруппе.
107. Пусть T1, T2, T3 — смежные классы. Доказать, что
(T1T2)T3 = T1(T2T3).
108.Пусть нормальная подгруппа обозначена буквой E. Доказать, что ET = T E = T для любого смежного класса .
109.Доказать, что для любого смежного класса T найдется класс T −1 такой, что T T −1 = T −1T = E.
36

Из утверждений задач 107–109 следует, что множество смежных классов с описанной выше бинарной операцией образует группу. Эта группа называется факторгруппой группы G по нормальной подгруппе N и обозначается G/N.
Очевидно, что G/{e} G и G/G {}. Очевидно так-
= =
же, что порядок факторгруппы равен натуральному числу n/m, где n — порядок группы G, а m — порядок нормальной подгруппы N. Например, факторгруппа группы симметрий квадрата по подгруппе центральных симметрий содержит 4 элемента.
110.Выяснить, будет ли факторгруппа группы симметрий квадрата по подгруппе центральных симметрий изоморфна группе вращений квадрата или группе симметрий ромба.
111.Найти все нормальные подгруппы и факторгруппы *) по ним в следующих группах: а) группа симметрий
треугольника, б) Z2 × Z2, в) группа симметрий квадрата, г) группа кватернионов (стр. 125).
112.Описать все нормальные подгруппы и факторгруппы по ним для групп: а) Zn, б) Z.
113.Найти все нормальные подгруппы и факторгруппы по ним в группе вращений тетраэдра.
114.В прямом произведении групп G1 × G2 рассмотрим подгруппу G1 × {e2}. Доказать, что это нормальная подгруппа и что факторгруппа по ней изоморфна группе G2.
§12. Коммутант
Напомним, что два элемента a и b группы G называются
перестановочными (или коммутирующими), если ab = ba. Степень некоммутативности двух элементов группы можно измерять с помощью произведения aba−1b−1, которое равно единице тогда и только тогда, когда a и b перестановочны (докажите).
О п р е д е л е н и е. Элемент aba−1b−1 называют коммутатором элементов a и b. Коммутантом K(G) группы G
называется множество всевозможных произведений конечного числа коммутаторов группы G.
*) В дальнейшем найти факторгруппу означает указать какуюлибо группу, рассмотренную ранее, которой искомая факторгруппа изоморфна.
37
115.Доказать, что коммутант является подгруппой.
116.Доказать, что коммутант является нормальной подгруппой группы.
117.Доказать, что коммутант совпадает с единичной подгруппой {e} тогда и только тогда, когда группа коммутативна.
118.Найти коммутант в группах: а) симметрий треугольника, б) симметрий квадрата, в) в группе кватернионов (стр. 125).
119.Доказать, что коммутант в группе симметрий правильного n-угольника изоморфен группе Zn при n нечетном
игруппе Zn/2 при n четном.
120.Найти коммутант в группе вращений тетраэдра.
121.Доказать, что если нормальная подгруппа в группе вращений или в группе симметрий тетраэдра содержит хотя бы одно вращение вокруг оси, проходящей через вершину, то она содержит всю группу вращений тетраэдра.
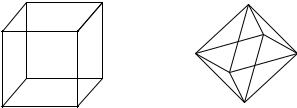
122.Найти коммутант в группе симметрий тетраэдра. Рассмотрим еще 2 группы: группу вращений куба и груп-
пу вращений правильного октаэдра (рис. 7).
Рис. 7
123.Сколько элементов в каждой из этих групп? Перечислить элементы группы вращений куба.
124.Доказать, что группы вращений куба и октаэдра изоморфны.
125.Сколькими различными способами можно закрасить грани куба 6 цветами (каждую грань своим цветом), если различными считаются раскраски, которые нельзя совместить друг с другом вращением куба? Тот же вопрос для спичечного коробка.
126.Каким из известных вам групп изоморфна группа
38
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
03.11.20184.26 Mб462.doc
- #
03.05.20151.86 Mб982.pdf
- #
- #
- #
- #
- #
РЕШЕТКИ НОРМАЛЬНЫХ ПОДГРУПП ПРАВИЛЬНОГО ТРЕУГОЛЬНИКА И КВАДРАТА
Д. Г. Гмыза, e-mail: [email protected]
АННОТАЦИЯ. Известно, что нормальные подгруппы любой группы образует модулярную решетку. В связи с этим в данной заметке построены решетки нормальных подгрупп группы симметрии треугольника и квадрата.
КЛЮЧЕВЫЕ СЛОВА: группа, нормальная подгруппа, модулярная решетка.
Группой называется множество G элементов произвольной природы, на котором задана бинарная операция 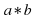
-
ассоциативность:
для любых элементов a, b, c из G;
-
в G существует такой элемент e, что
для любого элемента a из G, такой элемент e называется единицей группы G;
-
для любого элемента a из G существует такой элемент
из G, что
, такой элемент
называется обратным к элементу a.
Алгебра (L; ⋀, ⋁) называется решеткой, если L непустое множество, а ⋀ и ⋁ – бинарные операции на L, которые идемпотентны, коммутативны, ассоциативны и удовлетворяют двум тождествам поглащения.
Связь между группой и решеткой непосредственно видна из следующей теоремы.
ТЕОРЕМА 1[1,2]. Нормальные подгруппы любой группы G образуют модулярную решетку.
Подгруппа некоторой группы называется нормальной подгруппой, если она переходит в себя при всех внутренних автоморфизмах группы. Другими словами, подгруппа N группы G называется нормальной подгруппой в G, если для любого элемента a из N и любого g из G элемент 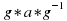
-
Решетка нормальных подгрупп правильного треугольника
Пусть А, В, С – вершины равностороннего треугольника АВС (рис. 1 а). Повернем треугольник вокруг его центра О на 1200 в направлении, указанном стрелкой. Тогда вершина А перейдет в вершину В, В в С, С в А. Таким образом, треугольник совместится со своим первоначальным положением (если не учитывать названия вершин), то есть поворот на 1200 вокруг точки О является преобразованием, переводящим данный треугольник в себя. Обозначим это преобразование через а. Его можно записать в виде 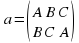
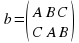
Можно составить таблицу умножения, где каждая строка, а также каждый столбец соответствует некоторому вращению, переводящему треугольник АВС в себя. На пересечении строки, соответствующей преобразованию g1, и столбца, соответствующего преобразованию g2, мы будем ставить преобразование, равное 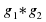
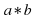
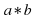
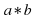
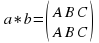
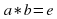
Любое преобразование некоторой фигуры в себя, сохраняющее расстояние между всеми ее точками, называется симметрией данной фигуры. Так, рассмотренные выше, вращения равностороннего треугольника являются его симметриями.
Кроме вращений, у равностороннего треугольника имеется еще три симметрии, а именно, отражение относительно осей l1, l2 и l3 (рис 1 б). Эти преобразования мы обозначим соответственно c, d, f так, что 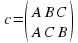
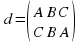
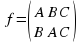
Здесь можно по-разному понимать композицию двух преобразований. Рассмотрим, например, композицию преобразования 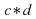
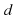
При таком подходе оказывается справедливыми рассуждения о вершинах фигуры, такие рассуждения удобно использовать для вычисления композиций преобразований.
Пусть некоторое множество преобразований G обладает следующими свойствами:
-
если преобразование g1 и g2 содержатся в G, то и их произведение g3=g1g2 содержатся в G;
-
если преобразование g содержатся в G, то и обратное ему преобразование g-1 содержатся в G.
Тогда такое множество преобразований G будем называть группой преобразований.
Нетрудно проверить, что множество преобразований представленных выше 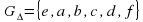
Теперь находим все подгруппы из 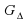
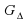
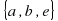
,
,
, две тривиальные подгруппы:
и вся группа
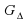
ТЕОРЕМА 2[3]. Подгруппа N группы G является нормальной подгруппой тогда и только тогда, когда левое и правое разложения группы G по подгруппе N совпадают.
Результаты применения теоремы 2 показывают, что среди выше указанных подгрупп из 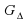
,
и вся группа
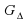
2 Решетка нормальных подгрупп группы симметрии квадрата
Пусть обозначают соответственно вращения квадрата на 00, на 1800, на 900 и на 2700 в направлении указанном стрелкой, то есть , , , (рис 2 а).
Можно составить таблицу умножения, где каждая строка, а также каждый столбец соответствует некоторому вращению, переводящему квадрат ABCD в себя. На пересечении строки, соответствующей преобразованию g2, мы будем ставить преобразование, равное 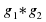
поставим: , то есть
.
Кроме вращений, у квадрата имеется 4 симметрии, а именно, отражения относительно осей d, f, g и h. Эти преобразования мы обозначим соответственно: , , , (рис 2 б).
Элемент g стоящий на пересечении столбца а и строки h вычисляется так: (таблица 2). Аналогично была заполнена другая часть таблицы 2.
Непосредственно проверяется, что множество преобразований квадрата с таблицей 2 образует группу, которая называется группой симметрии квадрата.
Далее, подгруппами в являются следующие: подгруппа вращений квадрата
, подгруппа центральных симметрий
, 4 подгруппы отражений относительно осей симметрии:
,
,
,
, и еще 2 подгруппы:
и
, 2 тривиальные подгруппы:
и вся группа
. Теперь среди этих 10 подгрупп выделим нормальных, для этого воспользуемся теоремой 2.
Если нормальная подгруппа в группе содержит элемент b или c, то она содержит всю подгруппу вращения квадрата, то есть получаем нормальную подгруппу
.
Имеем и
. Поэтому если один из элементов d, f входит в нормальную подгруппу, то и второй также входит в нормальную подгруппу. Так как
, то в этом случае элемент
также входит в нормальную подгруппу. Получаем нормальную подгруппу .
Так как ,
и
, то так же, как выше, получаем нормальную подгруппу .
Если же нормальная подгруппа не содержит элементов , то она совпадает с нормальной группой
.
Следовательно, в силу теоремы 1 имеет следующую решетку (рис 2 в).
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
-
Г. Гретцер, Общая теория решеток, М, Мир, 1982
-
Г. Биркгоф, Теория решеток, М, Наука, 1984
-
В. Н. Алексеев, Теория Абеля в задачах и решениях, М, Наука, 1976
и т.д.
|
. |
e |
a |
b |
c |
d |
f |
|
e |
e |
a |
b |
c |
d |
f |
|
a |
a |
b |
e |
f |
c |
d |
|
b |
b |
e |
a |
d |
f |
c |
|
c |
c |
d |
f |
e |
a |
b |
|
d |
d |
f |
c |
b |
e |
a |
|
f |
f |
c |
d |
a |
b |
e |
Таблица 1
А
С
В
а)
б)
в)
Рис. 1
|
. |
e |
a |
b |
c |
d |
f |
g |
h |
|
e |
e |
a |
b |
c |
d |
f |
g |
h |
|
a |
a |
e |
c |
b |
f |
d |
h |
g |
|
b |
b |
c |
a |
e |
g |
h |
f |
d |
|
c |
c |
b |
e |
a |
h |
g |
d |
f |
|
d |
d |
f |
h |
g |
e |
a |
c |
b |
|
f |
f |
d |
g |
h |
a |
e |
b |
c |
|
g |
g |
h |
d |
f |
b |
c |
e |
a |
|
h |
h |
g |
f |
d |
c |
b |
a |
e |
Таблица 2
а)
б)
в)
Рис. 2
 .
. , то подгруппы (нетривиальные) могут быть либо порядка 2, либо порядка 3. Учитывая, что любая подгруппа должна содержать нейтральный элемент остается проверить
, то подгруппы (нетривиальные) могут быть либо порядка 2, либо порядка 3. Учитывая, что любая подгруппа должна содержать нейтральный элемент остается проверить  вариантов для подгруппы порядка 2 и
вариантов для подгруппы порядка 2 и  вариантов для группы порядка 3. Ну все равно достаточно много работы… И для каждой нужно проверять нормальность? Не очень весело.
вариантов для группы порядка 3. Ну все равно достаточно много работы… И для каждой нужно проверять нормальность? Не очень весело. , который второго порядка, естественно, с
, который второго порядка, естественно, с  он образует подгруппу. Прав ли я буду, если скажу, что он не войдет больше ни в какую (нетривиальную) подгруппу? Наверное, это можно проще объяснить, но он войдет в другую подгруппу, только если она будет порядка 3, то есть к уже существующей нужно добавить еще один элемент. Однако каково будет произведение этого элемента с
он образует подгруппу. Прав ли я буду, если скажу, что он не войдет больше ни в какую (нетривиальную) подгруппу? Наверное, это можно проще объяснить, но он войдет в другую подгруппу, только если она будет порядка 3, то есть к уже существующей нужно добавить еще один элемент. Однако каково будет произведение этого элемента с  количество разных подгрупп у
количество разных подгрупп у  , естественно, растет очень быстро. К счастью нормальных подгрупп у
, естественно, растет очень быстро. К счастью нормальных подгрупп у 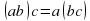 для любых элементов a, b, c из G;
для любых элементов a, b, c из G;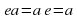 для любого элемента a из G, такой элемент e называется единицей группы G;
для любого элемента a из G, такой элемент e называется единицей группы G;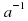 из G, что
из G, что 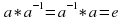 , такой элемент
, такой элемент