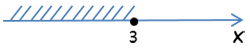Прежде чем перейти к определению и решению неравенств давайте вспомним, какие знаки используют в математике для
сравнения величин.
| Символ | Название | Тип знака |
|---|---|---|
| > | больше |
строгий знак (число на границе не включается) |
| < | меньше |
строгий знак (число на границе не включается) |
| ≥ | больше или равно |
нестрогий знак (число на границе включается) |
| ≤ | меньше или равно |
нестрогий знак (число на границе включается) |
Теперь мы можем разобраться, что называют линейным неравенством и чем неравенство
отличается от уравнения.
В отличии от уравнения в неравенстве вместо знака равно «=» используют любой
знак сравнения: «>», «<»,
«≤» или «≥».
Запомните!
Линейным
неравенством называют неравенство, в котором неизвестное стоит только в первой степени.
Рассмотрим пример линейного неравенства.
x − 6 < 8
Так как в неравенстве «x − 6 < 8»
неизвестное «x» стоит в первой степени, такое неравенство называют линейным.
Как решить линейное неравенство
Важно!
Чтобы решить неравенство, нужно чтобы в левой части осталось только неизвестное
в первой степени с
коэффициентом «1».
При решении линейных неравенств используют правило переноса и правило деления неравенства на число.
Правило переноса в неравенствах
Также как и в уравнениях,
в неравенствах можно переносить
любой член неравенства из левой части в правую и наоборот.
Запомните!
При переносе из левой части в правую (и наоборот) член неравенства меняет свой знак на
противоположный.
Вернемся к нашему неравенству и используем правило переноса.
x − 6 < 8
x < 8 + 6
x < 14
Итак, мы получили ответ к неравенству «x < 14». Но что означает такой
ответ?
Для того, чтобы понять, что получается при решении неравенства, нам нужно вспомнить,
понятие числовой оси.
Нарисуем числовую ось для неизвестного «x» и отметим на ней число «14».

Запомните!
При нанесении числа на числовую ось соблюдаются следующие правила:
Заштрихуем на числовой оси по полученному ответу «x < 14» все решения неравенства, то есть область
слева от числа «14».
Рисунок выше говорит о том, что любое число из заштрихованной области при подстановке в исходное неравенство
«x − 6 < 8»
даст верный результат.
Возьмем, например число «12» из заштрихованной области и подставим его
вместо «x» в исходное неравенство «x − 6 < 8».
Другими словами, можно утверждать, что любое число из заштрихованной области будет являться решением неравенства.
Важно!
Решить неравенство — это значит найти множество чисел, которые при подстановке в исходное неравенство
дают верный результат.
Решением неравенства
называют множество чисел из заштрихованной области на числовой оси.
В нашем примере ответ «x < 14» можно понимать так: любое число из
заштрихованной области (то есть любое число меньшее
«14») будет являться решением неравенства
«x − 6 < 8».
Правило умножения или деления неравенства на число
Рассмотрим другое неравенство.
2x − 16 > 0
Используем правило переноса и перенесём все числа без неизвестного, в правую часть.
2x − 16 > 0
2x > 16
Теперь нам нужно сделать так, чтобы при неизвестном «x»
стоял коэффициент «1». Для этого достаточно разделить и левую,
и правую часть на число «2».
Запомните!
При умножении или делении неравенства на число, на это число умножается (делится) и левая, и правая часть.
- Если неравенство умножается (делится) на положительное число,
то
знак самого неравенства остаётся прежним. - Если неравенство умножается (делится) на отрицательное число,
то
знак самого неравенства меняется на противоположный.
Разделим «2x > 16» на «2».
Так как «2» —
положительное число, знак неравенства останется прежним.
2x > 16 | (:2)
2x (:2) > 16 (:2)
x > 8
Ответ: x > 8
Рассмотрим другое неравенство.
9 − 3x ≥ 0
Используем правило переноса.
9 − 3x ≥ 0
−3x ≥ −9
Разделим неравенство на «−3».
Так как мы делим неравенство на отрицательное число, знак неравенства поменяется на противоположный.
−3x ≥ −9
−3x ≥ −9 | :(−3)
−3x : (−3) ≤ −9 :(−3)
x ≤ 3
Ответ: x ≤ 3
Примеры решения линейных неравенств
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
16 ноября 2021 в 16:44
Алина Кирщина
Профиль
Благодарили: 0
Сообщений: 1
Алина Кирщина
Профиль
Благодарили: 0
Сообщений: 1
Как правильно написать «больше 15» символом? <15 или >15?
0
Спасибо
Ответить
24 ноября 2021 в 12:56
Ответ для Алина Кирщина
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 27
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 27
> 15 Острый конец символа «птичка» > смотрит в сторону меньшего числа
Еще можно запомнить, как что где больше вершин у символа «птички», там большее число находится. У символа > слева две вершины, а справа одна, значит слева находится большее число.
0
Спасибо
Ответить
29 ноября 2021 в 7:32
Ответ для Алина Кирщина
Фархад Асланов
Профиль
Благодарили: 0
Сообщений: 1
Фархад Асланов
Профиль
Благодарили: 0
Сообщений: 1
>15
0
Спасибо
Ответить
5 марта 2020 в 23:01
Лина Недзвецкая
Профиль
Благодарили: 0
Сообщений: 1
Лина Недзвецкая
Профиль
Благодарили: 0
Сообщений: 1
Решите неравенство:
log3
≤1
0
Спасибо
Ответить
20 августа 2020 в 1:16
Ответ для Лина Недзвецкая
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
0 < (3x − 5)/(x+1) ≤ 3.
(3x − 5)/(x+1) > 0 ⇔ x < − 1 ∪ x > 5/3;
(3x − 5)/(x+1) ≤ 3 ⇔ 8/(x+1) ≥ 0 ⇔ x > − 1.
{(−∞; −1) ∪ (5/3; +∞)} ∩ (−1; +∞) = (5/3; +∞).
0
Спасибо
Ответить
17 июля 2016 в 15:37
Sergey Gurzhiy
Профиль
Благодарили: 0
Сообщений: 1
Sergey Gurzhiy
Профиль
Благодарили: 0
Сообщений: 1
Решите неравенство
2^3-6x<1
0
Спасибо
Ответить
21 сентября 2016 в 13:44
Ответ для Sergey Gurzhiy
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Странно, что для 11класса, но всё же:
23 ? 6x<1
8 ? 6x<1
? 6x< ? 7
x>
1
Спасибо
Ответить
6 июня 2016 в 17:05
Катя Петрова
Профиль
Благодарили: 0
Сообщений: 1
Катя Петрова
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
7 июня 2016 в 2:49
Ответ для Катя Петрова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Пусть 2x = y > 0.
Неравенство можно записать в виде
? 0.
Откуда y = 2 или 8 ? y < 9.
Стало быть, x = 1 или 3 ? x < log29.
0
Спасибо
Ответить
7 июня 2016 в 13:11
Ответ для Катя Петрова
Хачик Казанджян
Профиль
Благодарили: 0
Сообщений: 1
Хачик Казанджян
Профиль
Благодарили: 0
Сообщений: 1



-Tак как y>0, то сокращаем на y и преобразуем к виду
Учитывая, что y=2x получим x=1 или (3?x<log29) Ответ: (x=1)?(3?x<log2). или так {1?[3;log29)}
0
Спасибо
Ответить
8 июня 2016 в 12:10
Ответ для Катя Петрова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Списывать нехорошо.
0
Спасибо
Ответить
5 мая 2016 в 10:09
Влада Навдушевич
Профиль
Благодарили: 0
Сообщений: 1
Влада Навдушевич
Профиль
Благодарили: 0
Сообщений: 1
Как решить неравенство (х^2-4х+3)/(х^4-х^6) < или = 0
0
Спасибо
Ответить
8 июня 2016 в 12:28
Ответ для Влада Навдушевич
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
| (x — 1)(x — 3) |
| x4(1 — x)(1 + x) |
? 0.
и метод интервалов.
Ответ: (-oo; -1) U [3; +oo).
0
Спасибо
Ответить
3 августа 2015 в 16:54
Надие Рахимова
Профиль
Благодарили: 0
Сообщений: 1
Надие Рахимова
Профиль
Благодарили: 0
Сообщений: 1
область решения неравенства (х-4)>3х равна? решить
0
Спасибо
Ответить
31 августа 2016 в 10:31
Ответ для Надие Рахимова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
(x-4)>3x
x-4-3x>0
-4-2x>0
2x+4<0
2x<-4
x<-2
Проверка: Возьмём число меньшее -2, например -3
-3-4>-3 · 3
12>-9 Верно.
Ответ: x<-2
0
Спасибо
Ответить
Неравенство с одной переменной — это два выражения с переменной, соединенные знаком неравенства ((gt; ; lt; ; leq; ; geq)).
Решением неравенств с одной переменной называется такое значение переменной, которое обращает его в верное числовое неравенство.
Решить неравенство — это значит найти все его решения или доказать, что их нет, т.е. найти множество решений неравенства.
Решением неравенства с одной переменной, как правило, является числовой промежуток или совокупность промежутков.
Числовой промежуток — это множество чисел, удовлетворяющих одному из условий, перечисленных в первом столбце таблицы.
| Числовые промежутки | Обозначение | Название |
|---|---|---|
| (a lt x lt b) | ((a; b)) | Открытый промежуток, интервал |
| (x gt a) | ((a; +infty)) | |
| (x lt a) | ((-infty; a)) | |
| x — любое | ((-infty;+infty)) | |
| (a leq x leq b) | ([a;b]) | Закрытый промежуток, отрезок |
| (a lt x leq b) | ((a; b]) | Полуоткрытый промежуток, полуинтервал |
| (a leq x lt b) | ([a; b)) | |
| (x leq a) | ((-infty; a]) | |
| (x geq a) | ([a; +infty)) |
Равносильными (эквивалентами) называются неравенства, имеющие одно и то же множество решений (в частности, не имеющие решений).
Чтобы получить неравенство, равносильное данному, можно производить действия, вытекающие из свойств числовых неравенств:
- к обеим частям неравенства прибавлять одно и то же число;
- умножать обе части неравенства на одно и то же число;
- умножать обе части неравенства на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный.
Схема решения неравенств первой степени (линейных) с одной переменной
| (a cdot x geq b) | |||
|---|---|---|---|
| (a neq 0) |
(a = 0) (0 cdot x geq b) |
||
|
(a gt 0) (x ge frac{b}{a}) (x in left[frac{b}{a}; +inftyright)) |
(a lt 0) (x le frac{b}{a}) (x in left(-infty; frac{b}{a}right]) |
(b gt 0) нет решений |
(b le 0) ( x ) — любое число (x in (-infty; +infty) ) |
В случае строгого неравенства (ax gt b) схема аналогична, но все неравенства таже строгие, а интервалы — открытые.
Метод интервалов при решении неравенств
Этот метод удобен для решения неравенства вида ( P(x) gt 0 ; (lt; ; geq; ; leq) ), или ( frac{P(x)}{Q(x)} gt 0 ; (lt; ; geq; ; leq) ),
где P(x) и Q(x) — многочлены, раскладываемые на множетели.
-
Рассмотрим неравенство ( P(x) gt 0 ), и пусть многочлен ( P(x) ) раскладывается на множетели следующим образом:
(P(x)=(x-x_1)(x-x_2)…(x-x_n) gt 0) , где (x_1, x_2, …x_n) – корни данного многочлена и (n geq 2).Предположим, что все эти корни разные.
Знак левой части неравенства зависит от комбинации знаков линейных множителей и меняется в каждой из точек (x_1, x_2, …x_n).
Допустим, что (x_1 lt x_2 lt x_3 lt … lt x_n).
При (x gt x_n) все линейные множетели положительны, и вся левая часть тоже.
При (x_{n-1} lt x lt x_n) меняет знак только последний множитель, значит, и все выражение отрицательно.
При (x_{n-2} lt x lt x_{n-1}) отрицательны два последних множителя, значит левая часть опять положительна (т.к. «минус» умножить на «минус» получим «плюс») и т.д.Эти рассуждения позволяют сразу найти все решения неравенства, если воспользоваться числовой прямой.
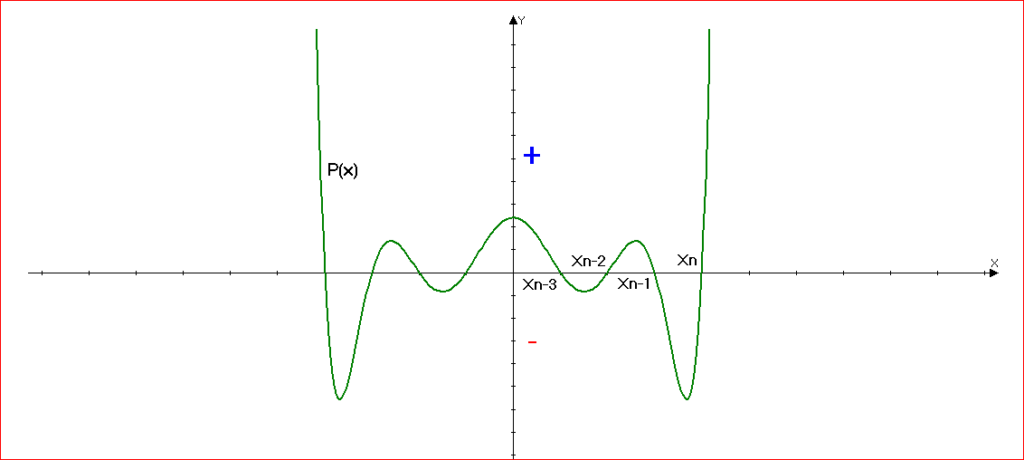
отметим на числовой прямой числа (x_1, x_2, …x_n) и проведём через них кривую (как показано на рисунке).В общем виде нельзя показать, как эта кривая пересечет прямую в точках (x_1 и x_2), т.к. мы не знаем, четно или нечетно n.
Если кривая проведена именно таким образом, то участки кривой, лежащие над числовой прямой, соответствует решению неравенства (P(x)gt 0),
а участки кривой, лежащие под осью – решение неравенства (P(x)lt 0),
(в случае строго неравенства берутся открытые промежутки, в случае нестрого — закрытые).Так в нашем случае:
(P(x)gt 0) при (x in …(x_{n-2};x_{n-1})bigcup{(x_n;+infty)} )
(P(x)leq 0) при (x in …[x_{n-3};x_{n-2}]bigcup{[x_{n-1};x_n]} )Пример
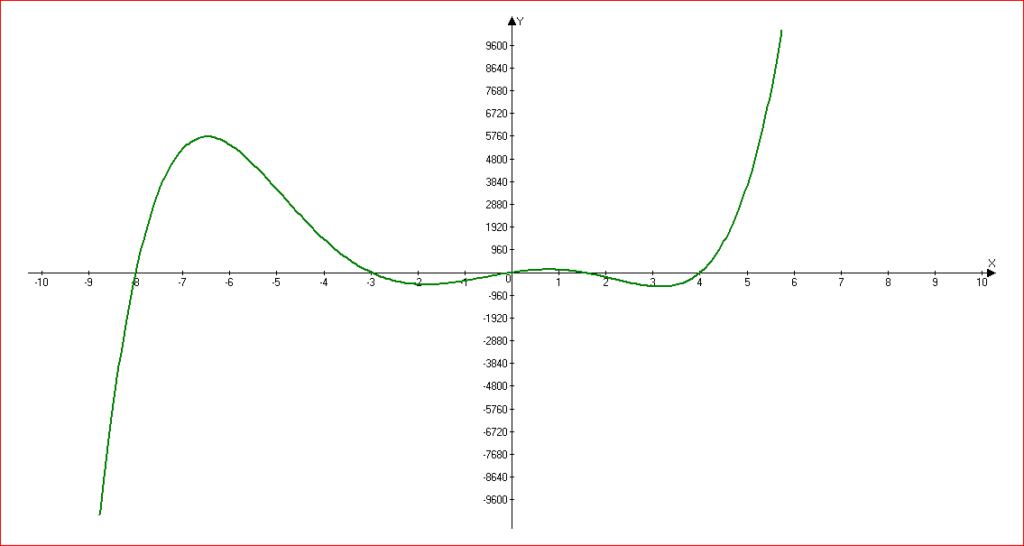
( x(x-4)(x+8)(x-1,5)(2x+6)geq 0 )
при (x in [-8; -3] bigcup [0; 1.5] bigcup [4; +infty) ) -
Пусть теперь среди множителей встречаются одинаковые (кратные).
Их произведение тогда можно записать с помощью степени в виде ((x-a)^2) или ((x+b)^3) и т.д.Если в разложении P(x) входит множитель вида ((x-a)^m), где m нечетно,
мы можем заменить его при решении неравенства множителем ((x-a)), т.к. у них знак один и тот же.Если в разложении P(x) входит множитель вида ((x-a)^m), где m четно,
то в нестрогом неравенстве его можно просто опустить, т.к. он положителен и никак не влияет на знак.
В случае строгого неравенства просто опустить множитель ((x-a)^2, ;; (x-a)^4) и т.д. нельзя,
т.к. мы должны включить в множество решений неравенства точку (x=a), для которой (P(x)=0).Пример
-
( x(x-3)^3 cdot (x-5) gt 0 )
т.к. корень x = 3 имеет кратность 3 (нечетная), то знак меняется.
решение: ( x in (0; 3) bigcup (5; +infty) ) -
( x(x-3)^2 cdot (x-5) leq 0 )
т.к. корень x = 3 имеет кратность 2 (четная), то знак не меняется.
решение: ( x in [0; 3] bigcup [3; 5] ) или ( x in [0; 5] ) -
( x(x-3)^2 cdot (x-5) lt 0 )
т.к. корень x = 3 имеет кратность 2 (четная), то знак не меняется.
решение: ( x in (0; 3) bigcup (3; 5) )
-
( x(x-3)^3 cdot (x-5) gt 0 )
-
В разложение многочлена входит квадратный трёхчлен, который не имеет действительных корней, а значит, не раскладывается на линейные множители.
В этом случае он нигде не обращается в нуль и не меняет знак, следовательно, его можно отбросить, если этот трёхчлен принимает только положительные значения.
Если же квадратный трёхчлен принимает только отрицательные значения, то его тоже можно отбросить, но при этом поменять знак неравенства на противоположный.Пример
( (x+3) cdot (x^2 + 3x + 10) gt 0 )
Т.к. трехчлен не имеет действительных корней ( (D lt 0) ) и коэффициент при (x^2) положителен,
то этот трёхчлен принимает положительные значения для всех ( x ),
т.е. решение исходного неравенства равносильно решению неравенства ( x+3 gt 0 ).
Откуда ( x gt -3 ). -
Пусть надо решить неравенство вида:
( frac{P(x)}{Q(x)} gt 0 ;; (lt, ; geq, ; leq) )
где ( P(x) ) и ( Q(x) ) — многочлены, которые можно разложить на множители.Поскольку на знак выражения не влияет, находится ли множитель в числителе или в знаменателе,
то это неравенство можно заменить неравенством (P(x) cdot Q(x)gt 0),
т.е. решение свести к первому случаю, но при этом обязательно исключить точки, в которых (Q(x)=0).
Если неравенство не строгое, то значения ( x ), при которых (Q(x)=0),
могут войти в множество решений неравенства (P(x) cdot Q(x)geq 0);
в этом случае их необходимо исключить из ответа, т.к. они не входят в ОДЗ исходного неравенства.
В случае же строгого неравенства этого можно не опасаться.Пример
$$ frac{x(x+5)}{(x-3)(x+7)^2}leq 0 $$
т.к. ( (x+7)^2 geq 0 ), то исходное неравенство равносильно следующей системе:
$$ begin{cases}
x(x+5)(x-3) leq 0 \
x neq 3 \
x neq -7
end{cases} $$решение выглядит так:
ответ: (x in (-infty; -7) bigcup (-7;-5) bigcup [0;3)). -
Прежде чем применить метод интервалов, необходимо привести линейные множители к виду (x-a),
разделив обе части неравенства на коэффициент при ( x ) (в каждой скобке).
многочлены при этом нужно разложить на множители.Пример
$$ (5x+3)(6-2x)(x^2-2x-3) geq 0 $$
Преобразуем выражение и получим:
$$ (x+frac{3}{5})(3-x)(x+1)(x-3) geq 0 $$
Ответ: (x in [-1; -3/5] bigcup [3; 3] ).
Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Неравенства
Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:
> больше,
≥ больше или равно,
< меньше,
≤ меньше или равно,
то получится неравенство.
Линейные неравенства
Линейные неравенства – это неравенства вида:
a x < b a x ≤ b a x > b a x ≥ b
где a и b – любые числа, причем a ≠ 0, x – переменная.
Примеры линейных неравенств:
3 x < 5 x − 2 ≥ 0 7 − 5 x < 1 x ≤ 0
Решить линейное неравенство – получить выражение вида:
x < c x ≤ c x > c x ≥ c
где c – некоторое число.
Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.
- Если знак неравенства строгий > , < , точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой.
Смысл выколотой точки в том, что сама точка в ответ не входит.
- Если знак неравенства нестрогий ≥ , ≤ , точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной.
Смысл жирной точки в том, что сама точка входит в ответ.
- Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.
Таблица числовых промежутков
| Неравенство | Графическое решение | Форма записи ответа |
|---|---|---|
| x < c |
|
x ∈ ( − ∞ ; c ) |
| x ≤ c |
|
x ∈ ( − ∞ ; c ] |
| x > c |
|
x ∈ ( c ; + ∞ ) |
| x ≥ c |
|
x ∈ [ c ; + ∞ ) |
Алгоритм решения линейного неравенства
- Раскрыть скобки (если они есть), перенести иксы в левую часть, числа в правую и привести подобные слагаемые. Должно получиться неравенство одного из следующих видов:
a x < b a x ≤ b a x > b a x ≥ b
- Пусть получилось неравенство вида a x ≤ b. Для того, чтобы его решить, необходимо поделить левую и правую часть неравенства на коэффициент a.
- Если a > 0 то неравенство приобретает вид x ≤ b a .
- Если a < 0 , то знак неравенства меняется на противоположный, неравенство приобретает вид x ≥ b a .
- Записываем ответ в соответствии с правилами, указанными в таблице числовых промежутков.
Примеры решения линейных неравенств:
№1. Решить неравенство 3 ( 2 − x ) > 18.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 − 3 x > 18
− 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 )
Делим обе части неравенства на (-3) – коэффициент, который стоит перед x. Так как − 3 < 0 , знак неравенства поменяется на противоположный. x < 12 − 3 ⇒ x < − 4 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x ∈ ( − ∞ ; − 4 )
№2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 x + 4 ≥ 3 x + 3 − 14
6 x − 3 x ≥ 3 − 14 − 4
3 x ≥ − 15 | ÷ 3 Делим обе части неравенства на (3) – коэффициент, который стоит перед x. Так как 3 > 0, знак неравенства после деления меняться не будет.
x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x ∈ [ − 5 ; + ∞ )
Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).
Примеры:
№1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 x − 1 ≤ 6 x − 1
6 x − 6 x ≤ − 1 + 1
0 ≤ 0
Получили верное неравенство, которое не зависит от переменной x. Возникает вопрос, какие значения может принимать переменная x, чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа.
Ответ:
- x – любое число
- x ∈ ( − ∞ ; + ∞ )
- x ∈ ℝ
№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
x + 6 − 9 x > − 8 x + 48
− 8 x + 8 x > 48 − 6
0 > 42
Получили неверное равенство, которое не зависит от переменной x. Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ.
Ответ: x ∈ ∅
Квадратные неравенства
Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c < 0 a x 2 + b x + c ≤ 0 где a, b, c – некоторые числа, причем a ≠ 0, x – переменная.
Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.
Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).
Алгоритм решения квадратного неравенства методом интервалов
- Решить уравнение a x 2 + b x + c = 0 и найти корни x 1 и x 2 .
- Отметить на числовой прямой корни трехчлена.
Если знак неравенства строгий > , < , точки будут выколотые.
Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный).
- Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A) и подставить её значение в выражение a x 2 + b x + c вместо x.
Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
- Выбрать подходящие интервалы (или интервал).
Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.
Если знак неравенства < или ≤ в ответ выбираем интервалы со знаком -.
- Записать ответ.
Примеры решения квадратных неравенств:
№1. Решить неравенство x 2 ≥ x + 12.
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
x 2 ≥ x + 12
x 2 − x − 12 ≥ 0
x 2 − x − 12 = 0
a = 1, b = − 1, c = − 12
D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6. Подставляем эту точку в исходное выражение:
x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0
Это значит, что знак на интервале, в котором лежит точка 6 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪ .
Точки -3 и 4 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ )
№2. Решить неравенство − 3 x − 2 ≥ x 2 .
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
− 3 x − 2 ≥ x 2
− x 2 − 3 x − 2 ≥ 0
− x 2 − 3 x − 2 = 0
a = − 1, b = − 3, c = − 2
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1
x 1 = − 2, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение:
− x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 < 0
Это значит, что знак на интервале, в котором лежит точка 0 будет − .
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥ , выбираем в ответ интервал со знаком +.
Точки -2 и -1 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ [ − 2 ; − 1 ]
№3. Решить неравенство 4 < x 2 + 3 x .
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
4 < x 2 + 3 x
− x 2 − 3 x + 4 < 0
− x 2 − 3 x + 4 = 0
a = − 1, b = − 3, c = 4
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1
x 1 = − 4, x 2 = 1
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение:
− x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 < 0
Это значит, что знак на интервале, в котором лежит точка 2, будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервалы со знаком − .
Точки -4 и 1 будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ )
№4. Решить неравенство x 2 − 5 x < 6.
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
x 2 − 5 x < 6
x 2 − 5 x − 6 < 0
x 2 − 5 x − 6 = 0
a = 1, b = − 5, c = − 6
D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1
x 1 = 6, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение:
x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0
Это значит, что знак на интервале, в котором лежит точка 10 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервал со знаком -.
Точки -1 и 6 будут в круглых скобках, так как они выколотые
Ответ: x ∈ ( − 1 ; 6 )
№5. Решить неравенство x 2 < 4.
Решение:
Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.
x 2 < 4
x 2 − 4 < 0
x 2 − 4 = 0
( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2
x 1 = 2, x 2 = − 2
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3. Подставляем эту точку в исходное выражение:
x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0
Это значит, что знак на интервале, в котором лежит точка 3 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервал со знаком − .
Точки -2 и 2 будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − 2 ; 2 )
№6. Решить неравенство x 2 + x ≥ 0.
Решение:
Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0.
x 2 + x ≥ 0
x 2 + x = 0
x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1
x 1 = 0, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1. Подставляем эту точку в исходное выражение:
x 2 + x = 1 2 + 1 = 2 > 0
Это значит, что знак на интервале, в котором лежит точка 1 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥ , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ )
Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.
Дробно рациональные неравенства
Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:
f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).
Примеры дробно рациональных неравенств:
x − 1 x + 3 < 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3
Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.
Алгоритм решения дробно рациональных неравенств:
- Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве):
f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
- Приравнять числитель дроби к нулю f ( x ) = 0. Найти нули числителя.
- Приравнять знаменатель дроби к нулю g ( x ) = 0. Найти нули знаменателя.
В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.
- Нанести нули числителя и нули знаменателя на ось x.
Вне зависимости от знака неравенства
при нанесении на ось x нули знаменателя всегда выколотые.
Если знак неравенства строгий,
при нанесении на ось x нули числителя выколотые.
Если знак неравенства нестрогий,
при нанесении на ось x нули числителя жирные.
- Расставить знаки на интервалах.
- Выбрать подходящие интервалы и записать ответ.
Примеры решения дробно рациональных неравенств:
№1. Решить неравенство x − 1 x + 3 > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравниваем числитель к нулю f ( x ) = 0.
x − 1 = 0
x = 1 – это ноль числителя. Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.
- Приравниваем знаменатель к нулю g ( x ) = 0.
x + 3 = 0
x = − 3 – это ноль знаменателя. При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x − 1 x + 3 = 2 − 1 2 + 3 = 1 5 > 0,
Это значит, что знак на интервале, в котором лежит точка 2 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые.
Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )
№2. Решить неравенство 3 ( x + 8 ) ≤ 5.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Привести неравенство к виду f ( x ) g ( x ) ≤ 0.
3 ( x + 8 ) ≤ 5
3 ( x + 8 ) − 5 x + 8 ≤ 0
3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 x − 40 x + 8 ≤ 0
− 5 x − 37 x + 8 ≤ 0
- Приравнять числитель к нулю f ( x ) = 0.
− 5 x − 37 = 0
− 5 x = 37
x = − 37 5 = − 37 5 = − 7,4
x = − 7,4 – ноль числителя. Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.
- Приравнять знаменатель к нулю g ( x ) = 0.
x + 8 = 0
x = − 8 – это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
− 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 < 0
Это значит, что знак на интервале, в котором лежит точка 0 будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства ≤ , выбираем в ответ интервалы со знаком -.
В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная.
Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ )
№3. Решить неравенство x 2 − 1 x > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравнять числитель к нулю f ( x ) = 0.
x 2 − 1 = 0
( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1
x 1 = 1, x 2 = − 1 – нули числителя. Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.
- Приравнять знаменатель к нулю g ( x ) = 0.
x = 0 – это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ )
Системы неравенств
Сперва давайте разберёмся, чем отличается знак { системы от знака [ совокупности. Система неравенств ищет пересечение решений, то есть те точки, которые являются решением и для первого неравенства системы, и для второго. Проще говоря, решить систему неравенств – это найти пересечение решений всех неравенств этой системы друг с другом. Совокупность неравенств ищет объединение решений, то есть те точки, которые являются решением либо для первого неравенства, либо для второго, либо одновременно и для первого неравенства, и для второго. Решить совокупность неравенств означает объединить решения обоих неравенств этой совокупности. Более подробно об этом смотрите короткий видео-урок.
Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.
Пример системы неравенств:
{ x + 4 > 0 2 x + 3 ≤ x 2
Алгоритм решения системы неравенств
- Решить первое неравенство системы, изобразить его графически на оси x.
- Решить второе неравенство системы, изобразить его графически на оси x.
- Нанести решения первого и второго неравенств на ось x.
- Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.
Примеры решений систем неравенств:
№1. Решить систему неравенств { 2 x − 3 ≤ 5 7 − 3 x ≤ 1
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2 x − 3 ≤ 5
2 x ≤ 8 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x ≤ 4 ;
Графическая интерпретация:
Точка 4 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
7 − 3 x ≤ 1
− 3 x ≤ 1 − 7
− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 < 0, знак неравенства после деления меняется на противоположный.
x ≥ 2
Графическая интерпретация решения:
Точка 2 на графике жирная, так как знак неравенства нестрогий.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на отрезке от 2 до 4. Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные.
Ответ: x ∈ [ 2 ; 4 ]
№2. Решить систему неравенств { 2 x − 1 ≤ 5 1 < − 3 x − 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2 x − 1 ≤ 5
2 x ≤ 6 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x ≤ 3
Графическая интерпретация:
Точка 3 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
1 < − 3 x − 2
3 x < − 1 − 2
3 x < − 3 | ÷ 3 , поскольку 3 > 0, знак неравенства после деления сохраняется.
x < − 1
Графическая интерпретация решения:
Точка -1 на графике выколотая, так как знак неравенства строгий.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая.
Ответ: x ∈ ( − ∞ ; − 1 )
№3. Решить систему неравенств { 3 x + 1 ≤ 2 x x − 7 > 5 − x
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
3 x + 1 ≤ 2 x
3 x − 2 x ≤ − 1
x ≤ − 1
Графическая интерпретация решения:
- Решаем второе неравенство системы
x − 7 > 5 − x
x + x > 5 + 7
2 x > 12 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x > 6
Графическая интерпретация решения:
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.
Ответ: x ∈ ∅
№4. Решить систему неравенств { x + 4 > 0 2 x + 3 ≤ x 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
x + 4 > 0
x > − 4
Графическая интерпретация решения первого неравенства:
- Решаем второе неравенство системы
2 x + 3 ≤ x 2
− x 2 + 2 x + 3 ≤ 0
Решаем методом интервалов.
− x 2 + 2 x + 3 = 0
a = − 1, b = 2, c = 3
D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16
D > 0 – два различных действительных корня.
x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1
Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.
Графическая интерпретация решения второго неравенства:
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪ .
Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные.
Ответ: x ∈ ( − 4 ; − 1 ] ∪ [ 3 ; + ∞ )
Скачать домашнее задание к уроку 8.
Сегодня посмотрим один вид задания №13 первой части ОГЭ, которое вызывает наибольшие трудности у девятиклассников.
Само задание звучит следующим образом:
Укажите неравенство, которое не имеет решений:
1) x²+x+36<0
2) x²+x+36>0
3) x²+x-36<0
4) x²+x-36>0
Это стандартное полное квадратное неравенство.
Если левая часть квадратного неравенства имеет корни, то неравенство всегда имеет решение.
Если левая часть не имеет корней, то неравенство либо имеет бесконечное множество решений, либо не имеет решений.
Значит, чтобы неравенство не имело решений необходимо выполнение нескольких условий, первое из которых: левая часть не имеет корней.
На этом этапе уже можно отсеять варианты 3) и 4)
Осталось теперь определить, какое из оставшихся неравенство имеет бесконечное множество решений, а какое не имеет решений.
Для этого изобразим решение на числовой прямой. Функция “у=x²+x+36” парабола. Ветки параболы смотрят вверх (a>0). Т.к. функция не имеет корней, то парабола не пересекает числовую прямую, а значит располагается выше оси.
Значит при любом значении х: x²+x+36>0.
А вот x²+x+36<0 не имеет решений
ОТВЕТ: 1
ПС Обратите внимание, что при отрицательном дискриминанте УРАВНЕНИЕ не имеет решений, на НЕРАВЕНСТВО либо не имеет решений, либо имеет бесконечное число решений. Поэтому выбор ответа требует дополнительного исследования функции.
Продолжение следует…
Не забудь нажать на пальчик вверх после прочтения и подписаться. За это отдельная благодарность
(✿◠‿◠)
Калькулятор онлайн.
Решение неравенств: линейные, квадратные и дробные.
Программа решения неравенств не просто даёт ответ задачи, она приводит подробное решение
с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Причём, если в процессе решения неравенства нужно решить, например, квадратное уравнение, то его подробное решение также
выводится (оно заключается в спойлер).
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Какие неравенства можно решить?
Примеры подробного решения >>
Правила ввода неравенств
В качестве переменной может выступать любая латинсая буква.
Например: ( x, y, z, a, b, c, o, p, q ) и т.д.
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5x – 3,5x^2
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 3&1/3 – 5&6/5y +1/7y^2
Результат: ( 3frac{1}{3} – 5frac{6}{5} y + frac{1}{7}y^2 )
При вводе выражений можно использовать скобки. В этом случае при решении неравенства выражения сначала упрощаются.
Например: 5(a+1)^2+2&3/5+a > 0,6(a-2)(a+3)
Нажмите на кнопку 
Выберите нужный знак неравенства и введите многочлены в поля ниже.
Наши игры, головоломки, эмуляторы:
Немного теории.
Сравнивать величины и количества при решении практических задач приходилось ещё с древних времён. Тогда же
появились и такие слова, как больше и меньше, выше и ниже, легче и тяжелее, тише и громче, дешевле и дороже и т.д.,
обозначающие результаты сравнения однородных величин.
Понятия больше и меньше возникли в связи со счётом предметов, измерением и сравнением величин. Например, математики Древней
Греции знали, что сторона любого треугольника меньше суммы двух других сторон и что против большего угла в треугольнике лежит
большая сторона. Архимед, занимаясь вычислением длины окружности, установил, что периметр всякого круга равен утроенному диаметру
с избытком, который меньше седьмой части диаметра, но больше десяти семьдесят первых диаметра.
Символически записывать соотношения между числами и величинами с помощью знаков > и < начали лишь в XVII—XVIII вв. Например,
вместо фразы «число а больше числа b» стали писать: а > b. Записи, в которых два числа соединены одним из знаков: > (больше),
< (меньше), ( geqslant ) (больше или равно), ( leqslant ) (меньше или равно), стали называть неравенствами.
С числовыми неравенствами вы встречались и в младших классах. Знаете, что неравенства могут быть верными, а могут быть и неверными.
Например, ( frac{1}{2} > frac{1}{3} ) верное числовое неравенство, 0,23 > 0,235 — неверное числовое неравенство.
Неравенства, в которые входят неизвестные, могут быть верными при одних значениях неизвестных и неверными при других.
Например, неравенство 2x+1>5 верное при х = 3, а при х = -3 — неверное. Для неравенства с одним неизвестным можно поставить
задачу: решить неравенство. Задачи решения неравенств на практике ставятся и решаются не реже, чем задачи решения уравнений.
Например, многие экономические проблемы сводятся к исследованию и решению систем линейных неравенств. Во многих разделах
математики неравенства встречаются чаще, чем уравнения.
Некоторые неравенства служат единственным вспомогательным средством, позволяющим доказать или опровергнуть существование
определённого объекта, например, корня уравнения.
Далее вы узнаете свойства неравенств, научитесь решать неравенства. Полученные умения вам понадобятся при изучении последующего
материала, для решения практических задач, а также задач физики и геометрии.
Числовые неравенства
Вы умеете сравнивать целые числа, десятичные дроби. Знаете правила сравнения обыкновенных дробей с одинаковыми знаменателями,
но разными числителями; с одинаковыми числителями, но разными знаменателями. Здесь вы научитесь сравнивать любые два числа с
помощью нахождения знака их разности.
Сравнение чисел широко применяется на практике. Например, экономист сравнивает плановые показатели с фактическими, врач
сравнивает температуру больного с нормальной, токарь сравнивает размеры вытачиваемой детали с эталоном. Во всех таких случаях
сравниваются некоторые числа. В результате сравнения чисел возникают числовые неравенства.
Определение. Число а больше числа b, если разность а-b положительна. Число а меньше числа b, если разность а-b отрицательна.
Если а больше b, то пишут: а > b; если а меньше b, то пишут: а < b.
Таким образом, неравенство а > b означает, что разность а – b положительна, т.е. а – b > 0. Неравенство а < b означает, что а – b < 0.
Для любых двух чисел а и b из следующих трёх соотношений a > b, a = b, a < b только одно является верным.
Сравнить числа а и b — значит выяснить, какой из знаков >, = или < нужно поставить между этими числами, чтобы получить верное
соотношение. Это можно сделать, определив знак разности а – b.
Теорема. Если a > b и b > с, то а > с.
Теорема. Если к обеим частям неравенства прибавить одно и то же число, то знак неравенства не изменится.
Следствие. Любое слагаемое можно перенести из одной части неравенства в другую, изменив знак этого слагаемого на
противоположный.
Теорема. Если обе части неравенства умножить на одно и то же положительное число, то знак неравенства не изменится.
Если обе части неравенства умножить на одно и то же отрицательное число, то знак неравенства изменится на противоположный.
Следствие. Если обе части неравенства разделить на одно и то же положительное число, то знак неравенства не изменится.
Если обе части неравенства разделить на одно и то же отрицательное число, то знак неравенства изменится на противоположный.
Вы знаете, что числовые равенства можно почленно складывать и умножать. Далее вы научитесь выполнять аналогичные действия
с неравенствами. Умения почленно складывать и умножать неравенства часто применяются на практике. Эти действия помогают решать
задачи оценивания и сравнения значений выражений.
При решении различных задач часто приходится складывать или умножать почленно левые и правые части неравенств. При этом
иногда говорят, что неравенства складываются или умножаются. Например, если турист прошёл в первый день более 20 км, а во
второй – более 25 км, то можно утверждать, что за два дня он прошёл более 45 км. Точно так же если длина прямоугольника меньше
13 см, а ширина меньше 5 см, то можно утверждать, что площадь этого прямоугольника меньше 65 см2.
При рассмотрении этих примеров применялись следующие теоремы о сложении и умножении неравенств:
Теорема. При сложении неравенств одинакового знака получается неравенство того же знака: если а > b и c > d, то
a + c > b + d.
Теорема. При умножении неравенств одинакового знака, у которых левые и правые части положительны, получается
неравенство того же знака: если а > b, c > d и а, b, с, d – положительные числа, то ac > bd.
Неравенства со знаком > (больше) и < (меньше) называют строгими. Например, 5/6 > 1/2, 3/4 < 1, a > b, c < d – строгие неравенства.
Наряду со знаками строгих неравенств > и < используются знаки ( geqslant ) (больше или равно) и ( leqslant ) (меньше или равно),
которые называют знаками нестрогих неравенств. Неравенство ( a leqslant b ) означает, что а < b или а = b, т. е. а не больше b.
Например, если число посадочных мест в самолёте 134, то число а пассажиров может быть меньшим или равным 134. В этом случае можно
записать: ( a leqslant 134 )
Точно так же неравенство ( a geqslant b ) означает, что число а больше или равно b, т. е. а не меньше b.
Неравенства, содержащие знак ( geqslant ) или знак ( leqslant ), называют нестрогими. Например,
( 18 geqslant 12 , ; 11 leqslant 12 ) – нестрогие неравенства.
Все свойства строгих неравенств справедливы и для нестрогих неравенств. При этом если для строгих неравенств противоположными
считались знаки > и <, то для нестрогих неравенств противоположными считаются знаки ( geqslant ) и ( leqslant ).
Вы знаете, что для решения ряда прикладных задач приходится составлять математическую модель в виде уравнения или системы
уравнений. Далее вы узнаете, что математическими моделями для решения многих задач являются неравенства с неизвестными.
Будет введено понятие решения неравенства и показано, как проверить, является ли данное число решением конкретного неравенства.
Неравенства вида
( ax > b, quad ax < b, quad ax geqslant b, quad ax leqslant b )
в которых а и b — заданные числа, а x — неизвестное, называют линейными неравенствами с одним неизвестным.
Определение. Решением неравенства с одним неизвестным называется то значение неизвестного, при котором это неравенство
обращается в верное числовое неравенство. Решить неравенство — это значит найти все его решения или установить, что их нет.
Решение уравнений вы осуществляли путём приведения их к простейшим уравнениям. Аналогично при решении неравенств их стремятся
с помощью свойств привести к виду простейших неравенств.
Решение неравенств второй степени с одной переменной
Неравенства вида
( ax^2+bx+c >0 ) и ( ax^2+bx+c <0 ),
где x — переменная, a, b и c — некоторые числа и ( a neq 0 ), называют неравенствами второй степени с одной переменной.
Решение неравенства
( ax^2+bx+c >0 ) или ( ax^2+bx+c <0 )
можно рассматривать как нахождение промежутков, в которых функция ( y= ax^2+bx+c ) принимает положительные или отрицательные
значения. Для этого достаточно проанализировать, как расположен график функции ( y= ax^2+bx+c ) в координатной плоскости:
куда направлены ветви параболы – вверх или вниз, пересекает ли парабола ось x и если пересекает, то в каких точках.
Алгоритм решения неравенств второй степени с одной переменной:
1) находят дискриминант квадратного трехчлена ( ax^2+bx+c ) и выясняют, имеет ли трехчлен корни;
2) если трехчлен имеет корни, то отмечают их на оси x и через отмеченные точки проводят схематически параболу, ветви которой
направлены вверх при a > 0 или вниз при a < 0; если трехчлен не имеет корней, то схематически изображают параболу, расположенную
в верхней полуплоскости при a > 0 или в нижней при a < 0;
3) находят на оси x промежутки, для которых точки параболы расположены выше оси x (если решают неравенство ( ax^2+bx+c >0 ) )
или ниже оси x (если решают неравенство
( ax^2+bx+c <0 ) ).
Решение неравенств методом интервалов
Рассмотрим функцию
f(x) = (х + 2)(х – 3)(х – 5)
Областью определения этой функции является множество всех чисел. Нулями функции служат числа -2, 3, 5. Они разбивают область
определения функции на промежутки ( (-infty; -2), ; (-2; 3), ; (3; 5) ) и ( (5; +infty) )
Выясним, каковы знаки этой функции в каждом из указанных промежутков.
Выражение (х + 2)(х – 3)(х – 5) представляет собой произведение трех множителей. Знак каждого из этих множителей в рассматриваемых
промежутках указан в таблице:
| ( (-infty; -2) ) | ( (-2; 3) ) | ( (3; 5) ) | ( (5; +infty) ) | |
| x+2 | – | + | + | + |
| x-3 | – | – | + | + |
| x-5 | – | – | – | + |
Отсюда ясно, что:
если ( x in (-infty;-2) ), то f(x)<0;
если ( x in (-2;3) ), то f(x)>0;
если ( x in (3;5) ), то f(x)<0;
если ( x in (5;+infty) ), то f(x)>0.
Мы видим, что в каждом из промежутков ( (-infty; -2), ; (-2; 3), ; (3; 5), ; (5; +infty) ) функция сохраняет знак,
а при переходе через точки -2, 3 и 5 ее знак изменяется.
Вообще пусть функция задана формулой
f(x) = (x-x1)(x-x2) … (x-xn),
где x–переменная, а x1, x2, …, xn – не равные друг другу числа. Числа
x1, x2, …, xn являются нулями функции. В каждом из промежутков, на которые область определения
разбивается нулями функции, знак функции сохраняется, а при переходе через нуль ее знак изменяется.
Это свойство используется для решения неравенств вида
(x-x1)(x-x2) … (x-xn) > 0,
(x-x1)(x-x2) … (x-xn) < 0,
где x1, x2, …, xn — не равные друг другу числа
Рассмотренный способ решения неравенств называют методом интервалов.
Приведем примеры решения неравенств методом интервалов.
Решить неравенство:
( x(0,5-x)(x+4) < 0 )
Очевидно, что нулями функции f(x) = x(0,5-x)(x+4) являются точки ( x=0, ; x=frac{1}{2} , ; x=-4 )
Наносим на числовую ось нули функции и вычисляем знак на каждом промежутке:
Выбираем те промежутки, на которых функция меньше нуля и записываем ответ.
Ответ:
( x in left( -4; ; 0 right) cup left( 0,5; ; +infty right) )
или
( -4 < x < 0 ;;; x > 0,5 )
Решить неравенство:
$$ frac{x+2}{x-1} leqslant 2 $$
Решение:
$$ frac{x+2}{x-1} leqslant 2 Rightarrow frac{x+2-2(x-1)}{x-1} leqslant 0 Rightarrow frac{-x+4}{x-1} leqslant 0 $$
Наносим на числовую ось нули и точки разрыва функции:
Выбираем те промежутки, на которых функция меньше или равна нулю и записываем ответ.
Ответ:
( x in left( -infty; ; 1 right) cup left[ 4; ; +infty right) )
или
( x < 1 ;;; x geqslant 4 )