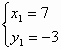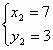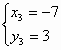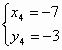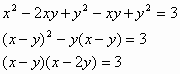Как найти все пары целых чисел уравнения - Сайт, где вы сможете решить свои вопросы

math4school.ru

Уравнения в целых числах

Немного теории

Уравнения в целых числах – это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами. Решениями такого уравнения являются все целочисленные (иногда натуральные или рациональные) наборы значений неизвестных переменных, удовлетворяющих этому уравнению. Такие уравнения ещё называют диофантовыми, в честь древнегреческого математика Диофанта Александрийского, который исследовал некоторые типы таких уравнений ещё до нашей эры.

Современной постановкой диофантовых задач мы обязаны французскому математику Ферма. Именно он поставил перед европейскими математиками вопрос о решении неопределённых уравнений только в целых числах. Наиболее известное уравнение в целых числах – великая теорема Ферма: уравнение

не имеет ненулевых рациональных решений для всех натуральных n > 2.

Теоретический интерес к уравнениям в целых числах достаточно велик, так как эти уравнения тесно связаны со многими проблемами теории чисел.

В 1970 году ленинградский математик Юрий Владимирович Матиясевич доказал, что общего способа, позволяющего за конечное число шагов решать в целых числах произвольные диофантовы уравнения, не существует и быть не может. Поэтому следует для разных типов уравнений выбирать собственные методы решения.

При решении уравнений в целых и натуральных числах можно условно выделить следующие методы:

способ перебора вариантов;

применение алгоритма Евклида;

представление чисел в виде непрерывных (цепных) дробей;

разложения на множители;

решение уравнений в целых числах как квадратных (или иных) относительно какой-либо переменной;

метод бесконечного спуска.

Задачи с решениями

1. Решить в целых числах уравнение x 2 – xy – 2y 2 = 7.

Запишем уравнение в виде (x – 2y)(x + y) = 7.

Так как х, у – целые числа, то находим решения исходного уравнения, как решения следующих четырёх систем:

1) x – 2y = 7, x + y = 1;

2) x – 2y = 1, x + y = 7;

3) x – 2y = –7, x + y = –1;

4) x – 2y = –1, x + y = –7.

Решив эти системы, получаем решения уравнения: (3; –2), (5; 2), (–3; 2) и (–5; –2).

Ответ: (3; –2), (5; 2), (–3; 2), (–5; –2).

2. Решить в целых числах уравнение:

а) 20х + 12у = 2013;

в) 201х – 1999у = 12.

а) Поскольку при любых целых значениях х и у левая часть уравнения делится на два, а правая является нечётным числом, то уравнение не имеет решений в целых числах.

Ответ: решений нет.

б) Подберём сначала некоторое конкретное решение. В данном случае, это просто, например,

Поскольку числа 5 и 7 взаимно простые, то

Значит, общее решение:

х = 1 + 7k, у = 2 – 5k,

где k – произвольное целое число.

Ответ: (1+7k; 2–5k), где k – целое число.

в) Найти некоторое конкретное решение подбором в данном случае достаточно сложно. Воспользуемся алгоритмом Евклида для чисел 1999 и 201:

НОД(1999, 201) = НОД(201, 190) = НОД(190, 11) = НОД(11, 3) = НОД(3 , 2) = НОД(2, 1) = 1.

Запишем этот процесс в обратном порядке:

1 = 2 – 1 = 2 – (3 – 2) = 2·2 – 3 = 2· (11 – 3·3) – 3 = 2·11 – 7·3 = 2·11 – 7(190 – 11·17) =

= 121·11 – 7·190 = 121(201 – 190) – 7·190 = 121·201 – 128·190 =

= 121·201 – 128(1999 – 9·201) = 1273·201 – 128·1999.

Значит, пара (1273, 128) является решением уравнения 201х – 1999у = 1. Тогда пара чисел

x₀ = 1273·12 = 15276, y₀ = 128·12 = 1536

является решением уравнения 201х – 1999у = 12.

Общее решение этого уравнения запишется в виде

х = 15276 + 1999k, у = 1536 + 201k, где k – целое число,

или, после переобозначения (используем, что 15276 = 1283 + 7·1999, 1536 = 129 + 7·201),

х = 1283 + 1999n, у = 129 + 201n, где n – целое число.

Ответ: (1283+1999n, 129+201n), где n – целое число.

3. Решить в целых числах уравнение:

а) x 3 + y 3 = 3333333;

б) x 3 + y 3 = 4(x 2 y + xy 2 + 1).

а) Так как x 3 и y 3 при делении на 9 могут давать только остатки 0, 1 и 8 (смотрите таблицу в разделе «Делимость целых чисел и остатки»), то x 3 + y 3 может давать только остатки 0, 1, 2, 7 и 8. Но число 3333333 при делении на 9 даёт остаток 3. Поэтому исходное уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

б) Перепишем исходное уравнение в виде (x + y) 3 = 7(x 2 y + xy 2 ) + 4. Так как кубы целых чисел при делении на 7 дают остатки 0, 1 и 6, но не 4, то уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

а) в простых числах уравнение х 2 – 7х – 144 = у 2 – 25у;

б) в целых числах уравнение x + y = x 2 – xy + y 2 .

а) Решим данное уравнение как квадратное относительно переменной у. Получим

у = х + 9 или у = 16 – х.

Поскольку при нечётном х число х + 9 является чётным, то единственной парой простых чисел, которая удовлетворяет первому равенству, является (2; 11).

Так как х, у – простые, то из равенства у = 16 – х имеем

С помощью перебора вариантов находим остальные решения: (3; 13), (5; 11), (11; 5), (13; 3).

Ответ: (2; 11), (3; 13), (5; 11), (11; 5), (13; 3).

б) Рассмотрим данное уравнение как квадратное уравнение относительно x:

x 2 – (y + 1)x + y 2 – y = 0.

Дискриминант этого уравнения равен –3y 2 + 6y + 1. Он положителен лишь для следующих значений у: 0, 1, 2. Для каждого из этих значений из исходного уравнения получаем квадратное уравнение относительно х, которое легко решается.

Ответ: (0; 0), (0; 1), (1; 0), (1; 2), (2; 1), (2; 2).

5. Существует ли бесконечное число троек целых чисел x, y, z таких, что x 2 + y 2 + z 2 = x 3 + y 3 + z 3 ?

Попробуем подбирать такие тройки, где у = –z. Тогда y 3 и z 3 будут всегда взаимно уничтожаться, и наше уравнение будет иметь вид

Чтобы пара целых чисел (x; y) удовлетворяла этому условию, достаточно, чтобы число x–1 было удвоенным квадратом целого числа. Таких чисел бесконечно много, а именно, это все числа вида 2n 2 +1. Подставляя в x 2 (x–1) = 2y 2 такое число, после несложных преобразований получаем:

y = xn = n(2n 2 +1) = 2n 3 +n.

Все тройки, полученные таким образом, имеют вид (2n 2 +1; 2n 3 +n; –2n 3 – n).

6. Найдите такие целые числа x, y, z, u, что x 2 + y 2 + z 2 + u 2 = 2xyzu.

Число x 2 + y 2 + z 2 + u 2 чётно, поэтому среди чисел x, y, z, u чётное число нечётных чисел.

Если все четыре числа x, y, z, u нечётны, то x 2 + y 2 + z 2 + u 2 делится на 4, но при этом 2xyzu не делится на 4 – несоответствие.

Если ровно два из чисел x, y, z, u нечётны, то x 2 + y 2 + z 2 + u 2 не делится на 4, а 2xyzu делится на 4 – опять несоответствие.

Поэтому все числа x, y, z, u чётны. Тогда можно записать, что

и исходное уравнение примет вид

Теперь заметим, что (2k + 1) 2 = 4k(k + 1) + 1 при делении на 8 даёт остаток 1. Поэтому если все числа x₁, y₁, z₁, u₁ нечётны, то x₁ 2 + y₁ 2 + z₁ 2 + u₁ 2 не делится на 8. А если ровно два из этих чисел нечётно, то x₁ 2 + y₁ 2 + z₁ 2 + u₁ 2 не делится даже на 4. Значит,

и мы получаем уравнение

Снова повторив те же самые рассуждения, получим, что x, y, z, u делятся на 2 n при всех натуральных n, что возможно лишь при x = y = z = u = 0.

7. Докажите, что уравнение

(х – у) 3 + (y – z) 3 + (z – x) 3 = 30

не имеет решений в целых числах.

Воспользуемся следующим тождеством:

(х – у) 3 + (y – z) 3 + (z – x) 3 = 3(х – у)(y – z)(z – x).

Тогда исходное уравнение можно записать в виде

(х – у)(y – z)(z – x) = 10.

Обозначим a = x – y, b = y – z, c = z – x и запишем полученное равенство в виде

Кроме того очевидно, a + b + c = 0. Легко убедиться, что с точностью до перестановки из равенства abc = 10 следует, что числа |a|, |b|, |c| равны либо 1, 2, 5, либо 1, 1, 10. Но во всех этих случаях при любом выборе знаков a, b, c сумма a + b + c отлична от нуля. Таким образом, исходное уравнение не имеет решений в целых числах.

8. Решить в целых числах уравнение 1! + 2! + . . . + х! = у 2 .

если х = 1, то у 2 = 1,

если х = 3, то у 2 = 9.

Этим случаям соответствуют следующие пары чисел:

Заметим, что при х = 2 имеем 1! + 2! = 3, при х = 4 имеем 1! + 2! + 3! + 4! = 33 и ни 3, ни 33 не являются квадратами целых чисел. Если же х > 5, то, так как

5! + 6! + . . . + х! = 10n,

можем записать, что

1! + 2! + 3! + 4! + 5! + . . . + х! = 33 + 10n.

Так как 33 + 10n – число, оканчивающееся цифрой 3, то оно не является квадратом целого числа.

Ответ: (1; 1), (1; –1), (3; 3), (3; –3).

9. Решите следующую систему уравнений в натуральных числах:

a 3 – b 3 – c 3 = 3abc, a 2 = 2(b + c).

3abc > 0, то a 3 > b 3 + c 3 ;

таким образом имеем

b 2 2 + х = у 4 + у 3 + у 2 + у.

Разложив на множители обе части данного уравнения, получим:

х(х + 1) = у(у + 1)(у 2 + 1),

х(х + 1) = (у 2 + у)(у 2 + 1)

Такое равенство возможно, если левая и правая части равны нулю, или представляют собой произведение двух последовательных целых чисел. Поэтому, приравнивая к нулю те или иные множители, получим 4 пары искомых значений переменных:

Произведение (у 2 + у)(у 2 + 1) можно рассматривать как произведение двух последовательных целых чисел, отличных от нуля, только при у = 2. Поэтому х(х + 1) = 30, откуда х₅ = 5, х₆ = –6. Значит, существуют ещё две пары целых чисел, удовлетворяющих исходному уравнению:

Ответ: (0; 0), (0; –1), (–1; 0), (–1; –1), (5; 2), (–6; 2.)

Задачи без решений

1. Решить в целых числах уравнение:

б) х 2 + у 2 = х + у + 2.

2. Решить в целых числах уравнение:

а) х 3 + 21у 2 + 5 = 0;

б) 15х 2 – 7у 2 = 9.

3. Решить в натуральных числах уравнение:

4. Доказать, что уравнение х 3 + 3у 3 + 9z 3 = 9xyz в рациональных числах имеет единственное решение

5. Доказать, что уравнение х 2 + 5 = у 3 в целых числах не имеет решений.

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №9. Решение уравнений в целых числах.

Перечень вопросов, рассматриваемых в теме

понятие диофантовых уравнений;
теоремы для решения уравнений в целых числах;
основные методы решения уравнений в целых числах.

Глоссарий по теме

Диофантовыми уравнениями называются уравнения вида

Неопределенные уравнения – уравнения, содержащие более одного неизвестного. Под одним решением неопределенного уравнения понимается совокупность значений неизвестных, которая обращает данное уравнение в верное равенство.

Теорема 1. Если НОД(а, b) = d, то существуют такие целые числа х и у, что имеет место равенство ах + bу = d.

Теорема 2. Если уравнение ах + bу = 1, если НОД(а, b) = 1, достаточно представить число 1 в виде линейной комбинации чисел а и b.

Теорема 3. Если в уравнении ах + bу = с НОД(а, b) = d>1 и с не делится на d, то уравнение целых решений не имеет.

Теорема 4. Если в уравнении ах + bу = с НОД(а, b) = d>1 и с 1 и с не делится на d, то уравнение целых решений не имеет.

Для доказательства теоремы достаточно предположить противное.

Найти целое решение уравнения 16х – 34у = 7.

(16,34)=2; 7 не делится на 2, уравнение целых решений не имеет.

Теорема 4. Если в уравнении ах + bу = с НОД(а, b) = d>1 и с 2 + 23 = у 2

Перепишем уравнение в виде: у 2 – х 2 = 23, (у – х)(у + х) = 23

Так как х и у – целые числа и 23 – простое число, то возможны случаи:

; ; ; ;

Решая полученные системы, находим:

; ;;;

4. Выражение одной переменной через другую и выделение целой части дроби.

Решить уравнение в целых числах: х 2 + ху – у – 2 = 0.

Выразим из данного уравнения у через х:

Так как х, у – целые числа, то дробь должна быть целым числом.

Это возможно, если х – 1 =

; ;

; ;

5. Методы, основанные на выделении полного квадрата.

Найдите все целочисленные решения уравнения: х 2 – 6ху + 13у 2 = 29.

Преобразуем левую часть уравнения, выделив полные квадраты,

х 2 – 6ху + 13у 2 = (х 2 – 6ху + 9у 2 ) + 4у 2 = (х – 3у) 2 + (2у) 2 = 29, значит (2у) 2 29.

Получаем, что у может быть равен .

1. у = 0, (х – 0) 2 = 29. Не имеет решений в целых числах.

2. у = -1, (х + 3) 2 + 4 =29, (х + 3) 2 = 25, х + 3 = 5 или х + 3 = -5

3. у = 1, (х – 3) 2 +4 =29,

(х – 3) 2 =25, х – 3 = 5 или х – 3 = -5

4. у = -2, (х + 6) 2 + 16 = 29, (х + 6) 2 = 13. Нет решений в целых числах.

5. у=2, (х-6) 2 +16=29, (х-6) 2 =13. Нет решений в целых числах.

Ответ: (2; -1); (-8; -1); (8; 1); (-2; 1).

6. Решение уравнений с двумя переменными как квадратных

относительно одной из переменных.

Решить уравнение в целых числах: 5х 2 +5у 2 +8ху+2у-2х+2=0.

Рассмотрим уравнение как квадратное относительно х:

5х 2 + (8у – 2)х + 5у 2 + 2у + 2 = 0

D = (8у – 2) 2 – 4·5(5у 2 + 2у + 2) = 64у 2 – 32у + 4 = -100у 2 – 40у – 40= = -36(у 2 + 2у + 1) = -36(у + 1) 2

Для того, чтобы уравнение имело решения, необходимо, чтобы D = 0.

-36(у + 1) 2 = 0. Это возможно при у = -1, тогда х = 1.

7. Оценка выражений, входящих в уравнение.

Решить в целых числах уравнение:

(х 2 + 4)(у 2 + 1) = 8ху

Заметим, что если – решение уравнения, то – тоже решение.

И так как х = 0 и у = 0 не являются решением уравнения, то, разделив обе части уравнения на ху, получим:

,

Пусть х > 0, у > 0, тогда, согласно неравенству Коши,

,

тогда их произведение , значит,

Отсюда находим х = 2 и у = 1 – решение, тогда х = -2 и у = -1 – тоже решение.

8.Примеры уравнений второй степени с тремя неизвестными.

Рассмотрим уравнение второй степени с тремя неизвестными: х 2 + у 2 = z 2 .

Геометрически решение этого уравнения в целых числах можно истолковать как нахождение всех пифагоровых треугольников, т.е. прямоугольник треугольников, у которых и катеты х,у и гипотенуза z выражаются целыми числами.

По формуле х = uv, , где u и v – нечетные взаимно простые числа (u > v > 0) можно найти те решения уравнения х 2 + у 2 = z 2 , в которых числа х,у и z не имеют общих делителей (т.е. взаимно простые).

Для начальных значений u и v формулы приводят к следующим часто встречающимся равенствам:

3 2 + 4 2 = 5 2 (u = 1, v = 3), 5 2 + 12 2 = 13 2 (u = 1, v = 5), 15 2 + 8 2 = 17 2 (u = 3, v = 5)

Все остальные целые положительные решения этого уравнения получаются умножением решений, содержащихся в формулах, на произвольный общий множитель а.

Разбор решения заданий тренировочного модуля

№1. Тип задания: выбор элемента из выпадающего списка

Решите уравнение 9х+22у-1=0

Решение: Решим данное уравнение, воспользовавшись теоремой 2:

2. 1 = 9 – 4∙2 = 9 – (22 – 9∙2) ∙2 = 9∙5 + 22∙(-2),

т.е. х₀= 5, у₀= -2 – решение данного уравнения

№2. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.

Найдите целое решение уравнения 3х+9у=3

Решение: Решим данное уравнение: 3х+9у=3

Разделим обе части уравнения на 3, получим:

3 = 1 ∙ 2 + 1

1 = 3 – 1∙2, т.е. х₀= 1, у₀= 0 – решение данного уравнения

Основные методы решения уравнений в целых числах

Введение

Существует множество математических задач, ответами к которым служат одно или несколько целых чисел. В качестве примера можно привести четыре классические задачи, решаемые в целых числах – задача о взвешивании, задача о разбиении числа, задача о размене и задача о четырёх квадратах. Стоит отметить, что, несмотря на достаточно простую формулировку этих задач, решаются они весьма сложно, с применением аппарата математического анализа и комбинаторики. Идеи решения первых двух задач принадлежат швейцарскому математику Леонарду Эйлеру (1707–1783). Однако наиболее часто можно встретить задачи, в которых предлагается решить уравнение в целых (или в натуральных) числах. Некоторые из таких уравнений довольно легко решаются методом подбора, но при этом возникает серьёзная проблема – необходимо доказать, что все решения данного уравнения исчерпываются подобранными (то есть решений, отличных от подобранных, не существует). Для этого могут потребоваться самые разнообразные приёмы, как стандартные, так и искусственные. Анализ дополнительной математической литературы показывает, что подобные задания достаточно часто встречаются в олимпиадах по математике разных лет и различных уровней, а также в задании 19 ЕГЭ по математике (профильный уровень). В то же время в школьном курсе математики данная тема практически не рассматривается, поэтому школьники, участвуя в математических олимпиадах или сдавая профильный ЕГЭ по математике, обычно сталкиваются со значительными трудностями при выполнении подобного рода заданий. В связи с этим целесообразно выделить систему основных методов решения уравнений в целых числах, тем более что в изученной математической литературе этот вопрос явно не оговаривается. Описанная проблема определила цель данной работы: выделить основные методы решения уравнений в целых числах. Для достижения поставленной цели необходимо было решить следующие задачи:

1) Проанализировать олимпиадные материалы, а также материалы профильного ЕГЭ по математике;

2) Обозначить методы решения уравнений в целых числах и выделить преобладающие;

3) Полученные результаты проиллюстрировать примерами;

4) Составить несколько тренировочных заданий по данной теме;

5) Применяя разработанные задания, определить степень готовности учащихся девятых классов МБОУ СОШ №59 к решению подобного рода задач и сделать практические выводы.

Основная часть

Анализ разнообразной математической литературы показывает, что среди методов решения уравнений в целых числах в качестве основных можно выделить следующие:

Представление уравнения в виде произведения нескольких множителей, равного некоторому целому числу;

Представление уравнения в виде суммы квадратов нескольких слагаемых, равной некоторому целому числу;

Использование свойств делимости, факториалов и точных квадратов;

Использование Малой и Великой теорем Ферма;

Метод бесконечного спуска;

Выражение одной неизвестной через другую;

Решение уравнения как квадратного относительно одной из неизвестных;

Рассмотрение остатков от деления обеих частей уравнения на некоторое число.

Сразу же нужно оговорить, что мы понимаем под основными методами решения уравнений. Основными будем называть наиболее часто применяющиеся методы, что, конечно, не исключает возможности периодического применения новых «неожиданных» приёмов. Кроме того, причём в подавляющем большинстве случаев, применяют их различные сочетания, то есть проводят комбинирование нескольких методов.
В качестве примера сочетания методов рассмотрим уравнение, предлагавшееся на ЕГЭ по математике в 2013 году (задание С6).

Задача. Решить в натуральных числах уравнение n! + 5n + 13 = k 2 .

Решение. Заметим, что оканчивается нулём при n > 4. Далее, при любых n ∈ N оканчивается либо цифрой 0, либо цифрой 5. Следовательно, при n > 4 левая часть уравнения оканчивается либо цифрой 3, либо цифрой 8. Но она же равна точному квадрату, который не может оканчиваться этими цифрами. Поэтому нужно перебрать только четыре варианта: n = 1, n = 2, n = 3, n = 4.

Значит, уравнение имеет единственное натуральное решение n = 2, k = 5.

В этой задаче использовались свойства точных квадратов, свойства факториалов, и остатки от деления обеих частей уравнения на 10.

Теперь приведём комплекс авторских задач.

Задача 1. Решить в целых числах уравнение n 2 – 4y! = 3.

Решение. Сначала перепишем исходное уравнение в виде n 2 = 4y! + 3. Если посмотреть на это соотношение с точки зрения теоремы о делении с остатком, то можно заметить, что точный квадрат, стоящий в левой части уравнения, даёт при делении на 4 остаток 3, что невозможно. Действительно, любое целое число представимо в одном из следующих четырёх видов:

Таким образом, точный квадрат при делении на 4 даёт в остатке либо 0, либо 1. Следовательно, исходное уравнение не имеет решений.

Ключевая идея – применение свойств точных квадратов.

Задача 2. Решить в целых числах уравнение 8z 2 = (t!) 2 + 2.

Решение. Непосредственная проверка показывает, что t = 0 и t = 1 не являются решениями уравнения. Если t > 1, то t! является чётным числом, то есть, оно представимо в виде t! = 2s. В таком случае уравнение можно преобразовать к виду 4z 2 = 2s 2 + 1. Однако, полученное уравнение заведомо не имеет решений, ибо в левой части стоит чётное число, а в правой – нечётное.

Ключевая идея – применение свойств факториалов.

Задача 3. Решить в целых числах уравнение x 2 + y 2 – 2x + 6y + 5 = 0.

Решение. Исходное уравнение можно переписать следующим образом: (x – 1) 2 + (y + 3) 2 = 5.

Из условия следует, что (x – 1), (y + 3) – целые числа. Следовательно, данное уравнение эквивалентно следующей совокупности:

Теперь можно выписать всевозможные целые решения уравнения.

Задача 4. Решить в целых числах уравнение zt + t – 2z = 7.

Решение. Исходное уравнение можно преобразовать к виду (z + 1) (t – 2) = 5. Числа (z + 1), (t – 2) являются целыми, поэтому имеют место следующие варианты:

Итак, уравнение имеет ровно четыре целых решения.

Ключевая идея – представление уравнения в виде произведения, равного целому числу.

Задача 5. Решить в целых числах уравнение n(n + 1) = (2k + 1)‼

Решение. Число (2k + 1)‼ нечётно при всех неотрицательных значениях k согласно определению (при отрицательных k оно вообще не определено). С другой стороны, оно равно числу n(n + 1), которое чётно при всех целых значениях k. Противоречие.

Ключевая идея – использование чётности/нечётности частей уравнения.

Задача 6. Решить в целых числах уравнение xy + x + 2y = 1.

Решение. Путём преобразований уравнение можно свести к следующему:

Данное преобразование не изменило ОДЗ неизвестных, входящих в уравнение, так как подстановка y = –1 в первоначальное уравнение приводит к абсурдному равенству –2 = 1. Согласно условию, x – целое число. Иначе говоря, тоже целое число. Но тогда число обязано быть целым. Дробь является целым числом тогда и только тогда, когда числитель делится на знаменатель. Делители числа 3: 1,3 –1, –3. Следовательно, для неизвестной возможны четыре случая: y = 0, y = 2, y = –2, y = –4. Теперь можно вычислить соответствующие значения неизвестной x. Итак, уравнение имеет ровно четыре целых решения: (–5;0), (–5;2), (1;–2), (1;–4).

Ключевая идея – выражение одной неизвестной через другую.

Задача 7. Решить в целых числах уравнение 5 m = n 2 + 2.

Решение. Если m = 0, то уравнение примет вид n 2 = –1. Оно не имеет целых решений. Если m 0. Тогда правая часть уравнения (как и левая) будет кратна 5. Но в таком случае n 2 при делении на 5 должно давать остаток 3, что невозможно (это доказывается методом перебора остатков, который был изложен при решении задачи 1). Следовательно, данное уравнение не имеет решений в целых числах.

Ключевая идея – нахождение остатков от деления обеих частей уравнения на некоторое натуральное число.

Задача 8. Решить в целых числах уравнение (x!) 4 + (y – 1) 4 = (z + 1) 4 .

Решение. Заметим, что в силу чётности показателей степеней уравнение эквивалентно следующему: (x!) 4 + |y – 1| 4 = |z + 1| 4 . Тогда x!, |y – 1|, |z + 1| – натуральные числа. Однако, согласно Великой теореме Ферма, эти натуральные числа не могут удовлетворять исходному уравнению. Таким образом, уравнение неразрешимо в целых числах.

Ключевая идея – использование Великой теоремы Ферма.

Задача 9. Решить в целых числах уравнение x 2 + 4y 2 = 16xy.

Решение. Из условия задачи следует, что x – чётное число. Тогда x 2 = 4x₁ 2 . Уравнение преобразуется к виду x₁ 2 + y 2 = 8x₁y. Отсюда вытекает, что числа x₁, y имеют одинаковую чётность. Рассмотрим два случая.

1 случай. Пусть x₁, y – нечётные числа. Тогда x₁ = 2t + 1, y = 2s + 1. Подставляя эти выражения в уравнение, получим:

Выполним соответствующие преобразования:

Сокращая обе части полученного уравнения на 2, получим?

В левой части стоит нечётное число, а в правой – чётное. Противоречие. Значит, 1 случай невозможен.

2 случай. Пусть x₁, y – чётные числа. Тогда x₁ = 2x₂ + 1, y = 2y₁. Подставляя эти значения в уравнение, получим:

Таким образом, получилось уравнение, точно такое же, как на предыдущем шаге. Исследуется оно аналогично, поэтому на следующем шаге получим уравнение и т.д. Фактически, проводя эти преобразования, опирающиеся на чётность неизвестных, мы получаем следующие разложения: . Но величины n и k не ограничены, так как на любом шаге (со сколь угодно большим номером) будем получать уравнение, эквивалентное предыдущему. То есть, данный процесс не может прекратиться. Другими словами, числа x, y бесконечно много раз делятся на 2. Но это имеет место, только при условии, что x = y = 0. Итак, уравнение имеет ровно одно целое решение (0; 0).

Ключевая идея – использование метода бесконечного спуска.

Задача 10. Решить в целых числах уравнение 5x 2 – 3xy + y 2 = 4.

Решение. Перепишем данное уравнение в виде 5x 2 – (3x)y + (y 2 – 4) = 0. Его можно рассмотреть как квадратное относительно неизвестной x. Вычислим дискриминант этого уравнения:

Для того чтобы уравнение имело решения, необходимо и достаточно, чтобы , то есть Отсюда имеем следующие возможности для y: y = 0, y = 1, y = –1, y = 2, y = –2.

Итак, уравнение имеет ровно 2 целых решения: (0;2), (0;–2).

Ключевая идея – рассмотрение уравнения как квадратного относительно одной из неизвестных.

Составленные автором задачи были использованы при проведении эксперимента, который состоял в следующем. Всем учащимся девятых классов были предложены разработанные задания с целью выявления уровня подготовки детей по данной теме. Каждому из учеников необходимо было предложить метод нахождения целочисленных решений уравнений. В эксперименте приняли участие 64 ученика. Полученные результаты представлены в таблице 1.

ТАБЛИЦА 1

Количество учащихся, справившихся с заданием (в процентах)

[spoiler title=”источники:”]

http://resh.edu.ru/subject/lesson/4728/conspect/

http://urok.1sept.ru/articles/671157

[/spoiler]

Источник

МБОУ «Высокогорская средняя общеобразовательная школа №2

Высокогорского муниципального района Республики Татарстан»

Олимпиадные задания.

Решение уравнений в целых числах

Разработала:

Аксанова Ильсияр Исмагиловна

Учитель математики высшей категории

МБОУ ВСОШ № 2

С. Высокая Гора – 2015 г.

Введение

Работа посвящена решению уравнений в целых числах. Актуальность этой темы обусловлена тем, что задачи, основанные на решении уравнений в целых числах, часто встречаются на вступительных экзаменах в высшие учебные заведения и на олимпиадах по математике и на ЕГЭ в старших классах. В школьной программе эта тема рассматривается в ознакомительном порядке. В работе представлены различные способы решения уравнений в целых числах, разобраны конкретные примеры. Данная работа будет полезна учителям старших классов для подготовки к ЕГЭ и олимпиадам.

Уравнения в целых числах – это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами. Решениями такого уравнения являются все целочисленные наборы значений неизвестных переменных, удовлетворяющих этому уравнению. Такие уравнения ещё называют диофантовыми, в честь древнегреческого математика Диофанта Аксандрийского, который исследовал некоторые типы таких уравнений ещё до нашей эры.

Наиболее известное уравнение в целых числах – великая теорема Ферма: уравнение

xn + yn = zn

не имеет ненулевых рациональных решений для всех натуральных n > 2.

При решении уравнений в целых и натуральных числах можно условно выделить следующие способы решения:

способ перебора вариантов;
применение алгоритма Евклида;
применение цепных дробей;
разложения на множители;
решение уравнений в целых числах как квадратных относительно какой-либо переменной;
метод остатков;
метод бесконечного спуска;
оценка выражений, входящих в уравнение.

В работе представлены два приложения: приложение 1. Таблица остатков при делении степеней (an:m); приложение 2. Задачи для самостоятельного решения

1. Способ перебора вариантов.

Пример 1.1. Найти множество всех пар натуральных чисел, которые являются решениями уравнения 49х + 51у = 602.

Решение. Выразим из уравнения переменную х через у х =, так как х и у – натуральные числа, то

х = 602 – 51у ≥ 49, 51у≤553, 1≤у≤10.

Полный перебор вариантов показывает, что натуральными решениями уравнения являются х=5, у=7.

Ответ: (5;7).

2. Применение алгоритма Евклида. Теорема.

Дано уравнение ax+by=c, где a, b, c-целые числа, a и b не равны 0.

Теорема: Если c не делится нацело на НОД(a,b), то уравнение не разрешимо в целых числах. Если НОД(a,b)=1или c делится на НОД(a,b), то уравнение разрешимо в целых числах. Если (x0, y0 )- какое-нибудь решение уравнения, то все решения уравнения задаются формулами:

x=x0-bt

y=y0+at , где t– принадлежит множеству целых чисел.

Пример 2.1. Решить уравнение в целых числах 5х + 7у = 19

Подберём сначала некоторое конкретное решение. В данном случае, это просто, например,

x0 = 1, y0 = 2.

Тогда 5x0 + 7y0 = 19, откуда

5(х – x0) + 7(у – y0) = 0,

5(х – x0) = –7(у – y0).

Поскольку числа 5 и 7 взаимно простые, то

х – x0 = 7k, у – y0 = –5k.

Значит, общее решение:

х = 1 + 7k, у = 2 – 5k,

где k – произвольное целое число.

Ответ: (1+7k; 2–5k), где k – целое число.

Пример 2.2. Решить уравнение 201х – 1999у = 12.

Найти некоторое конкретное решение подбором в данном случае достаточно сложно. Воспользуемся алгоритмом Евклида для чисел 1999 и 201:

НОД(1999, 201) = НОД(201, 190) = НОД(190, 11) = НОД(11, 3) = НОД(3 , 2) = НОД(2, 1) = 1.

Запишем этот процесс в обратном порядке:

1 = 2 – 1 = 2 – (3 – 2) = 2·2 – 3 = 2· (11 – 3·3) – 3 = 2·11 – 7·3 = 2·11 – 7(190 – 11·17) =

= 121·11 – 7·190 = 121(201 – 190) – 7·190 = 121·201 – 128·190 =

= 121·201 – 128(1999 – 9·201) = 1273·201 – 128·1999.

Значит, пара (1273, 128) является решением уравнения 201х – 1999у = 1. Тогда пара чисел

x0 = 1273·12 = 15276, y0 = 128·12 = 1536

является решением уравнения 201х – 1999у = 12.

Общее решение этого уравнения запишется в виде

х = 15276 + 1999k, у = 1536 + 201k, где k – целое число,

или, используя, что 15276 = 1283 + 7·1999, 1536 = 129 + 7·201, имеем

х = 1283 + 1999n, у = 129 + 201n, где n – целое число.

Ответ: (1283+1999n, 129+201n), где n – целое число.

3. Метод остатков.

Этот метод основан на исследовании возможных остатков левой и правой частей уравнения от деления на некоторое фиксированное натуральное число.

Замечание. Говоря строго математическим языком, для решения уравнения в данном случае применяется теория сравнений.

Рассмотрим примеры, которые раскрывают сущность данного метода.

Пример 3.1. Решить уравнение в целых числах x3 + y3 = 3333333;

Так как x3 и y3 при делении на 9 могут давать только остатки 0, 1 и 8 (смотрите таблицу в приложении 1), то x3 + y3 может давать только остатки 0, 1, 2, 7 и 8. Но число 3333333 при делении на 9 даёт остаток 3. Поэтому исходное уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

Пример 3.2. Решить уравнение в целых числах x3 + y3 = 4(x2y + xy2 + 1).

Перепишем исходное уравнение в виде (x + y)3 = 7(x2y + xy2) + 4. Так как кубы целых чисел при делении на 7 дают остатки 0, 1 и 6, но не 4, то уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

Пример 3.3. Решить в целых числах уравнение x2 + 1 = 3y.

Решение. Заметим, что правая часть уравнения делится на 3 при любом целом y.

Исследуем какие остатки может иметь при делении на три левая часть этого уравнения.По теореме о делении с остатком целое число х либо делится на 3, либо при делении на три в остатке дает 1 или 2.

Если х = 3k, то правая часть уравнения на 3 не делится.

Если х = 3k+1, то x2 + 1= (3k+1)2+1=3m+2, следовательно, опять левая часть на 3 не делится.

Если х = 3k+2, то x2 + 1= (3k+2)2+1=3m+2, следовательно, и в этом случае левая часть уравнения на три не делится.

Таким образом, мы получили, что ни при каких целых х левая часть уравнения на 3 не делится, при том, что левая часть уравнения делится на три при любых значениях переменной y. Следовательно, уравнение в целых числах решений не имеет.

Ответ: целочисленных решений нет.

Пример 3.4. Решить в целых числах x³ – 3y³ – 9z³ = 0 (1)

Решение. Очевидно, что решением уравнения будет тройка чисел (0; 0; 0).

Выясним, имеет ли уравнение другие решения. Для этого преобразуем уравнение (1) к виду

x³ = 3y³ + 9z³ (2)

Так как правая часть полученного уравнения делится на 3, то и левая должна делиться на три, следовательно, так как 3 – число простое, х делится на 3, т.е. х = 3k, подставим это выражение в уравнение (2), получим:

27k3 = 3y³ + 9z³, откуда

9k3 = y³ + 3z³ (3)

следовательно, y³ делится на 3 и y = 3m. Подставим полученное выражение в уравнение (3): 9k3 = 27m³ + 3z³, откуда

3k3 = 9m³ + z³ (4)

В свою очередь, из этого уравнения следует, что z3 делится на 3, и z = 3n. Подставив это выражение в (4), получим, что k3 должно делиться на 3.

Итак, оказалось, что числа, удовлетворяющие первоначальному уравнению, кратны трём, и сколько раз мы не делили бы их на 3, опять должны получаться числа, кратные трём. Единственное целое число, удовлетворяющее этому условию, будет нуль, т. е. решение данного уравнения (0; 0; 0) является единственным.

Ответ: (0;0;0).

4. Решение уравнений в целых числах сведением их к квадратным.

Пример 4.1. Решить в простых числах уравнение

х2 – 7х – 144 = у2 – 25у.

Решим данное уравнение как квадратное относительно переменной у. Получим: у = х + 9 или у = 16 – х.

Так как х, у – простые, то из равенства у = 16 – х, имеем

2 < х < 16, 2 < у < 16.

С помощью перебора вариантов находим остальные решения: (3; 13), (5; 11), (11; 5), (13; 3).

Ответ: (2; 11), (3; 13), (5; 11), (11; 5), (13; 3).

Пример 4.2. Решить в целых числах уравнение x + y = x2 – xy + y2.

Рассмотрим данное уравнение как квадратное уравнение относительно x:

x2 – (y + 1)x + y2 – y = 0.

Дискриминант этого уравнения равен –3y2 + 6y + 1. Он положителен лишь для следующих значений у: 0, 1, 2. Для каждого из этих значений из исходного уравнения получаем квадратное уравнение относительно х, которое легко решается.

Ответ: (0; 0), (0; 1), (1; 0), (1; 2), (2; 1), (2; 2).

Пример 4.3. Решить уравнение в целых числах: 5х2+5у2+8ху+2у-2х+2=0.

Решение:

Рассмотрим уравнение как квадратное относительно х:

5х2 + (8у – 2)х + 5у2 + 2у + 2 = 0

D = (8у – 2)2 – 4·5(5у2 + 2у + 2) = 64у2 – 32у + 4 = -100у2 – 40у – 40 = = -36(у2 + 2у + 1) = -36(у + 1)2

Для того, чтобы уравнение имело решения, необходимо, чтобы D = 0.

-36(у + 1)2 = 0. Это возможно при у = -1, тогда х = 1.

Ответ: (1;-1).

5. Разложение на множители.

Пример 5.1. Решить в целых числах уравнение x2 – xy – 2y2 = 7.

Разложим левую часть на множители (x – 2y)(x + y) = 7.

Так как х, у – целые числа, то находим решения исходного уравнения, как решения следующих четырёх систем:

1) x – 2y = 7, x + y = 1;

2) x – 2y = 1, x + y = 7;

3) x – 2y = –7, x + y = –1;

4) x – 2y = –1, x + y = –7.

Решив эти системы, получаем решения уравнения: (3; –2), (5; 2), (–3; 2) и (–5; –2).

Ответ: (3; –2), (5; 2), (–3; 2), (–5; –2).

Пример 5.2. Решить уравнение в целых числах: х2 + 23 = у2

Решение. Перепишем уравнение в виде:

у2 – х2 = 23, (у – х)(у + х) = 23

Так как х и у – целые числа и 23 – простое число, то возможны случаи:

Решая полученные системы, находим:

Ответ: (-11;12);(11;12);(11;-12);(-11;-12).

Пример 5.3. Решить уравнение в целых числах y3 – x3 = 91.

Решение. Используя формулы сокращенного умножения, разложим правую часть уравнения на множители:

(y – x)(y2 + xy + x2) = 91

Выпишем все делители числа 91: ± 1; ± 7; ± 13; ± 91

Проводим исследование. Заметим, что для любых целых x и y число

y2 + yx + x2 ≥ y2 – 2|y||x| + x2 = (|y| – |x|)2 ≥ 0,

следовательно, оба сомножителя в левой части уравнения должны быть положительными. Тогда уравнение равносильно совокупности систем уравнений:

; ; ;

Решив системы, получим: первая система имеет решения (5; 6), (-6; -5); третья (-3; 4),(-4;3); вторая и четвертая решений в целых числах не имеют.

Ответ: (5; 6); (-6; -5); (-3; 4); (-4;3).

Пример 5.4. Решить в целых числах уравнение x + y = xy.

Решение. Перенесем все члены уравнения влево и к обеим частям полученного уравнения прибавим (–1)

x + y – xy – 1 = – 1

Сгруппируем первое – четвертое и второе – третье слагаемые и вынесем общие множители, в результате получим уравнение: (x – 1)(y – 1) = 1

Произведение двух целых чисел может равняться 1 в том и только в том случае, когда оба этих числа равны или 1, или (–1). Записав соответствующие системы уравнений и, решив их, получим решение исходного уравнения.

Ответ: (0,0) и (2,2).

Пример 5.5. Доказать, что уравнение (x – y)3 + (y – z)3 + (z – x)3 = 30 не имеет решений в целых числах.

Решение. Разложим левую часть уравнения на множители и обе части уравнения разделим на 3, в результате получим уравнение:

(x – y)(y – z)(z – x) = 10

Делителями 10 являются числа ±1, ±2, ±5, ±10. Заметим также, что сумма сомножителей левой части уравнения равна 0. Нетрудно проверить, что сумма любых трех чисел из множества делителей числа 10, дающих в произведении 10, не будет равняться 0. Следовательно, исходное уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

6. Метод бесконечного спуска.

Метод спуска предполагает сначала последовательное выражение одной переменой чрез другую, пока в представлении переменной не останется дробей, а затем, последовательное «восхождение» по цепочке равенств для получения общего решения уравнения.

Пример 6.1. Решить уравнение в целых числах 5x + 8y = 39.

Выберем неизвестное, имеющее наименьший коэффициент , и выразим его через другое неизвестное: . Выделим целую часть: Очевидно, что х будет целым, если выражение окажется целым, что, в свою очередь, будет иметь место тогда, когда число 4 – 3y без остатка делится на 5.

Введем дополнительную целочисленную переменную z следующим образом: 4 –3y = 5z. В результате получим уравнение такого же типа, как и первоначальное, но уже с меньшими коэффициентами. Решать его будем уже относительно переменной y, рассуждая аналогично: . Выделяя целую часть, получим:

Рассуждая аналогично предыдущему, вводим новую переменную

u: 3u = 1 – 2z.

Выразим неизвестную с наименьшим коэффициентом, в этом случае переменную z: = . Требуя, чтобы было целым, получим: 1 – u = 2v, откуда u = 1 – 2v. Дробей больше нет, спуск закончен.

Теперь необходимо «подняться вверх». Выразим через переменную v сначала z, потом y и затем x:

z = = = 3v – 1; = 3 – 5v.

= = 3+8v.

Формулы x = 3+8v и y = 3 – 5v, где v – произвольное целое число, представляют общее решение исходного уравнения в целых числах.

Ответ: x = 3+8v и y = 3 – 5v.

7. Оценка выражений, входящих в уравнение.

Пример 7.1. Решить в целых числах уравнение (х2 + 4)(у2 + 1) = 8ху

Решение. Заметим, что если (х;у) – решение уравнения, то (-х;-у) – тоже решение.

И так как х = 0 и у = 0 не являются решением уравнения, то, разделив обе части уравнения на ху, получим:

∙ = 8, (х +)(у +) = 8.

Пусть х > 0, у > 0, тогда, согласно неравенству Коши,

х + = 4, у + = 2,

тогда их произведение (х + )(у +) = 4·2 = 8, значит, х + = 4 и у + = 2.

Отсюда находим х = 2 и у = 1 – решение, тогда х = -2 и у = -1 – тоже решение.

Ответ: (2;1); (-2;-1)

Пример 7.2. Решить уравнение в целых числах

x2 + 13y2 – 6xy = 100

Решение. x2+13y2–6xy=100 ↔ (x-3y)2+4y2=100. Так как (x-3y)2≥0, то 4y2≤100, или │2y│≤10. Аналогично, в силу 4y2≥0 должно выполняться │x-3y│≤10.

Возможны 12 случаев:

1.	↔	2.	↔

3.	↔	4.	↔

5.	↔	6.	↔

7.	↔	8.	↔

9.	↔	10.	↔

11.	↔	12.	↔

Ответ: (±15; ±5); (±10; ±0); (±18; ±4);

(±6; ±4); (±17; ±3); (±1; ±3).

8. Применение цепных дробей.

Пример 8.1. Решите в целых числах уравнение 25x-18y+1=0.

Найдем наибольший общий делитель пары чисел 25 и 18 с помощью цепных дробей, то есть используем один из вариантов алгоритма Евклида.

Преобразуем неправильную дробь , последовательно выделяя целые части неправильных дробей:

= 1 + = 1 + = 1 + = 1 + = 1 + = 1 + = 1 + ,

где выражение 1+ называется целой дробью.

Числа 1, 2, 1, 1, выделенные в этом выражении, являются последовательными частными алгоритма Евклида для нахождения наибольшего общего делителя пары чисел 25 и18.

Отбросим дробь и преобразуем получившуюся цепную дробь в обыкновенную:

1 + – 1 + – .

Вычтем полученную дробь из исходной дроби :

– = = .

Приведем ее к общему знаменателю: 25 ∙ 5 – 18 ∙ 7 + 1 = 0.

Получили частное решение исходного уравнения х = 5, у = 7.

Общее решение исходного уравнения: х = 5 + 18t; y = 7 + 25t, t Z.

Ответ: х = 5+18t; у = 7+25t.

Приложение 1. Таблица остатков при делении степеней (an:m)

an	2	3	4	5
3	0;1	0;1;2	0;1	0;1;2
4	0;1	0;1;3	0;1	0;1;3
5	0;1;4	0;1;2;3;4	0;1	0;1;2;3;4
6	0;1;3;4	0;1;2;3;4;5	0;1;3;4	0;1;2;3;4;5
7	0;1;2;4	0;1;6	0;1;2;4	0;1;2;3;4;5;6
8	0;1;4	0;1;3;5;7	0;1	0;1;3;5;7
9	0;1;4;7	0;1;8	0;1;4;7	0;1;2;3;4;5;7;8
10	0;1;4;5;6;9	0;1;2;3;4;5;6;7;8;9	0;1;5;6	0;1;2;3;4;5;6;7;8;9

Приложение 2. Задачи для самостоятельного решения

Решить в простых числах уравнение x2 – 2y2 = 1.
Доказать, что уравнение x3 + x + 10y = 20004 неразрешимо в целых числах.
Доказать, что уравнение x5 + 3x4y – 5x3y2 – 15x2y3 + 4xy4 + 12y5 = 33 неразрешимо в целых числах.
Решить в целых числах уравнение 2x3 + xy – 7 = 0.
Доказать, что уравнения не имеют целочисленных решений:

а) y2 = 5x2 + 6; б) x3 = 2 + 3y2

Решить в целых числах уравнения: а) x2 + x = y4 + y3 + y2 + y;

б) x² – y² = 91; в) 2ху = х² + 2y; г) 3x2 +4ху – 7y2 =13

Решите в натуральных числах уравнения:

а) 2х² + 5ху – 12у² = 28; б) х² – 4ху – 5у² = 1996.

Докажите, что система уравнений не имеет решений в целых числах.

Найти все пары целых чисел, удовлетворяющих уравнению

а) x2 = y2+ 2y +13; б) xy = 20 – 3x + y; в) xy + 1 = x + y; г) x2– 3xy + 2y2 = 3

Существуют ли целые числа m и n, удовлетворяющие уравнению

m2 + 1994 = n2

Найти все простые числа, которые одновременно являются суммой двух простых чисел и разностью двух простых чисел.
Докажите, что уравнение x2 – y2 = 30 не имеет решений в целых числах.
Решите уравнение x2 – 2х + y2 – 4y + 5 = 0.
Если первую цифру трехзначного числа увеличить на n, то полученное число будет в n раз больше исходного. Найдите число n и исходное число.
Решить в целых числах уравнение x2 + y2 + z2 = 2xyz.
Решить в целых числах уравнение x2 – 2y2 + 8z = 3.
Решите в натуральных числах систему уравнений:

а) б)

Найдите два натуральных числа, разность квадратов которых равна 45.
Найдите все пары натуральных чисел, удовлетворяющих уравнению:

а) x2 – y2 = 105; б) 2x2 + 5xy – 12y2 = 28

Решите в целых числах уравнение:

а) xy + 3x – 5y = – 3; б) x – y =

Докажите, что система не имеет целочисленных решений

Литература:

1. Бардушкин В.В., Кожухов И.Б., Прокофьев А.А., Фадеичева Т.П. Основы теории делимости чисел. Решение уравнений в целых числах. Факультативный курс. – М.: МГИЭТ(ТУ). 2003. – 224 с.

2. В. Серпинский. О решении уравнений в целых числах. 1961.

3. Карпова И.В. Решение уравнений в целых числах.

4. http://www.fmclass.ru/pic/48503321f105d/uravneniya-v-celyh-chislah.pdf

Образовательный портал «Физ/Мат класс» www.fmclass.ru.

5. http://diofant.na.by/

6. www.a-elita.net/userfiles/File/…/Integer%20solutions_2012_10.pdf

7. http://math4school.ru/uravnenija_v_celih_chislah.html

Источник

Алгебра и начала математического анализа, 10 класс

Урок №9. Решение уравнений в целых числах.

Перечень вопросов, рассматриваемых в теме

понятие диофантовых уравнений;
теоремы для решения уравнений в целых числах;
основные методы решения уравнений в целых числах.

Глоссарий по теме

Диофантовыми уравнениями называются уравнения вида

P(x₁, x₂, …, x_n) = 0,

где P(x₁, …, x_n) – многочлен с целыми коэффициентами.

Теорема 1. Если НОД(а, b) = d, то существуют такие целые числа х и у, что имеет место равенство ах + bу = d.

Теорема 3. Если в уравнении ах + bу = с НОД(а, b) = d>1 и с не делится на d, то уравнение целых решений не имеет.

Теорема 4. Если в уравнении ах + bу = с НОД(а, b) = d>1 и с<d, то оно равносильно уравнению , в котором НОД = 1.

Теорема 5. Если в уравнении ах + bу = с НОД(а, b) = 1, то все целые решения этого уравнения заключены в формулах:

х = + bt, у = -at, где – целое решение уравнения ах + bу = 1,

t – любое целое число.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017. Шабунин М.И., Ткачева М.В., Федорова Н.Е.

Теоретический материал для самостоятельного изучения

Решение в целых числах алгебраических уравнений с целыми коэффициентами более чем с одним неизвестным представляет собой одну из труднейших и древнейших математических задач. Этими задачами много занимались самые выдающиеся математики древности, например, греческий математик Пифагор (VI век до н.э.), александрийский математик Диофант (III век н.э.), П.Ферма(XVII в.), Л.Эйлер(XVIII век), Ж.Л.Лагранж(XVIII век), П.Дирихле(XIX век), К.Гаусс(XIX век), П.Чебышев(XIX в.) и многие другие.

Решение уравнений в целых числах является важной задачей и для современной математики. Теоретический интерес уравнений в целых числах достаточно велик, так как эти уравнения тесно связаны со многими проблемами теории чисел.

Ещё в начальной школе на уроках математики перед нами часто ставили задачу выяснить, при каких допустимых значениях буквы обе части того или иного равенства принимают одинаковые числовые значения. На равенство в этом случае мы смотрели как на уравнение относительно указанной неизвестной величины. В восьмом классе мы познакомились с решением квадратных уравнений с одной переменной. Но, готовясь к олимпиадам, рассматривая контрольно- измерительные материалы Единого государственного экзамена встречаемся с заданиями, в которых предлагали уравнения с двумя переменными.

Диофантовыми уравнениями называются уравнения вида

P(x₁, x₂, …, x_n) = 0,

где P(x₁, …, x_n) – многочлен с целыми коэффициентами.

Применение теории делимости к решению неопределенных уравнений в целых числах.

Для решения в целых числах уравнения вида ах + by = c, где а, b, c – целые числа, отличные от нуля, приведем ряд теоретических положений, которые позволят установить правило решения. Эти положения основаны также на уже известных фактах теории делимости.

Теорема 1. Если НОД(а, b) = d, то существуют такие целые числа х и у, что имеет место равенство ах + bу = d.

(Это равенство называется линейной комбинацией или линейным представлением наибольшего общего делителя двух чисел через сами эти числа.)

Доказательство теоремы основано на использовании равенства алгоритма Евклида для нахождения наибольшего общего делителя двух чисел (наибольший общий делитель выражается через неполные частные и остатки, начиная с последнего равенства в алгоритме Евклида).

Пример.

Найти линейное представление наибольшего общего делителя чисел 1232 и 1672.

Решение.

1. Составим равенства алгоритма Евклида:

1672 = 1232 ∙1 + 440,

1232 = 440 ∙ 2 + 352,

440 = 352 ∙ 1 + 88,

352 = 88 ∙ 4, т.е. (1672,352) = 88.

2) Выразим 88 последовательно через неполные частные и остатки, используя полученные выше равенства, начиная с конца:

88 = 440 – 352∙1 = (1672 – 1232) – (1232 – 1672∙2 + 1232∙2) = 1672∙3 – 1232∙4, т.е. 88 = 1672∙3 + 1232∙(-4).

Справедливость этой теоремы следует из теоремы 1. Таким образом, чтобы найти одно целое решение уравнения ах + bу = 1, если НОД (а, в) = 1, достаточно представить число 1 в виде линейной комбинации чисел а и в.

Пример.

Найти целое решение уравнения 15х + 37у = 1.

Решение.

1. 37 = 15 ∙ 2 + 7,

15 = 7 ∙ 2 + 1.

2. 1 = 15 – 7∙2 = 15 – (37 – 15∙2) ∙2 = 15∙5 + 37∙(-2),

т.е. – решение данного уравнения.

Теорема 3. Если в уравнении ах + bу = с НОД(а, b) = d>1 и с не делится на d, то уравнение целых решений не имеет.

Для доказательства теоремы достаточно предположить противное.

Пример.

Найти целое решение уравнения 16х – 34у = 7.

Решение.

(16,34)=2; 7 не делится на 2, уравнение целых решений не имеет.

Теорема 4. Если в уравнении ах + bу = с НОД(а, b) = d>1 и с<d, то оно равносильно уравнению , в котором НОД = 1.

При доказательстве теоремы следует показать, что произвольное целое решение первого уравнения является также решением второго уравнения и обратно.

Теорема 5. Если в уравнении ах + bу = с НОД(а, b) = 1, то все целые решения этого уравнения заключены в формулах:

х = х₀с + bt, у = y₀c-at, где х₀, y₀ – целое решение уравнения ах + bу = 1,

t – любое целое число.

При доказательстве теоремы следует показать, во-первых, что приведенные формулы действительно дают решения данного уравнения и, во-вторых, что произвольное целое решение этого уравнения заключено в приведенных формулах.

Приведенные теоремы позволяют установить следующее правило решения в целых числах уравнения ах+ bу = с НОД(а, b) = 1:

Находится целое решение уравнения ах + bу = 1 путем представления 1 как линейной комбинации чисел а и b (существуют и другие способы отыскания целых решений этого уравнения, например при использовании цепных дробей);
Составляется общая формула целых решений данного уравнения х = х₀с + bt, у = y₀c – at, где х₀, y₀ – целое решение уравнения ах + bу = 1, t – любое целое число.

Придавая t определенные целые значения, можно получить частные решения данного уравнения: наименьшие по абсолютной величине, наименьшие положительные (если можно) и т.д.

Пример.

Найти целые решения уравнения 407х – 2816у = 33.

Решение.

1. Упрощаем данное уравнение, приводя его к виду 37х – 256у = 3.

2.Решаем уравнение 37х – 256у = 1.

256 = 37∙ 6 + 34,

37 = 34 ∙1 + 3,

34 = 3 ∙11 + 1.

1 = 34 – 3∙11 = 256 – 37∙6 – 11 (37 – 256 + 37∙6) = 256∙12 – 37∙83 =

= 37∙(-83) – 256∙(-12),

т.е. х₀= -83, y₀= -12.

3. Общий вид всех целых решений данного уравнения:

х = -83∙3 – 256t = -249 – 256t,

у = -12∙3 – 37 t = -36 – 37 t.

Положив t = -1, получим х₁= 7, у₁= 1 и общие формулы решений примут вид: х = 7 – 256t, у = 1-37t.

2. Метод полного перебора всех возможных значений переменных,

входящих в уравнение.

Найти множество всех пар натуральных чисел, которые являются решениями уравнения 49х + 51у = 602.

Решение:

Выразим из уравнения переменную х через у , так как х и у – натуральные числа, то

602 – 51у ≥ 49,

51у≤553,

Полный перебор вариантов показывает, что натуральными решениями уравнения являются х=5, у=7.

Ответ: (5;7).

3. Решение уравнений методом разложения на множители.

Диофант наряду с линейными уравнениями рассматривал квадратные и кубические неопределенные уравнения. Решение их, как правило, сложно.

Рассмотрим такой случай, когда в уравнениях можно применить формулу разности квадратов или другой способ разложения на множители.

Решить уравнение в целых числах: х²+ 23 = у²

Решение:

Перепишем уравнение в виде: у²– х²= 23, (у – х)(у + х) = 23

Так как х и у – целые числа и 23 – простое число, то возможны случаи:

; ; ; ;

Решая полученные системы, находим:

; ;;;

Ответ: (-11;12);(11;12);(11;-12);(-11;-12).

4. Выражение одной переменной через другую и выделение целой части дроби.

Решить уравнение в целых числах: х²+ ху – у – 2 = 0.

Решение:

Выразим из данного уравнения у через х:

у(х – 1) =2 – х²,

Так как х, у – целые числа, то дробь должна быть целым числом.

Это возможно, если х – 1 =

; ;

Ответ: (0; -2); (2; -2).

5. Методы, основанные на выделении полного квадрата.

Найдите все целочисленные решения уравнения: х²– 6ху + 13у²= 29.

Решение:

Преобразуем левую часть уравнения, выделив полные квадраты,

х²– 6ху + 13у²= (х²– 6ху + 9у²) + 4у²= (х – 3у)²+ (2у)²= 29, значит (2у)² 29.

Получаем, что у может быть равен .

1. у = 0, (х – 0)²= 29. Не имеет решений в целых числах.

2. у = -1, (х + 3)²+ 4 =29, (х + 3)²= 25, х + 3 = 5 или х + 3 = -5

х=2 х=-8

3. у = 1, (х – 3)²+4 =29,

(х – 3)²=25, х – 3 = 5 или х – 3 = -5

х = 8 х = -2

4. у = -2, (х + 6)²+ 16 = 29, (х + 6)²= 13. Нет решений в целых числах.

5. у=2, (х-6)²+16=29, (х-6)²=13. Нет решений в целых числах.

Ответ: (2; -1); (-8; -1); (8; 1); (-2; 1).

6. Решение уравнений с двумя переменными как квадратных

относительно одной из переменных.

Решить уравнение в целых числах: 5х²+5у²+8ху+2у-2х+2=0.

Решение:

Рассмотрим уравнение как квадратное относительно х:

5х²+ (8у – 2)х + 5у²+ 2у + 2 = 0

D = (8у – 2)²– 4·5(5у²+ 2у + 2) = 64у²– 32у + 4 = -100у²– 40у – 40= = -36(у²+ 2у + 1) = -36(у + 1)²

Для того, чтобы уравнение имело решения, необходимо, чтобы D = 0.

-36(у + 1)²= 0. Это возможно при у = -1, тогда х = 1.

Ответ: (1; -1).

7. Оценка выражений, входящих в уравнение.

Решить в целых числах уравнение:

(х²+ 4)(у²+ 1) = 8ху

Решение:

Заметим, что если – решение уравнения, то – тоже решение.

И так как х = 0 и у = 0 не являются решением уравнения, то, разделив обе части уравнения на ху, получим:

Пусть х > 0, у > 0, тогда, согласно неравенству Коши,

тогда их произведение , значит,

Отсюда находим х = 2 и у = 1 – решение, тогда х = -2 и у = -1 – тоже решение.

Ответ: (2; 1); (-2; -1)

8.Примеры уравнений второй степени с тремя неизвестными.

Рассмотрим уравнение второй степени с тремя неизвестными: х²+ у²= z².

Геометрически решение этого уравнения в целых числах можно истолковать как нахождение всех пифагоровых треугольников, т.е. прямоугольник треугольников, у которых и катеты х,у и гипотенуза z выражаются целыми числами.

По формуле х = uv, , где u и v – нечетные взаимно простые числа (u > v > 0) можно найти те решения уравнения х²+ у²= z², в которых числа х,у и z не имеют общих делителей (т.е. взаимно простые).

Для начальных значений u и v формулы приводят к следующим часто встречающимся равенствам:

3²+ 4²= 5²(u = 1, v = 3), 5²+ 12²= 13²(u = 1, v = 5), 15²+ 8²= 17²(u = 3, v = 5)

Все остальные целые положительные решения этого уравнения получаются умножением решений, содержащихся в формулах, на произвольный общий множитель а.

Разбор решения заданий тренировочного модуля

№1. Тип задания: выбор элемента из выпадающего списка

Решите уравнение 9х+22у-1=0

Выпадающий список:

(-5; 2)
(5; 2)
(-5; -2)
(5; -2)

Решение: Решим данное уравнение, воспользовавшись теоремой 2:

1. 22 = 9 ∙ 2 + 4,

9 = 4 ∙ 2 + 1.

2. 1 = 9 – 4∙2 = 9 – (22 – 9∙2) ∙2 = 9∙5 + 22∙(-2),

т.е. х₀= 5, у₀= -2 – решение данного уравнения

Ответ: 4. (5; -2)

№2. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.

Найдите целое решение уравнения 3х+9у=3

х=____

у=____

Решение: Решим данное уравнение: 3х+9у=3

Разделим обе части уравнения на 3, получим:

х+3у=1

3 = 1 ∙ 2 + 1
1 = 3 – 1∙2, т.е. х₀= 1, у₀= 0 – решение данного уравнения

Ответ: х= 1, у= 0.

Источник

Уравнения в целых числах – уравнения с двумя и более неизвестными переменными и целыми коэффициентами. Решениями таких уравнений являются целые числа. Также такие уравнения называются диофантовыми, в честь древнегреческого математика Диофанта Александрийского, который изучал такие уравнения еще до нашей эры.

При решении уравнений в целых и натуральных числах можно выделить следующие способы.

1 способ. Метод перебора вариантов.

Решим уравнение $ (x-2)(y+3)=4 $ в целых числах.

Так как x и у целые числа, совершим перебор вариантов:

$ {x-2=1;; y+3=4rightarrow;x=3;;y=1\ x-2=4;; y+3=1rightarrow;x=6;;y=-2\ x-2=-1;; y+3=-4rightarrow;x=1;;y=-7\ x-2=-4;; y+3=-1rightarrow;x=-2;;y=-4\ x-2=2;; y+3=2rightarrow;x=4;;y=-1\ x-2=-2;; y+3=-2rightarrow;x=0;;y=-5\} $

Ответ: (3; 1), (6; -2), (1; -7), (-2; -4), (4; -1), (0; -5).

Решим уравнение 10х + 10у = 2019 в целых числах.

Поскольку при любых целых значениях х и у левая часть уравнения делится на два, а правая является нечётным числом, то уравнение не имеет решений в целых числах.

Ответ: решений нет.

Пусть нужно решить уравнение в целых числах: $ 5x+4y=22. $

Методом перебора находим решение $ x_1=2;;y_1=3. $

Получаем систему уравнений:

$ {begin{cases}5x=4y=22\5cdot2=4cdot3=22end{cases}\ 5(x-2)=4(y-3)=0\ 5(x-2)=-4(y-3)} $

$ x-2=frac{-4(y-3)}{5} $

Из полученного равенства видно, что число (х – 2) будет целым тогда и только тогда, когда (у – 3) делится на 5, т.е. у – 3 = 5n, где n какое-нибудь целое число.

Имеем:

$ { y=3+5n\ x-2=-4cdotfrac{5n}{5}=-4n\ x=2-4n} $

Тем самым все целые решения исходного уравнения можно записать в таком виде:

$ (2-4n;;3=5n),; где; n in Z. $

Ответ: $ (2-4n;;3=5n),; где; n in Z. $

2 способ. Алгоритм Евклида

Пусть нужно решить уравнение в целых числах: $ 5x+7y=6. $

Сделаем это с помощью Алгоритма Евклида. Ищем НОД чисел 5 и 7 с помощью него:

НОД (5, 7) = НОД (5, 7-5) = НОД (5, 2) = НОД (5 – 2∙2, 2) = НОД (1, 2) = 1

Запишем этот процесс в обратном порядке:

$ 1=2-1=2-(5-2cdot2)=2cdot3-5cdot1=(7-5)cdot3-5cdot1=7cdot3-5cdot4. $

То есть:

$ 1=5cdot(-4)+7cdot3 $

Тогда:

$ { 1cdot6=5cdot(-4)cdot6+7cdot3cdot6\ 6=5cdot(-24)+7cdot18\ 6=5x+7y} $

Тогда $ { x=-24 ;и ; y=18} $ является решением уравнения.

Общее решение записывается в виде:

$ { x=-24+7n; ; y=18+5n,} $ где n – любое целое число.

Выполним проверку:

$ { 5(-24+7n)+7(18+5n)=6\ -120+35n+126+35n=6\ 70n=0} $

$ { n} $ – любое целое.

Верно.

Это не всевозможные способы решения. Зачастую для решения диофантовых уравнений требуются более тонкие рассуждения, связанные с делимостью, перебором остатков, оценками частей уравнения, тождественными преобразованиями и т.п.

Пример.

Решим уравнение:

$ 3^{x}+4^{y}=5^{z} $

Разложить на множители и выразить переменную мы здесь не можем. Воспользуемся методом перебора остатков.

Если левая часть уравнения в целых числах кратна какому-то числу, то и другая обязательно должна быть кратна этому же числу. Отсюда следует, что и остатки от деления обеих частей уравнения на одно и то же число будут давать одинаковые остатки.

Будем делать выводы о делимости одной части уравнения на какое-либо число (или смотреть, какой остаток от деления при этом получается) и проверять, при каких значениях переменных вторая часть уравнения также делится на это число (либо даёт такой же остаток).

Левая часть кратна 5. И остатки от деления на 5 у обеих частей также будут равны.

Про пятёрку уже сказали, что правая часть делится на неё без остатка, значит и левая тоже должна делиться.

Рассмотрим остатки от деления на 4.

Z	$ 5^{z} $	Остаток при делении на 4
1	5	1
2	25	1
3	125	1
4	625	1

Видим простую закономерность, что 5 в любой степени при делении на 4 будет давать остаток 1.

Теперь левая часть: будет делиться на 4 без остатка.

Рассмотрим остатки от деления на 4 числа $ 3^{x} $

Z	$ 3^{x} $	Остаток при делении на 4
1	3	3
2	9	1
3	27	3
4	81	1
5	243	3

И так далее. Закономерность: при чётных х остаток 1, при нечётных остаток 3.

Отсюда делаем вывод, что х – число чётное, значит, мы можем представить его как х = 2n.

Теперь рассмотрим остатки при делении обеих частей на 3.

Правая часть:

Z	$ 5^{z} $	Остаток при делении на 3
1	5	2
2	25	1
3	125	2
4	625	1

И так далее. Видим закономерность, что при чётных z остаток равен 1, при нечетных z остаток равен 2.

Рассмотрим левую часть. Число $ 3^{x} $ даёт остаток 0 при делении на 3.

Рассмотрим остатки от деления на 3 числа $ 4^{y} $

Z	$ 4^{y} $	Остаток при делении на 3
1	4	1
2	16	1
3	64	1
4	256	1
5	1024	1

Получается, что левая часть при делении на 3 может давать только остаток 1. Значит, и правая тоже. Это происходит при чётных z.

Вернёмся к нашему уравнению $ 3^{x}+4^{y}=5^{z} $

Рассмотрев все остатки от деления, мы делаем выводы, что х и z – чётные числа. Тогда х = 2n, z = 2m, где m, n натуральные. Подставим в уравнение:

$ 3^{2n}+4^{y}=5^{2m} $ , заметим также, что $ 4^{y}=2^{2y} $

Теперь мы можем разложить на множители, используя формулу разности квадратов:

$ 2^{2y}=5^{2m}-3^{2n} $

$ (5^{m}-3^{n})(5^{m}+3^{n})=2^{2y} $ . Получается, что обе скобки должны быть степенями двойки. Мы не можем сделать никаких обоснованных выводов. Наша группировка неудачная. Попробуем иначе:

$ { 5^{2m}-2^{2y}=3^{2n}\ (5^{m}-2^{y})(5^{m}+2^{y})=3^{2n}} $

Теперь у нас обе скобки являются произведением троек. Рассмотрим такую ситуацию,

$ acdot b=3^{2n} $ , это означает, что и а, и b кратны 3. Либо одно из чисел кратно 3, а другое равно 1.

Рассмотрим случай, когда и а, и b кратны трём. Вспомним основные свойства делимости.

Ключевым признаком здесь будет второй: в нашем случае разность a-b также будет делиться на 3.

Рассмотрим разность скобок:

$ 5^{m}+2^{y}-(5^{m}-2^{y})=2cdot 2^{y} $ – это число никогда не будет кратно 3. Значит, в нашем произведении один из множителей равен 1, а другой равен 3²ⁿ. Так как $ 5^{m}+2^{y}> 1 $ ,

$ 5^{m}-2^{y}=1,5^{m}+2^{y})=3^{2n} $ Итак, мы с вами уже решаем немного другое уравнение, с переменными m и n, которые зависят от х и у. И пришли к выводу, что $ 5^{m}+2^{y}=1 $

m	$ 5^{m} $	y	$ 2^{y} $
0	1	0	1
1	5	1	2
2	25	2	4
3	125	3	8

Эта таблица показывает, что $ 5^{m}+2^{y}=1 $ только в одном случае при m = 1, y = 2. При их увеличении разница между и будет всё больше, поэтому это единственное решение.

Тогда z = 2m = 2, x = 2.

Ответ: (2, 2, 2)

Источник

Обращение автора к данной теме не является
случайным. Уравнения с двумя переменными впервые
встречаются в курсе 7-го класса. Одно уравнение с
двумя переменными имеет бесконечное множество
решений. Это наглядно демонстрирует график
линейной функции, заданный в виде ax + by=c. В
школьном курсе учащиеся изучают системы двух
уравнений с двумя переменными. В результате из
поля зрения учителя и, поэтому ученика, выпадает
целый ряд задач, с ограниченными условиями на
коэффициент уравнения, а также методы их решения.

Речь идет о решении уравнения с двумя
неизвестными в целых или натуральных числах.

В школе натуральные и целые числа изучаются в
4-6-х классах. К моменту окончания школы не все
ученики помнят различия между множествами этих
чисел.

Однако задача типа “решить уравнение вида ax +
by=c в целых числах” все чаще встречается на
вступительных экзаменах в ВУЗы и в материалах
ЕГЭ.

Решение неопределенных уравнений развивает
логическое мышление, сообразительность,
внимание анализировать.

Я предлагаю разработку нескольких уроков по
данной теме. У меня нет однозначных рекомендаций
по срокам проведения этих уроков. Отдельные
элементы можно использовать и в 7-м классе (для
сильного класса). Данные уроки можно взять за
основу и разработать небольшой элективный курс
по предпрофильной подготовке в 9-м классе. И,
конечно, этот материал можно использовать в 10-11
классах для подготовки к экзаменам.

Цель урока:

повторение и обобщение знаний по теме
“Уравнения первого и второго порядка”
воспитание познавательного интереса к учебному
предмету
формирование умений анализировать, проводить
обобщения, переносить знания в новую ситуацию

Урок 1.

Ход урока.

1) Орг. момент.

2) Актуализация опорных знаний.

Определение. Линейным уравнением с двумя
переменными называется уравнение вида

mx + ny = k, где m, n, k – числа, x, y – переменные.

Пример: 5x+2y=10

Определение. Решением уравнения с двумя
переменными называется пара значений
переменных, обращающая это уравнение в верное
равенство.

Уравнения с двумя переменными, имеющими одни и
те же решения, называются равносильными.

1. 5x+2y=12 (2)y =
-2.5x+6

Данное уравнение может иметь сколько угодно
решений. Для этого достаточно взять любое
значение x и найти соответствующее ему значение y.

Пусть x = 2, y = -2.5•2+6 = 1

x = 4, y = -2.5•4+6 =- 4

Пары чисел (2;1); (4;-4) – решения уравнения (1).

Данное уравнение имеет бесконечно много
решений.

3) Историческая справка

Неопределенные (диофантовы) уравнения – это
уравнения, содержащие более одной переменной.

В III в. н.э. – Диофант Александрийский написал
“Арифметику”, в которой расширил множество
чисел до рациональных, ввел алгебраическую
символику.

Так же Диофант рассмотрел проблемы решения
неопределенных уравнений и им даны методы
решения неопределенных уравнений второй и
третьей степени.

4) Изучение нового материала.

Определение: Неоднородным диофантовым
уравнением первого порядка с двумя неизвестными
x, y называется уравнение вида mx + ny = k, где m, n, k, x, y Z k0

Утверждение 1.

Если свободный член k в уравнении (1) не делится
на наибольший общий делитель (НОД) чисел m и n, то
уравнение (1) не имеет целых решений.

Пример: 34x – 17y = 3.

НОД (34; 17) = 17, 3 не делится нацело на 17, в целых
числах решения нет.

Пусть k делится на НОД (m, n). Делением всех
коэффициентов можно добиться, что m и n станут
взаимно простыми.

Утверждение 2.

Если m и n уравнения (1) взаимно простые числа, то
это уравнение имеет по крайней мере одно решение.

Утверждение 3.

Если коэффициенты m и n уравнения (1) являются
взаимно простыми числами, то это уравнение имеет
бесконечно много решений:

где (; ) –
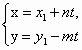
какое-либо решение уравнения (1), t Z

Определение. Однородным диофантовым
уравнением первого порядка с двумя неизвестными
x, y называется уравнение вида mx + ny = 0, где (2)

m, n, x, y Z

Утверждение 4.

Если m и n – взаимно простые числа, то всякое
решение уравнения (2) имеет вид

5) Домашнее задание. Решить уравнение в целых
числах:

9x – 18y = 5
x + y= xy
Несколько детей собирали яблоки. Каждый мальчик
собрал по 21 кг, а девочка по 15 кг. Всего они
собрали 174 кг. Сколько мальчиков и сколько
девочек собирали яблоки?

Замечание. На данном уроке не представлены
примеры решения уравнений в целых числах.
Поэтому домашнее задание дети решают исходя из
утверждения 1 и подбором.

Урок 2.

1) Организационный момент

2) Проверка домашнего задания

1) 9x – 18y = 5

НОД (9;18)=9

5 не делится нацело на 9, в целых числах решений
нет.

2) x + y= xy

Методом подбора можно найти решение

Ответ: (0;0), (2;2)

3) Составим уравнение:

Пусть мальчиков x, x Z, а девочек у, y Z, то можно составить уравнение 21x + 15y = 174

Многие учащиеся, составив уравнение, не смогут
его решить.

Ответ: мальчиков 4, девочек 6.

3) Изучение нового материала

Столкнувшись с трудностями при выполнении
домашнего задания, учащиеся убедились в
необходимости изучения их методов решений
неопределенных уравнений. Рассмотрим некоторые
из них.

I. Метод рассмотрения остатков от деления.

Пример. Решить уравнение в целых числах 3x – 4y
= 1.

3x = 4y + 1.

Левая часть уравнения делится на 3,
следовательно, должна делиться и правая часть.
Рассмотрим три случая.

Если y = 3m, m Z,
то 4y + 1= 4•3m + 1 = 12m + 1 не делится на 3.
Если y = 3 m + 1, то 4y +1 = 4• (3m + 1)+1 = 12m + 5 не делится на 3.
Если y = 3 m + 2, то 4y +1 = 4• (3m + 2)+1 = 12m + 9 делится на 3,
поэтому 3x = 12m + 9, следовательно, x = 4m + 3, а y = 3m + 2.

Ответ: где m Z.

Описанный метод удобно применять в случае, если
числа m и n не малы, но зато разлагаются на простые
сомножители.

Пример: Решить уравнения в целых числах.

8x + 14y = 32

4x + 7y = 16

4x = 16 – 7y

Пусть y = 4n, тогда 16 – 7y = 16 – 7•4n = 16 – 28n = 4*(4-7n)
делится на 4.

y = 4n+1, тогда 16 – 7y = 16 – 7• (4n + 1) = 16 – 28n – 7 = 9 – 28n
не делится на 4.

y = 4n+2, тогда 16 – 7y = 16 – 7• (4n + 2) = 16 – 28n – 14 = 2 – 28n
не делится на 4.

y = 4n+3, тогда 16 – 7y = 16 – 7• (4n + 3) = 16 – 28n – 21 = -5 – 28n
не делится на 4.

Следовательно, y = 4n, тогда

4x = 16 – 7•4n = 16 – 28n, x = 4 – 7n

Ответ: , где n Z.

II. Неопределенные уравнения 2-ой степени

Сегодня на уроке мы лишь коснемся решения
диофантовых уравнений второго порядка.

И из всех типов уравнений рассмотрим случай,
когда можно применить формулу разности
квадратов или другой способ разложения на
множители.

Пример: Решить уравнение в целых числах.

13 – простое число, поэтому оно может быть
разложено на множители лишь четырьмя способами:
13 = 13•1 = 1•13 = (-1)(-13) = (-13)(-1)

Рассмотрим эти случаи

а)
=>

б)
=>

в)
=>

г)
=>

Ответ: (7;-3), (7;3), (-7;3), (-7;-3).

4) Домашнее задание.

Примеры. Решить уравнение в целых числах:

а)

(x – y)(x + y)=4


2x = 4	2x = 5	2x = 5
x = 2	x = 5/2	x = 5/2
y = 0	не подходит	не подходит

2x = -4	не подходит	не подходит
x = -2
y = 0

Ответ: (-2;0), (2;0).

б)

Ответы: (-10;9), (-5;3), (-2;-3), (-1;-9), (1;9), (2;3), (5;-3), (10;-9).

в)

Ответ: (2;-3), (-1;-1), (-4;0), (2;2), (-1;3), (-4;5).

Итоги. Что значит решить уравнение в
целых числах?

Какие методы решения неопределенных уравнений
вы знаете?

Приложение:

Упражнения для тренировки.

1) Решите в целых числах.

а) 8x + 12y = 32	x = 1 + 3n, y = 2 – 2n, n Z
б) 7x + 5y = 29	x = 2 + 5n, y = 3 – 7n, n Z
в) 4x + 7y = 75	x = 3 + 7n, y = 9 – 4n, n Z
г) 9x – 2y = 1	x = 1 – 2m, y = 4 + 9m, m Z
д) 9x – 11y = 36	x = 4 + 11n, y = 9n, n Z
е) 7x – 4y = 29	x = 3 + 4n, y = -2 + 7n, n Z
ж) 19x – 5y = 119	x = 1 + 5p, y = -20 + 19p, p Z
з) 28x – 40y = 60	x = 45 + 10t, y = 30 + 7t, t Z

2) Найти целые неотрицательные решения
уравнения:

а) 8x + 65y = 81	x = 2, y = 1
б) 17x + 23y = 183	x = 4, y = 5

3) Найти все пары целых чисел (x; y),
удовлетворяющие следующим условиям

а) x + y = xy	(0;0), (2;2)
б)	(1;2), (5;2), (-1;-1), (-5;-2)

Решение:

Число 3 можно разложить на множители:

3 = 1•3 = 3·1 = (-1)·(-3) = (-3)·(-1)

Ответ: (-1; -2), (5; 2), (1;2), (-5; -2).

в)	(11;12), (-11;-12), (-11;12), (11;-12)
г)	(24;23), (24;-23), (-24;-23), (-24;23)
д)	(48;0), (24;1), (24;-1)
е)	x = 3m; y = 2m, mZ
ж) y = 2x – 1	x = m: y = 2m – 1, m Z
з)	x = 2m; y = m; x = 2m; y = -m, m Z
и)	решений нет

4) Решить уравнения в целых числах

	(-3;-2), (-1;1), (0;4), (2;-2), (3;1), (5;4)
(x – 3)(xy + 5) = 5	(-2;3), (2;-5), (4;0)
(y + 1)(xy – 1)=3	(0;-4), (1;-2), (1;2)
	(-4;-1), (-2;1), (2;-1), (4;1)
	(-11;-12), (-11;12), (11;-12), (11;12)
	(-24;23), (-24;23), (24;-23), (24;23)

5) Решить уравнения в целых числах.

Литература.

Детская энциклопедия “Педагогика”, Москва, 1972
г.
Алгебра-8, Н.Я. Виленкин, ВО “Наука”,
Новосибирск, 1992 г.
Конкурсные задачи, основанные на теории чисел.
В.Я. Галкин, Д.Ю. Сычугов. МГУ, ВМК, Москва, 2005г.
Задачи повышенной трудности в курсе алгебры 7-9
классов. Н.П. Косрыкина. “Просвещение”, Москва,
1991 г.
Алгебра 7, Макарычев Ю.Н., “Просвещение”.

Источник

math4school.ru

Уравнения в целых числах

Немного теории

Задачи с решениями

Задачи без решений

Алгебра и начала математического анализа. 10 класс

Конспект урока

Основные методы решения уравнений в целых числах

Урок 1.

Ход урока.

1) Орг. момент.

2) Актуализация опорных знаний.

3) Историческая справка

4) Изучение нового материала.

Урок 2.

1) Организационный момент

2) Проверка домашнего задания

3) Изучение нового материала

4) Домашнее задание.

Вам также может понравиться

Как найти квартиру по номеру объявления

Что за ошибка msvcp100 dll отсутствует как исправить windows 10

Как найди вершины функции

Добавить комментарий Отменить ответ