Как найти все перестановки массива

Алгоритм создания списка всех перестановок или размещений

Сразу оговорюсь, эта статья тематически похожа на опубликованную около года назад автором SemenovVV «Нерекурсивный алгоритм генерации перестановок», но подход тут, на мой взгляд, принципиально иной.

Я столкнулся с необходимостью составления списка всех перестановок из n элементов. Для n = 4 или даже 5, задача решается вручную в считанные минуты, но для 6! = 720 и выше исписывать страницы мне уже было лень – нужна была автоматизация. Я был уверен, что этот «велосипед» уже изобретён многократно и в различных вариациях, но было интересно разобраться самостоятельно – поэтому, намеренно не заглядывая в профильную литературу, я засел за создание алгоритма.

Первую же версию кода с рекурсией я отбросил как слишком тривиальную и ресурсоёмкую. Далее, сделав «финт ушами», разработал не очень эффективный алгоритм, перебирающий заведомо большее количество вариантов и отсеивающий лишь подходящие из них. Он работал, но мне хотелось чего-то элегантного – и, начав с чистого листа, я принялся искать закономерности в лексикографическом порядке перестановок для малых значений n. В итоге получился аккуратный код, который с минимальной «обвязкой» можно на Python представить строк в 10 (см. ниже). Более того, этот подход работает не только для перестановок, но и для размещений n элементов по m позициям (в случае когда, n≥m).
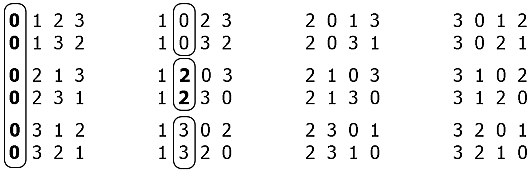
Если взглянуть на перечень всех перестановок для 4 по 4, то заметна определённая структура:

Весь массив перестановок (4! = 24) можно разбить на группы из (n-1)! = 3! – шести перестановок, а каждую группу в свою очередь разбить на (n-1-1)! = 2! –две комбинации и так далее. В рассмотренном случае, когда для n = 4, на этом – всё.

Итак, с точки зрения лексикографии этот набор перестановок можно представить себе как возрастающий ряд: так сказать, 0123 < 0132 < … < 3210. Мы наперёд знаем, сколько раз подряд будет повторяться один и тот же элемент в определённой позиции – это количество перестановок для массива порядком на единицу меньше, т.е. (a-1)!, где а – размерность текущего массива. Тогда признаком перехода к следующему значению будет новый результат целочисленного деления («//») порядкового номера i комбинации на количество таких перестановок: i // (a-1)!. Также, чтобы определить, каким будет номер этого элемента в списке ещё не задействованных (дабы не перебирать его по кругу), используем остаток от деления («%») полученной величины на длину этого списка. Т.о. имеем следующую конструкцию:

i // (a-1)! % r,

где r – размерность массива ещё не задействованных элементов.

Для наглядности рассмотрим конкретный случай. Из всех 24 перестановок i Є [0, 23] 4 элементов по 4 положениям, к примеру, 17-я будет представлять собой следующую последовательность:

[17 // (4-1)!] % r(0,1,2,3) = 2 % 4 = 2

(т.е., если считать с 0, третий элемент списка, – «2»). Следующим элементом этой перестановки будет:

[17 // (3-1)!] % r(0,1,3) = 8 % 3 = 2

(снова третий элемент – теперь это «3»)

Если продолжать в том же духе, в итоге получим массив «2 3 1 0». Следовательно, перебирая в цикле все значения i из количества перестановок [n!] или размещений [n!/(n-m)!, где m – количество положений в массиве], мы получим исчерпывающий набор искомых сочетаний.

Собственно, сам код выглядит так:

import math
elm=4				# к-во элементов, n
cells=4				# к-во положений, m
res=[]				# результирующий список
arrang = math.factorial(elm)/math.factorial(elm-cells)	# расчёт к-ва сочетаний
for i in range(arrang):
    res.append([])
    source=range(elm)	# массив ещё не задействованных элементов
    for j in range(cells):
        p=i//math.factorial(cells-1-j)%len(source)
        res[len(res)-1].append(source[p])
        source.pop(p)

UPD: со временем осознал, что метод недостаточно проверенный — поэтому, если кто-то станет его использовать, прошу быть бдительным (не хотелось бы кого-нибудь подвести)

Используйте один из двух алгоритмов перестановки, обсуждаемых далее.

Обсуждение

Функция pc_permute(), приведенная в примере 1 – это PHP модификация базовой рекурсивной функции.

примере 1

function pc_permute($items, $perms = array()) {
    if (empty($items)) {
        echo implode(' ', $perms) . "<br>";
    } else {
        for ($i = count($items) -1; $i >= 0; --$i) {
            $newitems = $items;
            $newperms = $perms;
            list($foo) = array_splice($newitems, $i, 1);
            array_unshift($newperms, $foo);
            pc_permute($newitems, $newperms);
        }
    }
}
pc_permute(explode(' ', 'she sells seashells'));

Эта рекурсия хотя и элегантна, но неэффективна, поскольку делает
повсюду копии. К тому же не так легко модифицировать эту функцию,
чтобы она возвращала значения вместо вывода на печать без накопле
ния их в глобальной переменной.

примере 2

function pc_next_permutation($p, $size) {
    // проходим массив сверху вниз в поисках числа, которое меньше следующего
    for ($i = $size - 1; $p[$i] >= $p[$i+1]; --$i) { }
    // если такого нет, прекращаем перестановки
    // массив перевернут: (1, 2, 3, 4) => (4, 3, 2, 1)
    if ($i == -1) { return false; }
    // проходим массив сверху вниз в поисках числа,
    // превосходящего найденное ранее
    for ($j = $size; $p[$j] <= $p[$i]; --$j) { }
    // переставляем их
    $tmp = $p[$i]; $p[$i] = $p[$j]; $p[$j] = $tmp;
    // теперь переворачиваем массив путем перестановки элементов,
    // начиная с конца
    for (++$i, $j = $size; $i < $j; ++$i, --$j) {
        $tmp = $p[$i]; $p[$i] = $p[$j]; $p[$j] = $tmp;
    }

    return $p;
}
$set = explode(' ', 'she sells seashells');
$size = count($set) -1;
$perm = range(0, $size);
$j = 0;
do {
    foreach ($perm as $i) { $perms[$j][] = $set[$i]; }
} while ($perm = pc_next_permutation($perm, $size) and ++$j);
foreach ($perms as $p) {
    echo implode(' ', $p) . "<br>";
}

Идея Доминуса состоит в том, что вместо манипуляций с самим массивом можно создавать перестановки целых чисел. Затем, чтобы получить истинную перестановку, снова ставим в соответствие числам элементы массива – оригинальная мысль.
Однако этот прием имеет некоторые недостатки. Для нас, программистов на PHP, более важными являются частые извлечения, вставки и
объединения массивов, т. е. то, что для Perl является центральным.
Затем процесс вычисления перестановок целых чисел проходит через
серию шагов, которые выполняются для каждой перестановки; и поскольку он не запоминает предыдущие перестановки, то каждый раз
начинает с исходной перестановки. Зачем работает повторное выполнение, если мы можем помочь ему?

Перестановки без повторений

Количество перестановок для N различных элементов составляет N!. Действительно:

• на первое место может быть помещен любой из N элементов (всего вариантов N),
• на вторую позицию может быть помещен любой из оставшихся (N-1) элементов (итого вариантов N·(N-1)),
• если продолжить данную последовательность для всех N мест, то получим: N·(N-1)·(N-2)· … ·1, то есть всего N! перестановок.

• Необходимо просмотреть текущую перестановку справа налево и при этом следить за тем, чтобы каждый следующий элемент перестановки (элемент с большим номером) был не более чем предыдущий (элемент с меньшим номером). Как только данное соотношение будет нарушено необходимо остановиться и отметить текущее число (позиция 1).
• Снова просмотреть пройденный путь справа налево пока не дойдем до первого числа, которое больше чем отмеченное на предыдущем шаге.
• Поменять местами два полученных элемента.
• Теперь в части массива, которая размещена справа от позиции 1 надо отсортировать все числа в порядке возрастания. Поскольку до этого они все были уже записаны в порядке убывания необходимо эту часть подпоследовательность просто перевернуть.

Перестановки с повторениями

Особого внимания заслуживает задача генерации перестановок N элементов в случае если элементы последовательности могут повторяться. Допустим, исходная последовательность состоит из элементов n₁, n₂… n_k, где элемент n₁ повторяется r₁ раз, n₂ повторяется r₂ раз и т.д. При этом n₁+n₂+…+n_k=N.  Если мы будем считать все n₁+n₂+…+n_k элементов перестановки с повторениями различными, то всего различных вариантов перестановок (n₁+n₂+…+n_k)! . Однако среди этих перестановок не все различны. В самом деле, все r₁ элементов n₁ мы можем переставлять местами друг с другом, и от этого перестановка не изменится. Точно так же, можем переставлять элементы n₂, n₃ и т. д. В итоге имеем r₁! вариантов записи одной и той же перестановки с различным расположением повторяющихся элементов n₁. Таким образом, всякая перестановка может быть записана r₁!·r₂!·…·r_k! способами. Следовательно, число различных перестановок с повторениями равно

Для генерации перестановок с повторениями можно использовать алгоритм генерации перестановок без повторений, приведенный выше. Введем повторяющийся элемент в массив a. Ниже приведен код программы для генерации перестановок с повторениями (изменен только код функции main()).

Результат работы приведенного выше алгоритма:

Назад: Алгоритмизация

Во время недавнего гугления по какому-то поводу попалась мне на глаза заметка, в которой автор приводил реализацию алгоритма получения всех перестановок (permutations) на PHP. Видимо, по той причине, что обработка входного массива выполнялась “по месту”, что существенно экономило память,  реализация алгоритма получилась весьма витиеватой. То есть, чтобы разобраться, как он работает, пришлось натурально браться за ручку и бумагу ))

И вот задумался я, а можно ли как-то все это реализовать в более понятном ключе ?….

Ведь что такое множество перестановок для некоторого массива размерности N ? Алгоритм его получения можно условно представить таким псевдокодом:

Функция ВсеПерестановки(ВходнойМассив)
       Результат = ПустойМассив();
       Цикл по I от 1 до РазмерВходногоМассиваN
             ПромежуточныйМассив = ВходнойМассив за вычетом элемента с индексом I;
             ПромежуточныеПерестановки = ВсеПерестановки(ПромежуточныйМассив);
             Цикл ПромежуточныеПерестановки как Перестановка
                       Перестановка = ЭлементВходногоМассива с индексом I + Перестановка; 
             КонецЦикла;
             Результат = Результат + ПромежуточныеПерестановки;
       КонецЦикла;
       Вернуть Результат;
КонецФункции;

То есть, налицо рекурсивный алгоритм, где каждое решение для массива размерности N основывается на решении задачи для массива размерности N-1. Для того, чтобы получить решение для массива размерности N,  нужно для каждого элемента этого массива выполнить следующие действия: получить промежуточный массив, который не содержит этого элемента
(размерность этого массива будет на 1 меньше), затем вызвать рекурсивно нашу функцию ВсеПерестановки() для этого промежуточного массива меньшей размерности, к полученным результатам функции “доклеить” в самое начало тот элемент, который мы удаляли из входного массива на первом шаге, а затем обработанный таким образом результат добавить для накопления в аккумулятор, значение которого будет возвращено по выходу из функции.

На мой взгляд, алгоритмически это решение весьма несложное для понимания. Попробуем реализовать этот алгоритм на PHP, применяя, по возможности, функциональный подход 🙂
Вот что получилось у меня:

===
function permutations($input) {
    if (count($input) <= 1) return array($input);
    $result = array();  
    foreach ($input as $v) {
          $reduce = array_filter($input,
                                 function ($e) use($v) { return $e !== $v; }
                    );
          $result = array_merge( $result, 
                        array_map(
                             function ($e) use ($v) { array_unshift( $e, $v); return $e; },
                             permutations( $reduce )
                        )
                    );
    }
    return $result;
}===
Вызов функции выглядит следующим образом:

$input = range(1, 5, 1);
$result = permutations($input);

Первый вызов – range() – возвращает нам массив, заполненный числам от 1 до 5 подряд.
Тут важный момент – все элементы массива должны быть различны, поэтому если вам нужно формировать перестановки для массива, в котором есть дубликаты, вы можете сформировать
массив индексов, как указано выше, получить перестановки для него, а потом использовать полученный результат для индексации оригинального массива.

Дальше этот массив поступает на вход функции, формирующей массив всех перестановок.
Количество перестановок будет равно факториалу от размерности входного массива.

Теперь давайте разберем, как работает permutations(). Она всегда возвращает массив массивов (даже для одного элемента). Это сделано специально, чтобы чуть упростить обработку результатов вложенного вызова самой себя. Итак, если на входе у нас пустой массив или массив, состоящий из одного элемента, мы возвращаем его же, но упакованным в массив.
То есть, на входе array(5), на выходе – array ( array (5) ).
Если же массив имеет более одного элемента, мы выполняем следующее: для каждого элемента $v массива мы формируем при помощи array_filter() промежуточный массив $reduce, который содержит все элементы входного массива за исключением этого элемента $v. После этого, мы вызываем permutations() для массива $reduce. Полученный результат обрабатываем при помощи array_map(), которая к каждому элементу массива перестановок добавляет в начало
элемент $v функцией array_unshift(). Далее, мы просто накапливаем полученные таким образом результаты в массиве $result, и после прохода по всему массиву $input возвращаем $result.
Все достаточно очевидно. Так как permutations() использует анонимные функции, то
требуется PHP версии не ниже 5.3 (это ограничение обходится написанием внешних функций, которые будут подаваться как callback в те же array_map() или array_filter().

 
Конечно, у такого подхода есть большой минус – он весьма “жруч” в плане памяти. Объясняется это, как минимум тем, что и array_map(), и array_merge(), и array_filter() в результате своей работы формируют новые массивы (функциональная иммутабельность! =)) Плюс еще и невозможность явно освобождать память в процессе работы. Я пытался вызывать внутри цикла unset(), но пользы это не принесло, к сожалению.
В общем, при попытке вызвать permutations() для входного массива, содержащего 10 элементов
(чуть более 3 с половиной миллионов перестановок), вываливается сообщение о нехватке ОЗУ:
==
Fatal error: Allowed memory size of 134217728 bytes exhausted (tried to allocate 36 bytes)
==
Так что функцию можно применять либо как учебную, либо на массивах весьма ограниченной размерности.

Вот, пожалуй, и все на данный момент.

Дополнение. 

Кстати, проверив работу функции, о которой я писал в самом начале этого поста, на размерности 10 элементов, я получил то же сообщение о нехватке памяти.  То есть, проблема, в первую очередь, определяется не тем, что array_* функции иммутабельны и в PHP нет явного управления выделением и освобождением памяти,  а тем, что все перестановки накапливаются в одном результирующем массиве, и уже этот массив целиком подается на выход функции permutations(). Решением проблемы может стать использование генераторов в PHP, которые появились в версии 5.5. То есть, вместо накопления результатов в массиве $result можно будет выдавать наверх каждую отдельную перестановку вызовом yield. По идее, это должно работать. Для более ранних версий PHP можно предусмотреть явный вызов из permutations() некоторой callback-функции с передачей в неё последней полученной перестановки  как параметра. Это, конечно, будет не так изящно, как использование генератора, но тоже вполне приемлемо.