Нами были рассмотрены действия сложения, вычитания и умножения матриц на число. Еще одним действием над ними является умножение. Выполняется оно сложнее, а само правило может показаться немного странным. При его выполнении важно уметь определять размер матриц. Это понятие было рассмотрено в теме «Что такое матрица».
Онлайн-калькулятор
Как умножать матрицы
Приступим к рассмотрению умножения матриц.
Нам известно, что складывать и вычитать можно матрицы, которые имеют одинаковый размер. С умножением дела обстоят немного сложнее.
Какие матрицы можно умножать
Матрицу P можно умножить на матрицу K только в том случае, если число столбцов матрицы P равняется числу строк матрицы K. Матрицы, для которых данное условие не выполняется, умножать нельзя.
Пример 1
Определим, можно ли умножить матрицу
K=(15271810)K=begin{pmatrix}15&27\18&10end{pmatrix} на матрицу L=(3516)L=begin{pmatrix}35\16end{pmatrix}.
Матрица KK состоит из 2 строк и 2 столбцов, а матрица LL — из 2 строк и 1 столбца. Число столбцов матрицы KK равно числу строк матрицы LL, значит, матрицу KK можно умножить на матрицу LL.
Пример 2
Переставим матрицы местами и определим, можно ли умножить матрицу
F=(3516)F=begin{pmatrix}35\16end{pmatrix} на матрицу C=(15271810)C=begin{pmatrix}15&27\18&10end{pmatrix}.
Матрица FF состоит из 2 строк и 1 столбца, а матрица CC — из 2 строк и 2 столбцов. Число столбцов матрицы FF не равно числу строк матрицы CC, значит, матрицу FF нельзя умножить на матрицу CC.
Произведение матрицы AA размера m×nmtimes n и матрицы BB размера n×kntimes k — это матрица CC размера m×kmtimes k, в которой элемент cijc_{ij} равен сумме произведений элементов ii строки матрицы AA на соответствующие элементы jj столбца матрицы B:cij=ai1b1j+ai2b2j+…+ainbnjB: c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+…+a_{in}b_{nj}.
Умножение матриц осуществляется путем умножения строки на столбец. Находятся произведения первого элемента строки и первого элемента столбца, второго элемента строки и второго элемента столбца и т.д. Затем полученные произведения суммируются.
Алгоритм нахождения произведения матриц
- определить размеры матриц;
- если число столбцов первой матрицы совпадает с числом строк второй матрицы, то выполнять умножение.
Рассмотрим пример умножения матрицы
A=(a11a12a21a22a31a32a41a42)A=begin{pmatrix}a_{11}&a_{12}\a_{21}&a_{22}\a_{31}&a_{32}\a_{41}&a_{42}end{pmatrix}
на матрицу
B=(b11b12b13b21b22b23)B=begin{pmatrix}b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}end{pmatrix}.
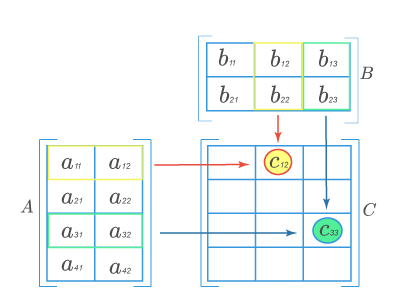
Матрица AA состоит из 4 строк и 2 столбцов, а матрица BB — из 2 строк и 3 столбцов. Число столбцов матрицы AA равно числу строк матрицы BB, значит, можно найти произведение C=A⋅BC=Acdot B. Причем матрица CC будет иметь размер 4×34times 3. Найдем элементы c12c_{12} (выделен красными стрелками) и c33c_{33} (выделен синими стрелками):
Для того чтобы найти элемент c12c_{12} нужно перемножать соответствующие элементы 1 строки матрицы AA и 2 столбца матрицы B:c12=a11⋅b12+a12⋅b22B: c_{12}=a_{11}cdot b_{12}+a_{12}cdot b_{22}. Для того чтобы найти элемент c33c_{33} нужно перемножать соответствующие элементы 3 строки матрицы AA и 3 столбца матрицы BB: c33=a31⋅b13+a32⋅b23c_{33}=a_{31}cdot b_{13}+a_{32}cdot b_{23}. Так находят все элементы.
Таким образом, матрица CC может быть найдена следующим образом:
A⋅B=(a11a12a21a22a31a32a41a42)⋅(b11b12b13b21b22b23)=Acdot B=begin{pmatrix}a_{11}&a_{12}\a_{21}&a_{22}\a_{31}&a_{32}\a_{41}&a_{42}end{pmatrix}cdot begin{pmatrix}b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}end{pmatrix}=
=(a11⋅b11+a12⋅b21a11⋅b12+a12⋅b22a11⋅b13+a12⋅b23a21⋅b11+a22⋅b21a21⋅b12+a22⋅b22a21⋅b13+a22⋅b23a31⋅b11+a32⋅b21a31⋅b12+a32⋅b22a31⋅b13+a32⋅b23a41⋅b11+a42⋅b21a41⋅b12+a42⋅b22a41⋅b13+a42⋅b23)=begin{pmatrix}a_{11}cdot b_{11}+a_{12}cdot b_{21}&a_{11}cdot b_{12}+a_{12}cdot b_{22}&a_{11}cdot b_{13}+a_{12}cdot b_{23}\a_{21}cdot b_{11}+a_{22}cdot b_{21}&a_{21}cdot b_{12}+a_{22}cdot b_{22}&a_{21}cdot b_{13}+a_{22}cdot b_{23}\a_{31}cdot b_{11}+a_{32}cdot b_{21}&a_{31}cdot b_{12}+a_{32}cdot b_{22}&a_{31}cdot b_{13}+a_{32}cdot b_{23}\a_{41}cdot b_{11}+a_{42}cdot b_{21}&a_{41}cdot b_{12}+a_{42}cdot b_{22}&a_{41}cdot b_{13}+a_{42}cdot b_{23}end{pmatrix}
Произведение B⋅ABcdot A нельзя найти, поскольку число столбцов матрицы BB неравно числу строк матрицы AA.
Найти произведение матрицы C=(15271810)C=begin{pmatrix}15&27\18&10end{pmatrix} на матрицу F=(3516)F=begin{pmatrix}35\16end{pmatrix}.
Матрица CC имеет размер 2×22times 2, матрица FF имеет размер 2×12times 1, значит, размер матрицы произведения будет 2×12times 1.
C⋅F=(15271810)⋅(3516)=(15⋅35+27⋅1618⋅35+10⋅16)=(957790)Ccdot F=begin{pmatrix}15&27\18&10end{pmatrix}cdot begin{pmatrix}35\16end{pmatrix}=begin{pmatrix}15cdot 35+27cdot 16\18cdot 35+10cdot 16end{pmatrix}=begin{pmatrix}957\790end{pmatrix}.
Как отмечалось выше, произведение матриц F⋅CFcdot C невозможно.
Найти произведение матриц K⋅LKcdot L и L⋅KLcdot K, если K=(12171314)K=begin{pmatrix}12&17\13&14end{pmatrix} на матрицу L=(18111210)L=begin{pmatrix}18&11\12&10end{pmatrix}.
Матрица KK имеет размер 2×22times 2, матрица LL имеет размер 2×22times 2, значит, размер матрицы произведения будет 2×22times 2.
K⋅L=(12171314)⋅(18111210)=(12⋅18+17⋅1212⋅11+17⋅1013⋅18+14⋅1213⋅11+14⋅10)=(420302402283)Kcdot L=begin{pmatrix}12&17\13&14end{pmatrix}cdot begin{pmatrix}18&11\12&10end{pmatrix}=begin{pmatrix}12cdot 18+17cdot 12&12cdot 11+17cdot 10\13cdot 18+14cdot 12&13cdot 11+14cdot 10end{pmatrix}=begin{pmatrix}420&302\402&283end{pmatrix}
Произведение L⋅KLcdot K существует и его размер — 2×22times 2.
L⋅K=(18111210)⋅(12171314)=(18⋅12+11⋅1318⋅17+11⋅1412⋅12+10⋅1312⋅17+10⋅14)=(359460274344)Lcdot K=begin{pmatrix}18&11\12&10end{pmatrix}cdot begin{pmatrix}12&17\13&14end{pmatrix}=begin{pmatrix}18cdot 12+11cdot 13&18cdot 17+11cdot 14\12cdot 12+10cdot 13&12cdot 17+10cdot 14end{pmatrix}=begin{pmatrix}359&460\274&344end{pmatrix}
Произведение двух матриц в общем случае зависит от порядка сомножителей, т.е. оно некоммутативно: A⋅B≠B⋅AAcdot Bneq Bcdot A.
Так, для матриц K=(12171314)K=begin{pmatrix}12&17\13&14end{pmatrix} и L=(18111210)L=begin{pmatrix}18&11\12&10end{pmatrix} из рассмотренного примера K⋅L≠L⋅KKcdot L neq Lcdot K.
Перестановочные матрицы
Перестановочные, или коммутирующие, матрицы – матрицы, для которых выполняется равенство A⋅B=B⋅AAcdot B=Bcdot A. Они обязательно квадратные.
Проверить, являются ли перестановочными матрицы CC и DD, если C=(2342)C=begin{pmatrix}2&3\4&2end{pmatrix}, D=(3343)D=begin{pmatrix}3&3\4&3end{pmatrix}.
Найдем произведения этих матриц C⋅DCcdot D и D⋅CDcdot C.
C⋅D=(2342)⋅(3343)=(2⋅3+3⋅42⋅3+3⋅34⋅3+2⋅44⋅3+2⋅3)=(18152018)Ccdot D=begin{pmatrix}2&3\4&2end{pmatrix}cdot begin{pmatrix}3&3\4&3end{pmatrix}=begin{pmatrix}2cdot 3+3cdot 4&2cdot 3+3cdot 3\4cdot 3+2cdot 4&4cdot 3+2cdot 3end{pmatrix}=begin{pmatrix}18&15\20&18end{pmatrix},
D⋅C=(3343)⋅(2342)=(3⋅2+3⋅43⋅3+3⋅24⋅2+3⋅44⋅3+3⋅2)=(18152018)Dcdot C=begin{pmatrix}3&3\4&3end{pmatrix}cdot begin{pmatrix}2&3\4&2end{pmatrix}=begin{pmatrix}3cdot 2+3cdot 4&3cdot 3+3cdot 2\4cdot 2+3cdot 4&4cdot 3+3cdot 2end{pmatrix}=begin{pmatrix}18&15\20&18end{pmatrix}.
Таким образом, для заданных матриц выполняется равенство C⋅DCcdot D и D⋅CDcdot C, поэтому они являются перестановочными.
Проверить, являются ли перестановочными матрицы FF и HH, если F=(3421)F=begin{pmatrix}3&4\2&1end{pmatrix}, H=(0593)H=begin{pmatrix}0&5\9&3end{pmatrix}.
Найдем произведения этих матриц F⋅HFcdot H и H⋅FHcdot F.
F⋅H=(3421)⋅(0593)=(3⋅0+4⋅93⋅5+4⋅32⋅0+1⋅92⋅5+1⋅3)=(3627913)Fcdot H=begin{pmatrix}3&4\2&1end{pmatrix}cdot begin{pmatrix}0&5\9&3end{pmatrix}=begin{pmatrix}3cdot 0+4cdot 9&3cdot 5+4cdot 3\2cdot 0+1cdot 9&2cdot 5+1cdot 3end{pmatrix}=begin{pmatrix}36&27\9&13end{pmatrix},
H⋅F=(0593)⋅(3421)=(0⋅3+5⋅20⋅4+5⋅19⋅3+3⋅29⋅4+3⋅1)=(1053339)Hcdot F=begin{pmatrix}0&5\9&3end{pmatrix}cdot begin{pmatrix}3&4\2&1end{pmatrix}=begin{pmatrix}0cdot 3+5cdot 2&0cdot 4+5cdot 1\9cdot 3+3cdot 2&9cdot 4+3cdot 1end{pmatrix}=begin{pmatrix}10&5\33&39end{pmatrix}.
Таким образом, для заданных матриц не выполняется равенство F⋅HFcdot H и H⋅FHcdot F, поэтому они не являются перестановочными.
Контрольные работы на заказ онлайн от практикующих исполнителей!
как найти перестановочную матрицу
Вы искали как найти перестановочную матрицу? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и найти все матрицы перестановочные с матрицей, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение.
Например, «как найти перестановочную матрицу».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как как найти перестановочную матрицу,найти все матрицы перестановочные с матрицей,найти все перестановочные матрицы с матрицей. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и как найти перестановочную матрицу. Просто введите задачу в окошко и нажмите
«решить» здесь (например, найти все перестановочные матрицы с матрицей).
Где можно решить любую задачу по математике, а так же как найти перестановочную матрицу Онлайн?
Решить задачу как найти перестановочную матрицу вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать – это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Найдите все матрицы перестановочные, с данной матрицей А:
rewer ne qwewer
Ученик
(172),
закрыт
6 лет назад
7 -3
5 -2
когда решал сам застрял на 4-ом уравнении помогите кто может
Дополнен 6 лет назад

Лучший ответ
Forestman
Гений
(81447)
6 лет назад
Ответ абсолютно верный. Чтобы в этом убедиться, достаточно сравнить произведения XA и AX. Вид ответа может не совпадать с тем, что приведен в Вашем задачнике. Он зависит от выбора базисного минора.
rewer ne qwewerУченик (172)
6 лет назад
Спасибо что уделили время) и благодарю за решение)
Остальные ответы
Alexander Alenitsyn
Высший разум
(754423)
6 лет назад
Ответ по строкам:
X=(p,q+3; -5q, p+9q) (строки разделены 😉
Здесь p и q произвольные параметры.
rewer ne qwewerУченик (172)
6 лет назад
что то я не совсем понял…. вот когда я решал 4 система не получилась
Alexander Alenitsyn
Высший разум
(754423)
У вас ошибка, см. фото

Похожие вопросы
Калькулятор матриц – действия с матрицами онлайн
С помощью калькулятора матриц вы сможете выполнять различные преобразования матриц, решать СЛАУ, а также находить некоторые характеристики, как, например, определитель, след и ранг. Подробнее о функционале и использовании калькулятора смотрите после блока с самим калькулятором.
Матричный калькулятор
Матрица A
Матрица B
Показатель степени:
Число:
Метод поиска обратной матрицы
Метод Гауса-Жордана
Метод союзной матрицы
Метод решения СЛАУ AX=B
Метод Гауса
Матричный метод
Метод Крамера
Элементарное преобразование
и
Выводить числа в виде
с знаками после запятой
Транспонирование — операция, при которой строки и столбцы матрицы меняются местами: aTij = aji
Выполнено действий:
Также может быть интересно:
- Калькулятор таблицы истинности. СДНФ. СКНФ. Полином Жегалкина
- Калькулятор комплексных чисел
Как пользоваться калькулятором матриц
- Выберите матрицу (или матрицы) с помощью переключателей ()
- Укажите размер с помощью выпадающих списков под матрицей ( × )
- Заполните элементы (нулевые элементы можно не заполнять.)
- Выберите в выпадающем списке требуемую функцию и, если требуется, введите дополнительные параметры.
- Нажмите кнопку .
- Если вывод чисел не устраивает, просто поменяйте его — доступны три варианта представления: правильные дроби (2), неправильные дроби () и десятичные дроби (2.4) с указанием числа знаков после запятой.
Ввод данных и функционал
- В качестве элементов используются обыкновенные правильные дроби (
1/2,29/7,-1/125), десятичные дроби (12,-0.01,3.14), а также числа в экспоненциальной форме (2.5e3,1e-2). - Длина вводимых чисел ничем не ограничена, вводите хоть 1000 цифр, правда, возможно, придётся подождать, пока будут идти вычисления!
- Используйте для работы одну или две матрицы (чтобы выполнять операции с двумя матрицами, передвиньте переключатель второй матрицы).
- Вставляйте результат в A или B с помощью кнопок “Вставить в A” и “Вставить в B”.
- Перетаскивайте (drag-and-drop) матрицы из результата в A или B.
- Используйте стрелки (
←,↑,→,↓) для перемещения по элементам
Что умеет наш калькулятор матриц?
С одной матрицей (только Матрица A или Матрица B)
- Транспонировать;
- Вычислять определитель;
- Находить ранг и след;
- Возводить в степень;
- Умножать на число;
- Вычислять обратную матрицу;
- Приводить к треугольному и ступенчатому вид;
- Находить LU-разложение;
- Выполнять элементарные преобразования;
- Выполнять действия с выражениями, содержащими матрицы.
С двумя матрицами (Матрица A и Матрица B)
- Складывать;
- Вычитать;
- Умножать;
- Решать системы линейных алгебраических уравнений (СЛАУ) вида AX=B;
- Выполнять действия с выражениями, содержащими матрицы.
Вычисление выражений с матрицами
Вы можете вычислять различные арифметические выражения с матрицами, а также с результатами некоторых преобразований этих матриц.
Из чего могут состоять выражения?
- Целые и дробные числа
- Матрицы A, B
- Знаки арифметических действий:
+-*/ - Круглые скобки для изменения приоритета операций:
() - Транспонирование:
^T - Возведение в целую степень:
^
Примеры корректных выражений
- Cложение двух матриц:
A+B,(A)+(B),((A) + B) - Возведение линейной комбинации матриц в степень:
(3A - 0.5B)^5 - Произведение транспонированной матрицы на исходную:
A^TA - Обратная матрица в квадрате для B:
B^-2
Что такое матрица?
Матрицей размера n×m называется прямоугольная таблица специального вида, состоящая из n строк и m столбцов, заполненная числами. Матрицы обозначаются заглавными латинскими буквами. При необходимости размер записывается следующим образом: An×m.
Примеры матриц
Элементы матрицы
Элементы A обозначаются aij, где i – номер строки, в которой находится элемент, j – номер столбца.
Некоторые теоретические сведения
Транспонирование — операция, при которой строки и столбцы матрицы меняются местами: aTij = aji
Главная диагональ квадратной матрицы — диагональ, которая проходит через верхний левый и нижний правый углы. Элементы главной диагонали — aii
Единичная матрица En×n — квадратная матрица из n столбцов и n строк с единицами на главной диагонали и нулями вне её.
Ранг — это максимальное количество линейно независимых строк (столбцов) этой матрицы. Обозначение: rank(A)
След — это сумма элементов, находящихся на её главной диагонали. Обозначение: tr(A) или track(A)
Умножение матрицы на число — матрица такой же размерности, что и исходная, каждый элемент которой является произведением соответствующего элемента исходной матрицы на заданное число.
Возведение в степень — умножение заданной матрицы саму на себя n-ое количество раз, где n – степень, в которую необходимо возвести исходную матрицу. Обозначение: An
Обратная матрица A−1 — матрица, произведение которой на исходную матрицу A равно единичной матрице: A-1×A = A×A-1 = E
Треугольная матрица — квадратная матрица, у которой выше (верхнетреугольная матрица) или ниже (нижнетреугольная матрица) главной диагонали находятся нули.
LU-разложение — представление матрицы в виде произведения двух матриц L и U, где L — нижнетреугольная матрица с еденичной диагональю, а U — верхнетреугольная матрица. A = L·U
Сложение матриц An×m и Bn×m — матрица Cn×m, получаемая попарной суммой соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: сij=aij+bij
Разность матриц An×m и Bn×m — матрица Cn×m, получаемая попарной разностью соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: сij=aij-bij
Умножение матриц An×k и Bk×m — матрица Cn×m, у которой элемент (cij) равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-того столбца матрицы B: cij = ai1·b1j + ai2·b2j + ... + aik·bkj
google.com/+ВикторЦекунов
Репетитор по математике, физике (Минск): Виктор Иванович.
Высшая математика и физика для студентов.
Профессиональный репетитор окажет помощь в решении задач, подготовит к экзаменам. Занятия в Серебрянке, индивидуально. (90 мин)
= 20 $.
Тел: +375(29) 127 61 86.___________________________________________________________________________
Оказываю
платные услуги: решение задач по высшей математике. Оплата WebMoney.
Заказы направляйте сюда: Платные услуги
___________________________________________________________________________
2.1. Арифметика целых чисел.
2.2. Матрицы и определители.
2.3.
Системы линейных уравнений.
2.4.
Множества и отображения.
2.5.
Комплексные числа.
2.6. Группы.
2.7. Кольца.
2.8. Алгебраические уравнения.
2.9.
Элементы теории полей.
2.10. Линейные пространства.
2.11. Линейные операторы.
2.12. Квадратичные формы.
2.13. Тензоры.
2.1. Арифметика целых чисел.
2.1-1.
Используя
алгоритм Евклида сократить дробь: 169/448.
Решение:
Применяя
алгоритм Евклида, получаем равенства (в правой части равенств после плюса стоят
остатки):
448 = 169∙2 + 110,
169 = 110∙1 + 59,
110 = 59∙1 + 51,
59 = 51∙1 + 8,
51 = 8∙6 + 3,
8 = 3∙2 + 2,
3 = 2∙1 + 1,
2 = 1∙2.
Так как последний отличный от нуля остаток равен 1, то наибольший общий
делитель чисел 448 и 169
НОД(448, 169) = 1.
Это означает, что числа 448 и 169 – взаимно простые. Следовательно, дробь
169/448 несократима.
2.1-2.
Используя
алгоритм Евклида сократить дроби: 490/1372; 92400/13960
Решение:
1) Дробь 490/1372:
Применяя алгоритм Евклида, получаем равенства (в правой части равенств после
плюса стоят остатки):
1372 = 490∙2 + 392,
490 = 392∙1 + 98,
392 = 98∙4.
Так как последний отличный от нуля остаток равен 98, то наибольший общий
делитель чисел 1372 и 490
НОД(1372, 490) = 98.
Сокращаем дробь на 98
(490:98)/(1372:98) = 5/14.
2) Дробь 92400/139600:
Применяя алгоритм Евклида, получаем равенства (в правой части равенств после
плюса стоят остатки):
139600 = 92400∙1 + 47200,
92400 = 47200∙1 + 45200,
47200 = 45200∙1 + 2000,
45200 = 2000∙22 + 1200,
2000 = 1200∙1 + 800,
1200 = 800∙1 + 400,
800 = 400∙2.
Так как последний отличный от нуля остаток равен 400, то наибольший общий
делитель чисел 139600 и 92400
НОД(139600, 92400) = 400.
Сокращаем
дробь на 400
(92400:400)/(139600:400) = 231/349.
Ответ: 490/1372 = 5/14; 92400/139600 = 231/349.
2.1-3.
Найти
наименьшее натуральное число x, удовлетворяющее условиям:
x = 6mod13
x = 33mod37
x = 19mod23
x = 14mod36
Решение:
x = 6 mod13
x = 33 mod37
x = 19 mod23
x = 14 mod36
x є N
x(min) – ?
Прежде
всего, уясним
x = 6 mod13 означает:
x/13
даёт в остатке 6 или иначе (x-6)/13 делится без остатка.
Имеем систему сравнений вида
x = aᵢ modnᵢ i=1,2,3,4,
где
a₁=6 , a₂=33 ,
a₃=19 ,
a₄=14 ,
n₁=13 ,
n₂=37 ,
n₃=23 ,
n₄=36.
Т.к. n₁, n₂, n₃, n₄
попарно взаимно простые, то согласно китайской теореме об остатках данная
система сравнений имеет единственное решение относительно x є Zn,
n = n₁n₂n₃n₄=
13·37·23·36=398268.
(Zn –
кольцо классов вычетов целых чисел по модулю n).
Решение будем искать по методу Гаусса:
x = (a₁N₁M₁ + a₂N₂M₂ + a₃N₃M₃ + a₄N₄M₄) modn, (1)
где
N₁=n/n₁=398268/13=30636,
N₂=n/n₂=398268/37=10764,
N₃=n/n₃=398268/23=17316,
N₄=n/n₄=398268/36=11063,
Mᵢ = Nᵢ⁻¹ modnᵢ. i=1,2,3,4.
Mᵢ –
мультипликативно обратный к Nᵢ элемент по модулю nᵢ.
Вычислим
M₁.
M₁ =
30636⁻¹ mod13 или
30636M₁ mod13=1,
30636 mod13·M₁ mod13=1,
8·M₁ mod13=1,
отсюда
8M₁
может принимать значения 14, 27, 40, …
Т.к. 40 делится на 8, то из уравнения
8M₁ = 40
находим
M₁=40/8=5.
Вычислим
M₂.
M₂ =
10764⁻¹ mod37 или
10764M₂ mod37=1,
10764 mod37·M₂ mod37=1,
34·M₂ mod37=1,
отсюда
34M₂
может принимать значения 38, 75, 112, 149, 186, 223, 260, 297, 334, 371, 408,
…
Т.к. 408 делится на 34, то из уравнения
34M₂ =
408 находим
M₂=408/34=12.
Вычислим
M₃.
M₃ =
17316⁻¹ mod23 или
17316M₃ mod23=1,
17316 mod23·M₃ mod23=1,
20·M₃ mod23=1,
отсюда
20M₃
может принимать значения 24, 47, 70, 93, 116, 139, 162, 185, 208, 231,
254, 277, 300, …
Т.к. 300 делится на 20, то из уравнения
20M₃ =
300 находим
M₃=300/20=15.
Вычислим
M₄.
M₄ =
11063⁻¹ mod36 или
11063M₄ mod36=1,
11063 mod36·M₄ mod36=1,
11·M₄ mod36=1,
отсюда
11M₄
может принимать значения 37, 73, 109, 145, 181, 217, 253, …
Т.к. 253 делится на 11, то из уравнения
11M₄ =
253 находим
M₄=253/11=23.Подставим
всё в (1)
x = (6·30636·5 + 33·10764·12 + 19·17316·15 + 14·11063·23) mod398268 =
= 13678970 mod398268 = 137858.
Ответ: x = 137858.
________________________________________________________________________________________________
2.2. Матрицы и определители.
2.2-2.
Найдите все матрицы, перестановочные с матрицей
Решение:
Пусть матрица
АВ = ВА. (1)
Вычислим произведения матриц: АВ и ВА.
Подставим в (1)
Равенство матриц означает равенство соответствующих элементов этих матриц.
Получаем систему уравнений:
{ a = a + 2b
{ b = b
{ 2a + c = c + 2d
{ 2b + d = d.
Отсюда получим: b = 0, a = d и матрица В примет вид
, где а, с є R.
Ответ:
, где a, c є R.
2.2-3.
Известно, что А – квадратная матрица 4-го порядка, причем det A = 3.
Чему тогда равен
det 3A?
Решение:
n = 4
det A = 3
det 3A − ?
Сначала докажем общую формулу, затем решим эту задачу.
1. Пусть А − квадратная матрица порядка
n (aij є R), λ − общий множитель (λ є R).
Доказать:
det(λA) = λⁿdetA. (1)
Доказательство:
Матрицы А, λА и
определитель detA
матрицы А:
_ _ _ _
| a₁₁ a₁₂ …
a₁n-1 a₁n | | λa₁₁ λa₁₂ …
λa₁n-1 λa₁n |
| a₂₁ a₂₂ … a₂nn-1 a₂n | | λa₂₁ λa₂₂ … λa₂n-1 λa₂n |
A = |
………………………………………..| λA = | ……………………………………..……… |
| an-1₁ an-1₂ … an-1 n-1 an–1n | | λan-1₁ λan-1₂ … λan-1 n-1 λan–1n |
| an₁ an₂ … ann-1 ann | | λan₁ λan₂ … λann-1 λann |
‾ ‾ ‾ ‾
| a₁₁ a₁₂ …
a₁n-1 a₁n |
| a₂₁ a₂₂ … a₂n-1 a₂n |
detA = |
……………………………………….|
| an-1₁ an-1₂ … an-1 n-1 an-1n |
| an₁ an₂ … ann-1 ann |.
Воспользуемся
свойством определителя:
общий множитель всех элементов произвольной строки (столбца) определителя можно
вынести за знак определителя. (*)
Тогда для определителя матрицы λA, в силу свойства (*), применённого последовательно к
строкам с номерами 1, 2, … , n-1, n, имеем
|
λa₁₁ λa₁₂ …
λa₁n-1 λa₁n | | a₁₁ a₁₂ …
a₁n-1 a₁n |
| λa₂₁ λa₂₂ … λa₂n-1 λa₂n | | λa₂₁ λa₂₂ … λa₂n-1 λa₂n |
det(λA) = |
……………………………………………… | = λ·| …………………………………………..… | =
| λan-1₁ λan-1₂ … λan-1 n-1 λan-1n | | λan-1₁ λan-1₂ … λan-1 n–1 λan-1n |
| λan₁ λan₂ … λann-1 λann | | λan₁ λan₂ … λann-1 λann |
|
a₁₁ a₁₂ …
a₁n-1 a₁n | | a₁₁ a₁₂
… a₁n-1 a₁n |
| a₂₁ a₂₂ … a₂n-1 a₂n | | a₂₁ a₂₂ … a₂n-1 a₂n |
= λ²·|
……………………………………………….| = … = λⁿ·| ………………………………..……. | = λⁿ·detA.
| λan-1₁ λan-1₂ … λan-1 n-1 λan-1n | | an-1₁ an-1₂ … an-1 n-1 an-1n |
| λan₁ λan₂ … λann-1 λann | | an₁ an₂ … ann-1 ann |
Итак, мы получили
det(λA) = λⁿ·detA и
формула (1) доказана!
2. Из формулы (1) при n = 4, det A = 3 получаем
det 3A = 3⁴·det A =
3⁴·3 = 3⁵= 243.
Ответ: det 3A = 3⁴·det A = 243.
________________________________________________________________________________________________
2.3.
Системы линейных уравнений.
2.3-1.
Определите коэффициенты a, b, c, d многочлена f(x) = ax³ + bx² + cx + d, если известно, что f(-1) =
-9, f(0) =
-2, f(1) =
-3, f(2) =
0.
Решение:
Подставляя в f(x) = ax³ + bx² + cx + d
соответственно х = -1, 0, 1 и 2, получим систему уравнений
{ – a + b – c + d = – 9
{ d = – 2
{ a + b + c + d = – 3
{ 8a + 4b + 2c + d = 0.
Решим данную систему уравнений методом Гаусса.
Составим расширенную матрицу данной системы и с помощью элементарных
преобразований строк приведём её к треугольному виду.
_ _ _ _
| -1 1 -1 1 | -9 | | -1 1 -1 1 | -9 | (1. К 2-й строке + 1-ю
| 0 0 0 1 | -2 | | 8 4 2 1 | 0 | строку, умноженную на 8;
| 1 1 1 1 | -3 | (переставим 2-ю и 4-ю строки) ~ | 1 1 1 1 | -3 | 2. К 3-й
строке + 1-ю
| 8 4 2 1 | 0 | | 0 0 0 1 | -2 | строку)
‾ ‾ ‾ ‾
_ _ _ _
| -1 1 -1 1 | -9 | | -1 1 -1 1 | -9 | (К 3-й строке + 2-ю
| 0 12 -6 9 | -72 | | 0 2 0 2 | -12 | строку, умноженную на
~ | 0 2 0 2 | -12 | (переставим 2-ю и 3-ю строки) ~ | 0 12 -6 9 | -72 | на -6)
| 0 0 0 1 | -2 | | 0 0 0 1 | -2 |
‾ ‾ ‾ ‾
_ _
| -1 1 -1 1 | -9 |
| 0 2 0 2 | -12 |
~ | 0 0 -6 -3 | 0 |
| 0 0 0 1 | -2 |
‾ ‾
По последней матрице выпишем систему, равносильную исходной системе
{ – a + b – c + d = – 9
{ 2b + 2d = –
12
{ – 6c – 3d = 0
{ d = –
2.
Из 4-го уравнения имеем: d = – 2.
Из 3-го уравнения имеем: – 6c – 3(-2) = 0, отсюда с = 1.
Из 2-го уравнения имеем: 2b + 2(-2) = – 12, отсюда b = –
4.
Из 1-го уравнения имеем: – a – 4 – 1 – 2 = – 9, отсюда a = 2.
Ответ:
a = 2, b = – 4, c = 1, d = – 2.
2.3-2. Дана система уравнений:
Как выглядит базисное решение этой системы?
Решение:
Перепишем
систему в виде
x₁ – 5x₂ +2x₄ = 4
4x₂ – x₃ = -1 (1)
2x₂ +3x₄ – x₅ = 0
Выпишем расширенную матрицу системы (1) и, с помощью элементарных преобразований
строк, приведём её к ступенчатому виду
_ _
| 1 -5 0 2 0 | 4 |
| 0 4 -1 0 0 | -1 | ~ ( к
2-й строке +3-ю строку, умноженную на (-2) ) ~
|_ 0 2 0 3 -1 | 0 _|
_ _
| 1 -5 0 2 0 | 4 |
~ | 0 0 -1 -6 2 | -1 | ~ (
поменяем местами 2-ю и 3-ю строки ) ~
|_ 0 2 0 3 -1 | 0 _|
_ _
| 1 -5 0 2 0 | 4 |
~| 0 2 0 3 -1 | 0 |
|_ 0 0 -1 -6 2 | -1 _|
Соответствующая ступенчатая система имеет вид
x₁ – 5x₂ + 2x₄ = 4
2x₂ + 3x₄ – x₅ = 0
–x₃ – 6x₄ + 2x₅ = -1
Неизвестные x₄ и x₅
объявим свободными и перепишем последнюю систему так:
x₁ – 5x₂ = 4 – 2x₄
2x₂ = – 3x₄ + x₅
x₃ = -6x₄+2x₅ + 1
Пусть x₄ = a, x₅ = b, a и b є R.
Получаем
x₁ – 5x₂ = 4 – 2a
2x₂ = -3a + b
x₃ = -6a + 2b + 1
откуда
x₃ = 2b-6a+1, x₂ = (b-3a)/2, x₁ = (5b-19a+8)/2.
Таким образом, система (1) имеет бесконечное множество решений вида
( (5b-19a+8)/2;
(b-3a)/2; 2b-6a+1; a; b ),
где a, b –
произвольные действительные числа.
Других
решений система не имеет.
Ответ: ( (5b-19a+8)/2;
(b-3a)/2; 2b-6a+1; a; b ), a, b є R.
2.3-3.
Объясните, как из матрицы:
(1 0 0 | 0)
(0 1 -1| 0)
(0 0 0 | 0)
получили такое решение:
( 0 )
X = (с1)
(с1).
Решение:
( 1 0 0 | 0 ) {x₁ = 0 {x₁ = 0
(0 1 -1 | 0 ) отсюда система уравнений { x₂ – x₃ = 0
или { x₂ = x₃ .
( 0 0 0 | 0 )
Обозначим x₃ = c₁ .
Тогда x₁ = 0,
x₂ = c₁ , x₃ = c₁ .
Или в виде матрицы-столбца
(0)
X = (c₁)
(c₁).2.3-4.
Проверить, является ли система линейных уравнений
(1)
невырожденной, и решить её по формулам Крамера.
Решение:
1. Матрица А данной системы:
Вычислим определитель ∆ матрицы А:
= ( к 2-й строке прибавим 1-ю строку, умноженную на (-1) ) =
= (разложим определитель по 1-му столбцу) =
= 1·1( 3·(-1) – 1·2 ) = -3 – 2 =
-5.
Так как ∆ = -5 ≠ 0, то система уравнений невырожденная и имеет решение.
Найдём решение системы по формулам Крамера:
х₁ = ∆₁/∆, х₂ = ∆₂/∆, х₃ = ∆₃/∆. (2)
2. Запишем определитель ∆₁ . Для этого в определитель ∆ вместо 1-го столбца
вставим столбец свободных членов системы (1):
0, 1, -3.
Имеем
= (к 3-й строке прибавим 2-ю строку, умноженную на 3) =
= (разложим определитель по 1-му столбцу) =
= 1·(-1)( (-1·2 – 7·(-1) ) = -(-2 +
7) = -5.
3. Запишем определитель ∆₂ . Для этого в определитель ∆ вместо 2-го столбца
вставим столбец свободных членов системы (1):
0, 1, -3.
Имеем
= ( к 2-й строке прибавим 1-ю строку, умноженную на (-1) ) =
= (разложим определитель по 1-му столбцу) =
= 1·1( 1·(-1) – (-3)·2 ) = -1 + 6 =
5.
4. Запишем определитель ∆₃ . Для этого в определитель ∆ вместо 3-го столбца
вставим столбец свободных членов системы (1):
0, 1, -3.
Имеем
= ( к 2-й строке прибавим 1-ю строку, умноженную на (-1) ) =
= (разложим определитель по 1-му столбцу) =
= 1·1( 3·(-3) – 1·1 ) = -9 – 1 =
-10.
Тогда по формулам (2) имеем
х₁ = -5/(-5) = 1, х₂ = 5/(-5) = -1, х₃ = -10/(-5) = 2.
Ответ: х₁ = 1, х₂ = -1,
х₃ = 2.
________________________________________________________________________________________________
2.5.
Комплексные числа.
2.5-1. Описать множество точек, изображающих на комплексной плоскости числа z,
удовлетворяющие условию |z+1-i| < |z-1+i|
Решение:
|z+1-i| < |z-1+i|
Подставим сюда z = x + iy
|x+iy+1-i| <
|x+iy-1+i| или
|x+1+i(y-1)|
< |x-1+i(y+1)| или
√( (x+1)²+(y-1)² )
< √( (x-1)²+(y+1)² ).
Возведём обе части полученного неравенства в квадрат
(x+1)²+(y-1)²
< (x-1)²+(y+1)².
Раскроем скобки и, после упрощения, получим
y > x.
Рисуем прямую y = x (она
направлена под углом 45⁰ к оси OX ).
Полуплоскость выше прямой y = x и будет искомое множество точек.
Ответ: полуплоскость выше прямой y = x.
________________________________________________________________________________________________
2.11. Линейные операторы.2.11-1.
Найти
матрицу оператора осевой симметрии относительно прямой x = – y.
Решение:
Пусть f –
оператор симметрии, М(x, y) – точка на плоскости, А – искомая матрица оператора f.
Оператор f
переводит точку М в точку М₁ : f( М(x, y) ) = М₁ (-y, –x).
Для вектора ОМ: f( ОМ(x, y) ) =
ОМ₁ (-y, –x).
Пусть е₁(1;0) и е₂(0;1) – единичные и взаимно ортогональные векторы, образующие
базис (е₁ направлен по оси X, е₂ – по оси Y).
Тогда f(
е₁(1;0) ) = (0;-1) = -е₂ , f( е₂(0;1) ) = (-1;0) = -е₁.
(0;-1) – первый столбец матрицы А.
(-1;0) – второй столбец матрицы А.
|‾ 0 -1 ‾|
Матрица А = | |
|_ -1 0 _|
|‾ 0 -1 ‾|
Ответ: А = | |
|_ -1 0 _|
2.11-2.
Найти собственные значения и собственные векторы матрицы
_ _
| 5 -1 1 |
A = | 0
4 -1 |.
| 0 -1 4 |
‾ ‾
Решение:
1. Матрица А имеет порядок n = 3. Запишем характеристическое уравнение матрицы А:
(1)
Разложим определитель по 1-му столбцу
= (
применим формулу: a² – b² = (a + b)(a – b) ) = (5 – λ)(4 – λ + 1) )(4 – λ – 1) = (5 – λ)(5 – λ)(3 – λ) =
= (5
– λ)²(3 –
λ).
Тогда уравнение (1) примет вид
(5 – λ)²(3 –
λ) = 0,
откуда находим корни λ₁ = 3, λ₂,₃ = 5, которые являются собственными значениями
матрицы А. Найдем соответствующие им собственные векторы.
Составляем систему для определения координат x₁ , x₂ , x₃
собственных векторов:
{ (5-λ)x₁ +
(-1)·x₂ + 1·x₃ = 0;
{ (4-λ)x₂ +
(-1)·x₃ = 0;
(2)
{ (-1)·x₂ +
(4-λ)x₃ = 0.
2. Подставляя λ = λ₁ = 3
в систему (2), имеем:
{ (5-3)x₁ +
(-1)·x₂ + 1·x₃ = 0
{ 2x₁ – x₂ + x₃ = 0
{ (4-3)x₂ +
(-1)·x₃ = 0
или { x₂ – x₃ = 0
{ (-1)·x₂ +
(4-3)x₃ = 0
{ – x₂ + x₃ = 0.
Решаем ее методом Гаусса. Выписываем расширенную матрицу
_ _
| 2 -1 1 0 |
A* = |
0 1 -1 0 |.
| 0 -1 1 0 |
‾ ‾
С помощью элементарных преобразований строк приведём матрицу А* к треугольному
виду.
_ _ _ _
| 2 -1 1 0 | (к 3-й строке прибавим 2-ю строку) | 2 -1 1 0 |
A* = |
0 1 -1 0 | ~ | 0 1 -1 0 |
| 0 -1 1 0 | | 0 0 0 0 |.
‾ ‾ ‾ ‾
В полученной матрице все миноры 3-го порядка равны нулю. Вычисляем левый верхний
минор 2-го порядка
_ _
| 2 -1 | = 2 ≠ 0. Получили не равный нулю минор 2-го порядка, значит ранг r = 2.
| 0 1 |
‾ ‾
По преобразованной матрице А* возвращаемся к системе уравнений
{ 2x₁ – x₂ + x₃ = 0
{ x₂ – x₃ = 0.
Так как r = 2,
то зависимых (базисных) переменных два, а свободное одно. Пусть x₃ –
свободное неизвестное, тогда
{ 2x₁ – x₂ = – x₃
{ x₂ = x₃.
Решая эту систему, находим общее решение: x₁ = 0,
x₂ = x₃.
Фундаментальная система решений состоит из одного решения, так как n – r = 3 –
2 = 1.
Множество собственных векторов, отвечающих собственному числу λ = 3,
имеет вид:
{0, x₃, x₃} = x₃{0,
1, 1}, где x₃ –
любое число (x₃ ≠ 0). Выберем из этого множества один вектор,
например, положив x₃ = 1: Х₁ = {0, 1, 1}.
Итак, собственному числу λ = 3 соответствует собственный вектор Х₁ = {0, 1, 1}.
3. Подставляя λ = λ₂,₃ =
5 в систему (2), имеем:
{ (5-5)x₁ +
(-1)·x₂ + 1·x₃ = 0
{ – x₂ + x₃ = 0
{ (4-5)x₂ +
(-1)·x₃ = 0
или { – x₂ – x₃ = 0
{ (-1)·x₂ +
(4-5)x₃ = 0
{ – x₂ – x₃ = 0.
Решаем ее методом Гаусса. Выписываем расширенную матрицу
_ _
| 0 -1 1 0 |
A** = |
0 -1 -1 0 |.
| 0 -1 -1 0 |
‾ ‾
С помощью элементарных преобразований строк приведём матрицу А** к треугольному
виду.
_ _ _ _
| 0 -1 1 0 |(к 3-й строке прибавим 2-ю строку, умноженную на (-1)) | 0 -1 1 0
|
A** = |
0 -1 -1 0 | ~ | 0 -1 -1 0 |
| 0 -1 -1 0 | | 0 0 0 0 |
‾ ‾ ‾ ‾
_ _
(к 2-й строке прибавим 1-ю строку, умноженную на (-1)) | 0 -1 1 0 |
~ | 0 0 -2 0 |
| 0 0 0 0 |.
‾ ‾
В полученной матрице все миноры 3-го порядка равны нулю. Не равный нулю
базисный минор 2-го порядка
_ _
| -1 1 | = 2 ≠ 0. Получили не равный нулю минор 2-го порядка, значит ранг r = 2.
| 0 -2 |
‾ ‾
По преобразованной матрице А** возвращаемся к системе уравнений
{ – x₂ + x₃ = 0
{ – 2x₃ = 0.
Отсюда получим x₂ = x₃ = 0.
Так как r = 2,
то зависимых (базисных) переменных два, а свободное одно. Так как базисный
минор стоит на пересечении 1-й и 2-й строки и 2-го и 3-го столбца, то x₂ и x₃ − базисные переменные, а x₁ ≠ 0 – свободная переменная, принимающая любое
значение. Общее решение: x₁ , x₂ = x₃ = 0.
Фундаментальная система решений состоит из одного решения, так как
n – r = 3 –
2 = 1.
Множество собственных векторов, отвечающих собственному числу λ = 5,
имеет вид:
{x₁ , 0,
0} = x₁{1,
0, 0}, где x₁ ≠ 0.
Выберем из этого множества один вектор, например, положив x₁ = 1:
Х₂ = {1, 0, 0}.
Итак, собственному числу λ = 5 соответствует собственный вектор Х₂ = {1, 0, 0}.
Легко видеть, что вектора Х₁ и Х₂ ортогональны (Х₁ _|_ Х₂), т.к. их скалярное
произведение равно нулю: 0·1 + 1·0 + 1·0 = 0.
Ответ:
λ₁ = 3, λ₂,₃ = 5; Х₁ = {0; 1; 1}, Х₂ = {1; 0; 0}.
________________________________________________________________________________________________
2.12. Квадратичные формы.
2.12-1. Как определить являются ли линейными преобразования каких-либо выражений?
Решение:
Пусть
выражение состоит из переменных
Х₁,
Х₂, …, Хn. (1)
Пусть дано произвольное поле P. Переход от переменных (1) к переменным
Y₁, Y₂, …, Yn (2)
С помощью формул
Х₁ = a₁₁Y₁+ a₁₂Y₂+ … a₁nYn
Х₂ = a₂₁Y₁+ a₂₂Y₂+ … a₂nYn (3)
……………………………………..
Хn = an₁Y₁+ an₂Y₂+ … annYn,
где аᵢᵧ –
произвольные элементы поля P, называется линейным преобразованием переменных над
полем P.________________________________________________________________________________________________
2.13. Тензоры.
2.13-1. Вычислить свертку Cijbkj+BmEikm
Решение:
Свёртка
выполняется по одинаковым индексам, конечный результат от них уже не зависит.
Свёртка (Cijbkj + Bmеikm) = С′ibk +
B′еik.
Свёртка Сii = С′
– константа.