-
Матрицы смежности и перечисления путей
Напомним, что
матрицей смежности А=||aij||
помеченного графа G(V,E) с n вершинами
называется (nxn)- матрица, в которой аij
=1 , если вершина viсмежна
с вершиной vj
и аij=0
в противном случае.
Если
граф не является связным, то путем
соответствующей нумерации вершин
матрицу смежности можно представить
блочной матрицей диагонального вида,
в которой каждый блок соответствует
одной из компонент связности, например:
Рис.20. Граф с тремя
компонентами и его блочная матрица
смежности
Поскольку компоненты
и в матрице смежности не имеют общих
элементов, то каждую из них можно
рассматривать отдельно.
С
помощью матриц смежности, используя
различные алгебры, можно определить
наличие путей различной длины между
произвольными вершинами, количество
таких путей и перечисление таких путей.
Если использовать
булеву алгебру, то элемент anij
показывает, есть ли между вершинами vi
и vj
путь, длиной меньше или равной n ребер.
При
этом о значении диагональных элементов
матрицы договариваются заранее исходя
из сущности решаемой задачи
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
||
|
А= |
1 |
1 |
0 |
1 |
; А21= |
1 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
||
|
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
||
|
А2= |
0 |
1 |
0 |
1 |
0 |
; А22= |
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
||
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
||
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
||
|
А32= |
0 |
1 |
0 |
1 |
0 |
А42= |
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
||
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
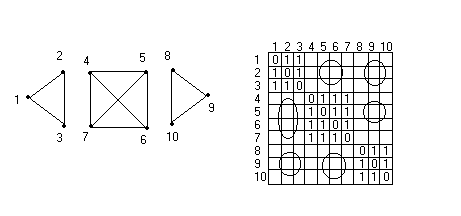
Графы G1
и G2,
соответствующие матрицам смежности А1
и А2
приведены на рис.21;
Рис.21. Графы G1
, G2
и G3
Граф G1
после возведения его матрицы смежности
А1
в квадрат становиться полносявзным,
т.е. каждая его вершина связана со всеми
остальными либо одним ребром в соответствии
с матрицей А1
, либо путем, состоящим из двух ребер в
соответствии с матрицей А21
.
Появляющиеся
петли при вершинах, соответствующие
диагональным элементам , можно принимать
или не принимать во внимание, в зависимости
от решаемой задачи.
При возведении
матрицы А2
в квадрат в графе G2
появляются дополнительные связи между
вершинами v1
иv3 (v3
и v1),
v2
и v4
(v4и
v2
), v3
и v5
( v5
и v3)
и граф G2
принимает вид, как показано на рис.22;
А)


в)

Рис.22.Механизм
появления новых связей при возведении
в степень {2,3,4}матрицы А2.
При возведении
матрицы А32
= А22
х А1
появляются новые пути из тех ребер,
связывающие вершины v1
иv2
; v1
иv4 и.т.д
произведя сложение матриц по правилам
булевой алгебры, получим :
АΣ= А2UА22UА32UА42
0 1 1 1 1
1 0 1 1 1
АΣ= 1 1 0 1 1
1 1 1 0 1
1 1 1 1 0
Граф, соответствующий
этой матрице, без учета петель является
полносвязным и показан на рис.22.
В матрицах А2
со степенью меньше 4 элементы а15
= а51
= 0. Поэтому
m = 4 является минимальной степенью, при
возведении в которую элементы матрицы
Аm
содержат только положительные элементы.
В
этом случае все вершины являются
достижимыми из любой вершины путем,
состоящим из не более чем m ребер (дуг)
.
Граф
G и соответствующая ему матрица смежности
А называются примитивными, а m – индексом
примитивности.
На рис.21 в граф G3
не является примитивным, поскольку из
его вершин 7 и 8 нет ребер , связывающих
их с другими вершинами.
Для
определения количества путей различной
длины применяют возведение в степень
матрицы смежности по правилам обычной
алгебры .
Так, при возведении
в квадрат матрицы А1,
соответствующей графу G1
на рис.21а получим :
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|||||
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|||||
|
А21 |
=А1 |
х А1= |
1 |
1 |
0 |
1 |
х |
1 |
1 |
0 |
1 |
|
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|||||
|
3 |
1 |
2 |
1 |
|||||||||
|
1 |
2 |
1 |
2 |
|||||||||
|
= |
2 |
1 |
3 |
1 |
||||||||
|
1 |
2 |
1 |
2 |
На главной диагонали
стоят степени вершин .
Из вершины v1
в v2
есть один
путь из двух ребер е2
е4
; в вершину v3
– два пути е1
е4
и е3
е5;
в вершину v4–
е2
е5
.
Эти пути можно
определить только визуально из графа,
по матрице же можно определить только
их количество.
Для перечисления
путей применяют так называемые структурные
матрицы и одну из равновидностей булевой
алгебры.
Структурная матрица
в определяется таким образом:
bij,
если вершины vi
и vj
соединены ребрам и i < j
В = 1, если i = j
bij,
если вершины vi
и vj
соединены ребром, но i>j
0 в остальных
случаях
алгебра такова:
1 U
1 = 1 ; 1.0 = 0.1=0 ; 1 U
0 = 0 U
1=1
ā .а=0 ; а
U
а = а ;а Uав
= а ; 1 U
а =1
для графа G1
рис 31а структурная матрица примет вид
:
|
1 |
а |
в |
С |
1 |
aUb |
bUadUcē |
cUbe |
|||
|
ā |
1 |
d |
0 |
ā |
1 |
dUāb |
ācU |
|||
|
В= |
b |
|
1 |
ē |
; |
B2= |
вUa |
|
1 |
eUbc |
|
|
0 |
ē |
1 |
|
acU |
ēU |
1 |
Для удобства
заполнения матрицы В2
записываем i-ю строку, под ней j-й столбец
и производим умножение строки на столбец
по изложенным правилам.
1 а в с
В211= 1 ā

*
1 а в с
В212= а 1

1 а в с
В213= в d 1 ē = 1*вUа dUвUс ē =
вUаdUс ē
1 а в с
В214= с 0 е 1 = сUа 0UвеUс =
сUве
Для того, чтобы
перечислить одно, двух и трехзвенные
пути, необходимо умножить матрицу В2хВ1
т.е. В3=
В2хВ.
Получим, например,
первую стоку матрицы В3
|
В311= |
1 |
аUb |
bUadVc |
cUbe |
|
1 |
ā |
|
|
= 1U ā b
a
UbceUcb ē = 1
|
В312= |
1 |
аUb |
bUadUc |
cUbe |
|
a |
1 |
|
0 |
=a U a b
b

ē = a U b
c ē
|
В313= |
1 |
аUb |
bUadUc |
cUbe |
|
b |
d |
1 |
ē |
= b U ad U b U ad U c ē U c ē = b U ad U c ē
|
В314= |
1 |
аUb |
bUadUc |
cUbe |
|
c |
0 |
e |
1 |
= c UbeUade
|
В323= |
ā U |
1 |
b Uā b |
c Ube |
|
b |
d |
1 |
|
= ā b UdUā
|
В324= |
ā U |
1 |
b Uā b |
c Ube |
|
c |
0 |
e |
1 |
= ā U c
U de U ā be
|
В334= |
|
|
1 |
e U |
|
c |
0 |
e |
1 |
=



матрица В3
имеет вид:
|
1 |
a Ub |
b UadUc ē |
c UbeUade |
|
ā U |
1 |
d Ua |
ā c U de U |
|
b UadU |
|
1 |
e U |
|
|
а c Ud eUа |
e U |
1 |
Дальнейшее
возведение в степень матрицы смежности
не дает новых путей (только циклы), а
алгоритм определения базисных циклов
был рассмотрен ранее.
В каждой из клеток
(n-1) степени структурной матрицы
представлены все пути, ведущие из вершины
vi
в вершину vj.
Каждую из клеток в связи с этим можно
представить отдельной матрицей путей
Мst
строкам которой соответствуют пути, а
столбцам –дуги, входящие в эти пути.
Например,
для клетки 13 матрица путей примет вид:
|
е1 |
е2 |
е3 |
е4 |
е5 |
||
|
a |
b |
c |
d |
e |
||
|
1 |
0 |
1 |
0 |
0 |
0 |
|
|
Мst= |
2 |
1 |
0 |
0 |
1 |
0 |
|
3 |
0 |
0 |
1 |
0 |
1 |
k13
= 113U213U313
= b U ad U c ē .
Перечисление
путей Мst
из произвольной вершины s в произвольную
вершину t может быть получено из
структурной матрицы В раскрытием
определителя подматрицы Вts,
получаемого из структурной матрицы В
вычергиванием s-го столбца и t –й строки:
Мst = detвts
= | вts
|
1
a b c a b c
в=
a 1 d o ;в13=
1 d o
b
d 1 e o e 1
c
o e 1
a
b c
k13=|в13|
= 1 d O =а
d OU b c UO = ad U b Ucе
o
e 1 e 1 e 1
Для вершин v1
и v3
таких
независимых путей 3 – это b(e2)
Uad(e1e4)
Uce(e3e5),
для вершин v2
и v3
таких пути
два :d(e4)
U
a b (e1e2).
Это является следствием того, что степень
вершины d(V4)
= 2 , поэтому и число независимых путей
в нее и из нее не может превышать этого
числа.
И
вообще число независимых путей из одной
вершины в другую не может превышать
минимальную степень одной из них.
В наших примерах
:
d(v1)
= 3; d(v2)
= 2; d(v3)
= 3; поэтому между v1
и v3
может быть не более трех независимых
путей, а между v2
и v3
не более двух .
В множестве путей
М23
пути ab и асе содержат общее ребро а,
поэтому они не могут быть независимыми.
Множество путей
между двумя произвольными вершинами
связано с понятием “сечение”, которое
является более общим случаем понятия
“разрез”.
Напомним,
что разрез – это минимальное число
ребер, удаление которых разбивает граф
на два связанных подграфа.
Сечением называется
минимальное число ребер или вершин,
удаление которых делает две вершины
графа vs
и vt
несвязными.
Для того, чтобы
сделать две вершины vs
и vtнесвязными,
нужно либо нарушить все пути Мst,
связывающие эти вершины, либо хотя бы
одно из сечений st
ε Sst
, где Sst
– множество сечений между вершинами
vs
и vt.
Между множеством
путей Мst
и множеством сечений Sst
, а также множеством базисных разрезов
существуют однозначные взаимосвязи.
Множество сечений
Sst
можно получить из дизъюнктивно-нормальной
формы записи множества путей Мst
, заменив знаки конъюнкции на знаки
дизъюнкции и наоборот, используя булеву
алгебру. Поскольку в булевой алгебре 1
U
1 = 1, то а.а = а; а U
а = а; 1.а = а;
1 U
а = 1; а(а U
в) = а; а Uав
= а; а. ā = 0; а U
ā =1.
Например,
М13
= b U ad Uce → S13
= b.(a U d).(c U e).
Здесь U
и (.) –знаки дизъюнкции и конъюнкции.
Скобки удобнее раскрывать последовательно.
b(a U d) = (b a U b d)
( b a U b d )( cU e ) = a b c U b c d U a b e U b
d e = S13
Аналогично из
перечисления сечений Sst
можно получить выражение для перечисления
множества путей Мst,
произведя замену знаков дизъюнкций и
конъюнкций. S13
=a b c U
b c d U
a b e U
b d e → М13
= ( a U
b U
c).(b U
c U
d).(a U
b U
c ).(b U
d U
c).(a U
b U
c).(b U
c U
d)= abUadUacU
b UcbUcdU
c = (adU
b U
c) посколку a Uab
= a такие пары скобок дает: (a U
b U
e)(b U
d U
e) = abUadUacU
b UbdUbcUacUbcU
e = adU
b U
e окончательно получим:
(adU
b
U
c)(adU
b
U
e)
= ad
UabdUabeUabdU
b
U
be
U
cad
Uce
= b
U
ad
Uce
= М13
.Запишем полученное множество сечений

|
a e1 |
b e2 |
с e3 |
d e4 |
е e5 |
|
|
|
1 |
1 |
1 |
0 |
0 |
|
|
0 |
1 |
1 |
1 |
0 |
|
|
1 |
1 |
0 |
0 |
1 |
|
|
0 |
1 |
0 |
1 |
1 |
Запишем также
матрицу базисных разрезов относительно
остовного дерева{e1
, e2
, e3},
полученную ранее
|
e1 |
e2 |
e3 |
e4 |
e5 |
|
|
s1 |
1 |
0 |
0 |
1 |
0 |
|
s2 |
0 |
1 |
0 |
1 |
1 |
|
s3 |
0 |
0 |
1 |
0 |
1 |
Из
соотношения матриц сечений и базисных
разрезов видно, что:
S113
= S1
S2
S3 =
S4
S213
= S2
S3 =
S5
S313
= S1
S2 =
S6
S413= S2 =
S2
Таким
образом, каждое сечение является
линейнной комбинацией базисных разрезов.
Запишем полученные разрезы в одну
матрицу.
|
e1 |
e2 |
e3 |
e4 |
e5 |
|
|
s1 |
1 |
0 |
0 |
0 |
1 |
|
s2 |
0 |
1 |
0 |
1 |
1 |
|
s3 |
0 |
0 |
1 |
0 |
1 |
|
s4 |
1 |
1 |
1 |
0 |
0 |
|
s5 |
0 |
1 |
1 |
1 |
0 |
|
s6 |
1 |
1 |
0 |
0 |
1 |
Как видно из графа
G1
на рис.21а, матрица охватывает все
возможные разрезы этого графа.
Множество сечений
Sst
является подмножеством всех возможных
сечений.
Таким
образом, нами рассмотрены способы
определения по матрице смежности или
структурной матрице наличия путей, их
количества и перечисления путей между
произвольными вершинами графа.
На
основе логическной формы записи множества
путей рассмотрен способ получения
сечений и установлена взаимосвязь между
множеством сечений и базисным множеством
разрезов.
Как видно из графа
G1
на рис.1.21а, матрица охватывает все
возможные разрезы этого графа.
Множество сечений
Sst
является подмножеством всех возможных
сечений.
Таким
образом, нами рассмотрены способы
определения по матрице смежности или
структурной матрице наличия путей, их
количества и перечисления путей между
произвольными вершинами графа.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
24.2 Матрицы и графы. Нахождение путей и сечений
с помощью структурной матрицы
Трудно переоценить роль матриц в теории графов (в частности, матрицы полезны, чтобы данный граф более “легко” воспринимался компьютером). Перечислим наиболее известные матрицы.
- Матрица смежности. Это квадратная матрица порядка п (п – число вершин), в которой нули стоят по главной диагонали (если в графе нет петель, а если петли есть в вершине k (и число этих петель равно р), то на главной диагонали в строчке с номером k стоит число р). Если вершина i связана с вершиной j одним ребром, то элемент матрицы смежности aij равен 1, если эти вершины связаны s ребрами, то аij= s. Аналогичным образом строятся матрицы смежности для орграфов и для мультиграфов.
Легко видеть, что матрица В =А2 = АА составлена из целых чисел bij, которые равны числу путей длины 2, соединяющих вершины i и j. Понятно, что А3 составлена из чисел, равных числу путей длины 3 (т. е. путей из 3-х ребер) из вершины i в вершину j и т. д.
- Матрица инциденций – это матрица размера n´ m, где n – число вершин, а m – число ребер графа, при этом ее элементы kij равны 1, если вершина с номером i является для ребра с номером j начальной или конечной (если ребро неориентировано) и начальной для ориентированных ребер. Заметим, что матрица инциденций сравнительно редко используется, так как в современных условиях (где число ребер часто очень велико) она имеет слишком большое число столбцов.
- Структурная матрица. Именно эта матрица имеет особое значение в теории сетей связи. Структурная матрица – это символьная матрица порядка п. Она составляется следующим образом: на главной диагонали стоит 1, т. е. aii = 1, остальные элементы – это символьные обозначения ребер (если вершины i и j не соединены ребром, то aii = 0). При этом, если при i<j вершины i и j соединены ребром а, то элемент sij = a, при i>j – это отрицание а, которое обычно отмечается чертой сверху. Если связи вершины i c вершиной j нет, то соответствующий элемент равен 0, структурная матрица может составляться и для орграфа и для мультиграфа без петель (здесь если два ребра а и b соединяют две вершины, то соответствующий элемент при i <j равен aÚ b, а при i>j этот элемент равен
Отметим, что в учебных целях, когда действия с матрицами осуществляются студентами “вручную” (число вершин в графе невелико), можно обозначать ребра латинскими буквами без индексов a, b, c и т. д., но при использовании компьютера гораздо удобнее обозначать ребра а(i,j), если это ребро соединяет вершины i и j при i<j и с чертой сверху, если i>j.
Теорема. Для того чтобы найти все пути (простые) из вершины i в вершину j достаточно раскрыть минор M(j,i) структурной матрицы методами булевой алгебры. При этом раскрытие минора производится обычными действиями с определителями, но при этом сложение заменяется дизъюнкцией, умножение – конъюнкцией, знаки умножения на числа не используются.
Подробно доказывать эту теорему не будем, но отметим, что определитель равен сумме (в данном случае дизъюнкции) элементов, взятых по одному из каждой строчки и каждого столбца с определенным знаком. В нашем случае знаки не присутствуют, а значит, любой член раскрытия определителя всей структурной матрицы S соответствует циклу в графе. Если же брать минор M(j,i), то его раскрытие соответствует тем членам определителя, в которых имелся элемент s(j,i), но без самого этого элемента (таким образом, индексы i и j встречаются вместо двух только один раз). Это и означает, что получаем маршрут от вершины с номером i к вершине с номером j.
Понятно, что раскрытие минора методами булевой алгебры предусматривает, что верны следующие соотношения: 1Ú a = 1, (это свойство нужно, для того чтобы не проходить по одному ребру дважды в противоположных направлениях), а также используется правило простого поглощения (хÚ ху = х). Видно, что если не использовать правило поглощения, то получим все маршруты (без повторения ребер), связывающие вершины i и j.
Примечание. 1. Если граф не ориентирован, то миноры M(j,i) и M(i,j) совпадают.
2. После получения ответа, черточки над обозначениями ребер (т. е. отрицания) можно убрать (на самом деле “черта” над ребром означает, что ребро проходится от вершины с большим номером к вершине с меньшим номером). Затем рекомендуется записать каждый путь по порядку прохождения ребер (в этом случае удобны обозначения ребер с индексами вершин).
Сечением (разрезом) между вершинами i и j называется неизбыточный набор ребер, при удалении которых из графа теряется связь между данными вершинами (не существует пути из вершины i в вершину j). Заметим, что сечений между данными вершинами может быть много, и они могут содержать разное количество ребер.
Слово “неизбыточный” означает, что если любое ребро из сечения снова возвратить в граф, то связь восстановится.
Естественно, что если известны все пути из вершины i в вершину j, причем эти пути заданы в виде ДНФ, т. е. дизъюнктивной нормальной формы (а именно такой вид получается после раскрытия соответствующего минора структурной матрицы), то все сечения между этими вершинами можно получить отрицанием этих путей (по правилу де Моргана конъюнкцию заменить на дизъюнкцию и наоборот), затем полученное выражение снова привести к ДНФ, используя раскрытие скобок по обычным правилам, при этом правило поглощения обеспечит неизбыточность набора ребер в каждом сечении. Ясно, что знаки отрицания (черточки над символами ребер) можно опустить.
Занятие 3-4: Графы — основные определения¶
Цель: Повторить на практике основные определения теории графов и освоить использование библиотеки визуализации NetworkX¶
Повторить¶
- Определение понятия граф, вершины, ребра, матрица смежности, ориентрованный и не ориентированный граф.
- Гамильтонов цикл.
- Задача коммивояжёра.
- Поиск длины кратчайшего пути при помощи алгоритма Дейкстры.
Основные определения¶
Графом называется конечное множество вершин и множество ребер. Каждому ребру сопоставлены две вершины – концы ребра.
В ориентированном графе одна вершина считается начальной, а другая – конечной.
Если некоторое ребро u соединяет две вершины A и B графа, то говорят, что ребро u инцидентно вершинам A и B, а вершины в свою очередь инцидентны ребру u.
Вершины, соединенные ребром, называются смежными.
Ребра называются кратными, если они соединяют одну и ту же пару вершин (а в случае ориентированного графа – если у них совпадают начала и концы).
Ребро называется петлей, если у него совпадают начало и конец.
Степенью вершины в неориентированном графе называется число инцидентных данной вершине ребер (при этом петля считается два раза, то есть степень – это количество «концов» ребер, входящих в вершину).
Путем на графе называется последовательность ребер, в которой конец одного ребра является началом следующего ребра. Начало первого ребра называется началом пути, конец последнего ребра – концом пути.
Если начало и конец пути совпадают, то такой путь называется циклом.
Путь, который проходит через каждую вершину не более одного раза называется простым путем. Аналогично определяется простой цикл.
Граф называется связным, если между любыми двумя его вершинами есть путь.
Если граф несвязный, то его можно разбить на несколько частей (подграфов), каждая из которых будет связной. Такие части называются компонентами связности.
Деревом называется связный граф не содержащий простых циклов.
Способы представления графов в памяти¶
Матрица смежности¶
При представлении графа матрицей смежности информация о ребрах графа хранится в квадратной матрице (двумерном списке), где элемент A[i][j] равен 1, если ребра i и j соединены ребром и равен 0 в противном случае.
Если граф неориентированный, то матрица смежности всегда симметрична относительно главной диагонали.
Задание 1 Напишите код, заполняющий матрицу смежности для графа, представленного на рисунке ниже
Список смежности¶
При представлении графа списками смежности для каждой вершины i хранится список W[i] смежных с ней вершин.
Например, для графа выше:
W[0] = [1, 2] W[1] = [0, 2] W[2] = [0, 1, 2]
Таким образом, весь граф можно представить одним списком, состоящим из вложенных списков смежности вершин.
W = [[1, 2], [0, 2], [0, 1, 2]]
В таком способе удобно перебирать ребра, выходящие из вершины i (это просто список W[i]), но сложно проверять наличие ребра между вершинами i и j – для этого необходимо проверить, содержится ли число j в списке W[i].
Но в языке Python можно эту часть сделать более эффективной, если заменить списки на множества – тогда проверка существования ребра между двумя вершинами также будет выполняться за О(1).
Задание 2 — В ячейке ниже реализуйте код, который строит список смежности на основе множеств из матрицы смежности, графа из задания 1. Проверьте в коде существование ребер между вершинами графа, изображенного выше. Для каждой пары вершин, между которыми существует ребро, выведите True и False в противном случае.
Взвешенные графы¶
Очень часто рассматриваются графы, в которых каждому ребру приписана некоторая числовая характеристика — вес. Соответствующие графы называются взвешенными.
При представлении графа матрицей смежности вес ребра можно хранить в матрице, то есть A[i][j] в данном случае будет равно весу ребра из i в j. При этом при отсутствии ребра можно хранить специальное значение, например, None.
При представлении графа списками смежности можно поступить двумя способами. Можно в списках смежности хранить пару (кортеж) из двух элементов – номер конечной вершины и вес ребра. Но в этом случае неудобно проверять наличие ребра между двумя вершинами.
Другой способ – хранить списки смежности как ранее, а веса ребер хранить в отдельном ассоциативном массиве (dict в Python), в котором ключом будет пара из двух номеров вершин (номер начальной и конечной вершины), а значением будет вес ребра между этими вершинами.
Гамильтонов цикл¶
Гамильтоновым циклом в графе называют цикл, проходящий через все вершины.
Гамильтонов путь — незамкнутый путь, проходящий через все вершины.
Ниже приведен переборный алгоритм поиска гамильтонова цикла в графе.
Если перенумеровать вершины в графе, то номера вершин в порядке следования их в гамильтоновом цикле образуют некоторую перестановку чисел от 1 до n. Можно перебрать все возможные перестановки и для каждой из них проверить, что данная перестановка соответствует циклу на графе, то есть каждые два соседних элемента в перестановке, а также первый и последний элемент перестановки соединены ребром.
Алгоритм поиска перестановок во многом напоминает алгоритм обхода в глубину, но главное его отличие заключается в том, что если из какой-то вершины не удается продолжить путь дальше (то есть были рассмотрены все ребра и все возможные продолжения привели в тупик), то алгоритм возвращается в предыдущую вершину, при этом покинутая вершина «перекрашивается», то есть с нее снимается отметка о том, что эта вершина была посещена ранее. При этом алгоритм может вернуться в эту вершину еще раз, уже по другому пути (и даже обязан это сделать, если в графе существует гамильтонов путь, так как гамильтонов путь проходит через все вершины).
Пусть n — число вершин в графе, вершины пронумерованы числами от 0 до n-1. Граф задан матрицей смежности A. В глобальной переменной Path будет храниться список вершин, входящих в путь. Функция hamilton() принимает в качестве параметра номер вершины, добавляемой к пути и возвращает значение True, если удалось построить гамильтонов путь и False, если не удалось. Причем если путь построить удалось, то построенный путь будет храниться в списке Path:
Visited = [False] * n Path = [] def hamilton(curr): Path.append(curr) if len(Path) == n: if A[Path[0]][Path[-1]] == 1: return True else: Path.pop() return False Visited[curr] = True for next in range(n): if A[curr][next] == 1 and not Visited[next]: if hamilton(next): return True Visited[curr] = False Path.pop() return False
Функция hamilton() прежде всего добавляет вершину curr в конец списка Path. При этом если длина списка стала равна n, то есть все вершины включены в путь Path, проверяется, что первая и последняя вершина в пути соединены ребром (это не требуется при помощи гамильтонова пути), если это так — то алгоритм возвращает True (цикл найден), в противном случае из списка Path удаляется последний элемент и алгоритм возвращает False (цикл не найден).
Если же длина списка меньше n, то вершина curr отмечается, как посещенная и осуществляется перебор дальнейших продолжений. Последовательно перебираются все оставшиеся вершины next и если вершина next соединена ребром с curr и вершина next не была посещена, то алгоритм рекурсивно запускается из вершины next, пытаясь сделать продолжение пути в вершину next. При этом если рекурсивный вызов из вершины next вернет True, то есть удалось построить цикл, то алгоритм сразу же возвращает True, при этом из списка Path ничего не удаляется, поэтому Path будет хранить полный гамильтонов цикл. Если же ни одно из продолжений не получилось, то осуществляется «откат» вершины curr — она помечается, как непосещенная, удаляется из конца списка Path и управление передается назад, на последнюю вершину в списке Path.
Видно, что сложность алгоритма может быть не менее, чем n!, поэтому для больших графов такой алгоритм непригоден.
Задание 3 — Для графа из задания 3 выведите на экран гамильтонов цикл.
Задача коммивояжера¶
Близкой задачей к задаче нахождения гамильтонова цикла является задача коммивояжера. Коммивояжеру необходимо посетить n городов и вернуться домой. Коммивояжер не хочет посещать города более одного раза и при этом хочет проделать наиболее короткий путь. То есть в неориентированном взвешенном графе необходимо найти путь наименьшей стоимости.
Задача коммивояжера решается аналогично задаче о гамильтоновом пути, но при этом нужно перебрать все возможные пути. При замыкании пути нужно вычислить его вес (лучше это делать не в конце замыкания, а одновременно с добавлением следующей вершины увеличивать вес построенного фрагмента пути на вес рассмотренного ребра) и сравнить вес найденного пути с весом наилучшего известного пути.
Алгоритм Дейкстры¶
Алгоритм Дейкстры назван в честь голландского ученого Эдсгера Дейкстры (Edsger Dijkstra). Алгоритм был предложен в 1959 году для нахождения кратчайших путей от одной вершины до всех остальных в ориентированном взвешенном графе, при условии, что все ребра в графе имеют неотрицательные веса.
Рассмотрим две модели хранения взвешенного графа в памяти. В первой модели (матрица смежности) будем считать, что вес ребра из вершины i в вершину j равен w[i][j], то есть в матрице w хранятся веса ребра для любых двух вершин. Если из вершины i в вершину j нет ребра, то w[i][j]==INF для некоторого специального значения константы INF. Значение INF следует выбирать исходя из задачи.
Алгоритм Дейкстры относится к так называемым «жадным» алгоритмам. Пусть расстояние от начальной вершины start до вершины i хранится в массиве dist[i]. Начальные значения dist[start]=0, dist[i]=INF для всех остальных вершин i. То есть в самом начале алгоритму известен путь из вершины start до вершины start длины 0, а до остальных вершин кратчайшие пути неизвестны. Между тем алгоритм будет постепенно улучшать значения в массиве dist, в результате получит кратчайшие расстояния до всех вершин.
Основная идея для улучшения называется «релаксацией ребра». Пусть из вершины i в вершину j есть ребро веса w[i][j], при этом выполнено неравенство dist[i] + w[i][j] < dist[j]. То есть можно построить маршрут из начальной вершины до вершины i и добавить к нему ребро из i в j, и суммарная стоимость такого маршрута будет меньше, чем известная ранее стоимость маршрута из начальной вершины в вершину j. Тогда можно улучшить значение dist[j], присвоив dist[j] = dist[i] + w[i][j].
В алгоритме Дейкстры вершины красятся в два цвета, будем говорить, что вершина «неокрашенная» или «окрашенная». Изначально все вершины неокрашенные. Если алгоритм Дейкстры покрасил вершину i, то это означает, что найденное значение dist[i] является наилучшим возможным и в последствии не будет улучшаться, то есть значение dist[i] является кратчайшим расстоянием от начальной вершины до вершины i. Если же вершина не покрашена, то величина dist[i] для такой вершины i равна кратчайшему пути из вершины start до вершины i, который проходит только по покрашенным вершинам (за исключением самой вершины i).
На каждом шаге алгоритма Дейкстры красится одна новая вершина. В качестве такой вершины выбирается неокрашенная вершина i с наименьшим значением D[i]. Затем рассматриваются все ребра, исходящие из вершины i, и производится релаксация этих ребер, то есть улучшаются расстояния до вершин, смежных с i.
Алгоритм заканчивается, когда на очередном шаге не останется неокрашенных вершин или если расстояние до всех неокрашенных вершин будет равно INF (то есть эти вершины являются недостижимыми).
Запишем алгоритм Дейкстры. Пусть — число вершин в графе, вершины пронумерованы от 0 до n-1. Номер начальной вершины — start и веса ребер хранятся в матрице w:
INF = 10 ** 10 dist = [INF] * n dist[start] = 0 used = [False] * n min_dist = 0 min_vertex = start while min_dist < INF: i = min_vertex used[i] = True for j in range(n): if dist[i] + w[i][j] < dist[j]: dist[j] = dist[i] + w[i][j] min_dist = INF for j in range(n): if not used[j] and dist[j] < min_dist: min_dist = dist[j] min_vertex = j
Массив used будет хранить информацию о том, была ли покрашена вершина. Сначала инициализируются массивы dist и used. Затем запускается внешний цикл алгоритма, который выбирает неокрашенную вершину с минимальным расстоянием, номер этой вершины хранится в переменной min_vertex, а расстояние до этой вершины — в переменной min_dist. Если же min_dist оказывается равно INF, то значит все неокрашенные вершины являются недостижимыми и алгоритм заканчивает свою работу. Иначе найденная вершина окрашивается и после этого релаксируются все ребра, исходящие из этой вершины.
Для восстановления ответа, то есть для нахождения пути из начальной вершины до всех остальных, необходимо построить дерево кратчайших путей. Это дерево будет состоять из тех ребер, которые были успешно срелаксированы в результате исполнения алгоритма. То есть если происходит релаксация ребра из i в j, то теперь кратчайший маршрут из вершины start до вершины j должен проходить через вершину i и затем содержать ребро i-j. Тем самым вершина i становится предшественником вершины j на кратчайшем пути из начальной вершины до вершины j.
Рассмотрим реализацию алгоритм Дейкстры с восстановлением ответа на графе, хранимым в виде списка смежности на языке Python. Набор вершин, смежных с вершиной i будет храниться в множестве w[i]. Также необходимо хранить веса ребер, будем считать, что для хранения весов ребер используется словарь weight, где ключом является кортеж из двух вершин. То есть вес ребра из i в j хранится в элементе weight[i, j] словаря весов:
dist = [INF] * n dist[start] = 0 prev = [None] * n used = [False] * n min_dist = 0 min_vertex = start while min_dist < INF: i = min_vertex used[i] = True for j in w[i]: if dist[i] + weight[i, j] < dist[j]: dist[j] = dist[i] + weight[i, j] prev[j] = i min_dist = INF for i in range(n): if not used[i] and dist[i] < min_dist: min_dist = dist[i] min_vertex = i
Для нахождения кратчайшего пути из вершины start до вершины j будем переходить от каждой вершины к ее предшественнику:
path = [] while j is not None: path.append(j) j = prev[j] path = path[::-1]
Алгоритм Дейкстры применим только в том случае, когда веса всех ребер неотрицательные. Это гарантирует то, что после окраски расстояние до вершины не может быть улучшено. Если в графе могут быть ребра отрицательного веса, то следует использовать другие алгоритмы.
Задание 4 — Для ненаправленного взвешенного графа, заданного парами вершин и их весов найдите кратчайший путь из вершины 0 в вершину 3 с помощью алгоритма Дейкстры:
- (0, 1, вес = 10)
- (0, 2, вес = 40)
- (1, 2, вес = 15)
- (0, 3, вес = 20)
- (3, 1, вес = 5)
Библиотека NetworkX для визуального представления графов¶
При решении задач контеста удобным инструментом для визуализации графов из примеров является библитотека NetworkX.
Установка библиотеки:
Подключение библиотеки:
NetworkX предназначена для изучения структуры, динамики и функционирования сложных сетей. Она позволяет создавать и хранить графы в стандартных и нестандартных форматах, генерировать много типов случайных и классических графов, анализировать их структуру, строить сетевые модели и создавать новые алгоритмы.
Документация на библиотеку находится по адресу.
Классы графов¶
NetworkX содержит четыре класса графов:
- Graph — граф без кратных рёбер (петли допустимы)
- DiGraph — ориентированный граф без кратных рёбер (петли допустимы)
- MultiGraph — граф с кратными рёбрами (в том числе с кратными
петлями) - MultiDiGraph — ориентированный граф с кратными рёбрами (в том
числе с кратными петлями)
Внутреннее представление графов реализовано в виде списков смежности (словарь словарей словарей). Однако во избежании появления несогласованности, все операции с графами должны производится с использованием API функций библиотеки.
Вершины и рёбра¶
Вершиной может быть любой неизменяемый тип с вычислимой функцией hash().
Например, подойдут соедующие типы Python:
- str
- int
- float
- кортеж из строк и чисел
- frozenset (неизменяемое множество)
Рёбра представляют собой связь двух вершин и чаще вершины имеют привязанные к ним данные — свойства рёбер. Для указания веса ребра, используйте свойство weight.
Создание графа¶
Графы могут быть созданы тремя основными способами:
- явное добавление узлов и рёбер
G = nx.Graph() # создаём экземпляр графа G.add_edge(1, 2) # ребро добавляется сразу со своими вершинами G.add_edge(2, 3) # стандартный вес ребра weight=1 G.add_edge(3, 4, weight = 0.9) # можно задать weight сразу при создании ребра G.add_node(5) # изолированный узел можно добавить отдельно G.add_node(6, x = 1.5, y = -5.0, data = ['any']) # и сразу задать ему любые свойства
- генераторами графов — алгоритмами порождения стандартных сетевых
топологий
G = nx.complete_graph(10) # полносвязный граф с 10 вершинами G = nx.path_graph(10) # 10 узлов, расположенных "в линеечку" G = nx.cycle_graph(10) # 10 узлов, связанных кольцом G = nx.star_graph(5) # звезда с 1 узлом в середине и 5 узлами-лучами G = nx.balanced_tree(2, 3) # сбалансированное двоичное дерево высоты 3 G = nx.empty_graph(10) # граф с 10 вершинами без рёбер
- импорт данных графа из некоторого формата (обычно из файла)
d = {0: {1: {'weight': 10}, 2: {'weight': 20}}, 1: {0: {'weight': 10}, 3: {'weight': 30}}, 2: {0: {'weight': 20}}, 3: {1: {'weight': 30}}} G = nx.Graph(d) dd = nx.to_dict_of_dicts(G) # d == dd
Визуализация графа¶
Визуализация графов — нетривиальная задача! Существует много полноценных библиотек, предназначенных именно для этого: Cytoscape, Gephi, Graphviz или PGF/TikZ для LaTeX. Для их использования можно экспортировать граф из NetworkX в формат GraphML.
Однако, есть и самый простой способ визуализации, встроенный в саму библиотеку NetworkX, при подключении библиотеки
matplotlib.pyplot.
nx.draw(G) # отобразить граф при помощи Matplotlib nx.draw_circular(G) # Использовать расположение circular layout nx.draw_random(G) # Использовать расположение random layout nx.draw_spectral(G) # Использовать расположение spectral layout nx.draw_spring(G) # Использовать расположение spring layout nx.draw_shell(G) # Использовать расположение shell layout nx.draw_graphviz(G) # Использовать graphviz для расположения вершин
Перед выполнением примера ниже не забудьте установить библиотеку matplotlib:
pip install -U matplotlib
Пример визуализации графа №1¶
Выполните приведенный ниже пример в ячейке code
import matplotlib.pyplot as plt import networkx as nx G=nx.path_graph(8) nx.draw(G) plt.savefig("simple_path.png") # сохранить как png файл plt.show() # вывести на экран
Пример визуализации графа №2¶
Пример добавления этикеток на вершины и подкрашивания рёбер:
""" Отрисовка графа через matplotlib, с разными цветами. """ __author__ = """Aric Hagberg (hagberg@lanl.gov)""" import matplotlib.pyplot as plt import networkx as nx G=nx.cubical_graph() pos=nx.spring_layout(G) # позиции всех вершин # вершины nx.draw_networkx_nodes(G, pos, nodelist=[0,1,2,3], # список вершин node_color='r', # красный цвет node_size=500, # размер alpha=0.8) # прозрачность nx.draw_networkx_nodes(G, pos, nodelist=[4,5,6,7], node_color='b', node_size=500, alpha=0.8) # рёбра nx.draw_networkx_edges(G, pos, width=1.0, alpha=0.5) # все рёбра nx.draw_networkx_edges(G, pos, edgelist=[(0,1),(1,2),(2,3),(3,0)], width=8, alpha=0.5, edge_color='r') # красные рёбра nx.draw_networkx_edges(G, pos, edgelist=[(4,5),(5,6),(6,7),(7,4)], width=8, alpha=0.5, edge_color='b') # синие рёбра # добавим математические названия вершин labels={} labels[0]=r'$a$' labels[1]=r'$b$' labels[2]=r'$c$' labels[3]=r'$d$' labels[4]=r'$alpha$' labels[5]=r'$beta$' labels[6]=r'$gamma$' labels[7]=r'$delta$' nx.draw_networkx_labels(G, pos, labels, font_size=16) plt.axis('off') plt.savefig("labels_and_colors.png") # сохранить как png картинку plt.show() # вывести на экран
Выполните пример в ячейке ниже.
Пример визуализации графа №3¶
Ещё один пример добавления этикеток на вершины и подкрашивания рёбер:
""" Пример использования Graph как взешенного. """ __author__ = """Aric Hagberg (hagberg@lanl.gov)""" import matplotlib.pyplot as plt import networkx as nx G = nx.Graph() # добавляем рёбра и вершины G.add_edge('a', 'b', weight=0.6) G.add_edge('a', 'c', weight=0.2) G.add_edge('c', 'd', weight=0.1) G.add_edge('c', 'e', weight=0.7) G.add_edge('c', 'f', weight=0.9) G.add_edge('a', 'd', weight=0.3) elarge = [(u,v) for (u,v,d) in G.edges(data=True) if d['weight'] >0.5] # "тяжёлые" esmall = [(u,v) for (u,v,d) in G.edges(data=True) if d['weight'] <=0.5] # "лёгкие" pos = nx.spring_layout(G) # позиции всех вершин # вершины nx.draw_networkx_nodes(G, pos, node_size=700) # рёбра nx.draw_networkx_edges(G, pos, edgelist=elarge, width=6) # "тяжёлые" nx.draw_networkx_edges(G, pos, edgelist=esmall, width=6, alpha=0.5, edge_color='b', style='dashed') # "лёгкие" # метки nx.draw_networkx_labels(G,pos,font_size=20,font_family='sans-serif') plt.axis('off') plt.savefig("weighted_graph.png") # сохранить как png картинку plt.show() # вывести на экран
|
anastasyi 1 / 1 / 0 Регистрация: 03.09.2021 Сообщений: 40 |
||||||||
|
1 |
||||||||
Алгоритм поиска количества всех возможных путей между двумя вершинами графа на основе графа матрицы смежности16.03.2023, 12:37. Показов 750. Ответов 6 Метки нет (Все метки)
Добрый всем день! помогите с заданием! Нужно найти количество всех возможных путей в графе, используя обход графа в глубину. Прошу помощи, поправьте код, что я делаю не так? Предисловие к заданию: Для решения задачи нужно модифицировать алгоритм обхода в глубину. Идея в том, что алгоритм запускается из какой-то из двух вершин, для которых ищется количество путей. После посещения очередной вершины, нужно проверить, не попал ли алгоритм в конечную вершину. В случае, если попал, нужно завершить обход для текущей рекурсивной ветви и увеличить количество найденных путей на единицу. Также нужно контролировать счетчик посещенных вершин visited. На каждой итерации он должен содержать набор вершин, которые присутствуют в пути на данной итерации. Имеется ввиду, что, например, когда алгоритм зашёл в тупик (у текущей вершины нет смежных непосещенных вершин), то при возвращении к предыдущей вершине текущую нужно обозначать как непосещеннуюvisited[current] = false. Таким образом в visited будут содержаться только те вершины, которые участвуют в текущем пути. В конце алгоритм должен пройти по всем возможным путям в графе. graph.h
Graph.cpp
0 |
|
SmallEvil 2339 / 1867 / 606 Регистрация: 29.06.2020 Сообщений: 7,056 |
||||||||||||
|
16.03.2023, 14:18 |
2 |
|||||||||||
|
Решение
Добавлено через 16 минут
Простой тест :
1 |
|
1 / 1 / 0 Регистрация: 03.09.2021 Сообщений: 40 |
|
|
17.03.2023, 06:43 [ТС] |
3 |
|
SmallEvil, Огромное вам спасибо! Очень сильно помогли!
0 |
|
SmallEvil 2339 / 1867 / 606 Регистрация: 29.06.2020 Сообщений: 7,056 |
||||
|
17.03.2023, 12:45 |
4 |
|||
|
Решение
Очень сильно помогли! Тут есть еще один нюанс. В вашем описании задания, как то упоминается массив посещенных вершин.
Код Pathes : 1 -> 2 -> 3 -> 4 -> 1 -> 2 -> 4 -> 1 -> 3 -> 2 -> 4 -> 1 -> 3 -> 4 -> Total : 4 Как видим есть два пути с вершинами 1 2 3 4, но различным порядком обхода. Добавлено через 4 минуты
Как видим есть два пути с вершинами 1 2 3 4, но различным порядком обхода. Теперь если вас спросят почему вы не брали вершины из таблицы посещений – у вас будет четкий ответ.
1 |
|
1 / 1 / 0 Регистрация: 03.09.2021 Сообщений: 40 |
|
|
17.03.2023, 12:56 [ТС] |
5 |
|
SmallEvil, спасибо, я себе законспектирую прям)Неожиданно быстрый и четкий ответ). Но спросят врядли. там бот проверяет задания.
0 |
|
2339 / 1867 / 606 Регистрация: 29.06.2020 Сообщений: 7,056 |
|
|
17.03.2023, 13:02 |
6 |
|
там бот проверяет задания Тогда будет лично для вас, для понимания.
0 |
|
1 / 1 / 0 Регистрация: 03.09.2021 Сообщений: 40 |
|
|
17.03.2023, 13:11 [ТС] |
7 |
|
SmallEvil, можно.Там только тесты у него скрыты. Остальные файлы можно перекроить, ну по идее можно и тестируемые данные вывести вначале из майна. но это и не важно. главное чтобы алгоритм сам работал. Что-то тяжело алгоритмы мне даются..
0 |
Трудно переоценить роль матриц в теории графов (в
частности, матрицы полезны, чтобы данный граф более “легко”
воспринимался компьютером). Перечислим наиболее известные матрицы.
- Матрица смежности. Это квадратная матрица порядка п (п – число вершин), в которой нули стоят по главной диагонали (если в графе нет петель, а если петли есть в вершине k (и число этих петель равно р), то на главной диагонали в строчке с номером k стоит число р). Если вершина i связана с вершиной j одним ребром, то элемент матрицы смежности aij равен 1, если эти вершины связаны s ребрами, то аij= s. Аналогичным образом строятся матрицы смежности для орграфов и для мультиграфов.
- Матрица инциденций – это матрица размера nґ
m, где n – число вершин, а m – число ребер графа, при этом ее элементы kij равны 1, если вершина с номером i является для ребра с номером j начальной
или конечной (если ребро неориентировано) и начальной для
ориентированных ребер. Заметим, что матрица инциденций сравнительно
редко используется, так как в современных условиях (где число ребер
часто очень велико) она имеет слишком большое число столбцов. - Структурная матрица. Именно эта матрица имеет особое значение в теории сетей связи. Структурная матрица – это символьная матрица порядка п. Она составляется следующим образом: на главной диагонали стоит 1, т. е. aii = 1, остальные элементы – это символьные обозначения ребер (если вершины i и j не соединены ребром, то aii = 0). При этом, если при i<j вершины i и j соединены ребром а, то элемент sij = a, при i>j – это отрицание а, которое обычно отмечается чертой сверху. Если связи вершины i c вершиной j нет,
то соответствующий элемент равен 0, структурная матрица может
составляться и для орграфа и для мультиграфа без петель (здесь если два ребра а и b соединяют две вершины, то соответствующий элемент при i <j равен aЪ
b, а при i>j этот элемент равен
Легко видеть, что матрица В =А2 = АА составлена из целых чисел bij, которые равны числу путей длины 2, соединяющих вершины i и j. Понятно, что А3 составлена из чисел, равных числу путей длины 3 (т. е. путей из 3-х ребер) из вершины i в вершину j и т. д.
Отметим, что в учебных целях, когда действия с матрицами осуществляются
студентами “вручную” (число вершин в графе невелико), можно обозначать
ребра латинскими буквами без индексов a, b, c и т. д., но при использовании компьютера гораздо удобнее обозначать ребра а(i,j), если это ребро соединяет вершины i и j при i<j и с чертой сверху, если i>j.
Теорема. Для того чтобы найти все пути (простые) из вершины i в вершину j достаточно раскрыть минор M(j,i)
структурной матрицы методами булевой алгебры. При этом раскрытие минора
производится обычными действиями с определителями, но при этом сложение
заменяется дизъюнкцией, умножение – конъюнкцией, знаки умножения на
числа не используются.
Подробно доказывать эту теорему не будем, но отметим,
что определитель равен сумме (в данном случае дизъюнкции) элементов,
взятых по одному из каждой строчки и каждого столбца с определенным
знаком. В нашем случае знаки не присутствуют, а значит, любой член
раскрытия определителя всей структурной матрицы S соответствует циклу в графе. Если же брать минор M(j,i), то его раскрытие соответствует тем членам определителя, в которых имелся элемент s(j,i), но без самого этого элемента (таким образом, индексы i и j встречаются вместо двух только один раз). Это и означает, что получаем маршрут от вершины с номером i к вершине с номером j.
Понятно, что раскрытие минора методами булевой алгебры предусматривает, что верны следующие соотношения: 1Ъ
a = 1, (это
свойство нужно, для того чтобы не проходить по одному ребру дважды в
противоположных направлениях), а также используется правило простого
поглощения (хЪ
ху = х). Видно, что если не использовать правило поглощения, то получим все маршруты (без повторения ребер), связывающие вершины i и j.
Примечание. 1. Если граф не ориентирован, то миноры M(j,i) и M(i,j) совпадают.
2. После получения ответа, черточки над обозначениями
ребер (т. е. отрицания) можно убрать (на самом деле “черта” над ребром
означает, что ребро проходится от вершины с большим номером к вершине с
меньшим номером). Затем рекомендуется записать каждый путь по порядку
прохождения ребер (в этом случае удобны обозначения ребер с индексами
вершин).
Сечением (разрезом) между вершинами i и j называется
неизбыточный набор ребер, при удалении которых из графа теряется связь
между данными вершинами (не существует пути из вершины i в вершину j). Заметим, что сечений между данными вершинами может быть много, и они могут содержать разное количество ребер.
Слово “неизбыточный” означает, что если любое ребро из сечения снова возвратить в граф, то связь восстановится.
Естественно, что если известны все пути из вершины i в вершину j, причем
эти пути заданы в виде ДНФ, т. е. дизъюнктивной нормальной формы (а
именно такой вид получается после раскрытия соответствующего минора
структурной матрицы), то все сечения между этими вершинами можно получить отрицанием этих
путей (по правилу де Моргана конъюнкцию заменить на дизъюнкцию и
наоборот), затем полученное выражение снова привести к ДНФ, используя
раскрытие скобок по обычным правилам, при этом правило поглощения
обеспечит неизбыточность набора ребер в каждом сечении. Ясно, что знаки
отрицания (черточки над символами ребер) можно опустить. Пример на эту
тему приведен в разд. 15 (примеры решения типовых задач).





 d
d e
e
 Uce
Uce Ua
Ua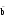

 Uē
Uē
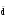 е
е c
c









 d
d
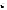 d
d Uā
Uā
 Ua
Ua
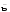 c
c Uс
Uс d
d Uā c ē
Uā c ē
 d
d e
e UabUa
UabUa e
e cUc a
cUc a
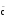 Uē
Uē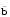 Uā
Uā ē
ē cU
cU b
b
 Ucad
Ucad



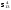





 Сообщение было отмечено anastasyi как решение
Сообщение было отмечено anastasyi как решение



