Как найти все пути в лабиринте

Алгоритмы поиска решений лабиринтов и их практическое применение в реальном мире — Кит Берроуз и Ванесса Клотцман

Истоки понятия «лабиринт»

Первое упоминание термина “maze” датируется тринадцатым веком, а “labyrinth” — к четырнадцатым. Сама концепция лабиринтов восходит к эпохе греческого мифологического героя Тесея — древнего героя, успешно прошедшего Кносский лабиринт и сразившего Минотавра.

Однако в более современном контексте лабиринты не имеют ничего общего с убийством мифологических существ. Теперь лабиринты чаще всего представляют из себя прямоугольную головоломку, состоящую из коридоров и поворотов, которые в конечном итоге ведут к выходу. И точно так же, как древний герой Тесей путешествовал по лабиринту, чтобы сразить Минотавра, современный человек решает задачу поиска пути в лабиринте не только для того, чтобы найти выход из лабиринта, но и для гораздо более широкого круга целей — решения связанных задач наиболее эффективным и доступным образом.

Введение

Лабиринты являются неотъемлемой частью нашей реальности. Хотя лабиринты в реальном физическом мире редко походят на стереотипное описание лабиринтов (черно-белая прямоугольная головоломка), общая идея и концепция лабиринтов находят свое отражение во многих аспектах нашего быта. В нашей повседневной жизни мы часто сталкиваемся с ситуациями, в которых необходимо найти самый быстрый и эффективный маршрут к заданному пункту назначения. Например, когда мы ищем в продуктовом магазине отдел с молоком, мы можем просто просмотреть каждый отдел, пока мы не найдем молоко. Однако это не самый эффективный способ. Если воспользоваться подсказками в магазине или полученными ранее воспоминаниями о том, куда ведут разные пути в магазине, поиск молока может стать гораздо более эффективным процессом. В некотором смысле мы должны использовать этот же процесс при решении задачи поиска пути в реальных лабиринтах. Метод/алгоритм, выбранный нами для поиска решения лабиринта, влияет на эффективность процесса.

Эффективность

Эффективность вычислительного алгоритма — это количество вычислительных ресурсов, используемых указанным алгоритмом, и время, необходимое для получения желаемого результата. Можно повысить эффективность алгоритма, удалив вложенные циклы for, кэшируя промежуточные или предыдущие результаты и уменьшив временную сложность алгоритма.

Временная сложность

Временная сложность измеряет время выполнения каждого оператора в коде алгоритма. При анализе фрагмента кода на предмет его временной сложности используется нотация большого “O”. Временная сложность — это функция от размера входных данных, равная максимальному количеству элементарных операций, проделываемых алгоритмом для решения экземпляра задачи указанного размера. «Существует связь между объемом входных данных (n) и количеством выполненных операций (N) относительно времени».

Константное (постоянное) время — O(1)

Линейное время — O(n)

Логарифмическое время — O(log(n))

Квадратичное время — O(n²)

Кубическое время — O(n³)

Как правило, мы стремимся создать алгоритм, который будет выполняться за константное время: O(1). Это значило бы, что время выполнения алгоритма одинаково независимо от размера набора данных или количества входных данных. Логарифмическая временная сложность — O(log (n)) — указывает на то, что по мере роста размера входных данных количество операций растет логарифмически (или достаточно медленно). С другой стороны, алгоритм, который может похвастаться кубической временной сложностью — O (n³) — имеет время выполнения, пропорциональное кубу размера набора данных. В результате добросовестный программист попытается свести к минимуму временную сложность своих алгоритмов и методов, чтобы уменьшить время выполнения и затрачиваемые ресурсы.

На приведенном ниже графике показано сравнение различных временных сложностей:

Длина кода

Не следует путать временную сложность с количеством строк кода. Такой показатель, как количество строк кода чрезвычайно легко измерить, но почти невозможно интерпретировать. В первую очередь это потому, что один алгоритм может иметь меньшую временную сложность при количестве строк кода большем, чем у другого алгоритма со сравнительно большей временной сложностью. Ошибочно считать, что временная сложность напрямую связана с количеством строк кода.

Давайте рассмотрим это на примере конкретной задачи: даны массив целых чисел nums и целое число target, нам нужно вернуть индексы двух чисел, которые в сумме равны target. Алгоритмы, решающие эту задачу, могут иметь разные временные сложности.

Реализация с временной сложностью O(n²):

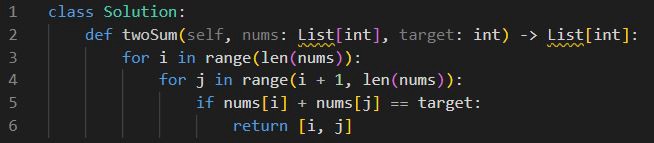
Реализация с временной сложностью O(n):

Оба этих подхода возвращают один и тот же результат. Однако мы прекрасно видим, что, несмотря на наличие дополнительной строки кода, второй пример выполняет задачу с временной сложностью O(n), а не O(n²), что в подавляющем большинстве случаев намного быстрее.

Несмотря на это, алгоритмы с меньшим количеством строк кода зачастую менее сложны, более читабельны и проще в использовании. Далее мы будем рассматривать разные алгоритмические подходы к одной и той же задаче, поэтому вполне ожидаемо, что все алгоритмы поиска решения лабиринта будут приблизительно одинакового объема. Следовательно, длину кода алгоритма все таки следует рассматривать как критерий при сравнении и противопоставлении рассматриваемых нами алгоритмов.

Алгоритмы поиска решения лабиринта

Алгоритмы поиска решения лабиринта представляют собой автоматизированные методы прохода. Отталкиваясь от конкретного лабиринт, можно использовать множество различных алгоритмов для нахождения его решения. В этой статье мы обсудим и проанализируем следующие хорошо известные алгоритмы поиска решения лабиринта:

• Полный перебор/”Грубая сила” (Bruteforce Algorithm)

• Алгоритм Тремо (Trémaux Algorithm)

• Алгоритм случайного поведения мыши (Random Mouse Algorithm)

• Метод следования вдоль стены (Wall-Follower Method)

• Метод обнаружения тупиков (Dead-End Filling)

Алгоритм полного перебора

Алгоритм поиска решения лабиринта путем полного перебора (в простонародье “брутфорс”) исследует каждый проход, пока не найдет правильный путь. Работа алгоритмов такого типа обычно заключается в проверке всех возможных путей через лабиринт с постоянным перезапуском, когда сгенерированный путь оказывается неудачным. Такой подход зачастую имеет высокую временную сложность и делает программу неэффективной, поскольку она выполняет избыточный код. В результате временная сложность алгоритма такого типа часто составляет O(n!). С другой стороны, алгоритм полного перебора очень легок в реализации, поскольку он не требует маркировки развилок (что требуется для алгоритма Тремо) и зачастую состоит из небольшого количества операторов повторяющихся в цикле.

Алгоритм Тремо

Алгоритм Тремо, изобретенный Шарлем Пьером Тремо (Charles Pierre Trémaux), представляет из себя метод поиска решения лабиринта, который, чтобы обозначить путь, рисует линии и точки на протяжении всего лабиринта. Существует ряд правил, которым необходимо следовать в рамках этого алгоритма:

• Выберите случайный проход и следуйте по нему до следующей развилки.

• Помечайте начало и конец каждого прохода по мере их прохождения (на анимации ниже в качестве меток используются точки).

• Если вы идете по проходу в первый раз, то вам нужно помечать его одной точкой. 

• Если вы зашли в тупик, вернитесь назад по тому же пути до первой развилки, пометив этот проход вторыми точками (на анимации две точки представлены крестом).

• Проход, который отмечен двумя точками (на анимации это крест), не подлежит проходу и считается тупиком.

• На развилке всегда выбирайте проход, отмеченный наименьшим количеством точек (в идеале не отмеченный ни одной точкой).

Этот алгоритм накладывает дополнительное требование помечать каждую пройденную развилку. Однако этот алгоритм более эффективен и имеет меньшую временную сложность, чем алгоритмы полного перебора и случайной мыши. Цена этой эффективности – более высокая сложность реализации. Впоследствии этот алгоритм был обобщен и назван “поиск в глубину”.

*Демонстрация работы алгоритма Тремо:

Пример реализации алгоритма Тремо на Python:

import random
from walker_base import WalkerBase
FOUND_COLOR = 'red'
VISITED_COLOR = 'gray70'
class Tremaux(WalkerBase):
    class Node(object):
        __slots__ = 'passages'
        def __init__(self):
            self.passages = set()
    def __init__(self, maze):
        super(Tremaux, self).__init__(maze, maze.start(), self.Node())
        self._maze.clean()
        self._last = None     # Заготовка на будущее
    def _is_junction(self, cell):
        return cell.count_halls() > 2
    def _is_visited(self, cell):
        return len(self.read_map(cell).passages) > 0
    def _backtracking(self, cell, last):
        return last in self.read_map(cell).passages
        

    def step(self):
        # Сердечно прошу простить меня за этот ход
        if self._cell is self._maze.finish():
            self._isDone = True
            self.paint(self._cell, FOUND_COLOR)
            return


        # print self._cell.get_position()
        paths = self._cell.get_paths(last=self._last)
        # print paths
        random.shuffle(paths)
        if self._is_visited(self._cell):
            # Мы уже были здесь раньше
            if self._backtracking(self._cell, self._last):
                # Возвращаемся назад; проверяем, если какие-нибудь непосещенные отрезки пути
                unvisited = filter(lambda c: not self._is_visited(c), paths)
                if len(unvisited) > 0:
                    self._last = self._cell
                    self._cell = unvisited.pop()
                else:   
                    # Непосещенных отрезков пути нет
                    self.paint(self._cell, VISITED_COLOR)
                    # Ищем путь назад
                    passages = self.read_map(self._cell).passages
                    unvisited = set(self._cell.get_paths()).difference(passages)
                    self._last = self._cell
                    self._cell = unvisited.pop()
            else:
                # Мы пришли к уже посещенному ранее отрезку; разворачиваемся назад
                self._cell, self._last = self._last, self._cell
        else:
            # Новый отрезок; двигаемся в случайном порядке
            if len(paths) > 0:
                # Не тупик
                self.paint(self._cell, FOUND_COLOR)
                self._last = self._cell
                self._cell = paths.pop()
            else:
                # Тупик; возвращаемся
                self.paint(self._cell, VISITED_COLOR)
                self._cell, self._last = self._last, self._cell

        self.read_map(self._last).passages.add(self._cell)
        # print self.read_map(self._cell).passages
        # print self.read_map(self._last).passages
        # raw_input('...')

Алгоритм случайного поведения мыши

Алгоритм случайного поведения мыши — крайне неинтеллектуальный и простой алгоритм. Часто он реализуется в качестве самого быстрого и простого варианта. В рамках этого алгоритма, как только мы начинаем двигаться по лабиринту и достигает развилки, мы “как мышь в лабиринте” случайным образом выбираем направление, в котором продолжим путь:

• Следуем по текущему проходу, пока на пути нам не встретится развилка.

• Затем мы случайным образом принимаем решение о следующем направлении, по которому мы будем следовать.

Этот алгоритм практически вслепую ищет выход из лабиринта и обычно занимает очень много времени. Несмотря на все это, мы всегда получим решение, так как алгоритм (“мышь”) в конечном итоге обязательно найдет правильный путь через лабиринт. Случайность и неэффективность, связанные с алгоритмами случайного поведения мыши, почти всегда являются причиной высокой временной сложности. Однако, этот алгоритм может случайным образом найти правильный путь с первой попытки/цикла, что дает нам временную сложность в лучшем случае O(1). Но, скорее всего, этот алгоритм будет неоднократно перебирать неудачные варианты, которые мы уже опробовали.

Пример кода алгоритма случайного поведения мыши на Python:

from random import choice
from maze_constants import *
from walker_base import WalkerBase
MOUSE_COLOR = 'brown'
class RandomMouse(WalkerBase):
    def __init__(self, maze):
        super(RandomMouse, self).__init__(maze, maze.start())
        self._maze.clean()
        self._last = None
        self._delay = 50
    def step(self):
        if self._cell is self._maze.finish():
            self._isDone = True
            return
        paths = self._cell.get_paths(last=self._last)
        if len(paths) == 0:
            # Мы попали в тупик
            self._cell, self._last = self._last, self._cell
        else:
            self._last = self._cell
            self._cell = choice(paths)
        self.paint(self._cell, MOUSE_COLOR)
        self.paint(self._last, OPEN_FILL)

Метод следования вдоль стены

Одним из наиболее широко известных методов поиска решения лабиринтов является метод следования вдоль стены, также известный как “правило левой/правой руки”. Этот метод основан на внешней связности лабиринта — все стены  должны быть соединены с внешней границей лабиринта. Если это так, то всегда можно найти выход из лабиринта, непрерывно следуя либо по левой, либо по правой стороне на протяжении всего лабиринта. Однако в тех случаях, когда не все стены соединены с внешними границами, этот метод не всегда будет находить решение. Этот метод/алгоритм полезен, если нам известно, что стены лабиринта связаны между собой. Алгоритм очень эффективен, так как не требует маркировки развилок или перезапуска при неудачных попытках; алгоритм просто следует по левой или правой стороне лабиринта.

Программирование метода следования вдоль стеной, вероятно, будет относительно простым и не потребует большого количества строк кода. В результате временная сложность, несомненно, будет лучше, чем у алгоритма полного перебора или случайного поведения мыши. Тем не менее, явная бесполезность этого метода для множество лабиринтов является большим минусом.

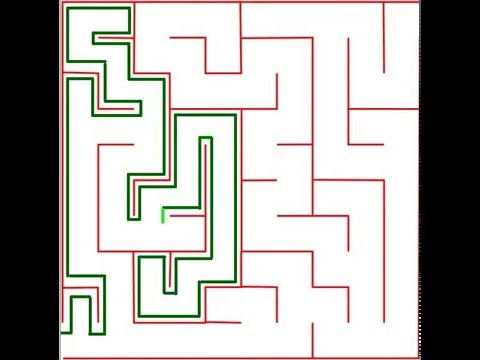
Пример реализации алгоритма следования вдоль стены.

Метод обнаружения тупиков

Алгоритм обнаружения тупиков использует другой подход к поиску решения лабиринта. Вместо того, чтобы пытаться пройти лабиринт как можно быстрее и эффективнее, алгоритм обнаружения тупиков заполняют все тупики, оставляя только правильный(е) путь(и). Правила этого алгоритма:

• Найти все тупики в лабиринте.

• Заполнить каждый путь из каждого тупика.

• Последний (оставшийся) путь является правильным путем.

Преимущества использования алгоритма обнаружения тупиков заключаются в том, что он может найти несколько решений лабиринта, если они существуют, и алгоритм должен работать для любого типа лабиринта. Несмотря на это, алгоритм очень неэффективен, особенно если лабиринт большой. Алгоритм должен проверять каждый тупик, а затем заполнять/отмечать его. Это отнимает много времени и наводит меня на мысль, что любая более-менее разумная программа с реализацией этого алгоритма будет иметь временную сложность не менее O(n²). Видео алгоритма в действии можно посмотреть ниже:

Пример приложения с роботом

Я решила внедрить вышеперечисленные алгоритмы поиска решения лабиринта в настоящего робота, который будет пытаться найти выход из реального лабиринта. Сделать это можно с помощью Raspberri Pi Pico и MicroPython.

В этом проекте используется робот Yahboom Raspberry Pi Pico Robot:

В рамках этого руководства вам не помешало бы некоторое знание Python. Робот Yahboom Pico поставляется с Raspberry Pi Pico, и вы также можете докупить множество дополнительных в рамках набора Pico Sensor Kit. В этом проекте не будут использоваться датчики из набора Sensor Kit, поэтому вам достаточно приобрести только Pico Robot.

Для начала нам нужно будет собрать робота Yahboom из отдельных частей и Raspberry Pi Pico, а затем подготовить для запуска MicroPython. Колеса должны быть тщательно выровнены, чтобы избежать ошибок в движений при выполнении кода. MicroPython — это язык программирования, написанный на C и оптимизированный для работы на микроконтроллерах и аппаратных средствах. Он позволяет нам управлять оборудованием, подключенным к Raspberry Pi Pico, не сталкиваясь с трудностями, связанными с языками более низкого уровня, такими как C или C++.

После того, как все будет подготовлено, мы сможем протестировать различные алгоритмы на реальном лабиринте, собранном из цветных листов бумаги и пенопласта.

Установка программного обеспечения

Raspberry Pi Pico можно запрограммировать, подключив его к компьютеру через кабель micro-USB. Но для начала нам нужно установить MicroPython, после чего мы сможем начать программирование на устройстве. Самые актуальные версии файлов MicroPython UF2 можно найти в документации Raspberri Pi по MicroPython.

*Обратите внимание, что на Pico нужно удерживать BOOTSEL, чтобы библиотека отобразилась в Windows/Mac.

Кроме того, должны быть установлены компиляторы Thonny Python и MicroPython. Thonny позволит нам общаться с Raspberry Pi Pico и устройствами, подключенными к его контактам. Если MicroPython установлен на Raspberry Pi Pico, то соответствующая опция должна быть доступна в настройках интерпретатора Thonny:

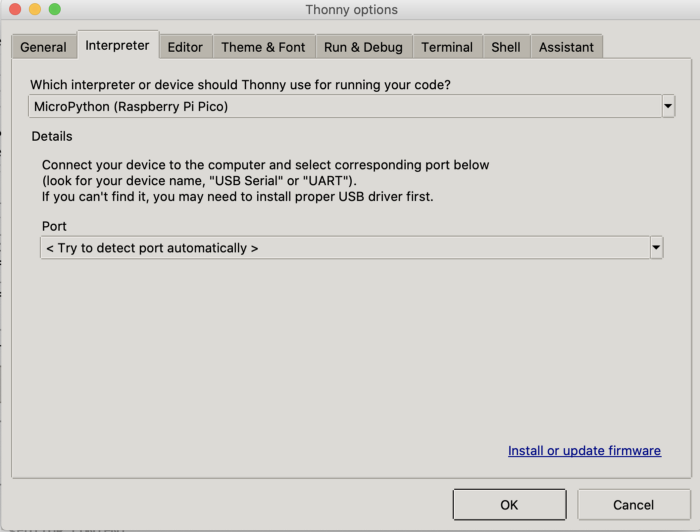
После успешного подключения к Thonny мы сможем получить доступ к Raspberry Pi Pico и начать программирование. Python-библиотека, которую рекомендуют производители робота, называется “Pico_Car”. Ее можно скачать здесь в разделе “библиотека” и впоследствии установить на Raspberry Pi Pico через Thonny. Кроме того, производители предоставляют приложение YahboomRobot на iOS для управления роботом. Чтобы использовать приложение, на Raspberry Pi Pico нужно загрузить и запустить “Bluetooth Control.py”. Файл можно скачать здесь в каталоге: “3. Robotics Course”. Если все правильно установлено и успешно запущено, то приложение должно выглядеть как на рисунке ниже, предоставляя нам возможность управлять роботом в режиме реального времени:

Чтобы управлять Raspberry Pi Pico без необходимости использовать это IOS-приложение, которое не позволяет нам запускать свой код, нам нужно реализовать управление через Bluetooth самостоятельно. Для этого мы должны использовать приложение для Android – Serial Bluetooth Terminal. Это приложение позволяет нам подключиться к Bluetooth-модулю Raspberry Pi Pico. Как только Pico получает ввод, определенный код может быть запущен или остановлен. Это позволяет нам запускать и останавливать программы по беспроводной связи и без необходимости подключать Pico к компьютеру каждый раз, когда нам нужно запустить фрагмент кода.

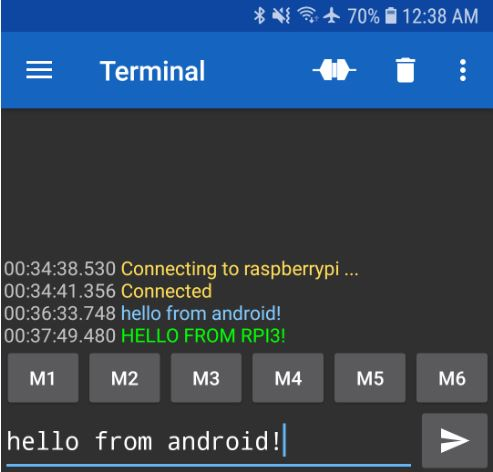
Значения M1 и M2 должны быть установлены в шестнадцатеричном формате в 31 и 32, чтобы запустить и остановить лабиринт соответственно.

Теперь наконец настало время реализовать на практике алгоритмы, которые мы обсуждали в первой части этой статьи. Для начала нам нужно написать код полного перебора, адаптированный к аппаратному обеспечению Raspberry Pi Pico. В этом случае нам не нужно беспокоиться об использовании датчика цвета, поскольку мы просто используем уже инициализированный 2D-массив в качестве нашего лабиринта. Используя шаги, которые программа возвращает для решения лабиринта (например, влево, вправо, вверх или вниз), мы можем заставить робота двигаться в этих направлениях. Адаптированный код можно посмотреть здесь.

Используя реализованный алгоритм поиска решения лабиринта методом полного перебора (ссылка выше), робот может пройти предварительно указанный ей лабиринт. Если немного подкорректировать размеры лабиринта и ввести в код в виде двумерного массива под именем maze, то алгоритм может быть приспособлен для решения любого лабиринта. Стены/границы представлены в массиве как 1, а открытое пространство, через которое робот может пройти, представлено как 0:

Если бы это был реальный лабиринт, он выглядел бы следующим образом (начиная с левого верхнего индекса):

Поскольку Raspberry Pi Pico и его код теперь настроены, мы можем воссоздать лабиринт в реальной жизни, чтобы наш робот мог его пройти. Обратите внимание, что для bruteforcesolverRPIPICO.py, может потребоваться корректировка переменных speed и runtime в соответствии с масштабом и размерами лабиринта. Значение по умолчанию:

runtime = 2 #seconds

rotate_pause = 2 #seconds

speed = 175

Теперь робот может успешно пройти описанный выше лабиринт. Однако мы должны воссоздать лабиринт в реальной жизни. В этом случае для строительства стен лабиринта я буду использовать блоки пенопласта.

Пример робота, проходящего через лабиринт, можно найти в видео на YouTube:

В результате мы:

1. Собрали робота

2. Установили необходимое программное обеспечение (MicroPython и Thonny)

3. Убедились, что MicroPython установлен на Raspberry Pi

4. Настроили и запустили скрипт, не забыв взглянуть на уже готовое приложение под iOS.

5. Построили лабиринт и запустите скрипт с помощью Thonny, подключив робота к ПК

Реальные сценарии

Способность проходить лабиринты с помощью робота захватывает, но может быть трудно реализовать альтернативные применения этих алгоритмов в реальной жизни. Поиск решения лабиринта — это упрощенная версия задачи навигации, поэтому реализация алгоритмов навигации зиждется на тех же концепциях, что и поиск решения лабиринта.

На примере ниже мы можем увидеть работу навигации Google Maps, где для построения пути от Mcdonald’s до Walgreens Google тоже использует алгоритм для определения самого быстрого маршрута. Дороги в этом случае эквивалентны проходам в лабиринте (индексы со значениями 0 в массиве лабиринта). Google также пытается найти самый быстрый маршрут — обычно маршрут с наименьшим количеством поворотов и совокупным расстоянием.

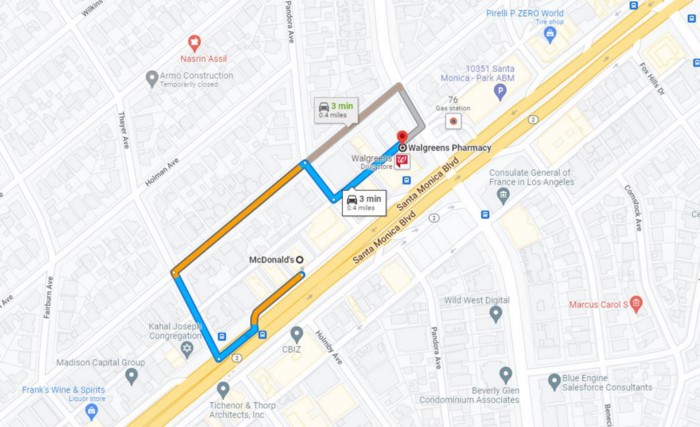
Кроме того, в 2022 году Uber начал эксперименты с доставкой еды при помощи роботов; используя технологию поиска пути и GPS, холодильник на колесах будет доставлять покупателям их еду.

Дело в том, что аналогичные процессы и алгоритмы, используемые для нахождения решений лабиринтов, используются в интересных и очень полезных реальных приложениях. Не следует рассматривать концепцию поиска решения лабиринтов как изолированную область с немногими полезными применениями в реальной жизни, это не так.

Заключение

Роботы, способные находить путь в лабиринтах, — это концепция, которую многие могут счесть неинтересной или не столь ценной для общества. Однако для реализации этого проекта потребовалось всего около сотни строк кода. Кроме того, если бы алгоритм решения лабиринта полным перебором был адаптирован для использования датчика света или цвета, робот мог бы пройти любой лабиринт, не требуя предварительной информации о его размерах и конфигурации стен. Если бы у меня было больше времени, я бы обязательно реализовала эту идею в данном проекте. В ходе этого исследования я погрузилась в новую область удивительного мира алгоритмов, временной сложности и эффективности программ. Этот проект позволил мне в комфортном для меня темпе открыть для себя ранее неизведанную область исследований и ее связь с системами GPS и множеством перспективных идей и стартапов. В мире, которым вполне вероятно скоро будет править ИИ и сложные роботы, я чувствую себя немного спокойнее, зная, что получила важный опыт, экспериментируя с основами робототехники и алгоритмов.

Полезные ссылки:

1. “A Brief History of Mazes: National Building Museum.” National Building Museum |, 17 Mar. 2017, https://www.nbm.org/brief-history-mazes/.

2. “Simple Maze Solution (Brute Force, Depth First), Python.” Gist, https://gist.github.com/Chuwiey/1e34ed9e65d41b735d8c.

3. mikeburnfire. “Trémaux’s Algorithm.” YouTube, YouTube, 10 July 2020, https://www.youtube.com/watch?v=RjWSlz-aEr8.

4. Maze Solution #3 — Tremaux’s Algorithm: V19FA Intro to Computer Science (CIS-1100-VU01). https://vsc.instructure.com/courses/6476/modules/items/713459.

5. Anubabajide. “Anubabajide/Maze-Runner: Autonomous Maze Navigation Robot Using a Raspberry Pi.” GitHub, https://github.com/anubabajide/Maze-Runner.

6. Genetic Algorithm for Maze Solving Bot — GitHub Pages. https://shepai.github.io/downloads/GeneticAlgorithmVsBrute_by_Dexter_Shepherd.pdf.

7. “Trémaux’s Algorithm” Sample Maze Solved [1] — Researchgate. https://www.researchgate.net/figure/Tremauxs-algorithm-sample-maze-solved-1_fig8_315969093.

8. Cedars-Sinai Medical Center. “With Smiles and Beeps.” Robots Help Nurses Get the Job Done, Cedars-Sinai Medical Center, 26 Nov. 2021, https://www.cedars-sinai.org/newsroom/robots-help-nurses-get-the-job-donewith-smiles-and-beeps/.

9. “Raspberry Pi Documentation.” MicroPython, https://www.raspberrypi.com/documentation/microcontrollers/micropython.html.

10. McFarland, Matt. “Uber to Test Delivering Food with Robots.” CNN, Cable News Network, 13 May 2022, https://www.cnn.com/2022/05/13/cars/uber-robot-delivery-la

11. Jarednielsen. “Big O Factorial Time Complexity.” Jarednielsencom RSS, https://jarednielsen.com/big-o-factorial-time-complexity/.

Сегодня вечером состоится открытый вебинар на тему «Создание ассоциативного массива», на котором мы начнем реализовывать популярную структуру данных «ассоциативный массив» для хранения пар (ключ, значение). Рассмотрим несколько алгоритмов для решения этой задачи и сравним их эффективность:

1. Параллельные массивы;
2. Отсортированные массивы;
3. Двоичные деревья поиска.

Регистрация для всех желающих доступна по ссылке.

From Wikipedia, the free encyclopedia

A maze-solving algorithm is an automated method for solving a maze. The random mouse, wall follower, Pledge, and Trémaux’s algorithms are designed to be used inside the maze by a traveler with no prior knowledge of the maze, whereas the dead-end filling and shortest path algorithms are designed to be used by a person or computer program that can see the whole maze at once.

Mazes containing no loops are known as “simply connected”, or “perfect” mazes, and are equivalent to a tree in graph theory. Maze-solving algorithms are closely related to graph theory. Intuitively, if one pulled and stretched out the paths in the maze in the proper way, the result could be made to resemble a tree.^[1]

Random mouse algorithm[edit]

This is a trivial method that can be implemented by a very unintelligent robot or perhaps a mouse. It is simply to proceed following the current passage until a junction is reached, and then to make a random decision about the next direction to follow. Although such a method would always eventually find the right solution, this algorithm can be extremely slow.

Wall follower[edit]

The best-known rule for traversing mazes is the wall follower, also known as either the left-hand rule or the right-hand rule. If the maze is simply connected, that is, all its walls are connected together or to the maze’s outer boundary, then by keeping one hand in contact with one wall of the maze the solver is guaranteed not to get lost and will reach a different exit if there is one; otherwise, the algorithm will return to the entrance having traversed every corridor next to that connected section of walls at least once. The algorithm is a depth-first in-order tree traversal.

Another perspective into why wall following works is topological. If the walls are connected, then they may be deformed into a loop or circle.^[2] Then wall following reduces to walking around a circle from start to finish. To further this idea, notice that by grouping together connected components of the maze walls, the boundaries between these are precisely the solutions, even if there is more than one solution (see figures on the right).

If the maze is not simply-connected (i.e. if the start or endpoints are in the center of the structure surrounded by passage loops, or the pathways cross over and under each other and such parts of the solution path are surrounded by passage loops), this method will not necessarily reach the goal.

Another concern is that care should be taken to begin wall-following at the entrance to the maze. If the maze is not simply-connected and one begins wall-following at an arbitrary point inside the maze, one could find themselves trapped along a separate wall that loops around on itself and containing no entrances or exits. Should it be the case that wall-following begins late, attempt to mark the position in which wall-following began. Because wall-following will always lead you back to where you started, if you come across your starting point a second time, you can conclude the maze is not simply-connected, and you should switch to an alternative wall not yet followed. See the Pledge Algorithm, below, for an alternative methodology.

Wall-following can be done in 3D or higher-dimensional mazes if its higher-dimensional passages can be projected onto the 2D plane in a deterministic manner. For example, if in a 3D maze “up” passages can be assumed to lead Northwest, and “down” passages can be assumed to lead southeast, then standard wall following rules can apply. However, unlike in 2D, this requires that the current orientation is known, to determine which direction is the first on the left or right.

Pledge algorithm[edit]

Disjoint (where walls are not connected to the outer boundary/boundary is not closed) mazes can be solved with the wall follower method, so long as the entrance and exit to the maze are on the outer walls of the maze. If however, the solver starts inside the maze, it might be on a section disjoint from the exit, and wall followers will continually go around their ring. The Pledge algorithm (named after John Pledge of Exeter) can solve this problem.^[3][4]

The Pledge algorithm, designed to circumvent obstacles, requires an arbitrarily chosen direction to go toward, which will be preferential. When an obstacle is met, one hand (say the right hand) is kept along the obstacle while the angles turned are counted (clockwise turn is positive, counter-clockwise turn is negative). When the solver is facing the original preferential direction again, and the angular sum of the turns made is 0, the solver leaves the obstacle and continues moving in its original direction.

The hand is removed from the wall only when both “sum of turns made” and “current heading” are at zero. This allows the algorithm to avoid traps shaped like an upper case letter “G”. Assuming the algorithm turns left at the first wall, one gets turned around a full 360 degrees by the walls. An algorithm that only keeps track of “current heading” leads into an infinite loop as it leaves the lower rightmost wall heading left and runs into the curved section on the left hand side again. The Pledge algorithm does not leave the rightmost wall due to the “sum of turns made” not being zero at that point (note 360 degrees is not equal to 0 degrees). It follows the wall all the way around, finally leaving it heading left outside and just underneath the letter shape.

This algorithm allows a person with a compass to find their way from any point inside to an outer exit of any finite two-dimensional maze, regardless of the initial position of the solver. However, this algorithm will not work in doing the reverse, namely finding the way from an entrance on the outside of a maze to some end goal within it.

Trémaux’s algorithm[edit]

Trémaux’s algorithm, invented by Charles Pierre Trémaux,^[5] is an efficient method to find the way out of a maze that requires drawing lines on the floor to mark a path, and is guaranteed to work for all mazes that have well-defined passages,^[6] but it is not guaranteed to find the shortest route.

An entrance of a passage is either unvisited, marked once or marked twice. Note that marking an entrance is not the same as marking a junction or a passage, because a junction may have multiple entrances, and a passage has an entrance at both ends. Dead ends can be thought of as junctions with one entrance (imagine there being a room at each dead end).

The algorithm works according to the following rules:

• Whenever you pass through an entrance of a passage, whether it is to enter or exit a junction, leave a mark at the entrance as you pass.
• When you are at a junction, use the first applicable rule below to pick an entrance to exit through:
  1. If only the entrance you just came from is marked, pick an arbitrary unmarked entrance, if any. This rule also applies if you’re just starting in the middle of the maze and there are no marked entrances at all.
  2. Pick the entrance you just came from, unless it is marked twice. This rule will apply whenever you reach a dead end.
  3. Pick any entrance with the fewest marks (zero if possible, else one).

The “turn around and return” rule effectively transforms any maze with loops into a simply connected one; whenever we find a path that would close a loop, we treat it as a dead end and return. Without this rule, it is possible to cut off one’s access to still-unexplored parts of a maze if, instead of turning back, we arbitrarily pick another entrance.

When you finally reach the solution, entrances marked exactly once will indicate a way back to the start. If there is no exit, this method will take you back to the start where all entrances are marked twice.
In this case each passage is walked down exactly twice, once in each direction. The resulting walk is called a bidirectional double-tracing.^[7]

Essentially, this algorithm, which was discovered in the 19th century, has been used about a hundred years later as depth-first search.^[8][9]

Dead-end filling[edit]

External video
Maze Strategy: Dead End Filling
Maze Solving algorithm

Dead-end filling is an algorithm for solving mazes that fills all dead ends, leaving only the correct ways unfilled. It can be used for solving mazes on paper or with a computer program, but it is not useful to a person inside an unknown maze since this method looks at the entire maze at once. The method is to

1. find all of the dead-ends in the maze, and then
2. “fill in” the path from each dead-end until the first junction is met.

Note that some passages won’t become parts of dead end passages until other dead ends are removed first. A video of dead-end filling in action can be seen to the right.

Dead-end filling cannot accidentally “cut off” the start from the finish since each step of the process preserves the topology of the maze. Furthermore, the process won’t stop “too soon” since the result cannot contain any dead-ends. Thus if dead-end filling is done on a perfect maze (maze with no loops), then only the solution will remain. If it is done on a partially braid maze (maze with some loops), then every possible solution will remain but nothing more. [1]

Recursive algorithm[edit]

If given an omniscient view of the maze, a simple recursive algorithm can tell one how to get to the end. The algorithm will be given a starting X and Y value. If the X and Y values are not on a wall, the method will call itself with all adjacent X and Y values, making sure that it did not already use those X and Y values before. If the X and Y values are those of the end location, it will save all the previous instances of the method as the correct path.

This is in effect a depth-first search expressed in term of grid points. The omniscient view prevents entering loops by memorization. Here is a sample code in Java:

boolean[][] maze = new boolean[width][height]; // The maze
boolean[][] wasHere = new boolean[width][height];
boolean[][] correctPath = new boolean[width][height]; // The solution to the maze
int startX, startY; // Starting X and Y values of maze
int endX, endY;     // Ending X and Y values of maze

public void solveMaze() {
    maze = generateMaze(); // Create Maze (false = path, true = wall)

    // Below assignment to false is redundant as Java assigns array elements to false by default 
    for (int row = 0; row < maze.length; row++)  
        // Sets boolean Arrays to default values
        for (int col = 0; col < maze[row].length; col++){
            wasHere[row][col] = false;
            correctPath[row][col] = false;
        }
    boolean b = recursiveSolve(startX, startY);
    // Will leave you with a boolean array (correctPath) 
    // with the path indicated by true values.
    // If b is false, there is no solution to the maze
}
public boolean recursiveSolve(int x, int y) {
    if (x == endX && y == endY) return true; // If you reached the end
    if (maze[x][y] || wasHere[x][y]) return false;
    // If you are on a wall or already were here
    wasHere[x][y] = true;
    if (x != 0) // Checks if not on left edge
        if (recursiveSolve(x-1, y)) { // Recalls method one to the left
            correctPath[x][y] = true; // Sets that path value to true;
            return true;
        }
    if (x != width - 1) // Checks if not on right edge
        if (recursiveSolve(x+1, y)) { // Recalls method one to the right
            correctPath[x][y] = true;
            return true;
        }
    if (y != 0)  // Checks if not on top edge
        if (recursiveSolve(x, y-1)) { // Recalls method one up
            correctPath[x][y] = true;
            return true;
        }
    if (y != height - 1) // Checks if not on bottom edge
        if (recursiveSolve(x, y+1)) { // Recalls method one down
            correctPath[x][y] = true;
            return true;
        }
    return false;
}

Maze-routing algorithm[edit]

The maze-routing algorithm ^[10] is a low overhead method to find the way between any two locations of the maze. The algorithm is initially proposed for chip multiprocessors (CMPs) domain and guarantees to work for any grid-based maze. In addition to finding paths between two locations of the grid (maze), the algorithm can detect when there is no path between the source and destination. Also, the algorithm is to be used by an inside traveler with no prior knowledge of the maze with fixed memory complexity regardless of the maze size; requiring 4 variables in total for finding the path and detecting the unreachable locations. Nevertheless, the algorithm is not to find the shortest path.

Maze-routing algorithm uses the notion of Manhattan distance (MD) and relies on the property of grids that the MD increments/decrements exactly by 1 when moving from one location to any 4 neighboring locations. Here is the pseudocode without the capability to detect unreachable locations.

Point src, dst;// Source and destination coordinates
// cur also indicates the coordinates of the current location
int MD_best = MD(src, dst);// It stores the closest MD we ever had to dst
// A productive path is the one that makes our MD to dst smaller
while (cur != dst) {
    if (there exists a productive path) {
        Take the productive path;
    } else {
        MD_best = MD(cur, dst);
        Imagine a line between cur and dst;
        Take the first path in the left/right of the line; // The left/right selection affects the following hand rule
        while (MD(cur, dst) != MD_best || there does not exist a productive path) {
            Follow the right-hand/left-hand rule; // The opposite of the selected side of the line
    }
}

Shortest path algorithm[edit]

When a maze has multiple solutions, the solver may want to find the shortest path from start to finish. There are several algorithms to find shortest paths, most of them coming from graph theory. One such algorithm finds the shortest path by implementing a breadth-first search, while another, the A* algorithm, uses a heuristic technique. The breadth-first search algorithm uses a queue to visit cells in increasing distance order from the start until the finish is reached. Each visited cell needs to keep track of its distance from the start or which adjacent cell nearer to the start caused it to be added to the queue. When the finish location is found, follow the path of cells backwards to the start, which is the shortest path. The breadth-first search in its simplest form has its limitations, like finding the shortest path in weighted graphs.

See also[edit]

• Mazes
• Maze generation algorithm

References[edit]

External links[edit]

• Think Labyrinth: Maze algorithms (details on these and other maze-solving algorithms)
• MazeBlog: Solving mazes using image analysis
• Video: Maze solving simulation
• Simon Ayrinhac, Electric current solves mazes, © 2014 IOP Publishing Ltd.

Учитывая лабиринт в виде бинарной прямоугольной матрицы найти длину кратчайшего пути в лабиринте от заданного источника до заданного пункта назначения.

Путь может быть построен только из ячеек со значением 1, и в любой момент мы можем двигаться только на один шаг в одном из четырех направлений. Допустимые ходы:

Go Top: (x, y) ——> (x – 1, y)
Go Left: (x, y) ——> (x, y – 1)
Go Down: (x, y) ——> (x + 1, y)
Go Right: (x, y) ——> (x, y + 1)

Например, рассмотрим следующую бинарную матрицу. Если source = (0, 0) а также destination = (7, 5), кратчайший путь от источника к месту назначения имеет длину 12.

 [ 1  1  1  1  1  0  0  1  1  1 ]
 [ 0  1  1  1  1  1  0  1  0  1 ]
 [ 0  0  1  0  1  1  1  0  0  1 ]
 [ 1  0  1  1  1  0  1  1  0  1 ]
 [ 0  0  0  1  0  0  0  1  0  1 ]
 [ 1  0  1  1  1  0  0  1  1  0 ]
 [ 0  0  0  0  1  0  0  1  0  1 ]
 [ 0  1  1  1  1  1  1  1  0  0 ]
 [ 1  1  1  1  1  0  0  1  1  1 ]
 [ 0  0  1  0  0  1  1  0  0  1 ]

Потренируйтесь в этой проблеме

Мы уже обсуждали Backtracking решение в предыдущий пост. Временная сложность решения с Backtracking будет выше, поскольку необходимо пройти все пути. Однако, поскольку это задача о кратчайшем пути, Поиск в ширину (BFS) будет идеальным выбором.

 
The Алгоритм Ли является одним из возможных решений задач маршрутизации в лабиринтах, основанных на поиске в ширину. Он всегда дает оптимальное решение, если оно существует, но работает медленно и требует много памяти. Вот полный алгоритм:

Обратите внимание, что в BFS сначала посещаются все ячейки, имеющие кратчайший путь, равный 1, а затем соседние ячейки, имеющие кратчайший путь, равный 1. 1 + 1 = 2 и т. д. Итак, если мы достигнем любого узла в BFS, его кратчайший путь на единицу больше, чем кратчайший путь родителя. Таким образом, первое вхождение ячейки назначения дает нам результат, и мы можем остановить наш поиск на этом. Невозможно, чтобы кратчайший путь существовал из какой-то другой клетки, для которой мы еще не достигли данного узла. Если бы такой путь был возможен, мы бы его уже исследовали.

Ниже приведена программа на C++, Java и Python, которая демонстрирует это:

Временная сложность предлагаемого решения равна O(M × N) и требует O(M × N) дополнительное пространство, где M а также N являются размерами матрицы.

 
Упражнение: Расширьте решение, чтобы напечатать кратчайший путь от источника к месту назначения.

Была ли эта статья полезной?

Недавно для решения задачи о прохождении лабиринта, которых, кстати, не мало, я решил воспользоваться «волновым алгоритмом», о котором ранее мне приходилось слышать. К моему сожаления, найти внятное объяснение его работы с примерами реализации на нужном мне языке не получилось, следствием чего является эта статья.

Итак, будем пытаться написать его самостоятельно, а для этого нужно продумать, как он должен работать. Для этого возьмём достаточно легкую задачу:

1. Для начала разберемся с входными данными: у нас есть матрица элементов, где 0 — пустые клетки, а 1 — стенки.
2. При вводе меняем «1» на “-1” (этого требует алгоритм)
3. Далее нужно выбрать ячейку, с которой начнется обход
4. Рекурсивно обойти лабиринт от выбранной ячейки, вставляя в ячейку текущий «уровень волны»

Ввод данных будет выглядеть следующим образом:

rdl = list(map(int,input().split()))
n, m = rdl
for i in range(n):
        rdl = input()
        cur = []
        for k in range(m):
            if int(rdl[k]) == 1:
                cur.append(-1)   
            else:    
                cur.append(int(rdl[k]))
        lab.append(cur)

Теперь у нас есть двумерная матрица, представляющая наш лабиринт.
Далее нам нужно написать функцию, которая будет обходить наш лабиринт:

def voln(x, y, cur, n, m, lab):

Где x, y — координаты текущей ячейки; cur — «уровень волны»; n, m — размеры лабиринта; lab — сам лабиринт.
Для начало нужно заполнить текущую ячейку уровнем воды:

lab[x][y] = cur

Далее проверим, есть ли у нас возможность «пойти» влево:

if y+1 < m:

Если есть такая возможность, то проверяем, нет ли там стенки или

текущий «уровень воды» меньше, чем в ячейке справа

:

if lab[x][y+1] == 0 or (lab[x][y+1] != -1 and lab[x][y+1] > cur):

И в случае «успеха» рекурсивно идем вправо:

voln(x,y+1,cur+1,n,m,lab)

Теперь нужно точно также проверить возможность пройти вниз, влево и вверх:

if x+1<n:
    if lab[x+1][y] == 0 or (lab[x+1][y] != -1 and lab[x+1][y] > cur):
            voln(x+1,y,cur+1,n,m)
if x-1>=0:
    if lab[x-1][y] == 0 or (lab[x-1][y] != -1 and lab[x-1][y] > cur):
            voln(x-1,y,cur+1,n,m)
if y-1>=0:
    if lab[x][y-1] == 0 or (lab[x][y-1] != -1 and lab[x][y-1] > cur):
            voln(x,y-1,cur+1,n,m)

Все, осталось в конце вернуть текущий лабиринт:

return lab

Готовая программа:

def main():
    lab = []
    rdl = list(map(int,input().split()))
    n, m = rdl
    for i in range(n):
        rdl = input()
        cur = []
        for k in range(m):
            if int(rdl[k]) == 1:
                cur.append(-1)   
            else:    
                cur.append(int(rdl[k]))
        lab.append(cur)
    rdl = list(map(int,input().split()))
    x1, y1 = rdl[0]-1, rdl[1]-1
    rdl = list(map(int,input().split()))
    x2, y2 = rdl[0]-1, rdl[1] -1
    lab = voln(x1,y1,1,n,m,lab)
    if lab[x2][y2] > 0:
        print("Mozhet")
    else:
        print("Ne mozhet")    
def voln(x,y,cur,n,m):
    lab[x][y] = cur
    if y+1<m:
        if lab[x][y+1] == 0 or (lab[x][y+1] != -1 and lab[x][y+1] > cur):
            voln(x,y+1,cur+1,n,m,lab)
    if x+1<n:
        if lab[x+1][y] == 0 or (lab[x+1][y] != -1 and lab[x+1][y] > cur):
            voln(x+1,y,cur+1,n,m,lab)
    if x-1>=0:
        if lab[x-1][y] == 0 or (lab[x-1][y] != -1 and lab[x-1][y] > cur):
            voln(x-1,y,cur+1,n,m,lab)
    if y-1>=0:
        if lab[x][y-1] == 0 or (lab[x][y-1] != -1 and lab[x][y-1] > cur):
            voln(x,y-1,cur+1,n,m,lab)
    return lab
main()

Спасибо за прочтение, надеюсь, кому-то будет полезно.