| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки
Примеры
-
рациональные:корни:x^3-7x+6
-
рациональные:корни:3x^3-5x^2+5x-2
-
рациональные:корни:6x^4-11x^3+8x^2-33x-30
-
рациональные:корни:2x^{2}+4x-6
- Показать больше
Описание
Найдите корни многочленов, используя теорему о рациональных корнях шаг за шагом
rational-roots-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
Middle School Math Solutions – Equation Calculator
Welcome to our new “Getting Started” math solutions series. Over the next few weeks, we’ll be showing how Symbolab…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
10.5. НАХОЖДЕНИЕ РАЦИОНАЛЬНЫХ КОРНЕЙ МНОГОЧЛЕНА С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ
Теорема 4. Если многочлен с целыми коэффициентами f (x) = anxn + an-1xn-1 + … + a1x+a0 имеет рациональный корень x=p/q (q ≠ 0, дробь p/q несократимая), то р является делителем свободного члена (a0), а q — делителем коэффициента при старшем члене аn.
Если p/q является корнем многочлена f (х), то f(p/q) = 0. Подставляем p/q вместо х в f(x) и из последнего равенства имеем
|
an * pn/qn + an-1 * pn-1/qn-1 + … + a1 * p/q + a0 = 0. |
(1) |
Умножим обе части равенства (1) на (q ≠ 0). Получаем
|
аnрn + an-1pn-1q + … + a1pqn-1 + a0qn = 0. |
(2) |
В равенстве (2) все слагаемые, кроме последнего, делятся на р. Поэтому
a0qn = -(аnрn + an-1pn-1q + … + a1pqn-1) делится на р.
Но когда мы записываем рациональное число в виде p/q, то эта дробь считается несократимой, то есть р и q не имеют общих делителей. Произведение a0qn может делиться на р (если р и q — взаимно простые числа) только тогда, когда a0 делится на р. Таким образом, р — делитель свободного члена a0.
Аналогично все слагаемые равенства (2), кроме первого, делятся на q. Тогда
anpn = -(an-1pn-1q + … + a1pq-1 + a0qn) делится на q. Поскольку р и q — взаимно простые числа, то an делится на q, следовательно, q — делитель коэффициента при старшем члене.
Отметим два следствия из этой теоремы. Если взять q = 1, то корнем многочлена будет целое число р — делитель a0. Таким образом, имеет место:
Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
Если в заданном многочлене f (х) коэффициент аn = 1, то делителями аn могут быть только числа ±1, то есть q =±1, и имеет место:
Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.
Задача 1 Найдите рациональные корни многочлена 2х3 – х2 + 12х – 6.
Пусть несократимая дробь p/q является корнем многочлена. Тогда р необходимо искать среди делителей свободного члена, то есть среди чисел ±1, ±2, ±3, ±6, а q — среди делителей старшего коэффициента: ±1, ±2.
Таким образом, рациональные корни многочлена необходимо искать среди чисел ±1/2, ±1, +±3/2, ±2, ±3, ±6. Проверять, является ли данное число корнем многочлена, целесообразно с помощью схемы Горнера. При x = 1/2 имеем следующую таблицу.
Кроме того, по схеме Горнера можно записать, что
2х3 – х2 + 12х – 6 = (x – 1/2) (2x2 + 12).
Многочлен 2х2 + 12 не имеет действительных корней (а тем более рациональных), поэтому заданный многочлен имеет единственный рациональный корень x =1/2.
Задача 2 Разложите многочлен Р (х) = 2х4 + 3х3 – 2х2 – х – 2 на множители.
Ищем целые корни многочлена среди делителей свободного члена: ±1, ±2. Подходит 1. Делим Р (х) на х – 1 с помощью схемы Горнера.
Тогда Р (х) = (х – 1)(2х3 + 5х2 + 3х + 2). Ищем целые корни кубического многочлена 2х3 + 5х2 + 3х + 2 среди делителей его свободного члена: ±1, ±2. Подходит (–2). Делим на х + 2
Имеем Р (х) = (х – 1)(х + 2)(2х2 + х +1).
Квадратный трехчлен 2х2 + х +1 не имеет действительных корней и на линейные множители не раскладывается.
Ответ: Р (х) = (х – 1)(х + 2)(2х2 + х +1).
Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен х2 + х + 1 не имеет действительных корней). Таким образом, многочлен n-й степени не всегда можно разложить на линейные множители. В курсах высшей алгебры доказывается, что многочлен нечетной степени всегда можно разложить на линейные и квадратные множители, а многочлен четной степени представить в виде произведения квадратных трехчленов.
Например, многочлен четвертой степени раскладывается в произведение двух квадратных трехчленов. Для нахождения коэффициентов этого разложения иногда можно применить метод неопределенных коэффициентов.
Задача 3 Разложите на множители многочлен х4 + х3 + 3х2 + х + 6.
Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.
Попытаемся разложить этот многочлен в произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:
|
х4 + х3 + 3х2 + х + 6 = (х2 + ах + b)(х2 + сх + d), |
(3) |
где а, b, с и d — неопределенные (пока что) коэффициенты. Многочлены, стоящие в левой и правой частях этого равенства, тождественно равны, поэтому и коэффициенты при одинаковых степенях х у них равны. Раскроем скобки в правой части равенства и приравняем соответствующие коэффициенты. Это удобно записать так:
х4 + х3 + 3х2 + х + 6 = x4 + cx3 + dx2 +
+ ax3 + acx2 + adx +
+ bx2 + bcx + bd.
Получаем систему
 |
(4) |
Попытка решить эту систему методом подстановки приводит к уравнению 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что b и d могут быть только делителями числа 6. Все возможные варианты запишем в таблицу.
Коэффициенты b и d в равенстве (3) равноправны, поэтому мы не рассматриваем случаи b = 6 и d = 1 или b = –6 и d = –1 и т. д.
Для каждой пары значений b и d из третьего равенства системы (4) найдем ас = 3 – (b + d), а из второго равенства имеем а + с = 1.
Зная а + с и ас, по теореме, обратной теореме Виета, находим а и с как корни квадратного уравнения. Найденные таким образом значения а, b, с, d подставим в четвертое равенство системы (4) bс + ad = 1, чтобы выбрать те числа, которые являются решениями системы (4). Удобно эти рассуждения оформить в виде таблицы:
Как видим, системе (4) удовлетворяет набор целых чисел а = –1, b = 2, с = 2, d = 3. Тогда равенство (3) имеет вид
|
x4 + х3 + 3х2 + х + 6 = (х2 – х + 2)(х2 + 2х + 3). |
(5) |
Поскольку квадратные трехчлены х2 – х + 2 и х2 + 2х + 3 не имеют не только рациональных, но и действительных корней, то равенство (5) дает окончательный ответ.
Упражнения
- Найдите целые корни многочлена:
1) х3 – 5х + 4;
2) 2x3 + x2 – 13x + 6;
3) 5х3 + 18х2 – 10х – 8;
4) 4х4 – 11х2 + 9х – 2.
- Найдите рациональные корни уравнения:
1) х3 – 3х2 + 2 = 0;
2) 2х3 – 5х2 – х + 1 = 0;
3) 3х4 + 5х3 – х2 – 5х – 2 = 0;
4) 3х4 – 8х3 – 2х2 + 7х – 2 = 0.
- Разложите многочлен на множители:
1) 2х3 – х2 – 5х – 2;
2) х3 + 9х2 + 23х +15;
3) х4 – 2х3 + 2х – 1;
4) х4 – 2х3 – 24х2 + 50х – 25.
- Найдите действительные корни уравнения:
1) х3 + х2 – 4х + 2 = 0;
2) х3 – 7х – 6 = 0;
3) 2х4 – 5х3 + 5х2 – 2 = 0;
4) 2х3 – 5х2 + 1 = 0.
5*. Разложите многочлен на множители методом неопределенных коэффициентов:
1) х4 + х3 – 5х2 + 13х – 6;
2) х4 – 4х3 – 20х2 + 13х – 2.
6*. Разложите многочлен на множители, заранее записав его с помощью метода неопределенных коэффициентов в виде (х2 + bх + с)2 – (mх + n)2: :
1) х4+ 4х – 1;
2) х4 – 4х3 – 1;
3) х4 + 4а3х – а4.
Вычисление корней многочлена любой степени
Вычисляет вещественные корни полинома любой степени численным методом или аналитически, если аналитическое решение существует
Статьи, описывающие этот калькулятор
- Вычисление корней полинома
Вычисление корней многочлена любой степени
Коэффициенты многочлена, разделенные пробелом.
Точность вычисления
Знаков после запятой: 5
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
График
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Этот калькулятор использует следующие калькуляторы
- Деление многочленов
- Изоляция корней многочлена методом VAS-CF
- Кубическое уравнение
- Наибольший общий делитель (НОД) двух многочленов
- Разложение многочлена на свободные от квадратов множители
- Решение квадратного уравнения
- Сдвиг многочлена
- Уравнение 4-й степени
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Изоляция корней многочлена
- • Вычисление корней полинома
- • Метод выделения полного квадрата
- • Интерполяционный многочлен Ньютона (полином Ньютона)
- • Интерполяционный многочлен Лагранжа (полином Лагранжа)
- • Раздел: Алгебра ( 46 калькуляторов )
PLANETCALC, Вычисление корней многочлена любой степени
Содержание:
- Теорема о рациональных корнях
- Задача пример №8
- Задача пример №9
- Задача пример №10
Теорема о рациональных корнях
Если для многочлена 
Доказательство:
Пусть несократимая дробь 

Умножим обе части равенства на 
Так как в последнем равенстве каждый член, кроме члена 







Задача пример №8
Найдите рациональные корни многочлена 
Решение:
свободный член 6, старший коэффициент 2.
Для 



Так как, 


Следствие 1. Если старший коэффициент ±1 и многочлен имеет рациональный корень, то он является целым числом.
Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.
Задача пример №9
Найдите корни многочлена 
Решение:
по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.
Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.
Так как 



Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения 
Например, для нахождения корней многочлена 


Для нахождения рациональных корней выполните следующие действия:
1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.
2. Из этих чисел выбирается число 

3. Для данного многочлена при помощи синтетического деления на двучлен 
4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.
5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена 
Проверим: 


Исследование:
1) Перепишите примеры в тетрадь и проведите обсуждение.
a) Многочлен первой степени 
b) Многочлен второй степени 


c) Многочлен третьей степени 
d) Многочлен четвертой степени 
e) Принимая во внимание, что уравнение 
2) Укажите степень и найдите корни многочленов, разложение на множители которых имеет вид 
3) Равна ли степень произвольного многочлена количеству его корней?
Покажем на примере, что многочлен n-ой степени имеет n корней.
Задача пример №10
Найдите все корни многочлена 
Решение:
рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:

Значит, 

В выражении 








Корни:
Во всех рассмотренных нами примерах уравнение n-ой степени всегда имеет n корней, включая кратные корни (действительных или комплексных).
Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:
Другие темы которые вам помогут понять математику:
|
|
|
|
Лекции:
- Свойства прямоугольного треугольника
- Частное решение дифференциального уравнения
- Интегрирование иррациональных функций
- Площадь поверхности. Интеграл по площади поверхности
- Формула Пуассона
- Найти производную функции
- Исследовать функцию на непрерывность: пример решения
- Преобразование графиков функций
- Полный дифференциал функции: пример решения
- Прямые и плоскости в пространстве
| Коэффициенты полинома 4 степени |
| Исходный многочлен |
| Кубическая резольвента |
| Корни кубической резольвенты |
| Корни заданного многочлена 4 степени |
| Вспомогательные коэффициенты |
| F2= |
| F1= |
| T= |
Данный калькулятор позволяет высчитывать корни произвольного полинома четвертой степени. Коэффициенты могут быть как вещественными так и комплексными числами.
Использовалась определенная методика, которая нигде не описана и не разобрана.
Формулами Феррари не стал пользоваться – не интересно.
Несмотря на свой собственный путь, все равно утыкаешься в задачу решения вспомогательного уравнения третьей степени, так называемой кубической резольвенты.
И по всей видимости избежать её никак не получится.
Но дальше все идет по другому.
По любому значения корня резольвенты, мы высчитываем три вспомогательный параметра.
Зная эти три параметра, мы можем легко найти все четыре корня исходного уравнения.
Есть только один нюанс с которым сталкивались предшественники, мне тоже надо иногда каким то определять знак + или – для одного вспомогательного параметра.
Теперь в виде формул
Заменой 
Решение данного уравнения ищем в виде сумм двух функций
Три вспомогательных параметра связаны к коэффициентами приведенного полинома через следующие соотношения
Выражая любой из вспомогательных параметров мы получаем, в том или ином виде кубическую резольвенту
Например, если выразим F2
Это кубическое уравнение которое подстановкой 
Теперь о нюансе о котором говорил раньше. Какой же знак брать когда высчитываем корни?
Критерий оказывается очень простой. Берем любой корень резольвенты и сравниваем его
если это условие верное то ставится +(плюс), если условие неверное то -(минус)
Дальше все эти параметры подставляются в формулу
+F(T,F_2))
Еще хотелось бы поговорить про критерий. Вдумчивый читатель спросит: “А что если любой корень резольвенты является комплексным числом? Какой в этом случае критерий?”
Лучшим способом, я посчитал для подстановка корня в исходное уравнение. Для этого есть простой алогритический способ описанный в статье Значение производной многочлена по методу Горнера. Если выражение обращается в ноль, то есть является верным, то знак не меняется. Если иначе то знак ставим минус.
Решать комплексные уравнения 4 степени теперь можно достаточно легко и быстро. В онлайн сервисах Вы такого не найдете.
Попробуйте решить уравнение 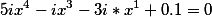
Один из корней равен
Кто считает что действительной частью можно принебречь и отбросить как “почти ноль” глубоко ошибается. Отбросив его у нас значение функции будет 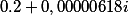
И только с учетом “такой маленькой” действительной части уравнение становиться тождественным.
Поэтому точность в вычислениях очень важны.
Если Вы вдруг заметили ошибку в расчетах ( а вдруг?) , просьба сообщить. Но я надеюсь, что такого не произойдет.
Несколько примеров:
| Исходный многочлен |
*x^3+(-9i)*x^2+(-4)*x^1+(-10i)) |
| Кубическая резольвента |
*x^2+(2620+2464i)*x^1+(-18432-34560i)) |
| Корни кубической резольвенты |
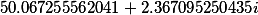 |
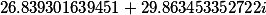 |
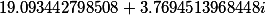 |
| Корни заданного многочлена 4 степени |
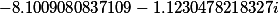 |
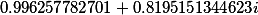 |
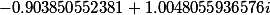 |
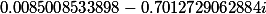 |
| Вспомогательные коэффициенты |
F2=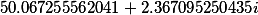 |
F1=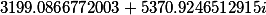 |
T=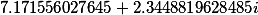 |
| Исходный многочлен |
*x^3+(-4)*x^2+(-20)*x^1+(-5)) |
| Кубическая резольвента |
*x^2+(272)*x^1+(-128)) |
| Корни кубической резольвенты |
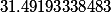 |
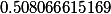 |
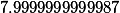 |
| Корни заданного многочлена 4 степени |
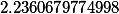 |
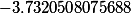 |
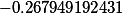 |
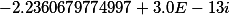 |
| Вспомогательные коэффициенты |
F2=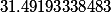 |
F1=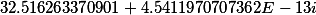 |
T=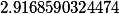 |






















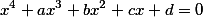
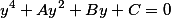
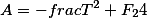
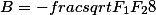
^2-frac{F_1}{2}}{64})
=8B^2)
)