Ряд Лорана и разложение функций по целым степеням
Ранее рассматривалась задача разложения функции в степенной ряд , при этом функция предполагалась аналитической в точке
, а ряд сходящимся в круге
.
Другим частным случаем функциональных рядов, наряду со степенными, является ряд ряд по целым степеням разности
. Такой ряд сходится в кольце
и его сумма — функция аналитическая внутри этого кольца.
Можно рассматривать задачу разложения функции, аналитической в кольце . Имеет место теорема, аналогичная теореме 3.3.
Теорема Лорана о разложении функции в ряд по целым степеням
Теорема 3.5 (Лорана). Функция , аналитическая в кольце, представляется в этом кольце сходящимся рядом по целым степеням, т.е. имеет место равенство
(3.24)
Коэффициенты ряда вычисляются по формуле
(3.25)
где — произвольный контур, принадлежащий кольцу и охватывающий точку
; в частности,
— окружность
.
Имеют место следующие определения.
1. Ряд коэффициенты которого вычисляются по формуле (3.25), называется рядом Лорана функции
.
Заметим, что формула (3.16) получается из формулы (3.25) при , но для коэффициентов ряда Лорана не имеет места формула вида (3.17), так как функция в точке
может быть не определена.
2. Совокупность членов ряда с неотрицательными степенями — называется правильной частью ряда Лорана; члены с отрицательными степенями образуют главную часть ряда Лорана:
или
.
3. При получаем частный случай кольца — вырожденное кольцо
. Это — круг с выколотым центром. Точка
— особая точка функции, и разложение в этом случае называется разложением функции в окрестности особой точки.
4. При область
есть внешность круга. В частном случае при
— внешность круга
. Разложение в этом случае называется разложением в окрестности бесконечно удаленной точки и имеет вид
(3.26)
или, что то же,
(3.27)
Здесь совокупность неотрицательных степеней образует главную часть ряда Лорана в окрестности бесконечно удаленной точки; совокупность отрицательных
— правильную часть ряда Лорана в окрестности бесконечно удаленной точки.
Пример 3.30. Исследовать возможность разложения функции в ряды Тейлора и Лорана.
Решение
Функцию нельзя разложить в ряд по степеням
ни в окрестности точки
(ряд Тейлора), ни в окрестности точки
(ряд Лорана), так как эти точки являются точками ветвления функции и в их окрестностях невозможно выделение однозначных ветвей.
Невозможны также разложения этой функции в ряды по степеням и
, поскольку точки
и
— также точки ветвления. Разложения по степеням
, где
, возможны.
Функция же раскладывается по степеням
и в ряд Тейлора в круге
и в ряд Лорана в области
(окрестность бесконечно удаленной точки), а также в кольце
. Возможны разложения и по степеням
и
в кольцевых областях, а также в окрестностях особых точек
.
Так как ряды по целым степеням обладают свойствами степенных рядов (см. утверждение 3.2), то, учитывая теорию и практику решения задачи разложения функции в степенной ряд (см. утверждения 3.3 и 3.4), можно сформулировать следующее утверждение.
Утверждение 3.6
1. Функция, аналитическая в кольце , разлагается в этом кольце в ряд Лорана (3.24), коэффициенты которого вычисляются по формуле (3.25).
2. Для коэффициентов ряда имеет место формула оценки коэффициентов — неравенство Коши:
(3.28)
где — радиус окружности (частный случай контура
), по которой производится интегрирование в (3.25).
3. На границах кольца сходимости ряда Лорана есть хотя бы по одной особой точке функции — его суммы.
4. Частными случаями рядов Лорана являются разложения функции в окрестности особой точки и окрестности бесконечно удаленной точки
.
5. Разложение в ряд Лорана сводится к разложению в ряд Тейлора, используются основные разложения и действия над рядами.
6. При разложении рациональных дробей, как и в случае рядов Тейлора, выдерется целая часть неправильной дроби, а правильная записывается в виде суммы элементарных дробей, для разложения которых используется формула суммы членов бесконечно убывающей геометрической прогрессии. При этом элементарные дроби преобразуются следующим образом:
– для получения правильной части, т.е. ряда, сходящегося в круге , разложение элементарной дроби записывается в виде
– для получения главной части, т.е. ряда, сходящегося вне круга , изложение элементарной дроби записывается в виде
Примеры разложения функций в ряд Лорана
Пример 3.31. Разложить функцию в ряд Лорана по степеням
.
Решение
Функция является аналитической всюду, кроме точек и
, в частности: в круге
, в кольце
и в окрестности бесконечно удаленной точки
(рис. 3.4).
В круге функция раскладывается в ряд Тейлора (см. пример 3.21). Получим разложения в двух других областях.
Рассмотрим разложение в кольце. Дробь правильная, ее разложение на элементарные дроби получено в примере (3.21):
Чтобы получить разложение в кольце, первое слагаемое раскладываем в области , т.е. записываем главную часть ряда, второе — в круге
— правильная часть. Получаем разложения:
Записываем окончательный результат:
Здесь первое слагаемое — главная часть, а второе — правильная часть ряда Лорана в кольце .
Чтобы получить разложение в области — окрестности бесконечно удаленной точки, нужно и второе слагаемое разложить по отрицательным степеням:
или
.
В результате получаем разложение в окрестности бесконечно удаленной точки:
Заметим, что главная часть ряда отсутствует, так как в разложении присутствуют только члены с отрицательными степенями.
Пример 3.32. Разложить функцию в ряд Лорана: а) по степеням
; б) по степеням
.
Решение
а) Особыми точками функции являются точки и
, причем вторая — ближайшая к центру разложения, т.е. к
(рис. 3.5,а); расстояние между
и
равно единице, поэтому в круге
функция раскладывается в ряд Тейлора. Расстояние от
до другой особой точки
равно трем, и в кольце
данная функция является аналитической и раскладывается в ряд Лорана. Аналитической она является и в области
и раскладывается в ней также в ряд Лорана по степеням
. Оба разложения получаем, как в предыдущем примере, причем замену
можно сделать в исходной дроби, а можно не вводить обозначения (см. пример 3.21). Запишем разложения в каждой из двух областей, учитывая представление функции в виде суммы элементарных дробей (см. примеры 3.21 и 3.31):
Разложение в кольце
Получаем ответ: .
Разложение в области
Получаем ответ: .
б) Задача решается так же, как и в предыдущем пункте. Различие заключается в том, что в данном случае обе особые точки расположены на одном расстоянии от центра — точки . Поэтому разложения по степеням
могут быть получены в круге
и в вырожденном кольце — в области
(рис. 3.5,б). Разложение в круге |
— ряд Тейлора — получено в примере 3.21. Запишем разложение в области
Получаем ответ: .
Пример 3.33. Записать разложения функции в окрестностях особых точек.
Решение
Особыми точками дроби являются . Решим задачу для каждой особой точки
.
Разложение в окрестности бесконечно удаленной точки получено в примере 3.31:
Заметим, что в разложении отсутствует главная часть — совокупность членов с положительными степенями .
Запишем разложение в окрестности точки . Расстояние до другой особой точки
равно четырем, поэтому окрестность точки
— проколотая окрестность, которая записывается в виде
(рис. 3.6).
В разложении исходной дроби на элементарные первое слагаемое записано по степеням
(уже разложено). Это разложение содержит только главную часть, состоящую из одного члена: здесь все
, кроме
, и разложение имеет место в области
. Второе слагаемое раскладываем в окрестности
и, так как для него эта точка не является особой, получим ряд Тейлора в круге
. Для исходной дроби это будет правильная часть ряда Лорана:
Получаем ответ: .
Для точки задача решается аналогично (рис. 3.6):
Получаем ответ: — разложение функции в окрестности особой точки
. Заметим, что в полученных разложениях в окрестности каждой особой точки главная часть содержит только одно слагаемое.
Пример 3.34. Исследовать разложения функции по степеням
. Записать разложения в окрестностях особых точек.
Решение
Функция может быть разложена в ряд Тейлора по степеням . окрестности любой конечной точки
; окрестностью будет круг
, где
— наименьшее из расстояний от точки
до особых точек (рис. 3.7,а).
В ряд Лорана по степеням функция может быть разложена в кольце
, где
и
, а также во внешности круга, т.е. в области
(рис. 3.7,а). Если
, то разложение будет иметь место только в вырожденном кольце вида
, так как в этом случае точка го одинаково удалена от обеих особых точек и
(рис. 3.7,б).
Особенностью примера является наличие в знаменателе множителя , поэтому в разложении дроби на элементарные присутствует дробь
, а именно имеет место равенство
Для разложения дроби по степеням
используется правило дифференцирования рядов (см. пример 3.22).
Запишем разложение функции в окрестности — особой точки.
В случае в разложении дроби на элементарные две первые дроби представляют собой слагаемые требуемого вида (уже разложены):
. Эти разложения справедливы во всей плоскости с выколотой точкой
, т.е. в области
.
От третьего слагаемого получаем правильную часть ряда Лорана:
Окончательный ответ: .
В главной части разложения присутствуют два члена, при этом .
В случае разложения в окрестности главная часть разложения содержит одно слагаемое
; правильная получается от разложения дробей
и
по степеням
.
Найдем эти разложения:
Записываем ответ:
Пример 3.35. Разложить функцию в окрестностях точек
и
.
Решение
Оба разложения — разложения по степеням и получаются из основного разложения, а именно
или
Различие разложений заключается в записи правильной и главной частей. Так, в случае точки правильная часть содержит конечное число слагаемых — четыре и ответ записывается в виде
В случае конечное число слагаемых образует главную часть и ответ записывается в виде
Пример 3.36. Разложить по степеням функции: а)
; б)
. С помощью полученных разложений найти
.
Решение
Применяем основные разложения для и
и записываем ряды для заданных функций:
а)
Таким образом, получаем результат: .
Справа записан степенной ряд, сходящийся всюду, его сумма при равна
, а при
, очевидно, равна
.
Получаем или
. Результат можно записать в виде асимптотической формулы:
б) .
Получен результат: . Отсюда
. Результат, как и в случае “а”, можно записать в виде асимптотической формулы:
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
4.1. Ряд Тейлора
Справедливы
следующие теоремы.
1.
Всякую функцию ![]() ,
,
аналитическую в круге с центром в точке
![]() можно представить внутри этого круга
можно представить внутри этого круга
в виде суммы ряда Тейлора:
![]()
 (1)
(1)
Во
всякой замкнутой области, принадлежащей
этому кругу, ряд Тейлора (1) сходится
равномерно.
2.
Всякую аналитическую функцию в каждой
внутренней точке области аналитичности
можно разложить в ряд Тейлора (1). Это
разложение справедливо в области
![]() ,
,
где![]() – расстояние от точки
– расстояние от точки![]() до ближайшей особой точки функции
до ближайшей особой точки функции![]() ,
,
то есть точки, в которой![]() не является аналитической.
не является аналитической.
3.
Если функция
![]() разлагается в окрестности точки
разлагается в окрестности точки![]() в степенной ряд
в степенной ряд ,
,
то этот ряд является ее рядом Тейлора,
то есть
 ,
, ![]() .
.
Пользуясь
теоремой 3, можно разложить данную
функцию
![]() в ряд по степеням
в ряд по степеням![]() ,
,
который является ее рядом Тейлора в
окрестности точки![]() .
.
Часто коэффициенты такого ряда находят,
используя известные разложения функций![]() и т.д.
и т.д.
Напомним
также разложение

(2)
сходящееся
в круге
![]() <1.
<1.
Пример 1.
Разложить
функцию
![]() в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки![]() .
.
Указать область, в которой справедливо
это разложение.
Решение.
В окрестности
точки
![]() функция
функция![]() является аналитической. Следовательно,
является аналитической. Следовательно,
согласно теореме 2, ее можно разложить
в ряд Тейлора. Для разложения в ряд
Тейлора преобразуем данную функцию к
виду
 .
.
Разложим
второй сомножитель в ряд по формуле
(2). Область сходимости этого ряда
 ,
,
отсюда![]() .
.
Искомое
разложение имеет вид:
 ,
,
или
 ;
; ![]() .
.
Пример 2.
Разложить функцию
![]() в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки![]() .
.
Указать область, в которой справедливо
это разложение.
Решение.
Для разложения
в ряд Тейлора преобразуем данную функцию
к виду
 и воспользуемся формулой (2).
и воспользуемся формулой (2).
Так
как
 ,
,
то![]() .
.
Получаем искомое разложение:
 ,
,
 ;
; ![]()
4.2. Ряд Лорана
Справедлива
теорема:
Функция
![]() ,аналитичная
,аналитичная
в кольце
![]() ,
,
представляется в этом кольце сходящимся
рядом Лорана
 ,
,
(3)
где
 ,
,
(4)
![]() ,
,
![]() – любая окружность, ориентированная
– любая окружность, ориентированная
против часовой стрелки и лежащая внутри
указанного кольца с центром в точке![]() .
.
Разложение в ряд Лорана единственно.
Первое
слагаемое в разложении (3) называется
правильной частью ряда Лорана, второе
слагаемое – главной частью ряда Лорана.
Правильная часть ряда Лорана сходится
в круге
![]() .
.
Главная часть ряда Лорана сходится во
внешности круга радиуса![]() ,
,
то есть при![]() .
.
Разложение
(3) иногда можно получить на практике,
не применяя формулы (4) для коэффициентов
![]() .
.
Пример 1.
Найти все разложения функции
 в ряд Лорана по степеням
в ряд Лорана по степеням![]() .
.
Решение.
Пусть
![]() .
.
Тогда данная функция может быть разложена
в ряд Лорана в кольцах:
I) ,II) ,III) ,
где
она является аналитической.
Разлагаем
![]() на элементарные дроби:
на элементарные дроби:
 .
.
I. Дробь
![]()
разлагается вне круга
![]() по степеням
по степеням![]()
с отрицательными показателями, то есть
 ,
,
при
 .
.
Дробь
![]()
разлагается внутри круга
![]() по степеням
по степеням![]()
с положительными показателями, то есть
 ,
,
при
 .
.
Итак,
 ,
,
при
![]() .
.
II.
Дроби ![]()
и ![]()
разложим в ряд по степеням ![]()
с положительными показателями внутри
круга  ,
,
 ,
, ![]()
Итак,
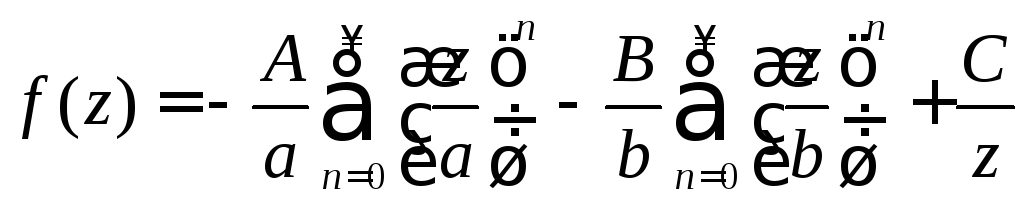 ,
,
при![]() .
.
III.
Дроби ![]()
и ![]()
разложим по степеням ![]()
с отрицательными показателями, то есть
 ,
,
где ![]() ;
;
 ,
,
где ![]() .
.
Итак,
 ,
,![]() .
.
Пример 2.
Найти все
лорановские разложения
![]() по степеням
по степеням![]() ,
,
если ,
,![]() .
.
Решение.
Пусть

Точки
![]() являются особыми точками функции
являются особыми точками функции![]() (в них
(в них![]() не аналитична). Тогда кольцами аналитичности
не аналитична). Тогда кольцами аналитичности![]() будут области:
будут области:
Возвращаясь
к переменной
![]() ,
,
получаем следующие области разложения![]() по степеням
по степеням![]()

Рассмотрим
разложение функции
![]() в ряд Лорана в кольце
в ряд Лорана в кольце![]() ,
,
то есть![]() .
.
Представим
функцию
![]() в виде
в виде
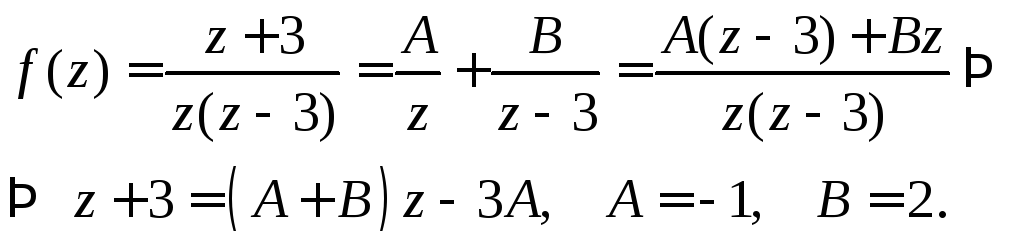
![]()
Таким
образом,
![]() .
.
Дробь
![]()
разложим по степеням
![]() с отрицательными показателями вне круга
с отрицательными показателями вне круга![]() ,
,
то есть
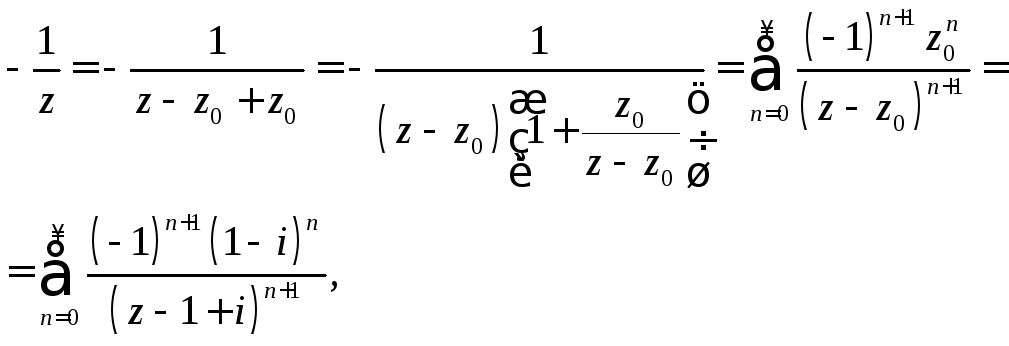
где
![]()
Дробь
![]()
разложим по степеням
![]() с положительными показателями внутри
с положительными показателями внутри
круга![]() ,
,
то есть


Итак,
 ,
,
где![]() .
.
Остальные
случаи разложения данной функции в ряд
Лорана предлагается рассмотреть
самостоятельно.
Для разложения
функции в ряд Лорана иногда используют
готовые разложения элементарных функций
в ряд Тейлора.



 (5)
(5)
которые
сходятся во всей комплексной плоскости.
Пример
3. Функцию
![]() разложить в ряд Лорана в окрестности
разложить в ряд Лорана в окрестности
точки![]() .
.
Решение.
Функция
![]() является аналитической в кольце
является аналитической в кольце![]() .
.
Следовательно, она разложима в ряд
Лорана. Воспользуемся разложением
функции![]() в ряд Тейлора
в ряд Тейлора .
.
и
положим
![]() :
:

(6)
В
силу единственности разложения в ряд
Лорана (6) является рядом Лорана для
функции
![]() в кольце
в кольце![]() .
.
Соседние файлы в папке ТФКП
- #
- #
1°. Ряд Тейлора. Функция ![]() однозначная и аналитическая в точке
однозначная и аналитическая в точке ![]() разлагается (то есть является суммой) в окрестности этой точки в степенной ряд – ряд Тейлора
разлагается (то есть является суммой) в окрестности этой точки в степенной ряд – ряд Тейлора
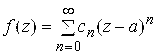 , (5.10)
, (5.10)
Где коэффициенты ![]() вычисляются по формулам
вычисляются по формулам
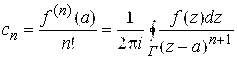
![]() , (5.11)
, (5.11)
Где Г – окружность с центром в точке ![]() , целиком лежащая в области аналитичности
, целиком лежащая в области аналитичности ![]() . Областью сходимости ряда является круг с центром в точке разложения радиуса R, равном расстоянию от центра разложения до ближайшей осо бой точки – точки, в которой
. Областью сходимости ряда является круг с центром в точке разложения радиуса R, равном расстоянию от центра разложения до ближайшей осо бой точки – точки, в которой ![]() теряет аналитичность.
теряет аналитичность.
Теорема Тейлора. Функция ![]() , аналитическая в круге
, аналитическая в круге ![]() однозначно представима в нем своим рядом Тейлора (5.10), коэффициенты которого определяются по формулам (5.11).
однозначно представима в нем своим рядом Тейлора (5.10), коэффициенты которого определяются по формулам (5.11).
Из этой теоремы и теоремы о возможности дифференцирования степенного ряда в круге сходимости любое число раз следует, что разложение функции в степенной ряд единственно. Это означает, что по любому методу разложения функции в степенной ряд мы получаем одно и то же разложение – ряд Тейлора. При ![]() ряд (5.10) называется рядом Маклорена.
ряд (5.10) называется рядом Маклорена.
При решении многих задач рекомендуется пользоваться следующими разложениями элементарных функций:
1) 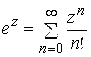 ,
, ![]() ; 2)
; 2) 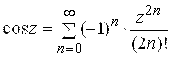 ,
, ![]() ;
;
3) 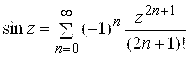 ,
,![]() ; 4)
; 4) 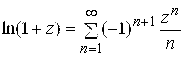 ,
, ![]() ; (5.12)
; (5.12)
5) 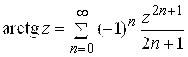 ,
, ![]() ; 6)
; 6) 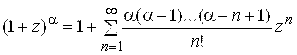 ,
,
![]() ,
, ![]() ; 7)
; 7) ![]()
![]() ;
;
8)  .
.
Для непосредственного разложения функции в степенной ряд (ряд Тейлора), необходимо найти закон получения производной N-го порядка (подобные примеры опустим).
Пример 1. Разложить в ряд по степеням ![]() функцию
функцию ![]() .
.
Решение. Рассмотрим сначала следующее преобразование данной логарифмической функции ![]() . Воспользуемся разложением 4) из (5.12) для
. Воспользуемся разложением 4) из (5.12) для ![]() , полагая
, полагая ![]() . Так как разложение 4) имеет место при
. Так как разложение 4) имеет место при ![]() , то наше разложение будет иметь место при
, то наше разложение будет иметь место при ![]() . Таким образом, для
. Таким образом, для ![]() :
: ![]()
 .
.
Часто при разложении функций в ряд удобно пользоваться дифференцированием или интегрированием известных разложений, а при разложении рациональной дроби – разложением ее на простейшие.
Пример 2. Разложить в ряд по степеням Z функцию 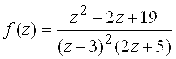 .
.
Решение. Разложим ![]() на простейшие дроби:
на простейшие дроби:  . По формуле суммы геометрической прогрессии 7) из (5.12) получим:
. По формуле суммы геометрической прогрессии 7) из (5.12) получим:
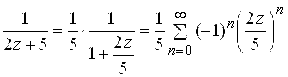 ,
, ![]() и
и  ,
,
![]() . Замечая, что
. Замечая, что ![]() и применяя теорему о возможном почленном дифференцировании степенного ряда в круге сходимости, получим
и применяя теорему о возможном почленном дифференцировании степенного ряда в круге сходимости, получим  ,
, ![]() . Складывая ряды для
. Складывая ряды для ![]() и
и 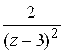 , имеем
, имеем  ,
, ![]() .
.
2°. Ряды Лорана.
Определение. Рядом Лорана называется ряд (5.6)
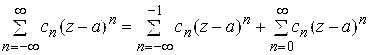 ; (5.6)
; (5.6)
При этом ряд  называется главной частью ряда Лорана, а ряд
называется главной частью ряда Лорана, а ряд  – правильной частью. Если
– правильной частью. Если  , то областью сходимости ряда (5.6) является кольцо
, то областью сходимости ряда (5.6) является кольцо ![]() .
.
Теорема Лорана. Если функция ![]() аналитична в кольце
аналитична в кольце ![]() , то в этом кольце она единственным образом представима в виде ряда Лорана (5.6), коэффициенты которого вычисляются по формулам:
, то в этом кольце она единственным образом представима в виде ряда Лорана (5.6), коэффициенты которого вычисляются по формулам:

![]() (5.13)
(5.13)
Заметим, что из этой теоремы “кольца разложимости” определяются через расстояния от центра разложения до двух “соседних” особых точек ![]() . Вычисление контурных интегралов (5.14), как правило, достаточно затруднительно. Поэтому для разложения функций в ряды Лорана используются различные искусственные приемы.
. Вычисление контурных интегралов (5.14), как правило, достаточно затруднительно. Поэтому для разложения функций в ряды Лорана используются различные искусственные приемы.
Пример 1. Разложить в ряд Лорана в кольце ![]() функцию
функцию  .
.
Решение. Преобразуем данную функцию:
 . (1)
. (1)
Первые два слагаемых в правой части (1) имеют нужный вид, так как представляют собой степени разности ![]() . Последние два слагаемых запишем в виде:
. Последние два слагаемых запишем в виде:  ,
,  . Применяя формулу 7), а затем 8) (из (5.12)), найдем
. Применяя формулу 7), а затем 8) (из (5.12)), найдем
 , (2)
, (2)
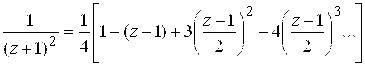 (3)
(3)
Подставляя (2) и (3) в (1), после несложных преобразований получим разложение ![]() в кольце
в кольце ![]() в ряд Лорана:
в ряд Лорана:
 .
.
Пример 2. Разложить в ряд Лорана функцию ![]() в окрестности
в окрестности ![]() .
.
Решение. Для любого комплексного ![]() имеем
имеем 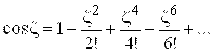
Полагая ![]() , получим:
, получим: 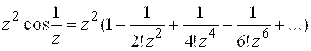
![]()

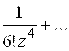 . Это разложение справедливо для любой точки
. Это разложение справедливо для любой точки ![]() . В данном случае “кольцо” представляет собой всю комплексную плоскость с одной выброшенной точкой
. В данном случае “кольцо” представляет собой всю комплексную плоскость с одной выброшенной точкой ![]() :
: ![]()
![]() .
.
Пример 3. Рассмотреть различные разложения в ряд Лорана функции ![]() .
.
Решение. Функция ![]() имеет две особые точки:
имеет две особые точки: ![]() и
и ![]() . Следовательно, имеется три “кольца” с центром в точке
. Следовательно, имеется три “кольца” с центром в точке ![]() , в каждом из которых
, в каждом из которых ![]() является аналитической: а) круг
является аналитической: а) круг ![]() ; б) кольцо
; б) кольцо ![]() ; в)
; в) ![]() – внешность круга
– внешность круга ![]() . Найдем ряды Лорана для функции
. Найдем ряды Лорана для функции ![]() В каждом из этих “колец”. Представим предварительно функцию в виде суммы простейших дробей:
В каждом из этих “колец”. Представим предварительно функцию в виде суммы простейших дробей: ![]() (1). а)разложение в круге
(1). а)разложение в круге ![]() . Преобразуем (1) следующим образом:
. Преобразуем (1) следующим образом: 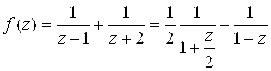 (2). Используя формулу 7) из (5.12), получим:
(2). Используя формулу 7) из (5.12), получим: ![]() ,
, ![]() (3);
(3);  ,
, ![]() (4). Подставляя эти разложения в (2), получим:
(4). Подставляя эти разложения в (2), получим: ![]()
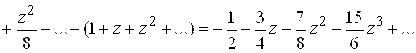 – это разложение есть ряд Маклорена функции
– это разложение есть ряд Маклорена функции ![]() . б) разложение в кольце
. б) разложение в кольце ![]() . Ряд (4) для функции
. Ряд (4) для функции ![]() остается сходящимся в этом кольце, так как
остается сходящимся в этом кольце, так как ![]() . Ряд (3) для функции
. Ряд (3) для функции ![]() расходится для
расходится для ![]() . Поэтому преобразуем
. Поэтому преобразуем ![]() следующим образом:
следующим образом:
 (5). Применяя формулу 7), получим:
(5). Применяя формулу 7), получим: 
![]() (6). Этот ряд сходится, если
(6). Этот ряд сходится, если ![]() , то есть при
, то есть при ![]() . Подставляя (4) и (6) в (5), найдем
. Подставляя (4) и (6) в (5), найдем  . в) разложение для
. в) разложение для ![]() . Ряд (4) для функции
. Ряд (4) для функции ![]() при
при ![]() расходится, а ряд (6) для функции
расходится, а ряд (6) для функции ![]() будет сходиться, так как, если
будет сходиться, так как, если ![]() , то и подавно
, то и подавно ![]() . Функцию
. Функцию ![]() представим в таком виде
представим в таком виде 
 . Используя формулу 7), получаем
. Используя формулу 7), получаем 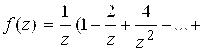
![]() . Заметим, что этот пример показывает, что для одной и той же функции ряд Лорана, вообще говоря, имеет разный вид для разных колец.
. Заметим, что этот пример показывает, что для одной и той же функции ряд Лорана, вообще говоря, имеет разный вид для разных колец.
Пример 4. Разложить в ряд Лорана функцию 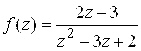 в окрестности ее особых точек.
в окрестности ее особых точек.
Решение. Особые точки функции: ![]() . а) разложение
. а) разложение ![]() в окрестности точки
в окрестности точки ![]() , то есть в кольце
, то есть в кольце ![]() . Представим функцию
. Представим функцию ![]() в виде суммы простейших дробей:
в виде суммы простейших дробей: 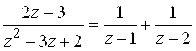 . Правую часть преобразуем так:
. Правую часть преобразуем так:  . Применяя разложение 7), в котором Z Заменим на
. Применяя разложение 7), в котором Z Заменим на ![]() , получим
, получим  или
или 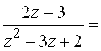
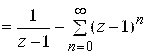 . б) разложение
. б) разложение ![]() в окрестности точки
в окрестности точки ![]() , то есть в кольце
, то есть в кольце ![]() . Имеем
. Имеем 
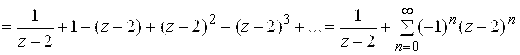 .
.
| < Предыдущая | Следующая > |
|---|
Введение
Теория функций комплексной переменной (ТФКП) дошла до наших дней почти в том виде, в котором оставил нам ее создатель великий французский математик Огюстен Коши (1789–1857 гг.).
ТФКП как продолжает, так и расширяет идеи математического анализа функций действительной переменной. Обычные определения, известные из алгебры чисел и математического анализа функций действительной переменной, остаются почти без изменений, но их содержание меняется весьма существенным образом. Хорошо известно, что уже обычные простейшие операции над действительными числами могут вывести за пределы их области. И решения большинства алгебраических уравнений не могут быть выражены только обычными действительными числами. Поэтому приходится расширять область действительных чисел, а таким расширением этой области и является область комплексных чисел.
Основное понятие комплексного анализа аналитическая функция. Это понятие позволяет доказать теоремы о существовании производных любого порядка от этих функций, о независимости интегралов от формы пути интегрирования. Позволяет сравнительно единообразно вычислять сложные интегралы с помощью вычетов и многое другое.
В данных методических указаниях изложены основные вопросы теории функций комплексной переменной в соответствии с действующими рабочими программами для студентов всех направлений подготовки бакалавров инженерно-технических специальностей вуза.
Каждый из выделенных параграфов содержит краткое изложение основных теоретических сведений, практическое руководство по решению стандартных математических задач. В конце предлагаются варианты заданий для расчетно-графической работы.
1. Функциональные ряды в комплексной области.
Степенные ряды
Пусть  – последовательность функций, определенных на множестве
– последовательность функций, определенных на множестве ![]() . Функциональным рядом в комплексной области называется выражение
. Функциональным рядом в комплексной области называется выражение
 , (1)
, (1)
где ![]() . Функции
. Функции  ,
, ![]() называются членами ряда. Функциональный ряд (1) называется сходящимся в точке
называются членами ряда. Функциональный ряд (1) называется сходящимся в точке  , если сходится числовой ряд
, если сходится числовой ряд  . Функциональный ряд (1) называется абсолютно сходящимся в точке
. Функциональный ряд (1) называется абсолютно сходящимся в точке ![]() , если сходится числовой ряд
, если сходится числовой ряд  . Множество
. Множество ![]() точек, в которых функциональный ряд (1) сходится, называется областью сходимости ряда, а функция
точек, в которых функциональный ряд (1) сходится, называется областью сходимости ряда, а функция  ,
, ![]() – суммой функционального ряда (1).
– суммой функционального ряда (1).
Функциональный ряд вида
 , (2)
, (2)
где ![]() ,
,  комплексные постоянные,
комплексные постоянные, ![]() – комплексная переменная, называется степенным рядом в комплексной области. Числа
– комплексная переменная, называется степенным рядом в комплексной области. Числа ![]()
 называются коэффициентами ряда,
называются коэффициентами ряда, ![]() – его центром.
– его центром.
Область определения степенного ряда – вся комплексная плоскость. Очевидно, что в точке  ряд (2) сходится. Следовательно, область сходимости любого степенного ряда состоит, по крайней мере, из одной точки.
ряд (2) сходится. Следовательно, область сходимости любого степенного ряда состоит, по крайней мере, из одной точки.
Теорема 1 (Абеля). Если степенной ряд (2) сходится в точке ![]() , то он сходится абсолютно при любом
, то он сходится абсолютно при любом ![]() , удовлетворяющем условию
, удовлетворяющем условию  .
.
Областью сходимости ряда (2) является круг с центром в точке ![]() . Радиус сходимости степенного ряда может быть найден по формулам:
. Радиус сходимости степенного ряда может быть найден по формулам:
 (3)
(3)
 , (4)
, (4)
если указанные пределы существуют.
Если  , то круг сходимости – вся конечная комплексная плоскость.
, то круг сходимости – вся конечная комплексная плоскость.
Если  , то круг вырождается в точку
, то круг вырождается в точку ![]() , а в его внешности, т. е. во всей комплексной плоскости, кроме точки
, а в его внешности, т. е. во всей комплексной плоскости, кроме точки ![]() , ряд расходится.
, ряд расходится.
На окружности  ряд (2) может вести себя по-разному: может сходиться во всех точках окружности, расходиться во всех точках, может в одних сходиться, а в других расходиться.
ряд (2) может вести себя по-разному: может сходиться во всех точках окружности, расходиться во всех точках, может в одних сходиться, а в других расходиться.
Пример 1.1. Найти радиус сходимости степенного ряда:  .
.
Решение. Воспользуемся формулой (3). Имеем
 ,
,
 .
.
Пример 1.2. Найти круг сходимости степенного ряда:  .
.
Решение. Воспользуемся формулой (4). Имеем
 ,
,  ,
,
 .
.
Следовательно,  – круг сходимости данного ряда.
– круг сходимости данного ряда.
2. Разложение функций в ряд Тейлора
Теорема 2 (о разложении аналитической функции в степенной ряд). Пусть ![]() – аналитическая функция в области
– аналитическая функция в области ![]() ,
,  и
и ![]() – расстояние от
– расстояние от ![]() до границы
до границы ![]() . Тогда в круге
. Тогда в круге ![]() функция
функция ![]() разлагается в степенной ряд
разлагается в степенной ряд
 , где
, где  , (5)
, (5)
называемый рядом Тейлора функции ![]() . При этом коэффициенты ряда удовлетворяют соотношениям
. При этом коэффициенты ряда удовлетворяют соотношениям
 (6)
(6)
при любых ![]() ,
,  .
.
Первый отличный от нуля член ряда Тейлора называется главным членом разложения в ряд Тейлора, а его степень – порядком главного члена.
Из этой теоремы следует еще одно определение аналитической функции.
Функция ![]() называется аналитической в точке
называется аналитической в точке ![]() , если она разлагается в степенной ряд в некоторой окрестности точки
, если она разлагается в степенной ряд в некоторой окрестности точки ![]() .
.
Функция ![]() называется аналитической в области
называется аналитической в области ![]() , если она разлагается в степенной ряд в некоторой окрестности каждой точки
, если она разлагается в степенной ряд в некоторой окрестности каждой точки ![]() .
.
Ряды Тейлора некоторых элементарных функций:
 ,
, ![]() ; (7)
; (7)
 ,
, ![]() ; (8)
; (8)
 ,
, ![]() ; (9)
; (9)
 ,
, ![]() ; (10)
; (10)
 ,
, ![]() ; (11)
; (11)
 ,
, ![]() . (12)
. (12)
Формула (12) называется суммой бесконечной геометрической прогрессии и является следствием (11) при  .
.
Пример 2.1. Разложить функцию  в ряд по степеням
в ряд по степеням ![]() и определить радиус сходимости ряда.
и определить радиус сходимости ряда.
Решение. Найдем коэффициенты ряда Тейлора, пользуясь формулой (5):
 .
.
Таким образом
 .
.
Поскольку функция ![]() аналитична на всей комплексной плоскости, то по теореме 2 этот ряд сходится также при всех
аналитична на всей комплексной плоскости, то по теореме 2 этот ряд сходится также при всех  .
.
Пример 2.2. Разложить функцию  в ряд по степеням
в ряд по степеням ![]() и определить радиус сходимости ряда.
и определить радиус сходимости ряда.
Решение. Преобразуем данную функцию:
 .
.
Обозначим  и воспользуемся разложением (12) для функции
и воспользуемся разложением (12) для функции ![]() при
при ![]() . Получим:
. Получим:
 .
.
Из условия ![]() следует, что полученный ряд сходится при
следует, что полученный ряд сходится при  , т. е. при
, т. е. при  .
.
Пример 2.3. Разложить функцию  в ряд по степеням
в ряд по степеням ![]() и определить радиус сходимости ряда.
и определить радиус сходимости ряда.
Решение. Найдем нули знаменателя дроби:  ,
, ![]() . Так как
. Так как  ,
, ![]() , то данная функция аналитична в круге
, то данная функция аналитична в круге ![]() как частное двух аналитических функций. Представим данную функцию в виде суммы простейших дробей:
как частное двух аналитических функций. Представим данную функцию в виде суммы простейших дробей:
 .
.
Каждое слагаемое разложим в ряд по степеням ![]() , пользуясь формулой (12):
, пользуясь формулой (12):
 ,
, ![]() ,
,
 ,
, ![]() .
.
Складывая полученные разложения и учитывая аналитичность функции ![]() в круге
в круге ![]() , получаем:
, получаем:
 ,
, ![]() .
.
Пример 2.4. Разложить функцию  в ряд по степеням
в ряд по степеням ![]() и определить радиус сходимости ряда.
и определить радиус сходимости ряда.
Решение. Преобразуем данную функцию и воспользуемся разложением (9):


 .
.
Полученный ряд сходится на всей комплексной плоскости, так как ряд (9) сходится при всех  .
.
3. Ряд Лорана
Рядом Лорана называется выражение
 , (13)
, (13)
где ![]() ,
,  . Ряд Лорана называется сходящимся на множестве
. Ряд Лорана называется сходящимся на множестве ![]() , если на этом множестве сходятся оба функциональных ряда:
, если на этом множестве сходятся оба функциональных ряда:
 (14)
(14)
и
 . (15)
. (15)
Суммой ряда Лорана (13) называется сумма  , где
, где ![]() и
и  – суммы рядов (14) и (15) соответственно. Ряд (14) называется главной, а ряд (15) – правильной частью ряда Лорана. Ряд Лорана называется абсолютно сходящимся на множестве
– суммы рядов (14) и (15) соответственно. Ряд (14) называется главной, а ряд (15) – правильной частью ряда Лорана. Ряд Лорана называется абсолютно сходящимся на множестве ![]() , если на этом множестве абсолютно сходятся ряды (14) и (15).
, если на этом множестве абсолютно сходятся ряды (14) и (15).
Ряды Лорана позволяют изучать функции, аналитические в кольцах ![]() , где
, где ![]() ,
, ![]() .
.
Теорема 3 (о сходимости ряда Лорана). Ряд Лорана сходится абсолютно внутри кольца ![]() , где
, где ![]() – радиус сходимости степенного ряда (15), а
– радиус сходимости степенного ряда (15), а  – радиус сходимости степенного ряда
– радиус сходимости степенного ряда
 , (16)
, (16)
если ![]() .
.
Теорема 4 (Лорана). Функция ![]() , аналитическая в кольце
, аналитическая в кольце ![]() , представляется в этом кольце сходящимся рядом Лорана
, представляется в этом кольце сходящимся рядом Лорана
 ,
,
где
 , (17)
, (17)
![]() ,
, ![]() .
.
Главная часть ряда Лорана сходится во внешности круга с центром в точке ![]() и радиусом
и радиусом ![]() , где
, где ![]() , как и в случае степенных рядов, может быть найден (если существуют соответствующие пределы) по формулам:
, как и в случае степенных рядов, может быть найден (если существуют соответствующие пределы) по формулам:
 (18)
(18)
или
![]() . (19)
. (19)
При ![]() эта область вырождается в в несобственную точку
эта область вырождается в в несобственную точку ![]() , а при
, а при ![]() – во всю плоскость, за исключением, возможно,
– во всю плоскость, за исключением, возможно,  .
.
Пример 3.1. Найти область сходимости ряда  .
.
Решение. Найдем круг сходимости правильной части ряда, т. е. ряда  . Воспользуемся формулой (4). Так как
. Воспользуемся формулой (4). Так как
 ,
,
то это круг ![]() . Для ряда
. Для ряда
 ,
,
представляющего собой главную часть данного ряда,
 ,
,
поэтому его область сходимости  . Исходный ряд сходится в кольце
. Исходный ряд сходится в кольце  .
.
Пример 3.2. Разложить функцию  в ряд Лорана в кольце
в ряд Лорана в кольце  .
.
Решение. Записав функцию в виде
 ,
,
замечаем, что данная функция является аналитической на всей комплексной плоскости, за исключением точек  и
и ![]() , в которых знаменатель дроби обращается в нуль. Эти точки лежат на границе данного кольца
, в которых знаменатель дроби обращается в нуль. Эти точки лежат на границе данного кольца  (рис. 1).
(рис. 1).

Рис. 1
Это означает, что в самом кольце функция аналитическая и, следовательно, по теореме 4 разлагается в ряд Лорана с центром в точке ![]() . Для получения этого разложения представим функцию в виде
. Для получения этого разложения представим функцию в виде
![]() , где
, где  ,
,  .
.
Функция ![]() аналитична в большем круге
аналитична в большем круге ![]() . Разложим ее в ряд Тейлора с центром в точке
. Разложим ее в ряд Тейлора с центром в точке ![]() . Преобразуем
. Преобразуем ![]() следующим образом:
следующим образом:
 .
.
Положим  и воспользуемся разложением (12). Получим:
и воспользуемся разложением (12). Получим:
 ,
, ![]() .
.
Функция  также разлагается в ряд по положительным степеням
также разлагается в ряд по положительным степеням ![]() , но этот ряд сходится лишь в круге
, но этот ряд сходится лишь в круге  , а мы хотим разложить функцию вне этого круга. Нужно получить разложение этой функции по отрицательным степеням. Преобразуем функцию
, а мы хотим разложить функцию вне этого круга. Нужно получить разложение этой функции по отрицательным степеням. Преобразуем функцию ![]() следующим образом:
следующим образом:
 .
.
Положим  и воспользуемся разложением (12). Получим:
и воспользуемся разложением (12). Получим:
 .
.
Этот ряд сходится при  , т. е. при
, т. е. при ![]() . Окончательно получаем:
. Окончательно получаем:
 ,
, ![]() .
.
Пример 3.3. Найти все возможные разложения в ряд Лорана по степеням ![]() функции
функции  .
.
Решение. Данная функция является аналитической на всей комплексной плоскости, за исключением точек  и
и ![]() , в которых знаменатель дроби обращается в нуль. Следовательно, по теореме 4 она разлагается в ряд Лорана в любом кольце с центром в точке
, в которых знаменатель дроби обращается в нуль. Следовательно, по теореме 4 она разлагается в ряд Лорана в любом кольце с центром в точке ![]() , не содержащем точку
, не содержащем точку ![]() . Получаем два кольца:
. Получаем два кольца:  и
и ![]() . Найдем разложение функции в ряд Лорана в кольце
. Найдем разложение функции в ряд Лорана в кольце ![]() . Имеем
. Имеем


 .
.
В кольце ![]() :
:


 .
.
Таким образом, получены два разложения данной функции в ряд Лорана по степеням ![]() :
:
 ,
, ![]() ,
,
 ,
, ![]() .
.
4. Изолированные особые точки аналитических функций
Точка  называется правильной точкой функции
называется правильной точкой функции ![]() , если функция
, если функция ![]() аналитична в этой точке. Если функция
аналитична в этой точке. Если функция ![]() не является аналитической в точке
не является аналитической в точке ![]() , но аналитична в некоторой ее проколотой окрестности
, но аналитична в некоторой ее проколотой окрестности ![]() , то точка
, то точка ![]() называется изолированной особой точкой функции
называется изолированной особой точкой функции ![]() .
.
Так как проколотую окрестность точки ![]() можно рассматривать как частный случай кольца, то функция
можно рассматривать как частный случай кольца, то функция ![]() разлагается в нем в ряд Лорана по степеням
разлагается в нем в ряд Лорана по степеням ![]() . В зависимости от вида этого ряда различают три типа изолированных особых точек.
. В зависимости от вида этого ряда различают три типа изолированных особых точек.
Изолированная особая точка ![]() для функции
для функции ![]() называется
называется
1) устранимой, если указанный ряд Лорана содержит только правильную часть:
![]() ;
;
2) полюсом, если главная часть ряда Лорана содержит лишь конечное число членов:
 ,
,
причем ![]() ,
, ![]() . Число
. Число ![]() называется порядком полюса, при
называется порядком полюса, при ![]() полюс называется простым.
полюс называется простым.
3) существенно особой, если главная часть ряда Лорана содержит бесконечное число членов:
 ,
,
причем ![]() для бесконечного числа отрицательных номеров
для бесконечного числа отрицательных номеров ![]() .
.
Во многих вопросах комплексного анализа удобно рассматривать расширенную комплексную плоскость, т. е. плоскость, дополненную символической точкой ![]() .
.
Точка  называется изолированной особой точкой функции
называется изолированной особой точкой функции ![]() , если
, если ![]() аналитична в области
аналитична в области  (в окрестности бесконечно удаленной точки). В этом случае точка
(в окрестности бесконечно удаленной точки). В этом случае точка ![]() является изолированной особой точкой функции
является изолированной особой точкой функции  . Точка
. Точка  называется устранимой особой точкой, полюсом порядка
называется устранимой особой точкой, полюсом порядка ![]() или существенно особой точкой функции
или существенно особой точкой функции ![]() в зависимости от того, является ли точка
в зависимости от того, является ли точка ![]() устранимой особой точкой, полюсом порядка
устранимой особой точкой, полюсом порядка ![]() или существенно особой точкой функции
или существенно особой точкой функции  .
.
Разложим  функцию в ряд Лорана в кольце
функцию в ряд Лорана в кольце 

и произведем замену переменной  . Получим ряд
. Получим ряд
 ,
,
который называется рядом Лорана функции ![]() в окрестности бесконечно удаленной точки. Ряд
в окрестности бесконечно удаленной точки. Ряд  называется главной, а ряд
называется главной, а ряд  – правильной частью ряда Лорана функции
– правильной частью ряда Лорана функции ![]() в окрестности бесконечно удаленной точки. Если главная часть разложения отсутствует, то точка
в окрестности бесконечно удаленной точки. Если главная часть разложения отсутствует, то точка  является устранимой особой точкой. В этом случае полагают по определению
является устранимой особой точкой. В этом случае полагают по определению  и говорят, что
и говорят, что  является правильной точкой функции
является правильной точкой функции ![]() . При этом, если
. При этом, если  является нулем порядка
является нулем порядка ![]() функции
функции  , то говорят, что
, то говорят, что ![]() является нулем порядка
является нулем порядка ![]() функции
функции ![]() .
.
Теорема 5 (о связи между нулем и полюсом). Точка ![]() является полюсом порядка
является полюсом порядка ![]() функции
функции ![]() тогда и только тогда, когда она является нулем порядка
тогда и только тогда, когда она является нулем порядка ![]() функции
функции  .
.
Теорема 6 (о существенно особой точке). Если существует окрестность существенно особой точки ![]() аналитической функции
аналитической функции ![]() , в которой
, в которой ![]() , то точка
, то точка ![]() является существенно особой и для функции
является существенно особой и для функции  .
.
Теорема 7 (Сохоцкого). Если ![]() – существенно особая точка функции
– существенно особая точка функции ![]() , то для любого
, то для любого  существует последовательность точек
существует последовательность точек  ,
, ![]() , сходящаяся к точке
, сходящаяся к точке ![]() , такая что
, такая что  .
.
Функция, аналитическая на всей комплексной плоскости, называется целой. Целая функция, для которой точка  является существенно особой точкой, называется целой трансцендентной. Функция, аналитическая в области
является существенно особой точкой, называется целой трансцендентной. Функция, аналитическая в области ![]() всюду, кроме полюсов, называется мероморфной в
всюду, кроме полюсов, называется мероморфной в ![]() .
.
На практике при определении вида особых точек часто бывает полезен следующий простой факт:
если ![]() – нуль порядка
– нуль порядка ![]() аналитической функции
аналитической функции ![]() , а функция
, а функция ![]() аналитична в точке
аналитична в точке ![]() и
и ![]() , то
, то ![]() – полюс порядка
– полюс порядка ![]() функции
функции  .
.
Пример 4.1. Найти изолированные особые точки функции  и определить их вид.
и определить их вид.
Решение. Данная функция представляет собой частное двух аналитических на всей комплексной плоскости функций, поэтому ее особыми точками могут быть только нули знаменателя. Найдем их:
![]()
![]()
 ,
, ![]() ,
,  .
.
Причем они являются простыми нулями.
Так как числитель ни в одной из этих точек не обращается в нуль, то по теореме 5 точки  ,
, ![]() ,
,  являются простыми полюсами исходной функции.
являются простыми полюсами исходной функции.
Пример 4.2. Найти изолированные особые точки функции  и определить их вид.
и определить их вид.
Решение. Данная функция как частное двух аналитических на всей комплексной плоскости функций может иметь особой точкой только нуль знаменателя, т. е. ![]() . Однако точка
. Однако точка ![]() является также и нулем числителя. Поэтому для выяснения вида особенности разложим функцию в ряд Лорана по степеням
является также и нулем числителя. Поэтому для выяснения вида особенности разложим функцию в ряд Лорана по степеням ![]() :
:
 .
.
Ряд не содержит отрицательных степеней ![]() , поэтому
, поэтому ![]() – устранимая особая точка.
– устранимая особая точка.
Пример 4.3. Найти изолированные особые точки функции  и определить их вид.
и определить их вид.
Решение. Данная функция определена и дифференцируема на всей комплексной плоскости, за исключением точки ![]() . Это изолированная особая точка. Запишем ряд Лорана для функции
. Это изолированная особая точка. Запишем ряд Лорана для функции ![]() в окрестности точки
в окрестности точки ![]() , пользуясь разложением (7) для функции
, пользуясь разложением (7) для функции ![]() , полагая
, полагая ![]() :
:
 .
.
Ряд содержит бесконечно много членов с отрицательными степенями. Поэтому точка ![]() – существенно особая.
– существенно особая.
Пример 4.4. Найти изолированные особые точки функции  и определить их вид.
и определить их вид.
Решение. Данная функция есть частное двух аналитических на всей комплексной плоскости функций. Поэтому ее особыми точками являются нули знаменателя:
![]()
![]()
 ,
, ![]() .
.
Так как числитель дроби в нуль не обращается, то эти точки являются полюсами. Определим порядки полюсов по порядкам нулей функции
 .
.
Вычислим:
![]() ,
,  ,
,  ,
,
![]() ,
,  ,
,  .
.
Следовательно, точки  (
(![]() ) являются нулями второго порядка функции
) являются нулями второго порядка функции ![]() и, по теореме 5, полюсами второго порядка функции
и, по теореме 5, полюсами второго порядка функции ![]() .
.
Вид изолированной особенности характеризует поведение функции в окрестности этой особенности:
если ![]() – устранимая особая точка функции
– устранимая особая точка функции ![]() , то существует конечный предел функции
, то существует конечный предел функции ![]() в точке
в точке ![]() ;
;
если ![]() – полюс, то
– полюс, то  при
при
если же ![]() – существенно особая точка, то указанного предела не существует.
– существенно особая точка, то указанного предела не существует.
Эти свойства являются характеристическими, т. е. справедливы и обратные утверждения.
Пример 4.5. Найти изолированные особые точки функции  и определить их вид, используя характеристические свойства особых точек.
и определить их вид, используя характеристические свойства особых точек.
Решение. Единственная особая точка данной функции – ![]() (см. пример 4.2). Так как
(см. пример 4.2). Так как
 ,
,
т. е. функция имеет конечный предел в точке ![]() , то
, то ![]() является устранимой особой точкой данной функции.
является устранимой особой точкой данной функции.
5. Вычеты и их применение
Пусть ![]() – изолированная особая точка однозначной аналитической функции
– изолированная особая точка однозначной аналитической функции ![]() и
и ![]() – окружность
– окружность  такая, что в замкнутом круге
такая, что в замкнутом круге  нет других особых точек функции
нет других особых точек функции ![]() , кроме точки
, кроме точки ![]() . Интеграл от функции
. Интеграл от функции ![]() по такой окружности
по такой окружности ![]() , деленный на
, деленный на ![]() , называется вычетом функции
, называется вычетом функции ![]() в точке
в точке ![]() и обозначается
и обозначается  .
.
Таким образом, по определению
 .
.
Вычислять вычеты, исходя из определения, довольно трудно. Поэтому на практике применяются следующие утверждения:
Теорема 8 (о вычете относительно изолированной особой точки). Вычет функции ![]() в изолированной особой точке
в изолированной особой точке ![]() равен коэффициенту при
равен коэффициенту при  в разложении функции в ряд Лорана в окрестности точки
в разложении функции в ряд Лорана в окрестности точки ![]() :
:
![]() .
.
Если точка ![]() – полюс, то для определения вычета иногда можно и не находить разложение функции в ряд Лорана. Имеются более простые способы.
– полюс, то для определения вычета иногда можно и не находить разложение функции в ряд Лорана. Имеются более простые способы.
Теорема 9 (о вычете относительно полюса). Пусть ![]() – полюс порядка
– полюс порядка ![]() функции
функции ![]() . Тогда
. Тогда
 . (20)
. (20)
Следствие. Если ![]() – простой полюс функции
– простой полюс функции ![]() , то
, то
![]() . (21)
. (21)
Вычисление вычета в простом полюсе еще более упрощается, если ![]() имеет вид:
имеет вид:
 ,
,
где ![]() ,
,  ,
, ![]() . Тогда
. Тогда
 . (22)
. (22)
Пример 5.1. Вычислить вычеты функции  относительно каждой из ее особых точек.
относительно каждой из ее особых точек.
Решение. В примере 4.3 установлено, что точка ![]() – существенно особая точка данной функции, и получено разложение функции в ряд Лорана в окрестности этой точки:
– существенно особая точка данной функции, и получено разложение функции в ряд Лорана в окрестности этой точки:
 ,
,
следовательно,
 .
.
Пример 5.2. Вычислить вычеты функции  относительно каждой из ее особых точек.
относительно каждой из ее особых точек.
Решение. Особыми точками данной функции являются нули знаменателя ![]() – простой полюс и
– простой полюс и ![]() – полюс второго порядка. Найдем вычет относительно точки
– полюс второго порядка. Найдем вычет относительно точки ![]() по формуле (21):
по формуле (21):
 .
.
Для определения вычета относительно точки ![]() воспользуемся формулой (20) при
воспользуемся формулой (20) при  :
:
 .
.
Теория вычетов находит широкое применение благодаря следующему утверждению:
Теорема 10 (о вычетах). Пусть функция ![]() является аналитической в области
является аналитической в области ![]() всюду, за исключением конечного числа точек
всюду, за исключением конечного числа точек ![]() ,
, ![]() . Пусть замкнутый контур
. Пусть замкнутый контур ![]() содержится в области
содержится в области ![]() и не проходит через особые точки. Тогда интеграл от функции
и не проходит через особые точки. Тогда интеграл от функции ![]() по контуру
по контуру ![]() равен сумме вычетов функции относительно всех особых точек
равен сумме вычетов функции относительно всех особых точек ![]() (
( ), заключенных внутри
), заключенных внутри ![]() , умноженной на
, умноженной на ![]() :
:
 .
.
Теорема 11 (о вычетах на расширенной комплексной плоскости). Пусть функция ![]() является аналитической на расширенной комплексной плоскости, кроме конечного числа точек
является аналитической на расширенной комплексной плоскости, кроме конечного числа точек  ,
, ![]() ,
, ![]() ,…,
,…, ![]() . Тогда
. Тогда
 .
.
Пример 5.3. Вычислить интеграл  .
.
Решение. Особыми точками подынтегральной функции  являются точки
являются точки ![]() ,
,  ,
, ![]() . Из них внутри окружности
. Из них внутри окружности ![]() лежат только две:
лежат только две:  и
и ![]() . Поэтому по теореме 10
. Поэтому по теореме 10
 .
.
Обе эти точки являются для данной функции простыми полюсами. Воспользуемся формулой (22):
 ,
,
 .
.
Следовательно,
 .
.
Пример 5.4. Вычислить интеграл  .
.
Решение. Внутри окружности  лежат восемь полюсов второго порядка, а вне ее – простой полюс
лежат восемь полюсов второго порядка, а вне ее – простой полюс ![]() и
и  . По формуле (21) найдем вычет в точке
. По формуле (21) найдем вычет в точке ![]() :
:
 .
.
Для определения вычета в точке  найдем несколько членов разложения подынтегральной функции в ряд Лорана в окрестности этой точки. Введем новую переменную
найдем несколько членов разложения подынтегральной функции в ряд Лорана в окрестности этой точки. Введем новую переменную ![]() , тогда
, тогда
 .
.
Так как функция ![]() аналитична в круге
аналитична в круге ![]() , то ее можно разложить в этом круге в степенной ряд:
, то ее можно разложить в этом круге в степенной ряд:
![]() ,
, ![]() .
.
Тогда
 ,
, ![]()
или
 ,
, ![]() .
.
В полученном разложении коэффициент при ![]() равен нулю, т. е.
равен нулю, т. е.  . Значит по теореме 11
. Значит по теореме 11
 .
.
Варианты заданий для РГР
Задание 1. Разложить функцию ![]() в ряд по степеням
в ряд по степеням  и определить радиус сходимости полученного ряда.
и определить радиус сходимости полученного ряда.
1. а) ![]() ,
,  ; б)
; б)  ,
, ![]() .
.
2. а) ![]() ,
,  ; б)
; б)  ,
, ![]() .
.
3. а) ![]() ,
,  ; б)
; б)  ,
, ![]() .
.
4. а) ![]() ,
,  ; б)
; б)  ,
, ![]() .
.
5. а) ![]() ,
,  ; б)
; б)  ,
, ![]() .
.
6. а) ![]() ,
,  ; б)
; б)  ,
, ![]() .
.
7. а) ![]() ,
,  ; б)
; б)  ,
, ![]() .
.
8. а) ![]() ,
,  ; б)
; б)  ,
, ![]() .
.
9. а) ![]() ,
,  ; б)
; б)  ,
, ![]() .
.
10. а)  ,
, ![]() ; б)
; б)  ,
, ![]() .
.
11. а)  ,
, ![]() ; б)
; б)  ,
, ![]() .
.
12. а)  ,
, ![]() ; б)
; б)  ,
, ![]() .
.
13. а)  ,
, ![]() ; б)
; б)  ,
, ![]() .
.
14. а)  ,
, ![]() ; б)
; б)  ,
, ![]() .
.
15. а)  ,
,  ; б)
; б)  ,
, ![]() .
.
16. а)  ,
, ![]() ; б)
; б)  ,
, ![]() .
.
17. а)  ,
, ![]() ; б)
; б)  ,
, ![]() .
.
18. а)  ,
, ![]() ; б)
; б)  ,
, ![]() .
.
19. а)  ,
, ![]() ; б)
; б)  ,
, ![]() .
.
20. а)  ,
, ![]() ; б)
; б)  ,
, ![]() .
.
21. а)  ,
, ![]() ; б)
; б)  ,
, ![]() .
.
22. а)  ,
, ![]() ; б)
; б)  ,
, ![]() .
.
23. а)  ,
, ![]() ; б)
; б)  ,
, ![]() .
.
24. а)  ,
, ![]() ; б)
; б)  ,
, ![]() .
.
25. а)  ,
, ![]() ; б)
; б)  ,
, ![]() .
.
26. а)  ,
, ![]() ; б)
; б)  ,
, ![]() .
.
27. а)  ,
, ![]() ; б)
; б)  ,
, ![]() .
.
28. а)  ,
, ![]() ; б)
; б)  ,
, ![]() .
.
29. а)  ,
, ![]() ; б)
; б)  ,
, ![]() .
.
30. а)  ,
, ![]() ; б)
; б)  ,
, ![]() .
.
Задание 2. Разложить функцию ![]() в ряд Лорана в указанном кольце.
в ряд Лорана в указанном кольце.
1.  ,
, ![]() ;
;
2.  ,
, ![]() ;
;
3.  ,
, ![]() ;
;
4.  ,
, ![]() ;
;
5.  ,
, ![]() ;
;
6.  ,
, ![]() ;
;
7.  ,
, ![]() ;
;
8.  ,
, ![]() ;
;
9.  ,
, ![]() ;
;
10.  ,
, ![]() ;
;
11.  ,
, ![]() ;
;
12.  ,
, ![]() ;
;
13.  ,
, ![]() ;
;
14.  ,
, ![]() ;
;
15.  ,
, ![]() ;
;
16.  ,
, ![]() ;
;
17.  ,
, ![]() ;
;
18.  ,
, ![]() ;
;
19.  ,
, ![]() ;
;
20.  ,
, ![]() ;
;
21.  ,
, ![]() ;
;
22.  ,
, ![]() ;
;
23.  ,
, ![]() ;
;
24.  ,
, ![]() ;
;
25.  ,
, ![]() ;
;
26.  ,
, ![]() ;
;
27.  ,
, ![]() ;
;
28.  ,
, ![]() ;
;
29.  ,
, ![]() ;
;
30.  ,
, ![]() .
.
Задание 3. Найти все возможные разложения функции ![]() в ряд Лорана по степеням
в ряд Лорана по степеням  .
.
1.  ,
, ![]() ;
;
2.  ,
, ![]() ;
;
3.  ,
, ![]() ;
;
4.  ,
, ![]() ;
;
5.  ,
, ![]() ;
;
6.  ,
, ![]() ;
;
7.  ,
, ![]() ;
;
8.  ,
, ![]() ;
;
9.  ,
, ![]() ;
;
10.  ,
, ![]() ;
;
11.  ,
, ![]() ;
;
12.  ,
, ![]() ;
;
13.  ,
, ![]() ;
;
14.  ,
, ![]() ;
;
15.  ,
, ![]() ;
;
16.  ,
, ![]() ;
;
17.  ,
, ![]() ;
;
18.  ,
, ![]() ;
;
19.  ,
, ![]() ;
;
20.  ,
, ![]() ;
;
21.  ,
, ![]() ;
;
22.  ,
, ![]() ;
;
23.  ,
, ![]() ;
;
24.  ,
, ![]() ;
;
25.  ,
, ![]() ;
;
26.  ,
, ![]() ;
;
27.  ,
, ![]() ;
;
28.  ,
, ![]() ;
;
29.  ,
, ![]() ;
;
30.  ,
, ![]() .
.
Задание 4. Найти изолированные особые точки функции ![]() и определить их вид.
и определить их вид.
1.  ;
;
2.  ;
;
3.  ;
;
4. ![]() ;
;
5.  ;
;
6.  ;
;
7.  ;
;
8.  ;
;
9.  ;
;
10.  ;
;
11.  ;
;
12.  ;
;
13.  ;
;
14.  ;
;
15.  ;
;
16.  ;
;
17.  ;
;
18.  ;
;
19. ![]() ;
;
20.  ;
;
21.  ;
;
22.  ;
;
23.  ;
;
24.  ;
;
25.  ;
;
26.  ;
;
27.  ;
;
28.  ;
;
29.  ;
;
30.  .
.
Задание 5. Вычислить вычеты функции ![]() относительно каждой из ее особых точек.
относительно каждой из ее особых точек.
1.  ;
;
2.  ;
;
3.  ;
;
4.  ;
;
5.  ;
;
6. ![]() ;
;
7. ![]() ;
;
8.  ;
;
9.  ;
;
10.  ;
;
11.  ;
;
12.  ;
;
13.  ;
;
14.  ;
;
15.  ;
;
16.  ;
;
17.  ;
;
18.  ;
;
19.  ;
;
20.  ;
;
21.  ;
;
22.  ;
;
23.  ;
;
24.  ;
;
25.  ;
;
26.  ;
;
27.  ;
;
28.  ;
;
29.  ;
;
30.  .
.
Задание 6. Вычислить интеграл.
1.  ;
;
2.  ;
;
3.  ;
;
4.  ;
;
5.  ;
;
6.  ;
;
7.  ;
;
8.  ;
;
9.  ;
;
10.  ;
;
11.  ;
;
12.  ;
;
13.  ;
;
14.  ;
;
15.  ;
;
16.  ;
;
17.  ;
;
18.  ;
;
19.  ;
;
20.  ;
;
21.  ;
;
22.  ;
;
23.  ;
;
24.  ;
;
25.  ;
;
26.  ;
;
27.  ;
;
28.  ;
;
29.  ;
;
30.  .
.
Литература
1. Волковыский Л. И., Лунц Г. Л., Араманович И. Г. Сборник задач по теории функций комплексного переменного. – М.: ФИЗМАТЛИТ, 2004.
2. Леонтьева Т. А. Лекции по теории функций комплексного переменного. – М.: Научный мир. 2004.
3. Лунц Г. Л., Эльсгольц Л. Э. Функции комплексного переменного (с элементами операционного исчисления). – М.: Лань, 2002.
4. Морозова В. Д. Теория функций комплексного переменного. – М.: Изд-во МГТУ им. Н. Э. Баумана, 2009.
5. Пантелеев А. В., Якимова А. С. Теория функций комплексного переменного и операционное исчисление в примерах и задачах. – М.: Вузовская книга, 2012.
6. Письменный Д. Т. Конспект лекций по высшей математике, 1, 2 часть. – М.: 2004.
7. Письменный Д. Т. Сборник задач по высшей математике, 1, 2 часть. – М.: 2004.
8. Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. – М.: ФИЗМАТЛИТ, 2005.
9. Шабунин М. И. Сборник задач по теории функций комплексного переменного. – М.: БИНОМ. Лаборатория знаний. 2006.
Антоненкова О. Е., Часова Н. А.
МАТЕМАТИКА
Теория функций
комплексной переменной
Методические указания и задания к расчетно-графической работе
для студентов всех направлений подготовки бакалавров
очной формы обучения
Формат Объем Тираж Заказ
Брянск, Станке Димитрова 3, Редакционно-издательский отдел
Отпечатано: Печатный цех БГИТА
Наташа — контент-маркетолог и блогер, но все это не мешает ей оставаться адекватным человеком. Верит во все цвета радуги и не верит в теорию всемирного заговора. Увлекается «нефрохиромантией» и тайно мечтает воссоздать дома Александрийскую библиотеку.
![]()
Пример 2.5. Найти сумму ряда ![]() .
.
Выясним интервал сходимости ряда. По признаку Даламбера для ряда из модулей ![]() получаем:
получаем: ![]() .На концах интервала сходимости ряд расходится, так как при
.На концах интервала сходимости ряд расходится, так как при ![]() и при
и при![]() получаем ряды
получаем ряды ![]() и
и ![]() , для которых не выполняется необходимый признак. Пусть сумма данного ряда
, для которых не выполняется необходимый признак. Пусть сумма данного ряда ![]() . Далее, в области сходимости данного ряда проинтегрируем ряд почленно:
. Далее, в области сходимости данного ряда проинтегрируем ряд почленно:![]()
![]() .
.
Получили сумму геометрической прогрессии, где b=x, q=x.
![]() , так как
, так как ![]() .
.
Итак, проинтегрированный ряд имеет сумму ![]() .
.
Следовательно, ![]() . Ответ:
. Ответ: ![]()
Пример 2.6. Найти сумму ряда ![]() .
.
Выясним интервал сходимости ряда с помощью признака Даламбера: ![]() .
.
В точке ![]() получаем гармонический ряд
получаем гармонический ряд ![]() . Он расходится. В точке
. Он расходится. В точке ![]() получаем ряд
получаем ряд ![]() ,сходящийся условно по признаку Лейбница. Следовательно, область сходимости степенного ряда
,сходящийся условно по признаку Лейбница. Следовательно, область сходимости степенного ряда ![]() .
.
Пусть сумма исходного ряда ![]() . В области сходимости почленно продифференцируем этот ряд:
. В области сходимости почленно продифференцируем этот ряд:
![]()
![]() .
.
Получили сумму геометрической прогрессии, где b=1, q=x.
![]() .
.
Ответ: ![]() .
.
Задачи для самостоятельной работы.
Найти область сходимости ряда:
1.  ; Ответ:
; Ответ:![]() 2.
2. ![]() ; Ответ:
; Ответ:![]()
3. ![]() ; Ответ:
; Ответ:![]()
4. ![]() ; Ответ:
; Ответ:![]() 5.
5. ![]() Ответ:
Ответ:![]()
![]() Часть 3. Разложение функций в степенные ряды.
Часть 3. Разложение функций в степенные ряды.
Возможность почленного дифференцирования и интегрирования степенного ряда внутри его интервала сходимости, а также простота степенной функции, делают степенные ряды незаменимыми в теоретических и практических исследованиях. Встаёт вопрос о разложении функции в степенной ряд и нахождении области его сходимости.
Теорема. Функция ![]() , бесконечно дифференцируемая в некотором интервале
, бесконечно дифференцируемая в некотором интервале![]() , может быть разложена в этом интервале в сходящийся к ней степенной ряд Тейлора
, может быть разложена в этом интервале в сходящийся к ней степенной ряд Тейлора ![]() , (3.1)
, (3.1)
если в этом интервале выполняется условие ![]() , где
, где
![]() -остаточный член формулы Тейлора,
-остаточный член формулы Тейлора, ![]() . При
. При ![]() получаем ряд Маклорена:
получаем ряд Маклорена: ![]() .(3.2)
.(3.2)
Замечание. Если в некотором интервале, содержащем точку ![]() , при любом n выполняется неравенство
, при любом n выполняется неравенство ![]() , М>0,то
, М>0,то ![]() , и
, и ![]() разложима в ряд Тейлора.
разложима в ряд Тейлора.
( Если последнее условие не выполняется, то формально построенный ряд Тейлора может быть сходящимся, но к другой функции.)
Пример 3.1. Можно ли разложить: а) ![]() в ряд Маклорена;
в ряд Маклорена;
б) ![]() в ряд Тейлора по степеням
в ряд Тейлора по степеням ![]() ;
;
в) ![]() в ряд Маклорена?
в ряд Маклорена?
Решение. а) ![]() нельзя разложить в ряд Маклорена, так как в точке
нельзя разложить в ряд Маклорена, так как в точке ![]() ни функция, ни её производные не определены; б)
ни функция, ни её производные не определены; б)![]() разложить по степеням
разложить по степеням ![]() нельзя, так как в точке
нельзя, так как в точке ![]()
функция определена, но ![]() является граничной точкой области определения, и производные в ней не определены;
является граничной точкой области определения, и производные в ней не определены;
в) ![]() можно разложить в ряд Маклорена, так как в точке
можно разложить в ряд Маклорена, так как в точке ![]() определена как сама функция, так и её производная любого порядка.
определена как сама функция, так и её производная любого порядка.
Притом очевидно, что ![]() , то есть полученный ряд будет сходиться именно к
, то есть полученный ряд будет сходиться именно к ![]() .
.
Приёмы разложения функций в степенные ряды.
-
Непосредственное разложение функции в ряд Тейлора.
В этом случае, находя все ![]() , формально составляют ряд
, формально составляют ряд
![]() и находят область сходимости этого ряда.
и находят область сходимости этого ряда.
Пример 3.2. Разложить ![]() в ряд Тейлора по степеням
в ряд Тейлора по степеням ![]() .
.
а) Составим ряд Тейлора в виде ![]() .
.
Вычислим производные до n порядка и найдём их значения при ![]() .
.
![]()
![]()
![]()
![]()
![]()
………………. ………………………
![]()
Подставим вычисленные производные в ряд Тейлора:
![]()
![]() .
.
б) Область сходимости полученного ряда:![]() .
.
На концах интервала: ![]() – расходится, как гармонический ряд.
– расходится, как гармонический ряд. ![]() – сходится условно.
– сходится условно.
Итак, область сходимости полученного ряда ![]() .
.
в) Чтобы ответить на вопрос, сходится ли полученный ряд именно к функции ![]() , проверим выполнимость условия
, проверим выполнимость условия ![]() .
.
 ,
,![]() ,
, ![]()
![]() .Следовательно, ряд
.Следовательно, ряд ![]() в области
в области ![]() сходится к функции
сходится к функции ![]() , т. е. является разложением данной функции по степеням
, т. е. является разложением данной функции по степеням ![]() .
.
Отметим, что непосредственное разложение функций в ряд Тейлора не всегда позволяет получить разложение вида ![]() ,
,
так как найти общую формулу ![]() бывает затруднительно. В таких случаях либо ограничиваются конечным числом членов степенного ряда, либо пользуются разложениями в степенной ряд элементарных функций.
бывает затруднительно. В таких случаях либо ограничиваются конечным числом членов степенного ряда, либо пользуются разложениями в степенной ряд элементарных функций.
-
Разложение в степенные ряды с использованием представления основных элементарных функций в виде ряда Маклорена.
Имеют место разложения в ряды Маклорена следующих функций:
![]()
![]()
![]()
![]()
![]()
![]()

 (3.9)
(3.9)
![]() Используя эти разложения, можно находить разложения других функций. При этом отпадает необходимость исследования поведения остаточного члена
Используя эти разложения, можно находить разложения других функций. При этом отпадает необходимость исследования поведения остаточного члена ![]() , так как интервалы сходимости рядов, полученных для основных элементарных функций, известны.
, так как интервалы сходимости рядов, полученных для основных элементарных функций, известны.
Прежде чем приступить к дальнейшему рассмотрению, напомним некоторые свойства элементарных функций и формулы, их связывающие:
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Пример 3.3. Разложить функцию![]() в ряд Тейлора по степеням
в ряд Тейлора по степеням ![]() . (Это второй способ решения примера 3.2.) Сведём задачу о
. (Это второй способ решения примера 3.2.) Сведём задачу о
разложении в ряд Тейлора к разложению в ряд Маклорена, используя замену переменной. ![]()
![]()
![]() .
.
Найдём область сходимости ряда к данной функции. Из разложения (3.8) имеем: ![]()
![]()
![]()
![]()
![]() .
.
Сравнивая результаты примеров 3.2 и 3.3, видим, что данный способ позволяет получить результат более рационально.
Пример 3.4. Разложить функцию ![]() по степеням
по степеням ![]() .
.
Как и в предыдущем примере, сведём задачу о разложении в ряд Тейлора к разложению в ряд Маклорена с помощью линейной замены:

![]()
 .
.
Область сходимости полученного ряда: ![]() .
.
Пример 3.5. Разложить функцию ![]() по степеням
по степеням ![]() .
.

(Далее, с помощью формул (3.4) и (3.5), считая ![]() , получаем):
, получаем):
![]()
Заметим, что в полученном разложении присутствуют все степени 2t, начиная с нулевой. Попробуем объединить оба ряда в один вида![]() :
:
![]()
![]()
![]()
 .
.
Окончательно, 
P.S. Чередование знака по два в общем элементе можно записать следующим образом:![]() , или
, или ![]() .
.
Пример 3.6. Разложить функцию ![]() по степеням
по степеням ![]() .
.
![]()
![]()
Далее, используя формулу (3.3), принимая в ней ![]() , получаем:
, получаем:
![]()
![]() . Получившиеся три ряда имеют одинаковые степени, начиная с
. Получившиеся три ряда имеют одинаковые степени, начиная с ![]() . Преобразуем результат в одну сумму вида
. Преобразуем результат в одну сумму вида ![]() . Сначала «сместим» индексы так, чтобы в каждой из сумм степени t были одинаковыми. Для этого в первой сумме заменим n+2 на n, во второй заменим n+1 на n. Суммы станут выглядеть так:
. Сначала «сместим» индексы так, чтобы в каждой из сумм степени t были одинаковыми. Для этого в первой сумме заменим n+2 на n, во второй заменим n+1 на n. Суммы станут выглядеть так:
 .
.
У всех трёх сумм одинаковы степени t, начиная с ![]() .Вычислим слагаемые с меньшими степенями t, т.е.
.Вычислим слагаемые с меньшими степенями t, т.е. ![]() и
и ![]() .
.


![]()
Ответ:![]()
![]() .
.
Пример 3.7. Разложить функцию ![]() по степеням
по степеням ![]() .
.
![]() .
.
Представим полученную дробь в виде суммы простых дробей методом неопределённых коэффициентов: ![]()
![]()
![]() . Итак, исходную функцию можно представить в виде:
. Итак, исходную функцию можно представить в виде:![]() .
.
Далее, с помощью (3.10),получим:![]() .
.
Так как ![]() , область сходимости этого ряда
, область сходимости этого ряда ![]()
![]()
![]() .
.
Аналогично, .
.
Так как ![]() , область сходимости этого ряда
, область сходимости этого ряда ![]()
![]()
![]() .
.
Окончательно,![]()
![]()
![]()
Область сходимости полученного ряда:![]() .
.
Пример 3.8. Разложить функцию ![]() по степеням x.
по степеням x.
![]()

![]()
![]() .
.
Область сходимости данного ряда:![]() .
.
Пример 3.9. Разложить функцию ![]() в ряд Маклорена.
в ряд Маклорена.
![]() . Напомним, что степенной ряд можно почленно интегрировать в области сходимости. Разложим с помощью формулы (3.9) для m=-1/2 в ряд Маклорена функцию
. Напомним, что степенной ряд можно почленно интегрировать в области сходимости. Разложим с помощью формулы (3.9) для m=-1/2 в ряд Маклорена функцию ![]() ,а затем, проинтегрировав полученный ряд, получим разложение исходной функции.
,а затем, проинтегрировав полученный ряд, получим разложение исходной функции.
![]()
![]()
![]()

![]() . Область сходимости полученного ряда
. Область сходимости полученного ряда ![]() .
.
Контрольное задание.
Разложить данные функции в ряды по степеням ![]() и найти
и найти
области сходимости полученных рядов:
1. ![]() ; Ответ: a)
; Ответ: a)![]()
![]() b)
b)![]() ,
,![]() .
.
2. ![]() Ответ:
Ответ: ![]() .
.![]()
3. ![]() Ответ:
Ответ: ![]() ,
,![]() .
.
4. ![]() Ответ:
Ответ: ![]() ,
,![]()
5. ![]() Ответ:
Ответ: ![]() ,
,![]() .
.
6. ![]() Ответ:
Ответ:![]()
![]() .
.
7.![]() Ответ: a)
Ответ: a)![]()
![]() , b)
, b) ![]()
![]() .
.
8. Используя метод интегрирования степенного ряда, разложить в ряд Маклорена и указать область сходимости:![]()
Ответ: ![]()
![]()
Часть 4. Приближённое вычисление определённых интегралов при помощи степенных рядов.
Многие определённые интегралы не могут быть вычислены с помощью формулы Ньютона-Лейбница, так как первообразная не всегда выражается в элементарных функциях. Если подынтегральная функция разлагается в степенной ряд, а пределы интегрирования принадлежат области сходимости этого ряда, то определённый интеграл можно вычислить приближённо.
Приближённое вычисление суммы S сходящегося числового ряда связано с оценкой погрешности, допускаемой при замене S частичной суммой ![]() .
. ![]() с точностью до
с точностью до ![]() .
.
Оценка остаточного члена ![]() числового ряда.
числового ряда.
а) Для знакочередующихся рядов, удовлетворяющих условиям признака Лейбница, ![]() .
.
б) Построение мажорирующей геометрической прогрессии![]() для оценки погрешности знакопостоянного ряда.(
для оценки погрешности знакопостоянного ряда.(![]() ).
).
![]() .
.
Пример 4.1. Вычислить интеграл ![]() с точностью до δ=0,001.Разложим подынтегральную функцию в ряд Маклорена:
с точностью до δ=0,001.Разложим подынтегральную функцию в ряд Маклорена: ![]()
![]()
![]() .
.
Получили знакочередующийся ряд. Его область сходимости ![]() Область интегрирования принадлежит области сходимости, следовательно, полученный ряд можно интегрировать:
Область интегрирования принадлежит области сходимости, следовательно, полученный ряд можно интегрировать:
![]()
![]()
![]()
![]() Ряд удовлетворяет условиям теоремы Лейбница, следовательно,
Ряд удовлетворяет условиям теоремы Лейбница, следовательно, ![]() , так как
, так как ![]() и
и
![]() . Ответ:
. Ответ: ![]() .
.
Пример 4.2. Вычислить ![]() с точностью δ=0,001.
с точностью δ=0,001.
