Как найти все решения диофантова уравнения - Сайт, где вы сможете решить свои вопросы

Загрузить PDF

Чтобы решить линейное диофантово уравнение, нужно найти значения переменных «x» и «y», которые являются целыми числами. Целочисленное решение сложнее обычного и требует определенного набора действий. Сначала необходимо вычислить наибольший общий делитель (НОД) коэффициентов, а затем найти решение. Если вы нашли одно целочисленное решение линейного уравнения, можно применить простой шаблон, чтобы найти бесконечное множество других решений.

1
2

Упростите уравнение (если можно). Когда вы запишете уравнение в стандартной форме, посмотрите на коэффициенты и . Если у этих коэффициентов есть НОД, разделите на него все три коэффициента. Решение такого упрощенного уравнения также будет решением исходного уравнения.
3

Проверьте, можно ли решить уравнение. В некоторых случаях можно сразу заявить, что уравнение не имеет решений. Если коэффициент «С» не делится на НОД коэффициентов «А» и «В», у уравнения нет решений.

Реклама

1

Уясните алгоритм Евклида. Это ряд повторных делений, в котором предыдущий остаток используется как следующий делитель. Последний делитель, который делит числа нацело, является наибольшим общим делителем (НОД) двух чисел.^[1]
2

Примените алгоритм Евклида к коэффициентам «A» и «B». Когда вы запишете линейное уравнение в стандартной форме, определите коэффициенты «A» и «B», а затем примените к ним алгоритм Евклида, чтобы найти НОД. Например, дано линейное уравнение .^[2]
3

Найдите наибольший общий делитель (НОД). Поскольку последним делителем было число 1, НОД 87 и 64 равен 1. Таким образом, 87 и 64 являются простыми числами по отношению друг к другу.^[3]
4

Реклама

1

Пронумеруйте шаги вычисления НОД. Чтобы найти решение линейного уравнения, нужно использовать алгоритм Евклида в качестве основы процесса подстановки и упрощения.^[5]
2
Обратите внимание на последний шаг, где есть остаток. Перепишите уравнение этого шага так, чтобы изолировать остаток.^[6]
- В нашем примере последний шаг с остатком — это шаг 6. Остаток равен 1. Перепишите уравнение шага 6 следующим образом:
3
Изолируйте остаток предыдущего шага. Этот процесс представляет собой пошаговое «перемещение вверх». Каждый раз вы будете изолировать остаток в уравнении предыдущего шага.^[7]
- Изолируйте остаток уравнения шага 5:
4
5

Повторите процесс подстановки и упрощения. Повторите описанный процесс, перемещаясь по алгоритму Евклида в обратном порядке. Каждый раз вы будете переписывать уравнение предыдущего шага и подставлять его в последнее полученное уравнение.^[9]
6

Продолжите процесс подстановки и упрощения. Этот процесс будет повторяться до тех пор, пока вы не достигнете первоначального шага алгоритма Евклида. Цель процесса — записать уравнение с коэффициентами 87 и 64 исходного уравнения, которое нужно решить. В нашем примере:^[10]
7

Перепишите полученное уравнение в соответствии с исходными коэффициентами. Когда вы вернетесь к первому шагу алгоритма Евклида, вы увидите, что полученное уравнение содержит два коэффициента исходного уравнения. Перепишите уравнение так, чтобы порядок его членов соответствовал коэффициентам исходного уравнения.^[11]
8
Примените соответствующий множитель, чтобы найти решение. Обратите внимание, что в нашем примере НОД=1, поэтому окончательное уравнение равно 1. Но исходное уравнение (87x-64y) равно 3. Поэтому все члены окончательного уравнения нужно умножить на 3, чтобы получить решение:^[12]
9
Запишите целочисленное решение уравнения. Числа, которые умножаются на коэффициенты исходного уравнения, являются решениями этого уравнения.
- В нашем примере запишите решение в виде пары координат: .
Реклама

1
Уясните, что существует бесконечное множество решений. Если линейное уравнение имеет одно целочисленное решение, то оно должно иметь бесконечно множество целочисленных решений. Вот краткое доказательство (в алгебраической форме):^[13]
- (если прибавить «B» к «x» и вычесть «A» из «y», значение исходного уравнения не изменится)
2
Запишите исходные значения «x» и «y». Шаблон для вычисления последующих (бесконечных) решений начинается с единственного решения, которое вы уже нашли.^[14]
- В нашем примере решение представляет собой пару координат .
3
Прибавьте коэффициент «B» к значению «x». Сделайте это, чтобы найти новое значение «x». ^[15]
- В нашем примере x=-75, а В=-64:
- Таким образом, новое значение «х»: x=-139.
4

Вычтите коэффициент «A» из значения «y». Чтобы значение исходного уравнения не изменилось, при прибавлении одного числа к «x» нужно вычесть другое число из «y».
5

Проверьте решение. Чтобы убедиться, что новая пара координат является решением исходного уравнения, подставьте значения в уравнение.^[16]
6

Запишите выражения для нахождения множества решений. Значения «x» будут равны исходному решению плюс любое кратное коэффициента «В». Это можно записать в виде следующего выражения:^[17]

Реклама

Об этой статье

Эту страницу просматривали 77 474 раза.

Была ли эта статья полезной?

Источник

Првило 1. Если с не делится на d, то уравнение ах +
ву = с не имеет решений в целых числах. Н.О.Д.(а,в) = d.

Правило 2. Чтобы найти решение уравнения ах + ву =
с при взаимно-простых а и в, нужно сначала найти
решение (Х_о; у_о) уравнения ах + ву = 1;
числа СХ_о, Су_о составляют решение
уравнения ах + ву = с.

Решить в целых числах (х,у) уравнение

5х – 8у = 19 … (1)

Решение.

Первый способ. Нахождение частного
решения методом подбора и запись общего решения.

Знаем, что если Н.О.Д.(а;в) =1, т.е. а и в
взаимно-простые числа, то уравнение (1)

имеет решение в целых числах х и у. Н.О.Д.(5;8) =1.
Методом подбора находим частное решение: Х_о=
7; у_о=2.

Итак, пара чисел (7;2) – частное решение уравнения
(1).

Значит, выполняется равенство: 5 x 7 – 8 x 2 = 19 … (2)

Вопрос: Как имея одно решение записать все
остальные решения?

Вычтем из уравнения (1) равенство (2) и получим: 5(х
-7) – 8(у – 2) =0.

Отсюда х – 7 = . Из полученного равенства видно, что
число (х – 7) будет целым тогда и только тогда,
когда (у – 2) делится на 5, т.е. у – 2 = 5n, где n
какое-нибудь целое число. Итак, у = 2 + 5n, х = 7 + 8n, где
n Z.

Тем самым все целые решения исходного
уравнения можно записать в таком виде:

n Z.

Второй способ. Решение уравнения
относительно одного неизвестного.

Решаем это уравнение относительно того из
неизвестных, при котором наименьший (по модулю)
коэффициент. 5х – 8у = 19 х = .

Остатки при делении на 5: 0,1,2,3,4. Подставим вместо
у эти числа.

Если у = 0, то х = =.

Если у =1, то х = =.

Если у = 2, то х = = = 7 Z.

Если у =3, то х = =.

Если у = 4 то х = =.

Итак, частным решением является пара (7;2).

Тогда общее решение: n Z.

Третий способ. Универсальный способ поиска
частного решения.

Для решения применим алгоритм Евклида. Мы
знаем, что для любых двух натуральных чисел а, в,
таких, что Н.О.Д.(а,в) = 1 существуют целые числа х,у
такие, что ах + ву = 1.

План решения:

1. Сначала решим уравнение 5m – 8n = 1 используя
алгоритм Евклида.

2. Затем найдем частное решение уравнения (1)по
правилу 2.

3. Запишем общее решение данного уравнения (1).

1. Найдем представление: 1 = 5m – 8n. Для этого
используем алгоритм Евклида.

8 = 5 1 +
3.

5 = 3

3 = 2 .

Из этого равенства выразим 1. 1 = 3 – 2 = 3 – (5 – 3 ) =

= 3 – 5 =
3 = (8 – 5 – 5 82 -5

= 5(-2).
Итак, m = -3, n = -2.

2. Частное решение уравнения (1): Х_о= 19m; у_о=19n.

Отсюда получим: Х_о=19; у_о=19 .

Пара (-57; -38)- частное решение (1).

3. Общее решение уравнения (1): n Z.

Четвертый способ. Геометрический.

План решения.

1. Решим уравнение 5х – 8у = 1 геометрически.

2. Запишем частное решение уравнения (1).

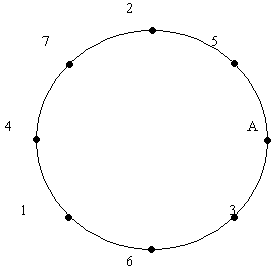
3. Запишем общее решение данного уравнения (1).

Отложим на окружности последовательно друг за
другом равные дуги, составляющие

-ю
часть полной окружности. За 8 шагов получим все
вершины правильного вписанного в окружность
8-угольника. При этом сделаем 5 полных оборотов.

На 5 – ом шаге получили вершину, соседнюю с
начальной, при этом сделали 3 полных оборота и еще
прошли – ю
часть окружности, так что х = у + .

Итак, Х_о= 5, у_о=3 является частным
решением уравнения 5х – 8у = 1.

2. Частное решение уравнения (1): Х_о= 19 у_о=19

3. Общее решение уравнения (1): n Z.

Источник

Диофа́нтово уравнение (также уравнение в целых числах) — это уравнение вида

$P(x_{1},dots ,x_{m})=0,$

где — целочисленная функция, например, полином с целыми коэффициентами, а переменные $x_{i}$ принимают целые значения. «Диофантовым» уравнение названо в честь древнегреческого математика Диофанта.

Также при рассмотрении вопроса разрешимости переменные часто разделяют на параметры (значения которых предполагаются фиксированными) и неизвестные. Так, уравнение

${displaystyle P(a_{1},dots ,a_{n},x_{1},dots ,x_{m})=0,}$

с параметрами $a_{1},dots ,a_{n}$ и неизвестными ${displaystyle x_{1},dots ,x_{m}}$ считается разрешимым при данных значениях набора параметров ${displaystyle (a_{1},dots ,a_{n})}$ , если существуют набор чисел ${displaystyle (x_{1},dots ,x_{m})}$ , при которых это равенство становится верным.

Таким образом, диофантовыми уравнениями называют уравнения с целыми коэффициентами, для которых требуется найти целочисленные (или натуральные) решения. При этом количество неизвестных в уравнении должно быть не менее двух^[1]. Своё название уравнения получили в честь выдающегося античного математика Диофанта Александрийского, который, как считается, первым систематически изучал неопределённые уравнения и описывал методы их решения^[2]. Все сохранившиеся записи собраны в книгу «Арифметика»^[3]. После Диофанта схожим изучением неопределённых уравнений занимались индусские математики, начиная примерно с пятого века^[4]. В Европе решением неопределённых уравнений занимались практически все крупные алгебраисты своего времени: Леонардо Фибоначчи (ок.1170 — 1250 гг.), Франсуа Виет (1540—1603 гг.), Симон Стевин (ок. 1549—1620 гг.)^[5].

Проблема решения уравнений в целых числах рассмотрена до конца для уравнений с одним неизвестным, а также для уравнений первой и второй степени с двумя неизвестными.

Примеры[править | править код]

Линейные диофантовы уравнения[править | править код]

Общий вид линейного диофантова уравнения:

$a_{1}x_{1}+a_{2}x_{2}+ldots +a_{k}x_{k}=d.$

В частности, линейное диофантово уравнение с двумя неизвестными имеет вид:

Если (то есть наибольший общий делитель (a,;b) не делит ), то уравнение (1) не разрешимо в целых числах. В самом деле, если , то число, стоящее слева в (1), делится на (a,;b) , а стоящее справа — нет. Справедливо и обратное: если в уравнении ax+by=c выполняется , то оно разрешимо в целых числах.

Пусть $(x_{0},;y_{0})$ — частное решение уравнения ax+by=c . Тогда все его решения находятся по формулам:

${displaystyle {begin{cases}x=x_{0}-n{frac {b}{(a,;b)}}\y=y_{0}+n{frac {a}{(a,;b)}}end{cases}}quad nin mathbb {Z} .}$

Частное решение $(x_{0},;y_{0})$ можно построить следующим образом. Если и делится на (a,b) , то после деления всех коэффициентов на (a,b) уравнение приобретает вид $a_{1}x+b_{1}y=c_{1}$ , где $(a_{1},b_{1})=1$ . Для последнего уравнения частное решение получается из соотношения Безу для ${displaystyle a_{1},b_{1}}$ :

$ua_{1}+vb_{1}=1,$

исходя из которого, можно положить $(x_{0},;y_{0})=(c_{1}cdot u,;c_{1}cdot v).$

Известна явная формула для серии решений линейного уравнения^[6]:

${displaystyle {begin{cases}x_{t}=ca^{varphi (b)-1}+bt,\y_{t}=c{frac {1-a^{varphi (b)}}{b}}-at,end{cases}}}$

где — функция Эйлера, а t — произвольный целый параметр.

Алгебраические диофантовы уравнения[править | править код]

При рассмотрении вопроса разрешимости алгебраических диофантовых уравнений можно воспользоваться тем, что любую систему таких уравнений можно преобразовать в одно диофантово уравнение степени не выше 4 в целых неотрицательных числах, разрешимое в том и только том случае, когда разрешима исходная система (при этом множество переменных и множество решений этого нового уравнения может оказаться совершенно другим).

Диофантовы множества[править | править код]

Диофантовым множеством называется множество состоящее из упорядоченных наборов из n целых чисел, для которого существует алгебраическое диофантово уравнение:

${displaystyle P(a_{1},dots ,a_{n},x_{1},dots ,x_{m})=0,}$

которое разрешимо тогда и только тогда, когда набор чисел ${displaystyle (a_{1},dots ,a_{n})}$ принадлежит этому множеству. Рассматриваемое диофантово уравнение называется диофантовым представлением этого множества. Важный результат, полученный Ю. В. Матиясевичем, состоит в том, что каждое перечислимое множество имеет диофантово представление^[7].

Неразрешимость в общем виде[править | править код]

Десятая проблема Гильберта, сформулированная в 1900 году, состоит в нахождении алгоритма решения произвольных алгебраических диофантовых уравнений. В 1970 году Ю. В. Матиясевич доказал алгоритмическую неразрешимость этой проблемы.^[8]

Экспоненциальные диофантовы уравнения[править | править код]

Если одна или более переменных в диофантовом уравнении входит в выражение показателя возведения в степень, такое диофантово уравнение называется экспоненциальным.

Примеры:

Уравнение Рамануджана — Нагеля
Уравнения гипотезы Ферма — Каталана
Гипотеза Била

Общая теория решения таких уравнений отсутствует; частные случаи, такие как Гипотеза Каталана, были исследованы. Однако большинство из этих уравнений всё же удаётся решить специальными методами, такими как теорема Стёрмера^[en] или даже метод проб и ошибок.

См. также[править | править код]

Малая теорема Ферма
Решение сравнений

Примечания[править | править код]

↑ . Абакумова С. И., Гусева А. Н. Диофантовы уравнения Фундаментальные и прикладные исследования в современном
мире. — 2014. — Т. 1, № 6. — С. 133—137.
↑ Башмакова И. Г. Диофант и диофантовы уравнения — Москва : Наука, 1972. — 68 с
↑ Жмурова, И. Ю. Диофантовы уравнения: от древности до нашихдней. Молодой учёный. — 2014. — № 9. -С. 1-5
↑ Кожаев, Ю. П. Греческий математик Диофант и диофантовы уравнения. Материалы IV Всероссийской научно — практической конференции «Культура и общество: история и современность»- Ставрополь : АГРУС. — 2015. — С. 150—154.
↑ Мельников Р. А. Краткий обзор этапов развития диофантовых уравнений. Материалы международной научно-практической конференции «Математика: фундаментальные и прикладные исследования и вопросы образования» — Рязань : издательство РГУ им. С. А. Есенина, 2016. — С. 429—435.
↑ Воробьёв Н. Н. Признаки делимости. — М.: Наука, 1988. — С. 60. — 96 с. — (Популярные лекции по математике).
↑ Диофантово множество — статья из Математической энциклопедии. Ю. В. Матиясевич
↑ Матиясевич Ю. В. Десятая проблема Гильберта. — М.: Наука, 1993.

Ссылки[править | править код]

Башмакова И. Г. Диофант и диофантовы уравнения. — М.: Наука, 1972. German translation: Diophant und diophantische Gleichungen. Birkhauser, Basel/ Stuttgart, 1974. English translation: Diophantus and Diophantine Equations. Translated by Abe Shenitzer with the editorial assistance of Hardy Grant and updated by Joseph Silverman. The Dolciani Mathematical Expositions, 20. Mathematical Association of America, Washington, DC. 1997.
Башмакова И. Г., Славутин Е. И. История диофантова анализа от Диофанта до Ферма. — М.: Наука, 1984.
Bashmakova, Izabella G. “Diophante et Fermat, ” Revue d’Histoire des Sciences 19 (1966), pp. 289—306
Bashmakova, Izabella G. «Arithmetic of Algebraic Curves from Diophantus to Poincaré,» Historia Mathematica 8 (1981), 393—416.
Гельфонд А. О. Решение уравнений в целых числах. — М.: Наука, 1978. — (Популярные лекции по математике).
Михайлов И. О диофантовом анализе // Квант. — 1980. — № 6. — С. 16—17,35.
Rashed, Roshdi, Houzel, Christian. Les Arithmétiques de Diophante : Lecture historique et mathématique, Berlin, New York : Walter de Gruyter, 2013.
Rashed, Roshdi, Histoire de l’analyse diophantienne classique : D’Abū Kāmil à Fermat, Berlin, New York : Walter de Gruyter.
Серпинский В. Н. О решении уравнений в целых числах. — М.: Физматлит, 1961. — 88 с.
Степанов С. А. Диофантовы уравнения // Тр. МИАН СССР. — 1984. — Т. 168. — С. 31–45.
Weisstein, Eric W. Diophantine Equation (англ.) на сайте Wolfram MathWorld.

Источник

Конспект урока

Алгебра

7 класс

Урок № 50

Линейные диофантовы уравнения

Перечень рассматриваемых вопросов:

Диофантово уравнение.
Разрешимость диофантова уравнения.
Решение задач с помощью диофантова уравнения.

Тезаурус:

Диофантовым уравнением называется уравнение вида ах + bу = с (а ≠ 0, b ≠ 0), где а, b, с, х и у – целые числа.

Если c делится на НОД(а; b), то уравнение ах + bу = с имеет решение в целых числах. Если c не делится на НОД (а; b), то уравнение ах + bу = с не имеет решений в целых числах.

Основная литература:

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

Дополнительная литература:

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Определение диофантова уравнения.

Пусть дано уравнение ах + bу = с (а ≠ 0, b ≠ 0), где а, b, с – целые числа. Если поставлена задача найти только такие его решения (х₀; у₀), где х_0, у₀– целые числа, то это уравнение называют линейным диофантовым уравнением.

Историческая справка.

Диофантовы уравнения связаны с именем древнегреческого математика Диофанта Александрийского. О подробностях жизни Диофанта Александрийского практически ничего не известно. С одной стороны, Диофант цитирует Гипсикла (II век до нашей эры); с другой стороны, о Диофанте пишет Теон Александрийский (около 350 года нашей эры). Откуда можно сделать вывод, что жил он приблизительно в III веке нашей эры.

Решение диофантовых уравнений.

Решим линейное диофантово уравнение

2х + 3у = 6.

Выразим у через х:

Из этого равенства видно, что у будет целым только тогда, когда целое число х делится на 3, т.е. х = 3х_1,где х_{1 –}некоторое целое число. Тогда у = 2 -2х₁.

Таким образом, решениями уравнения являются все пары чисел (3х_1;2 -2х₁).

Приведём некоторые частные решения этого уравнения.

Если х₁ = 0, то х = 3х_{1 =}0, а у = 2 – 2 х₁ = 2; решением уравнения является пара (0;2).

Если х_{1 =}1, то х = 3х_{1 =}3, а у = 2 – 2 х₁ = 0;

решением уравнения является пара (3; 0)

Аналогично можно найти и другие частные решения, их бесконечно много.

Запишем ответ: пары чисел (3х_1;2 -2х₁).

Решение задач при помощи линейных диофантовых уравнений.

Линейные диофантовы уравнения возникают при решении некоторых задач.

Рассмотрим задачу.

У покупателя и продавца имеются монеты только по 2р. и 5р. Сможет ли покупатель заплатить за покупку стоимостью 1р.?

Если покупатель даст х монет по 2р. и у монет по 5 р., то он заплатит (2х + 5у) р. А по условию задачи это 1р. Составим уравнение:

2х + 5у = 1.

Выразим х через у из уравнения:

Из равенства видно, что х будет целым только тогда, когда у будет нечетным числом: у = 2m + 1, где m – целое число.

Тогда х = -5m – 2.

Таким образом, решением уравнения являются все пары чисел (-5m – 2; 2m + 1), где m – любое целое число.

Таким образом, способов оплаты товара стоимостью 1р. Бесконечно много. Если х окажется отрицательным, то это означает, что покупатель должен получить сдачу: х монет по 2р.

Например, пара (-2; 1) является решением уравнения. Это означает, что покупатель далодну монету по 5 р. и получил сдачу 2 монеты по 2р.

Ответ: сможет.

Разрешимость диофантова уравнения.

Не каждое диофантово уравнение имеет решение в целых числах.

Рассмотрим на примере уравнения

3х + 6у = 2 алгоритм, с помощью которого можно определить, имеет оно решение в целых числах.

1 шаг. Надо найти наибольший общий делитель чисел 3 и 6. НОД(3; 6) = 3.

2 шаг. Определить, делится ли 2 на НОД(3; 6).

3 шаг. Если 2 делится на НОД(3; 6), то уравнение имеет решение в целых числах.

Если 2 не делится на НОД (3; 6), то уравнение не имеет решений в целых числах.

Расширенный алгоритм Евклида для решения диофантовых уравнений.

Для нахождения наибольшего общего делителя двух целых неотрицательных чисел используют алгоритм Евклида. Рассмотрим его реализацию на примере чисел 24 и 17.

Разделим большее из этих чисел на меньшее, то есть 24 на 17.

Получаем 24 : 17 = 1 (ост. 7), что можно записать в виде равенства:

24 = 17 · 1 + 7.

Теперь разделим делитель на остаток, то есть 17 на 7, получим:

17 = 7 · 2 + 3.

Снова разделим делитель на остаток:

7 = 3 · 2 + 1.

Выполним деление еще раз:

3 = 1 · 3 + 0.

Мы получили остаток, равный нулю, так как 3 делится на 1 без остатка.

В представленной последовательности действий мы получали остатки: 7, 3, 1, 0. Последний остаток, не считая 0, является наибольшим общим делителем чисел 24 и 17. То есть, НОД(24; 17) = 1.

Рассмотрим еще один пример: НОД(612; 342)?

612 = 342 ∙ 1 + 270,

342 = 270 ∙ 1 + 72,

270 = 72 ∙ 3 + 54,

72 = 54 ∙ 1 + 18,

54 = 18 ∙ 3 + 0.

НОД(612; 342) = 18.

Теперь выполним действия «в обратном направлении», то есть выразим 18 (остаток) через числа 612 и 342.

Для этого в каждой строчке последовательности Евклида выразим остатки через делимое и делитель (второй столбик таблицы):

612 = 342 ∙ 1 + 270

342 = 270 ∙ 1 + 72

270 = 72 ∙ 3 + 54

72 = 54 ∙ 1 + 18

54 = 18 ∙ 3 + 0

270 = 612 – 342 ∙ 1

72 = 342 – 270 ∙ 1

54 = 270 – 72 ∙ 3

18 = 72 – 54 ∙ 1

Получаем, 18 = 72 – 54 ∙ 1 = 72 – (270 – 72 ∙ 3) = 342 – 270 ∙ 1 – (270 – (342 – 270 ∙ 1) ∙3) =

342 – ((612 – 342 ∙1) ∙ 1) – (612 – 342 ∙ 1 – (342 – (612 – 342 ∙ 1)) ∙3) = 342 – 612 + 342 – 612 + 342 + 342 ∙ 3 – 612 ∙ 3 + 342 ∙ 3 = 342 ∙ 9 – 612 ∙ 5 = 342 ∙ 9 + 612 ∙ (-5).

То есть 18 = 9 ∙ 342 + (-5) ∙ 612.

Умение выполнять действия алгоритма «в обратном направлении» понадобится нам в решении диофантовых уравнений при помощи расширенного алгоритма Евклида.

Пример: решите уравнение 24x−17y=2.

Решение.

Найдем при помощи алгоритма Евклида НОД(24, 17):

24 = 17 · 1 + 7.

17 = 7 · 2 + 3.

7 = 3 · 2 + 1.

3 = 1 · 3 + 0.

НОД (24, 17) = 1.

Выполним действия «в обратном направлении»:

1 = 7 – 3 · 2 = 7 − (17 – 7 · 2) · 2 = 7 – 17 · 2 + 7 · 4 + 5 · 7 – 2 · 17 = 5 · (24 – 17 · 1) – 2 · 17 = 5 · 24 – 5 · 17 – 2 · 17 = 5 · 24 – 7 · 17 = 24 · 5 – 17 · 7.

24 · 5 – 17 · 7 = 1; В исходном уравнении в правой части стоит число 2. Поэтому умножим обе части уравнения на 2. Получим:

24 · 10 – 17 · 14 = 2.

То есть, x₀= 10, y₀= 14 – частные решения уравнения 24x −17y = 2.Если уравнение имеет одно решение в целых числах, то оно имеет бесконечное множество других решений.

Прибавим коэффициент b к значению х.

10 + (-17) = -7.

Чтобы значение исходного уравнения не изменилось, при прибавлении одного числа к х нужно вычесть другое число изу:

14 – 24 = -10.

(-7; -10) – еще одно решение уравнения.

Значения x будут равны сумме исходного решения (х₀) и любого кратного коэффициента b. То есть х = 10 + (-17t), где t – целое число.

А значение у – равны разности у₀ и любого кратного коэффициента а. То есть у = 14 – 24t.

Ответ: (10 − 17t, 14 − 24t), t ∈ Z.

Разбор заданий тренировочного модуля.

1. Решите задачу:

Некий чиновник купил ослов и быков за 1770 талеров. За каждого осла он уплатил по 31 талеру, а за каждого быка – по 21 талеру. Сколько ослов и быков купил чиновник?

Пусть чиновник купил х ослов и у быков. Тогда 31х + 21у = 1770.

По смыслу задачи х и у – натуральные числа. Так как 21 и 1770 делятся на 3, то 31х делится на 3, т. е. х делится на 3: х = 3n, где n – натуральное число. Тогда 31n + 7у = 590. Откуда n =

Очевидно, что n будет целым, если 7у – 1 делится на 31.

Наименьшее натуральное у, при котором это произойдет, равно 9. При этом n = 17, х = 51. Первое решение найдено: (51; 9).

Заметим, что следующие целые n будут получаться в результате увеличения у = 9 на число, кратное 31.

При у = 9 + 21 = 40 имеем n = 10, х = 30.

При у = 40 + 9 имеем n = 3, х = 9.

При следующих значениях у значения n отрицательны. Таким образом, исходное уравнение имеет 3 решения: (51, 9), (30, 40), (9, 71).

Ответ: (51, 9), (30, 40), (9, 71).

2. Решение уравнения.

Разделите уравнения на 2 группы: уравнение имеет решение в целых числах, уравнение не имеет решений в целых числах.

7х – 5у = 2

3х + 5у = 10

2х + 4у = -1

3х – 9у = 10

6х + 9у = 2

2х – 5у = 15

1) НОД(7; 5) = 1, 2 делится на 1, следовательно, 7х – 5у = 2 имеет решение в целых числах.

2) НОД(3; 5) = 1, 10 делится на 1, следовательно, 3х + 5у = 10 имеет решение в целых числах.

3) НОД(2; 4) = 2, -1 не делится на 2, следовательно, 2х + 4у = -1 не имеет решений в целых числах.

4) НОД(3; 9) = 3, 10 не делится на 3, следовательно, 3х – 9у = 10 не имеет решений в целых числах.

5) НОД(6; 9) = 3, 2 не делится на 3, следовательно, 6х + 9у = 2 не имеет решений в целых числах.

6) НОД(2; 5) = 1, 15 делится на 1, следовательно, 2х – 5у = 15 имеет решение в целых числах.

Источник

Основные понятия

Решением линейных уравнений начали заниматься ещё в Древнем Вавилоне и Греции. Особого успеха в их вычислении смог добиться древнегреческий философ и математик правителя Греции — Диофант Александрийский. В третьем веке до нашей эры он издал свой труд под названием «Арифметика», в котором описал возможные решения различных математических задач. Большая часть их была посвящена уравнениям, которые и были позже названы в его честь.

Диофантовыми уравнениями принято называть линейные выражения вида: a1x1 + a2x2 + … + anxn = c. В этих равенствах икс обозначает искомое неизвестное, а коэффициенты a и c являются целыми числами. Греческий учёный предложил несколько способов решения таких уравнений:

полный перебор;
разложение на множители;
выражение одной переменной через другую с выделением целой части при решении системы;
поиск частного решения;
алгоритм Евклида;
геометрический метод.

Методы решения диофантовых уравнений позволяют найти целые или рациональные решения для алгебраических равенств или их систем. Но при этом число переменных в выражении не должно превышать двух. Как правило, такие уравнения имеют несколько решений, поэтому их другое популярное название — неопределённые.

Чтобы воспользоваться способами, предложенными математиком при рассмотрении задач, нужно попробовать проанализировать исходные данные и свести их к линейному равенству или системе уравнений. При этом коэффициенты, как стоящие возле неизвестных, так и свободные, должны быть целыми. Ответом же должно получиться тоже целое число, обычно натуральное.

Чтобы понимать возможности применения уравнений в тех или иных исследовательских вычислениях, необходимо предварительно ответить на два вопроса: могут ли быть у задания целочисленные решения и ограничено ли число действительных ответов. Поэтому использование способов подходит только для простейших уравнений первой и второй степени. Для выражений высших порядков, например, 4x ³ + 6Y ³ — 2z ⁴ = 23, определить, является ли решением целое число, довольно проблематично.

Методы решения

Для начала следует рассмотреть однородное линейное уравнение вида: ax + by = 0. Это простой многочлен первой степени. Для него характерно то, что если для коэффициентов можно подобрать один делитель, то обе части возможно сократить на его величину не нарушив принципы записи. Наиболее простым способом определить этот делитель является метод разработанный великим математиком своего времени Евклидом.

Решение диофантовых уравнений по алгоритму Евклида заключается в нахождении общего делителя натуральных чисел с использованием деления с остатком. Для этого нужно взять большее число и просто разделить его на наименьшее. Затем полученный остаток нужно снова разделить на меньшее из чисел. Это действие необходимо повторять до тех пор, пока результатом операции не станет единица, то есть выполнится деление без остатка. Последнее полученное число и будет являться наибольшим общим делителем (НОД).

Существует три теоремы, которые используются при решении уравнений первой степени:

В случае, когда НОД равняется единице, выражение будет обязательно иметь хотя бы одну пару целого решения.
Если коэффициенты выражения больше единицы, и при этом свободный член нельзя нацело разделить на них, то корни равенства не имеют целого значения.
Когда коэффициенты равняются единице, все решения, состоящие из целых чисел, находятся с помощью формул: x = x0c + bt и y = y0c — at, где: х0, y0 — целые ответы, t — множество чисел.

Например, пусть есть равенство вида 54x + 37y = 1. Используя то, что a = 54, а b =37, можно записать: 54 — 37 *1 = 17. Теперь можно выполнить следующие вычисления:

37 — 17 * 2 = 3;
71 — 3 * 5 = 2;
3 — 2 * 1 = 1.

Далее нужно выразить значения коэффициентов через остаток:

3 — (17 — 3 * 5) = 1;
1 = 17 — 3 * 4;
1 = 17 — (37- 17 * 2) * 4;
1 = 17 — 37 * 4+17 * 8;
1 = 17 * 9 — 37 * 4;
1 = (54 — 37 * 1) * 9 — 37 * 4;
1 = 54 * 9 — 37 * 9 — 37 * 4;
1 = 54 * 9 — 37 * 13;
1 = 54х + 37у.

Исходя из приведённого следует, что x0 равняется девяти, а игрек нулевой — минус тринадцать. Таким образом, рассматриваемое уравнение будет иметь вид:

{x = 9 + 37t;

{y = -13 — 54t.

Этим же способом можно и определить, что целых решений в выражении быть не может, как, например, для равенства 17x + 36y = 7. В этом случае НОД не делится на два, поэтому и целых решений нет.

Способ подбора и разложения

Метод подбора используется для нахождения корней простых уравнений. Пожалуй, это самый простой способ, но вместе с тем и требующий повышенного внимания и большого количества операций. Его суть заключается в полном переборе всех допустимых значений переменных, входящих в равенство. Например, эта задача которая будет интересна и школьникам, только знакомящимся с уравнениями.

Пусть имеется зоопарк, в котором находятся птицы и млекопитающие. Всего у животных двадцать лап. Определить, какое количество может быть птиц, а какое — млекопитающих. Для нахождения ответа методом перебора следует принять число одних животных, равное x (пусть это будут четырёхпалые), а других — y (птицы). Таким образом, получится уравнение: 2x + 4 y = 20. Для простоты выражение можно упростить, сократив на два: x + 2y = 10.

Полученное выражение нужно преобразовать, разделив неизвестные знаком равно: x = 10 — 2y. Зная, что ответом могут быть только целые числа, вместо y нужно пробовать подставлять возможные варианты: 1 — 8; 2 — 6; 3 — 4; 4 — 2; 5 — 0. Это и есть все возможные ответы на поставленную задачу.

Разложение выражения на множители можно выполнять различными способами. Вот основные из них:

вынесение общего множителя: если каждый член многочлена можно разделить на одно и то же число, то его можно вынести за скобку;
использование формулы сокращённого умножения: оно выполняется по формуле: an — bn = (a-b) * (an-1 + an-2 * b +… a2bn-3 + abn-2 + bn-1);
применение свойства полного квадрата: это самый эффективный способ, заключающийся в вынесении полного квадрата за скобку с последующим использованием формул разности квадратов;
группировкой — в его основе лежит вынесение общего множителя таким образом, чтобы появилась возможность перегруппировки выражения, после которой получится значение, присутствующее во всех членах равенства.

Например, пусть имеется нелинейное уравнение вида: 8×4 + 32×2 = 8. Все его члены можно перенести в одну сторону, а равенство приравнять к нулю, при этом сократив каждый член на восемь: x4 + 4×2 — 1 = 0. Для преобразования такого выражения удобнее всего применить метод квадратов. Таким образом, уравнение можно расписать следующим образом: x4 + 2 * 2 * x2 + 4 — 4 — 1 = (x2 + 2)2 — 5 = (x2 + 2 — √5) * (x2 + 2 +√5).

Геометрический подход

Этот метод удобно применять для системы уравнений. Его принцип построен на изображении графиков уравнений и определения их точки пересечения. При этом координаты этой точки и будут являться корнями рассматриваемой системы.

Из этого утверждения можно сделать следующие выводы:

если графики уравнений представляют пересекающиеся прямые, то решением будет только одно число;
когда графики уравнений не имеют общих точек, то решения у системы уравнений нет;
в случае, когда графики совпадают, система будет иметь бесконечное множество корней.

Применять этот метод можно для уравнений, порядок которых не превышает единицы. В равенствах высшего порядка построить график обычно сложно. Например, дана система:

{2x — y = -9;

{3x + 2y = 4.

Из первого и второго равенства можно выразить одно неизвестное через другое, используя несколько произвольных чисел. Затем, подставляя их вместо неизвестного, можно построить график. Как только две прямые будут построены, можно будет определить, что точка их пересечения имеет координаты -2; 5. Эти значения и будут искомыми корнями.

Занимательная задача

На самом деле примеры диофантовых уравнений можно встретить в повседневной жизни. Например, при покупке чего-либо в магазине. На эту тему математики смогли придумать интересные задачи, обычно предлагающиеся ученикам на дополнительных занятиях.

Вот одна из них, появившаяся из реальной истории. Однажды математик пришёл в магазин приобрести свитер. Его цена составляла 19 рублей. У учёного же были с собой только купюры номиналом три рубля, а у кассира — пятирублёвки. Задача состоит в том, чтобы выяснить, сможет ли состояться сделка. Иными словами, необходимо найти, сколько нужно математику дать купюр, и какое их количество он получит от кассира.

Рассуждать нужно следующим образом. В задачи есть два неизвестных: количество трёхрублёвых и пятирублёвых купюр. Поэтому можно составить уравнение: 3x — 5y = 19. По сути, уравнение с двумя неизвестными может иметь бесчисленное число решений, но не всегда из них может найтись хотя бы одно целое положительное.

Итак, зная, что неизвестные должны быть целыми положительными числами, нужно выразить неизвестное с меньшим коэффициентом через остальные члены. Получится равенство: 3 x = 19 + 5 y. Левую и правую часть можно разделить на три, а после выполнить простейшие преобразования: x = (19 + 5y) / 3 = 6 + y + (1 + 2y) / 3. Учитывая, что неизвестные и свободный член это целые числа, выражение (1 + 2y) / 3 можно заменить буквой r, также являющимся каким-то целым числом.

Тогда уравнение можно переписать как x = 6 + y + t. Отсюда t = (1 + 2y) / 3 или y = t + (t — 1) / 2. Снова можно сделать вывод, что (t — 1) / 2 — какое-то целое число. Если заменить его на t1, выражение примет вид: y = t + t1.

Подставив t = 2t1 + l в равенство можно получить, что x = 8 + 5t1, а y = 1 + 3t1. Таким образом, решением уравнения будут полученные равенства. Исходя из того, что результат должен быть положительным, равенства можно переписать в неравенства вида:8 + 5t1> 0, 1 + 3t1 > 0. Отсюда определить диапазон, ограничивающий t1. Беря во внимание только плюсовую часть диапазона, можно сделать заключение, что возможные варианты решения лежать в пределе от нуля до плюс бесконечности.

Подставляя по очереди числа, можно определить значения x и y. Искомый ряд будет выглядеть следующим образом: {x = 8 + 5t} 1 = 8, 13, 18, 23, …, n; {у = 1 + 3t} 1 = 1, 4, 7, 10,…, m. То есть математик, дав восемь купюр, получит одну на сдачу, а если он отдаст 13 купюр, то продавец должен будет ему выдать четыре пятирублёвки. Этот ряд можно продолжать до бесконечности.

Использование онлайн-калькулятора

Существуют сайты, рассчитывающие линейные уравнения в автоматическом режиме. Они называются математическими онлайн-калькуляторами. Пользователю, желающему воспользоваться их услугами, нужно иметь лишь подключение к интернету и любой веб-браузер.

Свои услуги сервисы предоставляют бесплатно. При этом часто на их страницах содержится краткий теоретический материал, посвящённый решению диофантовых уравнений. Кроме того, пользователю предоставляется возможность ознакомиться с решением типовых примеров.

Из нескольких десятков таких сайтов на русском языке можно отметить следующие:

HostCiti;
PocketTeacher;
Upbyte;
Planetcalc;
Math24.

Все приведённые сайты имеют интуитивно понятный интерфейс и бесплатны. После того как пользователь введёт в предложенную форму нужные уравнения и запустит расчётчик, онлайн-сервисы не только выдадут ответ, но и выведут на экран пошаговое решение с объяснениями. Таким образом, эти сервисы помогают не только быстро и верно найти решение, но и дают возможность пользователю понять принципы вычисления, проверить самостоятельно выполненный расчёт.

Источник

Об этой статье

Была ли эта статья полезной?

Примеры[править | править код]

Линейные диофантовы уравнения[править | править код]

Алгебраические диофантовы уравнения[править | править код]

Диофантовы множества[править | править код]

Неразрешимость в общем виде[править | править код]

Экспоненциальные диофантовы уравнения[править | править код]

См. также[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Основные понятия

Методы решения

Способ подбора и разложения

Геометрический подход

Занимательная задача

Использование онлайн-калькулятора

Вам также может понравиться

Скайриме как найти призрак девочки

Как найти мошенника интернет магазина

Как найти корни квадратного уравнения не решая

Добавить комментарий Отменить ответ