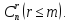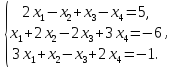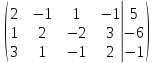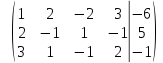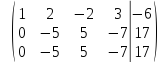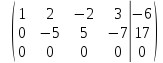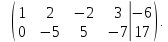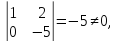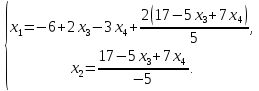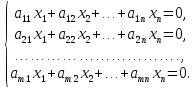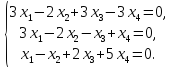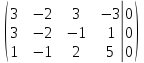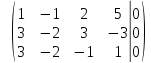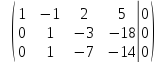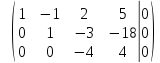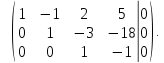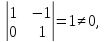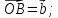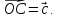Как найти все решения системы линейных уравнений

Время чтения: 7 минут.

Сегодня мы разберем, что такое система уравнений и какие существуют методы ее решения: быстро, кратко, понятно🧠

То есть, по итогу решения системы у нас будет пара значений x и y, которые мы можем подставить в два уравнения и получить верное равенство.

Способы решения систем уравнения:

• Графический метод 📈
• Способ подстановки 📝
• Способ сложения ➕

Ниже разберем каждый метод подробнее.

1. Графический метод решения

Чтобы решить систему графически, нам нужно:

• Выразить из каждого уравнения переменную y;
• Построить таблицы значений для каждого уравнения (см. картинку ниже);

• Построить графики по полученным в таблице точкам;
• Найти точку пересечения графиков – это и будет решение

Таким образом, решением данного уравнения будет являться точка (3;2), то есть x=3, y=2.

Памятка для системы уравнений графическим методом

По коэффициентам при х сразу можно понять, будет ли система иметь решения.

2. Способ подстановки

Способ подстановки говорит сам за себя – что-то берем и подставляем вместо другого. Ниже представлен алгоритм действий👇

Давай рассмотрим решение на конкретном примере.

То есть, мы выразили y из первого уравнения, подставили его во второе и нашли значение х. После чего нашли значение y. Все просто!💁‍♀️

3. Способ сложения

Напоминаю для тех, кто забыл:

• коэффициенты – это числа перед x и y;
• x и y – это переменные.

Получается, наша задача – это избавиться от одной из переменных, чтобы дальше решать обыкновенное уравнение с одной переменной.

Звучит не очень то и сложно. Давай разберем на примере!

В примере мы умножили первое уравнение на -2, чтобы при х вместо 5 стал коэффициент -10.

А затем сложили первое и второе уравнение: -10x + 10x = 0. Вот мы и избавились от х😏Дальше решение очень напоминает предыдущий способ.

На этом все! Ниже будет несколько примеров для тренировки. Если хочешь закрепить полученные знания, то обязательно реши их.

Остались вопросы? Можешь написать о них в комментариях!

#образование #математика #ОГЭ #егэ #впр

Прежде чем перейти к разбору как решать системы уравнений, давайте разберёмся, что называют системой уравнений
с двумя неизвестными.

Например, система уравнений может быть задана следующим образом.

Чтобы решить систему уравнений, нужно найти и «x», и «y».

Как решить систему уравнений

Существуют два основных способа решения систем уравнений. Рассмотрим оба способа решения.

Способ подстановки
или
«железобетонный» метод

Первый способ решения системы уравнений называют способом подстановки или «железобетонным».

Название «железобетонный» метод получил из-за того, что с помощью этого метода практически всегда можно
решить систему уравнений. Другими словами, если у вас не получается решить систему уравнений,
всегда пробуйте решить её методом подстановки.

Разберем способ подстановки на примере.

Выразим из первого уравнения «x + 5y = 7»
неизвестное «x».

Перенесём в первом уравнении «x + 5 y = 7» всё что
содержит «x» в левую часть,
а остальное в правую часть по
правилу переносу.

При «x» стоит коэффициент равный единице, поэтому дополнительно делить уравнение
на число не требуется.

Теперь, вместо «x» подставим во второе уравнение полученное выражение
«x = 7 − 5y» из первого уравнения.

	x = 7 − 5y
3(7 − 5y) − 2y = 4

Подставив вместо «x» выражение «(7 − 5y)»
во второе уравнение,
мы получили обычное линейное уравнение с одним неизвестным «y».
Решим его по правилам
решения линейных уравнений.

Чтобы каждый раз не писать всю систему уравнений заново, решим полученное уравнение
«3(7 − 5y) − 2y = 4» отдельно.
Вынесем его решение отдельно с помощью
обозначения звездочка (*).

	x = 7 − 5y
3(7 − 5y) − 2y = 4  (*)

(*)   3(7 − 5y) − 2y = 4
21 − 15y − 2y = 4
− 17y = 4 − 21
                 − 17y = − 17     | :(−17)
y = 1

Мы нашли, что «y = 1».
Вернемся к первому уравнению «x = 7 − 5y» и вместо «y» подставим в него полученное числовое значение.
Таким образом можно найти «x».
Запишем в ответ оба полученных значения.

Ответ: x = 2; y = 1

Способ сложения

Рассмотрим другой способ решения системы уравнений. Метод называется способ сложения.
Вернемся к нашей системе уравнений еще раз.

По правилам математики уравнения системы можно складывать. Наша задача в том, чтобы сложив исходные
уравнения, получить такое уравнение, в котором останется только одно неизвестное.

Давайте сейчас сложим уравнения системы и посмотрим, что из этого выйдет.

	x + 5y = 7		(x + 5y) + (3x − 2y) = 7 + 4
	+          =>	x + 5y + 3x − 2y = 11
3x − 2y = 4		4x + 3y = 11

При сложении уравнений мы получили уравнение «4x + 3y = 11».
По сути, сложение уравнений в исходном виде нам ничего
не дало, так как в полученном уравнении мы по прежнему имеем оба неизвестных.

Вернемся снова к исходной системе уравнений.

Чтобы при сложении неизвестное «x» взаимноуничтожилось,
нужно сделать так, чтобы в первом уравнении при «x» стоял коэффициент
«−3».

Для этого умножим первое уравнение на «−3».

	x + 5y = 7 | ·(−3)
3x − 2y = 4

	x ·(−3) + 5y · (−3) = 7 · (−3)
3x − 2y = 4

	−3x −15y = −21
3x − 2y = 4

Теперь сложим уравнения.

	−3x −15y = −21		(−3x −15y ) + (3x − 2y) = −21 + 4
	+          =>	−3x −15y + 3x − 2y = −21 + 4
3x − 2y = 4		−17y = −17 |:(−17)
		y = 1

Мы нашли «y = 1».
Вернемся к первому уравнению и подставим вместо «y» полученное числовое
значение и найдем «x».

Ответ: x = 2; y = 1

Пример решения системы уравнения
способом подстановки

Выразим из первого уравнения «x».

Подставим вместо «x» во второе уравнение полученное выражение.

	x = 17 + 3y
(17 + 3y) − 2y = −13 (*)

(*) (17 + 3y) − 2y = −13
17 + 3y − 2y = −13
17 + y = −13
y = −13 − 17
y = −30

Подставим в первое уравнение полученное числовое значение «y = −30» и
найдем «x».

	x = 17 + 3 · (−30)
y = −30

Ответ: x = −73; y = −30

Пример решения системы уравнения
способом сложения

Рассмотрим систему уравнений.

	3(x − y) + 5x = 2(3x − 2)
4x − 2(x + y) = 4 − 3y

Раскроем скобки и упростим выражения в обоих уравнениях.

	3x − 3y + 5x = 6x − 4
4x − 2x − 2y = 4 − 3y

	8x − 3y = 6x − 4
2x −2y = 4 − 3y

	8x − 3y − 6x = −4
2x −2y + 3y = 4

Мы видим, что в обоих уравнениях есть «2x».
Наша задача, чтобы при сложении уравнений «2x» взаимноуничтожились и в
полученном уравнении осталось только «y».

Для этого достаточно умножить первое уравнение на «−1».

	2x − 3y = −4      |·(−1)
2x + y = 4

	2x · (−1) − 3y · (−1) = −4 · (−1)
2x + y = 4

Теперь при сложении уравнений у нас останется только «y» в уравнении.

	−2x + 3y = 4		(−2x + 3y ) + (2x + y) = 4 + 4
	+          =>	−2x + 3y + 2x + y = 4 + 4
2x + y = 4		4y = 8         | :4
		y = 2

Подставим в первое уравнение полученное числовое значение «y = 2» и
найдем «x».

Ответ: x = 1; y = 2

---

Ваши комментарии

Оставить комментарий:

---

Пусть
переменныхназываются основными (или базисными),
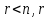
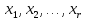
если определитель матрицы из коэффициентов
при них (т.е. базисный минор) отличен от
нуля. Остальныепеременных
называются неосновными (или свободными).
Каждому разбиению переменных на основные
и неосновные соответствует одно базисное
решение, а число способов разбиения не
превосходит числа сочетаний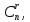то
и базисных решений имеется не более

Совместная
система
линейных уравнений спеременнымиимеет
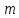
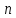
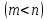
бесконечное множество решений, среди
которых базисных решений конечное
число, не превосходящее

Достоинства
метода Гаусса по сравнению с другими:

–
менее трудоемкий метод;

–
позволяет однозначно установить,
совместна система или нет и в случае
совместности найти ее решение;

–
дает возможность найти максимальное
число линейно независимых уравнений –
ранг матрицы системы.

Рассмотрим
пример. Найти
решение системы линейных алгебраических
уравнений

Составим
расширенную матрицу по данной системе

поменяем
местами первую и вторую строку

умножим
первую строку на
и сложим со второй строкой; умножим
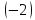
первую строку наи сложим с третьей строкой

умножим
вторую строку на
и сложим с третьей строкой

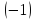
последняя
строка вычеркивается, так как все ее
элементы равны нулю

Ранг
основной матрицы
ранг
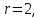
расширенной матрицы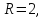следовательно, система совместна. Число
строк в основной матрице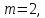число
столбцов в основной матрице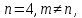следовательно, система имеет множество
решений.

Выявим
базисные переменные

следовательно,
базисные
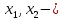
переменные, тогда

3.4. Однородные системы линейных алгебраических уравнений

Система
линейных уравнений спеременными называетсясистемой
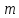
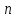
линейных однородных уравнений,
если все их свободные члены равны нулю.

Системы
линейных однородных уравнений:

Система
линейных однородных уравнений всегда
совместна, так как имеет, по крайней
мере, нулевое решение

Если
в однородной системе
а
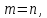
ее определитель отличен от нуля, то
такая система имеет только нулевое
решение.

Система
линейных однородных уравнений имеет
ненулевое решение тогда и только тогда,
когда ранг ее матрицы коэффициентов
при переменных меньше числа переменных,
т.е. при

Рассмотрим
пример. Найти
решение системы линейных алгебраических
уравнений

Составим
по данной системе расширенную матрицу

поменяем
местами первую и третью строки

умножим
первую строку на
и сложим со второй строкой, а затем с
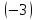
третьей строкой, получим

умножим
вторую строку на
и сложим с третьей строкой

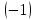
разделим
последнюю строку на

Таким
образом, ранг расширенной матрицы и
ранг основной матрицы равны
следовательно,
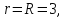
система совместна. Число строк в основной
матрице равно 3, а число столбцов равно
4, т.е. решений множество. Определим
базисные переменные

базисные
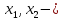
переменные.

Перейдем
от матрицы к системе, выразим переменные
через другие переменные

Контрольные
вопросы

1. Сформулировать
   теорему Кронекера
   – Капелли.

2. Сформулировать
   Метод Гаусса решения систем m
   линейных
   уравнений с n
   неизвестными.

3. Дать
   определение базисному решению систем
   линейных алгебраических уравнений.

4. Какие
   системы линейных алгебраических
   уравнений называют однородными?

Лекция
№4. Векторы

4.1.
Векторы в науке и технике. Понятие
вектора. Координаты вектора.

4.2.
Линейные операции над векторами.

4.3.
Декартова система координат. Базис
векторного пространства.

4.4.
Скалярное произведение векторов,
основные свойства и выражение в
координатной форме.

4.5.
Векторное произведение векторов.
Основные свойства векторного произведения
векторов и выражение в координатной
форме.

4.6.
Применение векторного произведения
векторов к решению задач.

4.7.
Смешанное произведение векторов.
Основные свойства смешанного произведения
векторов и выражение в координатной
форме.

4.8.
Применение смешанного произведения
векторов к решению задач.

1. Векторы
   в науке и технике. Понятие вектора.
   Координаты вектора

В
физике и математике вектор – это
величина, которая характеризуется
численным значением и направлением. В
физике встречается немало важных
величин, которые характеризуются
направлением. Например, сила, скорость,
ускорение, вращающий момент, импульс,
напряженность электрического и магнитного
полей. Их можно противопоставить другим
величинам, таким как масса, объем,
давление, температура, плотность, которые
можно описать обычным числом и называются
они скалярными величинами.

Векторная
запись используется при работе с
величинами, которые невозможно задать
полностью с помощью обычных чисел.
Например, необходимо описать положение
предмета, но полностью определить
местоположение предмета невозможно,
пока не будет известно направление, в
котором он находится. Таким образом,
местонахождение предмета характеризуется
численным значением (расстоянием в
километрах) и направлением.

При
изучении и расчете цепей переменного
тока удобно пользо­ваться векторными
диаграммами, на которых синусоидальные
напряжения и токи условно изображают
с помощью векто­ров. Применение этих
диаграмм упрощает изучение и расчет
цепей и вносит наглядность в рассматриваемые
соотношения.

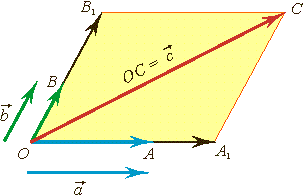
Вектором
на плоскости называется
направленный отрезок

с начальной точкой
и конечной точкойкоторый
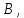
можно перемещать параллельно самому
себе.

Рис.
1

Вектор
на плоскости

От
любой точки можно отложить вектор,
равный данному, и притом только один,
используя параллельный перенос. При
параллельном переносе точки смещаются
по параллельным или совпадающим прямым
на одно и тоже расстояние.

Нулевой
вектор – точка
в пространстве. Начало и конец нулевого
вектора совпадают, и он не имеет длины
и направления.

Абсолютной
величиной или модулем вектора называется
длина отрезка, изображающего вектор.
Другими словами длина
вектора есть
расстояние между началом и концом
вектора

Векторы
называются коллинеарными,
если они
расположены на одной или на параллельных
прямых. Нулевой вектор коллинеарен
любому вектору. Если векторы
иколлинеарны и их лучи сонаправлены, то
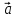
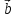
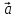
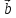
векторыиназываютсонаправленными.
Обозначают
Если векторыиколлинеарны,
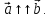
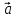
а их лучи не являются сонаправленными,
то векторы называютпротивоположно
направленными.
Обозначают
Нулевой вектор условились считать
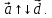
сонаправленным с любым вектором.

Рис.2

Коллинеарные
вектора

Свойство
коллинеарных векторов.

Если
векторы
иколлинеарны и,
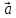
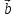
то существует число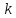такое,
что.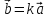
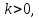
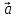
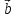
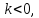
Причем, еслито векторыисонаправленные, еслито
противоположно направленные.

Векторы
называются компланарными,
если при
откладывании их от одной и той же точки
они будут лежать в одной плоскости.
Любые два вектора компланарны. Коллинеарные
векторы всегда компланарны, но не все
компланарные векторы коллинеарны.

Признак
компланарности трех векторов.

Если
вектор
можно разложить по векторами,
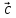
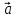
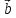
т.е. представить в виде,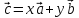
где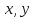-некоторые
числа, то векторы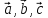-компланарны.

Рис.3

Компланарные
вектора

,
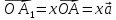
где
;

,
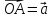
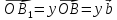
где

,
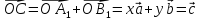
где

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #