Метод подсчёта количества решений

Линейные алгебраические уравнения — одни из самых простых уравнений, которые мы можем решить. Если в уравнении только одна переменная, решение тривиально, в то время как для системы линейных уравнений существует множество способов найти уникальные решения.
В этой статье нас интересует частный случай линейного уравнения с несколькими переменными. Хорошо известно, что подобное уравнение имеет бесконечное число решений. Мы наложим определённые ограничения и в значительной степени сократим количество решений.
Общая форма интересующего нас уравнения:

где n и m — положительные целые числа.
Наша задача — найти число решений этого уравнения, предполагая, что xᵢ являются целыми числами. Это предположение значительно снижает число решений заданного уравнения.
Нам нужен метод
Давайте начнём с частного случая общего уравнения:

Нетрудно найти все решения этого уравнения методом простого счёта. Решения заданы парами (x₁, x₂):

Мы видим, что уравнение имеет шесть решений. Также нетрудно предположить, что, если мы заменим правую часть определённым положительным целым числом m, решения будут выглядеть так:

и мы сможем подсчитать число решений — m+1.
Это было просто, верно?
Теперь возьмём немного более сложный вариант с тремя переменными, скажем:

С несколько большими усилиями, чем в предыдущем примере, находим решения в виде наборов из трёх чисел (x₁, x₂, x₃):

Число решений в этом случае равно 10.
Легко представить, что метод прямого счёта может стать очень утомительным для уравнения с большим количеством переменных. Он также становится утомительным, если целое число в правой части уравнения становится больше — например, если в правой части у нас будет 8, а не 3, решений будет уже 45. Разумеется, не хотелось бы искать все эти решения методом прямого счёта.
Значит, нужен эффективный метод.
Разрабатываем метод
Существует ещё один способ, которым можно решить предыдущие два уравнения. Давайте снова начнём с этого уравнения:

Одним из решений было (5, 0). Давайте преобразуем его в:

Мы разложили решение на нули и единицы, соответствующие каждому числу. Ненулевую часть (в данном случае 5) мы разложили на соответствующее число единиц, а ноль преобразовали в ноль. Таким же образом мы можем разложить и другое решение:

Мы поменяли прежнее расположение нуля, чтобы получить новое решение. Итак, два числа в парах (обозначенные красным и голубым) разделены нулём (чёрный) в разложенном виде. Таким же образом запишем оставшиеся решения:

Записав решения таким образом, видим закономерность. Кажется, все решения — это просто перестановки нулей и единиц. Вопрос о том, сколько существует решений, становится эквивалентным вопросу как много таких перестановок нулей и единиц может быть сделано, начиная с любой из конфигураций.
В данном случае у нас есть 6 местоположений в разложенной конфигурации для размещения нулей и единиц. Мы можем выбрать простейшее решение в качестве начальной конфигурации:

Теперь всё, что нам нужно найти, это общее число способов, которыми можно заполнить шесть местоположений пятью единицами и одним нулём.
Подобные задачи подсчёта мы можем решить различными способами, но наиболее эффективным будет способ, разработанный в такой области математики как комбинаторика, которая даёт нам формулу для числа способов перестановки r объектов в n местоположений:

где n! (читается как “n факториал”) определяется как произведение всех целых чисел от 1 до n, т.е. n! = 1 × 2 × 3 × ⋅ ⋅ ⋅ × n. Мы также определяем 0! = 1.
Эта формула обычно записывается в компактной форме как:

Теперь, возвращаясь к задаче, мы можем использовать эту формулу для нахождения числа способов перестановки пяти единиц в шести местоположениях:

Это то же самое число, что мы получили методом прямого счёта!
Выглядит многообещающе, поэтому давайте проверим, сможем ли мы найти таким способом число решений второго линейного уравнения:

Некоторые решения можно записать в разложенном виде:

В этот раз нам нужно заполнить тремя единицами и двумя нулями пять местоположений. Используя формулу мы можем найти число способов расположения чисел:

И опять то же число, что мы получили методом прямого счёта. Мы можем также найти число решений для нерешённого случая, где в правой части уравнения 8 вместо 3. Одним из решений будет:

а нам нужно найти число способов разместить 8 единиц в 10 местоположениях, и это будет:

как и утверждалось выше.
Если мы уверены в том, что этот метод работает для всех случаев, нам нужна общая формула. Напомним, что общее уравнение имеет вид:

Простейшее решение этого уравнения:

Поскольку существует n переменных, количество нулей в этом решении равно n-1. Таким образом, разложение выглядит так:

В разложенной конфигурации видим m и n-1 нулей (как утверждалось выше).
Следовательно, общее число местоположений, которые нужно заполнить, равно (m+n-1). Единственное, что остаётся — найти число способов, которыми можно заполнить m+n-1 местоположений m единиц, что определяется по формуле:
Как найти все решения уравнения информатика
Можно выделить различные способы решения систем логических уравнений. Это сведение к одному уравнению, построение таблицы истинности и декомпозиция.
Задача: Решить систему логических уравнений:
Рассмотрим метод сведения к одному уравнению. Данный метод предполагает преобразование логических уравнений, таким образом, чтобы правые их части были равны истинностному значению (то есть 1). Для этого применяют операцию логического отрицания. Затем, если в уравнениях есть сложные логические операции, заменяем их базовыми: «И», «ИЛИ», «НЕ». Следующим шагом объединяем уравнения в одно, равносильное системе, с помощью логической операции «И». После этого, следует сделать преобразования полученного уравнения на основе законов алгебры логики и получить конкретное решение системы.
Решение 1: Применяем инверсию к обеим частям первого уравнения:
Представим импликацию через базовые операции «ИЛИ», «НЕ»:
Поскольку левые части уравнений равны 1, можно объединить их с помощью операции “И” в одно уравнение, равносильное исходной системе:
Раскрываем первую скобку по закону де Моргана и преобразовываем полученный результат:
Полученное уравнение, имеет одно решение: A =0, B=0 и C=1.
Следующий способ – построение таблиц истинности. Поскольку логические величины имеют только два значения, можно просто перебрать все варианты и найти среди них те, при которых выполняется данная система уравнений. То есть, мы строим одну общую таблицу истинности для всех уравнений системы и находим строку с нужными значениями.
Решение 2: Составим таблицу истинности для системы:
Полужирным выделена строчка, для которой выполняются условия задачи. Таким образом, A=0, B=0 и C=1.
Способ декомпозиции. Идея состоит в том, чтобы зафиксировать значение одной из переменных (положить ее равной 0 или 1) и за счет этого упростить уравнения. Затем можно зафиксировать значение второй переменной и т.д.
Решение 3: Пусть A = 0, тогда:
Из первого уравнения получаем B =0, а из второго – С=1. Решение системы: A = 0, B = 0 и C = 1.
В ЕГЭ по информатике очень часто требуется определить количество решений системы логических уравнений, без нахождения самих решений, для этого тоже существуют определенные методы. Основной способ нахождения количества решений системы логических уравнений – замена переменных . Сначала необходимо максимально упростить каждое из уравнений на основе законов алгебры логики, а затем заменить сложные части уравнений новыми переменными и определить количество решений новой системы. Далее вернуться к замене и определить для нее количество решений.
Задача: Сколько решений имеет уравнение ( A → B ) + ( C → D ) = 1? Где A, B, C, D – логические переменные.
Решение: Введем новые переменные: X = A → B и Y = C → D . С учетом новых переменных уравнение запишется в виде: X + Y = 1.
Дизъюнкция верна в трех случаях: (0;1), (1;0) и (1;1), при этом X и Y является импликацией, то есть является истинной в трех случаях и ложной – в одном. Поэтому случай (0;1) будет соответствовать трем возможным сочетаниям параметров. Случай (1;1) – будет соответствовать девяти возможным сочетаниям параметров исходного уравнения. Значит, всего возможных решений данного уравнения 3+9=15.
Следующий способ определения количества решений системы логических уравнений – бинарное дерево. Рассмотрим данный метод на примере.
Задача: Сколько различных решений имеет система логических уравнений:
Приведенная система уравнений равносильна уравнению:
Предположим, что x 1 – истинно, тогда из первого уравнения получаем, что x 2 также истинно, из второго – x 3=1, и так далее до xm = 1. Значит набор (1; 1; …; 1) из m единиц является решением системы. Пусть теперь x 1=0, тогда из первого уравнения имеем x 2 =0 или x 2 =1.
Когда x 2 истинно получаем, что остальные переменные также истинны, то есть набор (0; 1; …; 1) является решением системы. При x 2=0 получаем, что x 3=0 или x 3=, и так далее. Продолжая до последней переменной, получаем, что решениями уравнения являются следующие наборы переменных ( m +1 решение, в каждом решении по m значений переменных):
Такой подход хорошо иллюстрируется с помощью построения бинарного дерева. Количество возможных решений – количество различных ветвей построенного дерева. Легко заметить, что оно равно m +1.
Как найти все решения уравнения информатика
Сколько различных решений имеет уравнение J ∧ ¬K ∧ L ∧ ¬M ∧ (N ∨ ¬N) = 0, где J, K, L, M, N — логические переменные?
В ответе не нужно перечислять все различные наборы значений J, K, L, M и N, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Выражение (N ∨ ¬N) истинно при любом N, поэтому
Применим отрицание к обеим частям логического уравнения и используем закон де Моргана ¬ (А ∧ В) = ¬ А ∨ ¬ В . Получим
Логическая сумма равна 1, если хотя бы одно из составляющих ее высказываний равно 1. Поэтому полученному уравнению удовлетворяют любые комбинации логических переменных кроме случая, когда все входящие в уравнение величины равны 0. Каждая из 4 переменных может быть равна либо 1, либо 0, поэтому всевозможных комбинаций 2·2·2·2 = 16. Следовательно, уравнение имеет 16 −1 = 15 решений.
Осталось заметить, что найденные 15 решений соответствуют любому из двух возможных значений логической переменной N, поэтому исходное уравнение имеет 30 решений.
[spoiler title=”источники:”]
http://www.sites.google.com/a/gkl-kemerovo.ru/informatics/logic/7-sistemy-logiceskih-uravnenij
http://inf-ege.sdamgia.ru/test?theme=263
[/spoiler]
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Сколько различных решений имеет уравнение J ∧ ¬K ∧ L ∧ ¬M ∧ (N ∨ ¬N) = 0, где J, K, L, M, N — логические переменные?
В ответе не нужно перечислять все различные наборы значений J, K, L, M и N, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
2
Сколько различных решений имеет уравнение
((J → K) → (M ∧ N ∧ L)) ∧ ((J ∧ ¬K) → ¬ (M ∧ N ∧ L)) ∧ (M → J) = 1
где J, K, L, M, N – логические переменные?
В ответе не нужно перечислять все различные наборы значений J, K, L, M и N, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
3
Сколько различных решений имеет уравнение
((K ∨ L) → (L ∧ M ∧ N)) = 0
где K, L, M, N – логические переменные? В Ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве Ответа Вам нужно указать количество таких наборов.
4
Сколько различных решений имеет уравнение
(K ∧ L) ∨ (M ∧ N) = 1
где K, L, M, N – логические переменные? В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.
5
Сколько различных решений имеет уравнение
(X ∧ Y ∨ Z) → (Z ∨ P) = 0
где X, Y, Z, P – логические переменные? В ответе не нужно перечислять все различные наборы значений, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.
Пройти тестирование по этим заданиям
Практическое занятие
Математические задачи. Решение уравнений и систем уравнений.
Пояснения к работе
Excel включает
большое число надстроек – откомпилированных программ, добавляющих табличному
процессору новые функциональные возможности. К таким надстройкам относятся
«Подбор параметра», «Поиск решения».
«Подбор параметра» помогает
находить в общем случае приближенные решения уравнений вида f(x)
= 0. Решим простое уравнение:
f(x) = x2 – 5x + 6 = 0
Для решения этого уравнения
подготовим рабочий лист. Ячейка B4 будет содержать значение неизвестной x, а
ячейка B5 – значение функции f(x).
Для этого в B5
поместим формулу = B4* B4 – 5* B4+6, как показано на рис. 1

Рис. 1. Подготовка к решению уравнения
Выберем команду. Сервис/Подбор
параметра. Excel отобразит диалоговое окно Подбор
параметра, приведенное на рисунке 2.В этом окне заполним все три окна в
соответствии с результатом, который мы хотим получить. В поле Установить в
ячейке введем адрес формулы (B5),
результаты которой будут подобраны. В поле Значение введем желаемый
результат вычисления формулы (0). Наконец, используя поле Изменяя значения
ячейки, определим адрес ячейки, которая содержит значение, которое нужно
изменить.

Рис. 2. Заполнение окна Подбор
параметра
После щелчка кнопкой Ok Excel выполнит необходимые вычисления и
выведет диалоговое окно Результат подбора параметра.

Рис. 3. Результат Подбора параметра
Ячейка B4 будет содержать найденный корень
уравнения.
Примечание. В нашем случае уравнение имеет
два корня x1 =2 и x2 = 3. Excel всегда дает только один корень в
зависимости от начального значения изменяемой ячейки.
Примечание. Решение уравнений можно выполнить,
представив функцию в табличном виде. Построив график функции на некотором
отрезке с заданным шагом изменения аргумента, грубо приближенно можно
определить корень уравнения. Затем, используя метод Подбора параметра,
уточнить корень уравнения.
Решение систем уравнений.
Для решения систем уравнений с несколькими
неизвестными используется надстройка «Поиск решения». Пусть требуется решить
систему уравнений
x2 + 5y = 29
5x + y2 = 31
Подготовим рабочий лист так, как показано
на рис. 4. Ячейки D4 и D5
содержат формулы, выражающие левые части уравнений, ячейки E1 и E2 – значения неизвестных x и y
(изменяемые ячейки).

Рис. 4. Подготовка к решению системы
уравнений
Выполним команду Сервис/Поиск решения, на
экране откроется диалоговое окно Поиск решения (рис.5).

Рис. 5. Поиск решения. Надстройки
Установим в поле Установить целевую ячейку
адрес первой формулы D4, в поле Равной значению – число 29 (правая
часть первого уравнения), а в поле Изменяя ячейки диапазон E1:E2 (рис.
6)

Рис. 6. Поиск решения
Второе уравнение мы запишем как ограниченное в поле Ограничения.
Для этого нажмите кнопку Добавить в открывшемся диалоговом окне Добавить
ограничения. Заполним соответствующие поля как показано на рис. 7

Рис. 7. Результат поиска решения
После нажатия кнопки ОК произойдет возврат в окно Поиск
решения. Нам остается только щелкнуть по кнопке Выполнить.
Результат поиска решения показан на рис. 7. Полученные
результаты можно сохранить, нажав кнопку ОК.
Чтобы решить систему из более, чем двух уравнений,
надо одно из них, например первое, выбрать как целевое, т.е. адрес
соответствующей формулы внести в поле Установить целевую ячейку, а
остальные как ограничения.
Надстройка «Поиск решения» как и «Выбор параметра»
позволяет находить только одно решение системы.
Надстройка «Поиск решения» помогает решать довольно
сложные задачи на экстремумы функций нескольких переменных при наличии
ограничений на эти переменные.
Варианты заданий
Задание 1
 На плоскости заданы координаты точек.
На плоскости заданы координаты точек.
Определить, сколько точек попадает в заданную фигуру, рис. 1а.
Результат определения принадлежности точек и подсчет
количества точек, принадлежащих заданной фигуре, представлен на рис. 2. В
ячейку C4 помещена формула для определения принадлежности
точек фигуре.

Рис. 2. Подсчет количества точек
Количество точек
находим с помощью автосуммы.
Задание 2. Решить
уравнения и системы уравнений
1.
x3 – x2 + 4 cos πx/2 = 0
2.
x = log x + 5
3.
x2 + xy = 7 –y2
x + 5y2 = 9 –x/3
4.
2x2 + 3y
= 10
–x
+ 6y2 =4
5.
3x
-4y = 3
6.
x3 – sinx – 0,5 = 0
7.
x2 –sinx + 0,1 = 0
8.
x3 + x2
-12x = 0
9.
x3 -19 x – 30 = 0
10.
x3 – x2 +
3x – 10 = 0
(Старый формат ЕГЭ) 23. Логические уравнения с множеством переменных
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Системы логических уравнений
Сколько существует различных наборов значений (x_1, x_2, … x_{10}), которые удовлетворяют всем перечисленным ниже условиям?
((x_1 wedge x_2) rightarrow (x_3 wedge x_4)=1)
((x_3 wedge x_4) rightarrow (x_5 wedge x_6)=1)
((x_5 wedge x_6) rightarrow (x_7 wedge x_8)=1)
((x_7 wedge x_8) rightarrow (x_9 wedge x_{10})=1)
В ответе не нужно перечислять все различные наборы значений переменных (x_1, x_2, … x_{10}), при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Внешняя операция в отдельно взятом уравнении — это импликация, в результате которой должна быть истина. Импликация будет истинна, если:
(0 rightarrow 1)
(0 rightarrow 0)
(1 rightarrow 1)
Если скобка ((x_1 wedge x_2)=1) ((x_1=1 , x_2=1)), то для скобки ((x_3 wedge x_4)) возможен только вариант ((x_3=1, x_4=1)), при любых других конъюнкция будет равна 0.
Если ((x_1 wedge x_2)=0) (это возможно в следующих случаях (x_1=0, x_2=1; x_1=1, x_2=0; x_1=0, x_2=0)), то для скобки ((x_3 wedge x_4)) возможны любые значения, импликация этих скобок будет истинна. Поскольку уравнения однотипные и отличаются только сдвигом номеров переменных на единицу, то будем использовать метод отображения, применяя его к каждой последующей комбинации (x_{i},x_{i+1}, i in [1; 9]).
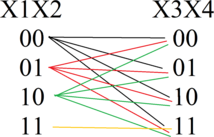
Теперь найдем общее количество решений, подставляя в отображении соответствующие x, учитывая предыдущие значения:
(begin{array}{|c|c|c|c|c|c|}
hline
& x_1 wedge x_2 & x_3 wedge x_4 & x_5 wedge x_6 & x_7 wedge x_8 & x_9 wedge x_{10}\
hline
00 & 1 & 3 & 9 & 27 & 81\
hline
01 & 1 & 3 & 9 & 27 & 81\
hline
10 & 1 & 3 & 9 & 27 & 81\
hline
11 & 1 & 4 & 13 & 40 & 121\
hline
end{array})
(begin{array}{|c|c|c|c|c|c|}
hline
& x_1 wedge x_2 & x_3 wedge x_4 & x_5 wedge x_6 & x_7 wedge x_8 & x_9 wedge x_{10}\
hline
00 & 1 & 1+1+1 & 3+3+3 & 9+9+9 & 27+27+27\
hline
01 & 1 & 1+1+1 & 3+3+3 & 9+9+9 & 27+27+27 \
hline
10 & 1 & 1+1+1 & 3+3+3 & 9+9+9 & 27+27+27\
hline
11 & 1 & 1+1+1+1 & 3+3+3+4 & 9+9+9+13 & 27+27+27+40\
hline
end{array})
В итоге получаем: (81+81+81+121=364).
Ответ: 364
Сколько существует различных наборов значений (x_1, x_2, …x_{10}), которые удовлетворяют всем перечисленным ниже условиям?
((x_1 wedge x_2) rightarrow (x_3 vee x_4)=1)
((x_3 wedge x_4) rightarrow (x_5 vee x_6)=1)
((x_5 wedge x_6) rightarrow (x_7 vee x_8)=1)
((x_7 wedge x_8) rightarrow (x_9 vee x_{10})=1)
В ответе не нужно перечислять все различные наборы значений переменных (x_1, x_2, … x_{10}), при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Внешняя операция в отдельно взятом уравнении — это импликация, в результате которой должна быть истина. Импликация истинна, если:
(0 rightarrow 1)
(0 rightarrow 0)
(1 rightarrow 1)
Если скобка ((x_1 wedge x_2)=1) (это верно в таких случаях (x_1=1 , x_2=1)), то для скобки ((x_3 wedge x_4)) возможны только варианты ((x_3=0 , x_4=1; x_3=1 , x_4=0; x_3=0 , x_4=0)), при ((x_3=0 , x_4=0)) ((x_3 vee x_4)=0) импликация становится равна 0.
Если ((x_1 wedge x_2)=0) (это верно в таких случаях (x_1=0 , x_2=1; x_1=1 , x_2=0; x_1=0 , x_2=0)), то для скобки ((x_3 wedge x_4)) возможны любые значения, импликация этих скобок будет истинна. Поскольку уравнения однотипные и отличаются только сдвигом номеров переменных на единицу, то будем использовать метод отображения, применяя его к каждой последующей комбинации (x_{i},x_{i+1}, i in [1; 9]).
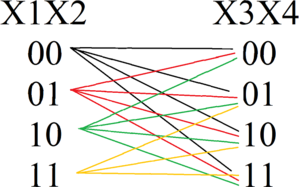
Теперь найдем общее количество решений, подставляя в отображении соответствующие x, учитывая предыдущие значения:
(begin{array}{|c|c|c|c|c|c|}
hline
& x_1 wedge x_2 & x_3 wedge x_4 & x_5 wedge x_6 & x_7 wedge x_8 & x_9 wedge x_{10}\
hline
00 & 1 & 3 & 11 & 41 & 153\
hline
01 & 1 & 4 & 15 & 56 & 209\
hline
10 & 1 & 4 & 15 & 56 & 209\
hline
11& 1 & 4 & 15 & 56 & 209\
hline
end{array})
(begin{array}{|c|c|c|c|c|c|}
hline
& x_1 wedge x_2 & x_3 wedge x_4 & x_5 wedge x_6 & x_7 wedge x_8 & x_9 wedge x_{10}\
hline
00 & 1 & 1+1+1+1 & 3+4+4 & 15+15+11 & 41+56+56\
hline
01 & 1 & 1+1+1+1 & 3+4+4+4 & 15+15+15+11 & 41+56+56+56\
hline
10 & 1 & 1+1+1+1 & 3+4+4+4 & 15+15+15+11 & 41+56+56+56\
hline
11 & 1 & 1+1+1+1 & 3+4+4+4 & 15+15+15+11 & 41+56+56+56\
hline
end{array})
В итоге получаем: (153+209+209+209=780).
Ответ: 780
Сколько существует различных наборов значений логических переменных (x_1, x_2, … x_6, y_1, y_2, … y_6,) которые удовлетворяют всем перечисленным ниже условиям?
((x_1 rightarrow (x_2 wedge y_1)) wedge (y_1 rightarrow y_2) = 1)
((x_2 rightarrow (x_3 wedge y_2)) wedge (y_2 rightarrow y_3) = 1)
…
((x_5 rightarrow (x_6 wedge y_5)) wedge (y_5 rightarrow y_6) = 1)
(x_6 rightarrow y_6 = 1)
В ответе не нужно перечислять все различные наборы значений переменных (x_1, x_2, … x_6, y_1, y_2, … y_6,) при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
(ЕГЭ 2017, Демонстрационная версия)
Поскольку уравнения однотипные и отличаются только сдвигом номеров переменных на единицу, то будем использовать метод отображения, применяя его к каждой последующей комбинации (x_i,y_{i},iin [1;6].)
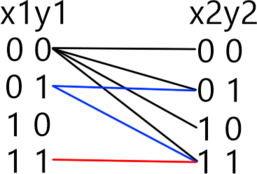
Также надо учитывать последнее уравнение, для которого не подходит только набор 1 0. Теперь найдем общее количество решений, подставляя в отображении соответствующие (x,y,) учитывая предыдущие значения:
[begin{array}{|c|c|c|c|c|c|c|} hline
&x_1y_1&x_2y_2&x_3y_3&x_4y_4&x_5y_5&x_6y_6\
hline
00&1&1&1&1&1&1\
hline
01&1&2&3&4&5&6\
hline
10&1&1&1&1&1&0\
hline
11&1&3&6&10&15&21\
hline
end{array}]
Суммируем и получаем ответ: (1+6+0+21=28.)
Ответ: 28
Сколько существует различных наборов значений логических переменных (x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8, x_9, x_{10},) которые удовлетворяют всем перечисленным ниже условиям:
(((x_1rightarrow x_2)rightarrow(x_3rightarrow x_4)) wedge ((x_3rightarrow x_4)rightarrow(x_5rightarrow x_6))= 1)
(((x_5rightarrow x_6)rightarrow(x_7rightarrow x_8)) wedge ((x_7rightarrow x_8)rightarrow(x_9rightarrow x_{10}))= 1)
(x_1wedge x_3wedge x_5wedge x_7wedge x_9= 1)
В ответе не нужно перечислять все различные наборы значений переменных (x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8, x_9, x_{10},) при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
(ЕГЭ 2017, СтатГрад, 30 сентября 2016)
Чтобы выполнилось последнее уравнение, все (x) с нечётными номерами должны быть равны 1.
Перепишем нашу систему, заменяя такие (x) на 1 и разделяя каждую конъюнкцию на два уравнения:
((x_1rightarrow x_2)rightarrow(x_3rightarrow x_4)= 1)
((x_3rightarrow x_4)rightarrow(x_5rightarrow x_6)= 1)
((x_5rightarrow x_6)rightarrow(x_7rightarrow x_8)= 1)
((x_7rightarrow x_8)rightarrow(x_9rightarrow x_{10})= 1)
Поскольку уравнения однотипные и отличаются только сдвигом номеров переменных на два, то будем использовать метод отображения, применяя его к каждой последующей комбинации (x_i,x_{i+1},iin {2, 4, 6, 8, 10}.)
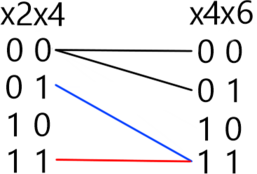
Также можно заметить, что для таких пар при наборе 1 0 уравнения истинны не будут, так как внешняя импликация будет равна 0 . Теперь найдем общее количество решений, подставляя в отображении соответствующие (x,) учитывая предыдущие значения:
[begin{array}{|c|c|c|c|c|} hline
&x_2x_4&x_4x_6&x_6x_8&x_8x_{10}\
hline
00&1&1&1&1\
hline
01&1&1&1&1\
hline
11&1&2&3&4\
hline
end{array}]
Суммируем и получаем ответ: (1+1+4=6.)
Ответ: 6
Сколько существует различных наборов значений логических переменных (x_1, x_2,…, x_{10},) которые удовлетворяют всем перечисленным ниже условиям?
(neg (x_1 equiv x_2) equiv (x_3 equiv x_4) = 1)
(neg (x_3 equiv x_4) equiv (x_5 equiv x_6) = 1)
(neg (x_5 equiv x_6) equiv (x_7 equiv x_8) = 1)
(neg (x_7 equiv x_8) equiv (x_9 equiv x_{10}) = 1)
В ответе не нужно перечислять все различные наборы значений переменных (x_1, x_2,…, x_{10},) при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
(ЕГЭ 2019, Основная волна)
Поскольку уравнения однотипные и отличаются только сдвигом номеров переменных на два, то будем использовать метод отображения, применяя его к каждой последующей комбинации (x_i,x_{i+1},iin {1, 3, 5, 7, 9}.)
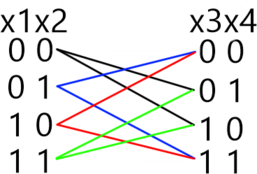
Теперь найдем общее количество решений, подставляя в отображении соответствующие (x,) учитывая предыдущие значения:
[begin{array}{|c|c|c|c|c|c|} hline
&x_1x_2&x_3x_4&x_5x_6&x_7x_8&x_9x_{10}\
hline
00&1&2&4&8&16\
hline
01&1&2&4&8&16\
hline
10&1&2&4&8&16\
hline
11&1&2&4&8&16\
hline
end{array}]
Суммируем и получаем ответ: (16+16+16+16=64.)
Ответ: 64
Сколько существует различных наборов значений логических переменных (x_1, x_2, …, x_8, y_1, y_2, …, y_8,) которые удовлетворяют всем перечисленным ниже условиям?
((x_1wedge y_1)equiv (neg x_2vee neg y_2 ))
((x_2wedge y_2)equiv (neg x_3vee neg y_3 ))
…
((x_7wedge y_7)equiv (neg x_8vee neg y_8 ))
В ответе не нужно перечислять все различные наборы значений переменных (x_1, x_2, …, x_8, y_1, y_2, …, y_8,) при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
(ЕГЭ 2019, Досрочная волна)
Поскольку уравнения однотипные и отличаются только сдвигом номеров переменных на единицу, то будем использовать метод отображения, применяя его к каждой последующей комбинации (x_i,y_{i},iin [1;8].)
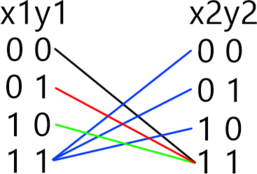
Теперь найдем общее количество решений, подставляя в отображении соответствующие (x,) учитывая предыдущие значения:
[begin{array}{|c|c|c|c|c|c|c|c|c|} hline
&x_1y_1&x_2y_2&x_3y_3&x_4y_4&x_5y_5&x_6y_6&x_7y_7&x_8y_8\
hline
00&1&1&3&3&9&9&27&27\
hline
01&1&1&3&3&9&9&27&27\
hline
10&1&1&3&3&9&9&27&27\
hline
11&1&3&3&9&9&27&27&81\
hline
end{array}]
Суммируем и получаем ответ: (27+27+27+81=162.)
Ответ: 162

УСТАЛ? Просто отдохни
- Пособие
- – Системы логических уравнений
Системы логических уравнений
Задача на подсчет количества решений системы логических уравнений является одним из самых сложных заданий ЕГЭ. Методы решения таких задач лучше изучать на примерах.
Задача: Сколько различных решений имеет система логических уравнений:
( begin{cases}x_1 ∨ x_2 = 1\ x_2 ∨ x_3 = 1\ … \ x_9 ∨ x_{10} = 1 end{cases} )
Решение: В общем случаем, при небольшом количестве переменных в одном уравнении лучше решать следующим методом, который называется методом отображения:
- Составляем таблицы наборов данных для каждого уравнения
- Выявляем связи между таблицами
- Подсчитываем количество наборов в каждой строке каждой таблицы
- Суммируем количество наборов в таблице, соответсвующей последнему уравнению
Составим таблицу для первого уравнения ( x_1 + x_2 = 1 ). Если подходить к составлению таблицы формально, то надо составить таблицу истинности для выражения в уравнении и вычеркнуть из нее все строки, которые не удовлетворяют уравнению:
| ( x_1 ) | ( x_2 ) | ( x_1 + x_2 ) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Первая строка, выделенная красным цветом, не удовлетворяет уравнению, потому что значение выражения ( x_1 + x_2 ) ложно, а по уравнению значение должно быть истинным. Поэтому вычеркиваем ее и составляем таблицу наборов данных первого уравнения:
| № | ( x_1 ) | ( x_2 ) | N |
| 1 | 0 | 1 | 1 |
| 2 | 1 | 0 | 1 |
| 3 | 1 | 1 | 1 |
В эту таблицу добавили столбец с номером строки и столбец с количеством наборов. В таблице для первого уравнения для всех строк это количество равно 1.
Для второго уравнения таблица будет такой же, потому что уравнение подобно первому только с другими переменными. Разместим эти таблицы рядом и выявим связи между строками (отобразим):
| Таблица 1 | Таблица 2 | ||||||
| № | ( x_1 ) | ( x_2 ) | N | ( x_2 ) | ( x_3 ) | N | |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | |
| 2 | 1 | 0 | 1 | 1 | 0 | 2 | |
| 3 | 1 | 1 | 1 | 1 | 1 | 2 |
В таблицах есть общая переменная ( x_2 ), по ней и будем строить связи. Для первой строки таблицы 2 значение ( x_2 ) ложно, что соответствует строке 2 таблицы 1. Проводим красную линию, а в столбец N таблицы 2 ставим значение количества набора данных таблицы 1 из строки 2.
Для второй строки таблицы 2 для переменной ( x_2 ) соответствуют значения строк 1 и 3 таблицы 1. Проводим зеленую линии, а в столбец N таблицы 2 ставим значение суммы количеств наборов данных таблицы 1 из строк 1 и 3.
Для третьей строки таблицы 2 для переменной ( x_2 ) также соответствуют значения строк 1 и 3 таблицы 1. Проводим синие линии, а в столбец N таблицы 2 ставим значение суммы количеств наборов данных таблицы 1 из строк 1 и 3.
Так как все уравнения подобны, то таблицы наборов и связи между ними будут такие же, поэтому все можно свести к одной таблице только со столбцами, соответствующими количеству наборов данных:
| ( x_1x_2 ) | ( x_2x_3 ) | ( x_3x_4 ) | ( x_4x_5 ) | ( x_5x_6 ) | ( x_6x_7 ) | ( x_7x_8 ) | ( x_8x_9 ) | ( x_9x_{10} ) |
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 |
| 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
| 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Столбец 1 содержит значения 1. Для каждого следующего столбца заполняем строки по выработанному алгоритму:
Для каждого следующего столбца для строки 1 берем значение из строки 2 предыдущего столбца. Для строк 2 и 3 – сумму значений из строк 1 и 3.
Суммируем последний столбец, соответствующий последнему уравнению: 34 + 55 + 55 = 144. Ответ: система имеет 144 решения – наборов данных.
Задача: Сколько различных решений имеет система логических уравнений:
( begin{cases}x_1 ∨ x_2 ∧ x_3= 1\ x_2 ∨ x_3 ∧ x_4 = 1\ … \ x_8 ∨ x_9 ∧ x_{10} = 1 end{cases} )
Решение: Составим таблицу наборов данных для первого уравнения ( x_1 + x_2 ⋅ x_3 = 1 ) . Можно это сделать формально как в предыдущем примере, но лучше попробуем заполнить методом рассуждений. Для ( x_1 = 0, x_2 = 0 ) нет решения уравнения, потому что каким бы не было значение переменной ( x_3), результат будет ложным. Для ( x_1 = 0, x_2 = 1 ) переменная ( x_3) должна быть истинна, чтобы результат удовлетворял бы уравнению, поэтому заполняем первую строку :
| ( x_1 ) | ( x_2 ) | ( x_3 ) |
| 0 | 1 | 1 |
Для ( x_1 = 1, x_2 = 0 ) переменная ( x_3) может быть как истинной, так и ложной, поэтому добавляем две строки 1,0,0 и 1,0,1:
| ( x_1 ) | ( x_2 ) | ( x_3 ) |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 0 | 1 |
Для ( x_1 = 1, x_2 = 1 ) переменная ( x_3) также может быть как истинной, так и ложной, поэтому добавляем еще две строки 1,1,0 и 1,1,1:
| ( x_1 ) | ( x_2 ) | ( x_3 ) |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 1 | 1 | 1 |
Для второго уравнения получим таблицу с такими же наборами данных, так как уравнения подобны. Добавим в таблицы столбцы для номера строк, количества наборов и расположим рядом для выявления связей:
| Таблица 1 | Таблица 2 | ||||||||
| № | ( x_1 ) | ( x_2 ) | ( x_3 ) | N | ( x_2 ) | ( x_3 ) | ( x_4 ) | N | |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | |
| 2 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | |
| 3 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | |
| 4 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 2 | |
| 5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 |
Таблицы связаны переменными ( x_2) и ( x_3), поэтому для набора значений ( x_2) и ( x_3) строки таблицы 2 ищем такие же наборы этих переменных в таблице 1. Вычисляем связи:
( N_{2-1} = N_{1-3})
( N_{2-2} = N_{1-4})
( N_{2-3} = N_{1-4})
( N_{2-4} = N_{1-1} + N_{1-5})
( N_{2-5} = N_{1-1} + N_{1-5})
В индексе для ( N) первая цифра – номер таблицы, вторая – номер строки.
Все уравнения подобны, поэтому и наборы данных и связи будут одинаковы. Строим таблицу системы только со столбцами количества набора данных:
| № | ( x_1x_2x_3 ) | ( x_2x_3x_4 ) | ( x_3x_4x_5 ) | ( x_4x_5x_6 ) | ( x_5x_6x_7 ) | ( x_6x_7x_8 ) | ( x_7x_8x_9 ) | ( x_8x_9x_{10} ) |
| 1 | 1 | 1 | 1 | 2 | 3 | 4 | 6 | 9 |
| 2 | 1 | 1 | 2 | 3 | 4 | 6 | 9 | 13 |
| 3 | 1 | 1 | 2 | 3 | 4 | 6 | 9 | 13 |
| 4 | 1 | 2 | 3 | 4 | 6 | 9 | 13 | 19 |
| 5 | 1 | 2 | 3 | 4 | 6 | 9 | 13 | 19 |
Суммируем последний столбец: 9 + 13 + 13 + 19 + 19 = 73. Ответ: 73 решения.
Задача: Сколько существует различных наборов значений логических переменных x1, x2,…, x5, y1, y2, …, y5, которые удовлетворяют всем перечисленным ниже условиям?
( (x_1 ∨ y_1) ≡ ¬(x_2 ∨ y_2) = 1 )
( (x_2 ∨ y_2) ≡ ¬(x_3 ∨ y_3) = 1 )
….
( (x_8 ∨ y_8) ≡ ¬(x_9 ∨ y_9) = 1 )
Решение: Преобразуем первое уравнение ( (x_1 + y_1) ≡ overline{(x_2 + y_2)} = 1 ).
( (x_1 + y_1) ≡ (overline{x_2} ⋅ overline{y_2}) = 1 ).
Заполним таблицу наборов данных этого уравнения методом рассуждений:
Для набора ( x_1 = 0, y_1 = 0 ) первое выражение в скобках будет ложно, поэтому и второе выражение в скобках также должно быть ложно, чтобы условие тождественного равенства этих выражений выполнилось. Второе выражение будет ложно при трех наборах данных: (( x_2 = 0, y_2 = 1 ) ), (( x_2 = 1, y_2 = 0 ) ), (( x_2 = 1, y_2 = 1 ) ). Добавим в таблицу полученные три набора:
| ( x_1 ) | ( y_1 ) | ( x_2 ) | ( y_2 ) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 |
Для набора (x_1 = 0, y_1 = 1 ) первое выражение в скобках будет истинно, поэтому и второе выражение должно быть истинно, что может быть только при ( x_2 = 0, y_2 = 0 ) . Для наборов ((x_1 = 1, y_1 = 0 ) ) и (( x_1 = 1, y_1 = 1 ) ) также будет выполняться условие тождественности только при наборе ( x_2 = 0, y_2 = 0 ). Добавим в таблицу еще три строки:
| ( x_1 ) | ( y_1 ) | ( x_2 ) | ( y_2 ) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 |
Для второго уравнения таблица наборов данных будет с такими же данными, так как уравнения подобны. Расположим таблицы для первого и второго уравнений рядом, добавил столбцы номера строки, количества наборов и выявим связи:
| Таблица 1 | Таблица 2 | ||||||||||
| № | ( x_1 ) | ( y_1 ) | ( x_2 ) | ( y_2 ) | N | ( x_2 ) | ( y_2 ) | ( x_3 ) | ( y_3 ) | N | |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 3 | |
| 2 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 3 | |
| 3 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 3 | |
| 4 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | |
| 5 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | |
| 6 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 |
В таблицах общими являются столбцы ( x_2) и ( y_2), поэтому для строки таблицы 2 ищем в таблице 1 строки с таким же набором ( x_2) и ( y_2). По полученным связям составляем выражения для подсчета количества наборов:
( N_{2-1} = N_{1-4} + N_{1-5} + N_{1-6} )
( N_{2-2} = N_{1-4} + N_{1-5} + N_{1-6} )
( N_{2-3} = N_{1-4} + N_{1-5} + N_{1-6} )
( N_{2-4} = N_{1-1} )
( N_{2-5} = N_{1-2} )
( N_{2-6} = N_{1-3} )
В индексах (N) первое число номер таблицы, а второе – номер строки. Строим таблицу всех уравнений:
| № | ( x_1y_1x_2y_2 ) | ( x_2y_2x_3y_3 ) | ( x_3y_3x_4y_4 ) | ( x_4y_4x_5y_5 ) | ( x_5y_5x_6y_6 ) | ( x_6y_6x_7y_7 ) | ( x_7y_7x_8y_8 ) | ( x_8y_8x_9y_9 ) |
| 1 | 1 | 3 | 3 | 9 | 9 | 27 | 27 | 81 |
| 2 | 1 | 3 | 3 | 9 | 9 | 27 | 27 | 81 |
| 3 | 1 | 3 | 3 | 9 | 9 | 27 | 27 | 81 |
| 4 | 1 | 1 | 3 | 3 | 9 | 9 | 27 | 27 |
| 5 | 1 | 1 | 3 | 3 | 9 | 9 | 27 | 27 |
| 5 | 1 | 1 | 3 | 3 | 9 | 9 | 27 | 27 |
Суммируем последний столбец: 81 + 81 + 81 + 27 + 27 + 27 = 324. Ответ: 324 набора значений.
Решим эту же задачу другим способом, при котором выявляем связи между парами переменных. Строим таблицу отображения следующим образом:
В столбце соответствующему паре переменных ( x_1y_1 ) записываем в строках все возможные наборы этих переменных. Во втором столбце – все возможные наборы данных для пары переменных ( x_2y_2 ). Устанавливаем связи тем же способом, каким мы заполняли таблицу уравнения в первом варианте решения задачи.
| ( x_1y_1 ) | ( x_2y_2 ) | Подсчет |
| 00 | 00 | 01 + 10 + 11 |
| 01 | 01 | 00 |
| 10 | 10 | 00 |
| 11 | 11 | 00 |
Рассматриваем первое уравнение: ( (x_1 + y_1) ≡ (overline{x_2} ⋅ overline{y_2}) = 1 )
Для набора ( x_1 = 0, y_1 = 0 ) первое выражение в скобках будет ложно, поэтому и второе выражение в скобках также должно быть ложно, чтобы условие тождественного равенства этих выражений выполнилось. Второе выражение будет ложно при трех наборах данных: (( x_2 = 0, y_2 = 1 ) ), (( x_2 = 1, y_2 = 0 ) ), (( x_2 = 1, y_2 = 1 ) ). Проводим линии от строки с набором 00 первого столбца к соответствующим строкам наборов второго столбца.
Для набора (x_1 = 0, y_1 = 1 ) первое выражение в скобках будет истинно, поэтому и второе выражение должно быть истинно, что может быть только при ( x_2 = 0, y_2 = 0 ) . Проводим линию от строки 01 первого столбца к строке 00 второго столбца. Для наборов ((x_1 = 1, y_1 = 0 ) ) и (( x_1 = 1, y_1 = 1 ) ) также будет выполняться условие тождественности только при наборе ( x_2 = 0, y_2 = 0 ). Проводим линии соответствующим образом.
В последнем столбце записываем формулу подсчета, в которой показано из каких наборов состоит количество наборов для пары переменных ( x_2y_2 ).
Строим таблицу со столбцами, соответствующим парам переменных всех уравнений. В этих столбцах будем подсчитывать количество наборов для пар:
| ( x_1y_1 ) | ( x_2y_2 ) | ( x_3y_3 ) | ( x_4y_4 ) | ( x_5y_5 ) | ( x_6y_6 ) | ( x_7y_7 ) | ( x_8y_8 ) | ( x_9y_9 ) | |
| 00 | 1 | 3 | 3 | 9 | 9 | 27 | 27 | 81 | 81 |
| 01 | 1 | 1 | 3 | 3 | 9 | 9 | 27 | 27 | 81 |
| 10 | 1 | 1 | 3 | 3 | 9 | 9 | 27 | 27 | 81 |
| 11 | 1 | 1 | 3 | 3 | 9 | 9 | 27 | 27 | 81 |
Заполняем таблицу по полученным формулам. В первом столбце ставим единицы. Во втором столбце в строку 00 записываем сумму значений строк 01, 10, 11 первого столбца. В строку 01 второго столбца – значение строки 00 первого столбца. В строки 10,11 второго столбца также записываем значение строки 00 первого столбца. В третьем столбце для подсчета используем значения строк предыдущего – второго столбца. Аналогичным образом заполняем и остальные столбцы.
Суммируем последний столбец: 81 + 81 + 81 + 81 = 324. Получили тот же ответ.
Задача: Сколько существует различных наборов значений логических переменных x1, x2,…, x5, y1, y2, …, y5, которые удовлетворяют всем перечисленным ниже условиям?
(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) ∧ (x4 → x5) = 1
(y1 → y2) ∧ (y2 →y3) ∧ (y3 → y4) ∧ (y4 → y5) = 1
(¬y1 ∨ x1) ∧ (¬y2 ∨ x2) ∧ (¬y3 ∨ x3) ∧ (¬y4 ∨ x4) ∧ (¬y5 ∨ x5) = 1
Решение: Составим таблицу наборов данных для первого уравнения. Как видно все члены конъюнкции должны быть истинны,чтобы результат был бы истинным, а истинны они могут быть при любом наборе в выражениях в скобках за исключением набора 1 0, то есть для соседних переменных запрещена эта комбинация. Исходя из этого таблица будет выглядеть так:
| x1 | x2 | x3 | x4 | x5 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Для второго уравнения таблица будет содержать такие же наборы данных. Расположим таблицы рядом. Так как в третьем уравнении переменных 10, то возможных наборов для таблицы – 1024. Метод отображения применить проблематично. Поэтому попробуем рассуждать. Если значения из первой строки таблицы первого уравнения подставить в третье уравнение, то можно заметить, что только один набор из второй таблицы позволит выражению третьего уравнения быть истинным, когда все переменные y1..y5 ложны. Записываем для первой строки количество наборов 1:
| x1 | x2 | x3 | x4 | x5 | y1 | y2 | y3 | y4 | y5 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | ||
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | ||
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | ||
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | ||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Если значения из второй строки таблицы первого уравнения подставить в третье уравнение, то необходимо, чтобы ложны были бы y1…y4, а значение y5 может быть как ложно, так и истинно. Таких наборов 2 – первая и вторая строка таблицы 2. Записываем для второй строки количество наборов 2:
| x1 | x2 | x3 | x4 | x5 | y1 | y2 | y3 | y4 | y5 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 2 | |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | ||
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | ||
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | ||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Аналогично рассуждая заметим, что для каждой следующей строки количество наборов из второй таблицы удовлетворяющих уравнению 3 увеличивается на 1. Наконец, для набора из последней строки первой таблицы все наборы из второй таблицы будут удовлетворять уравнению 3:
| x1 | x2 | x3 | x4 | x5 | y1 | y2 | y3 | y4 | y5 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 2 | |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 3 | |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 4 | |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 5 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 6 |
Просуммируем записанные значения количеств наборов для строк: 1 + 2 + 3 + 4 + 5 + 6 = 20. Ответ: 20
Задача: Сколько существует различных наборов значений логических переменных x1, x2,…, x6, y1, y2, …, y6, z1, z2, …, z6, которые удовлетворяют всем перечисленным ниже условиям?
(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) ∧ (x4 → x5) = 1
(y1 → y2) ∧ (y2 →y3) ∧ (y3 → y4) ∧ (y4 → y5) = 1
(z1 → z2) ∧ (z2 → z3) ∧ (z3 → z4) ∧ (z4 → z5) = 1
x5 ∧ y5 ∧ z5 = 0
Решение: Первые три уравнения этой задачи подобны уравнениям предыдущей задачи, поэтому просто скопируем таблицу наборов данных x1…x5:
| x1 | x2 | x3 | x4 | x5 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Для второго и третьего уравнений таблицы будут с такими же наборами данных, мы их не будем повторять. Составим таблицу наборов данных для уравнения 4. Конъюнкция будет ложна, когда ложна хотя бы одна переменная:
| x5 | y5 | z5 | |
| 0 | 0 | 0 | |
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 |
В первой строке таблицы значение x5 ложно. Смотрим в таблице для первого уравнения сколько наборов со значением x5 равным 0 – только одно. Аналогично для значения y5 = 0 находится один набор в таблице второго уравнения, а для z5 = 0 – один набор из таблицы третьего уравнения. Перемножаем найденные количества наборов и получаем количество наборов для первой строки (1 ⋅ 1 ⋅ 1 = 1). Для второй строки количество наборов для x5 и y5 уже известно, а для z5 = 1 из таблицы третьего уравнения находим 5 наборов, перемножаем и получаем 5 наборов для второй строки (1 ⋅ 1 ⋅ 5 = 5). Аналогично заполняем количество для остальных строк:
| x5 | y5 | z5 | |
| 0 | 0 | 0 | 1 ⋅ 1 ⋅ 1 = 1 |
| 0 | 0 | 1 | 1 ⋅ 1 ⋅ 5 = 5 |
| 0 | 1 | 0 | 1 ⋅ 5 ⋅ 1 = 5 |
| 0 | 1 | 1 | 1 ⋅ 5 ⋅ 5 = 25 |
| 1 | 0 | 0 | 5 ⋅ 1 ⋅ 1 = 5 |
| 1 | 0 | 1 | 5 ⋅ 1 ⋅ 5 = 25 |
| 1 | 1 | 0 | 5 ⋅ 5 ⋅ 1 = 25 |
Складываем полученные значения: 1 + 5 + 5 + 25 + 5 + 25 + 25 = 91. Ответ: 91.
