Как найти все стационарные точки функции

Как найти стационарные точки функции

Процесс исследования функции на наличие стационарных точек а также их нахождения является одним из важных элементов при построении графика функции. Найти стационарные точки функции можно, обладая определенным набором математических знаний.

Вам понадобится

• – функция, которую необходимо исследовать на наличие стационарных точек;
• – определение стационарных точек: стационарные точки функции – это точки (значения аргумента), в которых производная функции первого порядка обращается в нуль.

Инструкция

Используя таблицу производных и формулы дифференцирования функций, необходимо найти производную функции. Этот шаг является наиболее сложным и ответственным в ходе выполнения задачи. Если допустить ошибку на данном этапе, дальнейшие вычисления не будут иметь смысла.

Проверьте, зависит ли производная функции от аргумента. Если найденная производная не зависит от аргумента, то есть является числом (к примеру, f'(x) = 5), то в таком случае функция не имеет стационарных точек. Такое решение возможно, только если исследуемая функция является линейной функцией первого порядка (к примеру, f(x) = 5x+1). Если производная функции зависит от аргумента, то приступите к последнему этапу.

Составьте уравнение f'(x)= 0 и решите его. Уравнение может не иметь решений – в таком случае у функции стационарных точек не имеется. Если решения у уравнения есть, то именно эти найденные значения аргумента и будут являться стационарными точками функции. На данном этапе следует провести проверку решения уравнения методом подстановки аргумента.

Обратите внимание

При нахождении производной функции могут возникнуть трудности, если функция является сложной. В таком случае нужно использовать прием замены части функции промежуточным аргументом.

Полезный совет

Для выполнения данной задачи необходимо уделить особое внимание правилам дифференцирования.

Внимание и концентрация на задаче также помогут с ней справиться – перед выполнением задачи убедитесь в том, что вас ничто не будет отвлекать в процессе ее решения.
Знание стационарных точек функции значительно облегчает построение ее графика, так как именно в этих точках находится максимальное и минимальное значения функции.

Источники:

• Производная функции – Википедия
• Критическая точка (математика) – Википедия

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Онлайн калькулятор для определения стационарных точек.
Стационарные точки – это точки, в которых производная функции равна 0 или не существует.

Синтаксис
основных функций:
x^a: x^a
|x|: abs(x)
√x: Sqrt[x]
ⁿ√x: x^(1/n)
a^x: a^x
log^ax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]

sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]

arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]

areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция “И” ∧: &&
дизъюнкция “ИЛИ” ∨: ||
отрицание “НЕ” ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo

1. Стационарные точки функции.
   Необходимое условие локального
   экстремума функции

2. Первое достаточное условие локального
   экстремума

3. Второе и третье достаточные условия
   локального экстремума

4. Наименьшее и наибольшее
   значения функции на сегменте

5. Выпуклые функции и точки перегиба

1. Стационарные точки функции. Необходимое условие локального экстремума функции

_{Определение 1.}
Пусть функция
определена на _{.
Точка
называется стационарной точкой функции
,
если
дифференцирована в точке
и .}

Теорема 1 (необходимое
условие локального экстремума функции).
Пусть функция
определена на
_{и имеет в точке
локальный экстремум. Тогда выполняется
одно из условий:}

1. функция
   _{не имеет в точке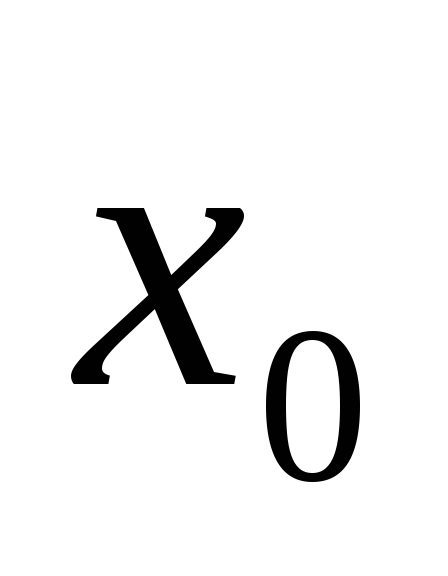
   производной;}

2. функция
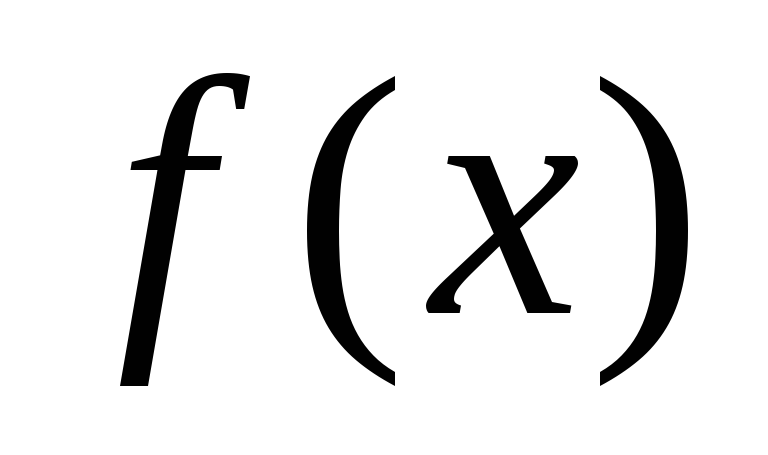
   _{имеет в точке
   производную и .}

_{Таким образом, для того,
чтобы найти точки, которые являются
подозрительными на экстремум, надо
найти стационарные точки функции и
точки, в которых производная функции
не существует, но которые принадлежат
области определения функции.}

_{Пример.
Пусть .
Найти для нее точки, которые являются
подозрительными на экстремум. Для
решения поставленной задачи, в первую
очередь, найдем область определения
функции: .
Найдем теперь производную функции:}

_.

_{Точки, в которых производная
не существует: .
Стационарные точки функции:}

_.

_{Поскольку и ,
и
принадлежат области определения функции,
то они обе будут подозрительными на
экстремум. Но для того, чтобы сделать
вывод, будет ли там действительно
экстремум, надо применять достаточные
условия экстремума.}

2. Первое достаточное условие локального экстремума

Теорема 1 (первое достаточное
условие локального экстремума).
Пусть функция
определена на
_{и дифференцирована на этом интервале
везде за исключением, возможно, точки
,
но в этой точке
функция является
непрерывной. Если
существуют такие правая и левая
полуокрестности точки ,
в каждой из которых
сохраняет определенный знак, то}

_{1) функция
имеет локальный экстремум в точке ,
если
принимает значения разных знаков в
соответствующих полуокрестностях;}

<sub>2) функция
не имеет локальный экстремум в точке
,
если справа и слева от точки

имеет одинаковый знак.</sub>

_{Доказательство.
1) Предположим, что в полуокрестности
производная ,
а в
.}

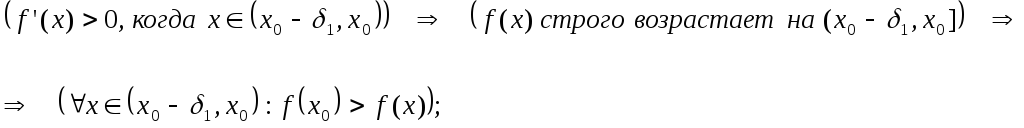
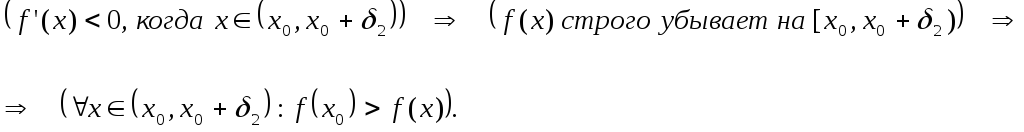
_{Таким образом в точке
функция
имеет локальный экстремум, а именно –
локальный максимум, что и нужно было
доказать.}

_{2) Предположим, что слева
и справа от точки
производная сохраняет свой знак,
например, .
Тогда на
и
функция
строго монотонно возрастает, то есть:}

_,

_.

_{Таким образом экстремума
в точке
функция
не имеет, что и нужно было доказать.}

_{Замечание 1.
Если производная
при прохождении через точку
меняет знак с «+» на «-», то в точке
функция
имеет локальный максимум, а если знак
меняется с «-» на «+», то локальный
минимум.}

_{Замечание 2.
Важным является условие непрерывности
функции
в точке .
Если это условие не выполняется, то
теорема 1 может не иметь места.}

_{Пример.
Рассматривается функция (рис.1):}

Эта функция определена на
<sub>и непрерывна везде, кроме точки ,
где она имеет устранимый разрыв. При
прохождении через точку

меняет знак с «-» на «+», но локального
минимума в этой точке функция не имеет,
а имеет локальный максимум по определению.
Действительно, около точки
можно построить такую окрестность, что
для всех аргументов из этой окрестности
значения функции будут меньше, чем
значение .
Теорема 1 не сработала потому, что в
точке
функция имела разрыв.</sub>

_{Замечание 3.
Первое достаточное условие локального
экстремума не может быть использовано,
когда производная функции
меняет свой знак в каждой левой и каждой
правой полуокрестности точки .}

_{Пример.
Рассматривается функция:}

_{Поскольку ,
то ,
а потому ,
но .
Таким образом:}

_,

_{т.е. в точке
функция
имеет локальный минимум по определению.
Посмотрим, сработает ли здесь первое
достаточное условие локального
экстремума.}

_{Для :}

_.

Для первого слагаемого правой
части полученной формулы имеем:

_,

_{а потому в малой окрестности
точки
знак производной определяется знаком
второго слагаемого, то есть:}

_,

<sub>а это означает, что в любой
окрестности точки

будет принимать как положительные, так
и отрицательные значения. Действительно,
рассмотрим произвольную окрестность
точки :
.
Когда</sub>

_,

_то

_{(рис.2), а
меняет свой знак здесь бесконечно много
раз. Таким образом, нельзя использовать
в приведенном примере первое достаточное
условие локального экстремума.}

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание:

Полная схема исследования функции:

1. Найти область определения функции.
2. Исследовать функцию на чётность и периодичность.
3. Найти точки пересечения графика функции с осями координат.
4. Найти интервалы знакопостоянства.
5. Найти первую производную, промежутки возрастания и убывания, точки экстремума и экстремумы функции.
6. Найти вторую производную. Определить интервалы выпуклости графика функции и точки перегиба.
7. Исследовать поведение функции на концах промежутков определения.
8. Найти асимптоты графика функции.
9. Построить график функции.

Пример:

Исследуйте функцию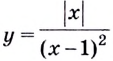

Решение:

1)    Область определения функции: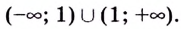 

2)    Функция ни чётная, ни нечётная, ни периодическая.

3) 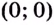    — точка пересечения графика функции с осями координат.

4)    

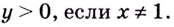
5)    Чтобы найти производную функции, запишем её в виде

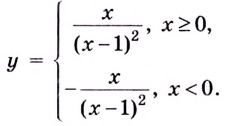
Поскольку в точке 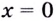 функция производной не имеет, то найдем производную отдельно для  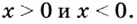Имеем:

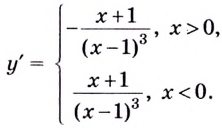
Функция имеет две критические точки:

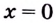 (производная не существует) и  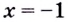(производная равна нулю).

Составим и заполним таблицу для первой производной

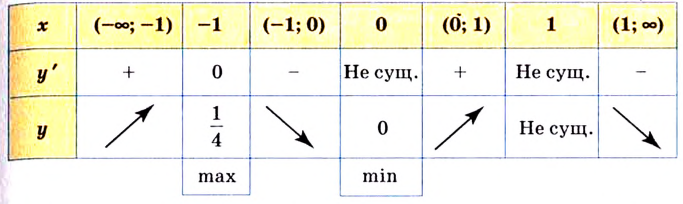
Из таблицы видно, что функция возрастает на промежутках 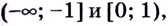 а убывает на промежутках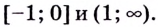 

Первая производная при переходе через точку  меняет знаке 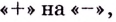 а при переходе через точку 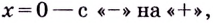поэтому  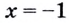— точка максимума, а  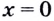— точка минимума.

6) Найдём вторую производную:

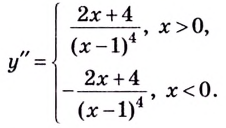
Функция имеет две критические точки второго рода: 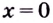 (вторая производная не существует) и  (вторая производная равна нулю).

Составим и заполним таблицу для второй производной

Как видим из таблицы, кривая выпуклая на промежутке 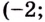 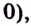а вогнутая на промежутках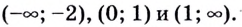 

Вторая производная при переходе через точку 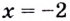 меняет знак 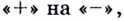а при переходе через точку  на 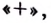 поэтому  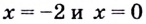— точки перегиба. В этих точках на графике выпуклость меняется на вогнутость и наоборот.

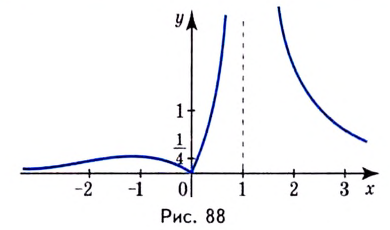
7) Исследуем поведение заданной функции на концах промежутков определения:

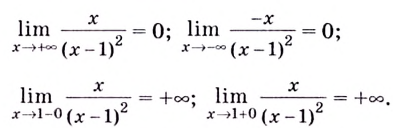
8) Найдём асимптоты. Функция не определена в точке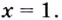 

Поскольку 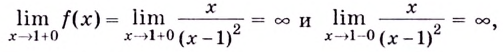 то 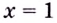 вертикальная асимптота.

Поскольку 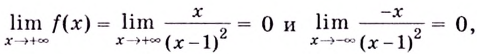 то  горизонтальная асимптота.

9) Используя полученные данные, построим график функции {рис. 88).

Пример:

Найдите интервалы выпуклости, вогнутости и точки перегиба кривых: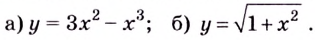 

Решение:

 

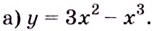
1)    Область определения функции —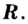 

2)    Найдём первую и вторую производные. Имеем: 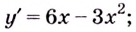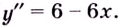Найдём критические точки второго рода: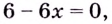 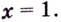 Других критических точек второго рода нет.

3)    Определим знак второй производной на каждом из интервалов 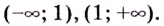 Для этого достаточно определить знак производной в произвольной внутренней точке каждого интервала.

Если 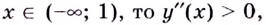 поэтому на интервале  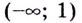кривая вогнутая.

Если 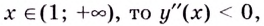 поэтому на интервале  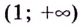кривая выпуклая.

Точка  является точкой перегиба, поскольку при переходе через эту точку вторая производная меняет знак.

Следовательно, 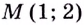 — точка перегиба.

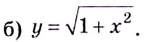
1) Область определения функции—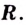 

2) Найдём критические точки второго рода: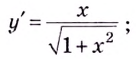 

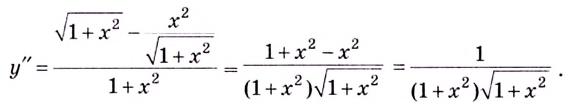
Как видим, вторая производная существует на множестве всех действительных чисел и ни в одной точке в ноль не превращается. А потому критических точек второго рода нет. Следовательно, нет и точек перегиба. На всей области определения 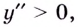 поэтому на множестве действительных чисел кривая вогнутая.

Пример:

Найдите асимптоты кривой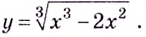 

Решение:

Область определения функции — 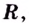 поэтому вертикальных асимптот нет.

Найдем наклонную асимптоту: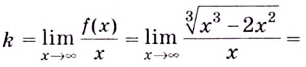 

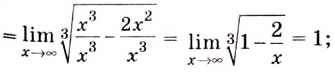
Следовательно, прямая 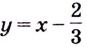 наклонная асимптота данной кривой. Других асимптот кривая не имеет.

Исследование функций

Процесс управления требует от менеджера компактного представления разносторонних знаний из разных областей хозяйственной, управленческой, налоговой, коммерческой и других видов деятельности в виде разнообразных функциональных зависимостей.

В процессе такой деятельности перед менеджером возникают задачи тактического и стратегического планирования, оценки возможностей предприятия и конкурентов, оптимального распределения ресурсов, разумного реагирования на налоговую политику, выбора ценовой и инвестиционной политики и др.

Важную роль при этом играет исследование функций, используемых при построении математической модели рассматриваемой проблемы. Такое исследование проводится с учетом свойств конкретных функций и позволяет уточнить сформулированную математическую задачу, решая которую (с учетом выбранного метода решения), рассчитывают получить определенный результат, требующий в дальнейшем интерпретации в терминах исследуемой проблемы.

Все это связано с выявлением таких свойств функций, используемых в модели, как характер изменения (монотонность), наличие точек с особыми свойствами (стационарные точки, экстремумы), геометрические свойства (выпуклость графика функции) и другие.

Настоящий раздел посвящен исследованию функций методами дифференциального исчисления и использованию полученных навыков для решения задач.

Монотонность функции

Функция y = y (x) называется возрастающей на промежутке l, если 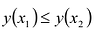для любых точек 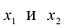, из промежутка l, удовлетворяющих неравенству 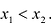,. Функция называется убывающей на l, если из условия 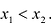следует .

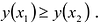Теорема. Если функция у = f(x) непрерывна на отрезке [a,b], дифференцируема на интервале (a,b), то для того, чтобы f(x) была возрастающей (убывающей) необходимо и достаточно, чтобы 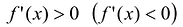в каждой внутренней точке интервала (a,b).

Дифференцируемая функция является возрастающей на промежутке l тогда и только тогда, когда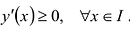

Пример:

Найти промежутки возрастания и убывания функции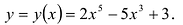

Вычислим: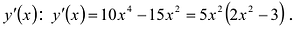

Точки 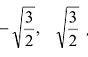делят числовую прямую R натри интервала: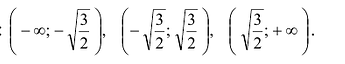

Производная 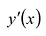положительна на интервалах 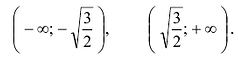. Следовательно, функция y(x) возрастает на каждом из этих интервалов. На интервале 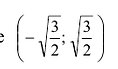производная 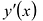неположительна, значит, у(х) убывает на этом интервале.

Локальный экстремум

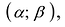Точка называется точкой локального максимума функции у = у{х) если существует интервал , содержащий точку такой что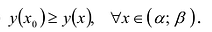

Точка называется точкой локального минимума функции 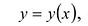если существует интервал 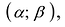содержащий точку такой что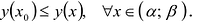

Точки локального минимума и локального максимума называются точками локального экстремума.

Необходимым условием локального экстремума дифференцируемой функции является выполнение равенства 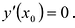. Поэтому точки, в которых дифференцируемая функция может иметь локальный экстремум, находят, решая уравнение: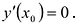

Решения этого уравнения называют стационарными точками.

Исследование стационарных точек

I правило. Если при возрастании .v при переходе через стационарную точку х0 производная у'(х) меняет знак с + на – , то – точка локального максимума. Если 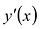меняет знак с – на + , то – точка локального минимума функции f(x). Если 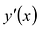не меняет знак в точке , то экстремума нет.

II правило. Если вторая производная 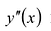в стационарной точке положительная, то – точка локального минимума функции Если вторая производная 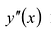в стационарной точке отрицательная, то – точка локального максимума функции y(x).

Точками локального экстремума функции могут быть такие точки, в которых производная не существует или обращается в бесконечность. Исследовать такие точки можно по I правилу. Экстремум в такой точке называется острым экстремумом.

Пример:

Найти экстремум функции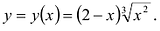

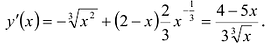
Функция имеет стационарную точку 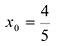(в этой точке производная равна нулю). В точке 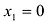производная обращается в бесконечность.

Поскольку 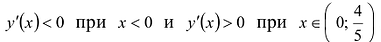то функция имеет в точке 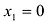локальный минимум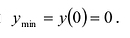

Это будет острый минимум.

При переходе через стационарную точку 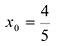производная меняет знак с – на +, значит, функция имеет локальный максимум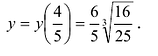

Глобальный экстремум

Непрерывная на отрезке [a;b] функция у = y(x) принимает свое наибольшее значение 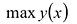и свое наименьшее значение min y(x) в точках этого отрезка. Эти значения могут достигаться либо в стационарных точках отрезка, либо в точках недифференцируемости функции, либо в граничных точках отрезка. Поэтому для нахождения значений 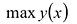и min y(x) поступают следующим образом.

• Находят стационарные точки 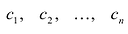функции;
• Находят точки 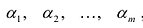в которых производная у'(x) не существует или обращается в бесконечность;
• Вычисляют значения: 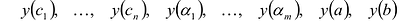– и выбирают среди этих чисел наибольшее и наименьшее.

Это и будут 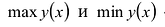– глобальные экстремальные значения.

Пример:

Найти наибольшее и наименьшее значения функции 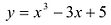на отрезке [ – 2; 2 ].

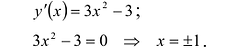
Вычисляем 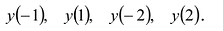Получаем числа 7, 3, 3, -7. Следовательно,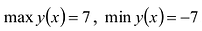

Выпуклость и перегибы графика функции

Графиком функции у = у(х), заданной на множестве X, называют множество точек плоскости с координатами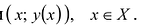. График называют выпуклым вниз на промежутке I, если касательная к графику в любой точке этого промежутка расположена ниже графика. Если касательная расположена выше графика, то график называют выпуклым вверх. Точка, в которой график меняет направление выпуклости, называется точкой перегиба.

Если на промежутке l вторая производная у'(х) положительна, то график является выпуклым вниз на этом промежутке. Если .у “(x) < 0 на промежутке l, то график является выпуклым вверх на промежутке l.

Точка М(с;у{с)) может быть точкой перегиба только в том случае, когда у'(x) = 0, либо у”(x) не существует – необходимое условие перегиба. Однако равенство нулю или не существование второй производной в точке с не означает еще, что в точке 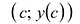будет перегиб графика. Поэтому нужно дополнительно исследовать такие точки.

Пример:

Найти промежутки выпуклости и точки перегиба графика функции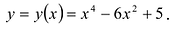

Вычислим вторую производную .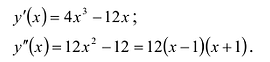

Точки -1 и 1 разбивают числовую прямую на три промежутка: 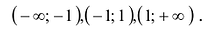. На промежутках 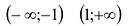вторая производная положительна, на промежутке (-l;l) – отрицательна. Следовательно, график функции является выпуклым вниз на 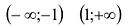и выпуклым вверх на (-l;l).

В точках 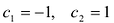вторая производная равна нулю. Вычислим 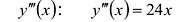. Поскольку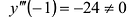 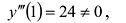, то в точке 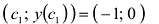и в точке 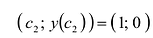график функции имеет перегиб.

Исследование функции и построение графика

График функции у = у(х)у заданной на множестве X, т.е. множество точек плоскости с координатами 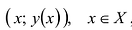обычно строят с некоторой степенью приближения, так как точное построение невозможно.

Для построения графика функции у = у{х) выясняют особенности поведения функции. Существенную роль при этом играют характерные точки: концевые точки промежутков задания функции, точки разрыва, стационарные точки и точки недифференцируемости функции и се производной и т.д. По этим точкам выделяются участки однообразного поведения функции, а именно: промежутки ее непрерывности; промежутки, на которых у'(х) и y”(x) сохраняют знак, что позволяет изучить характер монотонности функции и направление ее выпуклости.

Построение графика функции может быть осуществлено по следующему плану.

Если функция задана аналитическими выражениями, то выясняют естественную область определения функции, т.е. множество значений аргумента х, при которых y(x) имеет смысл.

Если функция периодическая, то находят ее период, т.е. число 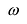такое, что 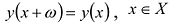(обычно рассматривают наименьший положительный период). Дальнейшее изучение функции и построение графика проводят для какого-либо отрезка длины 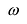, например, для [0;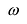], а затем периодически продолжают.

Для четной функции: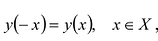, или нечетной: 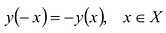. Исследование проводят на промежутке 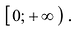Построенный график продолжают на все множество X.

Используя симметричное отражение относительно оси Oy для четной функции и относительно точки О – для нечетной функции.

Находят точки разрыва и промежутки, на которых она непрерывна. Выясняют характер точек разрыва. Вычисляют предельные значения функции в граничных точках множества X (если таковые имеются). Находят вертикальные асимптоты (в точках бесконечного скачка). Если X ограничено, то вычисляют пределы функции при 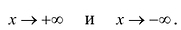. Если 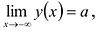, то график имеет горизонтальную левостороннюю асимптоту у = а, если 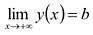, график имеет горизонтальную правостороннюю асимптоту у = b. Если пределы (или один из пределов) бесконечны, то график может иметь наклонные (левостороннюю и правостороннюю) асимптоты у = кх + b. Коэффициенты левосторонней асимптоты можно найти по формулам:

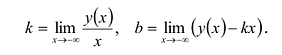
Аналогично находят коэффициенты правосторонней асимптоты (нужно вычислить пределы при ).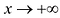

Вычисляют производную 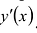. Находят критические точки функции у(х)у т.е. стационарные точки и точки, в которых y(x) не существует. Выделяют промежутки, на которых y”(x) сохраняет знак. Это позволяет исследовать монотонность функции y(x).

Вычисляют вторую производную . Находят критические точки производной 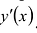Выделяют промежутки, на которых y”(x) сохраняет знак, и, следовательно, график функции y(x) сохраняет направление выпуклости. Находят точки перегиба, исследуя критические точки производной /(а) (т.е. точки, в которых у”(х) равны нулю или не существуют).

Исследуя стационарные точки функции у(х), находят точки локального экстремума и локальные экстремальные значения функции. Для этого можно изучить поведение производной 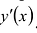в окрестности стационарной точки или значение y”(x) в стационарной точке. Изучают точки недифференцируемости функции, выясняя наличие локальных экстремумов в таких точках по поведению производной 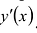в их окрестностях.

Опираясь на характерные точки функции, строят таблицу, в которую вносят все особенности функции.

На координатную плоскость в выбранном масштабе наносят характерные точки функции, асимптоты и строят график, руководствуясь п. 1-6. Если нужно, строят дополнительно несколько точек графика

Пример:

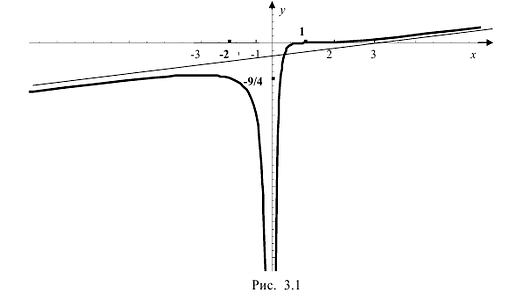
Построить график функции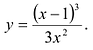

I. Область определения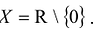

Функция не является периодической, четной, нечетной.

II. Поскольку 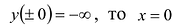– точка разрыва (точка бесконечного скачка). Прямая х = 0 является двусторонней вертикальной асимптотой.

Так как 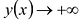при , 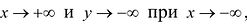то возможно существование наклонных асимптот (негоризонтальных). Учитывая, что 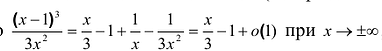делаем вывод, что прямая 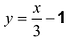является двусторонней наклонной асимптотой.

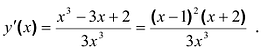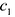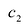3. Из уравнения у'(х)=0 находим стационарные точки: =-2, = 1.

IV. 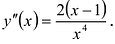Точка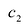=1 является стационарной точкой для производной у'(х), так как у”(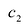) = 0.

V. Строим таблицу, в которой выделены промежутки однообразного поведения функции и ее характерные точки.

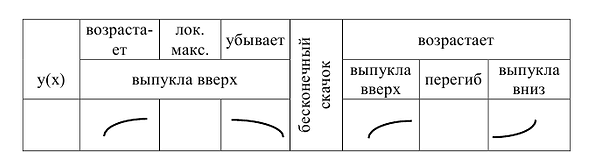
VI. На координатной плоскости отмечаем точки локального максимума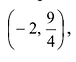 перегиба (1,0), асимптоты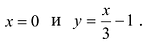

Строим схематично график функции с учетом выясненных ранее особенностей ее поведения.

Интерполяция и аппроксимация функций

При табличной форме задания функции часто возникает ситуация, когда аргумент функции задан с большей точностью, чем позволяет таблица. В этом случае приходится прибегнуть к интерполяции (или интерполированию) – приближенному нахождению неизвестных значений функций по известным ее значениям в заданных точках.

Наиболее простым является линейное интерполирование, при котором допускается, что приращение функции пропорционально приращению аргумента. Если заданное значение д: лежит между приведенными в таблице значениями 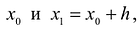которым соответствуют значения функци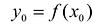и и 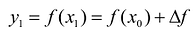то считают, что: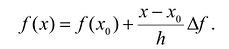

Если по заданным значениям функции необходимо найти приближенное значение аргумента, то такая операция называется обратным интерполированием.

В общем виде интерполяционная задача состоит в построении обобщенного многочлена Р(х), принимающего значения исследуемой функции у = f(x) на конечном множестве 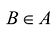(область задания функции). Указанный многочлен должен удовлетворять условиям 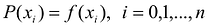. Точки х называются узлами интерполирования.

В частности, если A = [a,b] а множество 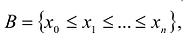, искомый многочлен имеет линейную структуру и может быть представлен в ви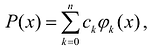де , где 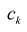– коэффициенты разложения, 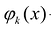— линейно независимые на 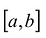функции.

Условия интерполирования 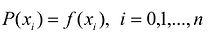можно представить в виде системы уравнений:

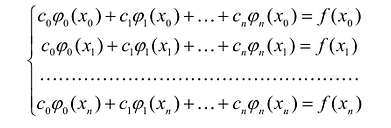
К системе можно применить векторно-матричную форму записи 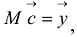если ввести обозначения:

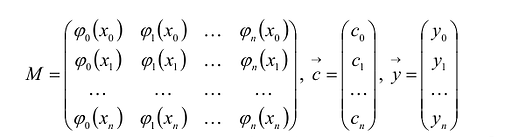
Если семейство функций 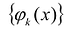составляет базис на [a,b], то условия интерполирования 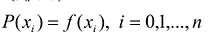однозначно удовлетворяются с помощью выбора коэффициентов. Если число узлов интерполирования не соответствует размерности базиса, то решение задачи интерполирования неоднозначно. Возникающую при этом неопределенность можно устранить путем введения дополнительных условий, налагаемых на значения коэффициентов. В частности, в узлах интерполяции можно задать не только значения функции, но и значения ее производной. В противном случае, задача интерполирования не имеет решения в общем виде, т.к. система условий может оказаться несовместной. В этом случае задача интерполирования заменяется задачей общей аппроксимации, которая заключается в построении многочлена низшей степени, наименее отклоняющегося от заданной функции.

• Заказать решение задач по высшей математике

Интерполяционный полином Лагранжа

Примером наипростейшей базисной системы функций можно считать систему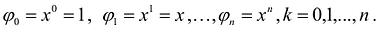

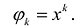
Утверждение 1. Если два многочлена степени 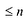принимают одинаковые значения при n +1 различных значениях переменной, то эти многочлены равны.

Пусть многочлены P(x) и Q(x) степени n, 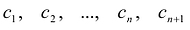– такие попарно различные числа, что 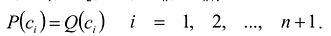. Рассмотрим многочлен

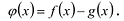Очевидно, что степень 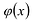не превосходит я, либо 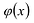– нулевой многочлен, причем 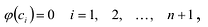т.е. многочлен 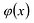имеет n + 1 различных корней, что невозможно. Следовательно,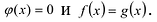

Это утверждение позволяет доказать следующую теорему.

Теорема. Для каждого натурального числа n существует один и только один многочлен степени 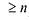, который принимает любые наперед заданные значения при n +1 значениях неизвестной.

Пусть 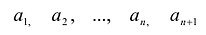– различные числа 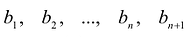– произвольные числа. Построим многочлен P (x)степени 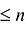такой, что 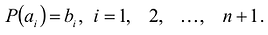. По утверждению 1, он определен однозначно:

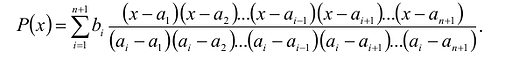
Степень и, очевидно, 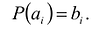Многочлен (1) называется интерполяционным многочленом Лагранжа.

Пример. Построить интерполяционный многочлен Лагранжа по заданной таблице значений: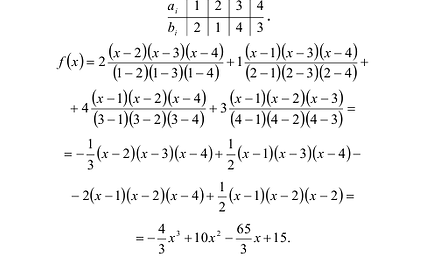

Формула Тейлора

Задача аппроксимации (приближенного вычисления) функции в окрестности данной точки, которую часто называют рабочей точкой, является одной из основных задач математического анализа. Для дифференцируемых функций эта задача решается с помощью формулы Тейлора.

Поскольку функция дифференцируема, то ее приращение представимо в виде:

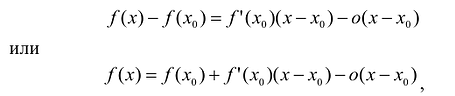
т.е. существует многочлен первой степени 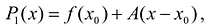такой, что при 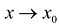выполняются условия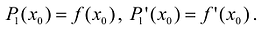

В более общем виде задачу можно сформулировать следующим образом. Пусть функция определена в некоторой окрестности точки 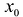и имеет в этой точке n производных f'(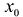), 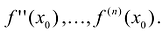Необходимо найти многочлен 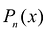степени не выше n, такой, что: 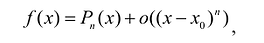где 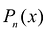удовлетворяет условиям:

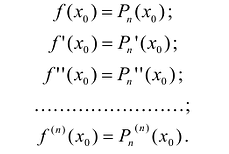
Предположим, что искомый аппроксимационный многочлен имеет вид: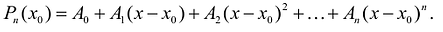

Тогда:

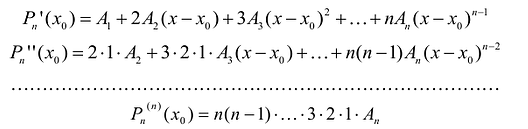
Тогда, с учетом условий (5), можно получить:

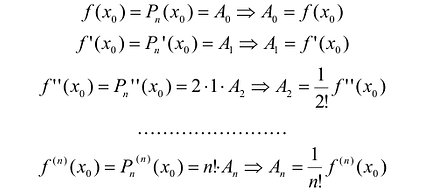
Таким образом, если в аппроксимационый полином подставить полученные значения коэффициентов, то полином можно записать следующим образом:

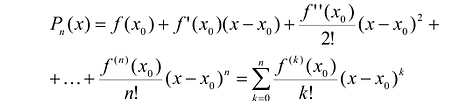
Этот многочлен называется многочленом Тейлора функции f. Можно показать, что он удовлетворяет условию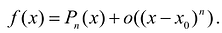

Рассмотрим функцию 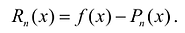Эта функция представляет собой погрешность при замене функции f многочленом 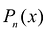в окрестности точки 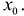. Из приведенных выше условий следует, что: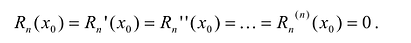

Для того, чтобы убедиться, что 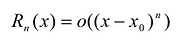ПРИ 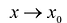необходимо показать, что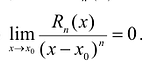. Для раскрытия этой неопределенности нужно применить n раз правило Лопиталя:

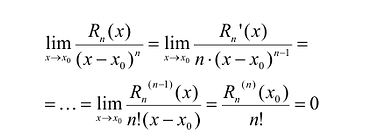
Полученные выводы можно сформулировать в виде теоремы.

Теорема. Пусть функция f определена в некоторой окрестности точки 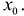и n раз дифференцируема в ней. Тогда, при 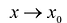имеет место формула:

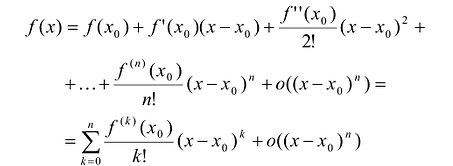
Полученный многочлен называется формулой Тейлора n -го порядка с остаточным членом в форме Пеано.

Если 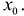= 0, то формула Тейлора называется формулой Маклорена и имеет вид:

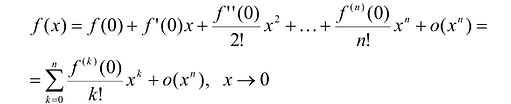
Для остаточного члена формулы Тейлора существуют и другие представления. Так, если функция f имеет производную n-го порядка в окрестности точки 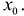, то остаточный член может быть представлен в форме Лагранжа:

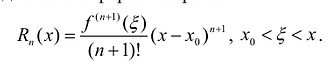
Основные разложения

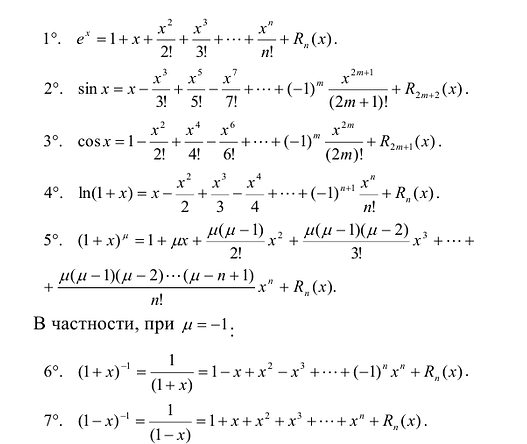
Используя основные разложения можно получать формулы Тейлора для других функций. При этом используют то, что:

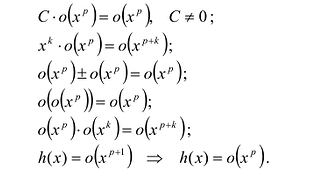
Понятие об эмпирических формулах

На практике часто возникает задача аппроксимации данных о зависимости между двумя переменными у их, полученных опытным путем и представленных в табличной форме. Это могут быть результаты опыта, наблюдений, статистической обработки результатов и т.д. При этом необходимо зависимость между этими переменными представить в виде аналитического выражения функции у = f(x) так, чтобы эта формула наилучшим образом отражала общую тенденцию зависимости у от fx, исключив при этом случайные отклонения, связанные с неизбежными погрешностями измерений или статистических наблюдений.

Формулы, служащие для аналитического представления опытных данных, называются эмпирическими. Задача нахождения эмпирических формул выполняется в два этапа:

• Установление вида зависимости у = f(x);
• Определение неизвестных параметров этой функции.

При определении вида эмпирической функции у-f{x)

обычно предполагается, что это наиболее гладкая кривая, согласованная с экспериментальными данными. Кроме того, для выбора этой функции привлекаются дополнительные соображения, как правило, не математического характера (теоретические модели, опыт предшествующих исследований, и т.п.).

Эта задача может быть решена в ходе регрессионного анализа, который изучается в курсе теории вероятностей, но решить ее можно и математическими методами. Согласно наиболее распространенному и теоретически обоснованному методу наименьших квадратов, в качестве неизвестных параметров функции у = f (х) выбираются такие значения, которые соответствуют минимальному значению суммы квадратов отклонений эмпирических значений у. от значений функции 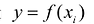вычисленных по соответствующим им значениям аргументов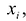, т.е.:

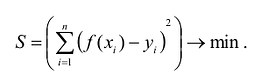
Разность 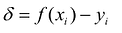называется невязкой. В качестве критерия согласия или величины отклонения можно было взять обычную сумму невязок или их абсолютных величин, но делать это нецелесообразно, поскольку в первом случае сумма невязок может быть малой или, даже, равняться нулю при значительном разбросе экспериментальных данных из-за того, что положительные отклонения будут скомпенсированы отрицательными. Сумма абсолютных величин невязок лишена этого недостатка, но она имеет другой – она не является дифференцируемой, что существенно затрудняет решение задачи.

В ходе решения задачи отыскания оптимальных параметров аппроксимационной функции y = f(x) возникает необходимость поиска экстремума функции нескольких переменных, поэтому, прежде чем решать эту задачу для конкретных эмпирический функций, необходимо рассмотреть свойства функций нескольких переменных.