Подсчёт точек на эллиптических кривых — группа методов, которые позволяют эффективно вычислять точки на эллиптических кривых. Подсчёт точек на эллиптических кривых используется при изучении теории чисел, криптографии[1][2] и создании цифровых подписей (см. Эллиптическая криптография и ECDSA). Уровень безопасности криптосистемы, построенной на эллиптической кривой 


Подходы к подсчёту точек на эллиптических кривых[править | править код]
Основными подходами являются простейший метод подсчёта точек на эллиптических кривых, алгоритм больших и малых шагов, подход, предложенный Рене Шуфом[en], и улучшения алгоритма Шуфа, предложенные Н. Элкисом и А. О. Л. Аткином[en].
Некоторые алгоритмы используют тот факт, что к группам вида 


Простейший подход[править | править код]
Простейший подход к подсчёту точек предполагает перебор всех элементов поля 
Пример[править | править код]
Пусть E будет кривой y2 = x3 + x + 1 над полем 
таблица из возможных значений x, квадратичных вычетов x mod 5 (только для поиска), x3 + x + 1 mod 5 и y (по x2 и x3 + x + 1 mod 5).

|

|

|

|
Points |
|---|---|---|---|---|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Последняя строка вычисляется следующим образом: в уравнение 




Таким образом, 
Вычислительная сложность алгоритма O(q), поскольку должны быть рассмотрены все значения 
Алгоритм больших и маленьких шагов[править | править код]
Снижение вычислительной сложности алгоритма было получено путём применения другого подхода: перебором случайных значений 





Теорема Хассе гласит, что 








Перебор всех значений 


Однако, применяя алгоритм больших и маленьких шагов к 
![{displaystyle 4{sqrt[{4}]{q}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/495c5b6948d76fd8c8445effd8bb9b9e20f64262)
Алгоритм[править | править код]
1. chooseinteger,
2. FOR{
to
} DO 3.
4. ENDFOR 5.
6.
7. REPEAT compute the points
8. UNTIL
:
\the
-coordinates are compared 9.
\note
10. Factor
. Let
be the distinct prime factors of
. 11. WHILE
DO 12. IF
13. THEN
14. ELSE
15. ENDIF 16. ENDWHILE 17.
\note
is the order of the point
18. WHILE
divides more than one integer
in
19. DO choose a new point
and go to 1. 20. ENDWHILE 21. RETURN
\it is the cardinality of

Пояснения к алгоритму[править | править код]
- в пункте 8. допускается существование такого совпадения. Следующая лемма гарантирует, что такое совпадение существует:
-
- Пусть
— целое,
. Существуют
и
такие, что
- Пусть
- Как только было подсчитано
, для вычисления
достаточно прибавить
к
вместо того, чтобы производить суммирование по всем
элементам. Таким образом, полный цикл вычислений требует
сложений.
может быть получено удвоением
. Вычисление
требует
удвоений и
сложений, где
число ненулевых элементов в бинарном представлении
; следует отметить, что знание
и
позволяет уменьшить число операций удвоения. Наконец, чтобы из
получить
, нужно просто прибавить
вместо того, чтобы производить суммирование с начала.
- Предполагается, что можно факторизовать
[3]. Если нет, то по крайней мере можно найти все маленькие простые факторы
и проверить, что для них
. Так,
является хорошим кандидатом в порядок
.
- Заключение шага 17 может быть доказано с использованием элементарной теории групп: поскольку
, порядок
делится на
без остатка. Если нет подходящего делителя
числа
, для которого
, то
— порядок
.
Одним из недостатков этого метода является то, что он требует много памяти, когда группа становится большой. В случае больших групп может быть эффективнее хранить только координаты 




Существуют и другие алгоритмы вычисления порядка элемента группы, которые будут требовать меньше памяти, такие как ро-алгоритм Полларда и алгоритм «кенгуру» Полларда. Алгоритм «кенгуру» Полларда позволяет найти решение в предписанном интервале, снижая число шагов до ![{displaystyle O({sqrt[{4}]{q}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4182beb722873e136c8cdbed3199b0a53d1c3271)

Алгоритм Шуфа[править | править код]
Теоретический прорыв в области вычисления порядка групп типа 
Шуф использует тот факт, что согласно теореме Хассе существует конечное число возможных значений 








Временная сложность алгоритма Шуфа 



Алгоритм Шуфа — Элкиса — Аткина[править | править код]
В 1990-х годах Ноам Элкис, а затем Артур Аткин[en] придумали улучшения базового алгоритма Шуфа путём разделения множества рассматриваемых простых чисел 




Вид простого 











Для эффективной имплементации алгоритма Шуфа — Элкиса — Аткина используются вероятностные алгоритмы поиска корней, что делает алгоритм алгоритмом Лас-Вегаса, а не детерминированным алгоритмом. Вычислительная сложность алгоритма определяется стоимостью вычислений модулярных полиномов 





См. также[править | править код]
- Алгоритм Шуфа
- Эллиптическая криптография
- Алгоритм Гельфонда-Шенкса
- Криптосистема с открытым ключом
- Алгоритм Шуфа — Элкиса — Аткина[en]
- Ро-алгоритм Полларда
- Алгоритм «кенгуру» Полларда
Примечания[править | править код]
- ↑ Jeffrey Hoffstein, Jill Pipher, Joseph H. Silverman. An introduction to mathematical cryptography. — Springer, 2008. — 524 с. — (Undergraduate Texts in Mathematics). — ISBN 9780387779942.
- ↑ Чалкин Т. А. Жданов О. Н. Применение эллиптических кривых в криптографии.
- ↑ Ишмухаметов Ш. Т. Методы факторизации натуральных чисел.
- ↑ Counting Points on Elliptic Curves over Finite Fields. J. Theor. Nombres Bordeaux 7:219-254, 1995, С. 15. Архивировано 27 января 2021 года. Дата обращения: 11 декабря 2019.
- ↑ «Remarks on the Schoof-Elkies-Atkin algorithm». Дата обращения: 20 декабря 2019. Архивировано 1 декабря 2008 года.
Литература[править | править код]
- I. Blake, G. Seroussi, and N. Smart: Elliptic Curves in Cryptography, Cambridge University Press, 1999.
- A. Enge: Elliptic Curves and their Applications to Cryptography: An Introduction. Kluwer Academic Publishers, Dordrecht, 1999.
- G. Musiker: Schoof’s Algorithm for Counting Points on
. Available at http://www.math.umn.edu/~musiker/schoof.pdf
- R. Schoof: Counting Points on Elliptic Curves over Finite Fields. J. Theor. Nombres Bordeaux 7:219-254, 1995. Available at http://www.mat.uniroma2.it/~schoof/ctg.pdf
- L. C. Washington: Elliptic Curves: Number Theory and Cryptography. Chapman & Hall/CRC, New York, 2003.
From Wikipedia, the free encyclopedia
An important aspect in the study of elliptic curves is devising effective ways of counting points on the curve. There have been several approaches to do so, and the algorithms devised have proved to be useful tools in the study of various fields such as number theory, and more recently in cryptography and Digital Signature Authentication (See elliptic curve cryptography and elliptic curve DSA). While in number theory they have important consequences in the solving of Diophantine equations, with respect to cryptography, they enable us to make effective use of the difficulty of the discrete logarithm problem (DLP) for the group 

Approaches to counting points on elliptic curves[edit]
There are several approaches to the problem. Beginning with the naive approach, we trace the developments up to Schoof’s definitive work on the subject, while also listing the improvements to Schoof’s algorithm made by Elkies (1990) and Atkin (1992).
Several algorithms make use of the fact that groups of the form 


Naive approach[edit]
The naive approach to counting points, which is the least sophisticated, involves running through all the elements of the field 
Example[edit]
Let E be the curve y2 = x3 + x + 1 over 
list of the possible values of x, then of the quadratic residues of x mod 5 (for lookup purpose only), then of x3 + x + 1 mod 5, then of y of x3 + x + 1 mod 5. This yields the points on E.

|

|

|

|
Points |
|---|---|---|---|---|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
E.g. the last row is computed as follows: If you insert 



Therefore, 
This algorithm requires running time O(q), because all the values of 
Baby-step giant-step[edit]
An improvement in running time is obtained using a different approach: we pick an element 




Hasse’s theorem tells us that 








Trying all values of 


However, by applying the baby-step giant-step algorithm to 
![4{sqrt[ {4}]{q}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/495c5b6948d76fd8c8445effd8bb9b9e20f64262)
The algorithm[edit]
1. chooseinteger,
2. FOR{
to
} DO 3.
4. ENDFOR 5.
6.
7. REPEAT compute the points
8. UNTIL
:
\the
-coordinates are compared 9.
\note
10. Factor
. Let
be the distinct prime factors of
. 11. WHILE
DO 12. IF
13. THEN
14. ELSE
15. ENDIF 16. ENDWHILE 17.
\note
is the order of the point
18. WHILE
divides more than one integer
in
19. DO choose a new point
and go to 1. 20. ENDWHILE 21. RETURN
\it is the cardinality of

Notes to the algorithm[edit]
- In line 8. we assume the existence of a match. Indeed, the following lemma assures that such a match exists:
-
- Let
be an integer with
. There exist integers
and
with
- Let
One drawback of this method is that there is a need for too much memory when the group becomes large. In order to address this, it might be more efficient to store only the 




There are other generic algorithms for computing the order of a group element that are more space efficient, such as Pollard’s rho algorithm and the Pollard kangaroo method. The Pollard kangaroo method allows one to search for a solution in a prescribed interval, yielding a running time of ![O({sqrt[ {4}]{q}})](https://wikimedia.org/api/rest_v1/media/math/render/svg/4182beb722873e136c8cdbed3199b0a53d1c3271)

Schoof’s algorithm[edit]
A theoretical breakthrough for the problem of computing the cardinality of groups of the type 
Schoof’s insight exploits the fact that, by Hasse’s theorem, there is a finite range of possible values for 








The running time of Schoof’s Algorithm is polynomial in 



Schoof–Elkies–Atkin algorithm[edit]
In the 1990s, Noam Elkies, followed by A. O. L. Atkin devised improvements to Schoof’s basic algorithm by making a distinction among the primes 




The status of a particular prime 











Unlike Schoof’s algorithm, the SEA algorithm is typically implemented as a probabilistic algorithm (of the Las Vegas type), so that root-finding and other operations can be performed more efficiently. Its computational complexity is dominated by the cost of computing the modular polynomials 





See also[edit]
- Schoof’s algorithm
- Elliptic curve cryptography
- Baby-step giant-step
- Public key cryptography
- Schoof–Elkies–Atkin algorithm
- Pollard rho
- Pollard kangaroo
- Elliptic curve primality proving
Bibliography[edit]
- I. Blake, G. Seroussi, and N. Smart: Elliptic Curves in Cryptography, Cambridge University Press, 1999.
- A. Enge: Elliptic Curves and their Applications to Cryptography: An Introduction. Kluwer Academic Publishers, Dordrecht, 1999.
- G. Musiker: Schoof’s Algorithm for Counting Points on
. Available at http://www.math.umn.edu/~musiker/schoof.pdf
- R. Schoof: Counting Points on Elliptic Curves over Finite Fields. J. Theor. Nombres Bordeaux 7:219-254, 1995. Available at http://www.mat.uniroma2.it/~schoof/ctg.pdf
- L. C. Washington: Elliptic Curves: Number Theory and Cryptography. Chapman & Hall/CRC, New York, 2003.
References[edit]
4.1.4 Эллиптические кривые над конечным полем
Рассмотрим эллиптические кривые над конечным полем  ,
,  , где
, где  – простое число. В зависимости от характетистики поля уравнение кривой можно привести к одному из видов:
– простое число. В зависимости от характетистики поля уравнение кривой можно привести к одному из видов:

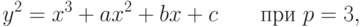
или к виду (4.2) при 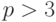 .
.
Особый интерес для криптографии представляет объект, называемый эллиптический группой по модулю  , где
, где  является простым числом.
является простым числом.
Далее мы, говоря об эллиптической кривой, если не оговорено противное, будем иметь в виду именно группу точек кривой над полем 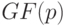 простого порядка
простого порядка  , заданной уравнением (4.2), причем
, заданной уравнением (4.2), причем  . Эту группу мы будем обозначать
. Эту группу мы будем обозначать 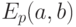 .
.
Пример 4.5 Пусть  . Рассмотрим эллиптическую кривую
. Рассмотрим эллиптическую кривую  .
.
В этом случае  и мы имеем
и мы имеем  , что удовлетворяет условиям эллиптической группы по модулю 23.
, что удовлетворяет условиям эллиптической группы по модулю 23.
Нас интересуют только целые значения от  до
до 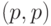 в квадранте неотрицательных чисел, удовлетворяющих уравнению по модулю
в квадранте неотрицательных чисел, удовлетворяющих уравнению по модулю  . В нашем случае список точек можно создать по следующим правилам.
. В нашем случае список точек можно создать по следующим правилам.
- Вычисляем значения
 (табл. 4.1).
(табл. 4.1).
- Вычисляем значения
 (табл. 4.2)
(табл. 4.2)
Теперь сравниваем числа в нижних строках табл. 4.1 и табл. 4.2. Число, попавшее в обе строки, определяет две точки кривой. Так, число 1 содержится и в нижней строке табл. 4.1, и в нижней строке табл. 4.2. Число 1 определяет точки 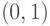 и
и  ; число 8 дает тоже две точки, находим по верхним строкам их координаты: это
; число 8 дает тоже две точки, находим по верхним строкам их координаты: это 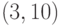 и
и 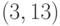 , и т. д. Таким образом, выбираем точки (отличные от
, и т. д. Таким образом, выбираем точки (отличные от 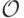 ), являющиеся элементами
), являющиеся элементами 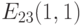 . Получаем табл. 4.3. Пара чисел
. Получаем табл. 4.3. Пара чисел  , для которой
, для которой 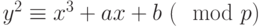 , включается в таблицу соответствий: это точка кривой.
, включается в таблицу соответствий: это точка кривой.
В криптографии применяются кривые, параметры которых являются большими (порядка 50 десятичных знаков) числами. В таких случаях перечисление всех точек кривой нереально за приемлемое время. Более того, даже определение количества точек кривой – весьма непростая задача.
Важной является
Теорема 4.1 (теорема Хассе) Пусть  – число точек на эллиптической кривой, определенной над
– число точек на эллиптической кривой, определенной над  . Тогда
. Тогда  .
.
4.1.5 Генерация точек эллиптической кривой
Для нахождения случайной точки эллиптической кривой  над полем простого порядка
над полем простого порядка  можно использовать следующий алгоритм:
можно использовать следующий алгоритм:
- Выбрать случайное
 .
. - Вычислить
 .
. - Вычислить символ Лежандра
 по
по  .
. - Если
 – квадратичный невычет, перейти к пункту 1.
– квадратичный невычет, перейти к пункту 1. - Вычислить
 – квадратный корень из
– квадратный корень из  по модулю
по модулю  (например, с помощью алгоритма Тонелли-Шенкса).
(например, с помощью алгоритма Тонелли-Шенкса).
Пример 4.6 Найти случайную точку эллиптической кривой  .
.
Решение. Пусть выбрано случайное число 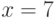 . Находим:
. Находим:  Вычисляем символ Лежандра-Якоби:
Вычисляем символ Лежандра-Якоби:

Следовательно,  не является квадратичным вычетом по модулю
не является квадратичным вычетом по модулю  ; выбираем другой
; выбираем другой  .
.
Пусть выбрано случайное число 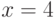 . Находим
. Находим  Вычисляем символ Лежандра-Якоби:
Вычисляем символ Лежандра-Якоби:

Итак,  – квадратичный вычет. Найдём корень из
– квадратичный вычет. Найдём корень из  по модулю
по модулю  .
.
Имеем:  . В алгоритме Тонелли-Шенкса получаем
. В алгоритме Тонелли-Шенкса получаем  . Мы уже знаем, что
. Мы уже знаем, что  является квадратичным невычетом; вычислим
является квадратичным невычетом; вычислим  . Вычисляем
. Вычисляем  При проверке видим, что
При проверке видим, что  Поэтому корнем из 22 будет число
Поэтому корнем из 22 будет число  . В самом деле,
. В самом деле, 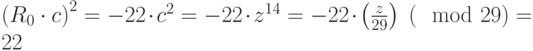 .
.
Итак, найдена точка  эллиптической кривой.
эллиптической кривой.
4.1.6 Сложение точек кривой над конечным полем
Проиллюстрируем примерами сложение точек кривой, построенной над конечным полем.
Пример 4.7 Выбрана кривая  , т. е.
, т. е.  . Найдем точку
. Найдем точку  .
.
Для нахождения  используем правила сложения точек эллиптической кривой (4.2).
используем правила сложения точек эллиптической кривой (4.2).
Вычисляем  :
:



Итак, мы нашли  . Теперь находим
. Теперь находим  :
:



Таким образом, мы нашли точку  .
.
4.1.7 Кратные точки
Данный алгоритм аналогичен алгоритму возведения в степень по модулю, см. параграф 1.2.2.
Рассмотрим алгоритм вычисления точки 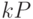 . Представим число
. Представим число  в двоичном виде:
в двоичном виде:

Далее, положим  ,
,  ,
, 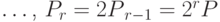 .
.
Откуда
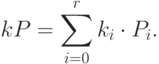
Таким образом, мы можем вычислить 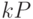 самое большее за
самое большее за  шагов, каждый из которых представляет собой сложение точек на кривой.
шагов, каждый из которых представляет собой сложение точек на кривой.
Пример 4.8 Найти  .
.
Представляем 100 в виде  Далее,
Далее,  ,
, 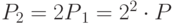 ,
, 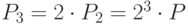 ,
, 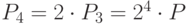 ,
,  ,
,  .
.
Теперь  .
.
Мы нашли точку 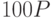 , произведя 6 удвоений и 2 сложения точек на кривой.
, произведя 6 удвоений и 2 сложения точек на кривой.
Пример 4.9 Найти точку  , кривая:
, кривая: 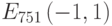 ,
, 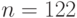 ,
,  .
.
Решение.

Пример 4.10 Найти порядок точки 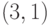 кривой
кривой  порядка
порядка 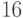 .
.
Решение. По теореме Лагранжа, порядок точки является делителем 16, то есть одним из чисел 2, 4, 8, 16. Пользуясь формулами (4.2), будем последовательно удваивать точку, пока не получим нейтральный элемент группы.

Следовательно, порядок точки 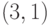 равен 4.
равен 4.
Пример 4.11 Найти порядок точки  кривой
кривой  порядка
порядка  .
.
Решение. Порядок точки является делителем числа 48, то есть одним из чисел: 2, 4, 8, 16, 3, 6, 12, 24. Нужно попробовать умножить точку на каждое из них. Расположим делители в узлах ориентированного дерева, где каждый потомок получается из родителя выполнением одной операции сложения точек. Пример такого дерева приведён на
рис.
4.2.

Рис.
4.2.
Дерево делителей числа 48
Совершая обход этого дерева, будем получать кратные точки. Например, чтобы получить  , сначала удвоим точку четыре раза, получив
, сначала удвоим точку четыре раза, получив  , затем от
, затем от  придём по стрелке к
придём по стрелке к  .
.
Заметим, что вариантов построения такого дерева может быть много. Число ребер в дереве с 10 вершинами – всегда 9, а операция удвоения точки всегда быстрее сложения произвольных двух точек. Поэтому оптимальным будет проводить вычисления по дереву на рисунке
рис.
4.3, содержащему наибольшее число удвоений.

Рис.
4.3.
Более оптимальное дерево делителей числа 48





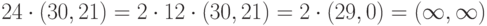
Теперь мы знаем, что порядок точки есть делитель числа 24, поэтому нам осталось пройти только те вершины дерева, в которых записаны делители числа 24. Например, вершину 16 мы рассматривать не будем.

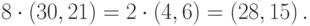
Итак, 24 – наименьшее число, при умножении точки на которое мы получим нейтральный элемент. Поэтому порядок точки равен 24.
Еще раз отметим, что во многих случаях определение порядка кривой является самостоятельной и весьма не простой задачей.
Список литературы
- Болоток А. А., Гашков С.Б., Фролов А. Б., Часовских А. А. Элементарное введение в эллиптическую криптографию – М.: КомКнига, 2006. – 328 с.
- Коблиц Н. Курс теории чисел и криптографии – М.: ТВП, 2003.
Важным аспектом в изучении эллиптических кривых является разработка эффективных способов подсчета точки на кривой . Для этого использовалось несколько подходов, и разработанные алгоритмы оказались полезными инструментами при изучении различных областей, таких как теория чисел, а в последнее время и криптография. и аутентификация цифровой подписи (см. криптография эллиптической кривой и эллиптическая кривая DSA ). Хотя в теории чисел они имеют важные последствия при решении диофантовых уравнений в отношении криптографии, они позволяют нам эффективно использовать сложность задачи дискретного логарифмирования (DLP) для группы E (F q) { displaystyle E ( mathbb {F} _ {q})}

Содержание
- 1 Подходы к подсчету точек на эллиптических кривых
- 2 Наивный подход
- 2.1 Пример
- 3 Гигантский шаг младенца
- 3.1 Алгоритм
- 3.2 Примечания к алгоритму
- 4 Алгоритм Шуфа
- 5 Алгоритм Шуфа – Элкиса – Аткина
- 6 См. Также
- 7 Библиография
- 8 Ссылки
Подходы к подсчету точек на эллиптических кривых
Есть несколько подходов к проблеме. Начиная с наивного подхода, мы прослеживаем развитие до окончательной работы Шуфа по этому вопросу, а также перечисляем улучшения в алгоритм Шуфа, сделанные Элкисом (1990) и Аткином (1992).
Некоторые алгоритмы используют тот факт, что группы вида E (F q) { displaystyle E ( mathbb {F} _ {q})}


- | | E (F q) | – (q + 1) | ≤ 2 кв. { displaystyle || E ( mathbb {F} _ {q}) | – (q + 1) | leq 2 { sqrt {q}}. ,}
Наивный подход
Наивный подход к подсчету очков, который является наименее изощренным, включает просмотр всех элементов поля F q { displaystyle mathbb {F} _ {q}}
- y 2 = x 3 + A x + B. { displaystyle y ^ {2} = x ^ {3} + Ax + B. ,}
Пример
Пусть E – кривая y = x + x + 1 над F 5 { displaystyle mathbb {F} _ {5}}
x { displaystyle x} |
x 2 { displaystyle x ^ {2}} |
x 3 + x + 1 { displaystyle x ^ {3} + x + 1} |
y { displaystyle y} |
Points |
|---|---|---|---|---|
0 { displaystyle quad 0} |
0 { displaystyle 0} |
1 { displaystyle 1} |
1, 4 { displaystyle 1,4} |
(0, 1), (0, 4) { displaystyle (0,1), (0,4)} |
1 { displaystyle quad 1} |
1 { displaystyle 1} |
3 { displaystyle 3} |
– { displaystyle -} |
– { displaystyle -} |
2 { displaystyle quad 2} |
4 { displaystyle 4} |
1 { displaystyle 1} |
1, 4 { displaystyle 1,4} |
(2, 1), (2, 4) { displaystyle (2,1), (2,4)} |
3 { displaystyle quad 3} |
4 { displaystyle 4} |
1 { displaystyle 1} |
1, 4 { displaystyle 1,4} |
(3, 1), (3, 4) { displaystyle (3,1), (3,4)} |
4 { displaystyle quad 4} |
1 { displaystyle 1} |
4 { displaystyle 4} |
2, 3 { displaystyle 2,3} |
(4, 2), ( 4, 3) { displaystyle (4,2), (4,3)} |
Например последняя строка вычисляется следующим образом: Если вы вставите x = 4 { displaystyle x = 4}




Следовательно, E (F 5) { displaystyle E ( mathbb {F} _ {5})}
Этот алгоритм требует времени выполнения O (q), потому что все значения x ∈ F q { displaystyle x in mathbb {F} _ {q}}
Baby-step гигантский-step
Уменьшение времени бега достигается с использованием другого подхода: мы выбираем элемент P = (x, y) ∈ E (F q) { displaystyle P = (x, y) in E ( mathbb {F} _ {q})}













Попытка всех значений M { displaystyle M}


Однако, применяя алгоритм гигантского шага к E (F q) { displaystyle E ( mathbb {F} _ {q})}
![4 { sqrt [{4}] {q}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/495c5b6948d76fd8c8445effd8bb9b9e20f64262)
Алгоритм
1. выберите m { displaystyle m} integer, m>q 4 { displaystyle m>{ sqrt [{4}] {q}}}
integer, m>q 4 { displaystyle m>{ sqrt [{4}] {q}}}![m>{ sqrt [{4}] {q}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c006dbed41ca9cdb6f040d0b2994b42b9a0f5005) 2. ДЛЯ {j = 0 { displaystyle j = 0}
2. ДЛЯ {j = 0 { displaystyle j = 0} до m { displaystyle m}
до m { displaystyle m} } DO3. P j ← j P { displaystyle P_ {j} leftarrow jP}
} DO3. P j ← j P { displaystyle P_ {j} leftarrow jP} 4. ENDFOR 5. L ← 1 { displaystyle L leftarrow 1}
4. ENDFOR 5. L ← 1 { displaystyle L leftarrow 1} 6. Q ← (q + 1) P { displaystyle Q leftarrow (q + 1) P}
6. Q ← (q + 1) P { displaystyle Q leftarrow (q + 1) P} 7. REPEAT вычисление точек Q + к (2 м п) { displaystyle Q + k (2mP)}
7. REPEAT вычисление точек Q + к (2 м п) { displaystyle Q + k (2mP)} 8. UNTIL∃ j { displaystyle exists j}
8. UNTIL∃ j { displaystyle exists j} : Q + k (2 м P) = ± P j { displaystyle Q + k (2mP) = pm P_ {j}}
: Q + k (2 м P) = ± P j { displaystyle Q + k (2mP) = pm P_ {j}} \ the x { displaystyle x}
\ the x { displaystyle x} -координаты сравниваются 9. M ← q + 1 + 2 mk ∓ j { displaystyle M leftarrow q + 1 + 2mk mp j}
-координаты сравниваются 9. M ← q + 1 + 2 mk ∓ j { displaystyle M leftarrow q + 1 + 2mk mp j} \ note MP = O { displaystyle MP = O}
\ note MP = O { displaystyle MP = O} 10. Коэффициент М { Displaystyle M}
10. Коэффициент М { Displaystyle M} . Пусть p 1,…, pr { displaystyle p_ {1}, ldots, p_ {r}}
. Пусть p 1,…, pr { displaystyle p_ {1}, ldots, p_ {r}} будут различными простыми множителями M { displaystyle M}
будут различными простыми множителями M { displaystyle M} . 11. WHILEi ≤ r { displaystyle i leq r}
. 11. WHILEi ≤ r { displaystyle i leq r} DO12. IFM п я P = O { displaystyle { frac {M} {p_ {i}}} P = O}
DO12. IFM п я P = O { displaystyle { frac {M} {p_ {i}}} P = O} 13. ЗАТЕМM ← M p i { displaystyle M leftarrow { frac {M} {p_ {i}}}}
13. ЗАТЕМM ← M p i { displaystyle M leftarrow { frac {M} {p_ {i}}}} 14. ELSEi ← i + 1 { displaystyle i leftarrow i + 1}
14. ELSEi ← i + 1 { displaystyle i leftarrow i + 1} 15. ENDIF 16. КОНЕЦ 17. L ← lcm (L, M) { displaystyle L leftarrow operatorname {lcm} (L, M)}
15. ENDIF 16. КОНЕЦ 17. L ← lcm (L, M) { displaystyle L leftarrow operatorname {lcm} (L, M)} \ note M { displaystyle M}
\ note M { displaystyle M} - это порядок точки P { displaystyle P}
- это порядок точки P { displaystyle P} 18. WHILEL { displaystyle L}
18. WHILEL { displaystyle L} делит более одного целого числа N { displaystyle N}
делит более одного целого числа N { displaystyle N} в (q + 1 - 2 q, q + 1 + 2 q) { displaystyle (q + 1-2 { sqrt {q}}, q + 1 + 2 { sqrt {q}})}
в (q + 1 - 2 q, q + 1 + 2 q) { displaystyle (q + 1-2 { sqrt {q}}, q + 1 + 2 { sqrt {q}})} 19. DO выберите новую точку P { displaystyle P}
19. DO выберите новую точку P { displaystyle P} и перейдите к 1. 20. ENDWHILE 21. RETURNN { displaystyle N}
и перейдите к 1. 20. ENDWHILE 21. RETURNN { displaystyle N} \ это мощность E (F q) { displaystyle E ( mathbb {F} _ {q })}
\ это мощность E (F q) { displaystyle E ( mathbb {F} _ {q })}
Примечания к алгоритму
- В строке 8. мы предполагаем наличие совпадения. Действительно, следующая лемма гарантирует, что такое совпадение существует:
-
- Пусть a { displaystyle a}
будет целым числом с | а | ≤ 2 м 2 { displaystyle | a | leq 2m ^ {2}}
. Существуют целые числа a 0 { displaystyle a_ {0}}
и a 1 { displaystyle a_ {1}}
с
- – m < a 0 ≤ m and − m ≤ a 1 ≤ m s.t. a = a 0 + 2 m a 1. {displaystyle -m
- Пусть a { displaystyle a}
- Вычисление (j + 1) P { displaystyle (j + 1) P}
после вычисления j P { displaystyle jP}
может быть выполнено путем добавления P { displaystyle P}
к j P { displaystyle jP}
вместо повторного вычисления полного скалярного умножения. Таким образом, полное вычисление требует m { displaystyle m}
сложений. 2 м P { displaystyle 2mP}
можно получить одним удвоением из m P { displaystyle mP}
. Для вычисления Q { displaystyle Q}
требуется log (q + 1) { displaystyle log (q + 1)}
удвоений и w { displaystyle w}
сложения, где w { displaystyle w}
– количество ненулевых цифр в двоичном представлении q + 1 { стиль отображения q + 1}
; обратите внимание, что знание j P { displaystyle jP}
и 2 m P { displaystyle 2mP}
позволяет нам уменьшить количество удвоений. Наконец, чтобы получить от Q + k (2 m P) { displaystyle Q + k (2mP)}
до Q + (k + 1) (2 m P) { displaystyle Q + (k + 1) (2mP)}
, просто добавьте 2 m P { displaystyle 2mP}
вместо того, чтобы пересчитывать все заново.
- Мы предполагая, что мы можем разложить на множители M { displaystyle M}
. Если нет, мы можем по крайней мере найти все малые простые множители pi { displaystyle p_ {i}}
и проверить, что M pi ≠ O { displaystyle { frac {M} {p_ {i}}} neq O}
для них. Тогда M { displaystyle M}
будет хорошим кандидатом для порядка из P { displaystyle P}
.
- . Результат шага 17 может быть следующим: доказано с помощью элементарной теории групп: поскольку MP = O { displaystyle MP = O}
, порядок P { displaystyle P}
делит M { Displaystyle M}
. Если нет собственного делителя M ¯ { displaystyle { bar {M}}}
of M { displaystyle M}
реализует M ¯ P = O { displaystyle { bar {M}} P = O}
, тогда M { displaystyle M}
– это порядок P { displaystyle P }
.
Одним из недостатков этого метода является необходимость в слишком большом объеме памяти, когда группа становится большой. Чтобы решить эту проблему, было бы более эффективно хранить только x { displaystyle x}




Есть и другие общие алгоритмы для вычисления порядка элементов группы, которые занимают больше места, такие как алгоритм ро Полларда и метод кенгуру Полларда. Метод кенгуру Полларда позволяет искать решение в заданном интервале, что дает время выполнения O (q 4) { displaystyle O ({ sqrt [{4}] {q}})}![O ({ sqrt [ {4}] {q}})](https://wikimedia.org/api/rest_v1/media/math/render/svg/4182beb722873e136c8cdbed3199b0a53d1c3271)

алгоритм Шуфа
Теоретический прорыв в проблеме вычисления мощности групп типа E (F q) { displaystyle E ( mathbb {F} _ {q })}
. Понимание Шуфа основано на том факте, что, согласно теореме Хассе, существует – конечный диапазон возможных значений для | E (F q) | { displaystyle | E ( mathbb {F} _ {q}) |}








время работы алгоритма Шуфа полиномиально от n = log q { displaystyle n = log {q}}



алгоритм Шуфа – Элкиса – Аткина
В 1990-е годы Ноам Элкис, за которым следует А. О.Л. Аткин разработал улучшения базового алгоритма Шуфа, выделив простые числа ℓ 1,…, ℓ s { displaystyle ell _ {1}, ldots, ell _ {s}}




Статус конкретного простого числа ℓ { displaystyle ell}











В отличие от алгоритма Шуфа, алгоритм SEA обычно реализуется как вероятностный алгоритм (из тип Лас-Вегас ), так что поиск корней и другие операции могут выполняться более эффективно. В его вычислительной сложности преобладает стоимость вычисления модульных многочленов Ψ ℓ (X, Y) { displaystyle Psi _ { ell} (X, Y)}





См. Также
- алгоритм Шуфа
- Криптография на эллиптических кривых
- Гигантский шаг маленького шага
- Криптография с открытым ключом
- Алгоритм Шуфа – Элкиса – Аткина
- Ро Полларда
- Кенгуру Полларда
- Доказательство простоты эллиптической кривой
Библиография
- I. Блейк, Дж. Серусси и Н. Смарт: Эллиптические кривые в криптографии, Cambridge University Press, 1999.
- A. Энге: Эллиптические кривые и их приложения в криптографии: Введение. Kluwer Academic Publishers, Dordrecht, 1999.
- Г. Musiker: алгоритм Шуфа для подсчета точек на E (F q) { displaystyle E ( mathbb {F} _ {q})}
. Доступно на http://www.math.umn.edu/~musiker/schoof.pdf
- R. Schoof: Подсчет точек на эллиптических кривых над конечными полями. J. Theor. Nombres Bordeaux 7: 219-254, 1995. Доступно на http://www.mat.uniroma2.it/~schoof/ctg.pdf
- L. К. Вашингтон: Эллиптические кривые: теория чисел и криптография. Chapman Hall / CRC, New York, 2003.
Источники
.
Важным аспектом изучения эллиптических кривых является разработка эффективных способов подсчета точек на кривой . Для этого использовалось несколько подходов, и разработанные алгоритмы оказались полезными инструментами при изучении различных областей, таких как теория чисел , а в последнее время – в криптографии и аутентификации цифровой подписи (см. Криптографию с эллиптической кривой и DSA с эллиптической кривой ). Хотя в теории чисел они имеют важные последствия при решении диофантовых уравнений , в отношении криптографии они позволяют нам эффективно использовать сложность задачи дискретного логарифмирования (DLP) для группы эллиптических кривых над конечным полем , где q = p k, а p простое число. DLP, как ее теперь называют, представляет собой широко используемый подход к криптографии с открытым ключом , и сложность решения этой проблемы определяет уровень безопасности криптосистемы. В этой статье рассматриваются алгоритмы подсчета точек на эллиптических кривых над полями большой характеристики, в частности p > 3. Для кривых над полями малой характеристики существуют более эффективные алгоритмы, основанные на p -адических методах.

Подходы к подсчету точек на эллиптических кривых
Есть несколько подходов к проблеме. Начиная с наивного подхода, мы прослеживаем развитие до окончательной работы Шуфа по этому вопросу, а также перечисляем улучшения в алгоритм Шуфа, сделанные Элкисом (1990) и Аткином (1992).
Некоторые алгоритмы используют тот факт, что группы формы подчиняются важной теореме Хассе, которая ограничивает количество рассматриваемых точек. Теорема Хассе утверждает , что если Е является эллиптической кривой над конечным полем , то мощность из удовлетворяет
Наивный подход
Наивный подход к подсчету точек, который является наименее изощренным, включает просмотр всех элементов поля и проверку того, какие из них удовлетворяют форме эллиптической кривой Вейерштрасса.
пример
Пусть E – кривая y 2 = x 3 + x + 1 над . Чтобы подсчитать точки на E , мы составляем список возможных значений x , затем квадратичных вычетов x по модулю 5 (только для целей поиска), затем x 3 + x + 1 по модулю 5, затем y из x 3. + х + 1 по модулю 5. Это дает точки на Е .

|

|

|

|
Точки |
|---|---|---|---|---|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Например, последняя строка вычисляется следующим образом: Если вы вставите уравнение, вы получите результат (3-й столбец). Этот результат может быть достигнут, если ( квадратичные остатки можно найти во 2-м столбце). Итак, баллы за последний ряд есть .
Следовательно, имеет мощность 9: 8 указанных выше точек и бесконечно удаленная точка.
Этот алгоритм требует времени работы O ( q ), потому что необходимо учитывать все значения .
Бэби-степ гигантский шаг
Уменьшение времени выполнения достигается с использованием другого подхода: мы выбираем элемент , выбирая случайные значения до тех пор, пока не будет квадрат, а затем вычисляем квадратный корень из этого значения, чтобы получить . Теорема Хассе говорит нам, что лежит в интервале . Таким образом, по теореме Лагранжа нахождение единственного, лежащего в этом интервале и удовлетворяющего , приводит к нахождению мощности . Алгоритм не работает, если существуют два различных целых числа и в интервале такие, что . В таком случае обычно достаточно повторить алгоритм с другой случайно выбранной точкой .
Испытание всех значений , чтобы найти то, которое удовлетворяет, требует нескольких шагов.
Однако, применяя алгоритм гигантских шагов baby-step к , мы можем ускорить это примерно до шагов. Алгоритм следующий.
Алгоритм
1. chooseinteger,
2. FOR{
to
} DO 3.
4. ENDFOR 5.
6.
7. REPEAT compute the points
8. UNTIL
:
\the
-coordinates are compared 9.
\note
10. Factor
. Let
be the distinct prime factors of
. 11. WHILE
DO 12. IF
13. THEN
14. ELSE
15. ENDIF 16. ENDWHILE 17.
\note
is the order of the point
18. WHILE
divides more than one integer
in
19. DO choose a new point
and go to 1. 20. ENDWHILE 21. RETURN
\it is the cardinality of

Примечания к алгоритму
- В строке 8 мы предполагаем наличие совпадения. Действительно, следующая лемма гарантирует, что такое совпадение существует:
-
- Позвольте быть целым числом с . Существуют целые числа и с
- Позвольте быть целым числом с . Существуют целые числа и с
Один из недостатков этого метода заключается в том, что при увеличении группы требуется слишком много памяти. Чтобы решить эту проблему, было бы более эффективно хранить только координаты точек (вместе с соответствующим целым числом ). Однако это приводит к дополнительному скалярному умножению для выбора между и .
Существует и другие общие алгоритмы для вычисления порядка группы элементов , которые являются более эффективным пространством, такими , как алгоритм ро – Полларда и Поллард кенгуру метода. Метод кенгуру Полларда позволяет искать решение в заданном интервале, давая время выполнения , используя пространство.
Алгоритм Шуфа
Теоретический прорыв в проблеме вычисления мощности групп этого типа был достигнут Рене Шуфом, который в 1985 году опубликовал первый детерминированный алгоритм с полиномиальным временем. Центральное место в алгоритме Шуфа занимает использование полиномов деления и теоремы Хассе , а также китайской теоремы об остатках .
Понимание Шуфа использует тот факт, что, согласно теореме Хассе, существует конечный диапазон возможных значений для . Достаточно вычислить по модулю целого числа . Это достигается путем вычисления по модулю простых чисел , произведение которых превышает , а затем применения китайской теоремы об остатках. Ключом к алгоритму является использование полинома деления для эффективного вычисления по модулю .
Время работы алгоритма Шуфа полиномиально от , с асимптотической сложностью , где обозначает сложность целочисленного умножения . Его космическая сложность составляет .
Алгоритм Шуфа – Элкиса – Аткина
В 1990-х годах Ноам Элкис , а затем AOL Atkin разработали улучшения базового алгоритма Шуфа, проведя различие между используемыми простыми числами . Простое число называется простым числом Элкиса, если характеристическое уравнение эндоморфизма Фробениуса,, расщепляется . В противном случае называется простым числом Аткина. Простые числа Элкиса являются ключом к улучшению асимптотической сложности алгоритма Шуфа. Информация, полученная с помощью простых чисел Аткина, допускает дальнейшее улучшение, которое асимптотически незначительно, но может быть весьма важным на практике. Модификация алгоритма Шуфа для использования простых чисел Элкиса и Аткина известна как алгоритм Шуфа – Элкиса – Аткина (SEA).
Статус конкретного простого числа зависит от эллиптической кривой и может быть определен с помощью модульного полинома . Если одномерный полином имеет корень в , где обозначающую J-инвариантные из , то является главным Elkies, а в противном случае он является главным Аткиным. В случае Элкиса для получения правильного множителя полинома деления используются дальнейшие вычисления с участием модулярных полиномов . Степень этого фактора есть , тогда как имеет степень .

В отличие от алгоритма Шуфа, алгоритм SEA обычно реализуется как вероятностный алгоритм (типа Лас-Вегаса ), так что поиск корня и другие операции могут выполняться более эффективно. В его вычислительной сложности преобладает стоимость вычисления модульных многочленов , но, поскольку они не зависят от них , они могут быть вычислены один раз и повторно использованы. При эвристическом предположении, что существует достаточно много малых простых чисел Элкиса, и без учета затрат на вычисление модульных многочленов, асимптотическое время работы алгоритма SEA равно , где . Его пространственная сложность равна , но при использовании предварительно вычисленных модульных многочленов она увеличивается до .
Смотрите также
- Алгоритм Шуфа
- Криптография на эллиптических кривых
- Бэби-степ гигантский шаг
- Криптография с открытым ключом
- Алгоритм Шуфа – Элкиса – Аткина
- Поллард ро
- Кенгуру Полларда
- Доказательство простоты эллиптической кривой
Библиография
- И. Блейк, Дж. Серусси и Н. Смарт: эллиптические кривые в криптографии , Cambridge University Press, 1999.
- А. Энге: Эллиптические кривые и их приложения в криптографии: Введение . Kluwer Academic Publishers, Дордрехт, 1999.
- Г. Мусикер: Алгоритм Шуфа для подсчета очков . Доступно на http://www.math.umn.edu/~musiker/schoof.pdf
- Р. Шоф: Подсчет точек на эллиптических кривых над конечными полями. J. Theor. Nombres Bordeaux 7: 219-254, 1995. Доступно на http://www.mat.uniroma2.it/~schoof/ctg.pdf
- LC Вашингтон: Эллиптические кривые: теория чисел и криптография. Chapman & Hall / CRC, Нью-Йорк, 2003.




