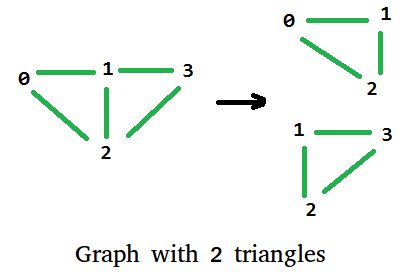
Корневые эвристики — это обобщённое название различных методов и структур данных, опирающихся на тот факт, что если мы разделим какое-то множество из $n$ элементов на блоки по $sqrt{n}$ элементов, то самих этих блоков будет не более $sqrt{n}$.
Центральное равенство этой статьи: $sqrt x = frac{x}{sqrt x}$.
#Деление на тяжелые и легкие объекты
Всем известный алгоритм факторизации за корень опирается на тот факт, что каждому «большому» делителю $d geq sqrt n$ числа $n$ соответствует какой-то «маленький» делитель $frac{n}{d} leq n$.
Подобное полезное свойство (что маленькие объекты маленькие, а больших объектов не много) можно найти и у других объектов.
#Длинные и короткие строки
Задача. Требуется в онлайне обрабатывать три типа операций над множеством строк:
- Добавить строку в множество.
- Удалить строку из множества.
- Для заданной строки, найти количество её вхождений как подстроку среди всех строк множества.
Одно из решений следующее: разделим все строки на короткие ($|s| < sqrt l$) и длинные ($|s| geq sqrt l$), где $l$ означает суммарную длину всех строк. Заметим, что длинных строк немного — не более $sqrt l$.
С запросами будем справляться так:
- Заведём хеш-таблицу, и когда будем обрабатывать запрос добавления или удаления, будем прибавлять или отнимать соответственно единицу по хешам всех её коротких подстрок. Это можно сделать суммарно за $O(l sqrt l)$: для каждой строки нужно перебрать $O(sqrt l)$ разных длин и окном пройтись по всей строке.
- Для запроса третьего типа для короткой строки, просто посчитаем её хеш и посмотрим на значение в хеш-таблице.
- Для запроса третьего типа для длинной строки, мы можем позволить себе посмотреть на все неудаленные строки, потому что таких случаев будет немного, и если мы можем за линейное время найти все вхождения новой строки, то работать это будет тоже за $O(l sqrt l)$. Например, можно посчитать z-функцию для всех строк вида
s#t, где $s$ это строка из запроса, а $t$ это строка из множества; здесь, правда, есть нюанс: $s$ может быть большой, а маленьких строк $t$ много — нужно посчитать z-функцию сначала только от $s$, а затем виртуально дописывать к ней каждую $t$ и досчитывать функцию.
Иногда отдельный подход к тяжелым и лёгким объектам не требуется, но сама идея помогает увидеть, что некоторые простые решения работают быстрее, чем кажется.
#Треугольники в графе
Задача. Дан граф из $n$ вершин и $m approx n$ рёбер. Требуется найти в нём количество циклов длины три.
Будем называть вершину тяжелой, если она соединена с более чем $sqrt n$ другими вершинами, и лёгкой в противном случае.
Попытаемся оценить количество соединённых вместе троек вершин, рассмотрев все возможные 4 варианта:
- В цикле нет тяжелых вершин. Рассмотрим какое-нибудь ребро $(a, b)$ цикла. Третья вершина $c$ должна лежать в объединении списков смежности $g_a$ и $g_b$, а раз обе эти вершины лёгкие, то таких вершин найдётся не более $sqrt n$. Значит, всего циклов этого типа может быть не более $O(m sqrt n)$.
- В цикле одна тяжелая вершина. Аналогично — есть одно «лёгкое» ребро, а значит таких циклов тоже $O(m sqrt n)$.
- В цикле две тяжелые вершины — обозначим их как $a$ и $b$, а лёгкую как $c$. Зафиксируем пару $(a, c)$ — способов это сделать $O(m)$, потому что всего столько рёбер. Для этого ребра будет не более $O(sqrt n)$ рёбер $(a, b)$, потому что столько всего тяжелых вершин. Получается, что всего таких циклов может быть не более $O(m sqrt n)$.
- Все вершины тяжелые. Аналогично — тип третьей вершины в разборе предыдущего случая нигде не использовался; важно лишь то, что тяжелых вершин $b$ немного.
Получается, что циклов длины 3 в графе может быть не так уж и много — не более $O(m sqrt n)$.
Само решение максимально простое: отсортируем вершины графа по их степени и будем перебирать все пути вида $v rightarrow u rightarrow w, v le u le w$ и проверять существование ребра $v rightarrow w$.
vector<int> g[maxn], p(n); // исходный граф и список номеров вершин
iota(p.begin(), p.end(), 0); // 0, 1, 2, 3, ...
// чтобы не копипастить сравнение:
auto cmp = [&](int a, int b) {
return g[a].size() < g[b].size() || (g[a].size() == g[b].size() && a < b);
};
// в таком порядке мы будем перебирать вершины
sort(p.begin(), p.end(), cmp);
// теперь отсортируем списки смежности каждой вершины
for (int v = 0; v < n; ++v)
sort(g[v].begin(), g[v].end(), cmp);
// рядом с каждой вершиной будем хранить количество
// ранее просмотренных входящих рёбер (v -> w)
vector<int> cnt(n, 0);
int ans = 0;
for (int v : p) {
for (int w : g[v])
cnt[w]++;
for (int u : g[v]) {
if (cmp(v, u))
break;
for (int w : g[u]) {
if (cmp(u, w))
break; // если ребро плохое -- не берем треугольник
ans += cnt[w]; // если в графе нет петель, то cnt[w] = {0, 1}
}
}
// при переходе к следующему v массив нужно занулить обратно
for (int w : g[v])
cnt[w]--;
}
#Рюкзак за $O(S sqrt S)$
Если у нас есть $n$ предметов с весами $w_1$, $w_2$, $ldots$, $w_n$, такими что $sum w_i = S$, то мы можем решить задачу о рюкзаке за время $O(S cdot n)$ стандартной динамикой. Чтобы решить задачу быстрее, попытаемся сделать так, чтобы число предметов стало $O(sqrt S)$.
Заметим, что количество различных весов будет $O(sqrt S)$, так как для любых $k$ различных чисел с суммой $S$
$$
S = w_1 + w_2 + ldots + w_n geq 1 + 2 + ldots + k = frac{k cdot (k+1)}{2}
$$
Откуда значит, что $k leq 2sqrt S = O(sqrt S)$.
Рассмотрим теперь некоторый вес $x$, который $k$ раз встречается в наборе весов. «Разложим» $k$ по степеням двойки и вместо всех $k$ вхождений этого веса добавим веса $x$, $2 cdot x$, $4 cdot x$, $ldots$, $(k – 1 – 2^t) cdot x$, где $t$ это максимальное целое число, для которого выполняется $2^t − 1 leq k$. Легко видеть, что все суммы вида $q cdot x$ ($q leq k$) и только их по-прежнему можно набрать.
Алгоритм в этом, собственно, и заключается: проведем данную операцию со всеми уникальными значениями весов и после чего запустим стандартное решение. Уже сейчас легко видеть, что новое количество предметов будет $O(sqrt S log S)$, потому что для каждого веса мы оставили не более $log S$ весов, а всего различных весов было $O(sqrt S)$.
Упражнение. Докажите, что предметов на самом деле будет $O(sqrt S)$.
Примечание. Классическое решение рюкзака можно ускорить на несколько порядков, если использовать bitset.
Также корневые эвристики можно использовать в контексте структур данных и обработки запросов.
Материал из Algocode wiki
Перейти к: навигация, поиск
Тяжелые и легкие вершины
Назовем $textit{тяжелой}$ вершину, имеющую более $sqrt{E}$ соседей. Все оставшиеся вершины назовем $textit{легкими}$.
Утверждение:
В графе не более $2 cdot sqrt{E}$ тяжелых вершин.
Доказательство:
Пусть в графе более $2 cdot sqrt{E}$ тяжелых вершин. Тогда число ребер в графе больше, чем $frac{2 cdot sqrt{E} cdot sqrt{E}}{2} = E$, чего не может быть.
Нахождение количества треугольников в графе за $O(E sqrt E)$
Мысленно разобьем все вершины графа на легкие и тяжелые. Заметим, что треугольников, образованных только тяжелыми вершинами, всего $O(Esqrt{E})$, как $C^3_{sqrt{E}}$. Теперь рассмотрим треугольники, которые содержат в себе легкие вершины. В таком треугольнике точно будут два ребра, инцидентных легкой вершине. Сколько таких пар может быть? Всего таких ребер $O(E)$, при этом для каждого ребра парными могут быть только $O(sqrt{E})$ ребер, в силу степени легкой вершины. Таким образом, textit{число треугольников в графе равно} $O(E sqrt{E})$.
Каким алгоритмом их искать? Можно явно провести процесс, описанный выше, но это не самое приятное в реализации решение этой задачи.
Можно переориентировать ребра от вершин с меньшей степенью к вершинам с большей. Теперь верно следующее
Утверждение:
Из каждой вершины выходит не более $O(sqrt E)$ ребер
Доказательство:
Степень легких вершин $O(sqrt E)$, а из тяжелых вершин ребра идут только в тяжелые, которых всего $O(sqrt E)$.
Теперь для каждой вершины пометим ее соседей, после чего запустим поиск путей длины 2 и будем фиксировать треугольник при нахождении пометки. Для каждого первого ребра пути мы посмотрим на $O(sqrt E)$ ребер, поэтому итоговая сложность алгоритма $O(E sqrt E)$
Автор конспекта: Константин Амеличев
По всем вопросам пишите в telegram @kik0s
Given an Undirected simple graph, We need to find how many triangles it can have. For example below graph have 2 triangles in it.
Let A[][] be the adjacency matrix representation of the graph. If we calculate A3, then the number of triangles in Undirected Graph is equal to trace(A3) / 6. Where trace(A) is the sum of the elements on the main diagonal of matrix A.
Trace of a graph represented as adjacency matrix A[V][V] is, trace(A[V][V]) = A[0][0] + A[1][1] + .... + A[V-1][V-1] Count of triangles = trace(A3) / 6
Below is the implementation of the above formula.
C++
#include <bits/stdc++.h>
using namespace std;
#define V 4
void multiply(int A[][V], int B[][V], int C[][V])
{
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
C[i][j] = 0;
for (int k = 0; k < V; k++)
C[i][j] += A[i][k]*B[k][j];
}
}
}
int getTrace(int graph[][V])
{
int trace = 0;
for (int i = 0; i < V; i++)
trace += graph[i][i];
return trace;
}
int triangleInGraph(int graph[][V])
{
int aux2[V][V];
int aux3[V][V];
for (int i = 0; i < V; ++i)
for (int j = 0; j < V; ++j)
aux2[i][j] = aux3[i][j] = 0;
multiply(graph, graph, aux2);
multiply(graph, aux2, aux3);
int trace = getTrace(aux3);
return trace / 6;
}
int main()
{
int graph[V][V] = {{0, 1, 1, 0},
{1, 0, 1, 1},
{1, 1, 0, 1},
{0, 1, 1, 0}
};
printf("Total number of Triangle in Graph : %dn",
triangleInGraph(graph));
return 0;
}
Java
import java.io.*;
class Directed
{
int V = 4;
void multiply(int A[][], int B[][],
int C[][])
{
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
C[i][j] = 0;
for (int k = 0; k < V;
k++)
{
C[i][j] += A[i][k]*
B[k][j];
}
}
}
}
int getTrace(int graph[][])
{
int trace = 0;
for (int i = 0; i < V; i++)
{
trace += graph[i][i];
}
return trace;
}
int triangleInGraph(int graph[][])
{
int[][] aux2 = new int[V][V];
int[][] aux3 = new int[V][V];
for (int i = 0; i < V; ++i)
{
for (int j = 0; j < V; ++j)
{
aux2[i][j] = aux3[i][j] = 0;
}
}
multiply(graph, graph, aux2);
multiply(graph, aux2, aux3);
int trace = getTrace(aux3);
return trace / 6;
}
public static void main(String args[])
{
Directed obj = new Directed();
int graph[][] = { {0, 1, 1, 0},
{1, 0, 1, 1},
{1, 1, 0, 1},
{0, 1, 1, 0}
};
System.out.println("Total number of Triangle in Graph : "+
obj.triangleInGraph(graph));
}
}
Python3
def multiply(A, B, C):
global V
for i in range(V):
for j in range(V):
C[i][j] = 0
for k in range(V):
C[i][j] += A[i][k] * B[k][j]
def getTrace(graph):
global V
trace = 0
for i in range(V):
trace += graph[i][i]
return trace
def triangleInGraph(graph):
global V
aux2 = [[None] * V for i in range(V)]
aux3 = [[None] * V for i in range(V)]
for i in range(V):
for j in range(V):
aux2[i][j] = aux3[i][j] = 0
multiply(graph, graph, aux2)
multiply(graph, aux2, aux3)
trace = getTrace(aux3)
return trace // 6
V = 4
graph = [[0, 1, 1, 0],
[1, 0, 1, 1],
[1, 1, 0, 1],
[0, 1, 1, 0]]
print("Total number of Triangle in Graph :",
triangleInGraph(graph))
C#
using System;
class GFG
{
int V = 4;
void multiply(int [,]A, int [,]B,
int [,]C)
{
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
C[i, j] = 0;
for (int k = 0; k < V;
k++)
{
C[i, j] += A[i, k]*
B[k, j];
}
}
}
}
int getTrace(int [,]graph)
{
int trace = 0;
for (int i = 0; i < V; i++)
{
trace += graph[i, i];
}
return trace;
}
int triangleInGraph(int [,]graph)
{
int[,] aux2 = new int[V, V];
int[,] aux3 = new int[V, V];
for (int i = 0; i < V; ++i)
{
for (int j = 0; j < V; ++j)
{
aux2[i, j] = aux3[i, j] = 0;
}
}
multiply(graph, graph, aux2);
multiply(graph, aux2, aux3);
int trace = getTrace(aux3);
return trace / 6;
}
public static void Main()
{
GFG obj = new GFG();
int [,]graph = {{0, 1, 1, 0},
{1, 0, 1, 1},
{1, 1, 0, 1},
{0, 1, 1, 0}};
Console.WriteLine("Total number of " +
"Triangle in Graph : "+
obj.triangleInGraph(graph));
}
}
Javascript
<script>
let V = 4;
function multiply(A, B, C)
{
for(let i = 0; i < V; i++)
{
for(let j = 0; j < V; j++)
{
C[i][j] = 0;
for(let k = 0; k < V; k++)
C[i][j] += A[i][k] * B[k][j];
}
}
}
function getTrace(graph)
{
let trace = 0;
for(let i = 0; i < V; i++)
trace += graph[i][i];
return trace;
}
function triangleInGraph(graph)
{
let aux2 = new Array(V);
let aux3 = new Array(V);
for(let i = 0; i < V; ++i)
{
aux2[i] = new Array(V);
aux3[i] = new Array(V);
for(let j = 0; j < V; ++j)
{
aux2[i][j] = aux3[i][j] = 0;
}
}
multiply(graph, graph, aux2);
multiply(graph, aux2, aux3);
let trace = getTrace(aux3);
return (trace / 6);
}
let graph = [ [ 0, 1, 1, 0 ],
[ 1, 0, 1, 1 ],
[ 1, 1, 0, 1 ],
[ 0, 1, 1, 0 ] ];
document.write("Total number of Triangle in Graph : " +
triangleInGraph(graph));
</script>
Output
Total number of Triangle in Graph : 2
How does this work?
If we compute An for an adjacency matrix representation of the graph, then a value An[i][j] represents the number of distinct walks between vertex i to j in the graph. In A3, we get all distinct paths of length 3 between every pair of vertices.
A triangle is a cyclic path of length three, i.e. begins and ends at the same vertex. So A3[i][i] represents a triangle beginning and ending with vertex i. Since a triangle has three vertices and it is counted for every vertex, we need to divide the result by 3. Furthermore, since the graph is undirected, every triangle twice as i-p-q-j and i-q-p-j, so we divide by 2 also. Therefore, the number of triangles is trace(A3) / 6.
Time Complexity: O(V3) (as here most time consuming part is multiplication of matrix which contains 3 nested for loops) Space Complexity: O(V2) (to store matrix of size V*V)
Time Complexity:
The time complexity of above algorithm is O(V3) where V is number of vertices in the graph, we can improve the performance to O(V2.8074) using Strassen’s matrix multiplication algorithm.
Another approach: Using Bitsets as adjacency lists.
- For each node in the graph compute the corresponding adjacency list as a bitmask.
- If two nodes, i & j, are adjacent compute the number of nodes that are adjacent to i & j and add it to the answer.
- In the end, divide the answer by 6 to avoid duplicates.
In order to compute the number of nodes adjacent to two nodes, i & j, we use the bitwise operation & (and) on the adjacency list of i and j, then we count the number of ones.
Below is the implementation of the above approach:
C++
#include<iostream>
#include<string>
#include<algorithm>
#include<cstring>
#include<vector>
#include<bitset>
using namespace std;
#define V 4
int main()
{
int graph[][V] = {{0, 1, 1, 0},
{1, 0, 1, 1},
{1, 1, 0, 1},
{0, 1, 1, 0}};
vector<bitset<V>> Bitset_Adj_List(V);
for (int i = 0; i < V;i++)
for (int j = 0; j < V;j++)
if(graph[i][j])
Bitset_Adj_List[i][j] = 1,
Bitset_Adj_List[j][i] = 1;
int ans = 0;
for (int i = 0; i < V;i++)
for (int j = 0; j < V;j++)
if(Bitset_Adj_List[i][j] == 1 && i != j){
bitset<V> Mask = Bitset_Adj_List[i] & Bitset_Adj_List[j];
ans += Mask.count();
}
ans /= 6;
cout << "The number of Triangles in the Graph is : " << ans;
}
Java
import java.util.*;
public class Main
{
static final int V = 4;
public static void main(String[] args) {
int graph[][] = {{0, 1, 1, 0},
{1, 0, 1, 1},
{1, 1, 0, 1},
{0, 1, 1, 0}};
Vector<BitSet> Bitset_Adj_List = new Vector<BitSet>();
for(int i=0; i<V; i++)
{
Bitset_Adj_List.add(new BitSet());
for(int j=0; j<V; j++)
{
if(graph[i][j] == 1)
Bitset_Adj_List.get(i).set(j, true);
}
}
int ans = 0;
for(int i=0; i<V; i++)
for(int j=0; j<V; j++)
if(Bitset_Adj_List.get(i).get(j) == true && i!=j)
{
BitSet Mask = (BitSet) Bitset_Adj_List.get(i).clone();
Mask.and(Bitset_Adj_List.get(j));
ans += Mask.cardinality();
}
ans /= 6;
System.out.println("The number of Triangles in the Graph is : " + ans);
}
}
Javascript
function main() {
const V = 4;
let graph = [[0, 1, 1, 0],
[1, 0, 1, 1],
[1, 1, 0, 1],
[0, 1, 1, 0]];
let Bitset_Adj_List = [];
for(let i=0; i<V; i++) {
Bitset_Adj_List[i] = new Array(V).fill(0);
for(let j=0; j<V; j++) {
if(graph[i][j] == 1) {
Bitset_Adj_List[i][j] = 1;
}
}
}
let ans = 0;
for(let i=0; i<V; i++) {
for(let j=0; j<V; j++) {
if(Bitset_Adj_List[i][j] == 1 && i!=j) {
let Mask = Bitset_Adj_List[i].slice();
for(let k = 0; k < Mask.length; k++) {
Mask[k] = Mask[k] & Bitset_Adj_List[j][k];
}
ans += Mask.filter(i => i==1).length;
}
}
}
ans /= 6;
console.log("The number of Triangles in the Graph is : " + ans);
}
main();
Python3
V = 4
Graph = [[0, 1, 1, 0],
[1, 0, 1, 1],
[1, 1, 0, 1],
[0, 1, 1, 0 ]]
def findNumberOfTriangles(graph):
count = 0
n = len(graph)
for i in range(n):
for j in range(n):
if(graph[i][j] == 1):
for k in range(n):
if(graph[j][k] == 1 and graph[k][i] == 1):
count += 1
return count // 6
ans = findNumberOfTriangles(Graph)
print("The number of Triangles in the Graph is : ", ans)
C#
using System;
using System.Collections;
class MainClass {
static int V = 4;
public static void Main() {
int[,] graph = {{0, 1, 1, 0},
{1, 0, 1, 1},
{1, 1, 0, 1},
{0, 1, 1, 0}};
ArrayList Bitset_Adj_List = new ArrayList();
for(int i=0; i<V; i++) {
Bitset_Adj_List.Add(new BitArray(V));
for(int j=0; j<V; j++) {
if(graph[i,j] == 1)
((BitArray)Bitset_Adj_List[i]).Set(j, true);
}
}
int ans = 0;
for(int i=0; i<V; i++) {
for(int j=0; j<V; j++) {
if(((BitArray)Bitset_Adj_List[i])[j] == true && i!=j) {
BitArray Mask = (BitArray)((BitArray)Bitset_Adj_List[i]).Clone();
Mask.And(Bitset_Adj_List[j] as BitArray);
int count = 0;
for(int k = 0; k < V; k++) {
if(Mask[k])
count++;
}
ans += count;
}
}
}
ans /= 6;
Console.WriteLine("The number of Triangles in the Graph is : " + ans);
}
}
Output
The number of Triangles in the Graph is : 2
Time Complexity: First we have the two for nested loops O(V2) flowed by Bitset operations & and count, both have a time complexity of O(V / Word RAM), where V = number of nodes in the graph and Word RAM is usually 32 or 64. So the final time complexity is O(V2 * V / 32) or O(V3).
Time Complexity: O(V3) Space Complexity: O(V2)
References:
http://www.d.umn.edu/math/Technical%20Reports/Technical%20Reports%202007-/TR%202012/yang.pdf
Number of Triangles in Directed and Undirected Graphs.
This article is contributed by Utkarsh Trivedi. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.
Last Updated :
28 Feb, 2023
Like Article
Save Article
Количество треугольников в графе
Алиса и Боб больше не играют ни в какие игры; теперь они дружно изучают свойства различных графов. Алиса придумала следующее занятие: из полного неориентированного графа с n вершинами она выбирает какие-то m ребер и оставляет их себе. Оставшиеся же 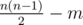
Алисе и Бобу очень нравятся «треугольники» в графах, то есть циклы длины 3. Поэтому они хотят узнать ответ на такой вопрос: какое суммарное количество треугольников находится в двух графах, образованных ребрами Алисы и ребрами Боба, соответственно?
Первая строка содержит два целых числа n и m ( 1 ≤ n ≤ 10 6 , 0 ≤ m ≤ 10 6 ), разделенные пробелом — количество вершин в изначальном полном графе, а также количество ребер в графе Алисы, соответственно. Далее следуют m строк: i -тая строка содержит два целых числа a i , b i ( 1 ≤ a i, b i ≤ n , a i ≠ b i ), разделенные пробелом — номера двух вершин, соединенных i -тым ребром графа Алисы. Гарантируется, что граф Алисы не содержит кратных ребер и петель. Изначальный полный граф также не содержит кратных ребер и петель.
Считайте, что вершины графа пронумерованы некоторым образом от 1 до n .
Выведите единственное число — суммарное количество циклов длины 3 в графах Алисы и Боба.
Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-битных чисел на С++. Рекомендуется использовать потоки cin , cout или спецификатор %I64d .
Каков эффективный алгоритм подсчета числа треугольников в графе?
каков эффективный алгоритм подсчета количества треугольников в неориентированном графе ) (где граф-это набор вершин и ребер)? Я искал Google и читал на полке учебники по несколько часов каждый день в течение трех дней подряд.
Это для домашнего задания, где мне нужен такой алгоритм, но разработка его ничего не значит на задании. Предполагается, что мы можем просто найти такой алгоритм извне ресурсы, но я на пределе.
для уточнения треугольник на графике представляет собой цикл длиной три. Фокус в том, что он должен работать на множествах вершин не более 10 000 узлов.
в настоящее время я работаю на C#, но больше забочусь об общем подходе к решению этой проблемы, чем о коде для копирования и вставки.
на высоком уровне, мои попытки до сих пор включено:
- широкий первый поиск, который отслеживал все уникальные циклы длины три. Это казалось мне прекрасной идеей, но я не мог заставить ее работать
- цикл по всем узлам в графе, чтобы увидеть, разделяют ли три вершины ребро. Это слишком медленное время работы для больших наборов данных. O (n^3).
сам алгоритм является частью вычисления коэффициента кластеризации.
6 ответов
эта проблема так же сложна, как умножение матрицы. Увидеть это ссылка.
вы знаете что-нибудь о графиках? Они редкие? Если нет, я не думаю, что вы сделаете намного лучше, чем O(n^3).
вам понадобится глубина первый поиск. Алгоритм такой:
1) для текущего узла прошу всех непосещенных смежных вершин
2) для каждого из этих узлов запустите depth two проверьте, является ли узел на глубине 2 вашим текущим узлом с шага one
3) отметить текущий узел как посещенный
4) Сделайте каждый незваный соседний узел своим текущим узлом (1 на 1) и запустите тот же алгоритм
зависит от того, как представлены ваши графики.
Если у вас есть матрица смежности A, Число треугольников должно быть tr (a^3)/6, другими словами, в 1/6 раза больше суммы диагональных элементов (разделение заботится об ориентации и вращении).
Если у вас есть списки смежности, просто начните с каждого узла и выполните поиск глубины-3. Подсчитайте, как часто вы достигаете этого узла – > разделить на 6 снова.
подсчет треугольников действительно труден и вычислительно дорогостоящ. Возможно, это хорошая отправная точка для понимания, почему:эффективный подсчет треугольников в больших графах с помощью разбиения вершин на градусы.
соответствующий цикл должен проверить для каждого из n узлов против каждого из их соседей(n*(n-1)) и продолжить цикл, чтобы увидеть, являются ли соседи соседа соседа n: (n*(n-1)) (n-1) (n-1), что почти 10^16 для 10000 n. С миллионом узлы эти петли становятся глупыми, но для ваших 10000 у вас не должно быть никаких проблем, если вы хотите, чтобы brute-force it:)
вы упомянули, что кодируете на C#, а graph (который доступен для C) имеет отличный алгоритм подсчета треугольников, написанных Габором Csardi. Он насчитал 1,3 миллиона треугольников в моем случайном графике 10000 узлов и один миллион ребер за 1,3 секунды на пятилетнем ноутбуке:) Габор Csardi был бы парнем, чтобы спросить 🙂
С точки зрения разных программные подходы, возможно, вам стоит посмотреть на данные, в которых вы храните свою сеть. Если хранится в матрице смежности, количество циклов фиксировано,но в списке ребер сети из трех ребер количество циклов кратно трем независимым от количества узлов. Вы можете запросить список ребер для соседей узла, не проверяя каждую комбинацию i – >j.
Я написал педагогический сценарий в R, чтобы проиллюстрировать подходы и измерить различные скорость алгоритмов очень простой способ. Есть много проблем со скоростью, присущих использованию R здесь (версия edge-list полностью завалена слишком большим количеством ребер), но я думаю, что пример кода должен получить некоторые идеи о том, как думать о скорости грубого принуждения треугольника. Это в R, и не очень аккуратно, но хорошо прокомментирован. Надеюсь, вы сможете преодолеть языковой барьер.
Если вас не волнует точное количество треугольников, существует очень простой алгоритм потоковой передачи, который обеспечивает беспристрастную оценку. См., например,здесь для объяснений.
самый быстрый алгоритм, известный для поиска и подсчета треугольников, опирается на быстрое матричное произведение и имеет временную сложность O(nw), где ω
Количество треугольников в неориентированном графе
Учитывая неориентированный простой граф, нам нужно найти, сколько треугольников у него может быть. Например, приведенный ниже график содержит 2 треугольника.
Пусть A [] [] будет матричным представлением графа смежности. Если мы вычислим A 3 , то число треугольников в Undirected Graph будет равно trace (A 3 ) / 6. Где trace (A) — это сумма элементов на главной диагонали матрицы A.
Ниже приведена реализация вышеприведенной формулы.
// C ++ программа для поиска
// количество треугольников в
// Неориентированный граф. Программа
// для матрицы смежности
// представление графика
#include
using namespace std;
// Количество вершин в графе
#define V 4
// Функция полезности для матрицы
// умножение
void multiply( int A[][V], int B[][V], int C[][V])
for ( int i = 0; i
for ( int j = 0; j
for ( int k = 0; k
// Сервисная функция для расчета
// трассировка матрицы (сумма
// диагностические элементы)
int getTrace( int graph[][V])
for ( int i = 0; i
// Сервисная функция для расчета
// количество треугольников в графе
int triangleInGraph( int graph[][V])
// Сохранить график ^ 2
// Сохранить график ^ 3
for ( int i = 0; i
for ( int j = 0; j
aux2[i][j] = aux3[i][j] = 0;
// aux2 – это график ^ 2 теперь printMatrix (aux2);
multiply(graph, graph, aux2);
// после этого умножения aux3
// график ^ 3 printMatrix (aux3);
multiply(graph, aux2, aux3);
int trace = getTrace(aux3);
return trace / 6;
printf ( “Total number of Triangle in Graph : %dn” ,
// Java программа для поиска номера
// треугольников в неориентированном
// График. Программа для
// матричное представление смежности
// графика
// Количество вершин в
// Сервисная функция для
void multiply( int A[][], int B[][],
for ( int i = 0 ; i
for ( int j = 0 ; j
for ( int k = 0 ; k
// Сервисная функция для расчета
// трассировка матрицы (сумма
int getTrace( int graph[][])
for ( int i = 0 ; i
// Сервисная функция для
// треугольники на графике
int triangleInGraph( int graph[][])
// Сохранить график ^ 2
int [][] aux2 = new int [V][V];
// Сохранить график ^ 3
int [][] aux3 = new int [V][V];
// Инициализация вспомогательных матриц
for ( int i = 0 ; i
for ( int j = 0 ; j
aux2[i][j] = aux3[i][j] = 0 ;
// aux2 теперь граф ^ 2
multiply(graph, graph, aux2);
// после этого умножения aux3
// является графиком ^ 3 printMatrix (aux3)
multiply(graph, aux2, aux3);
int trace = getTrace(aux3);
return trace / 6 ;
public static void main(String args[])
Directed obj = new Directed();
System.out.println( “Total number of Triangle in Graph : ” +
// Этот код предоставлен Аншикой Гоял.
# Программа Python3 для определения количества
# треугольники в неориентированном графе.
# программа для матрицы смежности
# представление графа
# Функция полезности для матрицы
# умножение
def multiply(A, B, C):
for i in range (V):
for j in range (V):
for k in range (V):
# Сервисная функция для расчета
# след матрицы (сумма
# диагностические элементы)
for i in range (V):
# Полезная функция для расчета
количество треугольников на графике
# Хранить график ^ 2
aux2 = [[ None ] * V for i in range (V)]
# Хранить график ^ 3
aux3 = [[ None ] * V for i in range (V)]
for i in range (V):
for j in range (V):
aux2[i][j] = aux3[i][j] = 0
# aux2 – это график ^ 2 теперь printMatrix (aux2)
multiply(graph, graph, aux2)
# после этого умножения aux3
# graph ^ 3 printMatrix (aux3)
multiply(graph, aux2, aux3)
return trace / / 6
# Количество вершин в графе
graph = [[ 0 , 1 , 1 , 0 ],
print ( “Total number of Triangle in Graph :” ,
# Этот код предоставлен PranchalK
// C # программа для поиска номера
// треугольников в неориентированном
// График. Программа для
// матричное представление смежности
// графика
<
// Количество вершин
// в графе
// Сервисная функция для
// матричное умножение
void multiply( int [,]A, int [,]B,
for ( int i = 0; i
for ( int j = 0; j
for ( int k = 0; k
// Функция полезности для
// вычислить след
// матрица (сумма
// диагностические элементы)
int getTrace( int [,]graph)
for ( int i = 0; i
trace += graph[i, i];
// Сервисная функция для
// вычисляем количество
// треугольники на графике
int triangleInGraph( int [,]graph)
// Сохранить график ^ 2
int [,] aux2 = new int [V, V];
// Сохранить график ^ 3
int [,] aux3 = new int [V, V];
// Инициализация вспомогательных матриц
for ( int i = 0; i
for ( int j = 0; j
aux2[i, j] = aux3[i, j] = 0;
// aux2 теперь граф ^ 2
multiply(graph, graph, aux2);
// после этого умножения aux3
// является графиком ^ 3 printMatrix (aux3)
multiply(graph, aux2, aux3);
int trace = getTrace(aux3);
return trace / 6;
public static void Main()
GFG obj = new GFG();
Console.WriteLine( “Total number of ” +
“Triangle in Graph : ” +
// Этот код предоставлен anuj_67.
Выход:
Как это работает?
Если мы вычисляем A n для представления графа в матрице смежности, то значение A n [i] [j] представляет количество различных переходов между вершинами i по j в графе. В A 3 мы получаем все различные пути длины 3 между каждой парой вершин.
Треугольник — это циклический путь длины три, т.е. начинается и заканчивается в одной и той же вершине. Таким образом, A 3 [i] [i] представляет треугольник, начинающийся и заканчивающийся вершиной i. Поскольку у треугольника есть три вершины, и он считается для каждой вершины, нам нужно разделить результат на 3. Кроме того, поскольку граф является ненаправленным, каждый треугольник в два раза больше, чем ipqj и iqpj, поэтому мы также делим на 2. Следовательно, количество треугольников является следом (A 3 ) / 6.
Сложность времени:
Временная сложность вышеупомянутого алгоритма составляет O (V 3 ), где V — количество вершин в графе, мы можем улучшить производительность до O (V 2.8074 ), используя алгоритм умножения матриц Штрассена .
Эта статья предоставлена Уткаршем Триведи. Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное или вы хотите поделиться дополнительной информацией по обсуждаемой выше теме.
[spoiler title=”источники:”]
http://askdev.ru/q/kakov-effektivnyy-algoritm-podscheta-chisla-treugolnikov-v-grafe-122592/
http://espressocode.top/number-of-triangles-in-a-undirected-graph/
[/spoiler]
Простой алгоритм перечисления всех циклов длины 3 неориентированного графа
1. Введение
Проблема перечисления всех элементов заданного типа в графе возникает при исследовании сетей различных видов. В статье [3], в частности, показано, каким образом алгоритмы подсчёта треугольных элементов графа могут быть использованы при определении Интернет-спама и в анализе характеристик пользователей социальной сети.
2. Постановка задачи
Неориентированный граф G = (V, E) состоит из множества вершин V и множества связывающих их рёбер E. Одним из наиболее удобных видов представления графа является матрица смежности A, каждый элемент которой содержит число, определяющее наличие ребра между вершиной-строкой и вершиной-столбцом. Совокупность последовательно соединённых вершин графа, в которой первая и последняя вершины совпадают, называется циклом. Требуется найти алгоритм, эффективно перечисляющий все треугольники (циклы длины 3) некоторого графа.
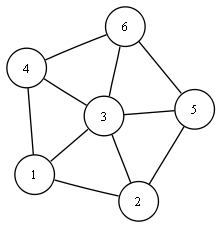
Пример графа, содержащего треугольники:
Рис. 1. Граф G
Множество вершин V = (1, 2, 3, 4, 5, 6).
Множество рёбер E = [(1, 2), (1, 3), (2, 3), (1, 4), (3, 4), (2, 5), (3, 5), (3, 6), (4, 6), (5, 6)].
Данный граф содержит 5 треугольников, T = [(1, 2, 3), (1, 3, 4), (2, 3, 5), (3, 4, 6), (3, 5, 6)].
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 2 | 1 | 0 | 1 | 0 | 1 | 0 |
| 3 | 1 | 1 | 0 | 1 | 1 | 1 |
| 4 | 1 | 0 | 1 | 0 | 0 | 1 |
| 5 | 0 | 1 | 1 | 0 | 0 | 1 |
| 6 | 0 | 0 | 1 | 1 | 1 | 0 |
Таблица 2. Матрица смежности A
3. Идея решения
Три вершины a, b и c графа G образуют треугольник, если в соответствующей матрице смежности ячейки A[a, b], A[b, c] и A[a, c] одновременно не равны нулю. Все возможные тройки вершин (a, b, c) составят тогда пространство поиска решений, удовлетворяющих данному условию.
Для всех a от 0 до n:
Для всех b от 0 до n:
Для всех c от 0 до n:
Если A[a, b], A[b, c] и A[a, c] не равны нулю, напечатать (a, b, c)
Данный алгоритм, однако, имеет серьёзные недостатки. При выводе результатов каждый треугольник будет повторен 6 (3! перестановок) раз, а количество проверок условия существования треугольника составит T = n^3. Для нашего графа G: T = 6^3 = 216.
Можно значительно сузить пространство поиска, перебирая комбинации троек (a, b, c), упорядоченных, например, по возрастанию(a < b < c).
Для всех a от 0 до n:
Для всех b от a + 1 до n:
Для всех c от b + 1 до n:
Если A[a, b], A[b, c] и A[a, c] не равны нулю, напечатать (a, b, c)
Этот алгоритм выдаст точный результат, без дублей. Количество проверяемых комбинаций в нём равно числу сочетаний без повторений из n по 3, T = C(n, 3). Для графа G: T = 20.
4. Алгоритм A
Пространство поиска можно сократить ещё более, заметив, что в отсутствие некоторого ребра (a, b) нет необходимости перебирать варианты в соответствующем внутреннем цикле по c.
Для всех a от 0 до n:
Для всех b от a + 1 до n:
Если A[a, b] = 0, переходим на следующий шаг цикла b
Для всех c от b + 1 до n:
Если A[b, c] и A[a, c] не равны нулю, напечатать (a, b, c)
Быстродействие данного алгоритма зависит от количества присутствующих в графе рёбер, и значение T лишь в худшем случае (матрица A состоит из одних единиц) достигает показателей предыдущего варианта. Для графа G: T = 16.
5. Алгоритм B
Впрочем, даже такой алгоритм возможно улучшить для случая разрежённых больших графов. Чтобы это осуществить, наряду с матрицей смежности, понадобится дополнительная структура, список связи L. Номер вершины графа соответствует очередному элементу списка связи, который хранит в себе внутренний список вершин, соединённых с вершиной данного номера. Важно, что элементы списка связи упорядочены, в частности каждый следующий элемент внутреннего списка должен быть больше предыдущего, а начальный — больше соответствующего номера вершины в основном списке.
Для всех a из L:
Для всех b из L[a]:
Для всех c из L[b]:
Если A[a, c] не нуль, напечатать (a, b, c)
Для графа G: T = 12.
6. Выводы
Алгоритм A отличается простотой реализации, не требует дополнительной памяти и успешно находит треугольники даже в несвязанных графах. Алгоритм B более эффективен, если есть возможность мириться с накладными расходами на создание списка связи.
7. Пример реализации
Ниже представлен исходный код алгоритма A на языке Python.
# Triangles enumeration algorithm(A)
def triangles(g):
n = len(g)
for a in range(0, n):
for b in range(a + 1, n):
if not g[a][b]:
continue
for c in range(b + 1, n):
if g[b][c] and g[a][c]:
print(a + 1, b + 1, c + 1)
g = [
[0, 1, 1, 1, 0, 0],
[1, 0, 1, 0, 1, 0],
[1, 1, 0, 1, 1, 1],
[1, 0, 1, 0, 0, 1],
[0, 1, 1, 0, 0, 1],
[0, 0, 1, 1, 1, 0]]
triangles(g)
Список литературы
| [1] | Р. Миллер, Л. Боксер. “Последовательные и параллельные алгоритмы”. Бином. Лаборатория знаний, 2006 г. |
| [2] | Альфред В. Ахо, Джон Хопкрофт, Джеффри Д. Ульман. “Структуры данных и алгоритмы”. Вильямс, 2000 г. |
| [3] | “Semi-Streaming Algorithms for Local Triangle Counting in Massive Graphs”. http://aeolus.ceid.upatras.gr/scientific-reports/2nd_year_reports/comm.pdf |