Имеются данные о распределении семей сотрудников финансовой корпорации по количеству детей:
| Число детей | Число семей сотрудников по подразделениям | ||
|---|---|---|---|
| первое | второе | третье | |
| 0 | 4 | 7 | 5 |
| 1 | 6 | 10 | 13 |
| 2 | 3 | 3 | 3 |
| 3 | 2 | 1 | – |
Вычислить:
а) внутригрупповые дисперсии;
б) среднюю из внутригрупповых дисперсий;
в) межгрупповую дисперсию;
г) общую дисперсию;
Проверьте правильность произведения расчётов с помощью правила сложения дисперсий.
Решение:
Совокупность семей сотрудников финансовой корпорации разбита на три группы по количеству детей.
а) Групповая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы от средней арифметической этой группы. Внутригрупповые дисперсии вычисляются по формуле:
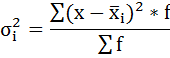
Нахождению внутригрупповой дисперсии предшествует расчёт средней арифметической по каждой группе.
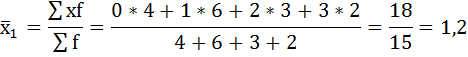
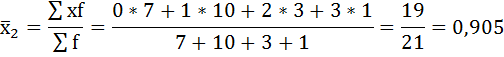
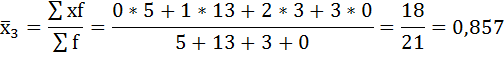
Рассчитаем внутригрупповые дисперсии:
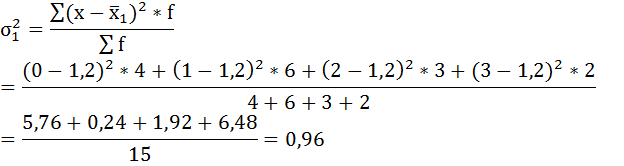
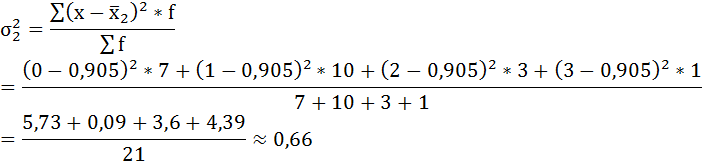
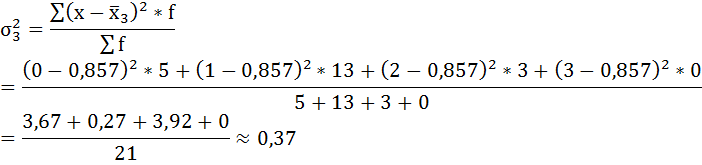
б) Средняя из внутригрупповых дисперсий – это средняя арифметическая взвешенная из дисперсий групповых:
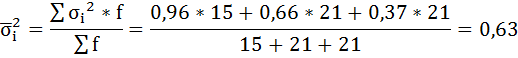
в) Межгрупповая дисперсия равна среднему квадрату отклонений групповых средних от общей средней:
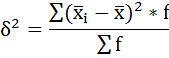
Для её расчета необходимо вычислить общую среднюю:
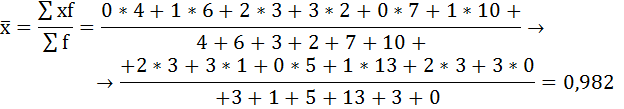
Определим межгрупповую дисперсию:
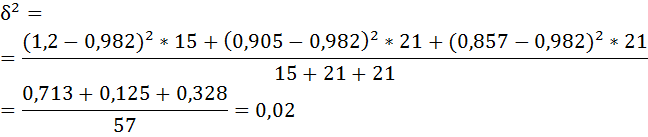
Вычислим общую дисперсию обычным способом:
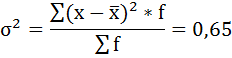
Проверим полученный результат, исчислив общую дисперсию по правилу сложения дисперсий: общая дисперсия равна сумме средней из внутригрупповых дисперсий и межгрупповой дисперсии:
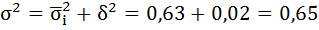
Для совокупности,
сгруппированной по определенному
признаку можно рассчитать три вида
дисперсий:
-
внутригрупповую
дисперсию; -
межгрупповую
дисперсию; -
общую дисперсию.
Внутригрупповая
дисперсия оценивает
колеблемость значения индивидуального
признака внутри группы. Эта вариация
возникает под влиянием неучтенных
факторов и не зависит от признака,
положенного в основу группировки. Она
исчисляется следующим образом:
![]() ,
,
(1.7.12)
где
![]() – средняя по изучаемой группе (групповая
– средняя по изучаемой группе (групповая
средняя).
Средняя из
внутригрупповых дисперсий
отражает ту часть вариации результативного
признака, которая обусловлена действием
всех прочих неучтенных факторов, кроме
фактора, по которому осуществлялась
группировка. Средняя из внутригрупповых
дисперсий определяется по формуле
арифметической взвешенной:
![]() (1.7.13)
(1.7.13)
Межгрупповая
дисперсия отражает ту часть вариации
результативного признака, которая
обусловлена воздействием признака
факторного. Это воздействие проявляется
в отклонении групповых средних от общей
средней:
![]() (1.7.14)
(1.7.14)
Общая дисперсия
оценивает вариацию изучаемого признака,
возникающего под влиянием всех факторов.
Между рассматриваемыми
видами дисперсий существует определенная
взаимосвязь, которая называется правилом
сложения дисперсий:
![]() (1.7.15)
(1.7.15)
Согласно правилу
сложения дисперсий общая дисперсия,
возникающая под влиянием всех факторов,
равна сумме дисперсий, возникающих под
влиянием всех прочих факторов, и
дисперсии, возникающей за счет
группировочного признака.
Зная любые два
вида дисперсий, можно определить или
проверить правильность расчета третьего
вида.
На основании
правила сложения дисперсий можно
измерить тесноту связи между группировочным
(факторным) и результативным признаками.
Для этого рассчитывается:
1) коэффициент
детерминации:
![]() (1.7.16)
(1.7.16)
Коэффициент
детерминации показывает, какая доля
вариации результативного признака
объясняется вариацией признака фактора,
положенного в основу группировки.
2) эмпирическое
корреляционное отношение:
 (1.7.17)
(1.7.17)
Величина показателя
изменяется в пределах от 0 до 1. Чем ближе
к 1, тем сильнее взаимосвязь между
рассматриваемыми признаками.
Пример: По
данным обследования коммерческих банков
города, 70% общего числа клиентов составили
юридические лица со средним размером
кредита 120 тыс. руб. и коэффициентом
вариации 25%, а 30% – физические лица со
средним размером ссуды 20 тыс. руб. при
среднем квадратическом отклонении 6
тыс. руб.
Используя правила
сложения дисперсий, определим тесноту
связи между размером кредита и типом
клиента, исчислив эмпирическое
корреляционное отношение.
Расчет эмпирического
корреляционного отношения включает
несколько этапов:
1) в данном примере
групповые средние нам даны по условию:
![]() = 120 тыс. руб.;
= 120 тыс. руб.;
![]() = 20 тыс. руб.;
= 20 тыс. руб.;
2) рассчитаем,
используя групповые средние, общую
среднюю:
![]()
3) затем вычислим
среднюю из внутригрупповых дисперсий.
Для этого сначала проведем расчеты
дисперсий по группам, используя исходные
данные:
![]() ;
;
 ;
;
Подставив полученные
значения в формулу, получим:
![]()
4) теперь определим
межгрупповую дисперсию:
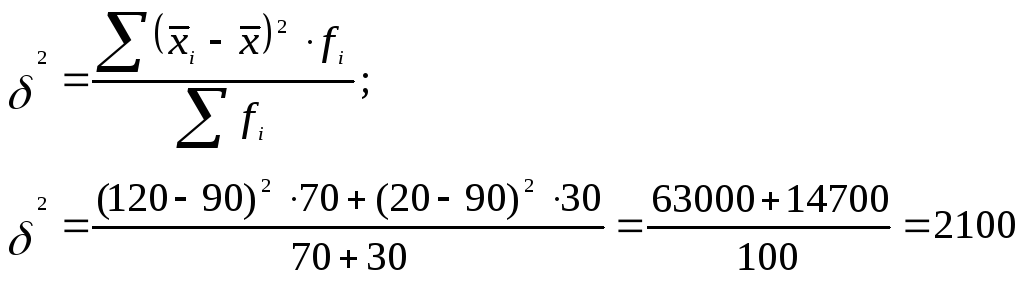
Таким образом,
общая дисперсия по правилу сложения
дисперсий равна:
![]()
5) рассчитаем
эмпирическое корреляционное отношение:
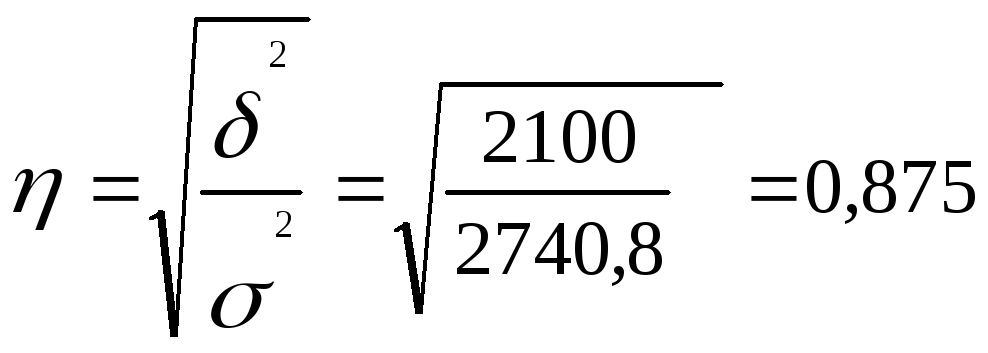
Полученная величина
свидетельствует о том, что
тип клиента
существенно влияет на размер
кредита.
Наряду с вариацией
индивидуальных значений признака вокруг
средней может наблюдаться и вариация
индивидуальных долей признака вокруг
средней доли. Для
анализа этой вариации вычисляются
следующие виды дисперсий.
Внутригрупповая
дисперсия доли
определяется по следующей формуле:
![]() (1.7.18)
(1.7.18)
Средняя из
внутригрупповых дисперсий:
![]() (1.7.19)
(1.7.19)
Межгрупповая
дисперсия:
![]() ,
,
(1.7.20)
где
![]() – численность единиц в отдельных группах;
– численность единиц в отдельных группах;
![]() – доля изучаемого
– доля изучаемого
признака во всей совокупности, которая
определяется по следующей формуле:
![]() (1.7.21)
(1.7.21)
Общая дисперсия
имеет вид:
![]() (1.7.22)
(1.7.22)
Три вида дисперсии
связаны между собой следующим образом:
![]() (1.7.23)
(1.7.23)
Данная взаимосвязь
дисперсий называется теоремой сложения
дисперсии доли признака. Эта теорема
широко используется в изучении
колеблемости качественных признаков.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
11.03.20154.03 Mб8УМК по Эконометрике.doc
- #
11.03.201517.75 Mб10УМК УЗДО Теплоснабжение.doc
- #
- #
- #
- #
- #
- #
Дисперсия, виды и свойства дисперсии
Понятие дисперсии
Дисперсия в статистике находится как среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической. В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий:
1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:
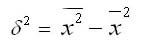
2. Взвешенная дисперсия (для вариационного ряда):
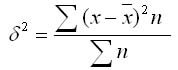
где n — частота (повторяемость фактора Х)
Пример нахождения дисперсии
На данной странице описан стандартный пример нахождения дисперсии, также Вы можете посмотреть другие задачи на её нахождение
Пример 1. Имеются следующие данные по группе из 20 студентов заочного отделения. Нужно построить интервальный ряд распределения признака, рассчитать среднее значение признака и изучить его дисперсию
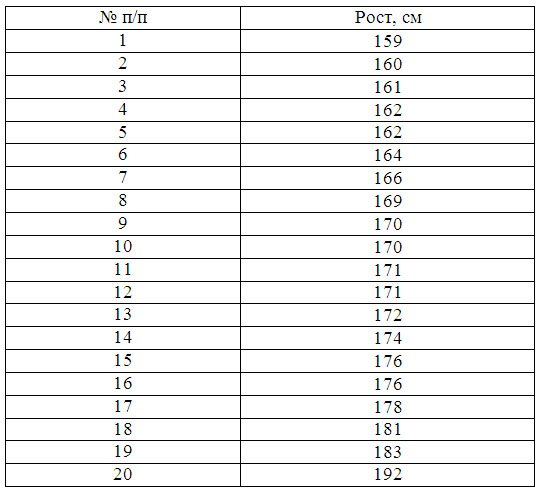
Построим интервальную группировку. Определим размах интервала по формуле:

где X max– максимальное значение группировочного признака;
X min–минимальное значение группировочного признака;
n – количество интервалов:
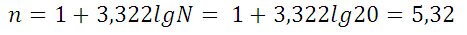
Принимаем n=5. Шаг равен: h = (192 — 159)/ 5 = 6,6
Составим интервальную группировку
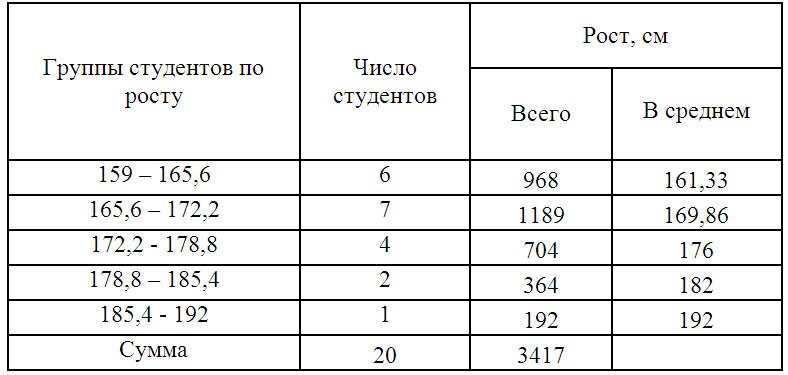
Для дальнейших расчетов построим вспомогательную таблицу:
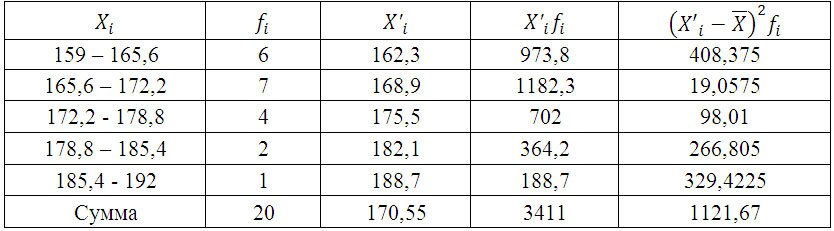
X’i– середина интервала. (например середина интервала 159 – 165,6 = 162,3)
Среднюю величину роста студентов определим по формуле средней арифметической взвешенной:
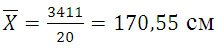
Определим дисперсию по формуле:
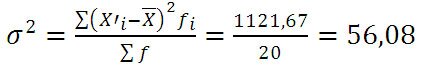
Пример 2. Определение групповой, средней из групповой, межгрупповой и общей дисперсии
Пример 3. Нахождение дисперсии и коэффициента вариации в группировочной таблице
Пример 4. Нахождение дисперсии в дискретном ряду
Формулу дисперсии можно преобразовать так:
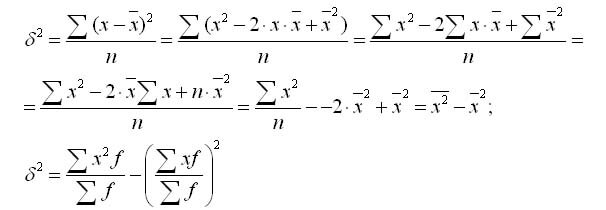
Из этой формулы следует, что дисперсия равна разности средней из квадратов вариантов и квадрата и средней.
Дисперсия в вариационных рядах с равными интервалами по способу моментов может быть рассчитана следующим способом при использовании второго свойства дисперсии (разделив все варианты на величину интервала). Определении дисперсии, вычисленной по способу моментов, по следующей формуле менее трудоемок:
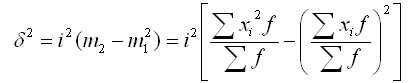
где i — величина интервала;
А — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой;
m1 — квадрат момента первого порядка;
m2 — момент второго порядка
Дисперсия альтернативного признака (если в статистической совокупности признак изменяется так, что имеются только два взаимно исключающих друг друга варианта, то такая изменчивость называется альтернативной) может быть вычислена по формуле:
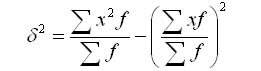
Подставляя в данную формулу дисперсии q =1- р, получаем:
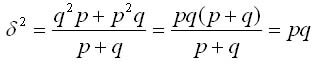
Виды дисперсии
Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.
Внутригрупповая дисперсия характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Такая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы X от средней арифметической группы и может быть вычислена как простая дисперсия или как взвешенная дисперсия.
Таким образом, внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле:
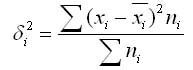
где хi — групповая средняя;
ni — число единиц в группе.
Например, внутригрупповые дисперсии, которые надо определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию).
Средняя из внутри групповых дисперсий отражает случайную вариацию, т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле:
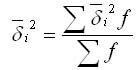
Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле:
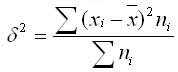
Правило сложения дисперсии в статистике
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:
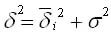
Смысл этого правила заключается в том, что общая дисперсия, которая возникает под влиянием всех факторов, равняется сумме дисперсий, которые возникают под влиянием всех прочих факторов, и дисперсии, возникающей за счет фактора группировки.
Пользуясь формулой сложения дисперсий, можно определить по двум известным дисперсиям третью неизвестную, а также судить о силе влияния группировочного признака.
Свойства дисперсии
1. Если все значения признака уменьшить (увеличить) на одну и ту же постоянную величину, то дисперсия от этого не изменится.
2. Если все значения признака уменьшить (увеличить) в одно и то же число раз n, то дисперсия соответственно уменьшится (увеличить) в n^2 раз.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
Что такое дисперсия в статистике
Статистика, в частности, оперирует рядами данных, характеризующих какой-либо признак, явление. Интересует их изменение.
Вариация представляет собой отличие величин одинакового показателя у разных предметов. Ее изучение позволит понять причины отклонений от нормы, анализировать их и в какой-то мере прогнозировать. Также станет возможным выявить факторы, влияющие на значения, отсеяв случайные.
Характеристики равномерного распределения представлены на картинке:

При значительном объеме статистики, средняя величина очевидно близка к нормальной. Об этом говорят и законы распределения. Отклонения от нее будут являться объективной характеристикой.
Только вот отрицательные значения этих разбросов будут сбивать с толку при расчетах, погашая положительные. А оставлять лишь модули – для математика не корректно. Напрашивается возвести в четную степень, а именно – во вторую.
Решение оказалось не только удобным. Оно открыло бо́льшие возможности в изучении отклонений. А важны именно они, поскольку сама по себе средняя мало что дает.

В качестве одного из важных показателей вариации, вводится понятие «дисперсия» – усредненный квадрат отклонений численных значений каких-либо событий от средней величины.
Кратко записывается D[X] в русскоязычных источниках и Var[X] (от «variance») в английских. В статистических выкладках используется σ2.

Никакого наглядного смысла величина не несет. Другое дело, среднее квадратическое отклонение – корень квадратный из дисперсии.
Виды дисперсии дискретной случайной величины
Для анализа данных цифр в таком виде недостаточно. Гораздо больше можно выжать из последовательности, если разбить ее на группы по определенному признаку.
Общая дисперсия
Как можно заметить, вычисленная по приведенному выше определению величина характеризует отклонения в целом. Без учета определяющих вариацию факторов. Вернее, с учетом всех, включая совершенно случайные. Поэтому и называется «общей» и рассчитывается по формулам, указанным ниже.
Простая дисперсия, без разделения на группы:
![]()
Или в несколько преобразованном виде:
![]()
Взвешенная дисперсия, для вариационного ряда:
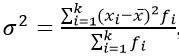
где xi – значение из ряда;
fi – частота, количество повторений;
k – групп;
n – число вариантов.
Черта сверху указывает на среднюю величину.
Межгрупповая дисперсия
Характеризует систематическое отклонение, возникающее из-за фактора, по которому производилось выделение признаков в группы. Поэтому также называется «факторной».
Как найти данную дисперсию? По формуле:
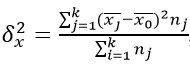
где k – количество групп;
nj – элементов в группе с индексом j.
Внутригрупповая дисперсия
Возникает по хаотичной причине, не связанной с причиной сделанной выборки. Неучтенный фактор. Еще обозначается как «остаточная».
Например, рассматривается количество выпущенных деталей за месяц каждым фрезеровщиком цеха.
В качестве критерия отбора в группу выбираем возраст оборудования. Он-то и не будет влиять на производительность внутри подборки: там станки у всех практически одинаковые.
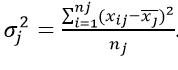
Если вычислить среднюю величину от всех групповых,
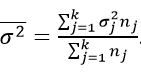
то получим характеристику случайного разброса. Иными словами, составляющую вариации, зависящую от чего угодно, кроме фактора отбора.
Взаимосвязь
В соответствии с правилом сложения, общая D[X] включает средние выражения остаточной и факторной. И это логично, поскольку учитывает и случайное изменение в группе, и систематическое в факторной.
Свойства дисперсии

Опишем основные:
-
Если последовательность состоит из одинаковых чисел, то D[X] будет нулевой.
-
Уменьшение всех значений на постоянную величину на дисперсию не влияет. Иначе говоря, рассчитать σ2 можно по отклонениям от фиксированного числа.
-
Уменьшение всех цифр в k раз приведет к падению D[X] в k2 раз. Можно, например, иметь в виду значения в метрах, а результат вычислить в футах. Достаточно учесть один раз то, на что следует умножить.
-
Средний квадрат отклонений от постоянной величины X отличается в большую сторону от того же с использованием среднего значения. Разница составит (Xcр – X)2.
Показатели вариаций
Кроме размаха (разницы максимального и минимального значений), среднего линейного и дисперсии, изменения описываются коэффициентом вариации:
![]()
Оценить масштаб разброса проще по относительной величине. Тем более, что измеряются в одних единицах.
Пример расчета дисперсии
Компания объявила конкурсный отбор для приема сотрудников. В качестве критерия принят стаж работы по специальности. Приведем исходные данные и расчеты.
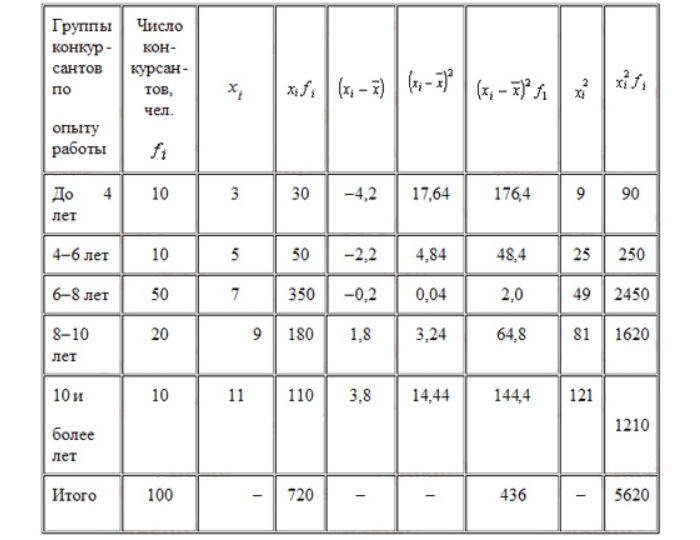
Усредненный стаж:
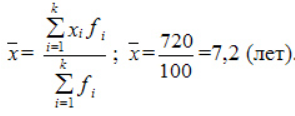
Дисперсия:
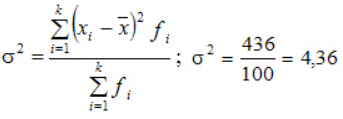
По альтернативной формуле:
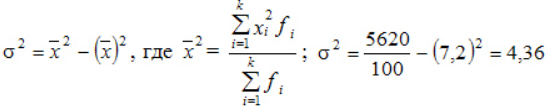
Среднеквадратическое:
![]()
Коэффициент вариации:
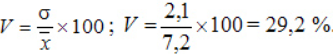
Заключение
Статистика оперирует значительными объемами данных. Вариация, как одно из основных понятий – не исключение. И дисперсия в качестве основной характеристики.
Для упрощения расчетов существует масса онлайн калькуляторов. Имеется упомянутый инструмент в MS Excel.
Дисперсия. Формула. Виды дисперсии
Вариация признака обусловлена различными факторами, некоторые из этих факторов можно выделить, если статистическую совокупность разбить на группы по какому-либо признаку, то есть построить аналитическую группировку. Тогда, наряду с изучением вариации признака по всей совокупности в целом, становится возможным изучить вариацию для каждой из составляющих ее группы, а также и между этими группами.
Дисперсия результативного признака внутри группы при относительном постоянстве признака-фактора возникает за счет других факторов (не связанных с изучаемым). Такая дисперсия называется остаточной (та колеблемость, которая осталась при закреплении изучаемого фактора ).
Межгрупповая дисперсия относится на счет изучаемого фактора (и факторов, связанных с ним), поэтому называется факторной.
В простейшем случае, когда совокупность расчленена на группы по одному фактору, изучение вариации достигается посредством исчисления и анализа трех видов дисперсий: общей, межгрупповой и внутри групповой.
Общая дисперсия 2 измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значений признака Х– от общей средней и может быть вычислена как простая дисперсия или взвешенная дисперсия по формуле (6) или (7).
Межгрупповая дисперсия 2 характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних , от общей средней
. Межгрупповая дисперсия вычисляется по формуле:
(15)
где mj – численность единиц в группе,
j – номер группы,
– среднее значение признака в j группе,
– общая средняя.
Внутригрупповая (частная) дисперсия , отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой группы
(групповой средней) и может быть исчислена как простая дисперсия или как взвешенная дисперсия по формулам, соответственно:
,
, (16)
– среднее значение признака в j группе,
– i значение признака (варианта),
– частот i варианты,
п – объем совокупности.
На основании внутри групповой дисперсии по каждой группе, т.е. на основании можно определить общую среднюю из внутригрупповых дисперсий
:
. (17)
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:
. (18)
Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью — неизвестную, а также судить о силе влияния группировочного признака.
Очевидно, чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака на изучаемый признак.
Поэтому в статистическом анализе широко используется эмпирический коэффициент детерминации (2) — показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации:
(19)
Эмпирический коэффициент детерминации показывает долю вариации результативного признака у под влиянием факторного признака х (остальная часть общей вариации у обуславливается вариацией прочих факторов). При отсутствии связи эмпирический коэффициент детерминации равен нулю, а при функциональной связи – единице.
Эмпирическое корреляционное отношение — это корень квадратный из эмпирического коэффициента детерминации:
оно показывает тесноту связи между группировочным и результативным признаками.
Эмпирическое корреляционное отношение , как и 2, может принимать значения от 0 до 1.
Если связь отсутствует, то корреляционное отношение равно нулю, т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет. Значит, группировочный признак никак не влияет на образование общей вариации.
Если связь функциональная, то корреляционное отношение будет равно единице. В этом случае дисперсия групповых средних равна обшей дисперсии (), т.е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого результативного признака.
Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками.
Для качественной оценки тесноты связи на основе показателя эмпирического корреляционного отношения можно воспользоваться соотношениями Чэддока:
|
э |
0,1-0,3 |
0,3-0,5 |
0,5-0,7 |
0,7-0,9 |
0,9-0,99 |
|
Сила связи |
Слабая |
Умеренная |
Заметная |
Тесная |
Весьма тесная |
Пример.
Имеются следующие данные о величине кредитов, выданных частным лицам, российскими и иностранными банками, функционирующими на территории РФ:
Таблица 3
|
Банки |
Выдано кредитов частным лицам, млн. руб. |
|
Российские |
2557,3; 2025,1; 1682,2; 1608,5; 1346,3; 1340,2; 1312,4; 1308,6 |
|
Иностранные |
410,1; 273,2; 187,5; 148,1 |
На основании приведенных данных проверить правило сложения дисперсий и определить влияние факторного признака на вариацию величины кредитов, выданных частным лицам.
Решение.
Проанализируем вариацию кредитов частным лицам по всем банкам. Для этого рассчитаем общую дисперсию по следующей формуле:
,
где значение признака по каждой единице;
общая средняя, рассчитанная по всем единицам.
Общая дисперсия характеризует вариацию объема кредитов частным лицам под влиянием всех факторов. Однако из таблицы видно, что вариация объема кредитов частным лицам зависит прежде всего от факторного признака.
Построим групповую таблицу, полученную по результатам аналитической группировки:
Таблица 4
|
Банки |
Число банков, nj |
Средний объем кредитов частным лицам, |
Дисперсия объема кредитов частным лицам в группе, 2j |
|
Российские |
8 |
1647,6 |
173186,45 |
|
Иностранные |
4 |
254,7 |
10105,44 |
|
Итого |
12 |
По каждой группе рассчитывается внутригрупповая дисперсия, характеризующая вариацию объема кредитов частным лицам под влиянием всех прочих случайных факторов (кроме фактора, положенного в основу группировки), по следующей формуле:
,
где j =1k (номер группы)
i = 1n (номер единицы)
Таким образом, имеем:
В целом для всех единиц рассчитывается средняя из внутригрупповых дисперсий:
Для оценки вариации объема кредитов частным лицам под влиянием факторного признака рассчитаем межгрупповую дисперсию:
Общую среднюю () определим по следующей формуле:
(млн. руб.)
Тогда
Общая дисперсия представляет собой сумму межгрупповой и средней из внутригрупповых дисперсий:
, что соответствует общей дисперсии, рассчитанной выше.
Для оценки влияния факторного признака на вариацию объема кредитов частным лицам рассчитаем долю межгрупповой дисперсии в общей, которая называется коэффициентом детерминации (2):
(78,4%)
Следовательно, на 78,4 % вариация объема кредитов частным лицам зависит от факторного признака и на 21,6 % (100-78,4) – от влияния всех прочих факторов.
Таким образом, в сочетании с методом группировок правило сложения дисперсий позволяет выявить факторы, оказывающие наибольшее влияние на вариацию признака в совокупности и дать количественную оценку степени влияния этих факторов.
