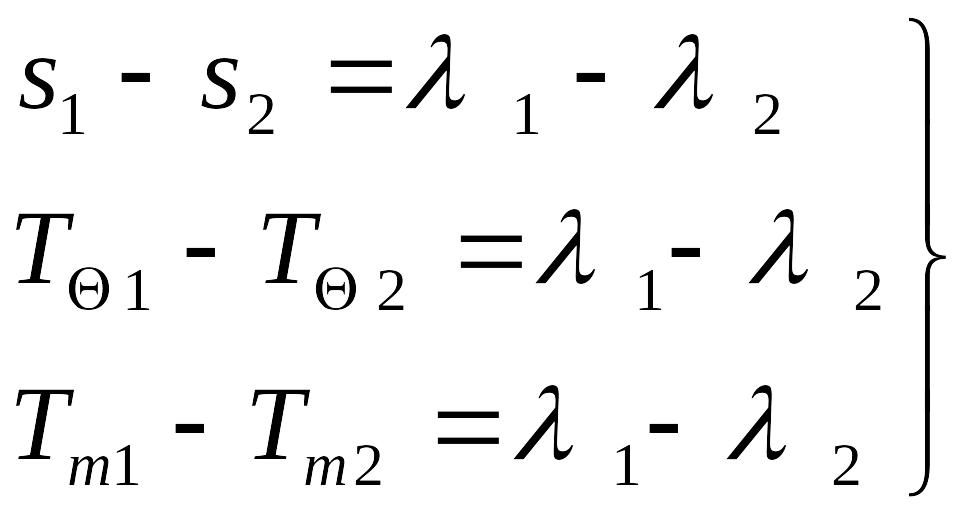На протяжении всей истории человечества времени отводилась важная роль. Время в астрономии, как и в любой сфере, играет важную и интересную роль. В своем роде, это продолжительность любого действия, оценка самой жизнидеятельности. Представьте, если бы его не было, то как бы мы определяли все вокруг.

Юлианские дни
Астрономы приняли определенную порядковую нумерацию дней. В ней существует цикл длиной 28 лет. В нём все дни и недели повторяются.

Данный способ измерения разработан Джоном Гершелем в 1849 году. Счёт времени начался с полудня 1 апреля с 4713 года до нашей эры. А предложил его использовать Иосиф Скалигер. Кстати, он и назвал его юлианским, в честь отца Юлия

«Вселенная и время бесконечны. Значит любое событие неизбежно, даже невозможное»
из фильма Трасса 60
Звёздное время в астрономии
Звёздные сутки соответствуют дистанции между двумя последовательными вершинами.
Такое время в астрономии можно определить как часовой угол точки весеннего равноденствия. Более того, по этому месту отсчитывают звёздное время.
Звёздные сутки подразумевают продолжительность оборота Земли вокруг своей оси. Их делят на часы, минуты и секунды. В одном году звездных суток больше на один, чем в средних солнечных.
Как видно, звёздные сутки короче, чем средние солнечные. Установленная разница составляет 3 минуты 56 секунд.
Притом, время обращения Земли к точке весеннего равноденствия всегда одно и то же. Итак, сутки постоянны.
Солнечное время в астрономии
Применение звёздного времени удобно в астрономии, но не для обыденной жизни человека. Поэтому было принято такое понятие как солнечное время.
Этот отрезок времени зависит от изменения часового угла Солнца.
Данный порядок расчёта времени основан на интервале между двумя последовательными кульминациями Солнца. Кстати, большую роль играет были эти кульминации верхними или нижними. От этого различают полдень сейчас или полночь.
Истинное и среднее солнечное время в астрономии
Солнечное время бывает истинным и средним. Зависит это того, по какому Солнцу его определяют.
Истинные солнечные сутки это время оборота Земли касательно Солнца.
Началом таких суток принято считать истинную полночь, то есть период нижней кульминации Солнца.

Передвижение солнца неравномерно. В результате этого, солнечные сутки 22 декабря длиннее, чем 23 сентября почти на одну минуту. Но такая неточность неудобна для расчёта.
В нашей жизни сутки составляют 24 часа. Как правило, измеряют всё в секундах. Кроме того, для определения времени человек различает утро, день, вечер и ночь. Это зависит, прежде всего, от того, где расположено Солнце относительно отдельного меридиана.
А вот средние солнечные сутки используются для точного определения времени.
Это время между двумя относительными кульминациями среднего экваториального Солнца на одном меридиане. Лучше сказать, что средние солнечные сутки соответствуют среднему значению истинных солнечных.
Эклиптическое Солнце размеренно двигается со средней скоростью Солнца. Сходятся они примерно 3 января и 4 июля.
Экваториальное также равномерно, но совпадает с эклиптическим солнцем в точке весеннего равноденствия. Среднее экваториальное солнце постоянно и равномерно относительно истинному солнечному времени.

Поясное время
В общем, используется оно в основном в географии.
Из школьных знаний нам известно, что Земля делится на меридианы. Всего их 24 и они отстают друг от друга на 15 градусов долготы.
Принято считать, что начальный меридиан с нулевой долготой является основным. Его ещё называют всемирным.
Меридианы простираются с запада на восток.
Такое время в соседних поясах отличается на один час. Для того, чтобы вычислить время отдельного пояса, необходимо узнать номер пояса.

Собственно говоря, поясное время это время часового пояса. Принято считать, что день состоит из 24 часов и начинается в полночь.
Декретное время
Например, на территории России выделено на 9 часовых поясов. В 1930 году определили понятие декретного времени. К поясному добавили один час.

Декретное время также называют московским.
Это определение времени по подразумевает использование времени соседнего пояса. Иначе говоря, декретное время это поясное время плюс один час.
По новым понятиям его называют местным временем.
Эфемеридное время
Это шкала времени, определяющая секунды. Расчёт такого времени не зависит от скорости вращения Земли.
Вдобавок, оно является основной единицей времени. Ввел это понятие в 1952 году Дж. М. Клеменс.
Эфемеридное время постоянно и применяется, на самом деле, для удобства исчисления.
«Отнять у человека час времени, отнять у человека жизнь-разница в масштабах»
Франк Герберт
Как видно, время отражает продолжительность чего-либо. Надо полагать, это самое уникальное течение и величина, которую определил человек. Помимо всего, для его расчёта придумали множество способов.

Безусловно, время очень много значит для человека. Так как это одна из основных составляющих его жизни.
Что будет дальше покажет нам время.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 12 августа 2021 года; проверки требуют 9 правок.

График уравнения времени (синяя линия) и двух его составляющих: от эллиптичности земной орбиты (зелёная) и наклона оси вращения земли (красная)

Уравнение времени (по «инвертированному» определению, принятому в англоязычной литературе). График выше нуля — солнечные часы «спешат», ниже нуля — солнечные часы «отстают»
Уравнение времени — разница между средним солнечным временем (ССВ) и истинным солнечным временем (ИСВ), то есть УВ = ССВ − ИСВ[1]. Эта разница в каждый конкретный момент времени одинакова для наблюдателя в любой точке Земли. Уравнение времени можно узнать из специализированных астрономических изданий, астрономических программ или вычислить по формуле, приведённой ниже.
В таких изданиях, как «Астрономический календарь», уравнение времени определяется как разность часовых углов среднего экваториального солнца и истинного солнца, то есть при таком определении УВ = ССВ − ИСВ[2].
В англоязычных изданиях часто применяется «инвертированное» определение уравнения времени: УВ = ИСВ − ССВ, то есть разница между истинным солнечным временем и средним солнечным временем.
Пояснения к определению[править | править код]
Можно встретить определение уравнения времени как разницы «местного истинного солнечного времени» и «местного среднего солнечного времени» (в англоязычной литературе — local apparent solar time и local mean solar time). Данное определение формально более точно, но не влияет на результат, так как для любой конкретной точки на Земле эта разница одинакова.
Кроме того, не следует путать ни местное истинное, ни местное среднее солнечное время с официальным местным временем (standard time).
Неравномерность движения истинного Солнца[править | править код]
В отличие от звёзд, чьё видимое суточное движение практически равномерно и обусловлено только вращением Земли вокруг своей оси, суточное движение Солнца не равномерно, так как обусловлено и вращением Земли вокруг своей оси, и обращением Земли вокруг Солнца, и наклоном земной оси к плоскости орбиты Земли.
Влияние эллиптичности орбиты[править | править код]
Вращение Земли вокруг Солнца происходит по эллиптической орбите. Согласно второму закону Кеплера, такое движение неравномерно, оно быстрее в области перигелия и медленнее в области афелия. Для наблюдателя, находящегося на Земле, это выражается в том, что видимое движение Солнца по эклиптике относительно неподвижных звёзд то ускоряется, то замедляется.
Влияние наклона земной оси[править | править код]
Поскольку плоскость эклиптики наклонена к плоскости небесного экватора, имеет место следующее явление:
- Солнце вблизи солнцестояний (зимнего и летнего) движется почти параллельно небесному экватору, и скорость его перемещения практически полностью вычитается из суточного движения небесной сферы — результирующая скорость изменения часового угла Солнца минимальна;
- Солнце вблизи равноденствий (осеннего и весеннего) движется под максимальным углом к небесному экватору, и скорость его перемещения лишь частично вычитается из суточного движения небесной сферы — результирующая скорость изменения часового угла Солнца максимальна.
Уравнение времени как сумма составляющих[править | править код]

Вверху слева: влияние эксцентриситета; вверху справа: влияние наклона эклиптики; внизу слева: сумма — уравнение времени; внизу справа: позиция истинного Солнца относительно среднего Солнца.
(Графики приведены в соответствии с «инвертированным» определением уравнения времени, принятым в англоязычной литературе.)
Кривая уравнения времени является суммой двух периодических кривых — с периодами 1 год и 6 месяцев. Практически синусоидальная кривая с годичным периодом обусловлена неравномерным движением Солнца по эклиптике. Эта часть уравнения времени называется уравнением центра или уравнением от эксцентриситета. Синусоида с периодом 6 месяцев представляет разность времён, вызванную наклоном эклиптики к небесному экватору и называется уравнением от наклона эклиптики[1].
Уравнение времени обращается в ноль четыре раза в году — приблизительно 15 апреля, 13 июня, 1 сентября и 25 декабря[3].
Соответственно, в каждое время года существует свой максимум уравнения времени: около 12 февраля — +14,3 мин, 15 мая — −3,8 мин, 27 июля — +6,4 мин и 4 ноября — −16,4 мин. Точные величины уравнения времени даются в астрономических ежегодниках.
Может применяться как дополнительная функция в некоторых моделях часов.
Расчёт[править | править код]
Уравнение можно аппроксимировать отрезком ряда Фурье как сумму двух синусоидальных кривых с периодами, соответственно, один год и шесть месяцев:
,
где
, если углы выражаются в градусах,
или
, если углы выражаются в радианах.
Там, где 
на 1 января,
на 2 января,
и так далее.
Программа расчета на Ruby для текущей даты[править | править код]
#!/usr/bin/env ruby puts puts "nt== You're using Ruby ver." + RUBY_VERSION + "t==" =begin Equation of Time calculation *** No guarantees are implied. Use at your own risk *** Written by E. Sevastyanov, 2017-05-14; clarified by E. Sevastyanov, 2022-01-20 Based on "Equation of time" WikiPedia article as of 2016-11-28 (which describes angles in a bewildering mixture of degrees and radians) and Del Smith, 2016-11-29 It appears to give a good result, but I make no claims for accuracy. =end pi = (Math::PI) # pi t = Time.now.getutc yd = t.yday yy = t.year delta = yd - 1 # (Текущий день года - 1) a = t.to_a; delta = delta + a[2] / 24.0 + a[1] / 1440.0 + a[0] / 86400.0 # Поправка на дробную часть дня np = case yy #The number np is the number of days from 1 January to the date of the Earth's perihelion. (http://www.astropixels.com/ephemeris/perap2001.html) when 2017 ; 3.59583333333333 when 2018 ; 2.23263888888889 when 2019 ; 2.22222222222222 when 2020 ; 4.325 when 2021 ; 1.57708333333333 when 2022 ; 2.28819444444444 when 2023 ; 3.67847222222222 when 2024 ; 2.02708333333333 when 2025 ; 3.56111111111111 when 2026 ; 2.71944444444444 when 2027 ; 2.10625 when 2028 ; 4.51944444444444 when 2029 ; 1.75902777777778 when 2030 ; 2.425 else; 2 end lambda = 23.4372 * pi / 180; # Earth's inclination in radians omega = 2 * pi / 365.25636 # angular velocity of annual revolution (radians/day) alpha = omega * ((delta + 10) % 365) # angle in (mean) circular orbit, solar year starts 21. Dec beta = alpha + 0.03340560188317 * Math.sin(omega * ((delta - np) % 365)) # angle in elliptical orbit, from perigee (radians) gamma = (alpha - Math.atan(Math.tan(beta) / Math.cos(lambda))) / pi # angular correction eot = (43200 * (gamma - gamma.round)) # equation of time in seconds (as The United States Naval Observatory defines it by placing itself at the center of the universe). puts "EOT = #{ eot * -1 } секунд" # (as "how many seconds the clock is ahead (+) or behind (−) the apparent sun")
См. также[править | править код]
- Аналемма
Примечания[править | править код]
- ↑ 1 2 Кононович Э. В., Мороз В. И. «Общий курс астрономии» Учебное пособие под ред. В. В. Иванова. Изд. 2-е, испр. М.: Едиториал УРСС, 2004. — 544 с. ISBN 5-354-00866-2, 3000 экз. (недоступная ссылка)
- ↑ Астрономический календарь. Постоянная часть / Ответственный редактор Абалакин В.К.. — 7-е изд. — М.: Наука, 1981. — С. 19.
- ↑ Мастерская истинного времени. www.analemma.ru. Дата обращения: 1 июля 2020. Архивировано 1 июля 2020 года.
Ссылки[править | править код]
- Величина колебаний уравнения времени в течение года на портале Гринвичской королевской обсерватории.
- Уравнение времени на сегодняшний день — визуализация.
- [bse.sci-lib.com/a_pictures/04/18/260109925.jpg Образец построения графика уравнения времени], где прорисованы:
- 1 — составляющая уравнения времени, определяемая неравномерностью движения Земли по орбите,
- 2 — составляющая уравнения времени, определяемая наклоном эклиптики к экватору,
- 3 — уравнение времени.
|
|
Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных ссылок
|
Вся наша жизнь связана со временем и регулируется периодической сменой дня и ночи, а также времён года. Вам известно, что Солнце всегда освещает только половину земного шара: на одном полушарии — день, а на другом в это время ночь. Следовательно, на нашей планете всегда есть точки, где в данный момент полдень, и Солнце находится в верхней кульминации, а есть полночь, когда Солнце находится в нижней кульминации.
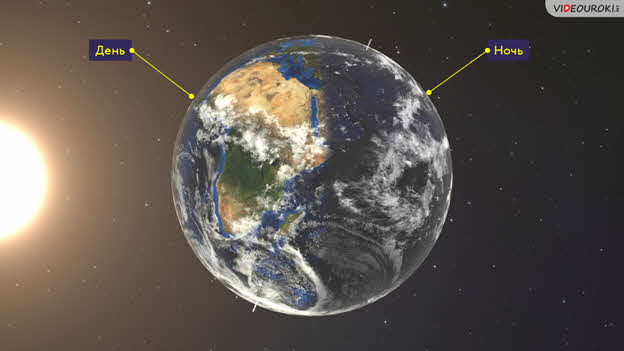
Момент верхней кульминации центра Солнца называется истинным полднем, момент нижней кульминации — истинной полночью. А промежуток времени между двумя последовательными одноимёнными кульминациями центра Солнца называется истинными солнечными сутками.
Казалось бы, их можно использовать для точного счёта времени. Однако из-за эллиптической орбиты Земли, солнечные сутки периодически меняют свою продолжительность. Так, когда Земля находится ближе всего к Солнцу, она движется по орбите примерно со 30,3 км/с. А через полгода Земля оказывается в самой удалённой точке от Солнца, где её скорость падает на 1 км/с. Такое неравномерно движение Земли по своей орбите вызывает неравномерное видимое перемещение Солнца по небесной сфере. Иными словами, в разное время года Солнце «перемещается» по небу с различной скоростью. Поэтому продолжительность истинных солнечных суток постоянно меняется и пользоваться ими в качестве единицы измерения времени неудобно. В связи с этим в повседневной жизни используются не истинные, а средние солнечные сутки, продолжительность которых принята постоянной и равной 24 часам. Каждый час среднего солнечного времени в свою очередь делится на 60 минут, а каждая минута — на 60 секунд.
Измерение времени солнечными сутками связано с географическим меридианом. Время, измеренное на данном меридиане, называется его местным временем, и оно одинаково для всех пунктов, находящихся на нём. При этом, чем восточнее земной меридиан, тем раньше на нём начинаются сутки. Если учесть, что за каждый час наша планета поворачивается вокруг своей оси на 15о, то разность времени двух пунктов в один час соответствует и разности долгот в 15°. Следовательно, местное время в двух пунктах будет отличаться ровно на столько, на сколько отличается их географическая долгота, выраженная в часовой мере:
T1 – T2 = λ1 – λ2.
Из курса географии вам известно, что за начальный (или, как его ещё называют, нулевой) меридиан принят меридиан, проходящий через Гринвичскую обсерваторию, находящуюся недалеко от Лондона. Местное среднее солнечное время Гринвичского меридиана называется всемирным временем — Universal Time (сокращённо UT).

Зная всемирное время и географическую долготу какого-либо пункта, можно легко определить его местное время:
T1 = UT + λ1.
Эта формула также позволяет находить географическую долготу по всемирному времени и местному времени, которое определяется из астрономических наблюдений.
Однако, если бы в повседневной жизни мы с вами пользовались местным временем, то по мере передвижения между населёнными пунктами, находящимися восточнее или западнее постоянного места проживания, нам бы приходилось непрерывно передвигать стрелки часов.
Для примера, давайте определим, на сколько позже наступает полдень в Санкт-Петербурге по сравнению с Москвой, если их географическая долгота заранее известна.

Иными словами, в Санкт-Петербурге полдень наступит примерно на 29 мин 12 с позднее, чем в Москве.
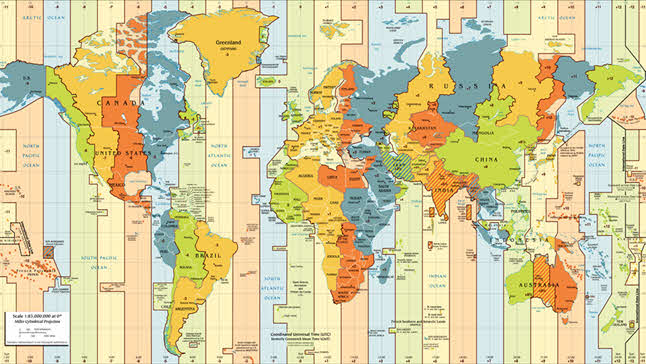
Возникающие неудобства столь очевидны, что в настоящее время практически всё население земного шара пользуется поясной системой счёта времени. Она была предложена преподавателем из США Чарльзом Даудом в 1872 году для использования на железных дорогах Америки. А уже в 1884 году в Вашингтоне прошла Международная меридианная конференция, итогом которой стала рекомендация применения гринвичского времени в качестве всемирного времени.
Согласно этой системе, весь земной шар разделён на 24 часовых пояса, каждый из которых простирается по долготе на 15° (или на один час). Часовой пояс Гринвичского меридиана считается нулевым. Остальным же поясам в направлении от нулевого на восток присвоены номера от 1 до 23. В пределах одного пояса во всех пунктах в каждый момент поясное время одинаково, а в соседних поясах оно отличается ровно на один час.
Таким образом, поясное время, которое принято в конкретном месте, отличается от всемирного на число часов, равных номеру его часового пояса:
Т = UT + n.
Если посмотреть на карту часовых поясов, то не трудно заметить, что их границы совпадают с меридианами только в малонаселённых местах, на морях и океанах. В остальных же местах границы поясов для большего удобства проведены по государственным и административным границам, горным хребтам, рекам и другим естественным рубежам.
Также от полюса до полюса по поверхности земного шара проходит условная линия, по разные стороны которой местное время отличается почти на сутки. Эта линия получила название линии перемены даты. Она примерно проходит по меридиану 180о.
В настоящее время более надёжным и удобным временем считается атомное время, которое было введено Международным комитетом мер и весов в 1964 году. А эталоном времени были приняты атомные часы, ошибка хода которых примерно составляет одну секунду за 50 тысяч лет. Поэтому с 1 января 1972 года страны земного шара ведут счёт времени по ним.
Для счёта длительных промежутков времени, в которых устанавливается определённая продолжительность месяцев, их порядок в году и начальный момент отсчёта лет, был введён календарь. В его основе лежат периодические астрономические явления: вращение Земли вокруг оси, изменение лунных фаз, обращение Земли вокруг Солнца. При этом любая календарная система (а их насчитывается более 200) опирается на три основные единицы измерения времени: средние солнечные сутки, синодический месяц и тропический (или солнечный) год.
Напомним, что синодический месяц — это промежуток времени между двумя последовательными одинаковыми фазами Луны. Он примерно равен 29,5 суток.
А тропический год — это промежуток времени между двумя последовательными прохождениями центра Солнца через точку весеннего равноденствия. Его средняя продолжительность с 1 января 2000 года составляет 365 д 05 ч 48 мин 45,19 с.
Как видим, синодический месяц и тропический год не содержат в себе целого числа средних солнечных суток. Поэтому многие народы по-своему пытались согласовать сутки, месяц и год. Это, в последствии, и привело к тому, что в разное время у разных народов была своя календарная система. Однако все календари можно условно разделить на три типа: лунные, лунно-солнечные и солнечные.

В лунном календаре год делится на 12 лунных месяцев, которые попеременно содержат в себе 30 или 29 суток. Вследствие этого, лунный календарь короче солнечного года примерно на десять суток. Такой календарь получил широкое распространение в современном исламском мире.
Лунно-солнечные календари самые сложные. В их основе лежит соотношение, что 19 солнечных лет равны 235 лунным месяцем. Вследствие этого, в году содержится 12 или 13 месяцев. В настоящее время такая система сохранилась в еврейском календаре.
В солнечном календаре за основу берётся продолжительность тропического года. Одним из первых солнечных календарей считается древнеегипетский календарь, созданный примерно в 5 тысячелетии до нашей эры. В нём год делился на 12 месяцев по 30 дней в каждом. А в конце года добавлялось ещё 5 праздничных дней.
Непосредственным предшественником современного календаря был календарь, разработанный 1 января 45 года до нашей эры в Древнем Риме по приказу Юлия Цезаря (отсюда и его название — юлианский).

Он содержал в себе 365,25 суток, что соответствовало известной в то время длине тропического года. Для удобства в нём три года считалось по 365 суток. А в каждый год, кратный четырём, добавлялись одни дополнительные сутки в феврале. Такой год был назван високосным.
Но и юлианский календарь не был совершенным, так как в нём продолжительность календарного года отличалась от тропического года на 11 минут и 14 секунд. Казалось бы, всего-ничего. Но к середине 16 века было замечено смещение дня весеннего равноденствия, с которыми связаны церковные праздники, на 10 суток.
Чтобы компенсировать накопившуюся ошибку и избежать подобного смещения в будущем, в 1582 году римский папа Григорий XIII провёл реформу календаря, передвинувшую счёт дней на 10 суток вперёд.

При этом, чтобы средний календарный год лучше соответствовал солнечному, Григорий XIII изменил правило високосных лет. По-прежнему високосным оставался год, номер которого кратен четырём, но исключение делалось для тех, которые были кратны ста. Такие годы были високосными только тогда, когда делились ещё и на 400. Например, 1700, 1800 и 1900 годы являлись простыми. А вот 1600 год и 2000 — високосными.
Исправленный календарь получил название григорианского календаря или календаря нового стиля.
В России новый стиль был введён лишь в 1918 году. К этому времени между ним и старым стилем накопилось разница в 13 дней.

Однако старый календарь всё ещё жив в памяти многих людей. Именно благодаря ему во многих странах бывшего СССР в ночь с 13 на 14 января отмечается «старый Новый год».
-
Местное время.
Время, измеренное
на данном географическом меридиане,
называется местным
временем
этого меридиана. Для всех мест на одном
и том же меридиане часовой угол точки
весеннего равноденствия (или Солнца,
или среднего солнца) в какой-либо момент
один и тот же. Поэтому на всем географическом
меридиане местное время (звездное или
солнечное) в один и тот же момент
одинаково.
Если разность
географических долгот двух мест есть
,
то в более восточном месте часовой угол
любого светила будет на
больше, чем часовой угол того же светила
в более западном месте. Поэтому разность
любых местных времен на двух меридианах
в один и тот же физический момент всегда
равна разности долгот этих меридианов,
выраженной в часовой мере (в единицах
времени):
|
|
(1.27) |
Непосредственно
из астрономических наблюдений получается
местное время того меридиана, на котором
эти наблюдения произведены.
2.
Всемирное
время. Местное
среднее солнечное время гринвичского
(нулевого) меридиана называется всемирным
временем
Т0 .
Полагая в формуле
(1.27) Tm2
= T0
и 2
= 0, Tm1
= Tm
и 1
=
, получим:
|
Tm |
(1.28) |
т.е.
местное
среднее время любого пункта на Земле
всегда равно всемирному времени в этот
момент плюс долгота данного пункта,
выраженная в часовой мере и считаемая
положительной к востоку от Гринвича.
В астрономических
календарях моменты большинства явлений
указываются по всемирному времени T0.
Моменты этих явлений по местному времени
Тт.
легко определяются по формуле (1.28).
3.
Поясное
время. В
повседневной жизни пользоваться как
местным средним солнечным временем,
так и всемирным временем неудобно.
Первым потому, что местных систем счета
времени в принципе столько же, сколько
географических меридианов, т.е.
бесчисленное множество. Поэтому для
установления последовательности событий
или явлений, отмеченных по местному
времени, совершенно необходимо знать,
кроме моментов, также и разность долгот
тех меридианов, на которых эти события
или явления имели место.
Последовательность
событий, отмеченных по всемирному
времени, устанавливается легко, но
большое различие между всемирным
временем и местным временем меридианов,
удаленных от гринвичского на значительные
расстояния, создает неудобства при
использовании всемирного времени в
повседневной жизни.
В 1884 г. была
предложена поясная
система счета среднего времени,
суть которой заключается в следующем.
Счет времени ведется только на 24 основных
географических меридианах, расположенных
друг от друга по долготе точно через
15° (или через 1h),
приблизительно посередине каждого
часового
пояса. Часовыми
поясами
называются участки земной поверхности,
на которые она условно разделена линиями,
идущими от ее северного полюса до южного
и отстоящими приблизительно на 7°,5 от
основных меридианов. Эти линии, или
границы часовых поясов, точно следуют
по географическим меридианам лишь в
открытых морях и океанах и в ненаселенных
местах суши. На остальном своем протяжении
они идут по государственным,
административно-хозяйственным или
географическим границам, отступая от
соответствующего меридиана в ту или
другую сторону. Часовые пояса занумерованы
от 0 до 23. За основной меридиан нулевого
пояса принят гринвичский. Основной
меридиан первого часового пояса
расположен от гринвичского точно на
15° к востоку, второго — на 30°, третьего
— на 45° и т. д. до 23 часового пояса,
основной меридиан которого имеет
восточную долготу от Гринвича 345° (или
западную долготу 15°).
Поясным временем
Тп
называется местное среднее солнечное
время, измеренное на основном меридиане
данного часового пояса. По нему ведется
счет времени на всей территории, лежащей
в данном часовом поясе.
Поясное время
данного пояса п
связано с всемирным временем очевидным
соотношением
|
Tn |
(1.29) |
Также совершенно
очевидно, что разность поясных времен
двух пунктов есть целое число часов,
равное разности номеров их часовых
поясов.
4.
Летнее время.
В целях более рационального распределения
электроэнергии, идущей на освещение
предприятий и жилых помещений, и наиболее
полного использования дневного света
в летние месяцы года во многих странах
(в том числе и в нашей республике)
переводят часовые стрелки часов, идущих
по поясному времени, вперед на 1 час или
полчаса. Вводится так называемое летнее
время. Осенью
же часы снова ставят по поясному времени.
Связь летнего
времени Tл
какого-либо пункта с его поясным временем
Тп
и с
всемирным временем Т0
дается следующими соотношениями:
|
|
(1.30) |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Скачать материал
без ожидания

Скачать материал
без ожидания


- Сейчас обучается 33 человека из 20 регионов






Описание презентации по отдельным слайдам:
-

1 слайд
Основы измерения времени
-

2 слайд
Древнегреческий
бог времени КроносГлавное свойство времени состоит в том, что оно длится, течет безостановочно.
Время необратимо – путешествия на машине времени в прошлое невозможны.
«Нельзя дважды войти в одну и ту же реку», – говорил Гераклит.
В древних мифах отражалось важное
значение времени.Время – это непрерывная череда сменяющих друг друга явлений.
-

3 слайд
В древности люди определяли время по Солнцу
Древняя индийская обсерватория в Дели, выполнявшая также роль солнечных часов.
Величественный Стоунхендж – одна из древнейших астрономических обсерваторий, построенная пять тысяч лет назад в Южной Англии.
Уже в те времена умели определять время по моменту восхода Солнца.
Солнечный календарь
древних ацтеков -

4 слайд
Тысячи лет назад люди заметили, что многое в природе повторяется:
Солнце встает на востоке и заходит на западе, лето сменяет зиму и наоборот.
Именно тогда возникли первые единицы времени – день, месяц и год.
С помощью простейших астрономических приборов было установлено, что в году около 360 дней, и приблизительно за 30 дней силуэт Луны проходит цикл от одного полнолуния к следующему.
Поэтому халдейские мудрецы приняли в основу шестидесятеричную систему счисления: сутки разбили на 12 ночных и 12 дневных часов, окружность – на 360 градусов. Каждый час и каждый градус были разделены на 60 минут, а каждая минута – на 60 секунд.
Сутки разделены на 24 часа,
каждый час – на 60 минут. -

5 слайд
Солнечные часы по форме очень разнообразны
Издавна отсчет времени измерялся сутками
по времени оборота Земли вокруг своей оси. -

6 слайд
Последующие более точные измерения показали, что Земля делает полный оборот вокруг Солнца за 365 суток 5 часов 48 минут и 46 секунд, т.е. в течение 365,25636 суток.
Луне же, чтобы обойти Землю, требуется от 29,25 до 29,85 суток.
Промежуток времени между двумя
кульминациями Солнца называется
солнечные сутки.
Они начинаются в момент нижней кульминации Солнца на данном меридиане (т.е. в полночь).Часы «Биг-Бен» в Лондоне
-

7 слайд
Солнечные сутки не одинаковы –
из-за эксцентриситета земной орбиты зимой в северном полушарии сутки длятся немного больше, чем летом, а в южном – наоборот.
Кроме того, плоскость эклиптики наклонена к плоскости земного экватора.
Поэтому были введены средние солнечные сутки, равные 24 часам.
Гринвич. Лондон
Среднее солнечное время, считаемое от полуночи, на гринвичском меридиане
называют всемирным временем. Обозначается UT (Universal Time).Для повседневной жизни удобно местное время – оно связано с чередованием дня и ночи в данной местности.
В местности с географической долготой λ местное время (Тλ) будет отличаться от всемирного (То) на число часов, минут и секунд, равное λ:
Тλ = То + λ
-

8 слайд
Для устранения разнобоя в счете
времени в разных населенных пунктах
принято деление земной поверхности
на часовые пояса.Были выбраны 24 земных меридиана
(через каждые 15 градусов).От каждого из этих 24 меридианов
отмерили 7,5° в обе стороны
и провели границы часовых поясов.Внутри часовых поясов
время всюду одинаково.Нулевой пояс – гринвичский.
Нулевой меридиан проходит через Гринвичскую обсерваторию, расположенную недалеко от Лондона. -

9 слайд
На каждом из этих меридианов поясное время отличается от всемирного на целое число часов, равное номеру пояса,
а минуты и секунды совпадают с гринвичскими.В нашей стране поясное время было введено с 1 июля 1919 года.
По территории России проходит 11 часовых поясов (от II до XII включительно). -

10 слайд
Зная всемирное время (То)
и номер пояса данного места (n ), можно легко найти поясное время (Тп):Тп = То + n
Нулевой меридиан. Гринвич. Лондон
-

11 слайд
В 1930 году на территории бывшего Советского Союза
все часы были переведены на час вперед.А в марте россияне переводят часы еще на час вперед
(т.е. уже на 2 часа по сравнению с поясным)
и до конца октября живут по летнему времени:Тл = Тп +2ч
-

12 слайд
Московское время – это местное время в столице России,
находящейся во II часовом поясе.
По московскому зимнему времени истинный полдень в Москве наступает в 12 часов 30 минут, по летнему – в 13 часов 30 минут. -

13 слайд
Календарь с високосными годами называется юлианским.
Он был разработан по поручению Юлия Цезаря в 45 году до н.э.
Юлианский календарь дает ошибку в одни сутки за 128 лет.Григорианский календарь (т.н. новый стиль) ввел папа Григорий XIII.
В соответствии со специальной буллой счет дней был передвинут на 10 суток вперед. Следующий день после 4 октября 1582 года стали считать 15 октября.
Григорианский календарь тоже с високосными годами, но в нем не считаются високосными годы столетий, у которых число сотен не делится без остатка на 4 (1700, 1800, 1900, 2100 и т.д.).
Подобная система даст ошибку в одни сутки за 3300 лет.На территории нашей страны григорианский календарь был введен в 1918 году.
В соответствии с декретом счет дней был передвинут на 13 суток вперед. Следующий день после 31 января стали считать 14 февраля.В настоящее время в большинстве стран мира применяется христианская эра. Счет лет начинается от Рождества Христова.
Эта дата была введена монахом Дионисием в 525 году.
Все годы до этой даты стали именоваться «до нашей эры», а все последующие даты стали «нашей эры». -

14 слайд
Задача
25 мая в Москве (n1 = 2) часы показывают 10ч45м. Какое среднее, поясное и летнее время в этот момент в Новосибирске (n2 = 6, 2 = 5ч31м)?
Дано: Тл1 = 10ч 45м;
n1 = 2;
n2 = 6;
2 = 5ч 3мНайти:Т2 – ? (среднее время – местное время в Новосибирске)
Тп2 – ?
Тл2 – ?
Решение: Находим всемирное время Т0:
Тп1 = Т0 + n1;
Тл1 = Тп1+ 2ч;
Т0 = Тл1– n1 – 2ч; Т0 = 10ч 45м – 2ч – 2ч = 6ч 45м;Находим среднее, поясное и летнее время в Новосибирске:
Т2 = Т0 + 2;Т2 = 6ч 45м + 5ч 31м = 12ч 16м;
Тп2 = Т0 + n2; Тп2 = 6ч 45м + 6ч = 12ч 45м;
Тл2 = Тп2+ 2ч; Тл2 = 12ч 45м + 2ч = 14ч 45м.Ответ:Т2 = 12ч 16м;
Тп2 = 12ч 45м;
Тл2 = 14ч 45м;
Краткое описание документа:
Цели мероприятия:
Дидактическая – формирование научных знаний об измерении времени, установление связей новых знаний с ранее полученными, расширение кругозора.
Развивающая – совершенствование, углубление знаний; расширение кругозора; формирование познавательной потребности; развитие познавательных интересов с положительной мотивацией.
Воспитательная – формирование умения формировать и осмысливать знания.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 257 915 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 13.10.2015
- 3142
- 99
Рейтинг:
4 из 5
- 13.10.2015
- 69246
- 2959
- 12.10.2015
- 1636
- 13
Рейтинг:
4 из 5
- 11.10.2015
- 12905
- 426
Рейтинг:
4 из 5
- 10.10.2015
- 9691
- 176
Рейтинг:
4 из 5
- 10.10.2015
- 15380
- 144

Вам будут интересны эти курсы:
-
Курс повышения квалификации «Подростковый возраст – важнейшая фаза становления личности»
-
Курс повышения квалификации «Экономика и право: налоги и налогообложение»
-
Курс повышения квалификации «Экономика предприятия: оценка эффективности деятельности»
-
Курс профессиональной переподготовки «Клиническая психология: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания конституционного права с учетом реализации ФГОС»
-
Курс повышения квалификации «Управление финансами: как уйти от банкротства»
-
Курс повышения квалификации «Специфика преподавания астрономии в средней школе»
-
Курс повышения квалификации «Финансы: управление структурой капитала»
-
Курс повышения квалификации «Организация маркетинга в туризме»
-
Курс профессиональной переподготовки «Астрономия: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Организация процесса страхования (перестрахования)»
-
Курс профессиональной переподготовки «Осуществление и координация продаж»
-
Курс профессиональной переподготовки «Организация и управление процессом по предоставлению услуг по кредитному брокериджу»
-
Курс профессиональной переподготовки «Гражданско-правовые дисциплины: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Управление качеством»