Содержание
- Определение всемирного времени астрономия формула
- Что такое всемирное время?
- Как определяется всемирное время?
- Формула определения всемирного времени
- Заключение
- Определение всемирного времени астрономия формула
- Что такое всемирное время?
- Как определяется UTC?
- Какая формула используется для определения UTC?
- Заключение
- Определение всемирного времени астрономия формула: что это такое?
- Формула для определения всемирного времени
- Как это работает?
- Вывод
Определение всемирного времени астрономия формула
Определение всемирного времени является фундаментальным понятием в астрономии. Оно используется для синхронизации времени наблюдений за объектами на небесной сфере. Точное определение всемирного времени (ВВ) основывается на множестве астрономических наблюдений и расчетов. В данной статье мы рассмотрим формулу определения ВВ и ее составляющие.
Что такое всемирное время?
Всемирное время (ВВ) — это система счета времени, используемая в научно-технических областях, связанных с астрономией и навигацией. Оно основано на скорости вращения Земли относительно Солнца и обновляется каждую секунду. ВВ является международным стандартом, который принимает во внимание время и положение Земли в отношении Солнца и других небесных тел.
Как определяется всемирное время?
Определение ВВ основано на расчетах, связанных с движением Земли вокруг своей оси. Определение ВВ включает в себя несколько компонентов, которые влияют на скорость вращения Земли. Эти компоненты включают в себя:
- Длительность дня, которая может изменяться на несколько миллисекунд из-за влияния приливных сил Луны.
- Вариации в скорости вращения Земли, связанные с изменениями в распределении массы на поверхности планеты.
- Дополнительные корректировки, необходимые для того, чтобы синхронизировать ВВ с другими системами счета времени.
Все эти компоненты учитываются при определении ВВ, что дает точный результат. Расчеты и измерения производятся в Международный Вселенский Час (МВЧ), который состоит из 86 400 секунд.
Формула определения всемирного времени
Формула для расчета ВВ выглядит следующим образом:
ВВ = UT1 + (DUT1/86 400) + (LOD*86400)
Где:
- UT1 — среднее звездное время на некотором меридиане;
- DUT1 — разница между UT1 и UTC (время в формате координированного всемирного времени);
- LOD — разница в длине дня относительно ее среднего значения. Она выражена в секундах и изменяется в пределах от -1 до +1 секунды.
Следует отметить, что формула определения ВВ меняется со временем, поскольку длительность дня и скорость вращения Земли также изменяются со временем.
Заключение
Таким образом, определение всемирного времени включает в себя множества параметров, которые влияют на скорость вращения Земли. Эти параметры должны быть учтены при вычислении ВВ для поддержания точности и стабильности этой системы счета времени. Формула определения ВВ позволяет производить эти расчеты и применять эту систему в различных сферах науки и техники.
Определение всемирного времени астрономия формула
Всемирное время (UTC) – это международный стандарт времени, который используется в большинстве стран мира. Для определения UTC астрономия применяет формулу, основанную на астрономических наблюдениях.
Что такое всемирное время?
Всемирное время – это одинаковое для всех стран мира время, которое рассчитывается с учетом зоны времени и восхода Солнца. Оно используется для синхронизации часов во всем мире и является основой для многих научных и технических приложений.
Как определяется UTC?
Определение UTC осуществляется с помощью атомных часов и астрономических наблюдений. Атомные часы используются для измерения точного количества времени, а наблюдения за движением Солнца и звезд позволяют вычислить корректирующие значения для UTC.
Формула для определения UTC основана на астрономических параметрах, таких как зона времени, длина дня, местное время в Greenwich и другие. Ее точность зависит от точности атомных часов и качества астрономических наблюдений.
Какая формула используется для определения UTC?
Формула для определения UTC выглядит следующим образом:
UTC = TAI + (leap seconds) + (UTC-TAI baseline)
TAI – это международное атомное время, которое используется в качестве стандарта времени для атомных часов. Leap seconds – это корректировка времени, которая вносится каждые несколько лет для синхронизации UTC со средним временем поворота Земли. UTC-TAI baseline – это разница между UTC и TAI, которая устанавливается с помощью астрономических наблюдений.
Заключение
Определение всемирного времени в астрономии основывается на точных атомных часах и астрономических наблюдениях. Формула для определения UTC учитывает зону времени, длину дня, местное время в Greenwich и другие факторы. Ее точность зависит от точности и качества используемых инструментов. Всемирное время имеет большое значение для многих научных и технических приложений, поэтому его определение является важной задачей в астрономии и других областях науки.
Определение всемирного времени астрономия формула: что это такое?
Всемирное время (UTC) – это мировое среднее время, которое используется везде на Земле. Оно привязано к атомному времени (TAI), которое отображает колебания атомов, а не движение Земли. Это позволяет избежать неточностей, связанных с плавными изменениями скорости вращения Земли.
В этой статье мы рассмотрим формулу, позволяющую определить всемирное время и разберемся, как это работает.
Формула для определения всемирного времени
В UTC = TAI – коррекция времени
где TAI — это число секунд, прошедших с 1 января 1958 года в полдень; коррекция времени — это разница между UTC и TAI в секундах.
Как было уже упомянуто, атомное время TAI имеет более высокую точность, чем устаревшее гринвичское время (GMT), которое было основано на движении Земли. Гринвичское время постепенно устаревает из-за не стабильности вращения Земли. Точно поэтому периодически проводятся вставки секунд, чтобы поддерживать синхронизацию между TAI и UTC.
Вставки секунды производятся на основании данных, полученных из Международной Земной вращательной Службы (IERS), которая отслеживает скорость вращения Земли и составляет таблицы для разных длительностей времений.
Как это работает?
Формула позволяет вычислить время UTC на основе TAI и коррекции времени. Коррекция времени может быть плюсовой или минусовой, в зависимости от того, насколько UTC отставляет от TAI в данный момент времени.
Это происходит, потому что UTC должно соответствовать местным условиям в разных частях света, как отстающими, так и продвинутыми. Например, в Гринвиче время должно быть одинаковым, что и UTC. Однако, для того чтобы это было возможно, в других частях света время может быть на несколько часов отличаться. Также, перевод на летнее время приводит к дополнительным к вставкам, которые должны быть учтены согласно формуле.
Как следствие, коррекция времени может быть плюсовой или минусовой, чтобы синхронизировать UTC и местное время.
Вывод
Таким образом, формула для вычисления всемирного времени UTC позволяет точно определить мировое время, отображая его на основе атомного времени TAI и учитывая разницу во времени на Земле. Система коррекции времени для UTC и постоянные вставки секунд позволяют поддерживать точность всемирного времени во всем мире.
Хотя формула использовалась в прошлом и может показаться слишком сложной для повседневного использования, для многих астрономических и научных приложений это является необходимой и важной концепцией.
- Всемирное время (UTC) — глобальный стандарт времени на основе атомного времени
- Формула UTC = TAI — коррекция времени используется для определения мирового времени на основе атомного времени TAI
- Коррекционный час может быть плюсовым или минусовым, чтобы учитывать различие между временем UTC и локальным временем в разных частях света
- Формула UTC = TAI — коррекция времени и система вставок секунд обеспечивают точность всемирного времени во всем мире
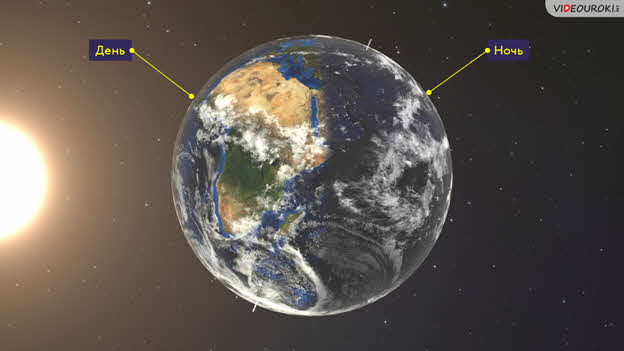
Вся наша жизнь связана со временем и регулируется периодической сменой дня и ночи, а также времён года. Вам известно, что Солнце всегда освещает только половину земного шара: на одном полушарии — день, а на другом в это время ночь. Следовательно, на нашей планете всегда есть точки, где в данный момент полдень, и Солнце находится в верхней кульминации, а есть полночь, когда Солнце находится в нижней кульминации.
Момент верхней кульминации центра Солнца называется истинным полднем, момент нижней кульминации — истинной полночью. А промежуток времени между двумя последовательными одноимёнными кульминациями центра Солнца называется истинными солнечными сутками.
Казалось бы, их можно использовать для точного счёта времени. Однако из-за эллиптической орбиты Земли, солнечные сутки периодически меняют свою продолжительность. Так, когда Земля находится ближе всего к Солнцу, она движется по орбите примерно со 30,3 км/с. А через полгода Земля оказывается в самой удалённой точке от Солнца, где её скорость падает на 1 км/с. Такое неравномерно движение Земли по своей орбите вызывает неравномерное видимое перемещение Солнца по небесной сфере. Иными словами, в разное время года Солнце «перемещается» по небу с различной скоростью. Поэтому продолжительность истинных солнечных суток постоянно меняется и пользоваться ими в качестве единицы измерения времени неудобно. В связи с этим в повседневной жизни используются не истинные, а средние солнечные сутки, продолжительность которых принята постоянной и равной 24 часам. Каждый час среднего солнечного времени в свою очередь делится на 60 минут, а каждая минута — на 60 секунд.
Измерение времени солнечными сутками связано с географическим меридианом. Время, измеренное на данном меридиане, называется его местным временем, и оно одинаково для всех пунктов, находящихся на нём. При этом, чем восточнее земной меридиан, тем раньше на нём начинаются сутки. Если учесть, что за каждый час наша планета поворачивается вокруг своей оси на 15о, то разность времени двух пунктов в один час соответствует и разности долгот в 15°. Следовательно, местное время в двух пунктах будет отличаться ровно на столько, на сколько отличается их географическая долгота, выраженная в часовой мере:
T1 – T2 = λ1 – λ2.
Из курса географии вам известно, что за начальный (или, как его ещё называют, нулевой) меридиан принят меридиан, проходящий через Гринвичскую обсерваторию, находящуюся недалеко от Лондона. Местное среднее солнечное время Гринвичского меридиана называется всемирным временем — Universal Time (сокращённо UT).
Зная всемирное время и географическую долготу какого-либо пункта, можно легко определить его местное время:
T1 = UT + λ1.
Эта формула также позволяет находить географическую долготу по всемирному времени и местному времени, которое определяется из астрономических наблюдений.
Однако, если бы в повседневной жизни мы с вами пользовались местным временем, то по мере передвижения между населёнными пунктами, находящимися восточнее или западнее постоянного места проживания, нам бы приходилось непрерывно передвигать стрелки часов.
Для примера, давайте определим, на сколько позже наступает полдень в Санкт-Петербурге по сравнению с Москвой, если их географическая долгота заранее известна.
Иными словами, в Санкт-Петербурге полдень наступит примерно на 29 мин 12 с позднее, чем в Москве.
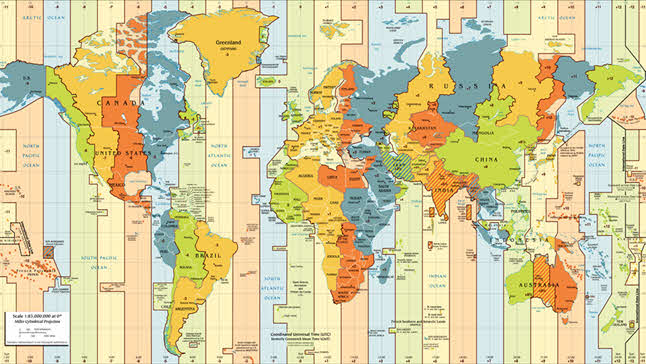
Возникающие неудобства столь очевидны, что в настоящее время практически всё население земного шара пользуется поясной системой счёта времени. Она была предложена преподавателем из США Чарльзом Даудом в 1872 году для использования на железных дорогах Америки. А уже в 1884 году в Вашингтоне прошла Международная меридианная конференция, итогом которой стала рекомендация применения гринвичского времени в качестве всемирного времени.
Согласно этой системе, весь земной шар разделён на 24 часовых пояса, каждый из которых простирается по долготе на 15° (или на один час). Часовой пояс Гринвичского меридиана считается нулевым. Остальным же поясам в направлении от нулевого на восток присвоены номера от 1 до 23. В пределах одного пояса во всех пунктах в каждый момент поясное время одинаково, а в соседних поясах оно отличается ровно на один час.
Таким образом, поясное время, которое принято в конкретном месте, отличается от всемирного на число часов, равных номеру его часового пояса:
Т = UT + n.
Если посмотреть на карту часовых поясов, то не трудно заметить, что их границы совпадают с меридианами только в малонаселённых местах, на морях и океанах. В остальных же местах границы поясов для большего удобства проведены по государственным и административным границам, горным хребтам, рекам и другим естественным рубежам.
Также от полюса до полюса по поверхности земного шара проходит условная линия, по разные стороны которой местное время отличается почти на сутки. Эта линия получила название линии перемены даты. Она примерно проходит по меридиану 180о.
В настоящее время более надёжным и удобным временем считается атомное время, которое было введено Международным комитетом мер и весов в 1964 году. А эталоном времени были приняты атомные часы, ошибка хода которых примерно составляет одну секунду за 50 тысяч лет. Поэтому с 1 января 1972 года страны земного шара ведут счёт времени по ним.
Для счёта длительных промежутков времени, в которых устанавливается определённая продолжительность месяцев, их порядок в году и начальный момент отсчёта лет, был введён календарь. В его основе лежат периодические астрономические явления: вращение Земли вокруг оси, изменение лунных фаз, обращение Земли вокруг Солнца. При этом любая календарная система (а их насчитывается более 200) опирается на три основные единицы измерения времени: средние солнечные сутки, синодический месяц и тропический (или солнечный) год.
Напомним, что синодический месяц — это промежуток времени между двумя последовательными одинаковыми фазами Луны. Он примерно равен 29,5 суток.
А тропический год — это промежуток времени между двумя последовательными прохождениями центра Солнца через точку весеннего равноденствия. Его средняя продолжительность с 1 января 2000 года составляет 365 д 05 ч 48 мин 45,19 с.
Как видим, синодический месяц и тропический год не содержат в себе целого числа средних солнечных суток. Поэтому многие народы по-своему пытались согласовать сутки, месяц и год. Это, в последствии, и привело к тому, что в разное время у разных народов была своя календарная система. Однако все календари можно условно разделить на три типа: лунные, лунно-солнечные и солнечные.
В лунном календаре год делится на 12 лунных месяцев, которые попеременно содержат в себе 30 или 29 суток. Вследствие этого, лунный календарь короче солнечного года примерно на десять суток. Такой календарь получил широкое распространение в современном исламском мире.
Лунно-солнечные календари самые сложные. В их основе лежит соотношение, что 19 солнечных лет равны 235 лунным месяцем. Вследствие этого, в году содержится 12 или 13 месяцев. В настоящее время такая система сохранилась в еврейском календаре.
В солнечном календаре за основу берётся продолжительность тропического года. Одним из первых солнечных календарей считается древнеегипетский календарь, созданный примерно в 5 тысячелетии до нашей эры. В нём год делился на 12 месяцев по 30 дней в каждом. А в конце года добавлялось ещё 5 праздничных дней.
Непосредственным предшественником современного календаря был календарь, разработанный 1 января 45 года до нашей эры в Древнем Риме по приказу Юлия Цезаря (отсюда и его название — юлианский).
Он содержал в себе 365,25 суток, что соответствовало известной в то время длине тропического года. Для удобства в нём три года считалось по 365 суток. А в каждый год, кратный четырём, добавлялись одни дополнительные сутки в феврале. Такой год был назван високосным.
Но и юлианский календарь не был совершенным, так как в нём продолжительность календарного года отличалась от тропического года на 11 минут и 14 секунд. Казалось бы, всего-ничего. Но к середине 16 века было замечено смещение дня весеннего равноденствия, с которыми связаны церковные праздники, на 10 суток.
Чтобы компенсировать накопившуюся ошибку и избежать подобного смещения в будущем, в 1582 году римский папа Григорий XIII провёл реформу календаря, передвинувшую счёт дней на 10 суток вперёд.
При этом, чтобы средний календарный год лучше соответствовал солнечному, Григорий XIII изменил правило високосных лет. По-прежнему високосным оставался год, номер которого кратен четырём, но исключение делалось для тех, которые были кратны ста. Такие годы были високосными только тогда, когда делились ещё и на 400. Например, 1700, 1800 и 1900 годы являлись простыми. А вот 1600 год и 2000 — високосными.
Исправленный календарь получил название григорианского календаря или календаря нового стиля.
В России новый стиль был введён лишь в 1918 году. К этому времени между ним и старым стилем накопилось разница в 13 дней.
Однако старый календарь всё ещё жив в памяти многих людей. Именно благодаря ему во многих странах бывшего СССР в ночь с 13 на 14 января отмечается «старый Новый год».
1. Измерение времени. Вся наша жизнь связана со временем и регулируется периодической сменой дня и ночи, а также времён года. На этих природных повторяющихся явлениях базируются основные единицы измерения времени — сутки, месяц, год. Широко используемая единица для измерения времени — сутки — связана с периодом вращения Земли вокруг своей оси.
Момент верхней кульминации центра Солнца называется истинным полднем, момент нижней кульминации — истинной полночью. Промежуток времени между двумя последовательными одноимёнными кульминациями центра Солнца называется истинными солнечными сутками. Время, прошедшее от момента нижней кульминации центра солнечного диска до любого другого его положения на одном и том же географическом меридиане, называется истинным солнечным временем (T¤).
Необходимо отметить, что истинные солнечные сутки периодически меняют свою продолжительность. Это вызывается двумя причинами: во-первых, наклоном плоскости эклиптики к плоскости небесного экватора, во-вторых, эллиптической формой орбиты Земли. Когда Земля находится на участке эллипса, расположенном ближе к Солнцу (на рис. 18 это положение показано слева), то она движется быстрее. Через полгода Земля окажется в противоположной части эллипса и будет перемещаться по орбите медленнее. Неравномерное движение Земли по своей орбите вызывает неравномерное видимое перемещение Солнца по небесной сфере, т. е. в разное время года Солнце перемещается с различной скоростью. Поэтому продолжительность истинных солнечных суток постоянно меняется и пользоваться ими в качестве единицы измерения времени неудобно. По этой причине в повседневной жизни используются не истинные, а средние солнечные сутки, продолжительность которых принята постоянной. Устанавливаются они по движению среднего экваториального Солнца — воображаемой точки, которая движется равномерно по небесному экватору и в точках весеннего и осеннего равноденствия совпадает с центром истинного Солнца. Верхнюю кульминацию среднего экваториального Солнца называют средним полднем, а промежуток времени между двумя последовательными средними полднями — средними солнечными сутками. Продолжительность их всегда одинакова. Средние солнечные сутки делят на 24 часа. Каждый час среднего солнечного времени в свою очередь делится на 60 минут, а каждая минута — на 60 секунд. За начало средних солнечных суток принимается средняя полночь, т. е. момент нижней кульминации среднего экваториального Солнца. Время, протёкшее от момента нижней кульминации среднего экваториального Солнца до любого другого его положения на одном и том же географическом меридиане, называется средним солнечным временем (Тср).
Разность между средним солнечным временем и истинным солнечным временем в один и тот же момент называется уравнением времени. Оно обозначается греческой буквой п. Можно записать следующее равенство:
Величина уравнения времени п обычно приводится в астрономических календарях. Приблизительно её можно найти по графику (рис. 19), из которого видно, что четыре раза в год уравнение времени п равно нулю. Это происходит примерно 14 апреля, 14 июня, 2 сентября и 24 декабря. Уравнение времени п принимает наибольшие численные значения около 14 февраля (h = +14 мин) и 3 ноября (h = -16 мин).
Различают также звёздные сутки (около 23 ч 56 мин 4 с). Звёздные сутки равны промежутку времени между двумя последовательными одноимёнными кульминациями точки весеннего равноденствия. Момент верхней кульминации этой точки, принимаемый за начало звёздных суток, считается 0 часов звёздного времени. Время, протёкшее от момента верхней кульминации точки весеннего равноденствия до любого другого её положения на одном и том же географическом меридиане, называется звёздным временем.
Рисунок 19 — График уравнения времени
2. Определение географической долготы. Измерение времени солнечными сутками связано с географическим меридианом. Время, измеренное на данном меридиане, называется местным временем данного меридиана, и оно одинаково для всех пунктов, находящихся на нём. Кульминация любой точки небесной сферы происходит в разное время на разных меридианах земного шара. Причём, чем восточнее земной меридиан, тем раньше в пунктах, лежащих на нём, происходит кульминация или начинаются сутки. Так как Земля за каждый час поворачивается на 15°, то разность времени двух пунктов в один час соответствует и разности долгот в 15° (в часовой мере 1 час). Отсюда можно сделать вывод: разность местного времени двух пунктов на Земле численно равна разности значений долготы, выраженных в часовой мере. Для пунктов земной поверхности, расположенных на географических долготах l1 и l2, получим:
Формула (1)
За начальный (нулевой) меридиан для отсчёта географической долготы принят меридиан, проходящий через Гринвичскую обсерваторию близ Лондона. Местное среднее солнечное время Гринвичского меридиана называется всемирным временем. Все сигналы точного времени соответствуют минутам и секундам всемирного времени. В астрономических календарях и ежегодниках моменты большинства явлений указываются по всемирному времени. Моменты этих явлений по местному времени какого-либо пункта легко определить, зная долготу этого пункта от Гринвича.
Если в данный момент на Гринвичском меридиане всемирное время будет Т0, то в местности с географической долготой l будет Тl. Следовательно, формула (1) при l0 = 0 примет вид:

Данная формула позволяет находить географическую долготу по всемирному времени (Т0) и местному времени (Тl), которое определяется из астрономических наблюдений. С другой стороны, зная долготу места наблюдения (l) и всемирное время (Т0), можно определить местное время (Тl):
Различие между местным временем даже не очень далеко расположенных друг от друга населённых пунктов создаёт неудобства в повседневной жизни. Так, например, местное время в Бресте и Витебске отличается на 26 мин. Жители этих городов, приезжая друг к другу в гости, должны были бы постоянно переводить стрелки часов. Отсюда возникла необходимость введения поясной системы счёта времени. Согласно этой системе, весь земной шар разделён на 24 часовых пояса, каждый из которых простирается по долготе на 15° (или 1 ч). Часовой пояс Гринвичского меридиана считается нулевым. Остальным поясам в направлении от нулевого на восток присвоены номера от 1 до 23. В пределах одного пояса во всех пунктах в каждый момент поясное время одинаково. В соседних поясах оно отличается ровно на один час. Границы поясов в малонаселённых местах, на морях и океанах проходят по меридианам, отстоящим на 7,5° к востоку и западу от центрального меридиана данного часового пояса. В остальных районах границы поясов для большего удобства проведены по государственным и административным границам, горным хребтам, рекам и другим естественным рубежам.
Зная всемирное время (Т0) и номер пояса данного места (n), можно найти поясное время:
Формула (3)
Исключив из формул (1) и (3) Т0, получим соотношение, позволяющее определять географическую долготу по поясному времени (Тn) и времени для местности с географической долготой l (Тl):

Фильм. Измерение времени.
В целях экономии и рационального распределения электроэнергии в течение суток на летний период в некоторых странах весной стрелки часов переводят на час вперёд — вводят летнее время, а осенью снова на час назад.
Существует граница, открывающая новую дату и день недели. Международная линия перемены дат проходит через Берингов пролив между островами Тихого океана от Северного полюса до Южного полюса (меридиан 180°).
Более надёжным и удобным временем считается атомное время, которое было введено Международным комитетом мер и весов в 1964 г. За эталон приняты атомные (квантовые) часы. По таким часам секунда — это промежуток времени, за который проходит 9 192 631 770 колебаний электромагнитной волны, излучаемой атомом цезия. С 1 января 1972 г. все страны земного шара ведут счёт времени по атомным часам.
Атомное время очень удобно для исследования Земли, потому что с его помощью можно изучать неравномерности во вращении нашей планеты. Ошибка хода атомных часов невелика — примерно 1 с за 50 тыс. лет.
3. Календарь. Календарь — это система счёта длительных промежутков времени, в основе которой лежат периодические астрономические явления: вращение Земли вокруг оси, изменение лунных фаз, обращение Земли вокруг Солнца. Любая календарная система опирается на три основные единицы измерения времени, а именно: средние солнечные сутки, синодический (или лунный) месяц и тропический (или солнечный) год.
Рис. 20. Антикитерский механизм (фрагмент, найденный археологами, и воссозданная на его основе модель)
Синодический месяц — это промежуток времени между двумя последовательными одинаковыми фазами Луны. Он равен 29,5306 суток. Тропический год — промежуток времени между двумя последовательными прохождениями центра Солнца через точку весеннего равноденствия. Он равен 365,2422 суток. Из-за медленного движения точки весеннего равноденствия навстречу Солнцу, вызванного прецессией, Солнце оказывается в той же точке неба относительно звёзд через промежуток времени на 20 мин 28 с больший, чем тропический год. Он называется звёздным годом и содержит 365,2564 средних солнечных суток.
Синодический месяц и тропический год не содержат целого числа средних солнечных суток, поэтому невозможно подобрать такое целое число тропических лет, в которых содержалось бы целое число синодических месяцев и целое число средних солнечных суток. Стремление согласовать между собой сутки, месяц и год привело к тому, что в разные эпохи у различных народов было создано много видов календарей, которые можно условно разделить на три типа: лунные, лунно-солнечные и солнечные. На рисунке 20 показано механическое приспособление, созданное древнегреческими астрономами во II в. до н. э. для расчёта движения Луны, Солнца и планет в календарных целях.
Рисунок 21 — Древний римский календарь
В лунном календаре год делится на 12 месяцев, содержащих попеременно 30 или 29 суток. Всего в лунном календаре 354 или 355 средних солнечных суток, т. е. он короче солнечного года примерно на 10 суток. Этот календарь получил широкое распространение в странах Ближнего Востока и принят в современном исламском мире. Из-за того что лунный год имеет меньше дней, чем тропический, у мусульман начало года постоянно перемещается по сезонам и выпадает то на весну, то на лето, то на зиму, то на осень.
Лунно-солнечные календари наиболее сложные. В них сумма некоторого количества лунных месяцев приблизительно соответствует продолжительности тропического года. В основе этих календарей лежит соотношение: 19 солнечных лет равны 235 лунным месяцам (с ошибкой около 2 ч). Год делится на 12 месяцев, каждый из которых начинается с новолуния. В настоящее время такая система сохранилась в еврейском календаре. Он содержит 12 или 13 месяцев в году. Продолжительность некоторых месяцев каждый год меняется, начало года всегда приходится на осень, но не совпадает с одной и той же датой григорианского календаря.
Римляне первоначально исчисляли время лунными годами. Новый год начинался 1 марта. До сих пор некоторые месяцы современного календаря называются в соответствии с этой традицией: сентябрь — «седьмой», декабрь — «десятый» и т. д. Впоследствии первый день года был перенесён римлянами на 1 января, так как с 153 г. до н. э. в этот день вступали в должность консулы (рис. 21).
Рисунок 22 — Медаль, выпущенная в память о введении григорианского календаря
Одним из первых солнечных календарей считается египетский, созданный в 4-м тыс. до н. э. По этому календарю год состоял из 12 месяцев по 30 дней в каждом, а в конце года добавлялось ещё 5 праздничных дней. Современный календарь берёт начало от солнечного римского календаря, появившегося в результате реформы Юлия Цезаря (отсюда его название — юлианский), проведённой 1 января 45 г. до н. э. Средняя продолжительность года, согласно этому календарю, была равна 365,25 суток, что соответствовало известной в то время длине тропического года. Для удобства три года подряд считали по 365 дней, а на четвёртый (високосный) добавляли лишние сутки — 366 дней. Год состоял из 12 месяцев: нечётные месяцы — 31 день, чётные — 30 дней; только февраль простого, невисокосного, года содержал 28 дней.
Вследствие того что продолжительность юлианского года длиннее тропического на 11 мин 15 с, за 128 лет накапливалась ошибка в целые сутки, а за 400 лет — около трёх суток. С течением времени календарь запаздывал всё больше и больше. Поэтому в конце XVI в. весеннее равноденствие наступало не 21, а 11 марта. Ошибка была исправлена в 1582 г., когда глава католической церкви папа Григорий ХШ создал специальную комиссию по реформе календаря, передвинувшую счёт дней на 10 суток вперёд и вернувшую весеннее равноденствие на 21 марта. Исправленный календарь получил название григорианского календаря или календаря нового стиля. В честь его введения была отчеканена памятная медаль (рис. 22). Систему счёта времени по юлианскому календарю сейчас называют старым стилем.
Високосный год в григорианском календаре — каждый четвёртый, за исключением годов с целым числом столетий (например, 1700, 1800). Такой год считается високосным только тогда, когда число сотен делится на 4 без остатка.
В России этот календарь был введён со среды 31 января 1918 г. Следующий день уже был 14 февраля, так как к тому времени календарная разница между новым и старым стилем достигла 13 дней. Это различие в 13 суток будет сохраняться до 15 февраля 2100 г. по старому стилю, или до 28 февраля 2100 г. по новому стилю. После этой даты оно увеличится на одни сутки и станет равным 14 суткам.
Григорианский календарный год длиннее солнечного года на 26 с. Лишние сутки накопятся только в L в. н. э., потому что разница в один день набегает за 3280 лет.
Необходимо отметить, что и григорианский календарь не лишён недостатков: неодинаковая продолжительность месяцев, неравные кварталы, несогласованность чисел месяцев с днями недели.
Много вопросов вызывают и привычные названия месяцев. Так, июль назван в память о римском императоре Юлии Цезаре, август — в честь римского императора Октавиана Августа. Остальные месяцы календаря получили свои названия по-разному: например, январь — в честь римского бога Януса, февраль — в честь ежегодных языческих обрядов очищения, март — по имени бога Марса, май — богини Майи, июнь — богини Юноны. Названия «сентябрь», «октябрь», «ноябрь», «декабрь» переводятся с латинского языка соответственно как «седьмой», «восьмой», «девятый», «десятый» и в настоящее время не соответствуют этой нумерации.
Кроме счёта месяцев в годах, следует вести счёт и самим годам. Для этой цели издревле использовались эры, т. е. длительные промежутки счёта лет. Эрой называется исходный пункт каждого летоисчисления. У разных народов эры были разные и связывались с какими-либо знаменательными событиями или с годами правления царей и императоров.
В Риме использовалась эра от основания Рима (753 г. до н. э.) и счёт годов от назначения консулов. В средневековой Европе была распространена эра Диоклетиана, считавшаяся от восшествия на престол императора Диоклетиана (29 августа 284 г. н. э.). Она применялась до XV в.
В Древней Греции применялась эра Олимпиад (начало 776 г. до н. э.). Олимпиады проводились раз в четыре года.
Иудеи отсчитывают начало эры от сотворения мира — от 3761 г. до н. э.
Христиане использовали эру от сотворения мира, принимая начало в 5508 г. до н. э. Эру от Рождества Христова рассчитал папский архивариус Дионисий Малый в 525 г. Он приравнял 248 г. эры Диоклетиана к 532 г. от рождения Христа. Эра от Рождества Христова, или новая эра (наша эра), частично начала применяться с Х в., а повсеместно в католических странах — лишь с XV в. В России она была введена в 1700 г. указом Петра I, согласно которому после 31 декабря 7208 г. от сотворения мира наступило 1 января 1700 г.
Мусульмане всего мира используют свою эру, которая называется хиджра и ведёт счёт лет от даты переселения пророка Мухаммеда из Мекки в Медину, что произошло в сентябре 622 г. н. э.
Главные выводы 1. Промежуток времени между двумя последовательными одноимёнными кульминациями центра солнечного диска на одном и том же географическом меридиане называется истинными солнечными сутками. 2. Из-за неравномерности истинных солнечных суток в повседневной жизни используются средние солнечные сутки, продолжительность которых постоянна. 3. Звёздные сутки — промежуток времени между двумя последовательными одноимёнными кульминациями точки весеннего равноденствия на одном и том же географическом меридиане. 4. Географическая долгота данной местности определяется разностью между местным и всемирным временем. 5. Календарь — это система счёта длительных промежутков времени, в основе которой лежат периодические астрономические явления. Мы живём по григорианскому календарю.
Контрольные вопросы и задания
1. Чем отличаются истинные солнечные сутки от средних солнечных суток?
2. Что называют звездными сутками?
3. Что понимают под уравнением времени?
4. Что понимают под всемирным временем?
5. Что понимают под линией перемены дат? Где она проходит?
6. Назовите календарные системы. На каких принципах они строятся?
7. В чем состоит отличие григорианского календаря от юлианского?
8. Почему нельзя создать абсолютно точный календарь?
9. Найдите разницу в местном времени для городов Гродно и Могилев.
10. В местный полдень капитан корабля отметил 14 ч 13 мин 46 с по хронометру, идущему по гринвичскому времени. Определите географическую долготу корабля.
11. 22 июня наблюдатель определил, что средний местный полдень наступил в 8 ч 40 мин всемирного времени, а высота Солнца в этот момент была равна 62°10′. Склонение Солнца в этот день δ = +23°26′. Определите географические координаты наблюдателя.
Проверь себя
Выбор тем
Универсальное время Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Всемирное время: 4 Второй –> 4 Второй Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
25.1327412287183 Радиан –>1440.00000000027 степень (Проверьте преобразование здесь)
12 Орбитальные параметры Калькуляторы
Универсальное время формула
Всемирная степень времени = (Всемирное время*2*pi)
UT° = (U.T*2*pi)
Как сейчас называется всемирное время?
До 1972 года это время называлось средним временем по Гринвичу (GMT), но теперь называется всемирным скоординированным временем или универсальным скоординированным временем (UTC). Это согласованная шкала времени, поддерживаемая Международным бюро мер и весов (BIPM). Он также известен как «время Z» или «время зулусов».
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 12 августа 2021 года; проверки требуют 9 правок.
График уравнения времени (синяя линия) и двух его составляющих: от эллиптичности земной орбиты (зелёная) и наклона оси вращения земли (красная)
Уравнение времени (по «инвертированному» определению, принятому в англоязычной литературе). График выше нуля — солнечные часы «спешат», ниже нуля — солнечные часы «отстают»
Уравнение времени — разница между средним солнечным временем (ССВ) и истинным солнечным временем (ИСВ), то есть УВ = ССВ − ИСВ[1]. Эта разница в каждый конкретный момент времени одинакова для наблюдателя в любой точке Земли. Уравнение времени можно узнать из специализированных астрономических изданий, астрономических программ или вычислить по формуле, приведённой ниже.
В таких изданиях, как «Астрономический календарь», уравнение времени определяется как разность часовых углов среднего экваториального солнца и истинного солнца, то есть при таком определении УВ = ССВ − ИСВ[2].
В англоязычных изданиях часто применяется «инвертированное» определение уравнения времени: УВ = ИСВ − ССВ, то есть разница между истинным солнечным временем и средним солнечным временем.
Пояснения к определению[править | править код]
Можно встретить определение уравнения времени как разницы «местного истинного солнечного времени» и «местного среднего солнечного времени» (в англоязычной литературе — local apparent solar time и local mean solar time). Данное определение формально более точно, но не влияет на результат, так как для любой конкретной точки на Земле эта разница одинакова.
Кроме того, не следует путать ни местное истинное, ни местное среднее солнечное время с официальным местным временем (standard time).
Неравномерность движения истинного Солнца[править | править код]
В отличие от звёзд, чьё видимое суточное движение практически равномерно и обусловлено только вращением Земли вокруг своей оси, суточное движение Солнца не равномерно, так как обусловлено и вращением Земли вокруг своей оси, и обращением Земли вокруг Солнца, и наклоном земной оси к плоскости орбиты Земли.
Влияние эллиптичности орбиты[править | править код]
Вращение Земли вокруг Солнца происходит по эллиптической орбите. Согласно второму закону Кеплера, такое движение неравномерно, оно быстрее в области перигелия и медленнее в области афелия. Для наблюдателя, находящегося на Земле, это выражается в том, что видимое движение Солнца по эклиптике относительно неподвижных звёзд то ускоряется, то замедляется.
Влияние наклона земной оси[править | править код]
Поскольку плоскость эклиптики наклонена к плоскости небесного экватора, имеет место следующее явление:
- Солнце вблизи солнцестояний (зимнего и летнего) движется почти параллельно небесному экватору, и скорость его перемещения практически полностью вычитается из суточного движения небесной сферы — результирующая скорость изменения часового угла Солнца минимальна;
- Солнце вблизи равноденствий (осеннего и весеннего) движется под максимальным углом к небесному экватору, и скорость его перемещения лишь частично вычитается из суточного движения небесной сферы — результирующая скорость изменения часового угла Солнца максимальна.
Уравнение времени как сумма составляющих[править | править код]
Вверху слева: влияние эксцентриситета; вверху справа: влияние наклона эклиптики; внизу слева: сумма — уравнение времени; внизу справа: позиция истинного Солнца относительно среднего Солнца.
(Графики приведены в соответствии с «инвертированным» определением уравнения времени, принятым в англоязычной литературе.)
Кривая уравнения времени является суммой двух периодических кривых — с периодами 1 год и 6 месяцев. Практически синусоидальная кривая с годичным периодом обусловлена неравномерным движением Солнца по эклиптике. Эта часть уравнения времени называется уравнением центра или уравнением от эксцентриситета. Синусоида с периодом 6 месяцев представляет разность времён, вызванную наклоном эклиптики к небесному экватору и называется уравнением от наклона эклиптики[1].
Уравнение времени обращается в ноль четыре раза в году — приблизительно 15 апреля, 13 июня, 1 сентября и 25 декабря[3].
Соответственно, в каждое время года существует свой максимум уравнения времени: около 12 февраля — +14,3 мин, 15 мая — −3,8 мин, 27 июля — +6,4 мин и 4 ноября — −16,4 мин. Точные величины уравнения времени даются в астрономических ежегодниках.
Может применяться как дополнительная функция в некоторых моделях часов.
Расчёт[править | править код]
Уравнение можно аппроксимировать отрезком ряда Фурье как сумму двух синусоидальных кривых с периодами, соответственно, один год и шесть месяцев:
,
где
, если углы выражаются в градусах,
или
, если углы выражаются в радианах.
Там, где 
на 1 января,
на 2 января,
и так далее.
Программа расчета на Ruby для текущей даты[править | править код]
#!/usr/bin/env ruby puts puts "nt== You're using Ruby ver." + RUBY_VERSION + "t==" =begin Equation of Time calculation *** No guarantees are implied. Use at your own risk *** Written by E. Sevastyanov, 2017-05-14; clarified by E. Sevastyanov, 2022-01-20 Based on "Equation of time" WikiPedia article as of 2016-11-28 (which describes angles in a bewildering mixture of degrees and radians) and Del Smith, 2016-11-29 It appears to give a good result, but I make no claims for accuracy. =end pi = (Math::PI) # pi t = Time.now.getutc yd = t.yday yy = t.year delta = yd - 1 # (Текущий день года - 1) a = t.to_a; delta = delta + a[2] / 24.0 + a[1] / 1440.0 + a[0] / 86400.0 # Поправка на дробную часть дня np = case yy #The number np is the number of days from 1 January to the date of the Earth's perihelion. (http://www.astropixels.com/ephemeris/perap2001.html) when 2017 ; 3.59583333333333 when 2018 ; 2.23263888888889 when 2019 ; 2.22222222222222 when 2020 ; 4.325 when 2021 ; 1.57708333333333 when 2022 ; 2.28819444444444 when 2023 ; 3.67847222222222 when 2024 ; 2.02708333333333 when 2025 ; 3.56111111111111 when 2026 ; 2.71944444444444 when 2027 ; 2.10625 when 2028 ; 4.51944444444444 when 2029 ; 1.75902777777778 when 2030 ; 2.425 else; 2 end lambda = 23.4372 * pi / 180; # Earth's inclination in radians omega = 2 * pi / 365.25636 # angular velocity of annual revolution (radians/day) alpha = omega * ((delta + 10) % 365) # angle in (mean) circular orbit, solar year starts 21. Dec beta = alpha + 0.03340560188317 * Math.sin(omega * ((delta - np) % 365)) # angle in elliptical orbit, from perigee (radians) gamma = (alpha - Math.atan(Math.tan(beta) / Math.cos(lambda))) / pi # angular correction eot = (43200 * (gamma - gamma.round)) # equation of time in seconds (as The United States Naval Observatory defines it by placing itself at the center of the universe). puts "EOT = #{ eot * -1 } секунд" # (as "how many seconds the clock is ahead (+) or behind (−) the apparent sun")
См. также[править | править код]
- Аналемма
Примечания[править | править код]
- ↑ 1 2 Кононович Э. В., Мороз В. И. «Общий курс астрономии» Учебное пособие под ред. В. В. Иванова. Изд. 2-е, испр. М.: Едиториал УРСС, 2004. — 544 с. ISBN 5-354-00866-2, 3000 экз. (недоступная ссылка)
- ↑ Астрономический календарь. Постоянная часть / Ответственный редактор Абалакин В.К.. — 7-е изд. — М.: Наука, 1981. — С. 19.
- ↑ Мастерская истинного времени. www.analemma.ru. Дата обращения: 1 июля 2020. Архивировано 1 июля 2020 года.
Ссылки[править | править код]
- Величина колебаний уравнения времени в течение года на портале Гринвичской королевской обсерватории.
- Уравнение времени на сегодняшний день — визуализация.
- [bse.sci-lib.com/a_pictures/04/18/260109925.jpg Образец построения графика уравнения времени], где прорисованы:
- 1 — составляющая уравнения времени, определяемая неравномерностью движения Земли по орбите,
- 2 — составляющая уравнения времени, определяемая наклоном эклиптики к экватору,
- 3 — уравнение времени.
|
|
Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных ссылок
|